Numerical Simulation of Two-Dimensional Dam Failure and Free-Side Deformation Flow Studies
Abstract
:1. Introduction
2. Numerical Models and the Proposed Method
2.1. Governing Equations
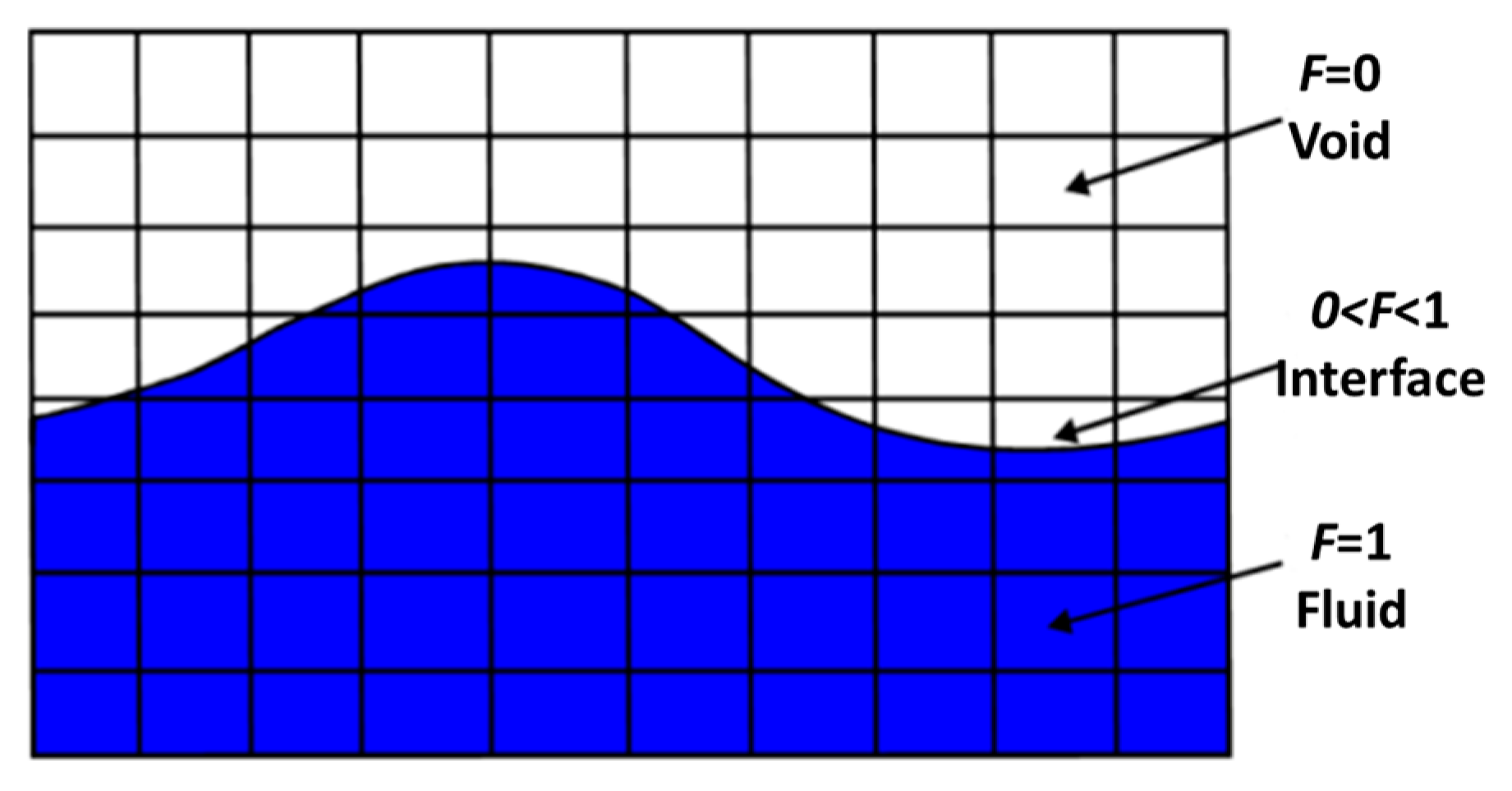
2.2. VOF Method
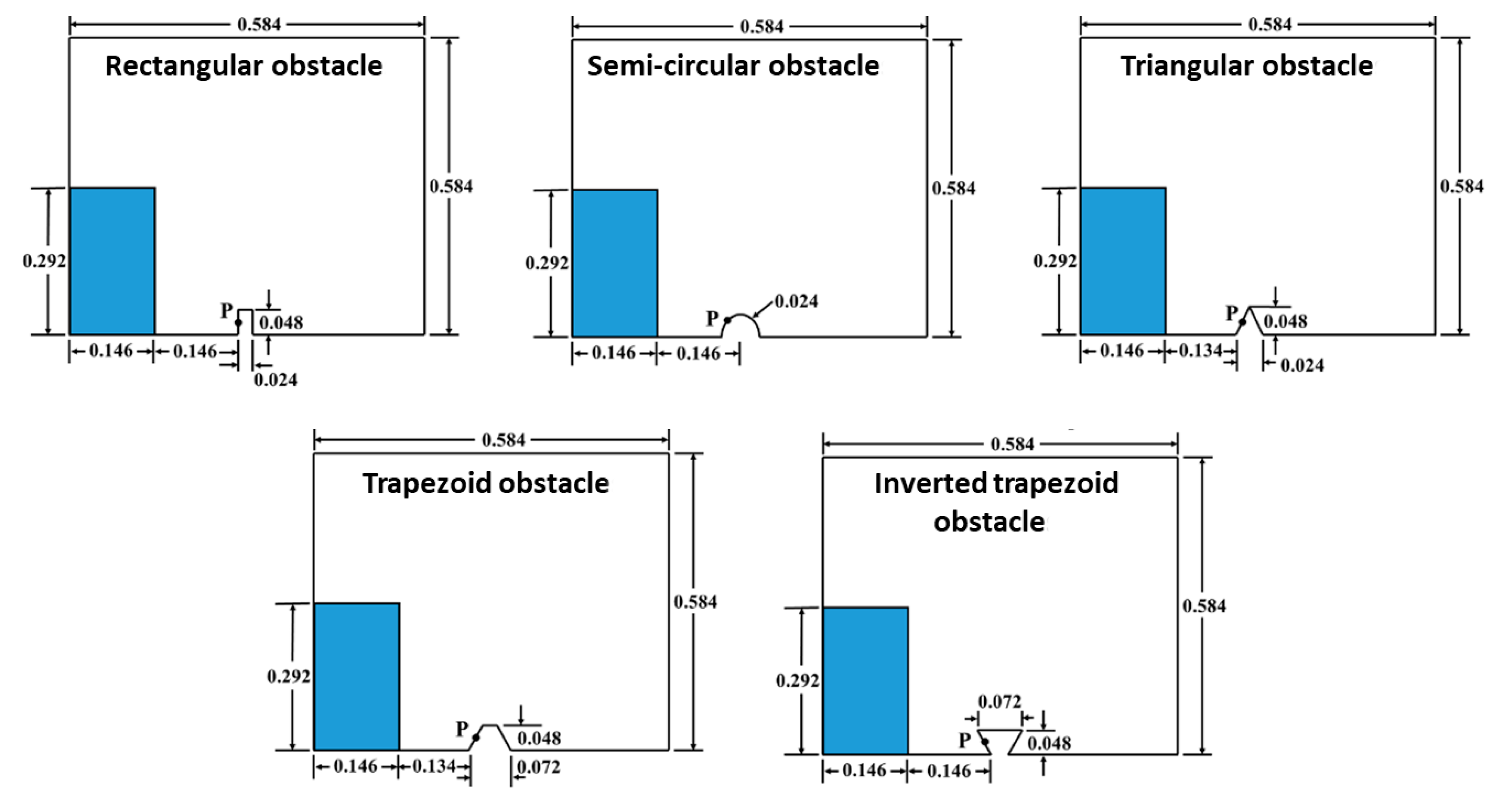
3. Single Liquid Dam Failure Simulation with Different Shapes of Obstacles Downstream
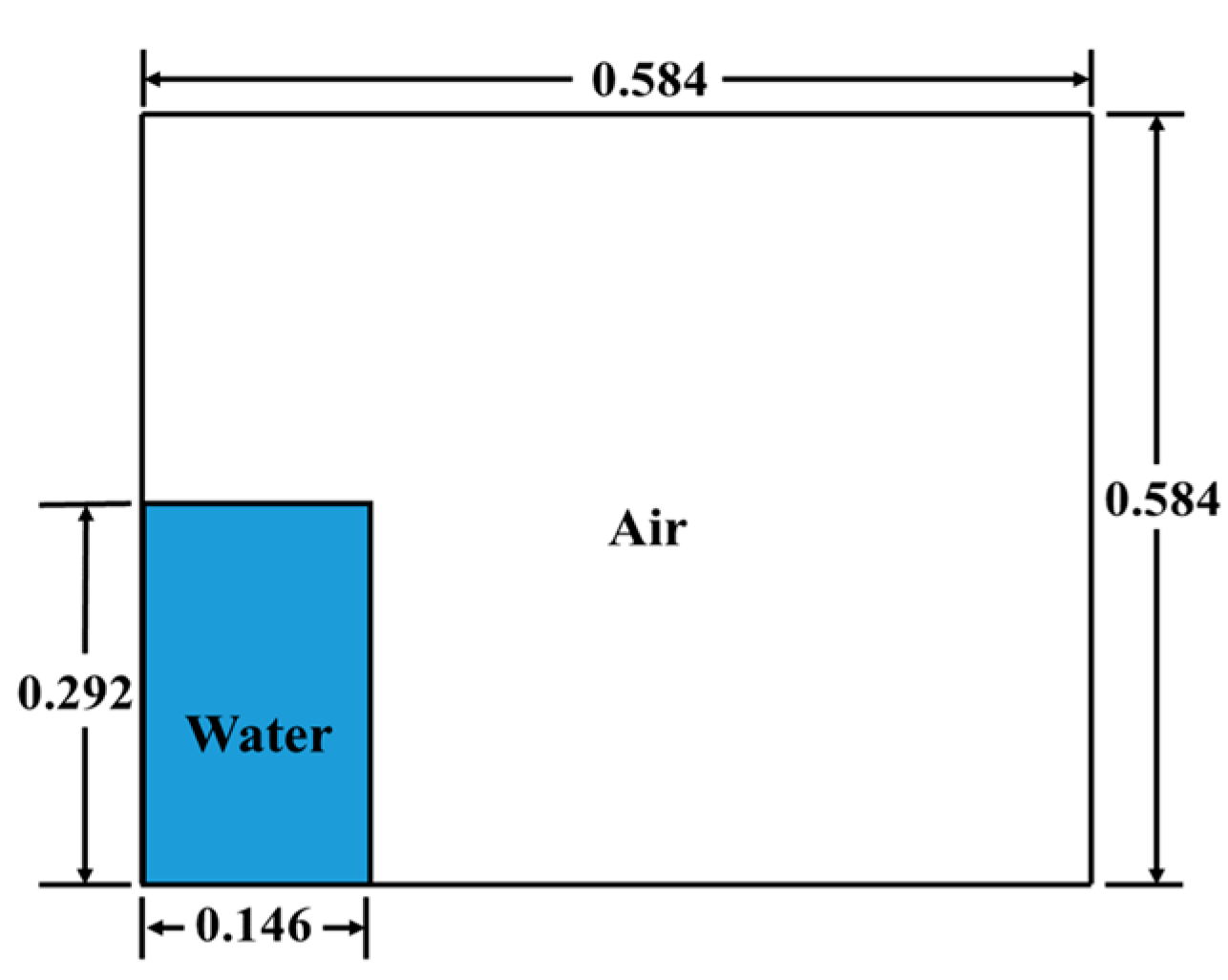
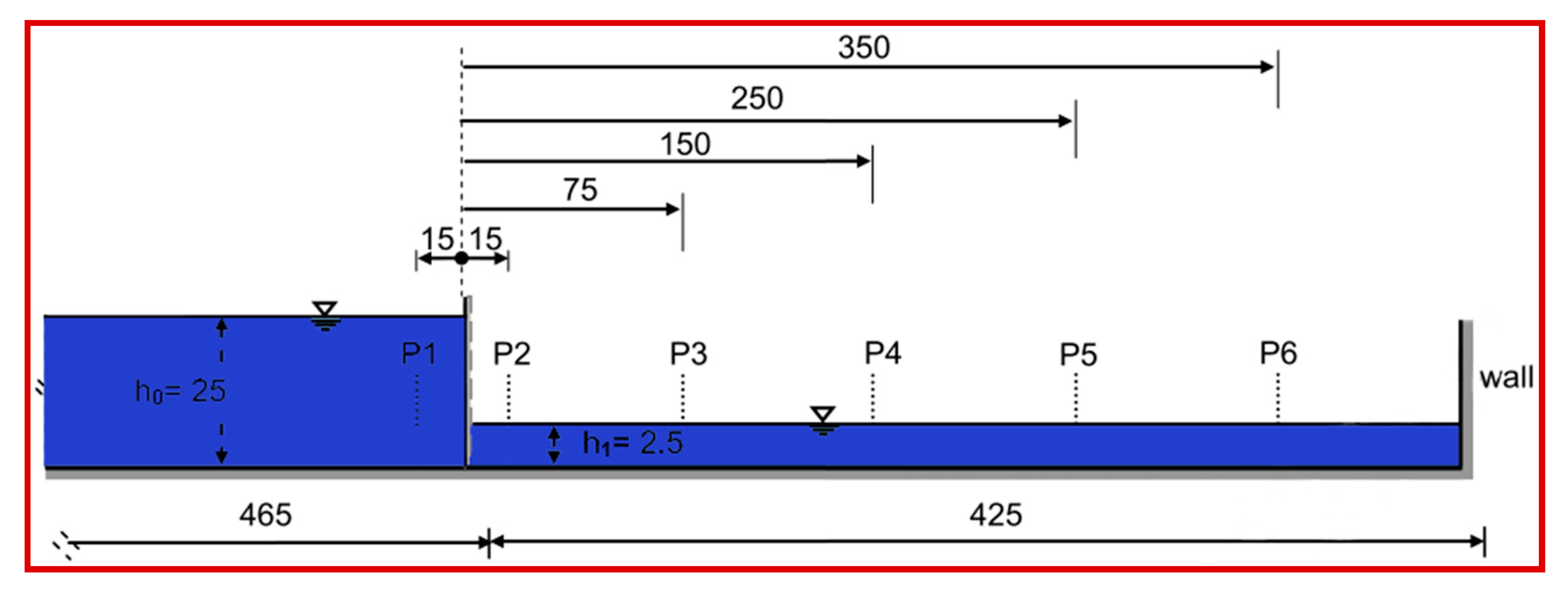
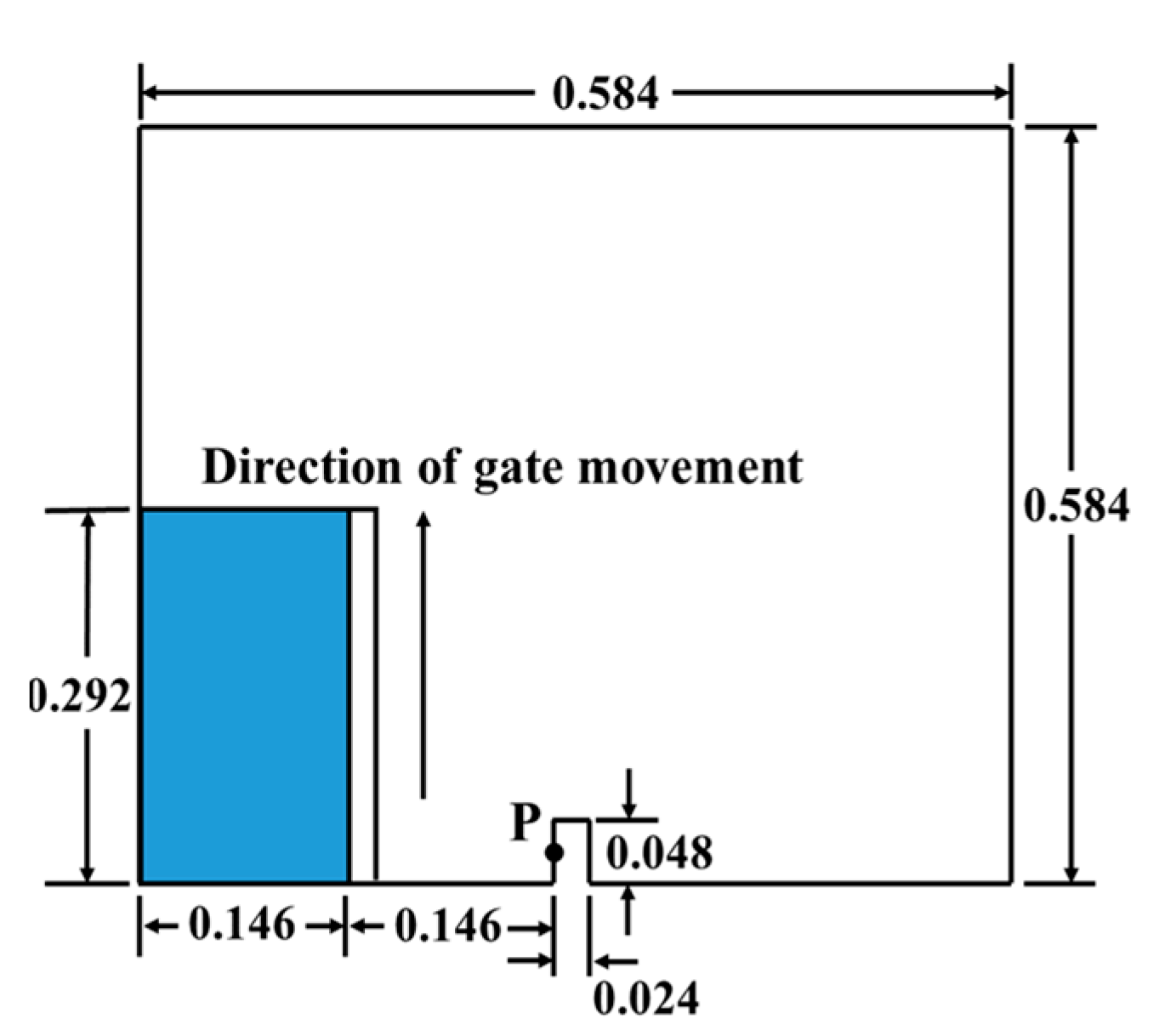
3.1. Basic Calculation Model Parameters
3.2. Mesh Division and Boundary Conditions of Foundation Dam Failure Computational Model
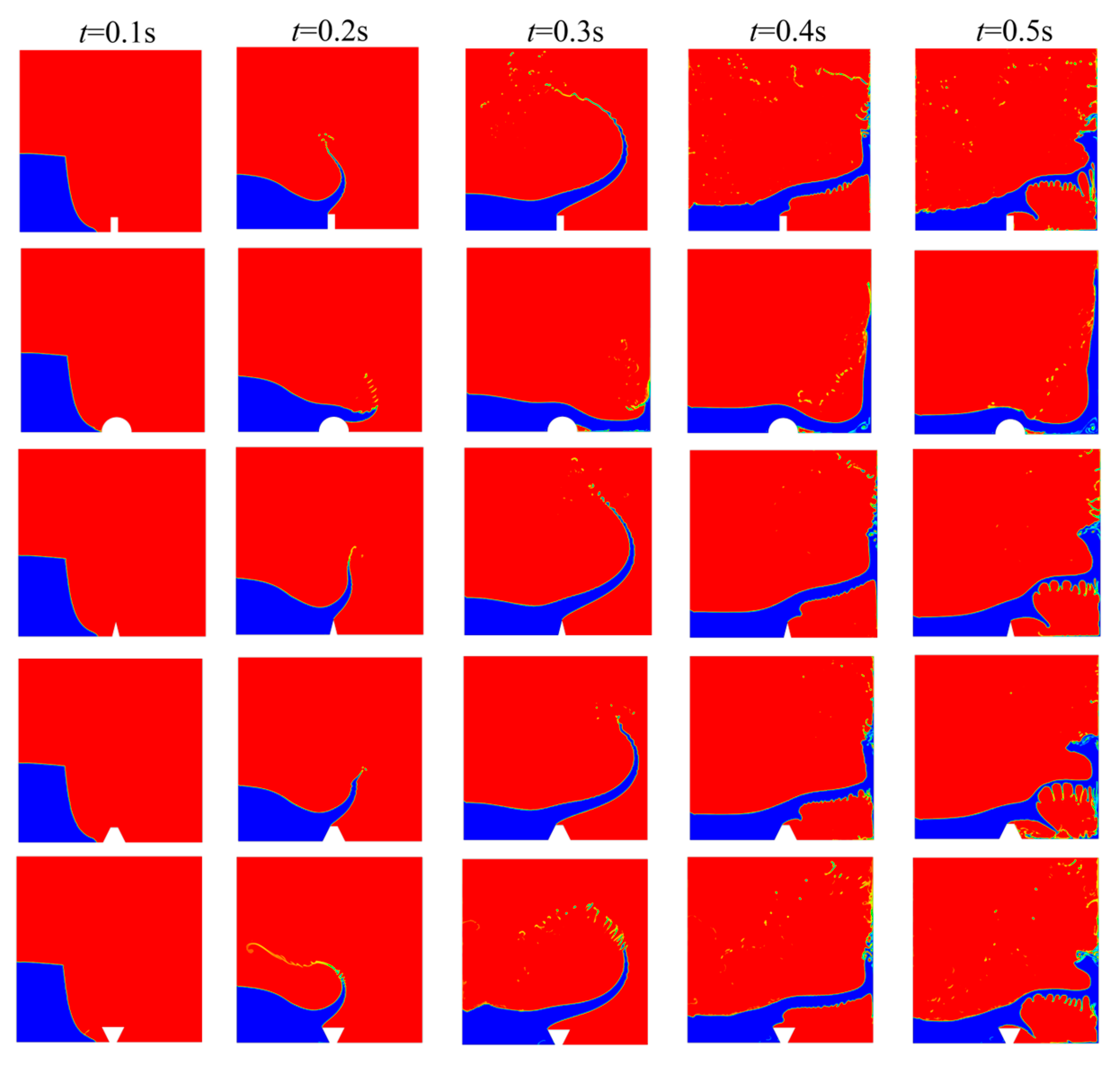
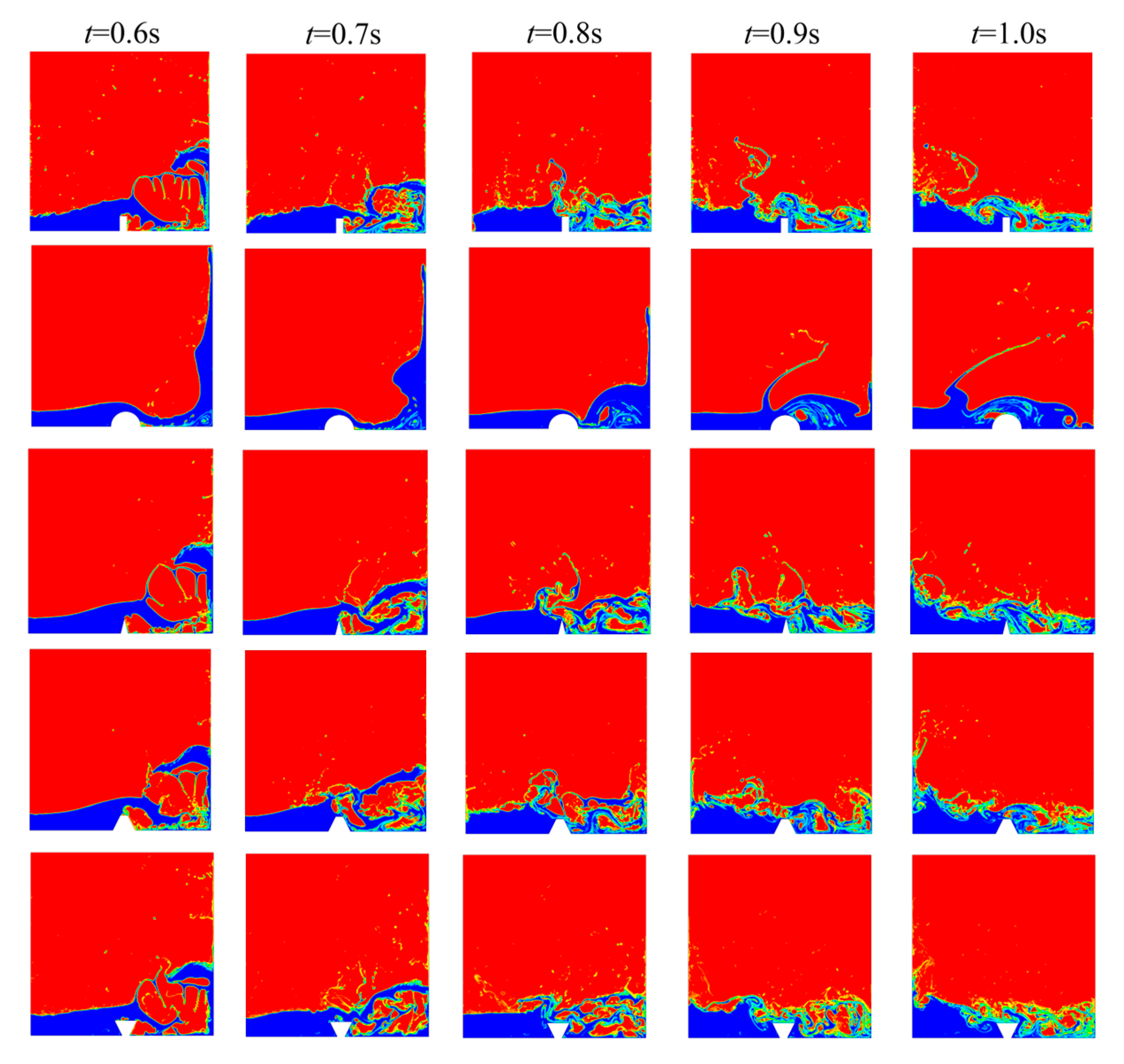
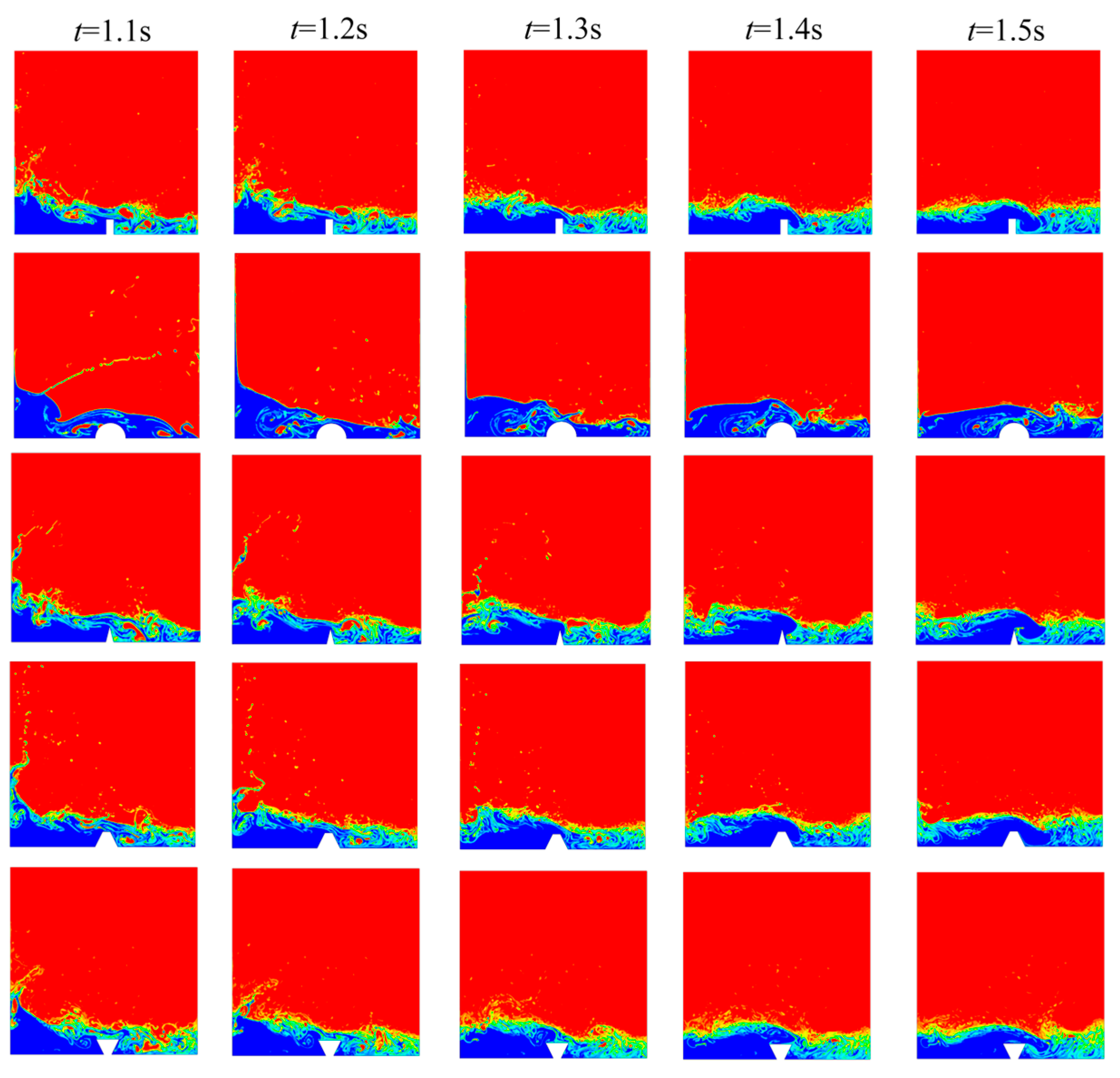
3.3. Data Analysis of Basic Dam Model Calculation Results
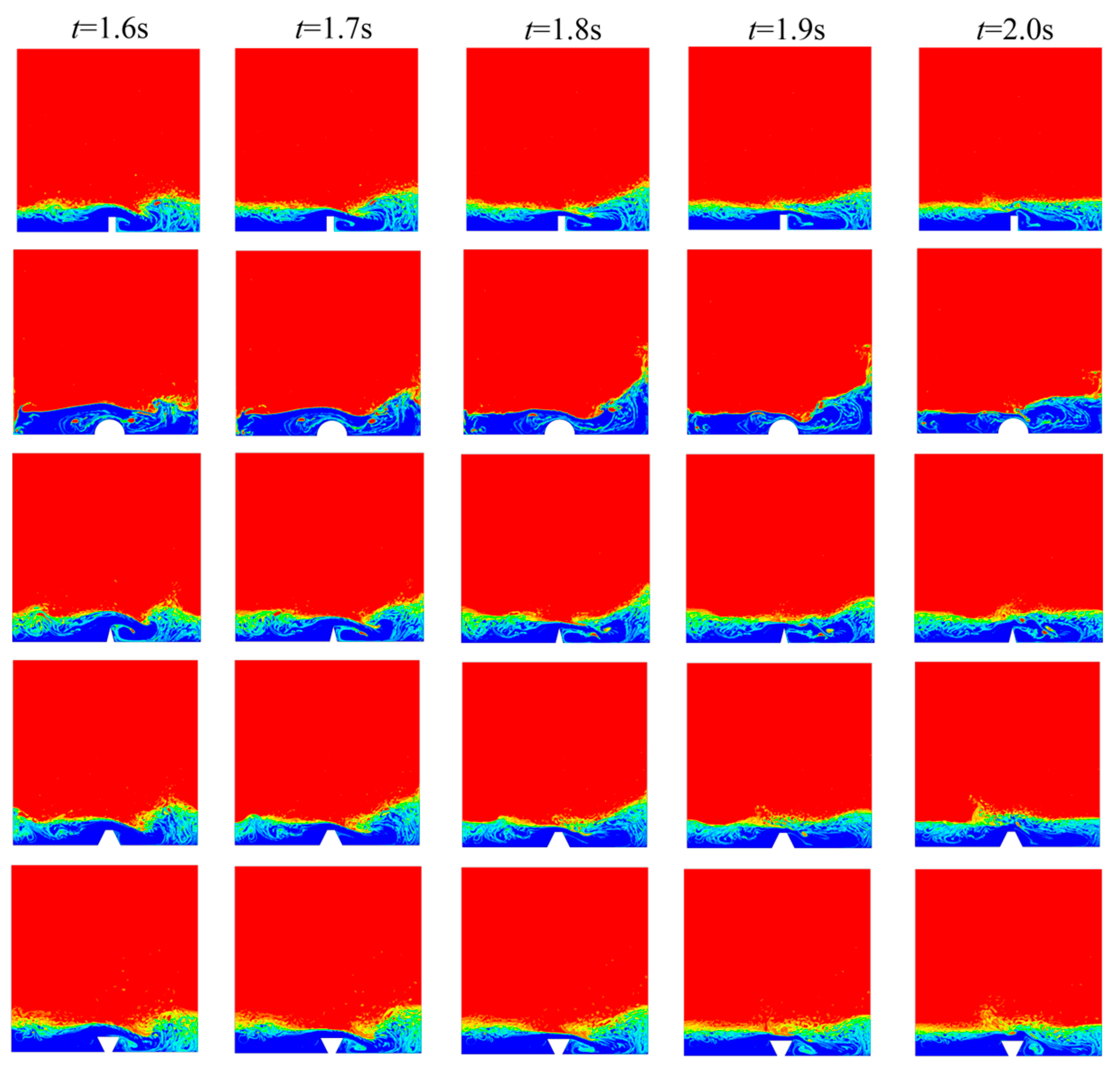
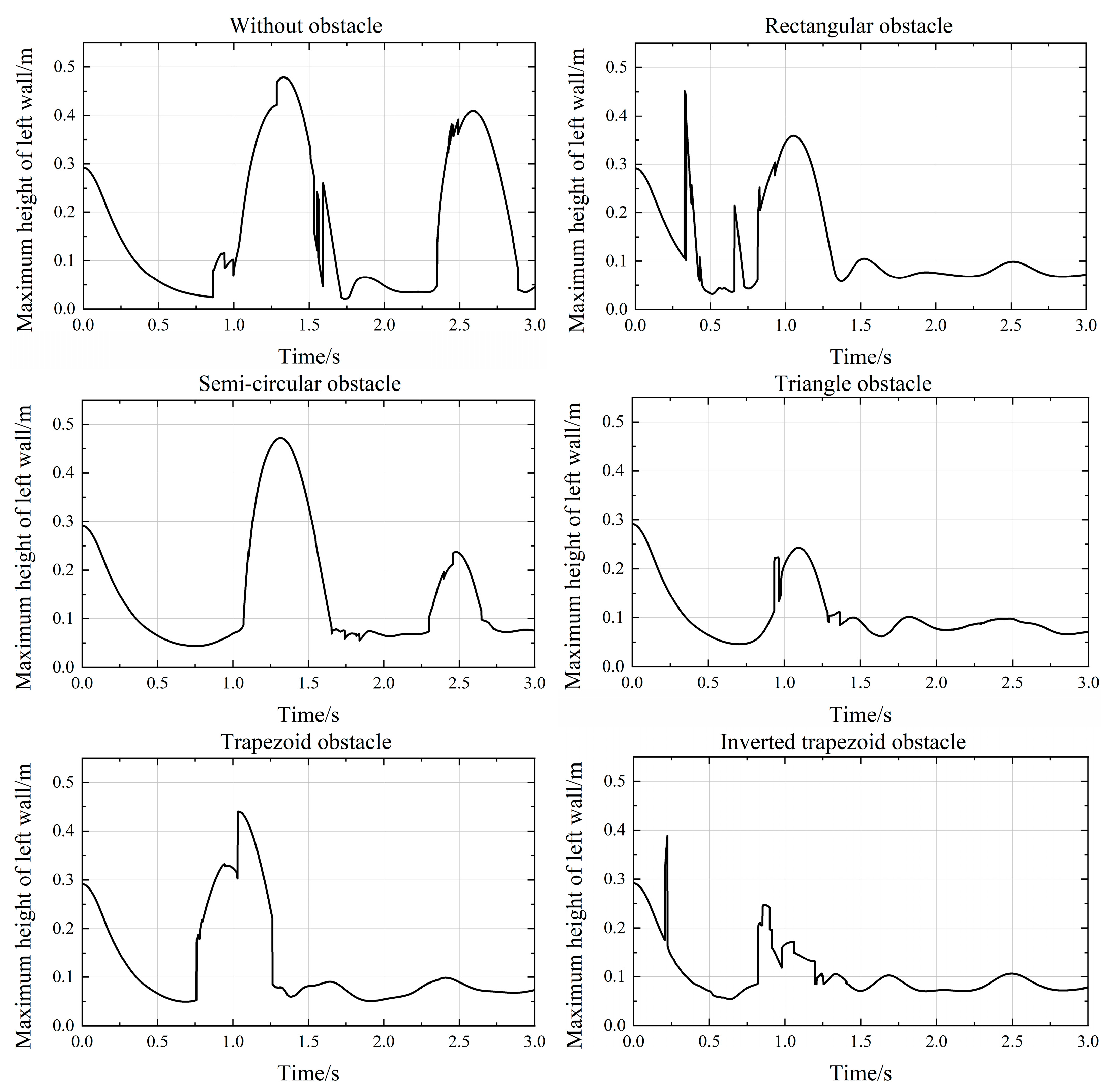
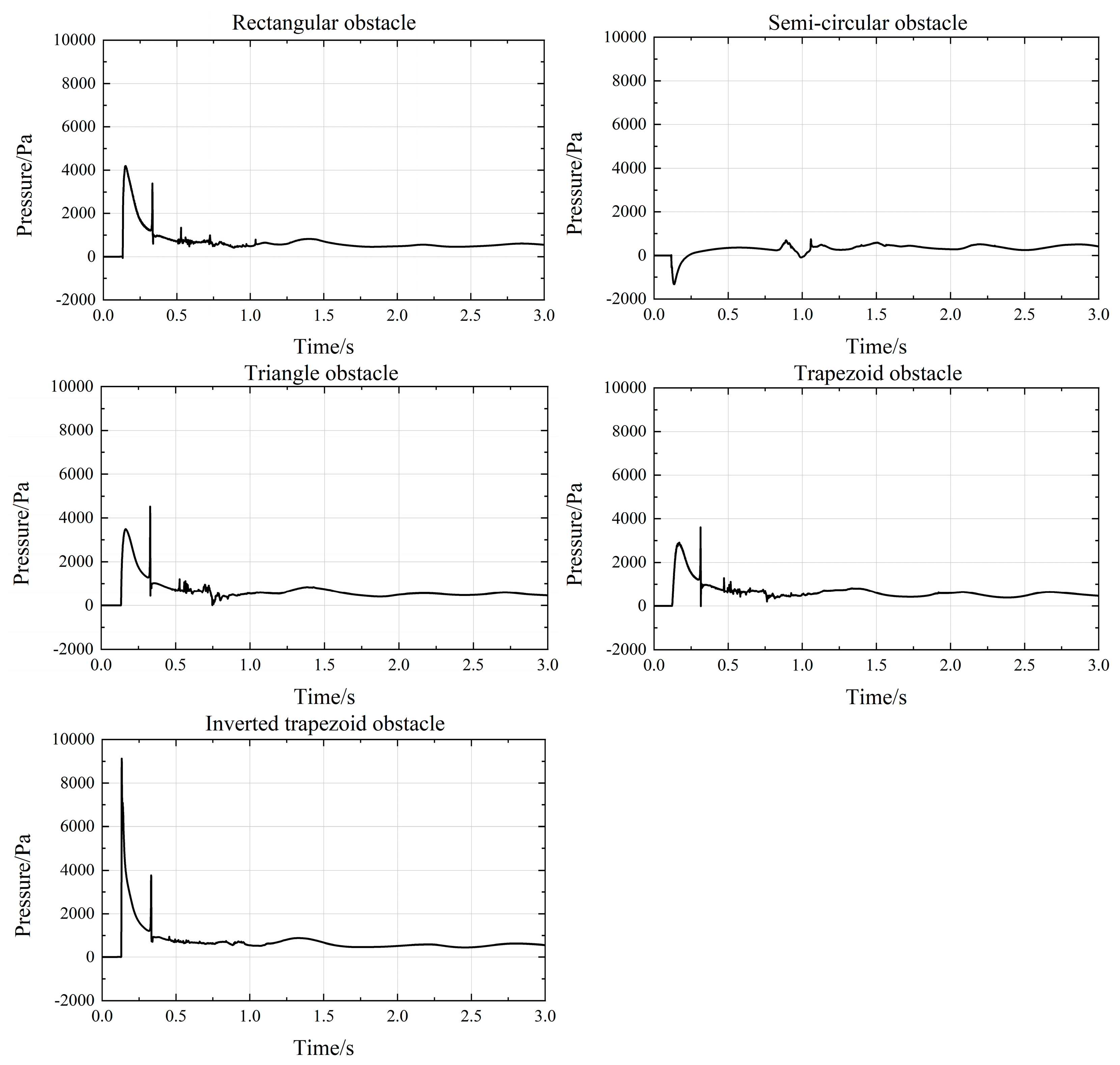
3.4. Comparative Analysis of Dam Failure Models with Diverse Obstacles Shapes Down-Stream
4. Simulation and Analysis of Single Liquid Dam with Wet Bed Downstream
4.1. Calculation Model of Wet Bed
4.2. Computational Model of Grid Division with Wet Bed
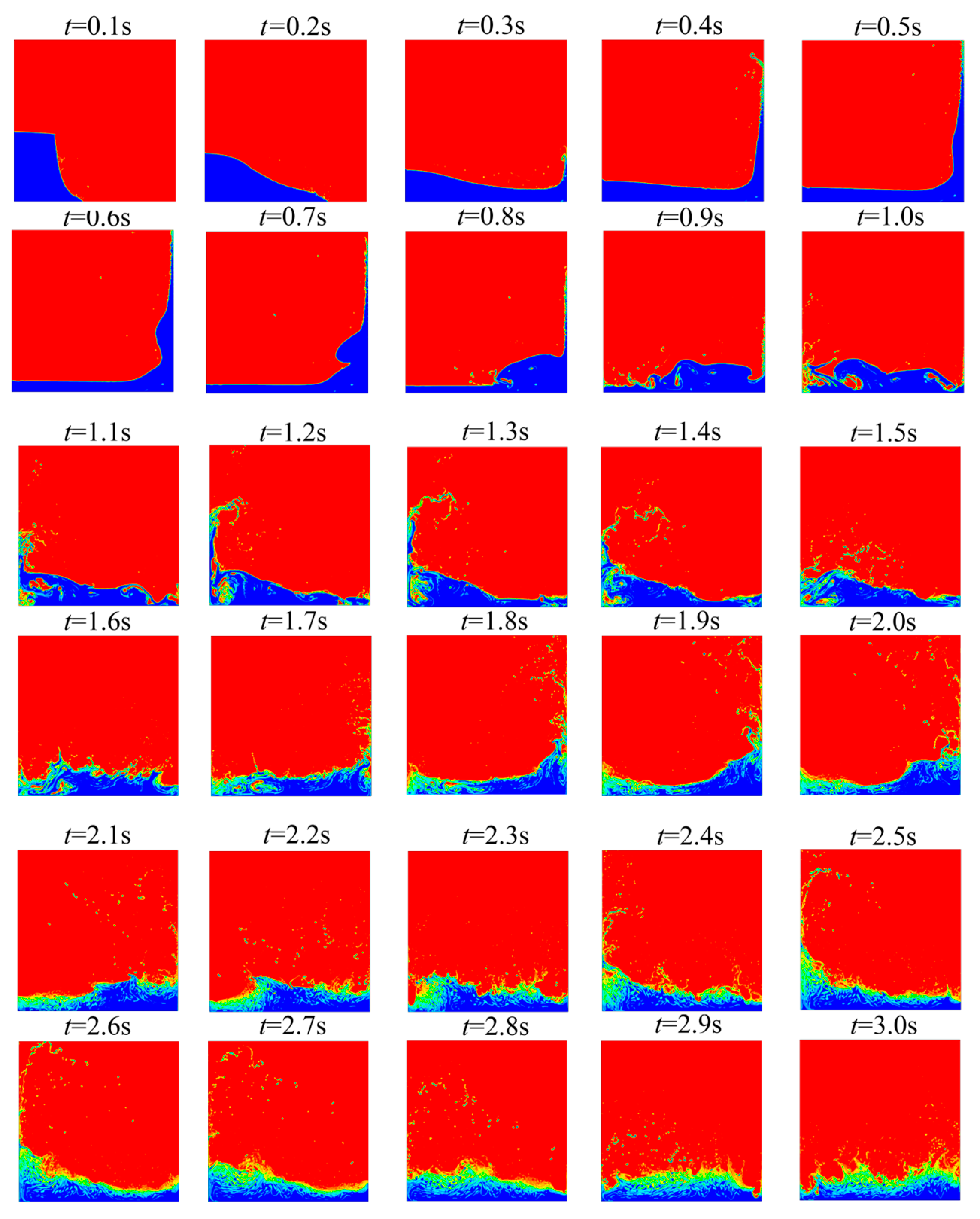
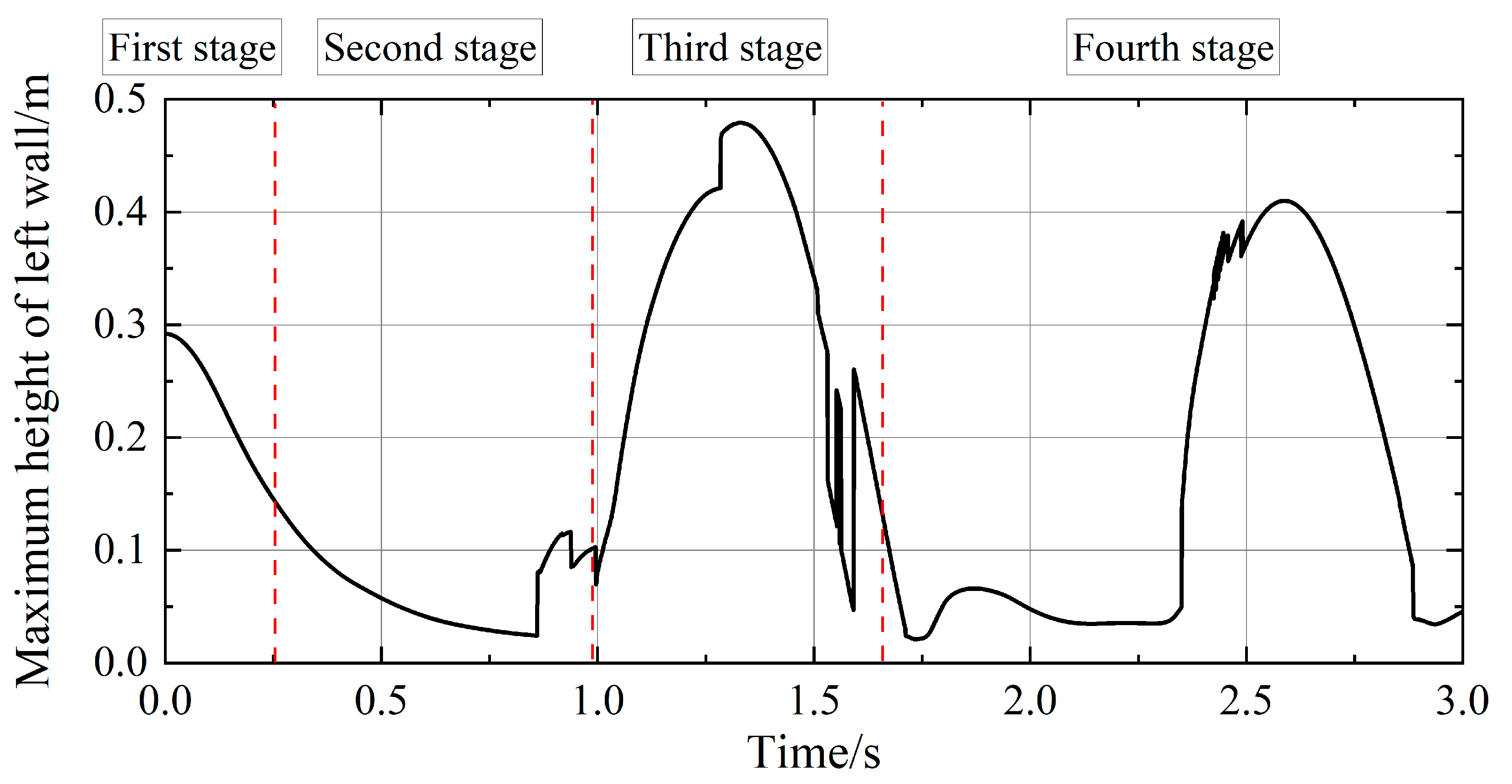
4.3. Distribution and Evolution of Free Surface Flow Field
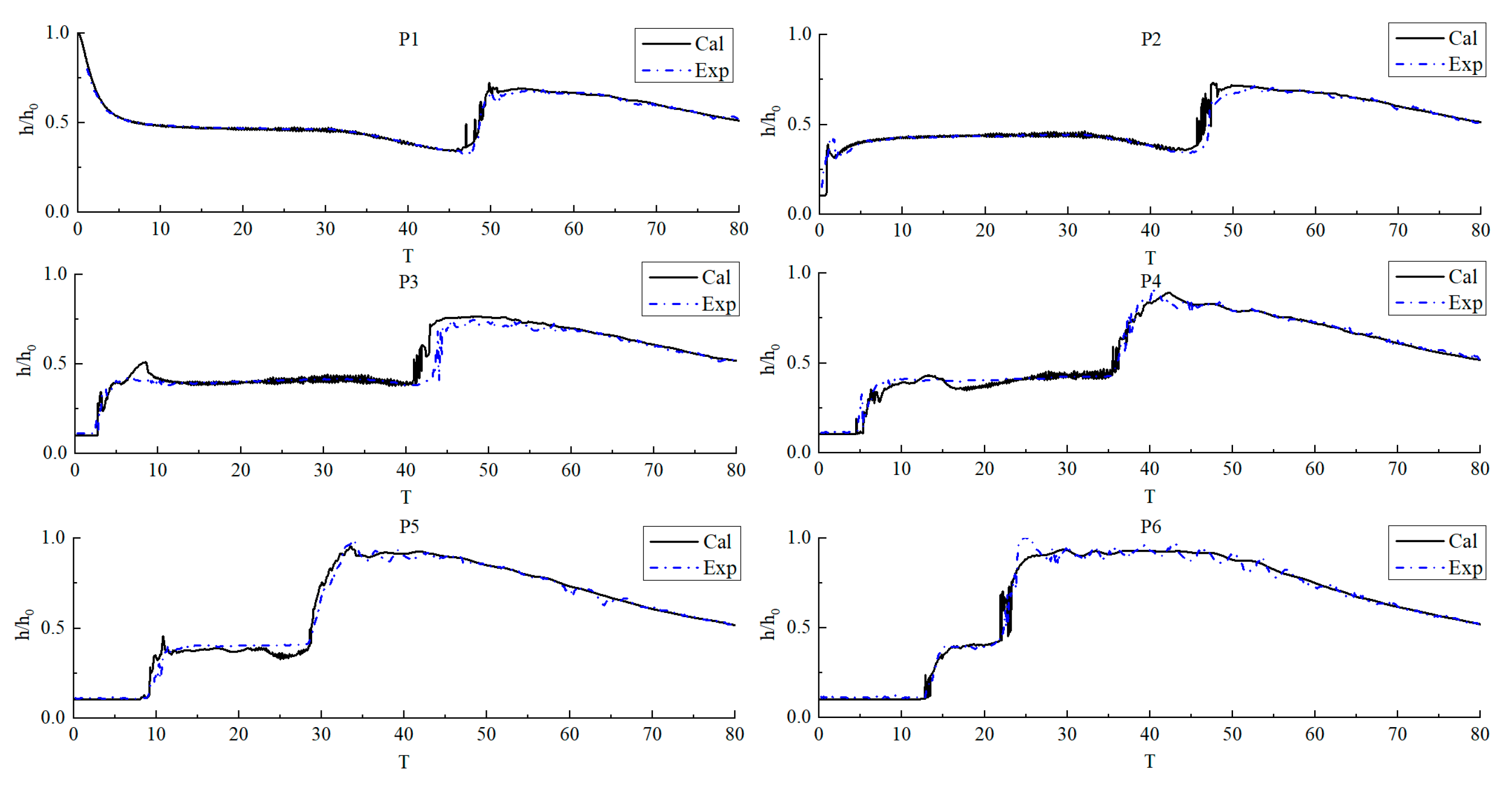
4.4. Free Surface Height Variation at Different Positions
5. Simulation and Analysis of Single Liquid Dam Failure during Gate Twitching
5.1. Dam Breaking Model When the Gate Twitches
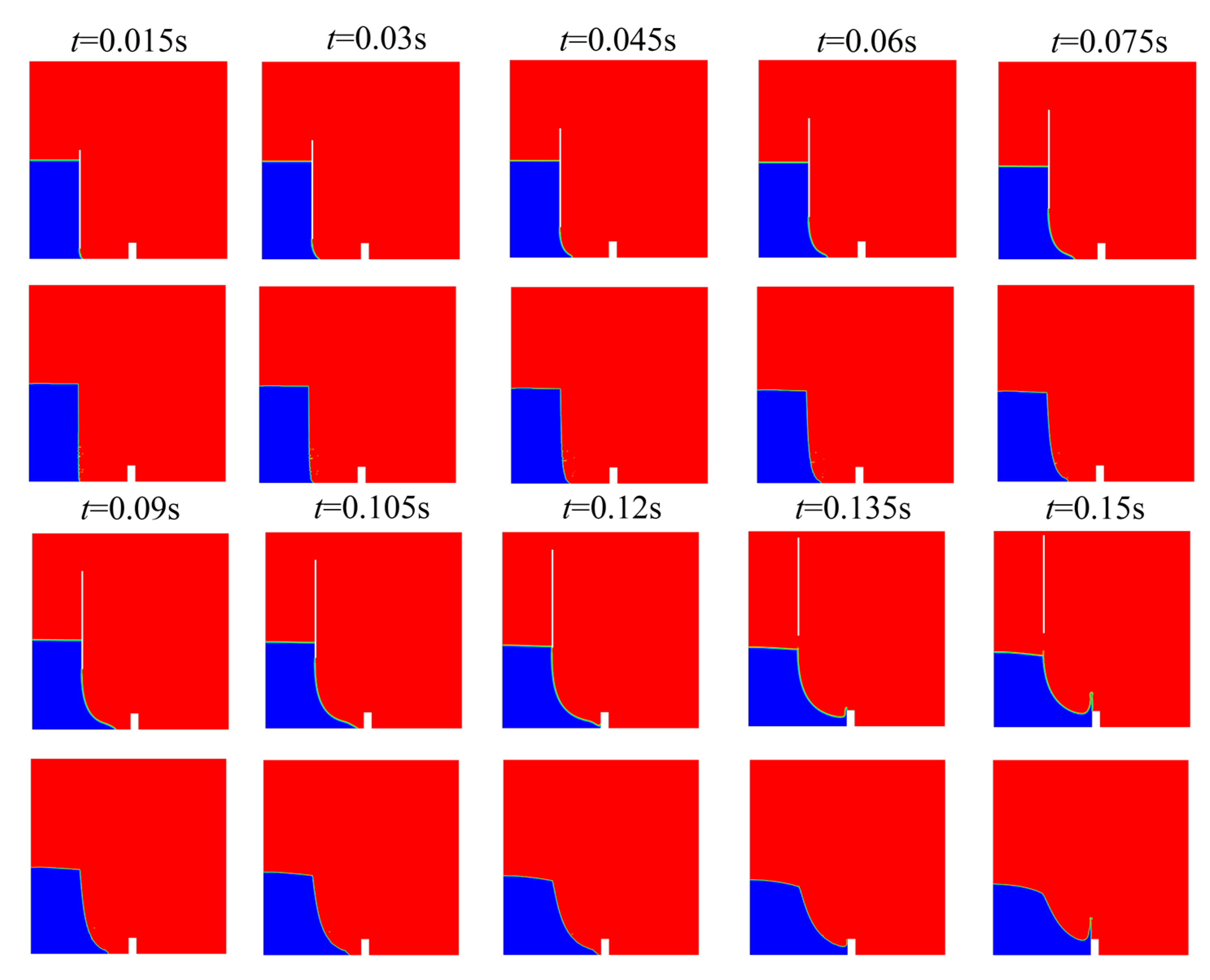
5.2. Free Surface Flow Field Distribution
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shuang, W.U. Statistics and Analysis of Dam Failures in United States since 2010. Dam Saf. 2020, 5, 61. [Google Scholar]
- Li, H.E.; Sheng, J.B.; He, Y.J. Global dam break events raise an alert about dam safety management. China Water Res. 2020, 16, 19–22+30. (In Chinese) [Google Scholar]
- Xie, J.B.; Sun, D.Y. Statistics of dam failures in China and analysis on failure causations. Water Resou. Hydro. Eng. 2009, 40, 124–128. [Google Scholar]
- You, L.; Li, C.; Min, X.; Xiaolei, T. Review of dam-break research of earth-rock dam combining with dam safety management. Proc. Eng. 2012, 28, 382–388. [Google Scholar] [CrossRef]
- Huang, B.; Ge, L.; Xu, X.; Wang, Y. Application of HEC-RAS in 2D Dam Break Simulation—A Case Study of Hongqi Reservoir. Pearl River 2021, 42, 73–79. (In Chinese) [Google Scholar]
- Yilmaz, A.; Kocaman, S.; Demirci, M. Numerical Modeling of the Dam-Break Wave Impact on Elastic Sluice Gate: A New Benchmark Case for Hydroelasticity Problems. Ocean Eng. 2021, 231, 108870. [Google Scholar] [CrossRef]
- Kocaman, S.; Evangelista, S.; Guzel, H.; Dal, K.; Yilmaz, A.; Viccione, G. Experimental and Numerical Investigation of 3d Dam-Break Wave Propagation in an Enclosed Domain with Dry and Wet Bottom. Appl. Sci. 2021, 11, 5638. [Google Scholar] [CrossRef]
- Kocaman, S.; Dal, K. A New Experimental Study and SPH Comparison for the Sequential Dam-Break Problem. J. Mar. Sci. Eng. 2020, 8, 905. [Google Scholar] [CrossRef]
- Kocaman, S.; Ozmen-Cagatay, H. Investigation of Dam-Break Induced Shock Waves Impact on a Vertical Wall. J. Hydrol. 2015, 525, 1–12. [Google Scholar] [CrossRef]
- Kocaman, S.; Ozmen-Cagatay, H. The Effect of Lateral Channel Contraction on Dam Break Flows: Laboratory Experiment. J. Hydrol. 2012, 432, 145–153. [Google Scholar] [CrossRef]
- Issakhov, A.; Zhandaulet, Y.; Nogaeva, A. Numerical simulation of dam break flow for various forms of the obstacle by VOF method. Int. J. Multi. Flow. 2018, 109, 191–206. [Google Scholar] [CrossRef]
- Issakhov, A.; Imanberdiyeva, M. Numerical simulation of the movement of water surface of dam break flow by VOF methods for various obstacles. Int. J. Heat. Mass. Transfer 2019, 136, 1030–1051. [Google Scholar] [CrossRef]
- Li, Y.L.; Wan, L.; Wang, Y.H.; Ma, C.P.; Ren, L. Numerical investigation of interface capturing method by the Rayleigh-Taylor instability, dambreak and solitary wave problems. Ocean Eng. 2020, 194, 106583. [Google Scholar] [CrossRef]
- Issakhov, A.; Imanberdiyeva, M. Numerical modelling of the water surface movement with macroscopic particles of dam break flow for various obstacles. J. Hydro. Resour. 2021, 59, 523–544. [Google Scholar] [CrossRef]
- Mokrani, C.; Abadie, S. Conditions for peak pressure stability in VOF simulations of dam break flow impact. J. Fluids Struc. 2016, 62, 86–103. [Google Scholar] [CrossRef]
- Khoshkonesh, A.; Nsom, B.; Bahmanpouri, F.; Dehrashid, F.A.; Adeli, A. Numerical study of the dynamics and structure of a partial dam-break flow using the VOF method. Water Resou. Mana. 2021, 35, 1513–1528. [Google Scholar] [CrossRef]
- Munoz, D.H.; Constantinescu, G. 3-D dam break flow simulations in simplified and complex domains. Adv. Water Resour. 2020, 137, 103510. [Google Scholar] [CrossRef]
- Chang, T.J.; Kao, H.M.; Chang, K.H.; Hsu, M.H. Numerical simulation of shallow-water dam break flows in open channels using smoothed particle hydrodynamics. J. Hydro. 2011, 408, 78–90. [Google Scholar] [CrossRef]
- Xu, X. An improved SPH approach for simulating 3D dam-break flows with breaking waves. Comput. Methods Appl. Mech. Eng. 2016, 311, 723–742. [Google Scholar] [CrossRef]
- Wu, Y.; Tian, L.; Rubinato, M.; Gu, S.; Yu, T.; Xu, Z.; Cao, P.; Wang, X.; Zhao, Q. A New Parallel Framework of SPH-SWE for Dam Break Simulation Based on OpenMP. Water 2020, 12, 1395. [Google Scholar] [CrossRef]
- Soleimani, K.; Ketabdari, M.J. Meshfree modeling of near field two-liquid mixing process in the presence of different obstacles. Ocean Eng. 2020, 213, 107625. [Google Scholar] [CrossRef]
- Gu, Z.H.; Wen, H.L.; Yu, C.-H.; Sheu, T.W. Interface-Preserving Level Set Method for Simulating Dam-Break Flows. J. Comput. Phys. 2018, 374, 249–280. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J. Numerical Simulation of 2-D Dambreak Wave by Using Conservation Element and Solution Element Method. J. Hydraul. Eng. 2005, 36, 1224–1229. [Google Scholar]
- Miao, J.; Huang, C.; Zhang, X. Research on Dambreak Flow Simulation by Meshfree SPH Method. C.R. Wat. Hyd. 2012, 01, 134–136. [Google Scholar]
- Xu, X.; Jiang, Y.; Yu, P. SPH simulations of 3D dam-break flow against various forms of the obstacle: Toward an optimal design. Ocean Eng. 2021, 229, 108978. [Google Scholar] [CrossRef]
- Hervouet, J.M. Hydrodynamics of Free Surface Flows: Modelling with the Finite Element Method; John Wiley and Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Seyedashraf, O.; Akhtari, A.A. Two-dimensional numerical modeling of dam-break flow using a new TVD finite-element scheme. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4393–4401. [Google Scholar] [CrossRef]
- Harlan, D.; Adityawan, M.B.; Natakusumah, D.K.; Zendrato, N.L.H. Application of numerical filter to a Taylor Galerkin finite element model for movable bed dam break flows. GEOMATE J. 2019, 16, 209–216. [Google Scholar] [CrossRef]
- Larese, A.N.T.O.N.I.A.; Rossi, R.; Oñate, E.; Idelsohn, S.R. Validation of the particle finite element method (PFEM) for simulation of free surface flows. Eng. Comput. 2013, 10, 385–425. [Google Scholar] [CrossRef]
- Savant, G.; Berger, C.; McAlpin, T.O.; Tate, J.N. Efficient implicit finite-element hydrodynamic model for dam and levee breach. J. Hydra. Eng. 2011, 137, 1005–1018. [Google Scholar] [CrossRef]
- Zhang, T.; Peng, L.; Feng, P. Evaluation of a 3D unstructured-mesh finite element model for dam-break floods. Comput. Fluids 2018, 160, 64–77. [Google Scholar] [CrossRef]
- Hosseini Boosari, S.S. Predicting the Dynamic Parameters of Multiphase Flow in CFD (Dam-Break Simulation) Using Artificial Intelligence-(Cascading Deployment). Fluids 2019, 4, 44. [Google Scholar] [CrossRef]
- Nourani, V.; Hakimzadeh, H.; Amini, A.B. Implementation of artificial neural network technique in the simulation of dam breach hydrograph. J. Hydro. 2012, 14, 478–496. [Google Scholar] [CrossRef]
- Mu, D.; Chen, L.; Ning, D. Three-D Numerical Study of Interaction between Dam-break Wave and Circular Cylinder. S.C. 2020, 61, 231–239. [Google Scholar]
- Wang, B.; Chen, Y.; Wu, C.; Peng, Y.; Song, J.; Liu, W.; Liu, X. Empirical and semi-analytical models for predicting peak outflows caused by embankment dam failures. J. Hydrol. 2018, 562, 692–702. [Google Scholar] [CrossRef]
- Aureli, F.; Maranzoni, A.; Petaccia, G. Review of historical dam-break events and laboratory tests on real topography for the validation of numerical models. Water-Sui 2021, 13, 1968. [Google Scholar] [CrossRef]
- Li, W.; Zhu, J.; Fu, L.; Zhu, Q.; Guo, Y.; Gong, Y. A rapid 3D reproduction system of dam-break floods constrained by post-disaster information. Environ. Modell. Softw. 2021, 139, 104994. [Google Scholar] [CrossRef]
- Azeez, O.; Elfeki, A.; Kamis, A.S.; Chaabani, A. Dam break analysis and flood disaster simulation in arid urban environment: The Um Al-Khair dam case study, Jeddah, Saudi Arabia. Nat. Hazards 2020, 100, 995–1011. [Google Scholar] [CrossRef]
- Ye, Y.; Xu, T.; Zhu, D.Z. Numerical analysis of dam-break waves propagating over dry and wet beds by the mesh-free method. Ocean Eng. 2020, 217, 107969. [Google Scholar] [CrossRef]
- Bahmanpouri, F.; Daliri, M.; Khoshkonesh, A.; Namin, M.M.; Buccino, M. Bed compaction effect on dam break flow over erodible bed; experimental and numerical modeling. J. Hydrol. 2021, 594, 125645. [Google Scholar] [CrossRef]
- Ahmadi, S.M.; Yamamoto, Y. A New Dam-Break Outflow-Rate Concept and Its Installation to a Hydro-Morphodynamics Simulation Model Based on FDM (An Example on Amagase Dam of Japan). Water 2021, 13, 1759. [Google Scholar] [CrossRef]
- Cai, W.; Zhu, X.; Peng, A.; Wang, X.; Fan, Z. Flood Risk Analysis for Cascade Dam Systems: A Case Study in the Dadu River Basin in China. Water 2019, 11, 1365. [Google Scholar] [CrossRef]
- Cantero-Chinchilla, F.N.; Bergillos, R.J.; Gamero, P.; Castro-Orgaz, O.; Cea, L.; Hager, W.H. Vertically Averaged and Moment Equations for Dam-Break Wave Modeling: Shallow Water Hypotheses. Water 2020, 12, 3232. [Google Scholar] [CrossRef]
- Bello, D.; Alcayaga, H.; Caamaño, D.; Pizarro, A. Influence of Dam Breach Parameter Statistical Definition on Resulting Rupture Maximum Discharge. Water 2022, 14, 1776. [Google Scholar] [CrossRef]
- Issakhov, A.; Zhandaulet, Y. Numerical study of dam break waves on movable beds for various forms of the obstacle by VOF method. Ocean Eng. 2020, 209, 107459. [Google Scholar] [CrossRef]
- Hernández-Fontes, J.V.; Vitola, M.A.; Esperança, P.T.; Sphaier, S.H.; Silva, R. Patterns and vertical loads in water shipping in systematic wet dam-break experiments. Ocean Eng. 2020, 197, 106891. [Google Scholar] [CrossRef]
- Wang, C.N.; Yang, F.C.; Nguyen, V.T.T.; Vo, N.T.M. CFD Analysis and Optimum Design for a Centrifugal Pump Using an Effectively Artificial Intelligent Algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef]
- Nguyen, V.T.T.; Vo, T.M.N. Centrifugal Pump Design: An Optimization. Eurasia Procee. Sci. Techn. Engi Math. 2022, 17, 136–151. [Google Scholar] [CrossRef]
- Yao, Z.; Peng, Y. Numerical Simulation of Dam Break Flood and Its Application; China Water & Power Press: Beijing, China, 2013. (In Chinese) [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Zhao, B.; Dapeng, Z.; Zhu, K. Numerical Simulation of Two-Dimensional Dam Failure and Free-Side Deformation Flow Studies. Water 2023, 15, 1515. https://doi.org/10.3390/w15081515
Jiang H, Zhao B, Dapeng Z, Zhu K. Numerical Simulation of Two-Dimensional Dam Failure and Free-Side Deformation Flow Studies. Water. 2023; 15(8):1515. https://doi.org/10.3390/w15081515
Chicago/Turabian StyleJiang, Haoyu, Bowen Zhao, Zhang Dapeng, and Keqiang Zhu. 2023. "Numerical Simulation of Two-Dimensional Dam Failure and Free-Side Deformation Flow Studies" Water 15, no. 8: 1515. https://doi.org/10.3390/w15081515
APA StyleJiang, H., Zhao, B., Dapeng, Z., & Zhu, K. (2023). Numerical Simulation of Two-Dimensional Dam Failure and Free-Side Deformation Flow Studies. Water, 15(8), 1515. https://doi.org/10.3390/w15081515









