Assessment of ERA5-Land Data in Medium-Term Drinking Water Demand Modelling with Deep Learning
Abstract
:1. Introduction
2. Materials and Methods
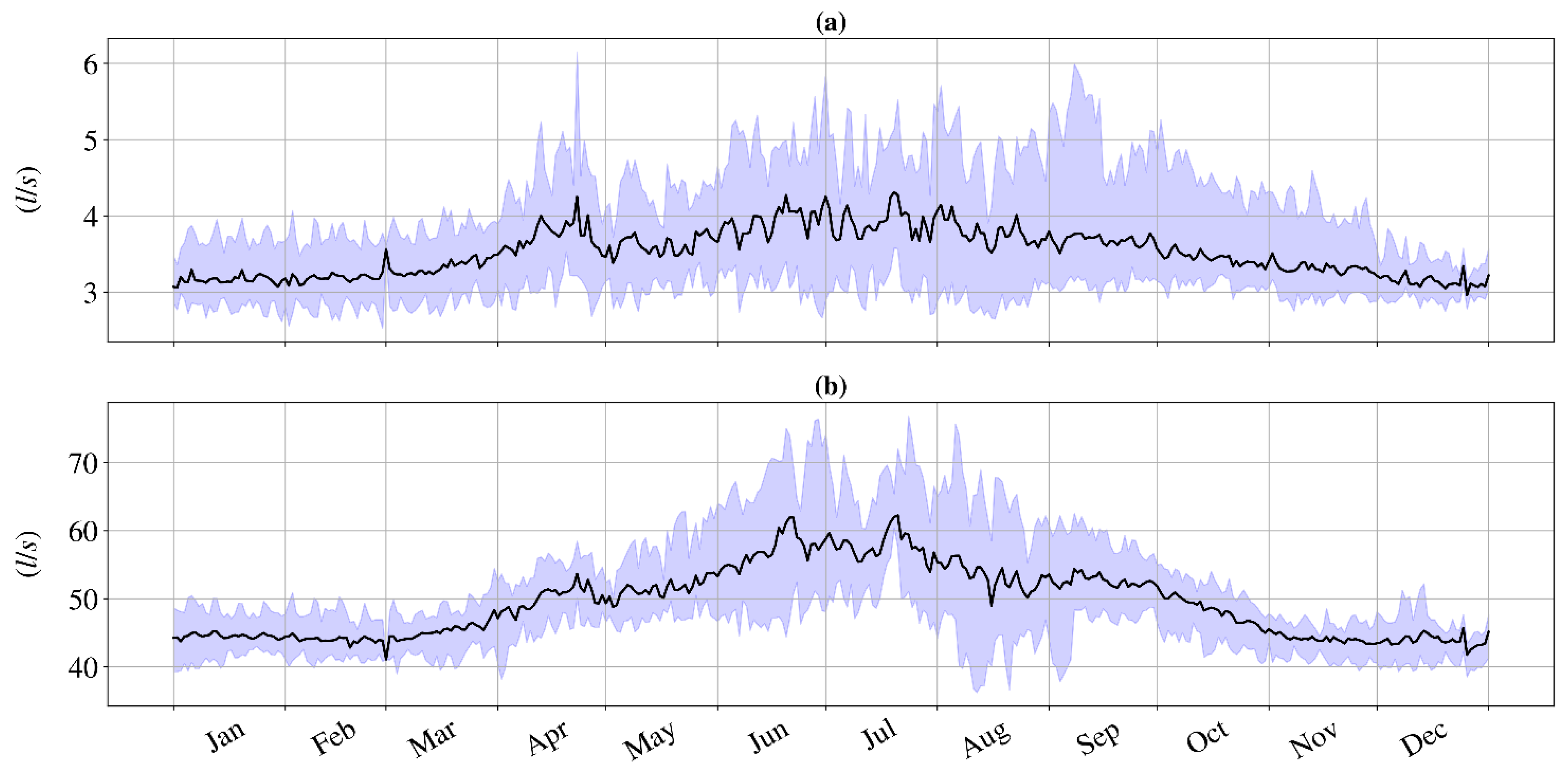
2.1. Water Demand
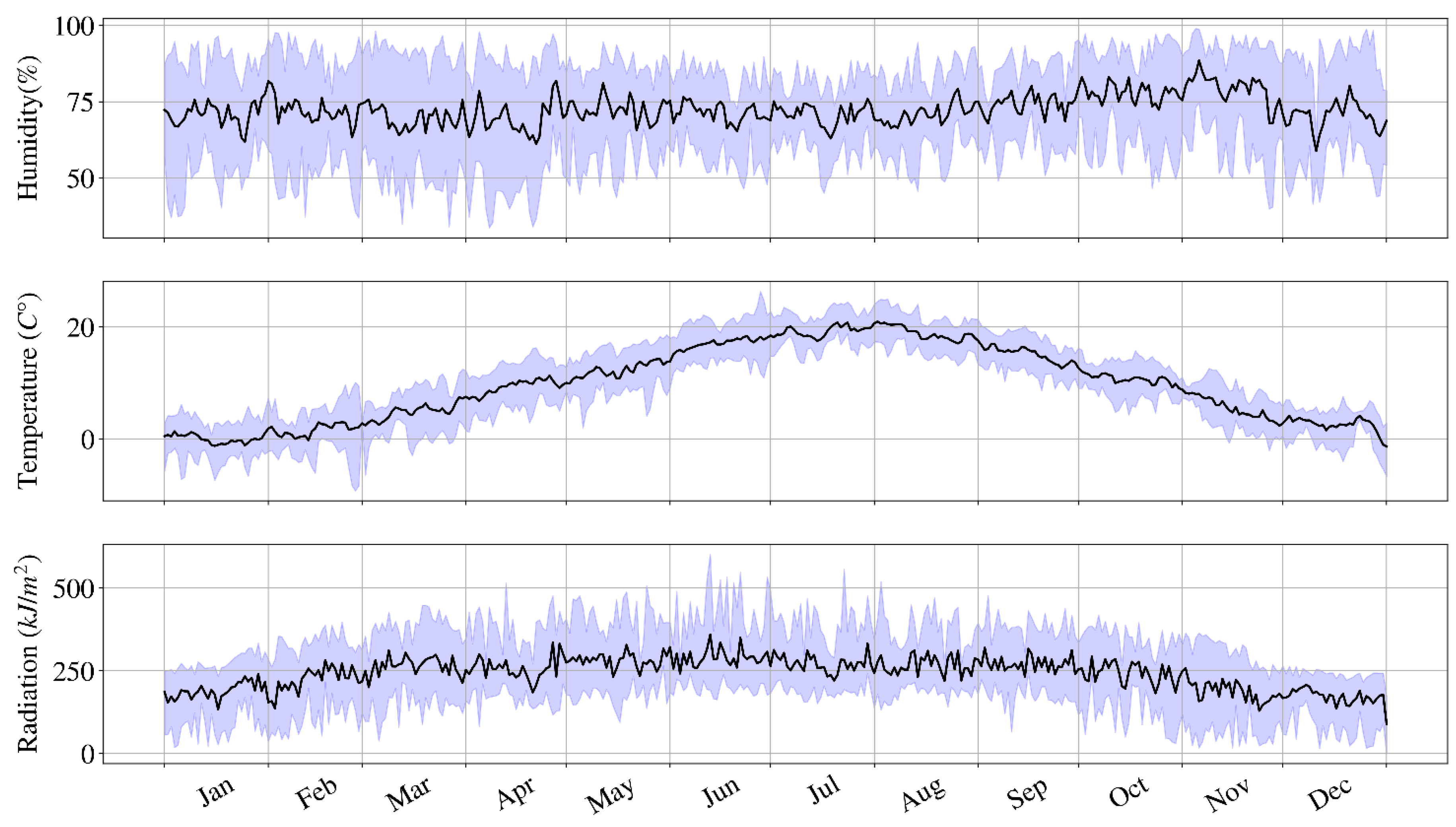
2.2. Meteorological Data
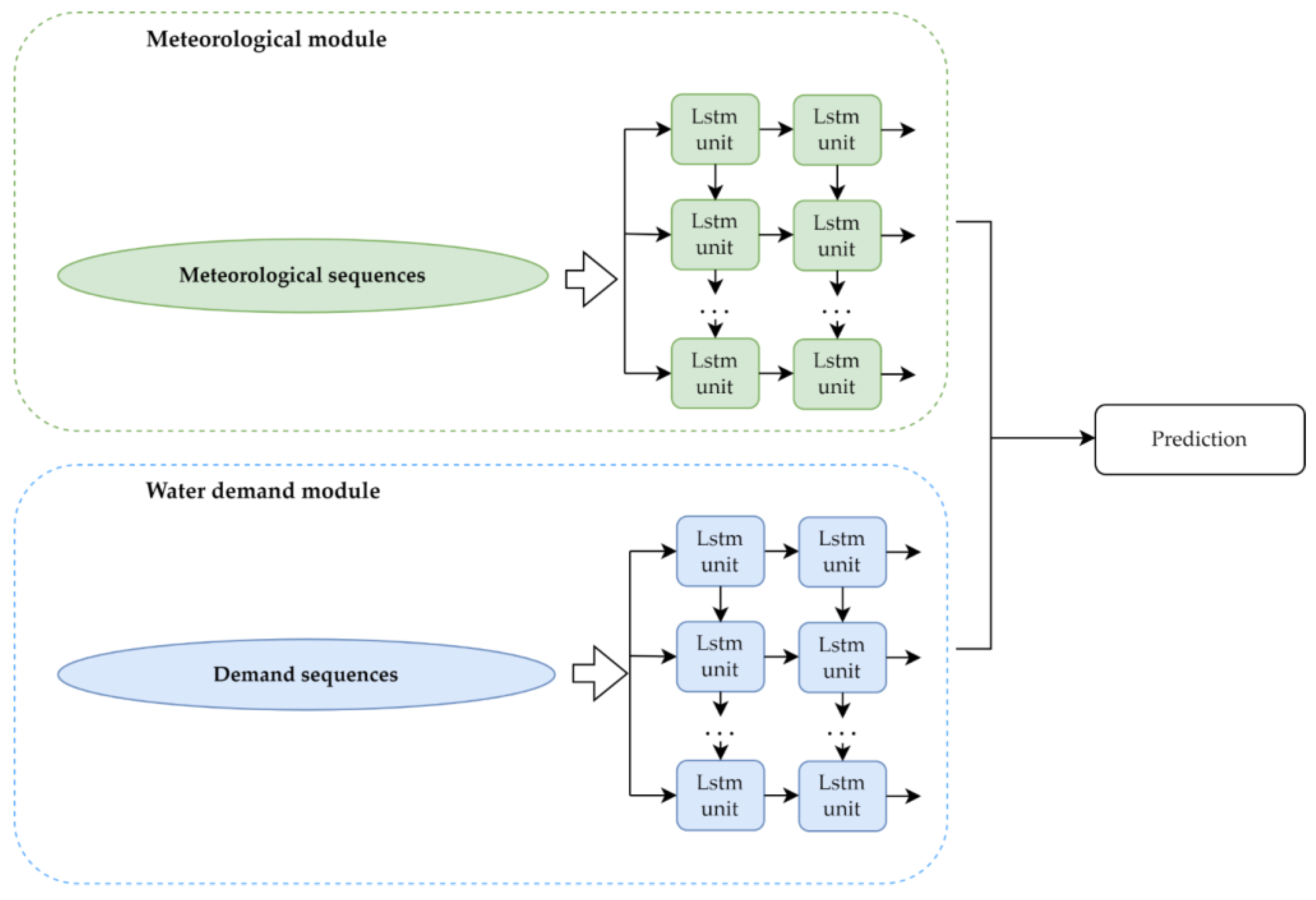
2.3. Forecasting Model
2.4. Evaluation Metrics
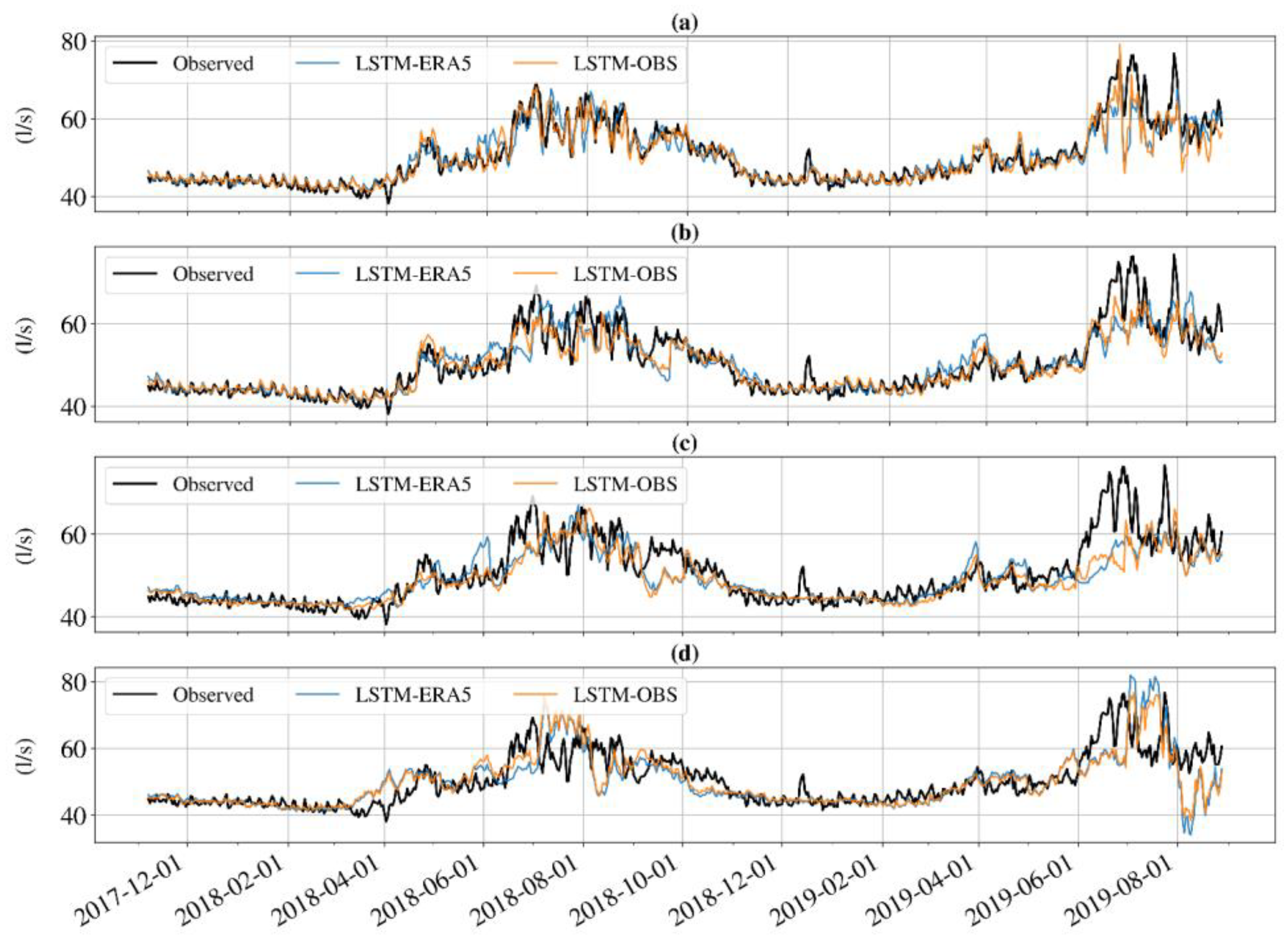
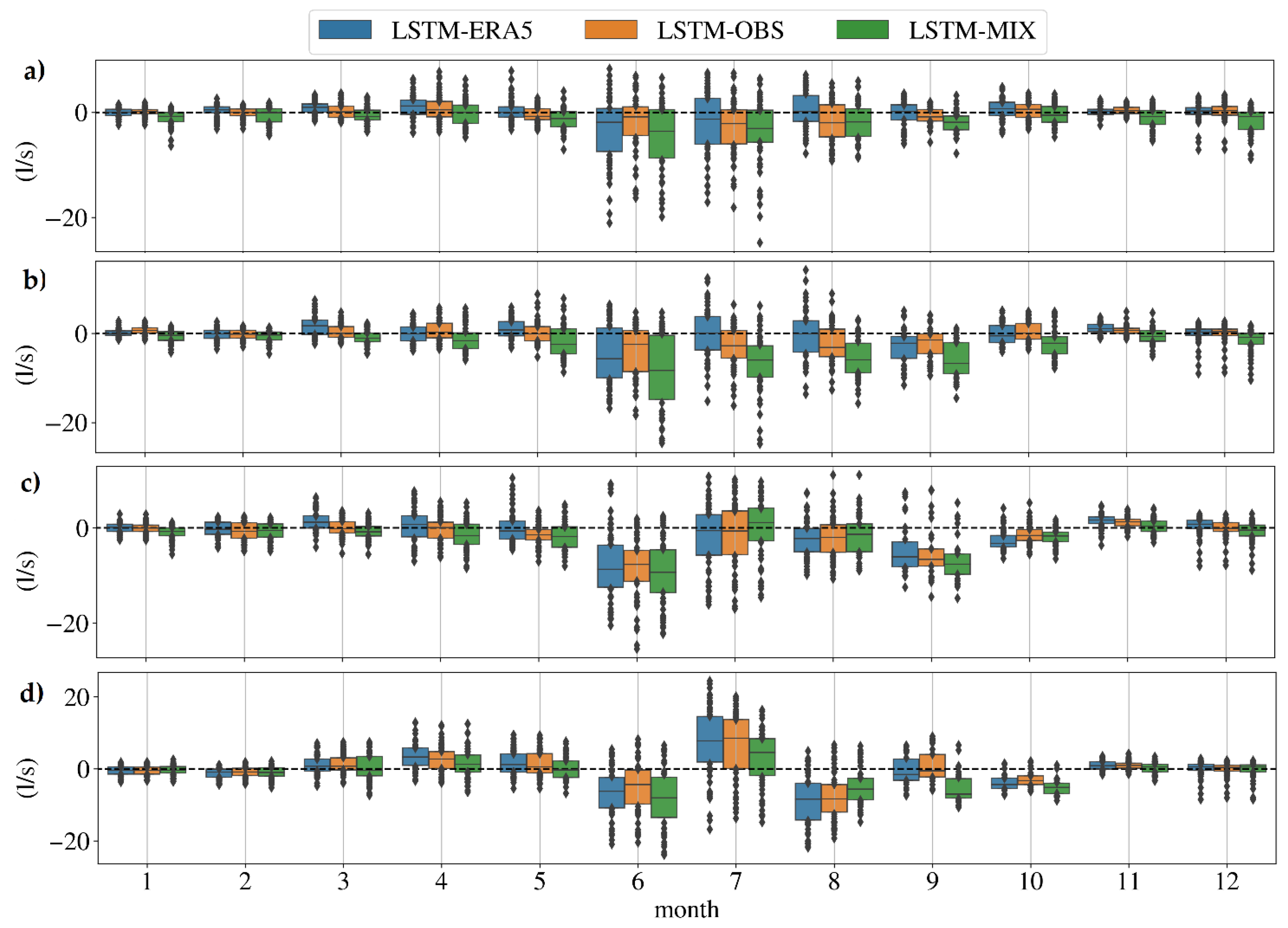
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sharif, M.N.; Haider, H.; Farahat, A.; Hewage, K.; Sadiq, R. Water–energy nexus for water distribution systems: A literature review. Environ. Rev. 2019, 27, 519–544. [Google Scholar] [CrossRef]
- Fuertes, P.C.; Alzamora, F.M.; Carot, M.H.; Campos, J.A. Building and exploiting a Digital Twin for the management of drinking water distribution networks. Urban Water J. 2020, 17, 704–713. [Google Scholar] [CrossRef]
- Laucelli, D.; Berardi, L.; Giustolisi, O. WDNetXL: Efficient Research Transfer for Management, Planning and Design of Water Distribution Networks. In Proceedings of the 11th International Conference on Hydroinformatics HIC 2014, New York, NY, USA, 17–21 August 2014. [Google Scholar]
- Butler, D.; Memon, F. Water Demand Management; IWA Publishing: London, UK, 2006. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M. Assessment of predictive uncertainty within the framework of water demand forecasting using the Model Conditional Processor (MCP). Urban Water J. 2017, 14, 1–10. [Google Scholar] [CrossRef]
- Meuleman, A.; Cirkel, G.; Zwolsman, G. When climate change is a fact! Adaptive strategies for drinking water production in a changing natural environment. Water Sci. Technol. 2007, 56, 137–144. [Google Scholar] [CrossRef]
- Delpla, I.; Jung, A.-V.; Baures, E.; Clement, M.; Thomas, O. Impacts of climate change on surface water quality in relation to drinking water production. Environ. Int. 2009, 35, 1225–1233. [Google Scholar] [CrossRef]
- Doll, P.; Jiménez-Cisneros, B.; Oki, T.; Arnell, N.; Benito, G.; Cogley, J.; Jiang, T.; Kundzewicz, Z.; Mwakalila, S.; Nishijima, A. Integrating risks of climate change into water management. Hydrol. Sci. J. 2015, 60, 4–13. [Google Scholar] [CrossRef] [Green Version]
- Joshi, N.; Tamaddun, K.; Parajuli, R.; Kalra, A.; Maheshwari, P.; Mastino, L.; Velotta, M. Future Changes in Water Supply and Demand for Las Vegas Valley: A System Dynamic Approach based on CMIP3 and CMIP5 Climate Projections. Hydrology 2020, 7, 16. [Google Scholar] [CrossRef] [Green Version]
- Babel, M.S.; Maporn, N.; Shinde, V.R. Incorporating Future Climatic and Socioeconomic Variables in Water Demand Forecasting: A Case Study in Bangkok. Water Resour. Manag. 2014, 28, 2049–2062. [Google Scholar] [CrossRef]
- Ougougdal, H.A.; Khebiza, M.Y.; Messouli, M.; Lachir, A. Assessment of Future Water Demand and Supply under IPCC Climate Change and Socio-Economic Scenarios, Using a Combination of Models in Ourika Watershed, High Atlas, Morocco. Water 2020, 12, 1751. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Ortega-Martorell, S.; Al-Bugharbee, H.; Olier, I.; Hashim, K.S.; Gharghan, S.K.; Kot, P.; Al-Khaddar, R. Urban Water Demand Prediction for a City That Suffers from Climate Change and Population Growth: Gauteng Province Case Study. Water 2020, 12, 1885. [Google Scholar] [CrossRef]
- Righetti, M.; Bort, C.M.G.; Bottazzi, M.; Menapace, A.; Zanfei, A. Optimal Selection and Monitoring of Nodes Aimed at Supporting Leakages Identification in WDS. Water 2019, 11, 629. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, E.G.; Zeleke, E.B.; Abebe, S.L. Water leakage detection and localization using hydraulic modeling and classification. J. Hydroinformatics 2021, 23, 782–794. [Google Scholar] [CrossRef]
- Menapace, A.; Zanfei, A.; Felicetti, M.; Avesani, D.; Righetti, M.; Gargano, R. Burst Detection in Water Distribution Systems: The Issue of Dataset Collection. Appl. Sci. 2020, 10, 8219. [Google Scholar] [CrossRef]
- Zanfei, A.; Menapace, A.; Santopietro, S.; Righetti, M. Calibration Procedure for Water Distribution Systems: Comparison among Hydraulic Models. Water 2020, 12, 1421. [Google Scholar] [CrossRef]
- Lima, G.M.; Brentan, B.M.; Manzi, D.; Luvizotto, E. Metamodel for nodal pressure estimation at near real-time in water distribution systems using artificial neural networks. J. Hydroinformatics 2018, 20, 486–496. [Google Scholar] [CrossRef]
- Xing, L.; Sela, L. Graph Neural Networks for State Estimation in Water Distribution Systems: Application of Supervised and Semisupervised Learning. J. Water Resour. Plan. Manag. 2022, 148, 4022018. [Google Scholar] [CrossRef]
- Giustolisi, O.; Savic, D.A. Advances in data-driven analyses and modelling using EPR-MOGA. J. Hydroinformatics 2009, 11, 225–236. [Google Scholar] [CrossRef]
- Guarnaccia, C.; Tepedino, C.; Viccione, G.; Quartieri, J. Short-Term Forecasting of Tank Water Levels Serving Urban Water Distribution Networks with ARIMA Models. In Frontiers in Water-Energy-Nexus—Nature-Based Solutions, Advanced Technologies and Best Practices for Environmental Sustainability; Springer: Berlin/Heidelberg, Germany, 2020; pp. 25–28. [Google Scholar] [CrossRef]
- Birylo, M.; Rzepecka, Z.; Kuczynska-Siehien, J.; Nastula, J. Analysis of water budget prediction accuracy using ARIMA models. Water Supply 2017, 18, 819–830. [Google Scholar] [CrossRef]
- Wei, S.; Lei, A.; Islam, S.N. Modeling and simulation of industrial water demand of Beijing municipality in China. Front. Environ. Sci. Eng. China 2010, 4, 91–101. [Google Scholar] [CrossRef]
- Guo, G.; Liu, S.; Wu, Y.; Li, J.; Zhou, R.; Zhu, X. Short-Term Water Demand Forecast Based on Deep Learning Method. J. Water Resour. Plan. Manag. 2018, 144, 4018076. [Google Scholar] [CrossRef]
- Rezaali, M.; Quilty, J.; Karimi, A. Probabilistic urban water demand forecasting using wavelet-based machine learning models. J. Hydrol. 2021, 600, 126358. [Google Scholar] [CrossRef]
- Du, B.; Zhou, Q.; Guo, J.; Guo, S.; Wang, L. Deep learning with long short-term memory neural networks combining wavelet transform and principal component analysis for daily urban water demand forecasting. Expert Syst. Appl. 2021, 171, 114571. [Google Scholar] [CrossRef]
- Niknam, A.; Zare, H.K.; Hosseininasab, H.; Mostafaeipour, A.; Herrera, M. A Critical Review of Short-Term Water Demand Forecasting Tools—What Method Should I Use? Sustainability 2022, 14, 5412. [Google Scholar] [CrossRef]
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Brentan, B.M.; Luvizotto, E., Jr.; Herrera, M.; Izquierdo, J.; Pérez-García, R. Hybrid regression model for near real-time urban water demand forecasting. J. Comput. Appl. Math. 2017, 309, 532–541. [Google Scholar] [CrossRef]
- Zanfei, A.; Menapace, A.; Granata, F.; Gargano, R.; Frisinghelli, M.; Righetti, M. An Ensemble Neural Network Model to Forecast Drinking Water Consumption. J. Water Resour. Plan. Manag. 2022, 148, 4022014. [Google Scholar] [CrossRef]
- Mu, L.; Zheng, F.; Tao, R.; Zhang, Q.; Kapelan, Z. Hourly and Daily Urban Water Demand Predictions Using a Long Short-Term Memory Based Model. J. Water Resour. Plan. Manag. 2020, 146, 5020017. [Google Scholar] [CrossRef]
- Kühnert, C.; Gonuguntla, N.; Krieg, H.; Nowak, D.; Thomas, J. Application of LSTM Networks for Water Demand Prediction in Optimal Pump Control. Water 2021, 13, 644. [Google Scholar] [CrossRef]
- Ajbar, A.; Ali, E.M. Prediction of municipal water production in touristic Mecca City in Saudi Arabia using neural networks. J. King Saud Univ. Eng. Sci. 2015, 27, 83–91. [Google Scholar] [CrossRef] [Green Version]
- Bata, M.H.; Carriveau, R.; Ting, D.S.-K. Short-Term Water Demand Forecasting Using Nonlinear Autoregressive Artificial Neural Networks. J. Water Resour. Plan. Manag. 2020, 146, 04020008. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Adamowski, J. Urban water demand forecasting and uncertainty assessment using ensemble wavelet-bootstrap-neural network models. Water Resour. Res. 2013, 49, 6486–6507. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Adamowski, J.F. Medium-Term Urban Water Demand Forecasting with Limited Data Using an Ensemble Wavelet–Bootstrap Machine-Learning Approach. J. Water Resour. Plan. Manag. 2015, 141, 04014053. [Google Scholar] [CrossRef] [Green Version]
- Shah, S.; Hosseini, M.; Ben Miled, Z.; Shafer, R.; Berube, S. A Water Demand Prediction Model for Central Indiana. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–3 February 2018; Volume 32. [Google Scholar] [CrossRef]
- Roushangar, K.; Alizadeh, F. Investigating effect of socio-economic and climatic variables in urban water consumption prediction via Gaussian process regression approach. Water Sci. Technol. Water Supply 2017, 18, 84–93. [Google Scholar] [CrossRef] [Green Version]
- Parandvash, G.H.; Chang, H. Analysis of long-term climate change on per capita water demand in urban versus suburban areas in the Portland metropolitan area, USA. J. Hydrol. 2016, 538, 574–586. [Google Scholar] [CrossRef]
- Stelzl, A.; Pointl, M.; Fuchs-Hanusch, D. Estimating Future Peak Water Demand with a Regression Model Considering Climate Indices. Water 2021, 13, 1912. [Google Scholar] [CrossRef]
- Fiorillo, D.; Kapelan, Z.; Xenochristou, M.; De Paola, F.; Giugni, M. Assessing the Impact of Climate Change on Future Water Demand using Weather Data. Water Resour. Manag. 2021, 35, 1449–1462. [Google Scholar] [CrossRef]
- Bakker, M.; van Duist, H.; van Schagen, K.; Vreeburg, J.; Rietveld, L. Improving the Performance of Water Demand Forecasting Models by Using Weather Input. Procedia Eng. 2014, 70, 93–102. [Google Scholar] [CrossRef] [Green Version]
- Zubaidi, S.L.; Gharghan, S.K.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M. Short-Term Urban Water Demand Prediction Considering Weather Factors. Water Resour. Manag. 2018, 32, 4527–4542. [Google Scholar] [CrossRef]
- Parker, W.S. Reanalyses and Observations: What’s the Difference? Bull. Am. Meteorol. Soc. 2016, 97, 1565–1572. [Google Scholar] [CrossRef] [Green Version]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Olauson, J. ERA5: The new champion of wind power modelling? Renew. Energy 2018, 126, 322–331. [Google Scholar] [CrossRef] [Green Version]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-De-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Johnson, S.J.; Stockdale, T.N.; Ferranti, L.; Balmaseda, M.A.; Molteni, F.; Magnusson, L.; Tietsche, S.; Decremer, D.; Weisheimer, A.; Balsamo, G.; et al. SEAS5: The new ECMWF seasonal forecast system. Geosci. Model Dev. 2019, 12, 1087–1117. [Google Scholar] [CrossRef] [Green Version]
- Ghiassi, M.; Zimbra, D.K.; Saidane, H. Urban Water Demand Forecasting with a Dynamic Artificial Neural Network Model. J. Water Resour. Plan. Manag. 2008, 134, 138–146. [Google Scholar] [CrossRef]
- Antunes, A.; Andrade-Campos, A.; Sardinha-Lourenço, A.; Oliveira, M. Short-term water demand forecasting using machine learning techniques. J. Hydroinformatics 2018, 20, 1343–1366. [Google Scholar] [CrossRef] [Green Version]
- Gagliardi, F.; Alvisi, S.; Kapelan, Z.; Franchini, M. A Probabilistic Short-Term Water Demand Forecasting Model Based on the Markov Chain. Water 2017, 9, 507. [Google Scholar] [CrossRef]
- Mouatadid, S.; Adamowski, J. Using extreme learning machines for short-term urban water demand forecasting. Urban Water J. 2016, 14, 630–638. [Google Scholar] [CrossRef]
- Haque, M.; Rahman, A.; Hagare, D.; Chowdhury, R.K. A Comparative Assessment of Variable Selection Methods in Urban Water Demand Forecasting. Water 2018, 10, 419. [Google Scholar] [CrossRef] [Green Version]
- Behboudian, S.; Tabesh, M.; Falahnezhad, M.; Ghavanini, F.A. A long-term prediction of domestic water demand using preprocessing in artificial neural network. J. Water Supply Res. Technol. 2013, 63, 31–42. [Google Scholar] [CrossRef]
- Adamowski, J.; Chan, H.F.; Prasher, S.O.; Ozga-Zielinski, B.; Sliusarieva, A. Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 2012, 48, W01528. [Google Scholar] [CrossRef]
- Polebitski, A.S.; Palmer, R.N. Seasonal Residential Water Demand Forecasting for Census Tracts. J. Water Resour. Plan. Manag. 2010, 136, 27–36. [Google Scholar] [CrossRef]
- Zanfei, A.; Brentan, B.M.; Menapace, A.; Righetti, M. A short-term water demand forecasting model using multivariate long short-term memory with meteorological data. J. Hydroinformatics 2022, 24, 1053–1065. [Google Scholar] [CrossRef]
- Menapace, A.; Zanfei, A.; Righetti, M. Tuning ANN Hyperparameters for Forecasting Drinking Water Demand. Appl. Sci. 2021, 11, 4290. [Google Scholar] [CrossRef]
- Chollet, F.; Watson, M.; Bursztein, E.; Zhu, Q.S.; Jin, H. Keras. 2015. Available online: https://keras.io/getting_started/faq/#how-should-i-cite-keras (accessed on 5 January 2023).
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
| Case Study 1 | Case Study 2 | |
|---|---|---|
| Number of Inhabitants | 861 | 20,482 |
| Mean (L/s) | 3.53 | 49.57 |
| Standard deviation (L/s) | 0.56 | 6.70 |
| Minimum (L/s) | 2.53 | 36.25 |
| Q1/4 (L/s) | 3.13 | 44.50 |
| Q1/2 (L/s) | 3.39 | 48.03 |
| Q3/4 (L/s) | 3.80 | 52.94 |
| Maximum (L/s) | 6.15 | 76.81 |
| Humidity (%) | Radiation (kJ m−2) | Temperature (°C) | ||||
|---|---|---|---|---|---|---|
| ERA5 | OBS | ERA5 | OBS | ERA5 | OBS | |
| Mean | 72.40 | 65.93 | 542.88 | 520.69 | 9.94 | 13.20 |
| Standard deviation | 12.24 | 16.79 | 777.22 | 851.88 | 7.15 | 7.61 |
| Minimum | 33.65 | 1.04 | 0.00 | 0.00 | −9.24 | −3.55 |
| Q1/4 | 63.96 | 55.08 | 0.00 | 0.00 | 3.74 | 6.44 |
| Q1/2 | 72.99 | 65.93 | 24.13 | 0.10 | 10.21 | 13.59 |
| Q3/4 | 81.39 | 77.89 | 972.18 | 806.82 | 16.06 | 19.60 |
| Maximum | 98.99 | 100.00 | 3443.94 | 3932.30 | 26.36 | 30.15 |
| Time Horizon | 7 Days | 14 Days | 30 Days | 60 Days |
|---|---|---|---|---|
| Number of layers | 3 | 3 | 3 | 3 |
| Number of units | 48-72-48 | 48-72-48 | 32-48-32 | 32-48-32 |
| Activation function | tanh/sigmoid | tanh/sigmoid | tanh/sigmoid | tanh/sigmoid |
| Optimiser | Adam | Adam | Adam | Adam |
| Loss function | mse | mse | mse | mse |
| Number of epochs | 100 | 100 | 150 | 200 |
| Case Study 1 | Case Study 2 | ||||
|---|---|---|---|---|---|
| Meteo | MAPE (%) | MAE (L/s) | MAPE (%) | MAE (L/s) | |
| 7 days | LSTM-OBS | 6.16 | 0.23 | 3.49 | 1.89 |
| LSTM-ERA5 | 6.51 | 0.24 | 3.88 | 2.10 | |
| LSTM-MIX | 8.20 | 0.31 | 4.60 | 2.49 | |
| 14 days | LSTM-OBS | 6.47 | 0.24 | 4.14 | 2.25 |
| LSTM-ERA5 | 6.93 | 0.25 | 4.84 | 2.62 | |
| LSTM-MIX | 9.16 | 0.34 | 6.62 | 3.67 | |
| 30 days | LSTM-OBS | 7.86 | 0.29 | 5.47 | 3.02 |
| LSTM-ERA5 | 8.44 | 0.31 | 6.07 | 3.29 | |
| LSTM-MIX | 8.88 | 0.33 | 5.88 | 3.23 | |
| 60 days | LSTM-OBS | 9.29 | 0.34 | 7.29 | 3.95 |
| LSTM-ERA5 | 9.80 | 0.36 | 7.75 | 4.22 | |
| LSTM-MIX | 9.68 | 0.36 | 7.24 | 3.93 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhawan, P.; Dalla Torre, D.; Zanfei, A.; Menapace, A.; Larcher, M.; Righetti, M. Assessment of ERA5-Land Data in Medium-Term Drinking Water Demand Modelling with Deep Learning. Water 2023, 15, 1495. https://doi.org/10.3390/w15081495
Dhawan P, Dalla Torre D, Zanfei A, Menapace A, Larcher M, Righetti M. Assessment of ERA5-Land Data in Medium-Term Drinking Water Demand Modelling with Deep Learning. Water. 2023; 15(8):1495. https://doi.org/10.3390/w15081495
Chicago/Turabian StyleDhawan, Pranav, Daniele Dalla Torre, Ariele Zanfei, Andrea Menapace, Michele Larcher, and Maurizio Righetti. 2023. "Assessment of ERA5-Land Data in Medium-Term Drinking Water Demand Modelling with Deep Learning" Water 15, no. 8: 1495. https://doi.org/10.3390/w15081495







