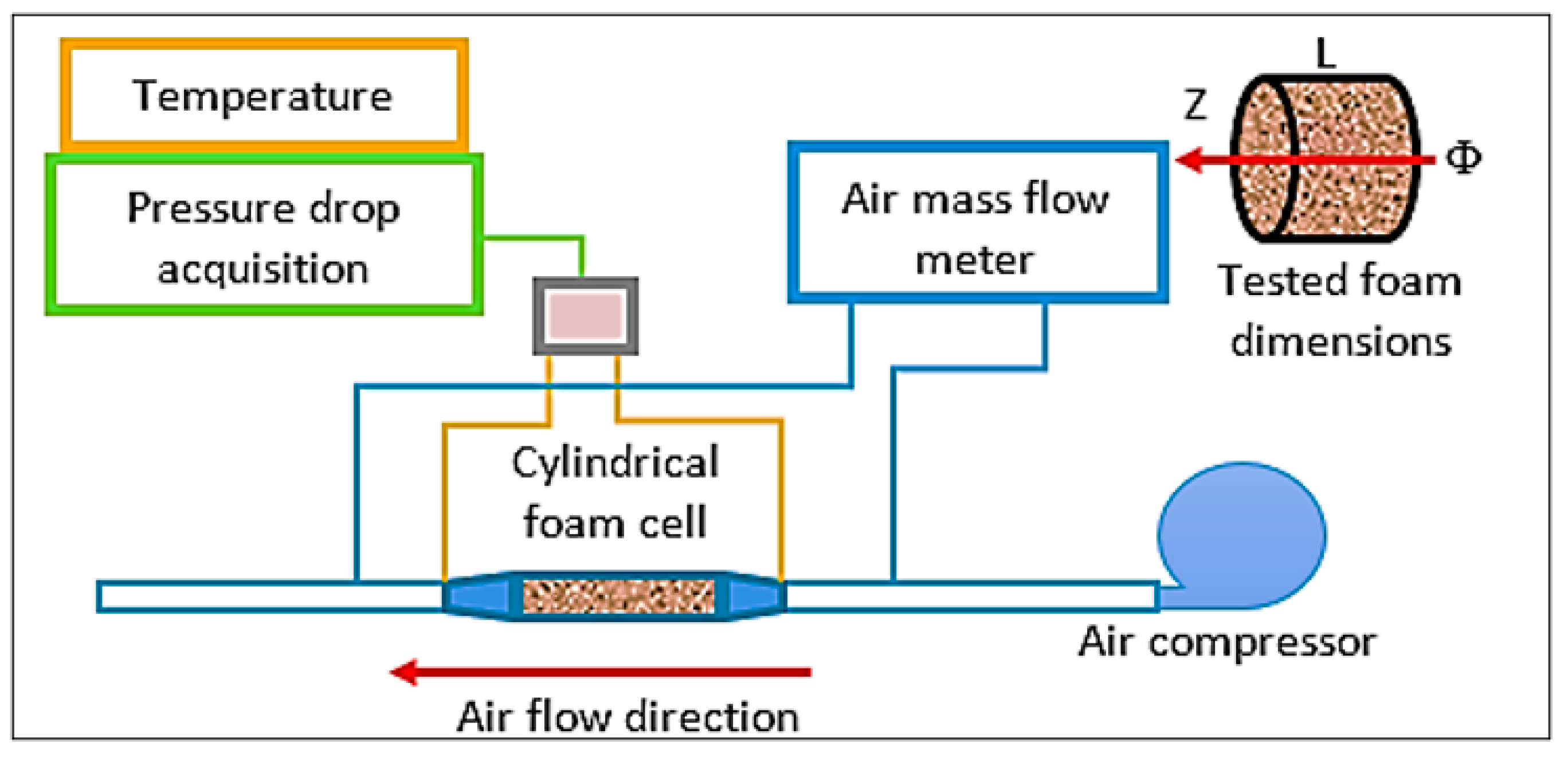
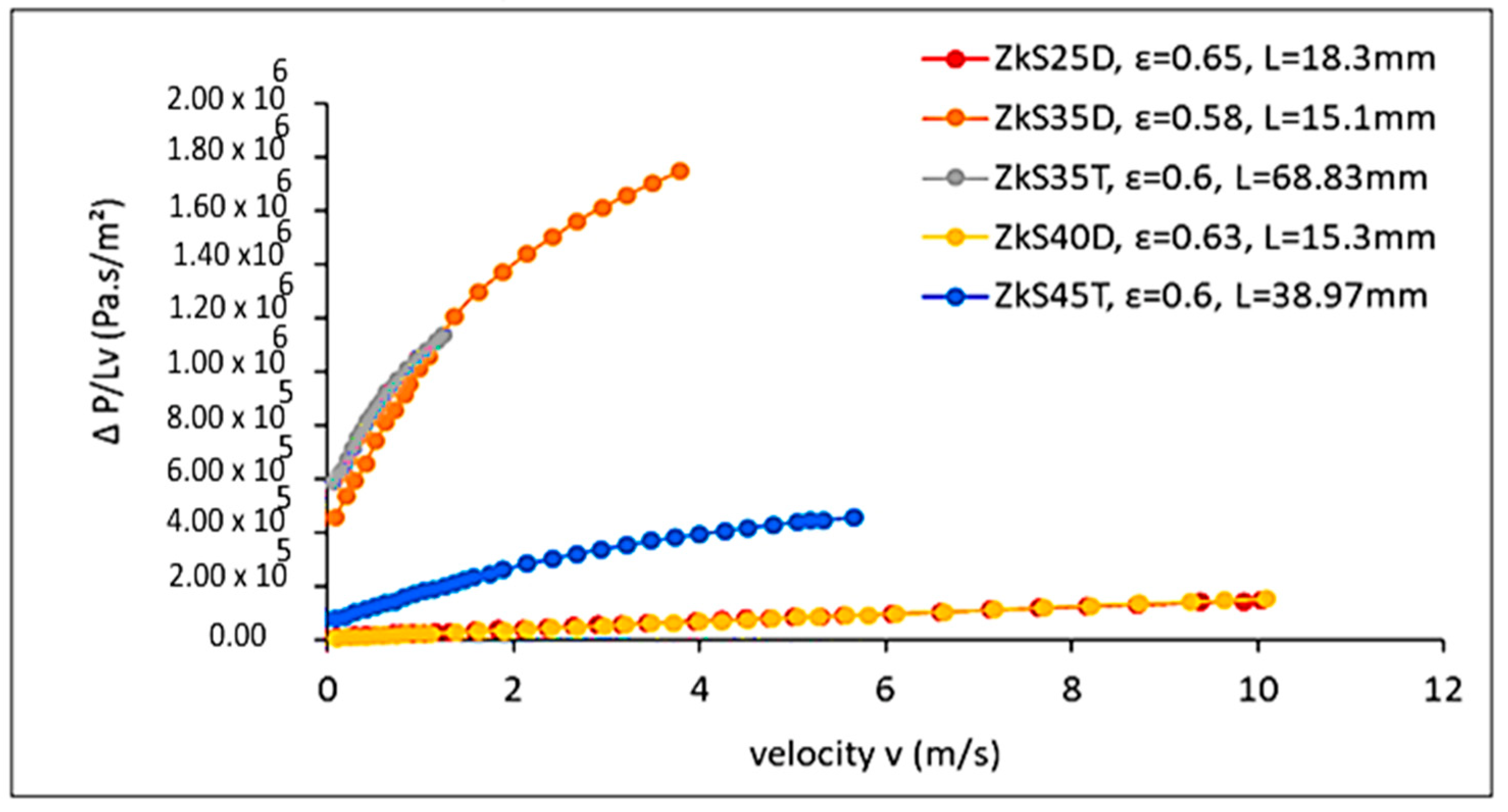
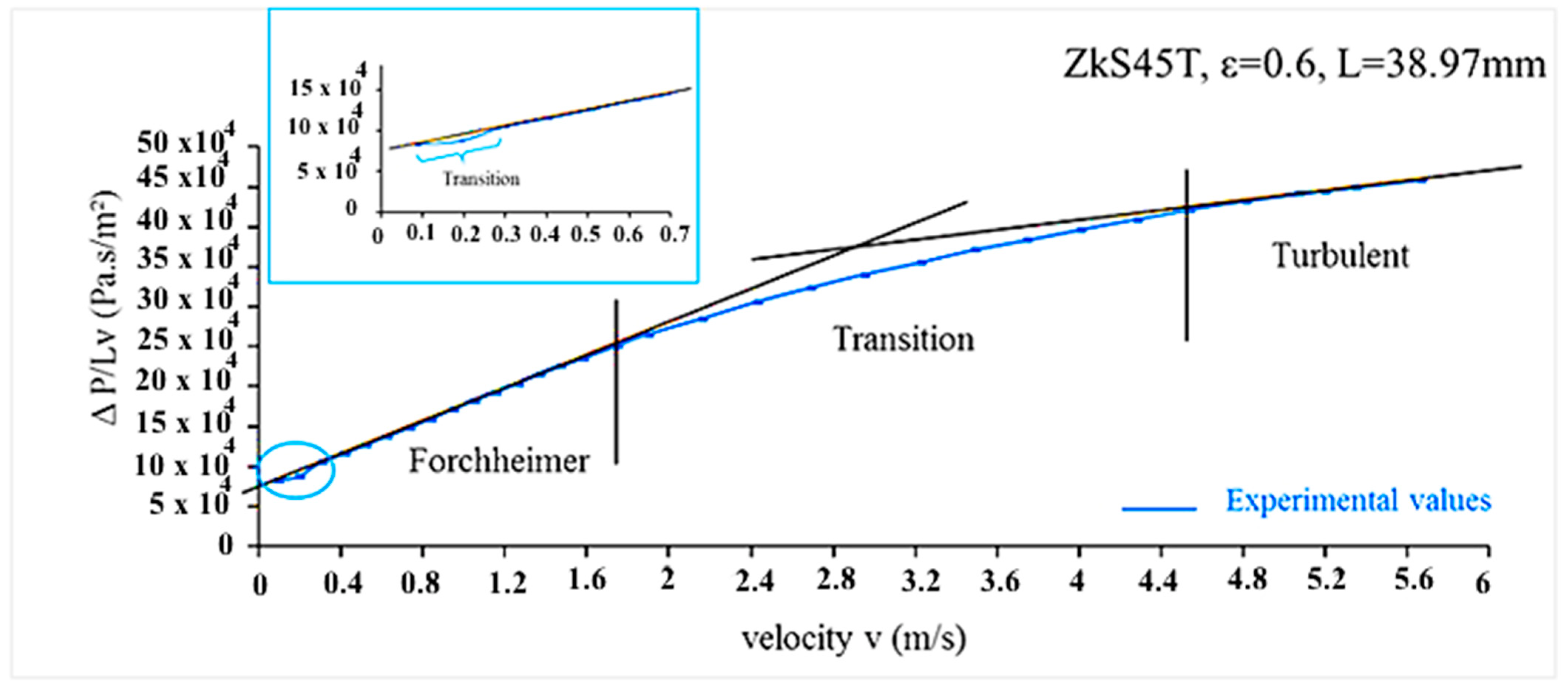
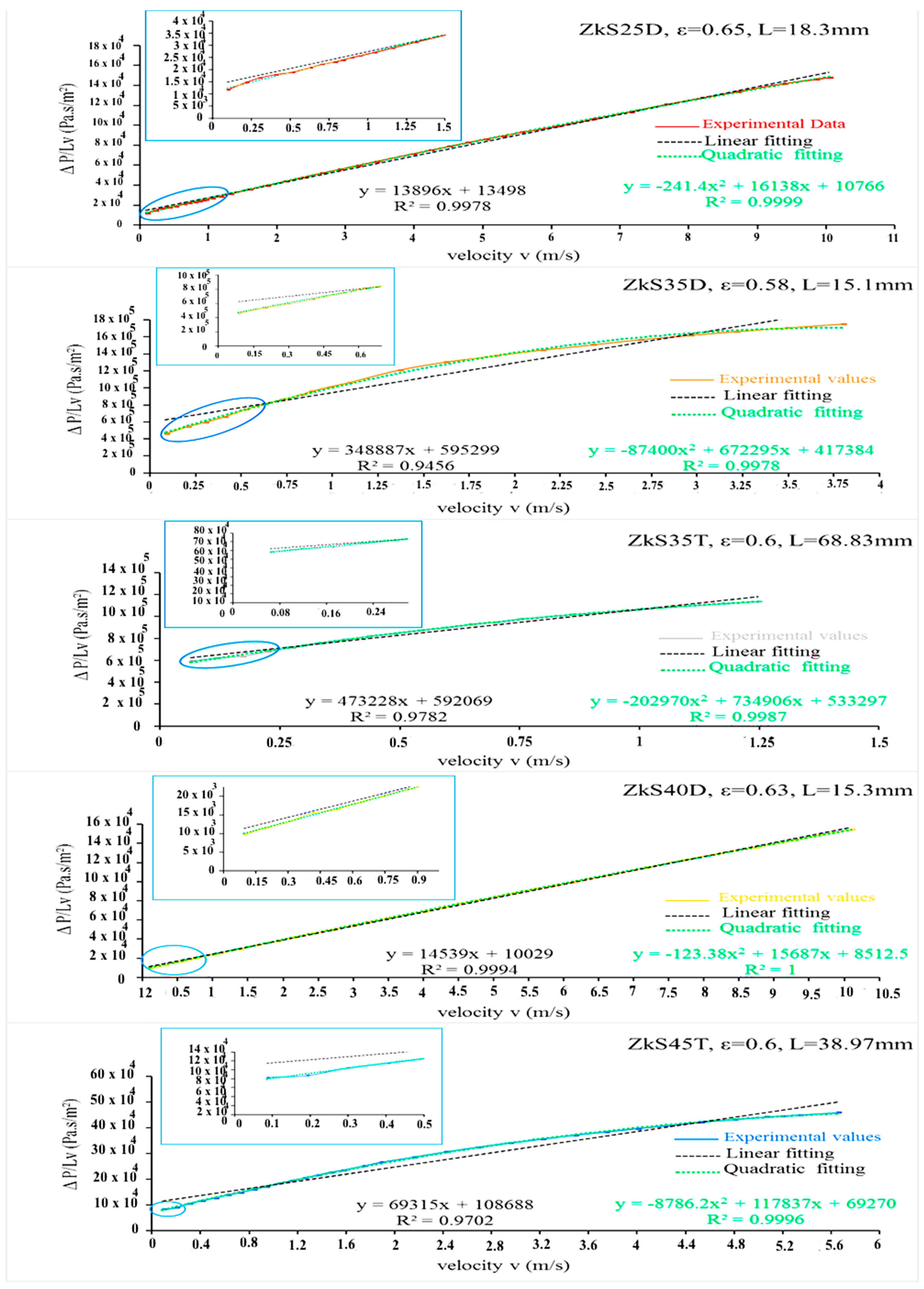
Flow Laws
Permeability indicates the material’s ability to allow the passage of a fluid, and each porous medium has its own permeability. If the open-cell metal foam had lower resistance to fluid flow through, the energy spent on driving it is lower. With known permeability for a particular porous medium, the control of fluid flow, internal residual time, optimal flow analysis, and practical designs can be carried out.
The permeability of open-cell porous materials has been the subject of several prior investigations. Special attention was given to low-density microcellular metals of the type derived from polyurethane foams: rigid and “hyperporous” materials [
16] made with the best thermal or electrical conductors or noble materials for special applications. However, understanding fluid flow performance in porous materials with a porosity between 0.4 and 0.8 is necessary. This paper contributes experimentally to improve this understanding.
Recently, there was a general agreement on the classification of flow regimes in porous media. According to this classification, flow regimes are generally characterized by the dimensionless number (the Reynolds number (Re)), which has the following changes (from small to large Re): Darcy, transition from Darcy to Forchheimer (Weak inertia), Forchheimer (strong inertia), transition from Forchheimer to turbulence (we will call it strong transition), and turbulence [
17]. Some researchers [
15,
18,
19] reported the existence of a pre-Darcy regime at very low velocity whose data are very scarce because of the difficulty of measuring an ultra-low pressure drop and velocity.
The Reynolds number Re based on cell diameter (D
C) is defined by Equation (1)
where
ρ is the fluid density, which is air (kg m
−3) in this study,
v is the superficial velocity (known also as seepage velocity or Darcy velocity) (m s
−1), l is the characteristic length (D
C in this case) (m), μ is the dynamic viscosity of air (kg m
−1s
−1), and
ν is the kinematic viscosity of air (m²s
−1).
The flow at very low Reynolds (creeping flow) is governed by the famous Darcy’s law (Equation (2)), which assumes that viscous forces dominate over inertial forces in porous media; hence, inertial forces can be neglected:
where Δ
P/
L is the pressure drop along the main flow z-direction,
v is Darcy’s velocity, and
K (m
2) is the Darcy’s permeability of the foam of length
L (m). It is obvious that this relation is linear in terms of
v but only for lower velocities (
v < 1 m s
−1); then permeability can be deduced knowing
μ. Creeping flows are difficult to sustain in the laboratory, and measurements of velocity and pressure drop are challenging, as these quantities may be too small to capture with good accuracy using common instruments, as stated by Dukhan [
20], which is the case in this study.
For high Reynolds numbers (strong inertia regime), the empirical Forchheimer–Dupuit equation expressed by Equation (3) is often used in homogeneous porous media. Thus, Equation (2) became the sum of two terms: a viscous (
v, Darcy’s law) term and an inertia (
v²) term
Equation (3) can be rearranged to Equation (4)
where K is the Forchheimer permeability,
β is the inertia coefficient or the Forchheimer coefficient or form drag coefficient (m
−1), and ρ is the fluid (air) density in (kg m
−3). The coefficient
β represents the blockage of the internal structure (ligaments, nodes, and occasional closed faces of open-cell metal foam) to the flow.
Mauroy et al. [
21] reported a major problem when working on modelling flow through trees that arises from the fact that, due to inertial effects, Darcy’s law breaks down as a phenomenological description for large Reynolds numbers. Even at moderate Reynolds numbers, the inertial nonlinearities become relevant as compared to viscous effects. Firoozabadi et al. [
22] concluded that Darcy’s law is inadequate to represent high-velocity flow and that the effect of gas properties does not account for high-velocity flow in porous media.
Andrade Jr et al. [
23] investigated the origin of the deviations from the classical Darcy’s law by numerical simulation of the Navier–Stokes equations in two-dimensional disordered porous media. They applied the Forchheimer equation as a phenomenological model to correlate variations of the friction factor for different porosities and flow conditions. At sufficiently high Reynolds numbers, when inertia becomes relevant, they observed a transition from linear to nonlinear behaviour, which is typical of experiments. They found that such a transition can be understood and statistically characterized in terms of the spatial distribution of kinetic energy in the system. Then they concluded that the Forchheimer model should be valid for low Re and also for a limited range of high Re numbers, even when inertial nonlinearities can significantly affect the momentum transport at the pore scale.
Coulaud et al. [
24] numerically solved the flow equations at a pore scale by introduction of a nonlinear term into Darcy’s equation (Equation (3)) to describe inertial effects in a porous medium modelled by cylinders of either equal or unequal diameters arranged in a regular pattern with a square or triangular base. This work corroborated certain experiments by confirming that Darcy’s and Forchheimer’s laws were only valid in well-established ranges of Reynolds numbers.
However, Takhanov [
25] and Skjetne and Auriault [
26] explained that as the flow rate (Reynolds number) increases, inertial forces become more significant, and Darcy’s law is generally corrected by a cubic term as in Equation (5)
where
K is the foam’s permeability (Darcy permeability) (m
2),
C is the weak inertia factor or dimensionless
C—cubic factor (-). Weak inertia is a regime in which the inertial force is of the same order as the viscous force.
Sivanesapillai et al. [
27], when discussing numerical results for macroscopically steady and unidirectional flow through a rigid fully saturated fibrous porous medium for Re up to 10
3, claimed that the necessity of using a cubic transition equation in the weak inertia regime, where the Forchheimer equation is often observed to fail, was quite possibly due to the fact that 𝛾 > 1 for certain pore space morphologies (while 𝛾 was a free parameter dictating the effective width of inertial transition).
Lage et al. [
16] tried fitting their experimental results with a cubic law of the form in Equation (6)
where the cubic term coefficient
C had the units (Pa s
3 m
−4). They found that the permeability and the inertia coefficients were the same as the ones obtained interpolating the low velocity range. Thus, they concluded that the fitting of the high-velocity range was affected only by the cubic term.
Panfilov and Fourar [
28] described an explicit model for the high flow rate obtained by Bues et al. in [
29] when working on a macroscale model and viscous–inertia effects for Navier–Stokes flow in a radial fracture with corrugated walls, which was conducted by asymptotic expansions over a channel diameter that was much smaller than the channel length. The obtained series for a corrugated channel revealed a full cubic law for moderate Re~1–10 given by Equation (7)
where the new parameters β′ and α′ can be negative or positive depending on channel geometry.
A general cubic formula including quadratic term, shown in Equation (8), has also been proposed by [
16,
30,
31] to better depict flow in this transitional regime
where C
1 and C
2 are dimensionless experimental parameters.
Rojas and Koplik [
30] studied the flow of an incompressible liquid at a nonzero Reynolds number Re in a two-dimensional model porous medium via numerical simulation. The geometry was a random array of cylinders of square cross section. Additionally, they re-casted the reduced pressure drop equation (Equation (7)) into a fully dimensionless form using the Reynolds number based on the square root of permeability by defining a dimensionless pressure gradient normalized to Darcy flow (F) as F = 1 + b (Re) + c (Re)², where the coefficients b and c are dimensionless. A transition from linear Darcy flow at vanishing Re to a cubic transitional regime at low Re, and then a quadratic Forchheimer was found when Re = 1.
Venkataraman and Rao [
32] demonstrated that the empirical power law of the form proposed by Missbach [
33], as given in Equation (9), was simple in form and accurate enough to describe the behaviour of flow through porous media at large Reynolds numbers in practical field problems
where
i is the hydraulic gradient,
b is a coefficient depending upon the fluid and porous media properties, and
m is an index; they are both to be determined experimentally. This law was not investigated during this study.
The conclusion is that the creeping flow and Forchheimer flow have been understood quite well in various porous media with different fluids, and various reasons were suggested by different researchers cited in [
28] to explain the nonlinear relationship between pressure gradient and superficial velocity, but the situation at higher velocities has received less attention for relatively dense foams such as the ESR foams, which are the subject of this study.
All previous laws described very well packed beds and hyper-porous materials, and many outcomes have been established among what was reported. For instance, a single sample displayed completely distinct permeability constants depending only on the range of data chosen for analysis, and the Darcian permeability constant
K had higher variation than the non-Darcian permeability constants [
34].
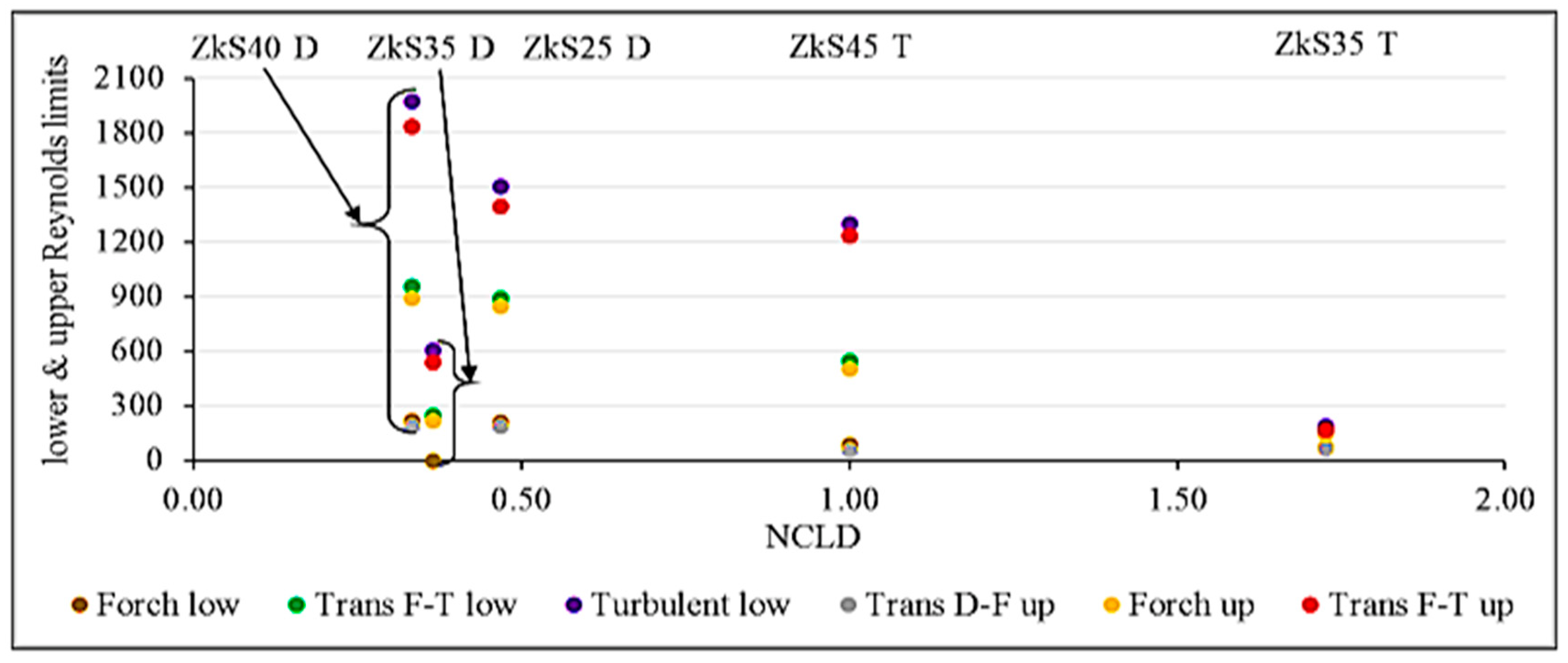
In this paper, various air flow regimes were analysed, and their boundaries were established for the ESR foams. Works dedicated to such a delimitation of fluid flow regimes through such metal foams are very scarce. Among the most recent and modest studies purposely geared toward establishing various flow regimes from pre-Darcy to turbulent in porous media include the following: Yang et al. [
35] experimentally investigated the flow domain division in beds packed with differently sized particles; Kundu et al. [
36] investigated the flow in homogeneous and mixed isotropic porous media; Dukhan et al. [
19] investigated the flow in 20 ppi/87% porous metal foams; and Chai et al. [
31] investigated the flow in disordered porous media.
In fact, the pressure drop in a porous medium is supposed to be due to two effects related to the energy losses caused by both viscous and inertial attrition [
37]. Different contributions of these last two effects on behaviour in open-cell foams made by the ESR process are to be expected because of their proper intrinsic rigid matrix and moderate porosity situated between packed beds (ε < 0.4) and hyper-porous materials (ε > 0.9).
To simplify the calculations, it is assumed that:
The flow is horizontal and uniform all along the main flow z-direction (Figure 2);
Air is treated as a monophasic Newtonian fluid;
The dense wall effect in our case is neglected because the tested foams are relatively dense [
2];
The static gas pressure was constant throughout the porous medium and was equal to the difference between the inlet and outlet pressures of the test section.
Among the abundant literature on the calculation of the permeability K and the inertia coefficient C, there is no explicit agreement on the method of their calculations, and many discrepancies exist. This led Dukhan and Minjeur [
38] to insist on the necessity of a distinction between the Darcy and Forchheimer permeabilities that was usually either absent or overlooked in several studies, which may lead to significant errors. This was also claimed earlier by Innocentini et al. [
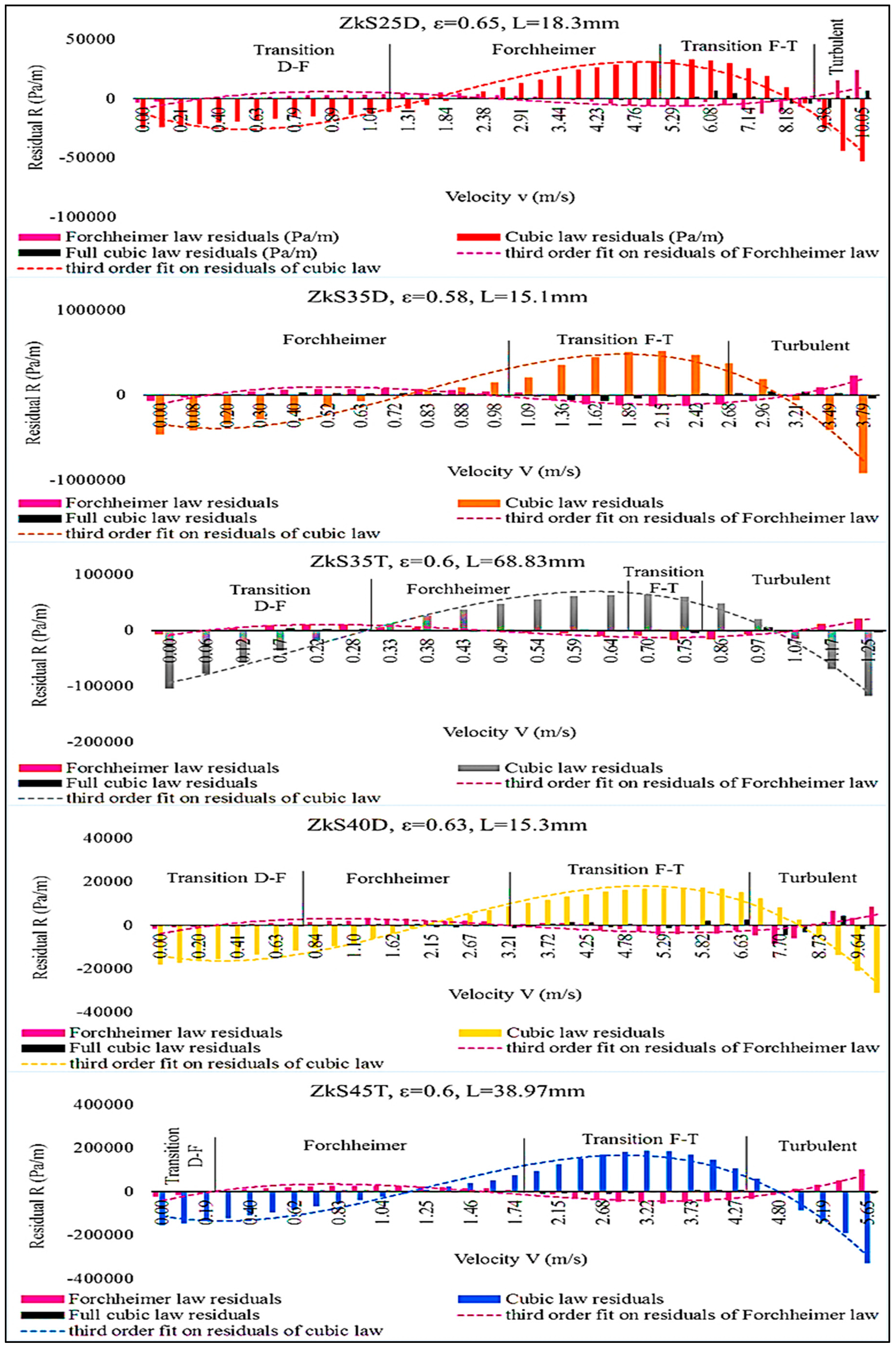
37] when they said that if experimental results were used only to predict permeability within a short range of low velocity, then the Darcian permeability term was reliable. On the other hand, if prediction of pressure drop at a higher flow rate was the purpose, errors could be high depending only on the velocity chosen. The current study compared three air flow laws: Forchheimer (Equation (4)), cubic (Equation (5)), and full cubic laws (Equation (8)). It also determined which law best describes the flow through the ESR foams using the minimum residuals method, as was conducted in [
19]. However, the first step was to carefully delimit the flow regime in terms of superficial velocity for all foams. The permeability and fluid transport properties through these foams were obtained from least-squares fitting of the full cubic equation, and they are discussed.