1. Introduction
A hydraulic transient corresponds to an intermediate state between two stationary flows, generated by valve maneuvers, pumps or turbines. This phenomenon can occur not only in water supply systems, but also in hydropower systems, the aircraft industry, railways tunnels, etc. [
1,
2,
3]. Hydraulic transient analysis is particularly important in the design stage of pressurized systems in order to specify the pipe material and wall thickness, and, whenever necessary, to design surge protection devices.
Classic transient analysis, considering steady-state friction formulas (amongst other assumptions), is commonly used for design purposes, as it describes the maximum and minimum pressure variations reasonably well [
2,
3,
4]. However, these models cannot accurately represent the complete transient phenomenon due to the wave propagation and complex diffusion mechanisms that significantly affect the pressure wave dissipation, dispersion and shape. This is particularly relevant in fast and high-frequency transient events, in which unsteady friction has a dominant effect [
5,
6]. Several efforts have been made to develop models with more accurate, simpler and lower computational demands, and the description of energy dissipation in pressurized transient flows has been a major challenge over the past decades; these models can be one-dimensional (1D), two-dimensional (2D) and three dimensional (3D) models, as briefly described in the following paragraphs.
In 1D models, several formulations have been proposed to compute unsteady friction for both laminar [
5,
7,
8,
9] and turbulent flows [
10,
11,
12,
13,
14,
15]. These formulations can be classified as instantaneous acceleration-based [
16,
17,
18] or convolution-based [
5,
9,
14,
19,
20,
21,
22]. Acceleration-based approaches introduce an additional term relating the local and the convective acceleration to the momentum equation. This formulation is quick to compute, but has a low accuracy; some formulations (e.g., [
16,
17,
18]) must be calibrated based on experimental results. Convolution-based formulations consider the complete history of the local acceleration. This approach is consistent and theoretically more robust, but is very time-consuming, which is why several approximate solutions have been developed (e.g., [
12,
20,
22]).
Axisymmetric models, also referred as quasi-two-dimensional models (Q2D), have been traditionally considered a good compromise between accuracy and computational time [
6,
23]. Q2D models have demonstrated consistency, regarding the physics of the phenomenon, and numerical robustness, ensuring the calculation of energy dissipation with high accuracy. More efficient versions than that initially proposed by Vardy and Hwang [
6] have also been developed [
24,
25,
26,
27]. A second promising feature is the enhanced definition of the radial grid, which can ensure higher accuracy simulations with fewer cylinders and reduced computation time.
Finally, tri-dimensional computational fluid dynamics (3D-CFD) models, integrating turbulent models, are the most powerful and comprehensive hydraulic analysis models in pressurized pipes, though extremely computationally expensive in terms of time and data storage for regular use in engineering practice [
28,
29,
30,
31,
32].
In any numerical model (1D, Q2D or 3D-CFD), the mesh size and configuration strongly affects the computational effort, as well as the accuracy of the results [
6,
33]. Not so intuitive, but equally important, is that the mesh must adapt to geometrical boundaries and to the flow physics to ensure that the velocity variation is of the same order along the numerical mesh. In practice, a non-uniform grid should be generated, with a higher resolution near the pipe wall, due to the high gradients observed. Calibrating the grid according to the velocity gradient history can reduce the number of mesh points at the same accuracy level [
34]. Q2D models have a high potential for future improvements, particularly as concerns the mesh definition and optimization to be used in engineering practice.
This paper aims at the assessment of radial mesh influence on the computation of unsteady energy dissipation in pressurized pipes using a Q2D model. An extensive numerical analysis of the effect of the numerical schemes and of the radial mesh on the computation of unsteady energy is carried out. Several radial meshes are defined, as a compromise between flow dynamics and total mesh points. A comprehensive analysis and comparison of the Q2D results obtained with experimental data with results from 1D model are conducted for laminar flows and for two valve closure maneuvers (i.e., an instantaneous and a S-shape closure).
The key innovative features of the current paper are: (i) the analysis of a new optimized equal-area mesh (divided into high and low-resolution regions) applying transient laminar flows created by an instantaneous valve closure; (ii) the application of the new mesh to transient tests observed in an experimental facility, created by a S-shaped valve closure; and (iii) the assessment of the advantages of neglecting the lateral velocity transfer for both instantaneous and calibrated valve maneuvers.
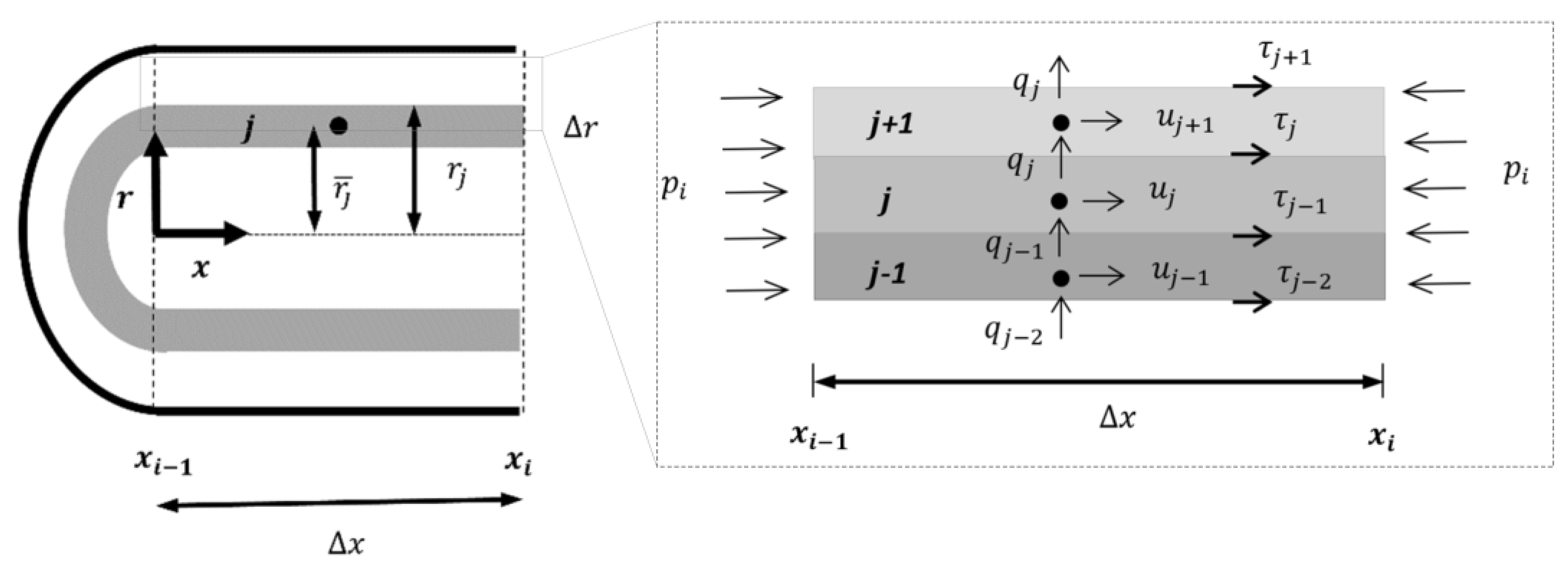
3. Experimental Facility Description
Transient tests for laminar flow conditions were carried out in the experimental facility assembled at the Laboratory of Hydraulics and Water Resources of the Instituto Superior Técnico (
Figure 3). These tests were conducted for a discharge of 0.016 L/s, corresponding to a Reynolds number (
Re = UD/ν) equal to 1000. Water was at 20 °C with a density
ρ = 1000 kg/m
3 and a kinematic viscosity
ν = 1.01 × 10
−6 m
2/s.
The system has a reservoir-pipe-valve configuration, with a rigidly supported straight copper pipe with an inner diameter,
D, of 20 mm, wall thickness,
e, of 0.001 m and a total length,
L, of 15.2 m. A centrifugal pump with a hydro-pneumatic vessel is installed at the upstream end of the pipe to simulate a constant level reservoir. Two in-line ball valves are installed at the downstream end of the pipe: one valve, manually actuated, is used to control the flow rate and the other valve, pneumatically actuated, is used to generate the transient event. Different closure times are attained by varying the operating pressure of the pneumatic valve [
36].
The data acquisition system (DAS) is composed of a computer, a Picoscope 3424 oscilloscope, a trigger-synchronizer, an electromagnetic flowmeter (with a 0.4% accuracy) and two strain-gauge type pressure transducers (WIKA S-10, 25 bars nominal pressure and 0.25% full-scale span accuracy). The first transducer is at the upstream end of the ball valve and the second is at the pipe mid-length.
The experimental wave speed,
c, estimated based on the travelling time of the pressure wave between the two transducers, is 1250 m/s, which is consistent with values of previous studies carried out in the same experimental facility [
36,
37,
38,
39,
40,
41].
The valve closure law of the ball valve was thoroughly studied by Ferreira et al. [
36]. The authors concluded that, despite the valve total closure time being higher than the system characteristic time,
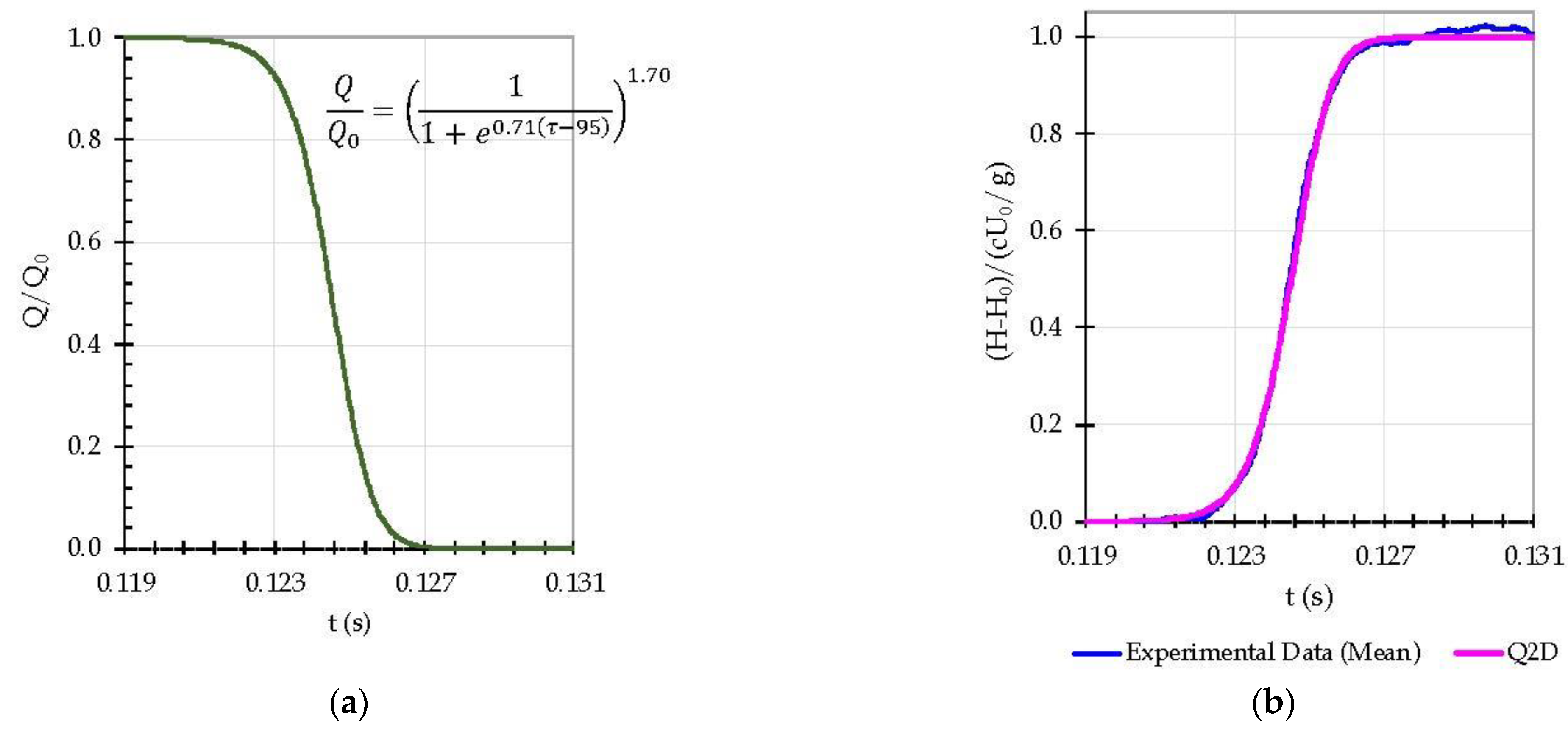
2L/c, the effective closure of the ball valve corresponds to 1/10 to 1/8 of the total closure time, and a rapid maneuver is always attained. The maneuver can be described by the sigmoidal-type closure law, as follows:
where
is the valve closure percentage, and
and
are the coefficients that best fit the numerical results with collected pressure-head data.
In the current study, the considered manoeuvre has total and effective closure times of 0.045 and 0.005 s, respectively. Accordingly, the experimental and Q2D models’ calibrated results are presented in
Figure 4. The calibrated flow rate variation is shown in
Figure 4a. The piezometric head obtained in the Q2D model fits almost perfectly with the collected data (
Figure 4b).
4. Numerical Results for the Instantaneous Valve Closure
4.1. Introduction
This section presents the results obtained by the Q2D model proposed by Zhao and Ghidaoui (2003) applied to an experimental pipe system for simulation of an instantaneous maneuver in a laminar flow. First, the effect of the mesh size near the pipe wall is analyzed for several standard equal area meshes, and results are compared with the reference Zielke’s solution implemented in 1D models. Secondly, results from the Q2D model with an optimized equal-area cylinder, and with 40 cylinders, are compared with those from standard equal area meshes.
4.2. Standard Equal-Area Cylinder Mesh: Effect of the Mesh Discretization
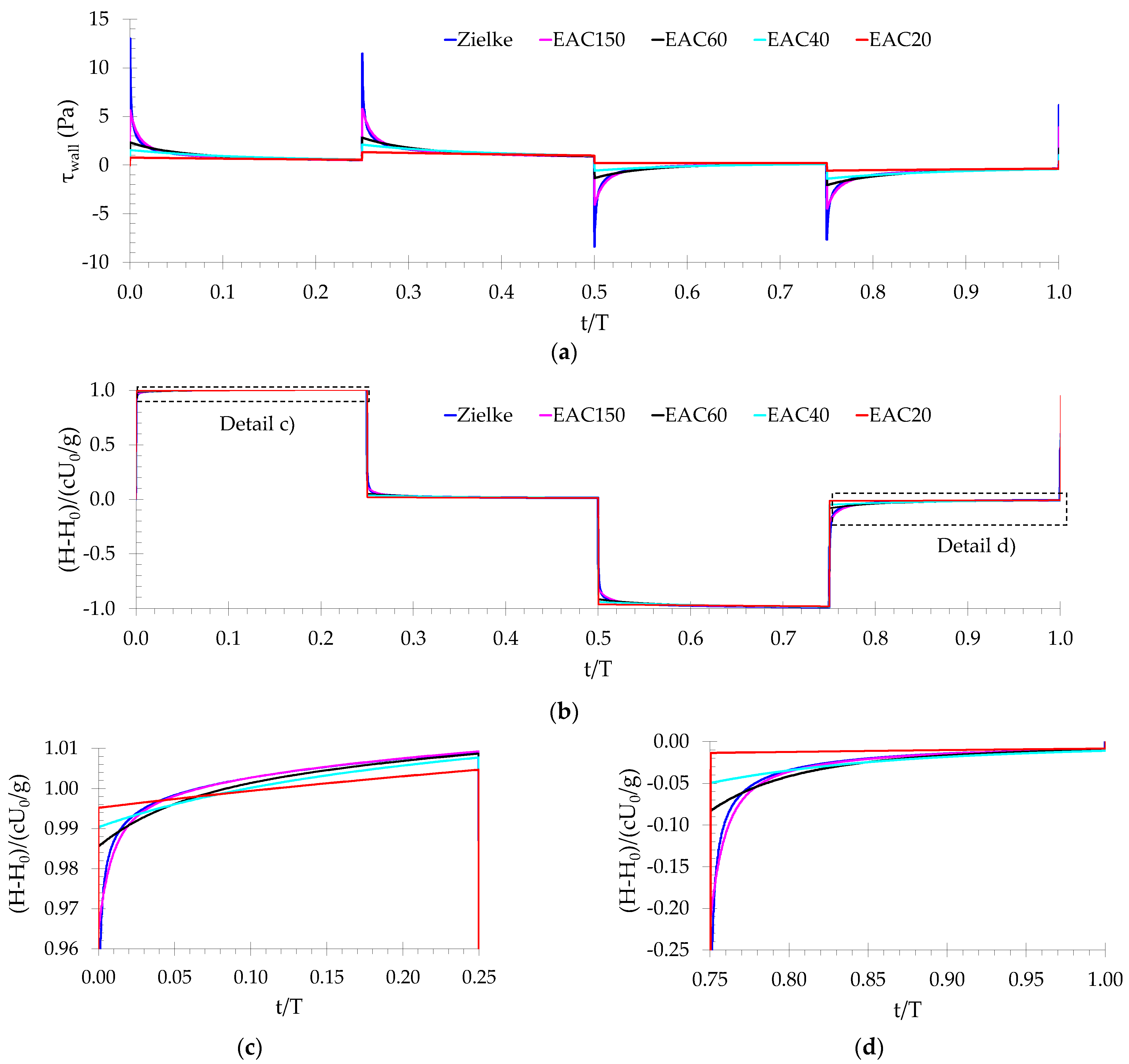
The numerical Q2D results for the wall shear stress and the piezometric-head with the standard equal-area cylinder mesh (EAC) and a variable number of cylinders (
Nc = 20, 40, 60 and 150) are depicted in
Figure 5. Zielke’s 1D model is also plotted in this figure and used as the benchmark solution for comparison.
The effect of the number of cylinders,
NC, is observed immediately after the first pressure wave arrival. The 1D model shows a high wall shear stress peak after each pressure surge, followed by an exponential decay (
Figure 5a). Low
NC meshes show a lower peak and a linear decay with time. Increasing the
NC value brings the Q2D model simulation closer to Zielke’s 1D solution. The
NC = 20 mesh reduces the Zielke’s peak more than 17 times; the
NC = 150 mesh increases the previous value almost eight times but is still approximately half the 1D model peak.
As expected, a more precise wall shear stress calculation leads to a better piezometric description. For the
NC = 20 mesh, the Q2D model piezometric-head results (
Figure 5b–d) do not depict the correct wave shape (the round-shape), showing a square shape geometry, and present a poor calculation of the wave damping (e.g., for t/T = 0.25, the difference to the 1D model is noticeable). Increasing the number of cylinders allows progressive approximation of Zielke’s results.
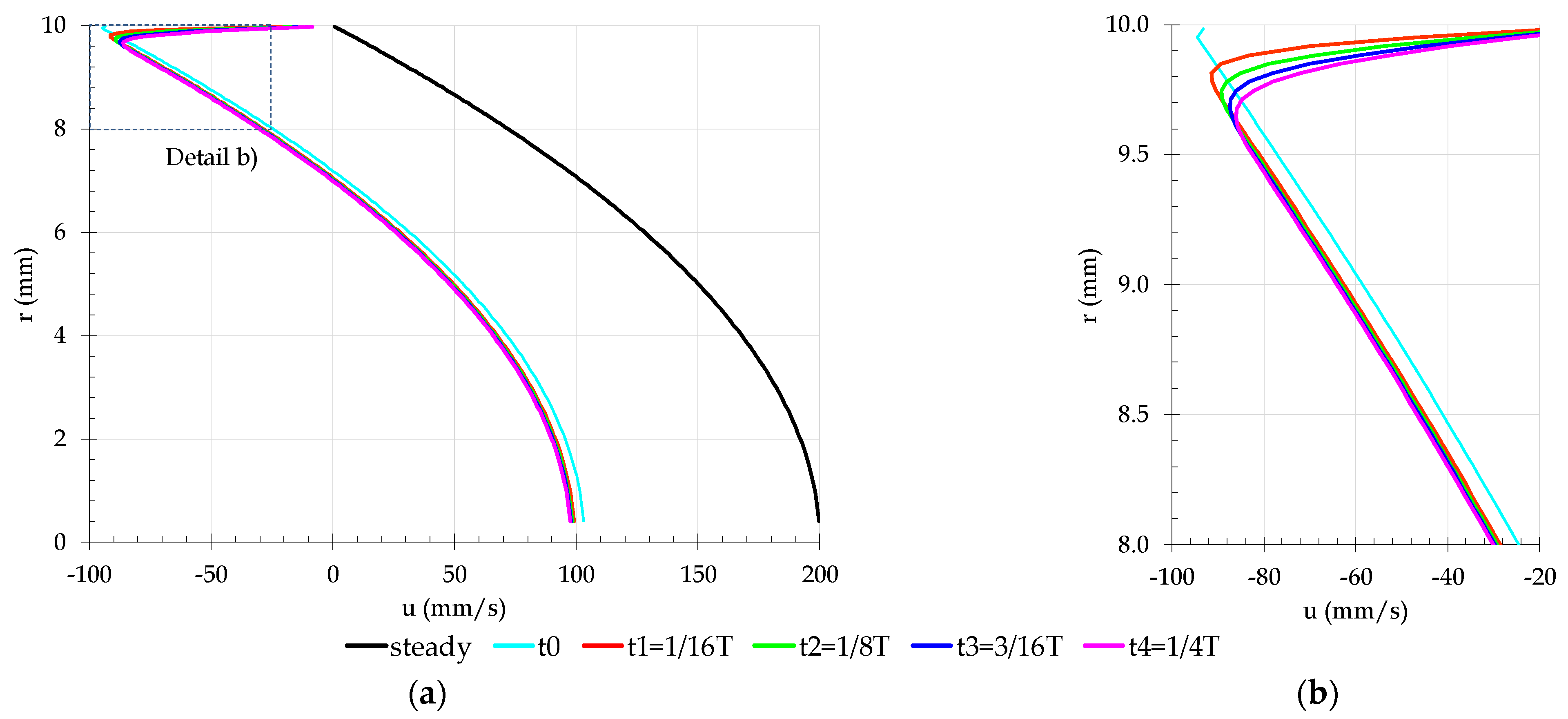
The Q2D model computes the wall shear stress and the piezometric-head at a given time based on the axial velocity calculation.
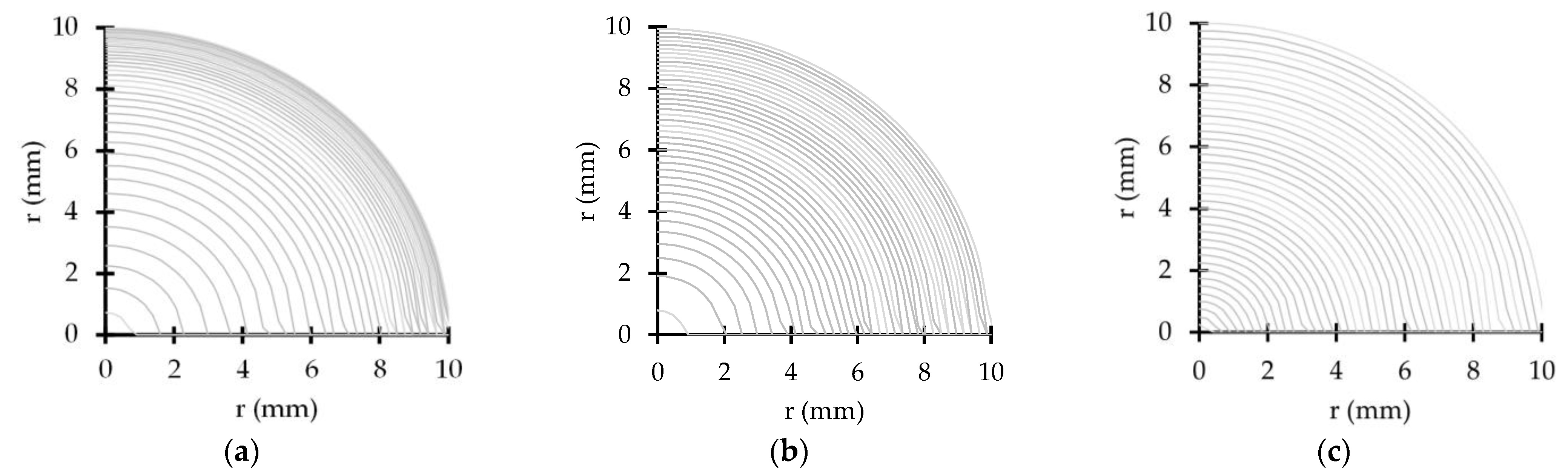
Figure 6 shows the axial velocity profile for the EAC150 mesh simulation at five-time steps during the first pressure surge (0 ≤
t/
T ≤ 0.25). The time steps are equally spaced:
t0 is the velocity profile immediately after the pressure wave arrival, and each new time adds
t/16
T to the previous one (
t0 = 0,
t1 =
t/16
T,
t2 =
t/8
T,
t3 = 3/16
T and
t4 = 1/4
T).
The pressure surge arrival shifts the steady-state axial velocity profile and an inflection point with a high axial velocity gradient appears near the pipe wall because of the no-slip condition. From t0 to t5, the velocity profile gradient near the wall reduces as the inflection point moves into the pipe core. The transient flow changes occur close to the pipe wall. At t4, just before the next pressure surge, the inflection point maximum displacement from the pipe wall is less than 4% of the pipe radius. Therefore, a high percentage of the pipe profile is unaffected and the Q2D model’s cylinders maintain a steady-state profile axial velocity.
The Q2D model numerical scheme accuracy is estimated by the finite difference truncation error, Equation (10). This means that high axial velocity variations must be followed by considerably lower grid intervals, , to achieve the same accuracy. The formation of the inflection point leads to a high numerical error in the pipe wall area and a low error in the pipe core, because it maintains the steady-state axial velocity profile with a parabolic variation (). The mesh refinement should focus on the wall area where the high axial velocity variations occur.
The EAC mesh geometry uniformly reduces the grid space in the pipe section, implying a considerable computational effort to approximate the 1D model results, especially immediately after each pressure surge. The use of EAC150 mesh corresponds to almost eight times the EAC20 computational effort, as it increases linearly with the number of cylinders for the implemented numerical scheme.
4.3. Optimized Equal-Area Cylinder Mesh
4.3.1. Mesh Description
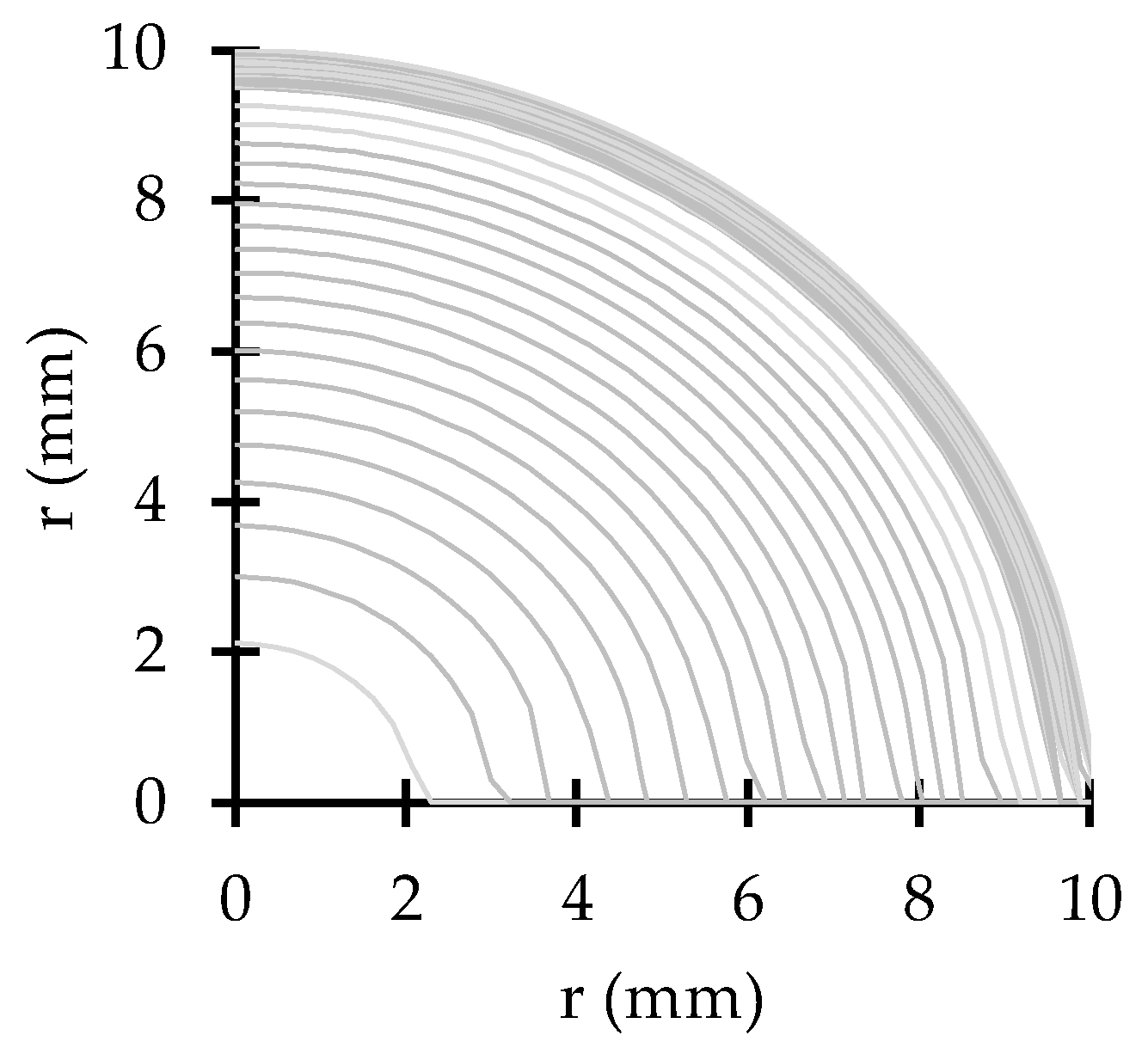
The optimized equal-area cylinder (OEAC) mesh, innovatively proposed in this research, has a high-resolution grid close to the pipe wall and a low-resolution grid in the pipe core, as presented in
Figure 7. Two equal-area cylinder meshes are implemented, with the lowest cylinder area near the wall. The underlying principle is to use a finer mesh in areas with high-velocity gradients and a coarse mesh in the low-velocity gradient region, thus, reducing the computational effort.
The new mesh is characterized by three parameters: (i) the total number of cylinders, NC; (ii) the limit of the high-resolution grid, r, defined as a percentage of the pipe radius and measured from the pipe wall; and (iii) the number of cylinders in the high-resolution region, NHR. Thus, the optimized equal area cylinder (OEAC) meshes are expressed as follows, OEACNC Nr = NHR. For instances, OEAC40 N5% = 20 stands for a mesh that has a total of 40 cylinders (NC = 40); the limit of the high-resolution mesh occurs at r = 9.5 mm (r/R = 5%) and has 20 cylinders in this high-resolution region.
This mesh is referred to as optimized since it provides better results than those for the standard EAC meshes for the same number of cylinders, as demonstrated in the following sections. This analysis will be carried out for
NC = 40, because the EAC mesh with 40 cylinders does not lead to an accurate simulation of the piezometric head (
Figure 5b), representing a good comparison with optimized mesh.
4.3.2. Shear Stress Results
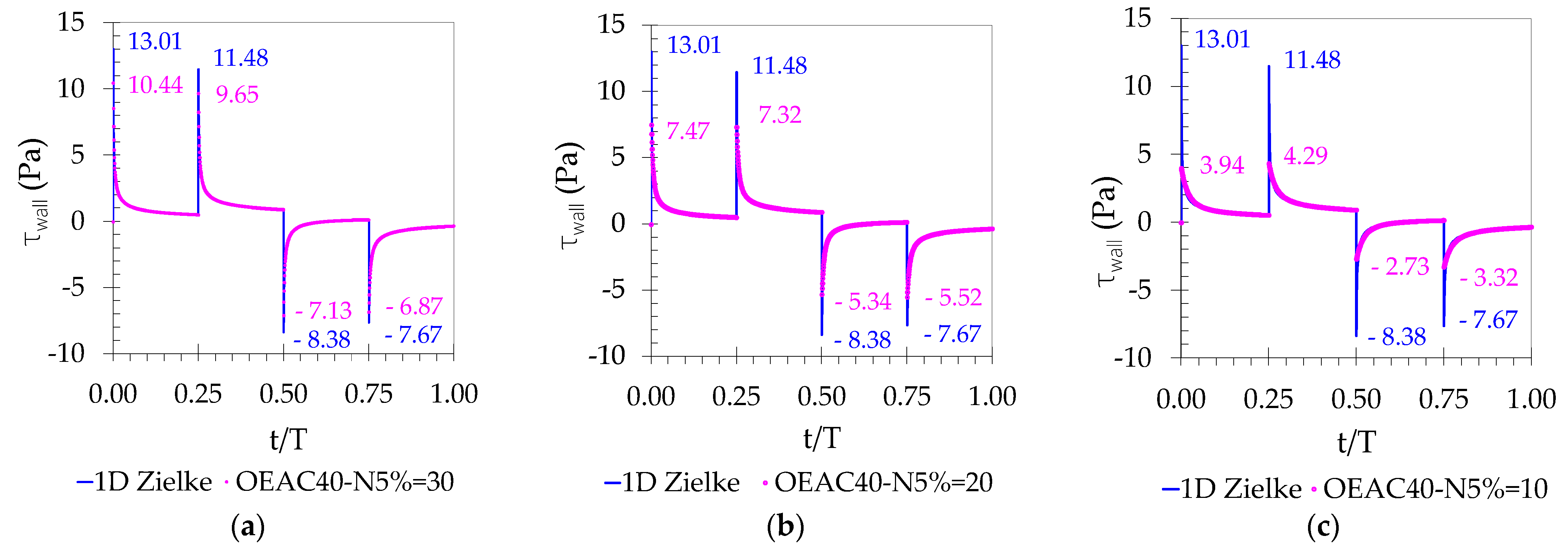
The wall shear stress obtained by the Q2D model for the optimized equal-area cylinder (OEAC) meshes with
NHR between 10 to 30,
r = 5% and
NC = 40 are presented in
Figure 8. The
r = 5% corresponds to the inflection point maximum displacement determined in the previous analysis (
Figure 6). All simulations’ accuracy has significantly improved compared to the EAC results (
Figure 4), for the same total number of cylinders (
NC = 40). The new mesh with more than 20 cylinders in the wall region (OEAC40 N
5% = 20) also presents better results than the 150 equal area cylinder meshes (EAC150). These results are compared with those obtained by the Zielke formulation used in the 1D model.
The OEAC40 N
5% = 30 mesh allows an almost perfect adjustment to Zielke’s results (
Figure 8a), whereas the OEAC40 N
5% = 10 mesh leads to a maximum wall shear stress four times lower than the Zielke’s value. This shows that the higher the number of cylinders in the high-resolution area, the more accurate the prediction of the maximum wall stress and of the subsequent decay. A second aspect concerns the relation between the wall shear stress peak values in the deceleration (
t/T = 0 and
t/T = 0.25) and the acceleration (t/T = 0.50 and t/T = 0.75) phases. For the meshes with higher resolution near the wall (
NHR ≥ 20), the peaks decay with time, as in the Zielke model; on the contrary, for the low resolution mesh (
Figure 8c), the peaks increase compared with the previous surge for t/T = 0.25 and t/T = 0.75, as observed for the standard meshes (
Figure 8a).
The mean absolute error (MAE) is used to measure the Q2D accuracy, using paired observation from the 1D Zielke model, and is given by:
in which
n is the total number of time step at the pipe middle section,
y is the Zielke model value (assumed as exact) and
x is the Q2D predicted value, both for the same instance
i.
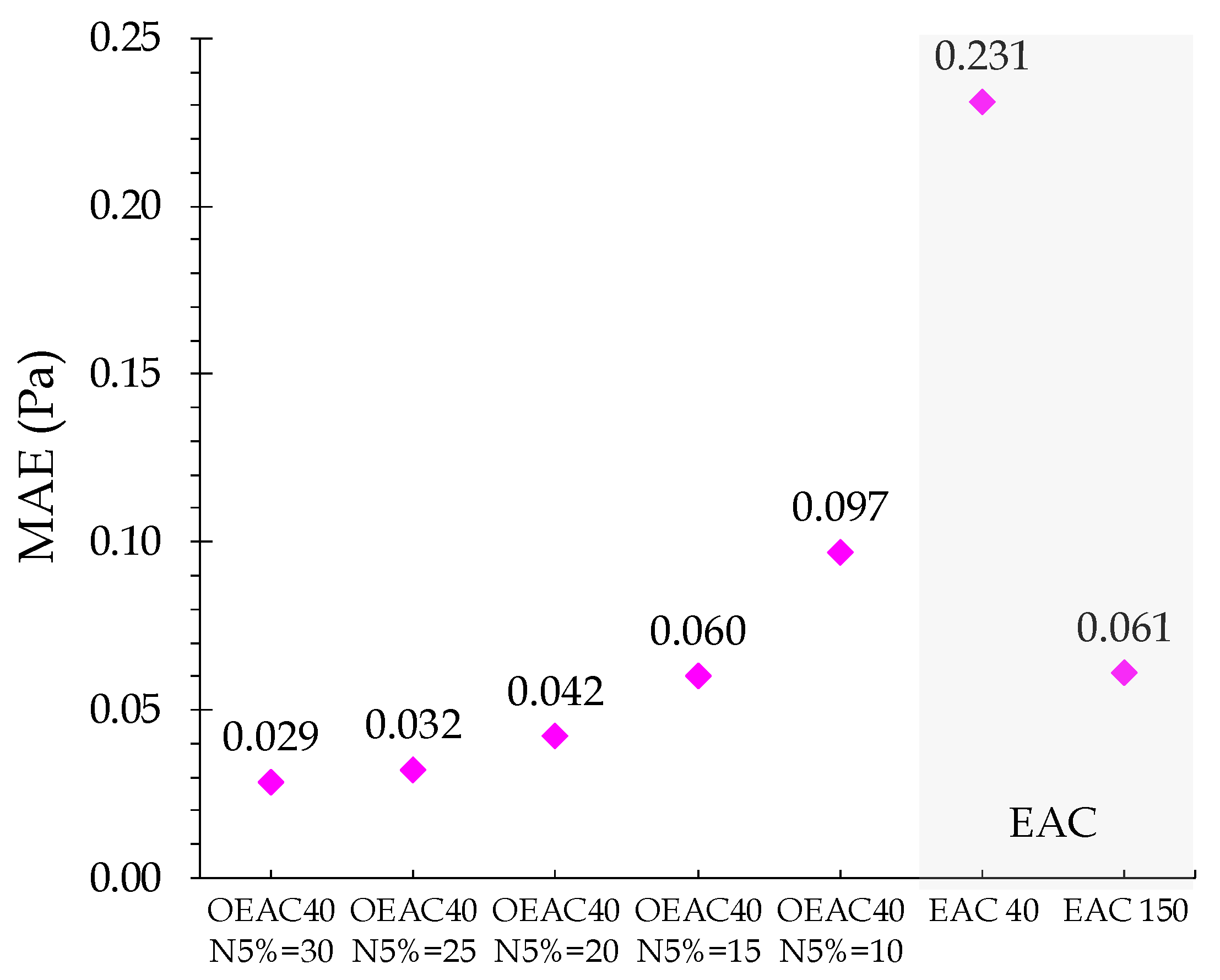
The MAE calculation for the wall shear stress simulation during the first pressure wave period (0 <
t/T ≤ 1) confirms the previous assessment (
Figure 9). MAE shows an almost exponential increase along with the
NHR reduction. For the same number of cylinders, the EAC40 mesh results have an error almost 10 times higher than that of the best OEAC mesh (OEAC40 N
5% = 30). The EAC150 results present the same MAE as the OEAC40 N
5% = 15 and a higher error than when using a higher
NHR value. This analysis highlights that a higher accuracy can be achieved with one-quarter of the number of standard mesh cylinders (40/150). OEAC mesh’s results are clearly better than those obtained for the EAC grid, considering the same (EAC40), or even a higher (EAC150), value of the total number of cylinders.
4.3.3. Mean Velocity and Piezometric Head Results
The Q2D model simulation accuracy for the mean velocity and piezometric head depends not only on the unsteady wall shear stress calculation, but also on the steady-state velocity profile calculation.
Figure 10 shows the relative steady-state mean velocity error for EAC and OEAC meshes, described by
, in which
1D is the steady-state mean velocity obtained by Hagen–Poiseuille solution and
U2D is the Q2D model steady-state flow approximation for each mesh. Firstly, OEAC meshes have a worse steady-state velocity representation than the EAC meshes (i.e., the EAC40 mesh leads to a lower error). Secondly, this error increases exponentially with the
NHR increase. The OEAC40 N
5% = 10 mesh has a 0.08% error, which is close to EAC40 (0.06%), but the OEAC40 N
5% = 30 error rises to 0.64% (i.e., 8 to 10 times higher).
All meshes show similar wall shear stress values close to the pipe wall (see
r = 10 mm in
Figure 11b). Nevertheless, the highest resolution OEAC meshes tend to have higher shear stress values in the pipe core (see
r < 2 mm in
Figure 11a). Increasing the distance between grid points,
, towards the pipe axis implies a higher numerical error in the pipe core. Additionally, the OEAC meshes have a discontinuity between the high and the low-resolution regions, this discontinuity being more pronounced for higher values of
NHR (
Figure 11b; see black and green curves for
r = 9.5 mm). This discontinuity occurs in the transition between the two regions of the OEAC meshes (i.e., at
r= 9.5 mm), being more noticeable for the OEAC40 N
5% = 30 mesh.
The OEAC meshes with high
NHR values allow a considerable improvement in the wall shear stress simulation results without increasing
NC; however, a balance with higher steady-state error must be accomplished. The MAE of the mean velocity simulation is calculated in the first wave period (
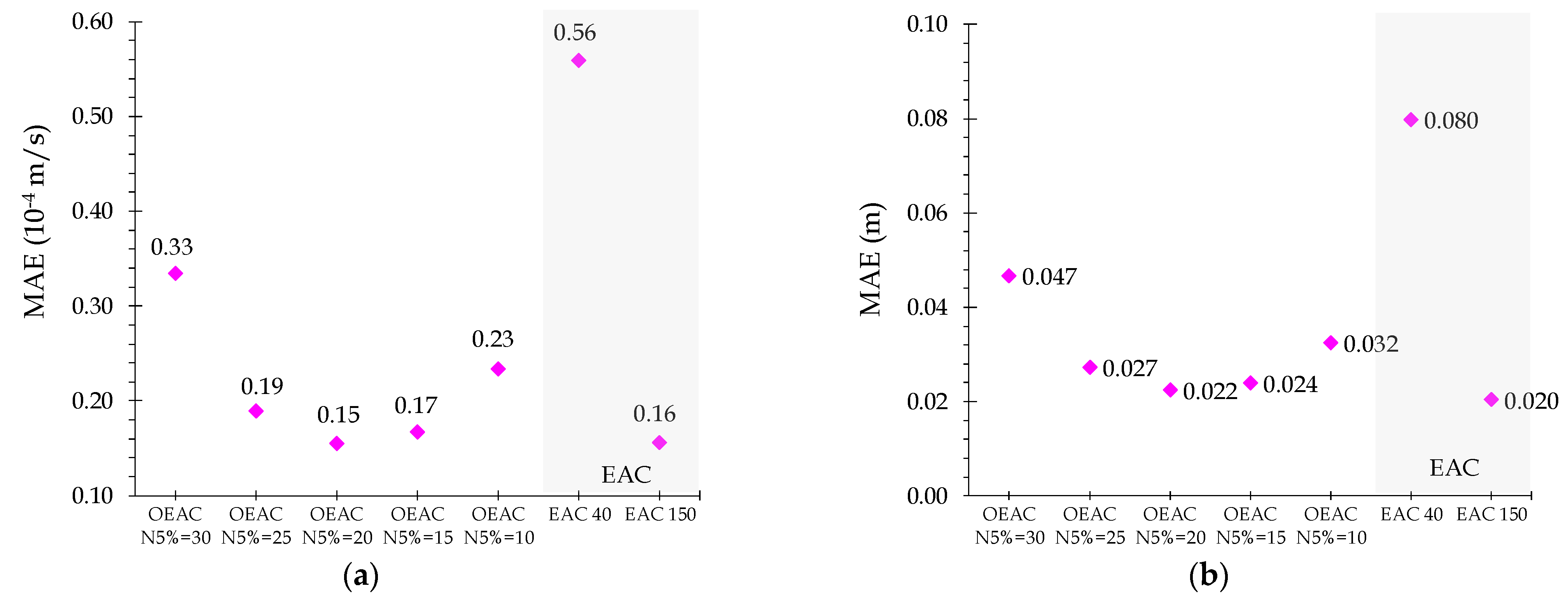
t/T < 1) using Zielke’s model as benchmark, as depicted in
Figure 12a. The EAC meshes (EAC40 and EAC150) and OEAC meshes with
NC = 40, and varying the
NHR values from 30 to 10, are considered. OEAC40 N
5% = 20 has the lowest error (MAE = 0.15), close to that of the standard EAC150 (MAE = 0.16) and five times lower than that for the standard EAC40 mesh (with the same number of cylinders). Increasing the number of cylinders in the wall region (
NHR from 20 to 30) increases the MAE value because a higher wall shear stress accuracy does not compensate for a lower steady velocity profile accuracy; decreasing the number of cylinders in the wall region also increases the error for the opposite reason. The piezometric-head results lead to the same conclusions (
Figure 12b).
6. Complete Versus Simplified Q2D Models
Results presented in previous sections refer to the complete Q2D model from Vardy and Hwang (1981) [
6], with Zhao and Ghidaoui’s implementation [
24]. The simplified Q2D model neglects the lateral mass transfer and allows a computation effort reduction of 30% and 40% with
θ1 = 0.5 and
θ1 = 1.0, respectively. The accuracy of the three models—complete Q2D, simplified Q2D (
θ1 = 0.5) and simplified Q2D (
θ1 = 1)—is assessed herein for the instantaneous and for the calibrated valve maneuvers.
6.1. Instantaneous Valve Manoeuvre
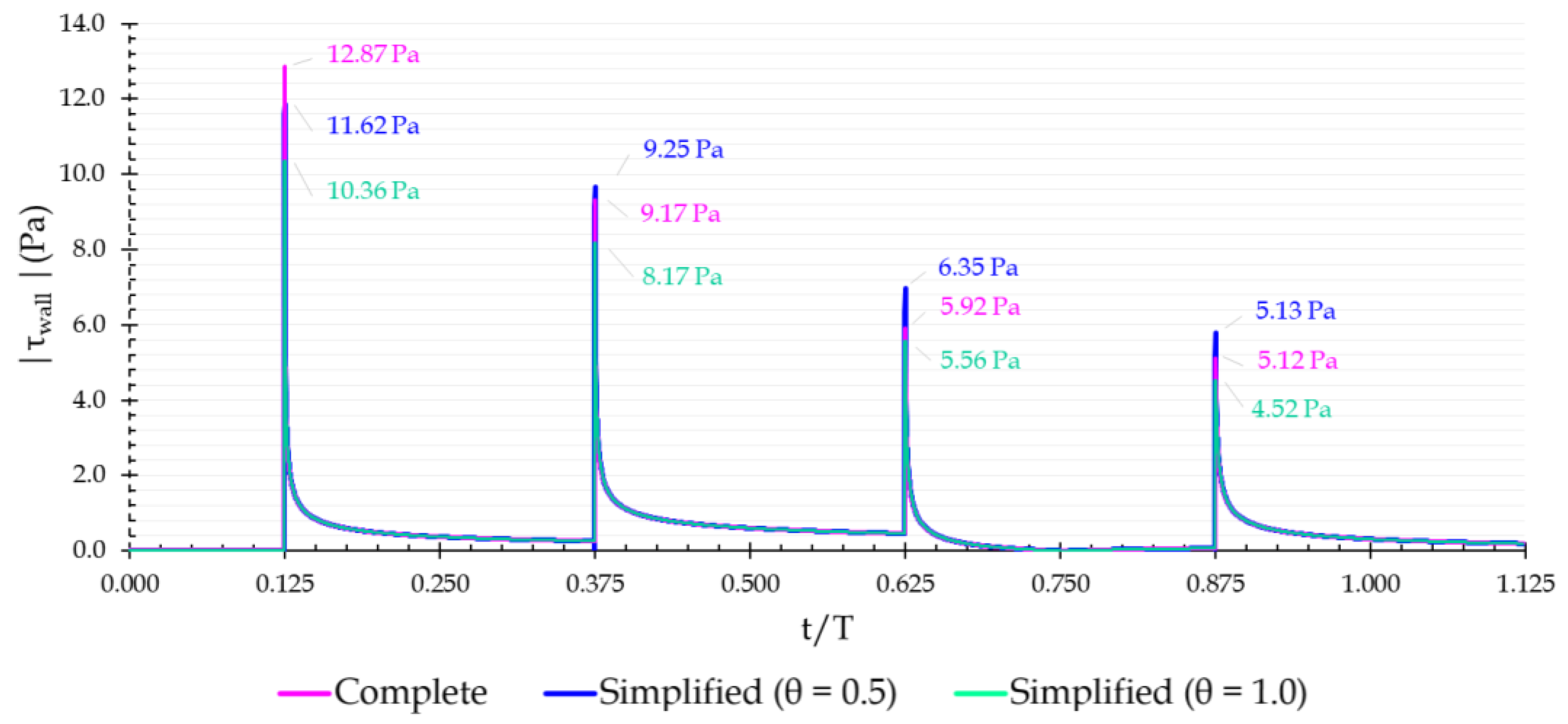
The wall shear stress results are analysed for
NC values from 20 to 100 and compared with the Zielke’s analytical solution for ∆
x = 0.01m. For
NC = 100, a slight difference is registered between the three models during the high velocity-gradient immediately after the pressure surge and fades shortly after (
Figure 17). The complete model has the best accuracy, and the simplified model with
θ1 = 1.0 the worst. Nevertheless, for the lowest
NC meshes (
NC = 60 and
NC = 80), the differences between the three models are hardly observed because the period immediately after the pressure surge is not described so accurately.
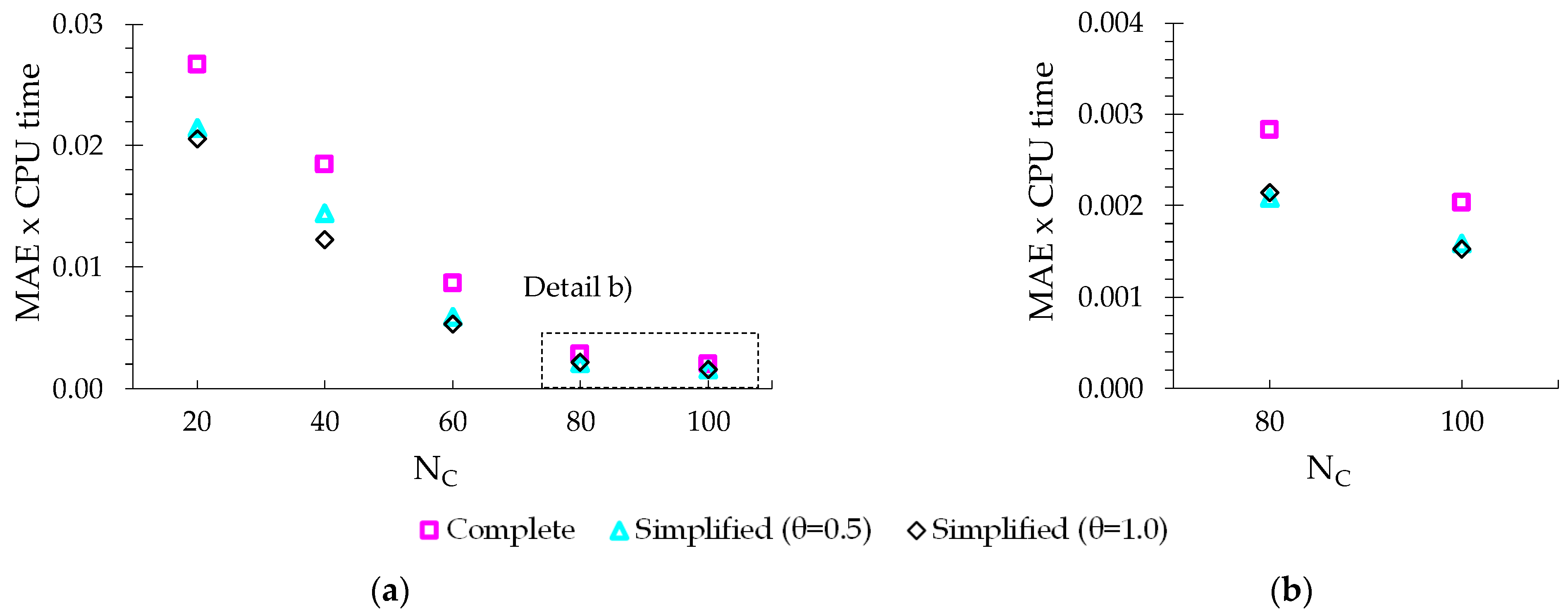
Figure 18 shows the product between the accuracy (described by MAE) and the CPU time for the different
NC values. The rationale is to combine these two aspects in a single parameter for best selection of the numerical model. The MAE value exponentially decreases with
NC. Increasing the
NC value ensures a better simulation accuracy independently of the numerical model selected. Increasing the model complexity is not justifiable for meshes with low
NC, and the simplified model with
θ1 = 1.0 is the best option. For higher
NC values the simplified model with
θ1 = 0.5 compensates for the additional computation time. The complete model is only recommended for a detailed evaluation in the period immediately after the pressure surge.
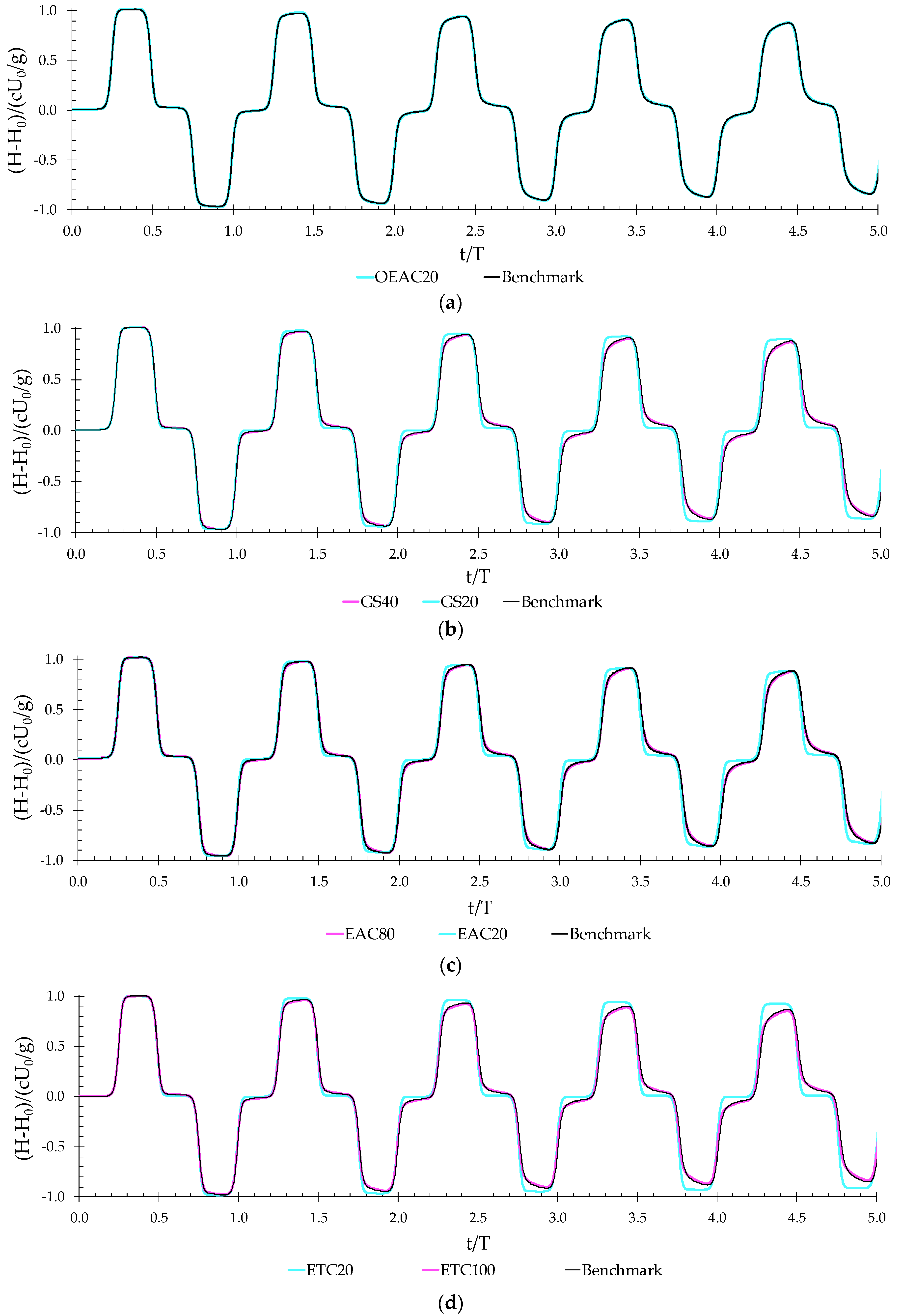
6.2. Calibrated Valve Manoeuvre
The calibrated valve closure (
Figure 4) is used to analyze the accuracy of the three numerical models results for the traditional mesh geometries (GS, EAC and ETC) and the new optimized mesh (OEAC). For the sake of simplicity, only the
NC = 100 meshes are considered, since the results for lower
NC values were negligible for instantaneous valve closure.
A slower valve closure maneuver reduces the wall shear stress peak and, consequently, approximates the results for the three traditional mesh geometry models, compared to the instantaneous valve closure. Additionally, the EAC and ETC meshes show a low accuracy and the simulation results are independent of the selected Q2D model, thus, the fastest numerical scheme should be considered (simplified model with θ1 = 0.5). On the contrary, the results of the high-resolution grids (OEAC and GS) are influenced by the model, and the conclusions are similar to those obtained for the instantaneous valve maneuver.
7. Conclusions
An optimized equal area cylinder (OEAC) radial mesh is proposed to ensure the Q2D model accuracy without increasing the computation effort. The new mesh, with 40 cylinders, is defined by a high-resolution grid near the pipe wall and a lower-resolution grid in the pipe core. For an instantaneous valve closure, this mesh reduced the calculation time by four times with similar simulation error, compared to the standard equal area cylinder (EAC) mesh.
The results of the new mesh are compared with those obtained for the traditional mesh geometries (GS, ETC and EAC) for a calibrated S-shape valve closure. Compared to the geometric sequence (GS) mesh, the new geometry achieved a significant improvement in accuracy for meshes with fewer cylinders (NC ≤ 60). The other two radial meshes (ETC and EAC) do not provide the same accuracy. The new mesh correctly describes the experimental data with only 20 cylinders, which is not achieved by the fastest 1D models.
The simplified Q2D model (i.e., neglecting the lateral velocity) reduces the computational effort without significant loss of accuracy for low resolution meshes in the wall region. If a higher accuracy simulation is required, it is recommended to increase the number of cylinders instead of using the complete Q2D model.
The new two-region mesh has been applied herein to laminar flows, for which there is an exact analytical solution for unsteady friction (Zielke’s formulation) that is used as a benchmark solution for comparison. In future works, the same approach can be applied to turbulent flows by including an adequate turbulent model in the fundamental equations, and the results obtained can be analyzed and compared with experimental data. Additionally, future research could explore the possibility of using a dynamic-mesh, reconfigured during the transient event according to the axial velocity gradient, in order to reduce the computation effort, but maintaining a high accuracy; this will imply the development of a new specific numerical scheme, adequate for non-uniform meshes, to avoid the loss of accuracy due to high grid space variations.