Deep Learning Optical Flow with Compound Loss for Dense Fluid Motion Estimation
Abstract
:1. Introduction
2. Approach and Materials
2.1. Flownet2 Network Structure
2.2. Compound Loss Function
2.2.1. RMSE Loss Function
2.2.2. AAE Loss Function
2.2.3. Div-Curl Smooth Loss Function
2.2.4. Compound Form
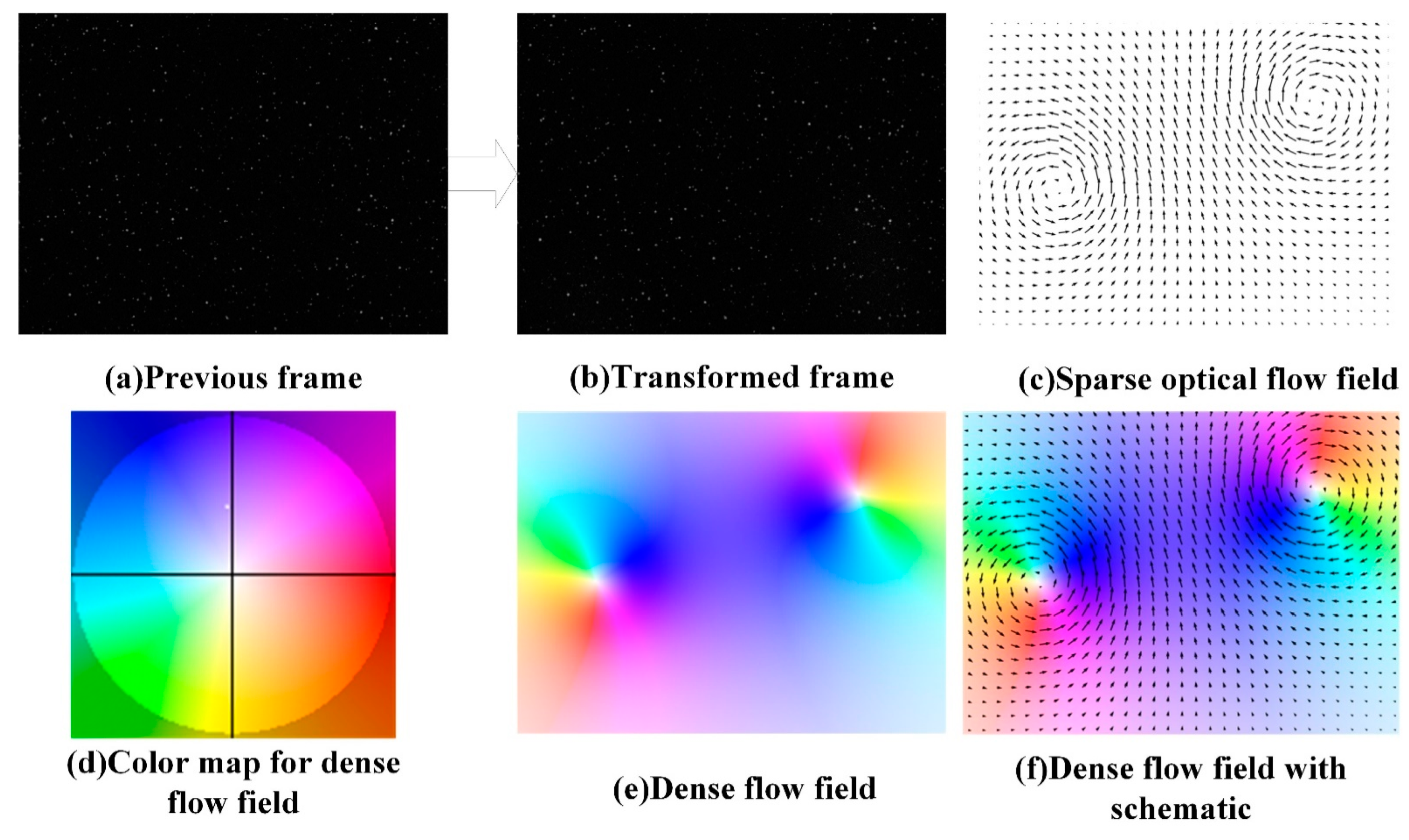
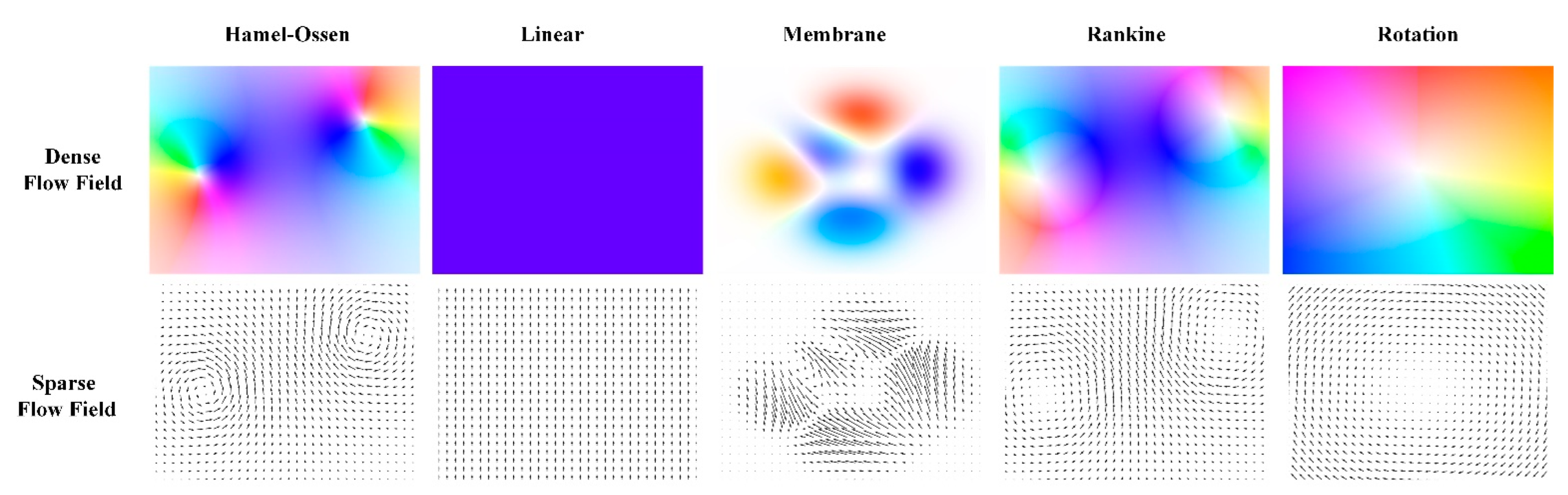
2.3. Synthetic PIV Data Set
3. Results and Analysis
3.1. Index of Performance Measurement
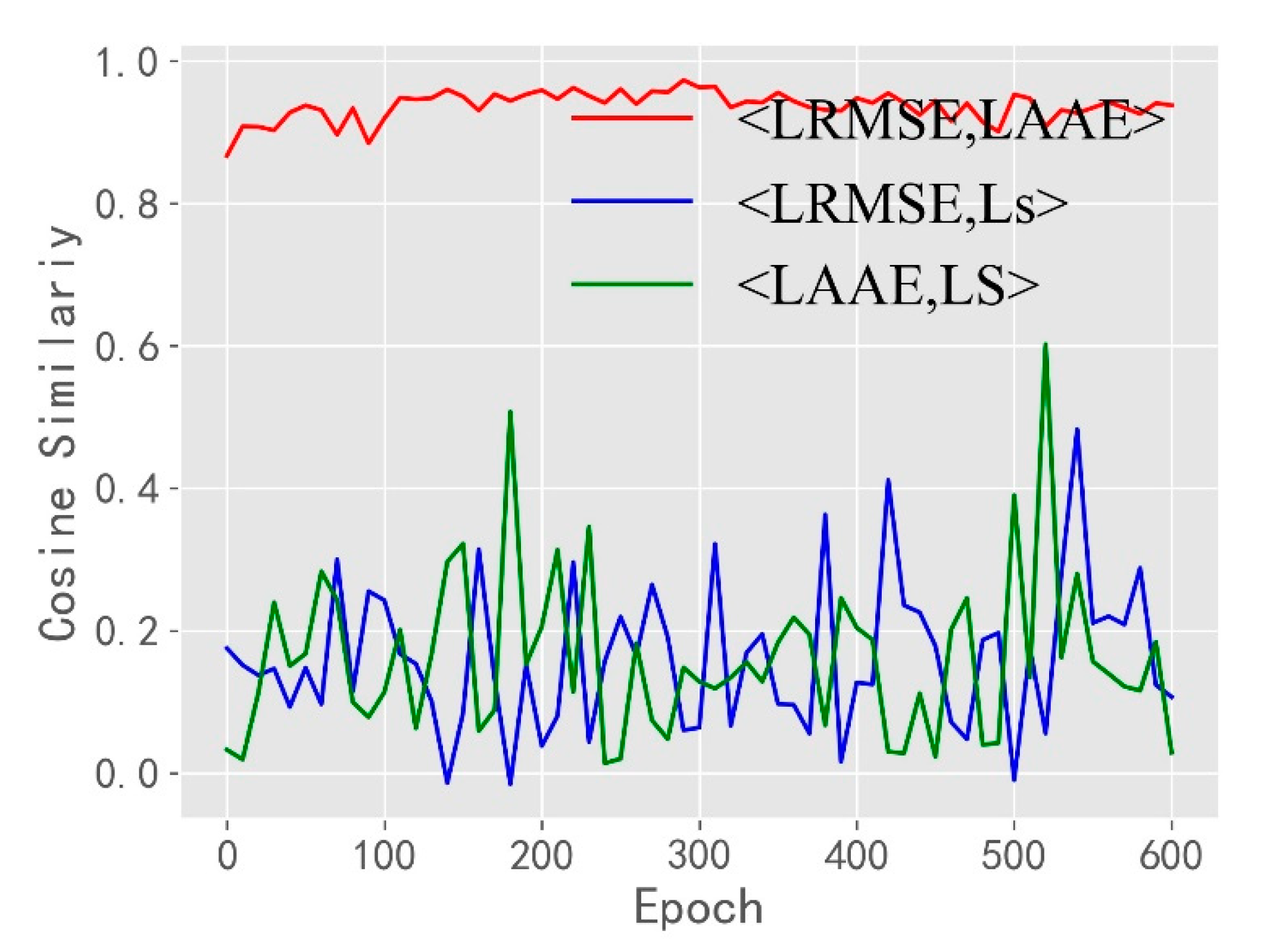
3.2. Cosine Similarity Verification of Compound Loss Function
3.3. Sensitivity Analysis of Compound Loss Function Parameters
3.4. Results of Compound Form of Loss Function on Training Data Set
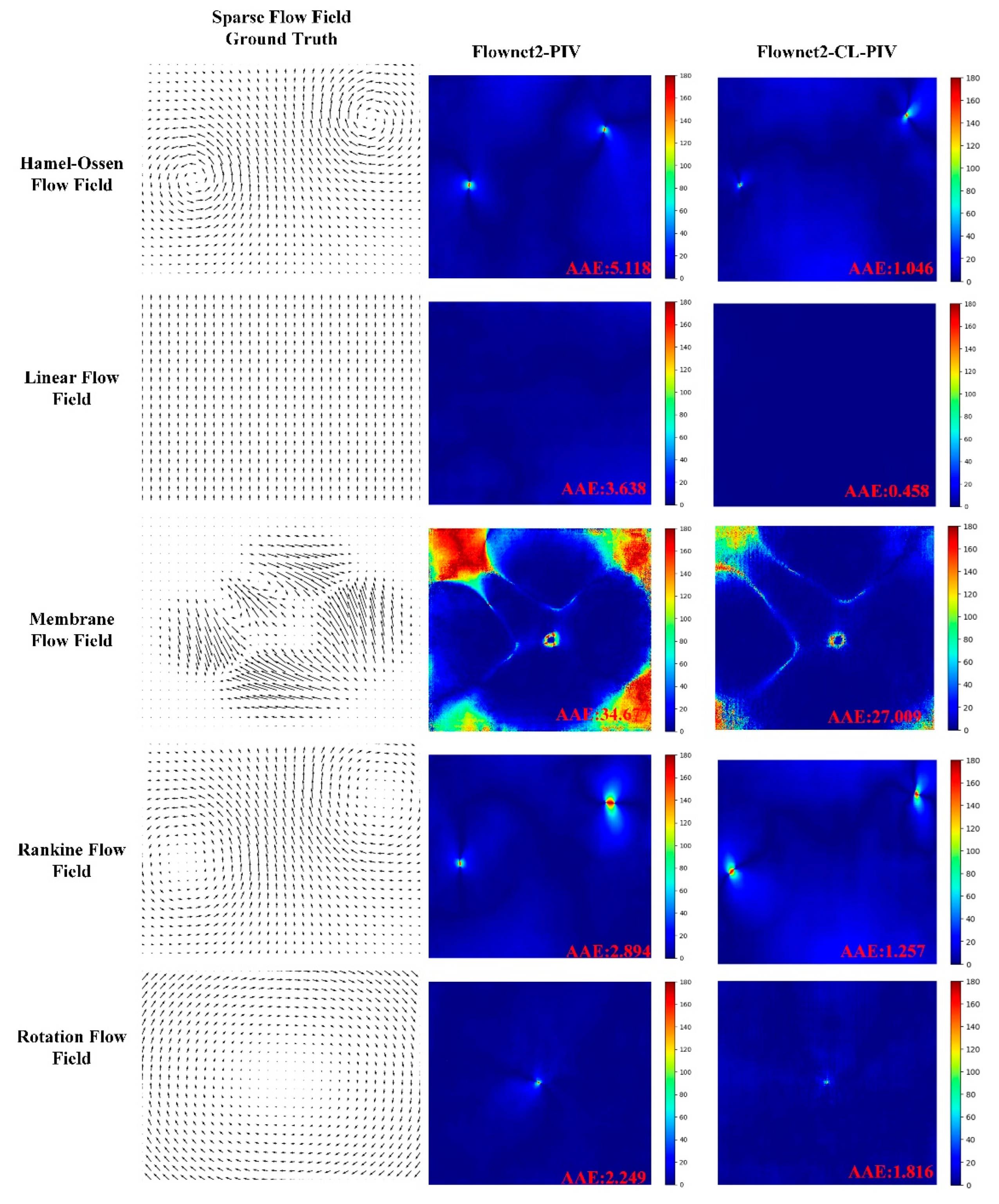
3.5. Analysis of RMSE Calculation Results
3.6. Analysis of AAE Calculation Results
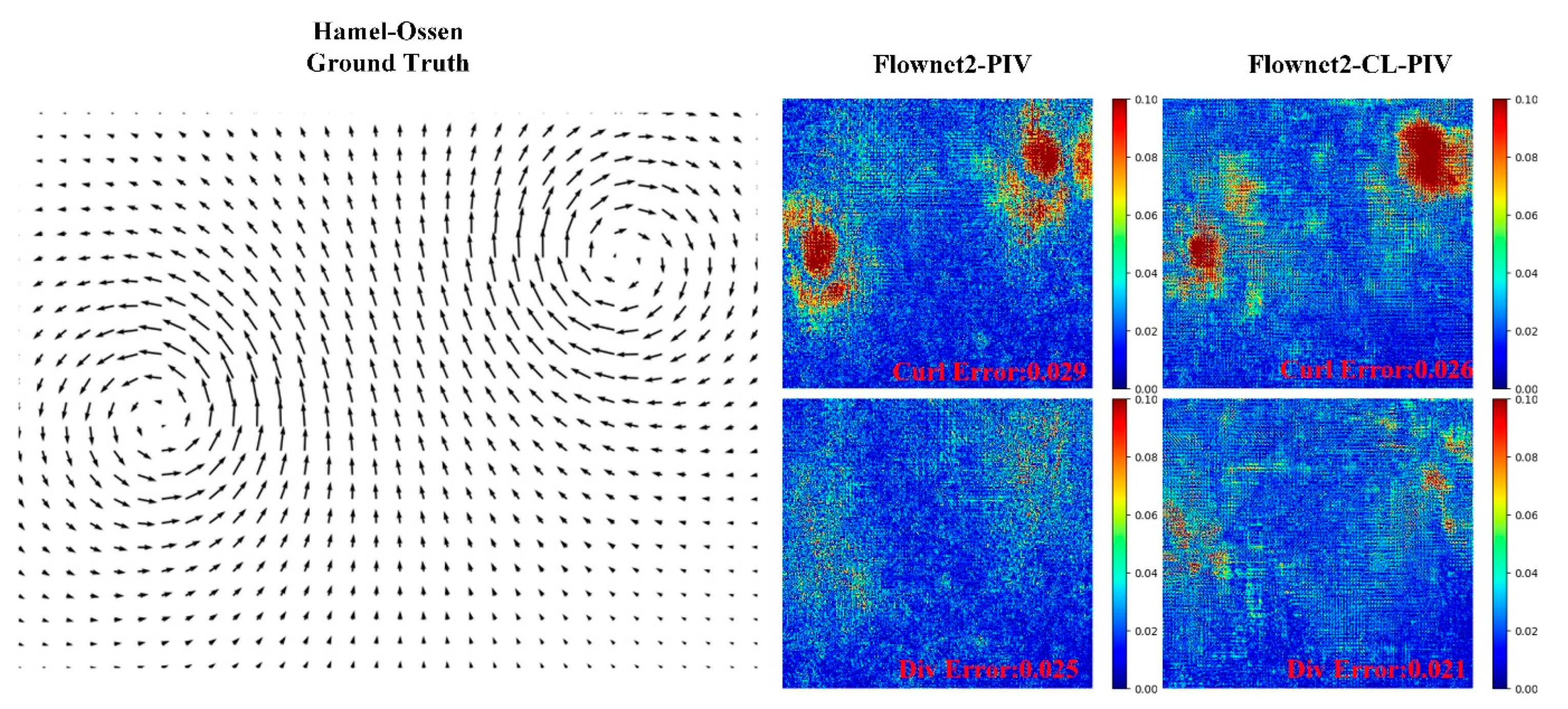
3.7. Analysis of Div-Curl Error Calculation Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raffel, M.; Willert, C.; Wereley, S.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer: Cham, Switzerland, 2007. [Google Scholar]
- Cai, S. Optical Flow-Based Motion Estimation of Complex Flows; Zhejiang University: Hangzhou, China, 2019. [Google Scholar]
- Wang, J.; Shi, T.; Yu, D.; Teng, D.; Ge, X.; Zhang, Z.; Yang, X.; Wang, H.; Wu, G. Ensemble machine-learning-based framework for estimating total nitrogen concentration in water using drone-borne hyperspectral imagery of emergent plants: A case study in an arid oasis, NW China. Environ. Pollut. 2020, 266, 115412. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, K.; Sugii, Y.; Aota, A.; Hibara, A.; Tokeshi, M.; Kitamori, T.; Okamoto, K. High-Speed Micro PIV Measurements of Micro Counter-Current Flow. Proc. JSME Annu. Meet. 2004, 2004, 111–112. [Google Scholar] [CrossRef]
- Westerweel, J. Digital Particle Image Velocimetry: Theory and Application. Ph.D. Thesis, Delft University, Delft, The Netherlands, 1995. [Google Scholar]
- Scarano, F.; Riethmuller, M.L. Iterative Multigrid Approach in PIV Image Processing with Discrete Window Offset. Exp. Fluids 1999, 26, 513–523. [Google Scholar] [CrossRef]
- Horn, B.; Schunck, B. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef] [Green Version]
- Corpetti, T.; Memin, E.; Perez, P. Dense Estimation of Fluid Flows. Pattern Anal. Mach. Intell. IEEE Trans. 2002, 24, 365–380. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.S.; Shen, L.X. Fluid flow and optical flow. J. Fluid Mech. 2008, 614, 253–291. [Google Scholar] [CrossRef]
- Tauro, F.; Tosi, F.; Mattoccia, S.; Toth, E.; Piscopia, R.; Grimaldi, S. Optical Tracking Velocimetry (OTV): Leveraging Optical Flow and Trajectory-Based Filtering for Surface Streamflow Observations. Remote Sens. 2018, 10, 2010. [Google Scholar] [CrossRef] [Green Version]
- Khalid, M.; Pénard, L.; Mémin, E. Optical flow for image-based river velocity estimation. Flow Meas. Instrum. 2019, 65, 110–121. [Google Scholar] [CrossRef] [Green Version]
- Hui, T.W.; Tang, X.; Loy, C.C. LiteFlowNet: A Lightweight Convolutional Neural Network for Optical Flow Estimation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Fischer, P.; Dosovitskiy, A.; Ilg, E.; Häusser, P.; Hazırbaş, C.; Golkov, V.; Van der Smagt, P.; Cremers, D.; Brox, T. FlowNet: Learning Optical Flow with Convolutional Networks. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Sun, D.; Yang, X.; Liu, M.Y.; Kautz, J. PWC-Net: CNNs for Optical Flow Using Pyramid, Warping, and Cost Volume. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Teed, Z.; Deng, J. RAFT: Recurrent All-Pairs Field Transforms for Optical Flow; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Ilg, E.; Mayer, N.; Saikia, T.; Keuper, M.; Dosovitskiy, A.; Brox, T. FlowNet 2.0: Evolution of Optical Flow Estimation with Deep Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Lee, Y.; Yang, H.; Yin, Z. PIV-DCNN: Cascaded deep convolutional neural networks for particle image velocimetry. Exp. Fluids 2017, 58, 171. [Google Scholar] [CrossRef]
- Kondor, S.; Chan, D.; Sitterle, J. Application of Optical Surface Flow Measurement to Composite Resin Shrinkage. In Proceedings of the ADEA/AADR/CADR Meeting & Exhibition, Orlando, FL, USA, 8–9 March 2006. [Google Scholar]
- Cai, S.; Liang, J.; Gao, Q.; Xu, C.; Wei, R. Particle Image Velocimetry Based on a Deep Learning Motion Estimator. IEEE Trans. Instrum. Meas. 2020, 69, 3538–3554. [Google Scholar] [CrossRef]
- Cai, S.; Zhou, S.; Xu, C.; Gao, Q. Dense motion estimation of particle images via a convolutional neural network. Exp. Fluids 2019, 60, 73. [Google Scholar] [CrossRef]
- Dickson, M.C.; Bosman, A.S.; Malan, K.M. Hybridised loss functions for improved neural network generalization. In Proceedings of the Pan-African Artificial Intelligence and Smart Systems: First International Conference, PAAISS 2021, Windhoek, Namibia, 6–8 September 2021; Springer International Publishing: Cham, Switzerland, 2022; pp. 169–181. [Google Scholar]
- Kendall, A.; Gal, Y.; Cipolla, R. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7482–7491. [Google Scholar]
- Sener, O.; Koltun, V. Multi-task learning as multi-objective optimization. Adv. Neural Inf. Process. Syst. 2018, 31, 1–12. [Google Scholar]
- Yu, C.D.; Fan, Y.W.; Bi, X.J.; Han, Y.; Kuai, Y.F. Deep particle image velocimetry supervised learning under light conditions. Flow Meas. Instrum. 2021, 80, 102000. [Google Scholar] [CrossRef]
- Yu, C.; Luo, H.; Fan, Y.; Bi, X.; He, M. A cascaded convolutional neural network for two-phase flow PIV of an object entering water. IEEE Trans. Instrum. Meas. 2021, 71, 1–10. [Google Scholar] [CrossRef]
- Baker, S.; Scharstein, D.; Lewis, J.P.; Roth, S.; Black, M.J.; Szeliski, R. A Database and Evaluation Methodology for Optical Flow. Int. J. Comput. Vis. 2011, 92, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Yu, T.; Kumar, S.; Gupta, A.; Levine, S.; Hausman, K.; Finn, C. Gradient surgery for multi-task learning. Adv. Neural Inf. Process. Syst. 2020, 33, 5824–5836. [Google Scholar]


| Method | Train | Test | ||
|---|---|---|---|---|
| Sintel Clean | Sintel Final | Sintel Clean | Sintel Final | |
| FlowNetS | 4.50 | 5.45 | 7.42 | 8.43 |
| FlowNetC | 4.31 | 5.87 | 7.28 | 8.81 |
| FlowNet2 | 2.02 | 3.54 | 3.96 | 6.02 |
| LiteFlowNet | 2.48 | 4.04 | - | - |
| PWC-Net | 2.55 | 3.93 | - | - |
| Flow Field Type | Max Displacement (Pixel) | Step (Pixel) | Amount |
|---|---|---|---|
| Linear | ±5~ ± 20 | 0.1 | 4500 |
| Rankine | 5~25 | 0.1 | 2400 |
| Hamel-Ossen | 5–20 | 0.1 | 1280 |
| Rotation | ±5–±20 | 0.1 | 600 |
| Membrane | 3 | 0 | 600 |
| (LRMSE) | (LAAE) | (LS) | RMSE (Pixel) | AAE (°) |
|---|---|---|---|---|
| 1 | 1 | 1 | 4.886 | 17.658 |
| 1 | 0.1 | 10 | 2.791 | 5.314 |
| 1 | 0.05 | 10 | 2.368 | 4.254 |
| 10 | 1 | 10 | 3.081 | 4.346 |
| 10 | 1 | 1 | 3.427 | 4.891 |
| Loss Function | RMSE (Pixel) | AAE (°) | Curl Error | Div Error |
|---|---|---|---|---|
| LRMSE | 0.201 | 3.73 | 0.084 | 0.065 |
| LRMSE + LAAE | 0.193 | 2.56 | 0.046 | 0.038 |
| LRMSE + LS | 0.224 | 4.34 | 0.022 | 0.019 |
| LRMSE + LAAE + LS | 0.182 | 1.724 | 0.024 | 0.017 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, Z.; Wang, Z.; Chen, L. Deep Learning Optical Flow with Compound Loss for Dense Fluid Motion Estimation. Water 2023, 15, 1365. https://doi.org/10.3390/w15071365
Wang J, Zhang Z, Wang Z, Chen L. Deep Learning Optical Flow with Compound Loss for Dense Fluid Motion Estimation. Water. 2023; 15(7):1365. https://doi.org/10.3390/w15071365
Chicago/Turabian StyleWang, Jie, Zhen Zhang, Zhijian Wang, and Lin Chen. 2023. "Deep Learning Optical Flow with Compound Loss for Dense Fluid Motion Estimation" Water 15, no. 7: 1365. https://doi.org/10.3390/w15071365
APA StyleWang, J., Zhang, Z., Wang, Z., & Chen, L. (2023). Deep Learning Optical Flow with Compound Loss for Dense Fluid Motion Estimation. Water, 15(7), 1365. https://doi.org/10.3390/w15071365







