A Laboratory Scale of the Physical Model for Inclined and Porous Breakwaters on the Coastline of Soc Trang Province (Mekong Delta)
Abstract
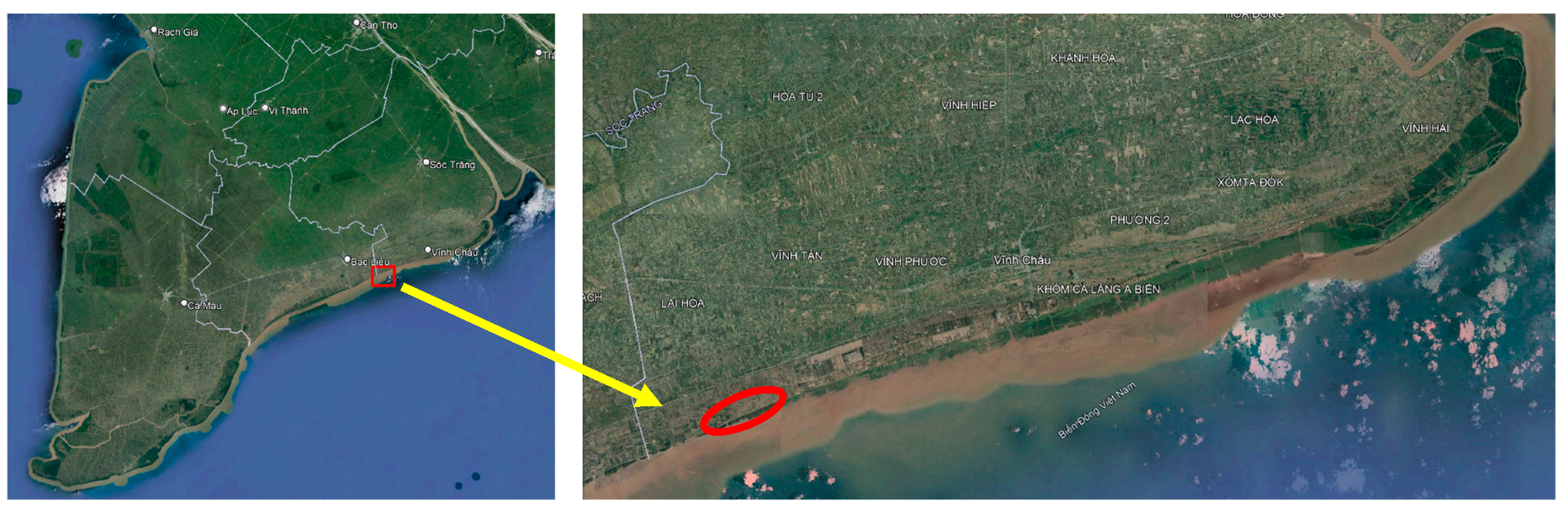
:1. Introduction
2. Breakwater Block Designs
2.1. Water Level and Wave Condition
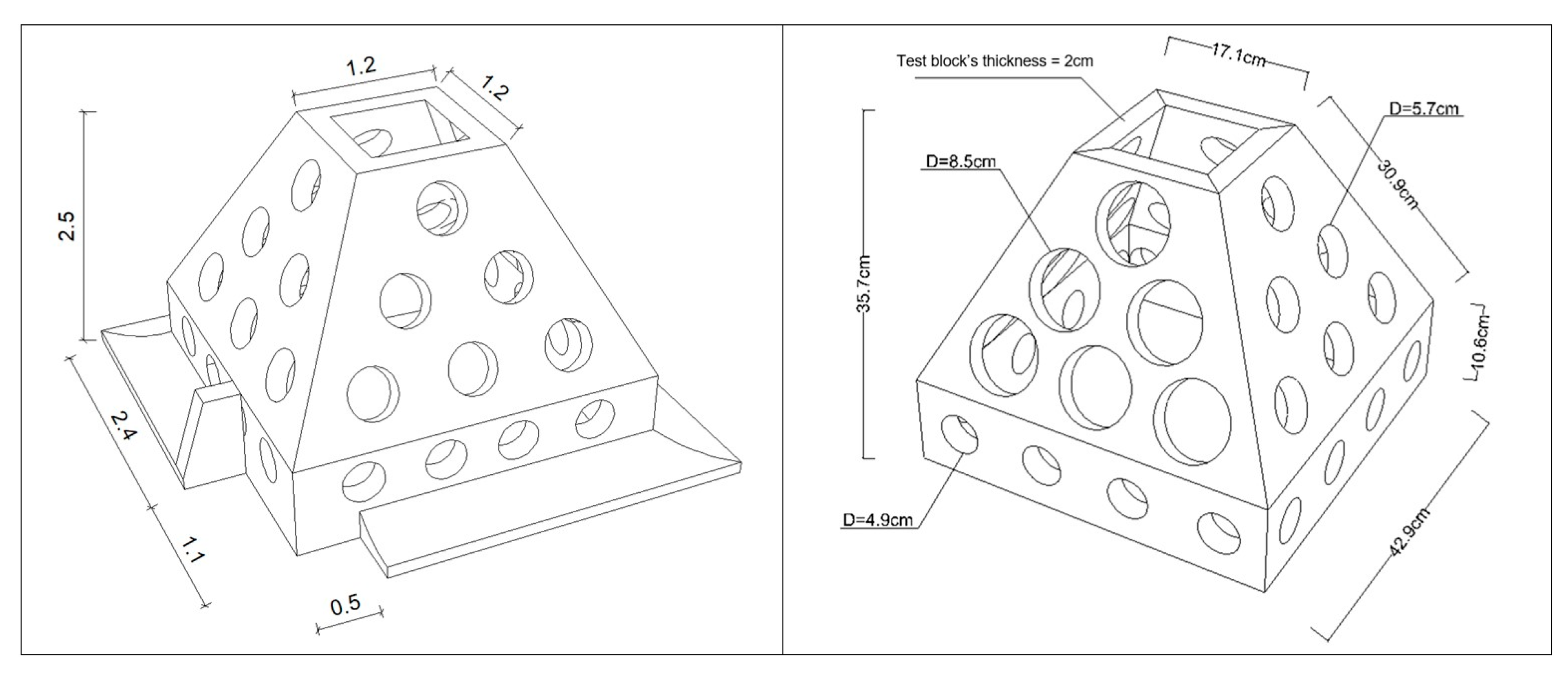
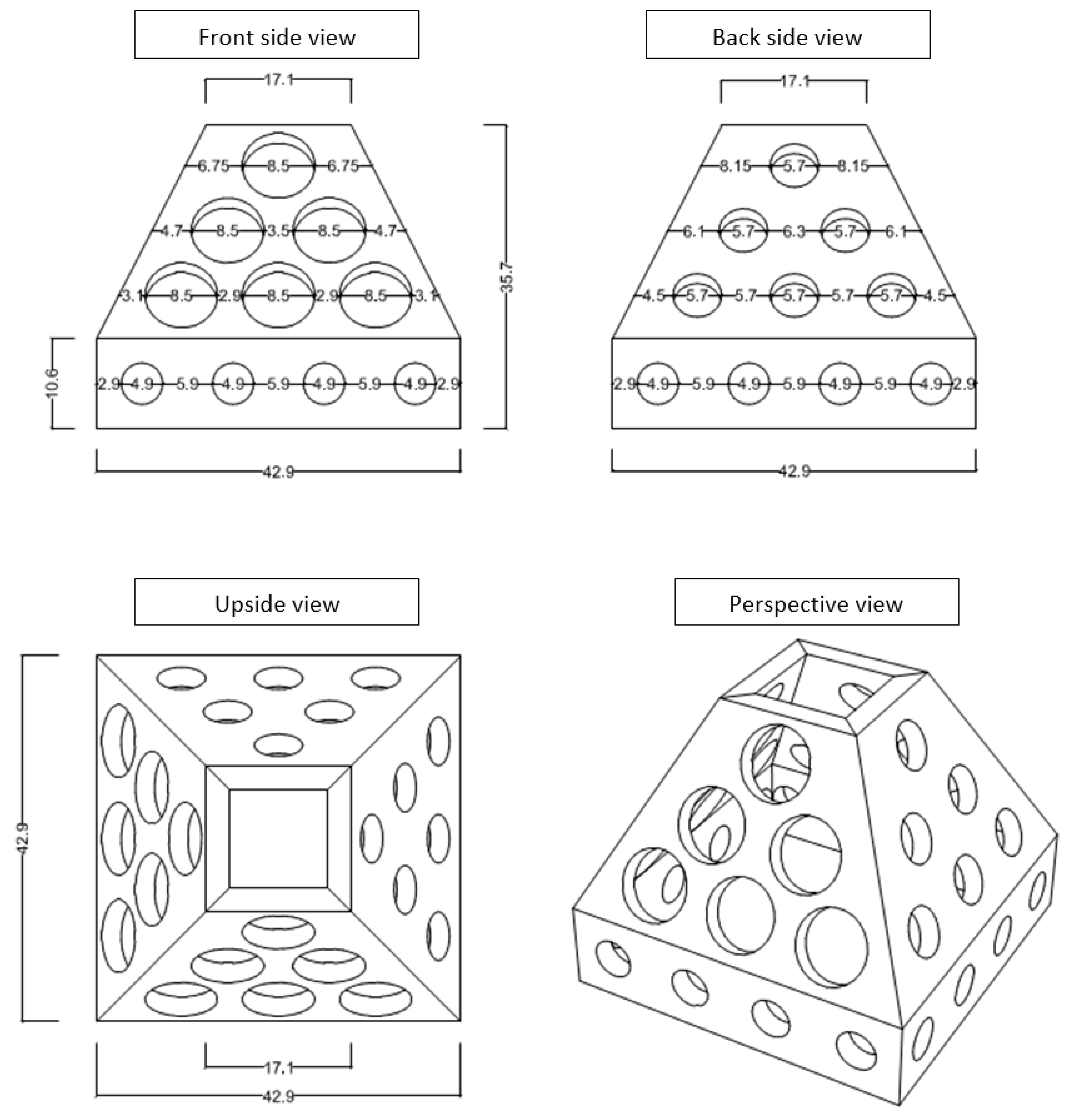
2.2. Breakwater Parameters
2.2.1. Submerged Breakwater
2.2.2. Emerged Breakwater
3. Physical Models
3.1. Modelling Scales
3.2. Model Construction and Scenarios
- -
- Defining an optimal diameter of the pores in the breakwater surfaces; the pores could be on either the front or the back side or on both sides;
- -
- Defining the wave energy dissipation ability of the block with chosen pores (presented in Table 3 below).
- -
- On the back side, the diameter of the largest pore is 5.7 cm, whereas the diameter of the smallest pore is 4.1 cm.
- -
- On the front side, the diameter of the largest pore is 8.9 cm. It is 5.7 cm for the smallest pore.
4. Results and Discussion
4.1. Wave Parameter Estimations
- ❖
- Wave height at zero moment
- -
- is the variance density of the spectrum corresponding to frequency f;where—Spectral width parameters.
- ❖
- Wave peak periods and
- ❖
- Wave transmission coefficient of the breakwater
- ❖
- Wave reflection coefficient
- ❖
- Wave dissipation coefficient
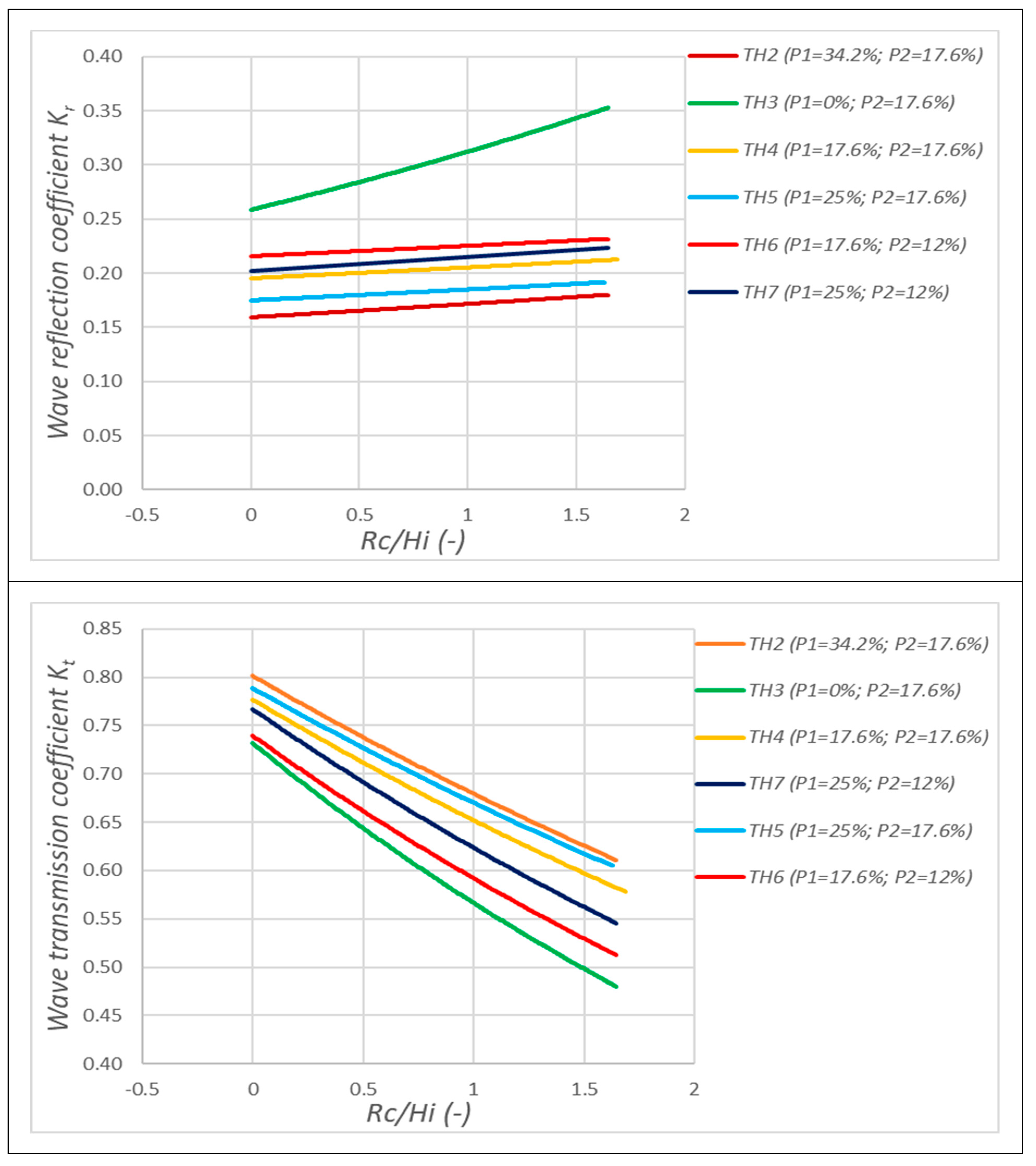
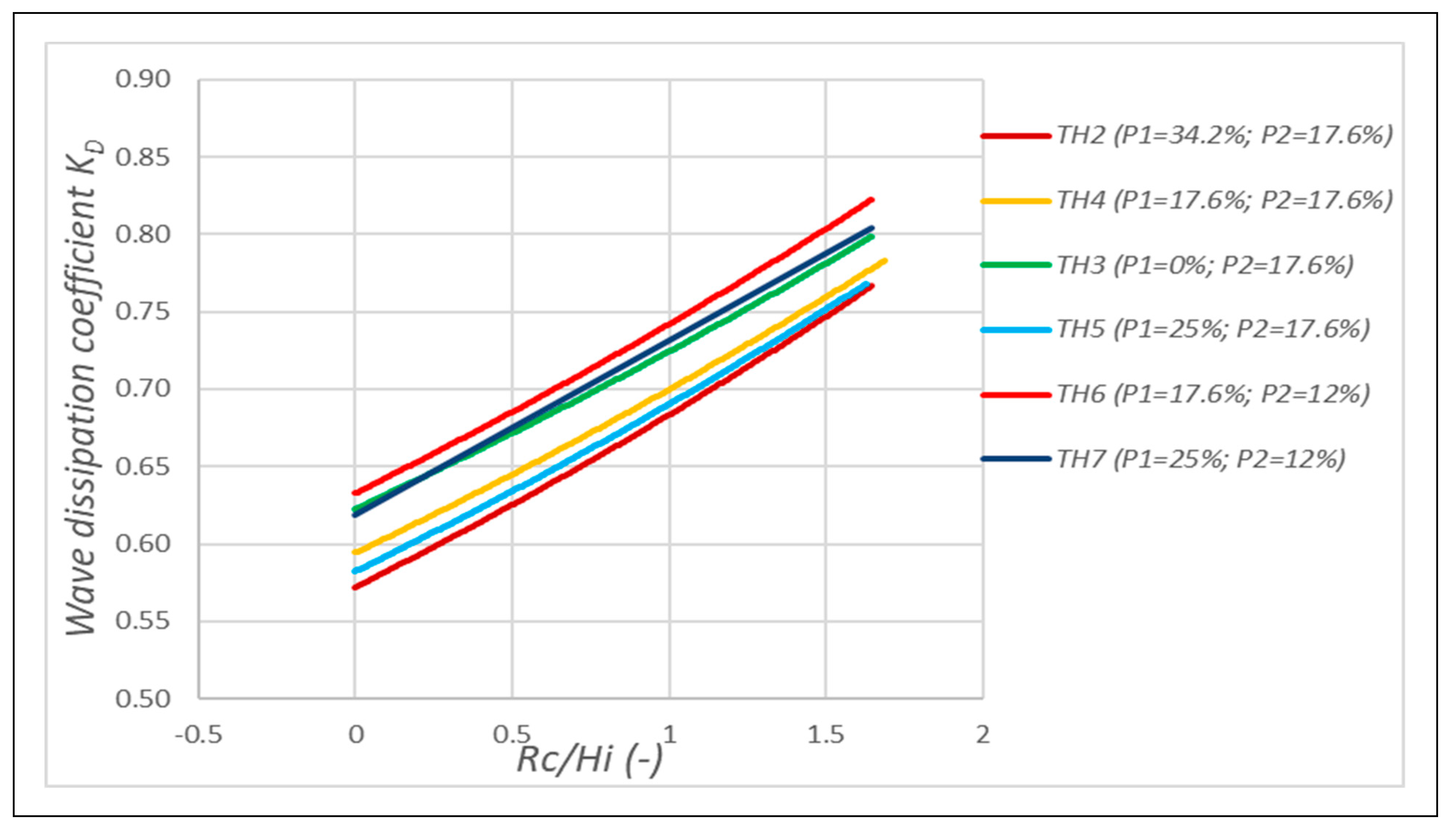
4.2. Dependency of Wave Dissipation Capacity on Pore Diameters of Breakwater
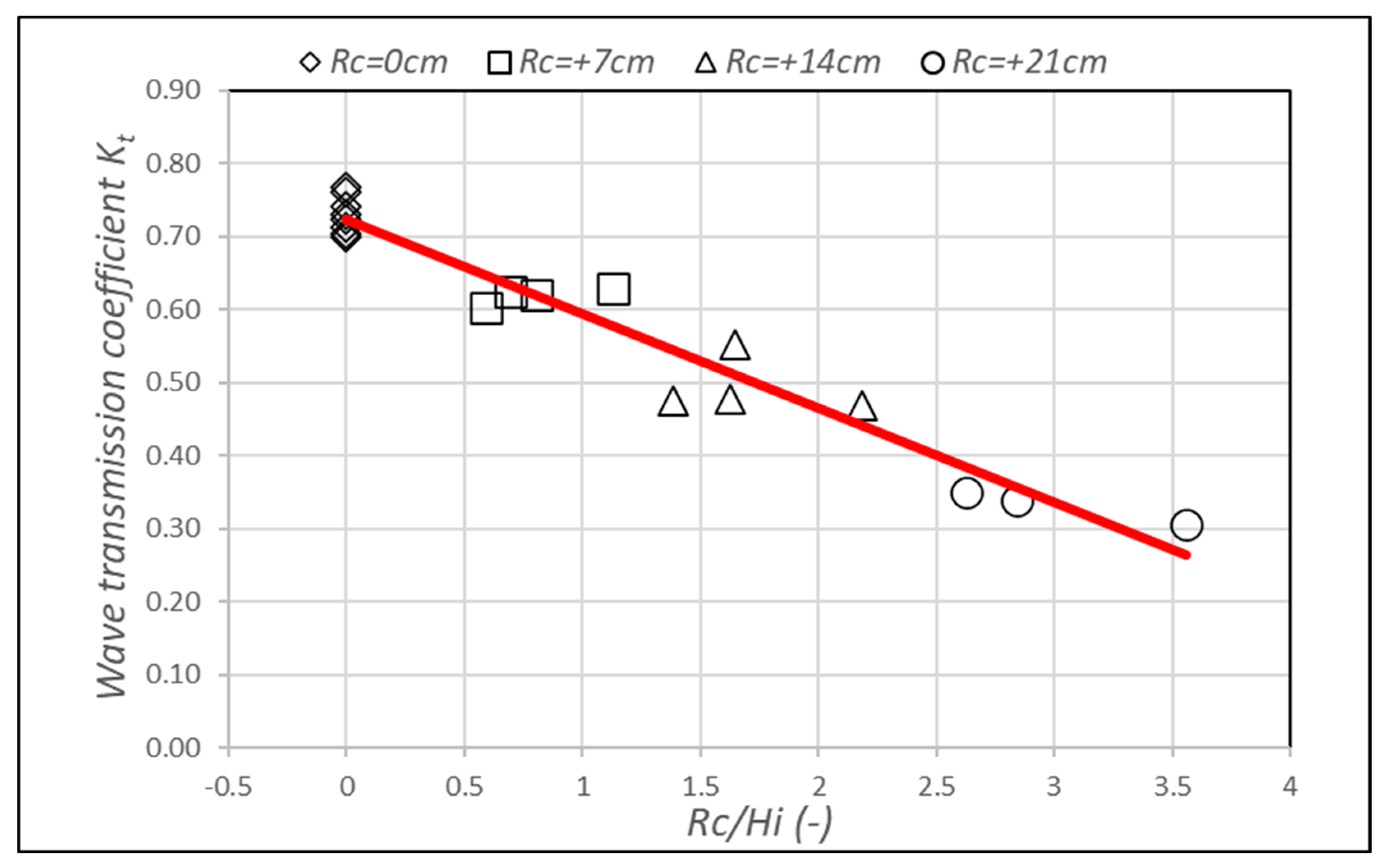
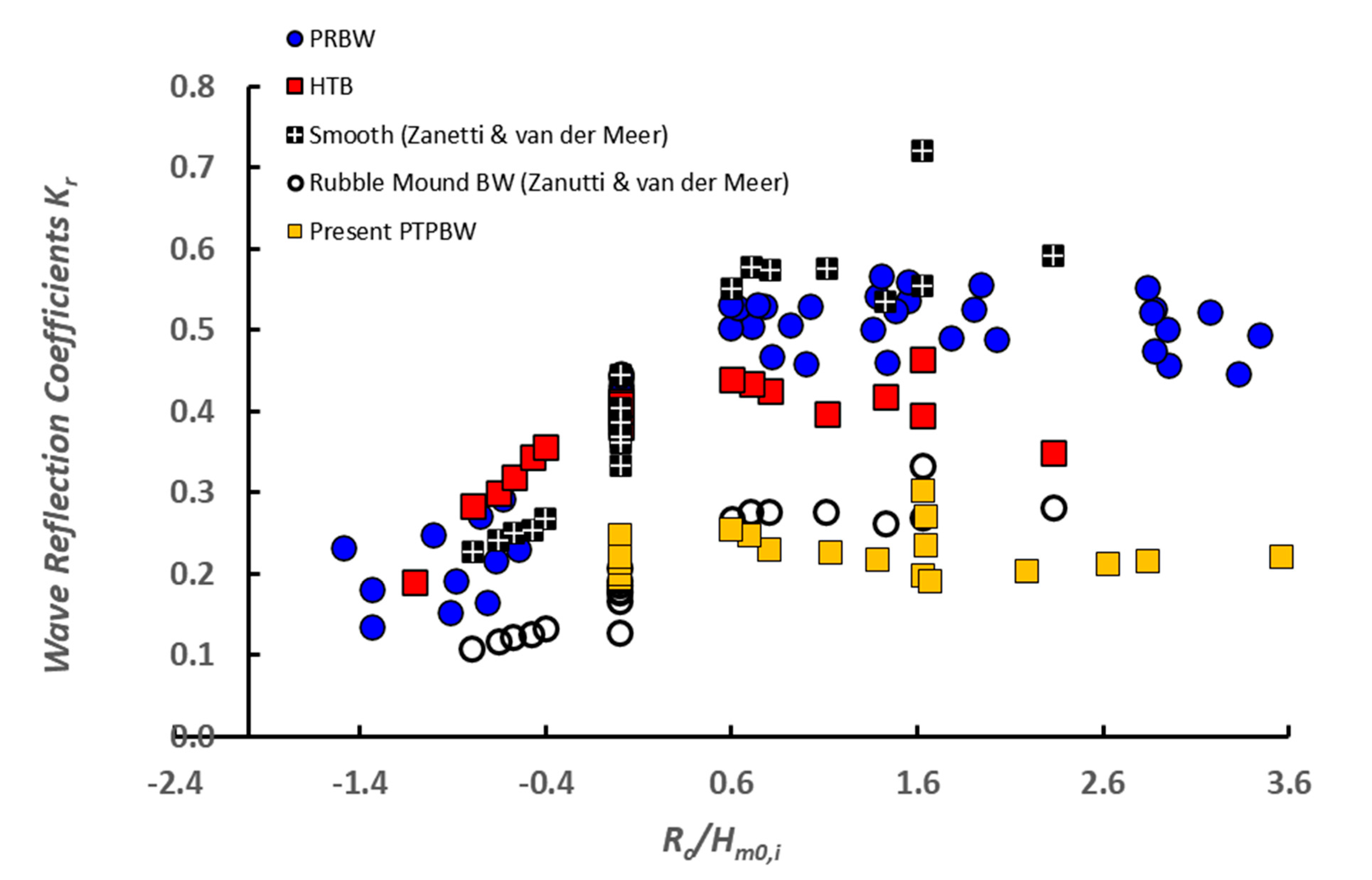
4.3. Wave-Reducing Effects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| α—Angle of the incident wave; |
| β—Spectral energy parameter; |
| γ—Peak enhancement factor; |
| D—Pore diameter; |
| Do—Outer diameter (of the rings composing the pore in the model block); |
| Di—Inner diameter (of the rings composing the pore in the model block); |
| Ds—Back-side pore diameter; |
| fm— Value of pick frequency; |
| Hs—Deep-water wave height; |
| Hm0—Wave height at zero moment; |
| Hm0,i—Incident wave height at zero moment in front of the structure at a distance of 1.5 m from the breakwater; |
| Hm0,r—Reflected wave height in front of the structure at a distance of 1.5 m from the breakwater. |
| Kt—Wave transmission coefficient; |
| KD—Wave dissipation coefficient; |
| Kr—Wave reflection coefficient at the front of the breakwater; |
| Lm—Wave length; |
| m0—Zero moment of the spectrum; |
| m-1—Zero moment of the spectrum; |
| NL—Length scale; |
| Nt—Time scale; |
| Rc—Crest freeboard; |
| S—Planned subsidence height; |
| Sop = Hm0/Lm—Wave steepness; |
| Tp—Deep-water wave period; |
| Tm-1,0—Wave period; |
| Ztp—Sea water level; |
| Z1%—Sea water level at the probability 1%; |
| Zs—Crest level of the submerged breakwater; |
| Ze—Crest level for the emerged breakwater. |
References
- Zapata, M.U.; Van Bang, D.P.; Nguyen, K.D. Unstructured Finite-Volume Model of Sediment Scouring Due to Wave Impact on Vertical Seawalls. J. Mar. Sci. Eng. 2021, 9, 1440. [Google Scholar] [CrossRef]
- Neelamani, S.; Sandhya, N. Wave reflection characteristics of plane, dentated and serrated seawalls. Ocean. Eng. 2003, 30, 1507–1533. [Google Scholar] [CrossRef]
- Tofany, N.; Ahmad, M.; Kartono, A.; Mamat, M.; Mohd-Lokman, H. Numerical modeling of the hydrodynamics of standing wave and scouring in front of impermeable breakwaters with different steepnesses. Ocean Eng. 2014, 88, 255–270. [Google Scholar] [CrossRef]
- Zanuttigh, B.; van der Meer, J.W. Wave reflection from coastal structures in design conditions. Coast. Eng. 2008, 55, 771–779. [Google Scholar] [CrossRef]
- d’Angremond, K.; Van Der Meer, J.W.; De Jong, R.J. Wave Transmission at Low-Crested Structures. In Proceedings of the 25th International Conference on Coastal Engineering, Orlando, FL, USA, 2–6 September 1996; ASCE: Reston, VA, USA, 1997; pp. 2418–2427. [Google Scholar]
- Santanu, K.; Panduranga, K.; Almashan, N.; Neelamani, S.; Al-Ragum, A. Numerical and experimental modelling of water wave interaction with rubble mound offshore porous breakwaters. Ocean. Eng. 2020, 218, 108218. [Google Scholar]
- Liu, H.-W.; Luo, H.; Zeng, H.-D. Optimal Collocation of Three Kinds of Bragg Breakwaters for Bragg Resonant Reflection by Long Waves. J. Waterw. Port Coast. Ocean. Eng. 2015, 141, 04014039. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Zang, J.; Dong, G.; Ma, X.; Zhu, Y.; Zhou, L. Numerical investigation of harbor oscillations induced by focused transient wave groups. Coast. Eng. 2020, 158, 103670. [Google Scholar] [CrossRef]
- Le Xuan, T.; Ba, H.T.; Le Manh, H.; Van, D.D.; Nguyen, N.M.; Wright, D.P.; Bui, V.H.; Mai, S.T.; Anh, D.T. Hydraulic performance and wave transmission through pile-rock breakwaters. Ocean Eng. 2020, 218, 108229. [Google Scholar] [CrossRef]
- Le Xuan, T.; Le Manh, H.; Ba, H.T.; Van, D.D.; Vu, H.T.D.; Wright, D.; Bui, V.H.; Anh, D.T. Wave energy dissipation through a hollow triangle breakwater on the coastal Mekong Delta. Ocean Eng. 2022, 245, 110419. [Google Scholar] [CrossRef]
- Nguyen, N.-M.; Van, D.D.; Le, D.T.; Nguyen, Q.; Pham, N.T.; Tanim, A.H.; Gagnon, A.S.; Wright, D.P.; Thanh, P.N.; Anh, D.T. Experimental modeling of bed morphological changes and toe erosion of emerged breakwaters due to wave-structure interactions in a deltaic coast. Mar. Geol. 2022, 454, 106932. [Google Scholar] [CrossRef]
- Chuong, L.T.; Phong, N.C. Computation of Wave and Water Level Combinations for Physical Model Test; Southern Institute of Water Resources Research: Ho-Chi-Minh City, Vietnam, 2019. [Google Scholar]
- TCVN-9901:2014; Hydraulic Structures. Sea Structure Design Standard. Available online: http://tlu.edu.vn/Portals/0/CRA/TCVN%209901.rar (accessed on 16 February 2022).
- HR Wallingford. Wave Probe Monitor—User Manual; HR Wallingford: Wallingford, UK, 2008.
- Mansard EP, D.; Funke, E.R. The Measurement of Incident and Reflected Spectra Using a Least squares Method. In Proceedings of the 17th International Conference on Coastal Engineering, Sydney, Australia, 23–28 March 1980. [Google Scholar]
- Tien, N.V.; Tuan, T.Q.; Truyen, L.K. Research of submerged breakwater and upstream zone effects on wave reducing effects using physical model with wave flume. J. Water Ressour. Environ. Technol. 2013, 4100011, 69–79. (In Vietnamese) [Google Scholar]

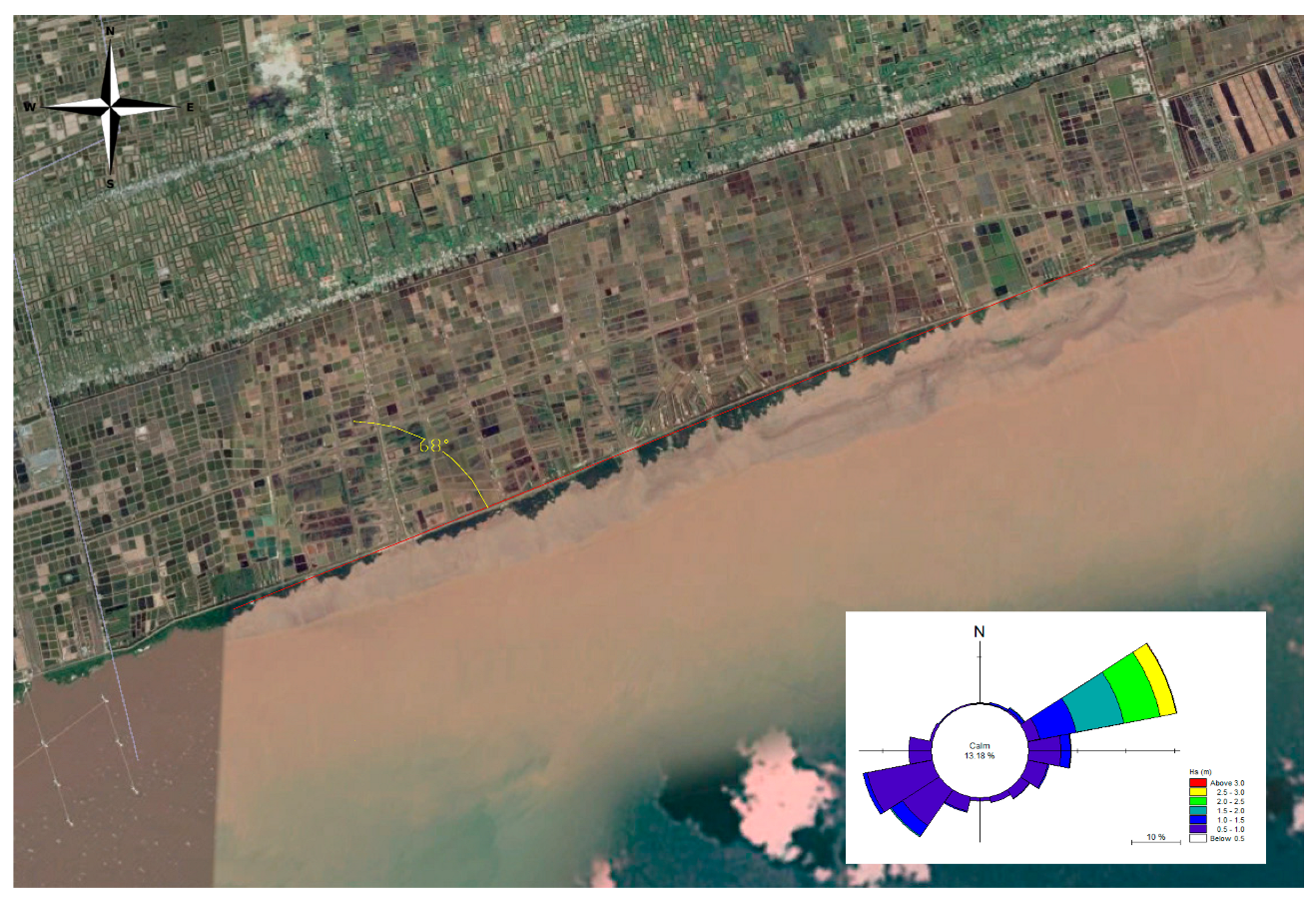










| Simulation Cases | Water Level (m) | Design Deep-Water Monsoon Wave: Hs = 3.03 m, T = 5.82 s | |
|---|---|---|---|
| Hs (m) | Tm-1,0 (s) | ||
| Tide level of Probability P = 1% | 1.53 | 0.81 | 4.83 |
| Model Scale | Value |
|---|---|
| Length scale NL | 7 |
| Time scale Nt | 2.65 |
| No | Experimental Model Pore Diameter | Prototype Pore Diameter |
|---|---|---|
| 1 | D = 4.1 cm | D = 30 cm |
| 2 | D = 5.7 cm | D = 40 cm |
| 3 | D = 7.3 cm | D = 50 cm |
| 4 | D = 8.9 cm | D = 60 cm |
| Test Cases | Front-Side and Back-Side Pore Diameter (cm) | Front-Side Pore Percentage (P1) | Back-Side Pore Percentage (P2) |
|---|---|---|---|
| TH2 | Di = 8.9 cm; Ds = 5.7 cm | 34.2% | 17.6% |
| TH3 (without pore on front side) | Di = 0.0 cm; Ds = 5.7 cm | 0.0% | 17.6% |
| TH4 | Di = 5.7 cm; Ds = 5.7 cm | 17.6% | 17.6% |
| TH5 | Di = 7.3 cm; Ds = 5.7 cm | 25.0% | 17.6% |
| TH6 | Di = 5.7 cm; Ds = 4.1 cm | 17.6% | 12.0% |
| TH7 | Di = 7.3 cm; Ds = 4.1 cm | 25.0% | 12.0% |
| Test Cases | Front-Side and Back-Side Pore Diameter (cm) | Water Depth d (cm) Crest Freeboard Rc (cm) | Wave Parameters |
|---|---|---|---|
| TH2 | Di = 8.9 cm; Ds = 5.7 cm | d = 47 cm (Rc = 0 cm) d = 33 cm (Rc = +14 cm) | Hs = 0.1 m; Tp = 1.5 s Hs = 0.1 m; Tp = 2.5 s Hs = 0.14 m; Tp = 1.5 s Hs = 0.14 m; Tp = 2.5 s |
| TH3 | Di = 0.0 cm; Ds = 5.7 cm | ||
| TH4 | Di = 5.7 cm; Ds = 5.7 cm | ||
| TH5 | Di = 7.3 cm; Ds = 5.7 cm | ||
| TH6 | Di = 5.7 cm; Ds = 4.1 cm | ||
| TH7 | Di = 7.3 cm; Ds = 4.1 cm |
| Test Cases | Water Depth d (cm) Crest Freeboard Rc (cm) | Wave Parameters |
|---|---|---|
| No structure | d = 47 cm (Rc = 0 cm) d = 40 cm (Rc = +7 cm) d = 33 cm (Rc = +14 cm) d = 26 cm (Rc = +21 cm) | Hs = 0.07 m; Tp = 1.2 s Hs = 0.10 m; Tp = 1.5 s Hs = 0.12 m; Tp = 1.6 s Hs = 0.14 m; Tp = 1.7 s Hs = 0.17 m; Tp = 1.8 s |
| With structure |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, C.T.; Do, D.V.; Nguyen, D.B.; Wang, P. A Laboratory Scale of the Physical Model for Inclined and Porous Breakwaters on the Coastline of Soc Trang Province (Mekong Delta). Water 2023, 15, 1366. https://doi.org/10.3390/w15071366
Le CT, Do DV, Nguyen DB, Wang P. A Laboratory Scale of the Physical Model for Inclined and Porous Breakwaters on the Coastline of Soc Trang Province (Mekong Delta). Water. 2023; 15(7):1366. https://doi.org/10.3390/w15071366
Chicago/Turabian StyleLe, Chuong Thanh, Duong Van Do, Duong Binh Nguyen, and Ping Wang. 2023. "A Laboratory Scale of the Physical Model for Inclined and Porous Breakwaters on the Coastline of Soc Trang Province (Mekong Delta)" Water 15, no. 7: 1366. https://doi.org/10.3390/w15071366
APA StyleLe, C. T., Do, D. V., Nguyen, D. B., & Wang, P. (2023). A Laboratory Scale of the Physical Model for Inclined and Porous Breakwaters on the Coastline of Soc Trang Province (Mekong Delta). Water, 15(7), 1366. https://doi.org/10.3390/w15071366







