Application of Newton–Raphson Method for Computing the Final Air–Water Interface Location in a Pipe Water Filling
Abstract
:1. Introduction
2. Numerical Approach
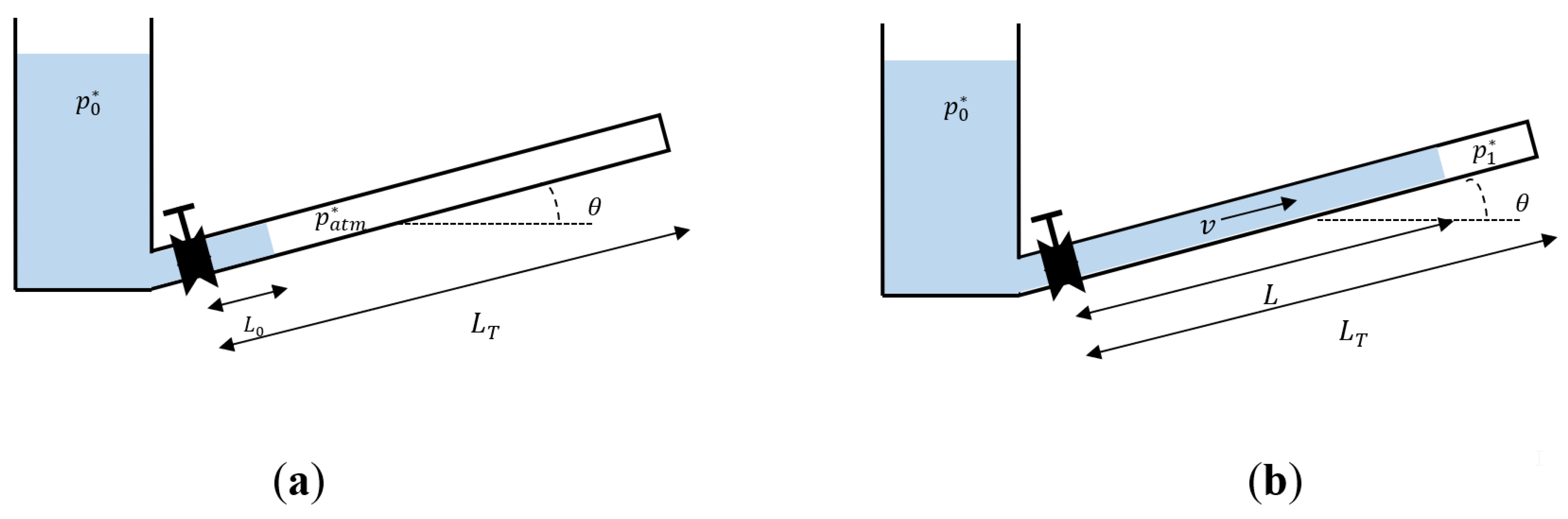
2.1. Filling Operation
2.2. Governing Equations
- Air–water interface position is given by:
- Polytropic model: this formulation describes how the air pocket size changes with air pocket pressure pulses. These changes are described by the polytropic law (see Equation (3)), which is applied without injected air into hydraulic installations.
2.3. Initial Conditions
2.4. Velocity Field
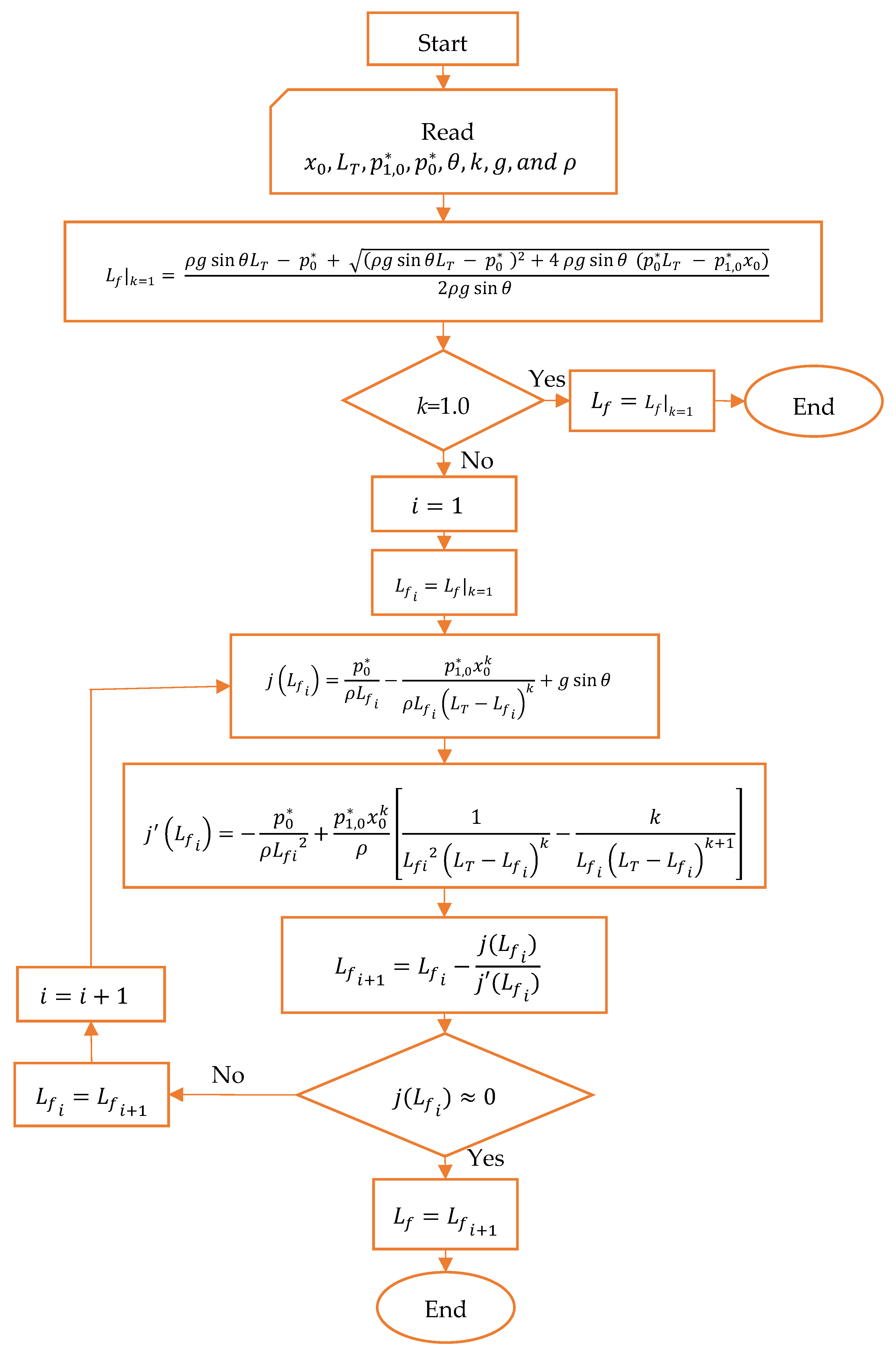
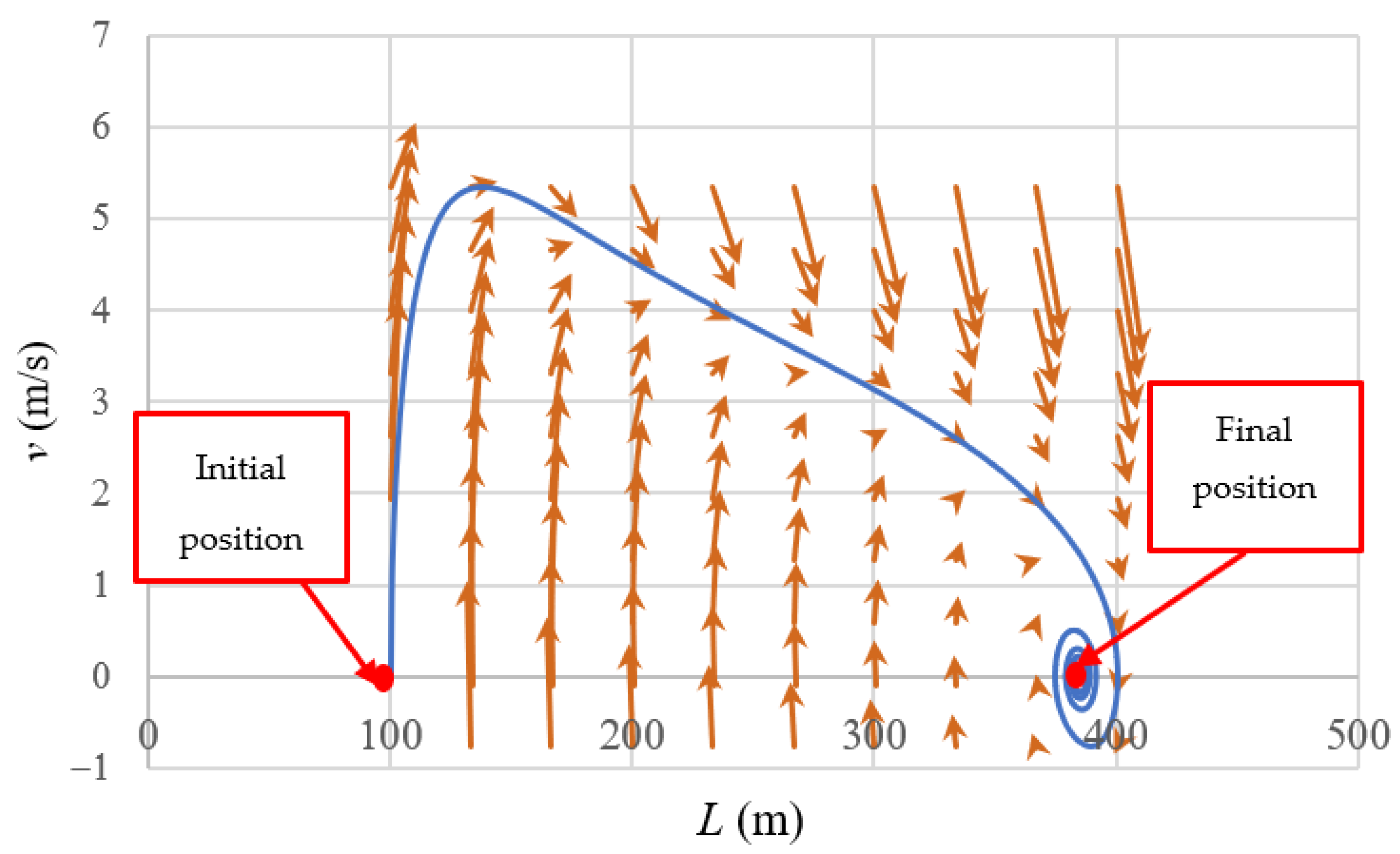
2.5. Computation of Critical Point
3. Analysis of Results and Discussion
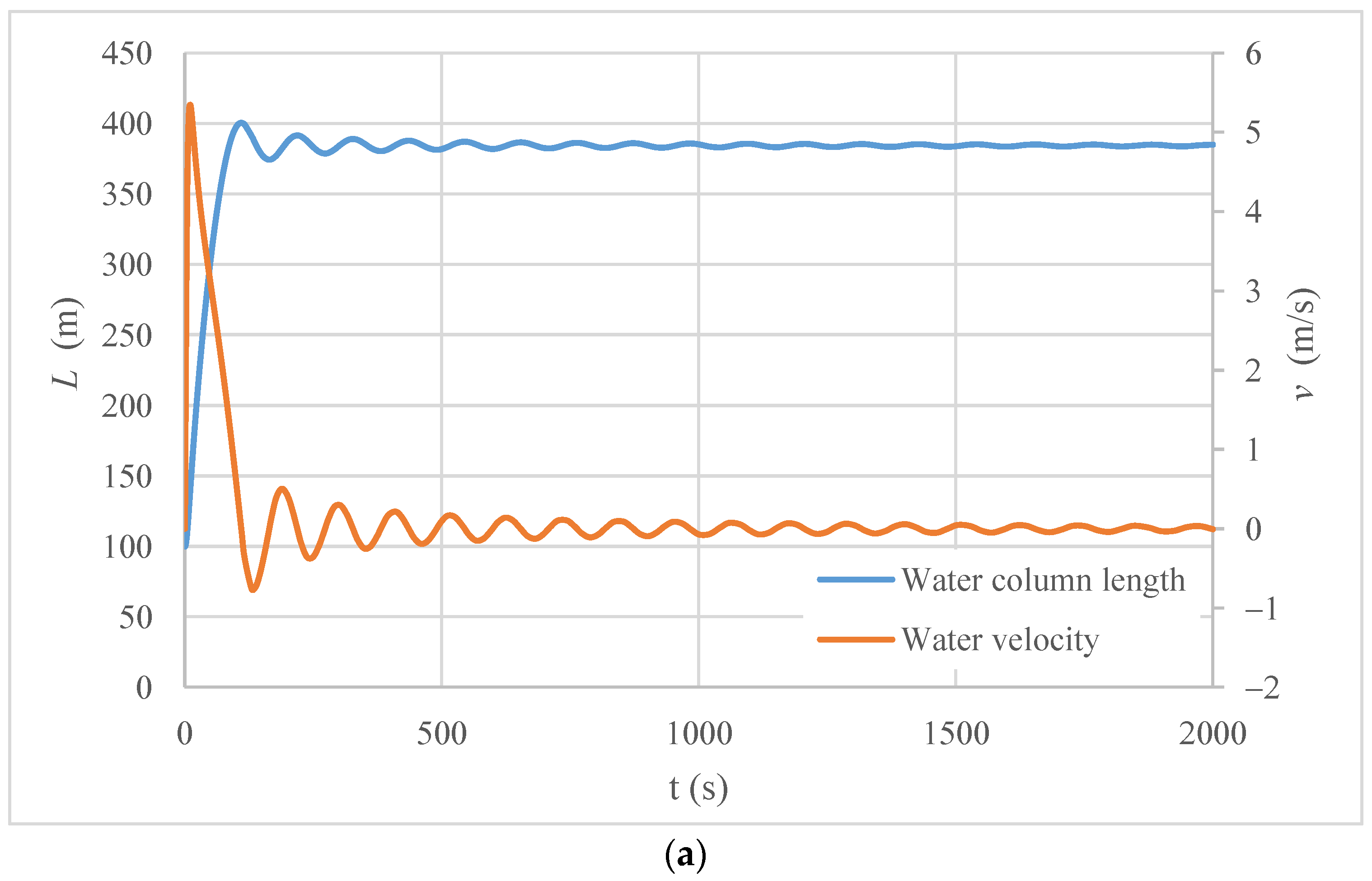
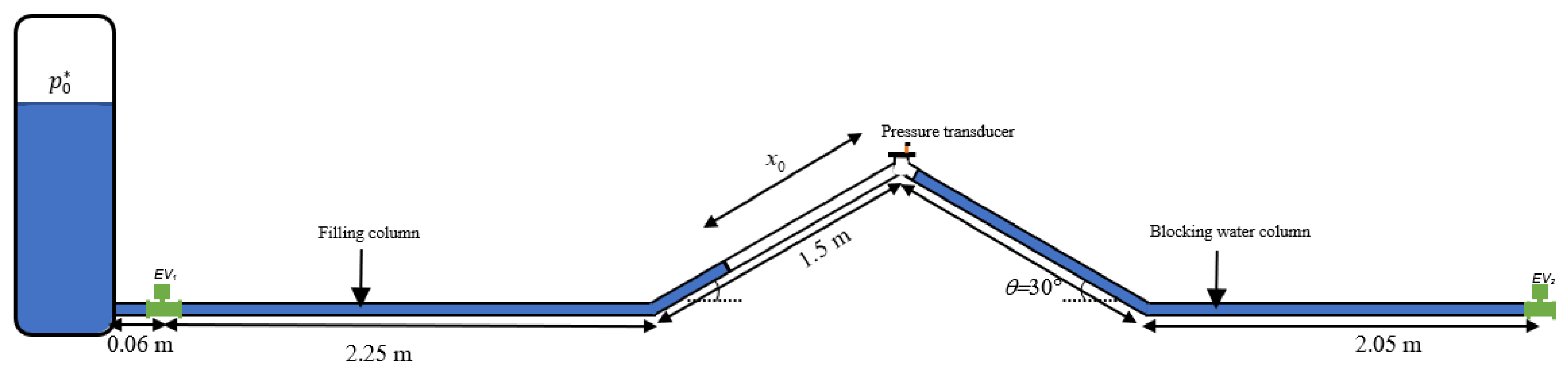
3.1. Case Study
3.2. Final Position of Air–Water Interface
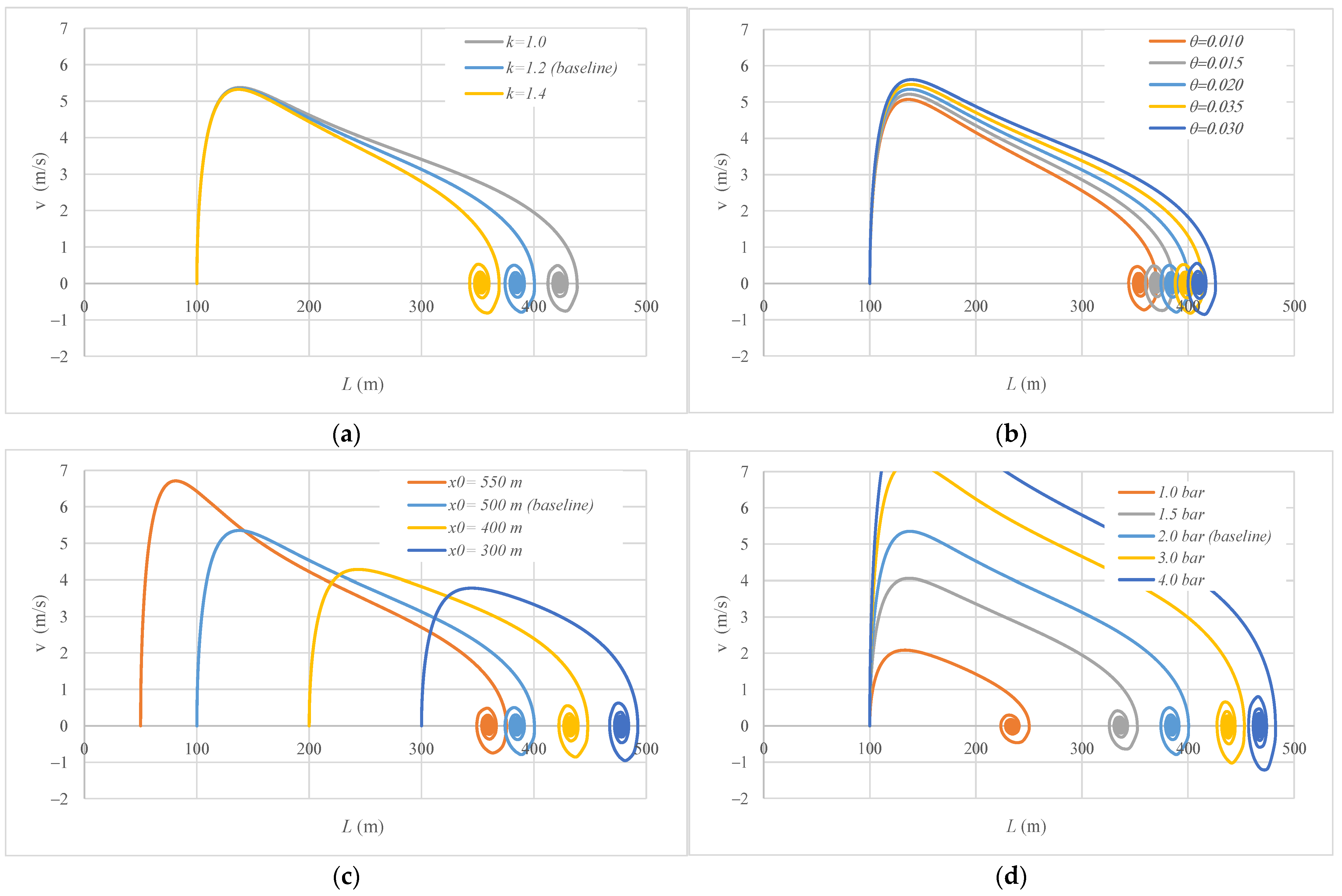
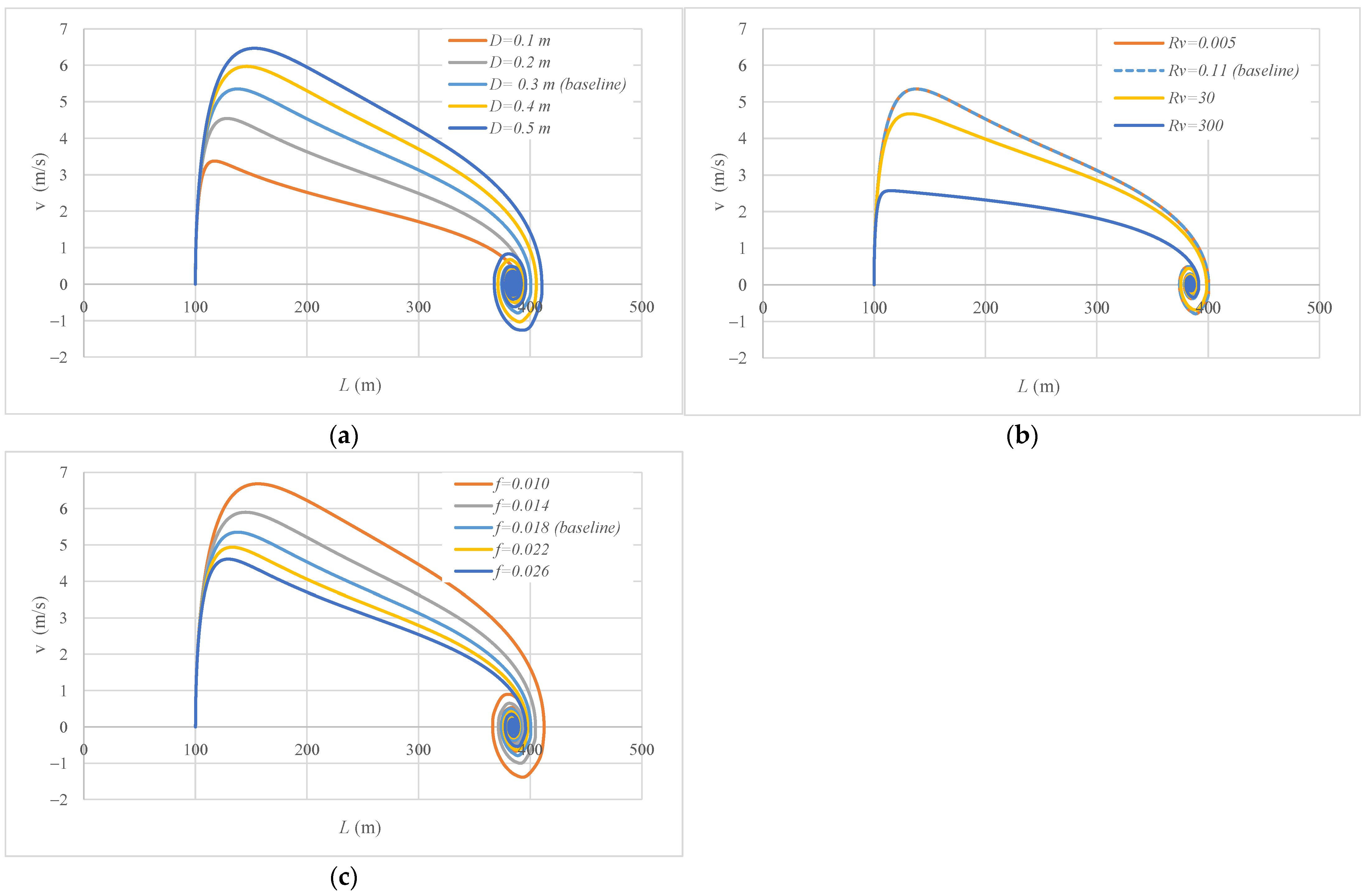
3.3. Sensitivity Analysis
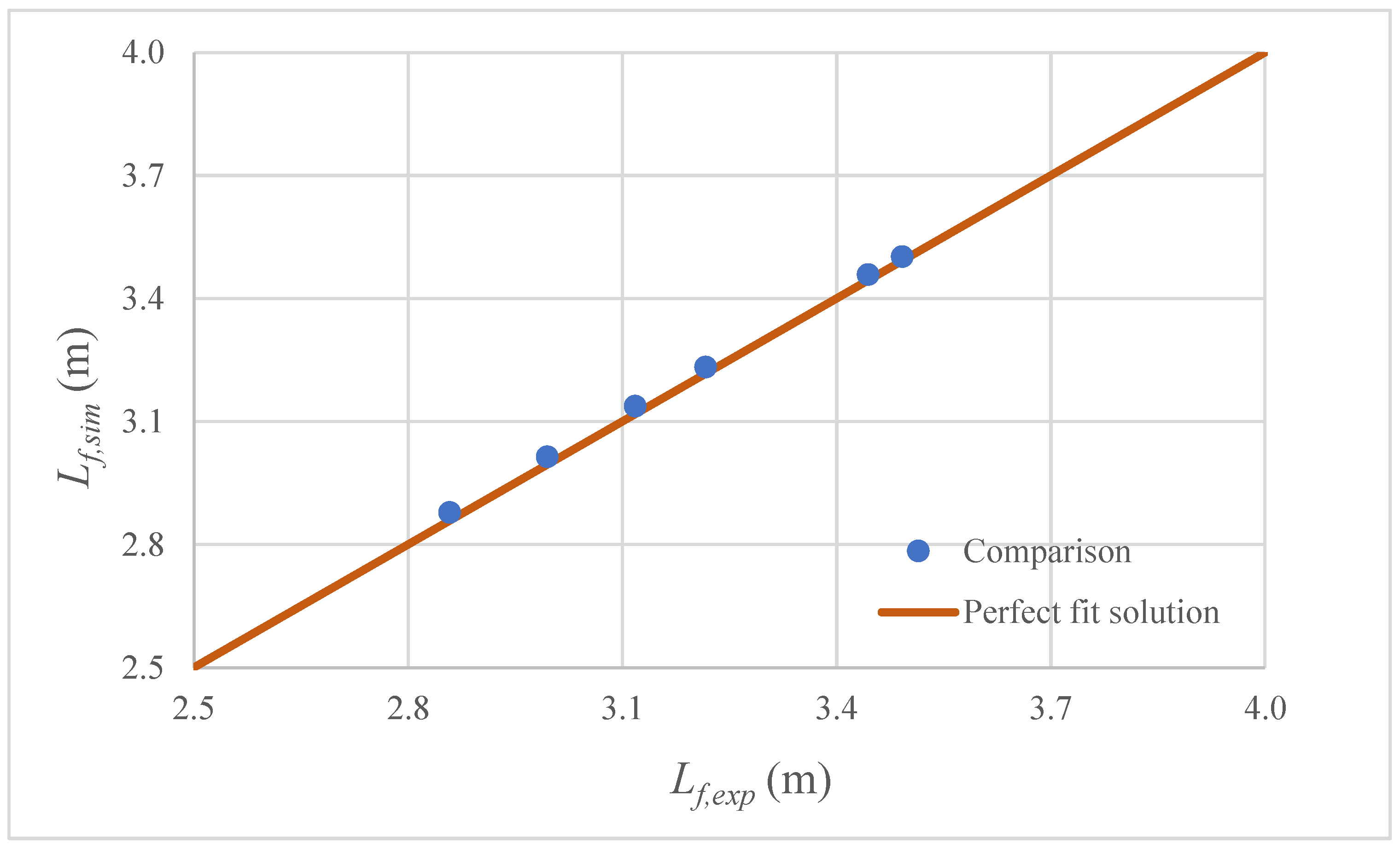
3.4. Experimental Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Cross-sectional area of pipe (m2) |
| D | Internal pipe diameter (m) |
| f | Friction factor (-) |
| g | Gravity acceleration (m s−2) |
| k | Polytropic coefficient (-) |
| j | Used function in the Newton–Raphson equation |
| L | Water column length (m) |
| LT | Pipe length (m) |
| p0* | Initial absolute pressure supplied by an energy source (Pa) |
| patm* | Atmospheric pressure (101,325 Pa) |
| p*1 | Air pocket pressure (Pa) |
| Rv | Resistance coefficient (ms2m−6) |
| t | Time (s) |
| v | Water velocity (m s−1) |
| V | Vector field on a region in the plane (L, v) |
| x | Air pocket size (m) |
| X | Vector function of t |
| Water density (kg m−3) | |
| θ | Pipe slope (rad) |
| γw | Water unit weight (N m−3) |
| Subscripts | |
| 0 | Refers to an initial condition |
| f | Refers to a final condition |
| i | Iteration number |
| s | Specific experimental test |
| Superscripts | |
| ‘ | Derivative |
References
- Tasca, E.; Besharat, M.; Ramos, H.M.; Luvizotto, E., Jr.; Karney, B. Contribution of Air Management to the Energy Efficiency of Water Pipelines. Sustainability 2023, 15, 3875. [Google Scholar] [CrossRef]
- Martins, N.M.; Soares, A.K.; Ramos, H.M.; Covas, D.I. CFD modeling of transient flow in pressurized pipes. Comput. Fluids 2016, 126, 129–140. [Google Scholar] [CrossRef]
- Maddahian, R.; Shaygan, F.; Bucur, D.M. Developing a 1D-3D model to investigate the effect of entrapped air on pressure surge during the rapid filling of a pipe. IOP Conf. Ser. Earth Environ. Sci. 2021, 774, 012069. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Mora-Melia, D.; Iglesias-Rey, P.L. Hydraulic Modeling during Filling and Emptying Processes in Pressurized Pipelines: A Literature Review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- AWWA (American Water Works Association). Manual of Water Supply Practices M51—Air Valves: Air Release, Air/Vacuum and Combination; AWWA: Denver, CO, USA, 2016. [Google Scholar]
- Zhou, L.; Liu, D. Experimental Investigation of Entrapped Air Pocket in a Partially Full Water Pipe. J. Hydraul. Res. 2013, 51, 469–474. [Google Scholar] [CrossRef]
- Tijsseling, A.S.; Hou, Q.; Bozkuş, Z. Rapid Liquid Filling of a Pipe With Venting Entrapped Gas: Analytical and Numerical Solutions. J. Press. Vessel. Technol. 2019, 141, 041301. [Google Scholar] [CrossRef]
- Liou, C.P.; Hunt, W.A. Filling of pipelines with undulating elevation profiles. J. Hydraul. Eng. 1996, 122, 534–539. [Google Scholar] [CrossRef]
- Izquierdo, J.; Fuertes, V.; Cabrera, E.; Iglesias, P.; Garcia-Serra, J. Pipeline start-up with entrapped air. J. Hydraul. Res. 1999, 37, 579–590. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, L.; Liu, D.; Karney, B.; Wang, P.; Xia, L.; Ma, J.; Xu, C. CFD approach for column separation in water pipelines. J. Hydraul. Eng. 2016, 142, 04016036. [Google Scholar] [CrossRef] [Green Version]
- Chan, S.N.; Cong, J.; Lee, J.H. 3d numerical modeling of geyser formation by release of entrapped air from horizontal pipe into vertical shaft. J. Hydraul. Eng. 2018, 144, 04017071. [Google Scholar] [CrossRef]
- Wang, J.; Vasconcelos, J. Manhole cover displacement caused by the release of entrapped air pockets. J. Water Manag. Model. 2018, 26, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Martins, N.M.; Delgado, J.N.; Ramos, H.M.; Covas, D.I. Maximum transient pressures in a rapidly filling pipeline with entrapped air using a CFD model. J. Hydraul. Res. 2017, 55, 506–519. [Google Scholar] [CrossRef]
- Tijsseling, A.; Hou, Q.; Bozku¸s, Z.; Laanearu, J. Improved One-Dimensional Models for Rapid Emptying and Filling of Pipelines. J. Press. Vessel Technol. 2016, 138, 031301. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Cao, Y.; Karney, B.; Vasconcelos, J.; Liu, D.; Wang, P. Unsteady friction in transient vertical-pipe flow with trapped air. J. Hydraul. Res. 2021, 59, 820–834. [Google Scholar] [CrossRef]
- Zhou, L.; Pan, T.; Wang, H.; Liu, D.; Wang, P. Rapid air expulsion through an orifice in a vertical water pipe. J. Hydraul. Res. 2019, 57, 307–317. [Google Scholar] [CrossRef]
- Zhou, L.; Cao, Y.; Karney, B.; Bergant, A.; Tijsseling, A.S.; Liu, D.; Wang, P. Expulsion of Entrapped Air in a Rapidly Filling Horizontal Pipe. J. Hydraul. Eng. 2020, 146, 04020047. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Bonilla-Correa, D.M.; Lovo, A.; Fuertes-Miquel, V.S.; Gatica, G.; Linfati, R.; Coronado-Hernández, J.R. An Implicit Formulation for Calculating Final Conditions in Drainage Maneuvers in Pressurized Water Installations. Water 2022, 14, 3364. [Google Scholar] [CrossRef]
- Canelon, D.J. Pivoting Strategies in the Solution of the Saint-Venant Equations. J. Irrig. Drain. Eng. 2009, 135, 96–101. [Google Scholar] [CrossRef]
- Martin, C.S. Entrapped Air in Pipelines. In Proceedings of the Second International Conference on Pressure Surges, London, UK, 22–24 September 1976. [Google Scholar]
- Chapra, S.; Canale, R. Numerical Methods for Engineers, 7th ed.; Mcgraw-Hill Education, Cop: New York, NY, USA, 2015. [Google Scholar]



| 0 | 422.58 | −0.15559 | −0.00479 | 390.10 | −32.48 |
| 1 | 390.10 | −0.02036 | −0.00365 | 384.53 | −5.57 |
| 2 | 384.53 | −0.00038 | −0.00352 | 384.42 | −0.11 |
| 3 | 384.42 | 0.00000 | −0.00352 | 384.42 | 0.00 |
| Test No. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| x0 (m) | 0.46 | 0.96 | 1.36 | 0.46 | 0.96 | 1.36 |
| (bar) | 1.75 | 1.75 | 1.75 | 2.25 | 2.25 | 2.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonilla-Correa, D.M.; Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Application of Newton–Raphson Method for Computing the Final Air–Water Interface Location in a Pipe Water Filling. Water 2023, 15, 1304. https://doi.org/10.3390/w15071304
Bonilla-Correa DM, Coronado-Hernández ÓE, Fuertes-Miquel VS, Besharat M, Ramos HM. Application of Newton–Raphson Method for Computing the Final Air–Water Interface Location in a Pipe Water Filling. Water. 2023; 15(7):1304. https://doi.org/10.3390/w15071304
Chicago/Turabian StyleBonilla-Correa, Dalia M., Óscar E. Coronado-Hernández, Vicente S. Fuertes-Miquel, Mohsen Besharat, and Helena M. Ramos. 2023. "Application of Newton–Raphson Method for Computing the Final Air–Water Interface Location in a Pipe Water Filling" Water 15, no. 7: 1304. https://doi.org/10.3390/w15071304







