Shoreline Temporal Variability Inferred from Satellite Images at Mar del Plata, Argentina
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Shoreline Detection
2.3. Beach Width Variation
3. Results
3.1. Seasonal Variability
3.2. Interannual Variability
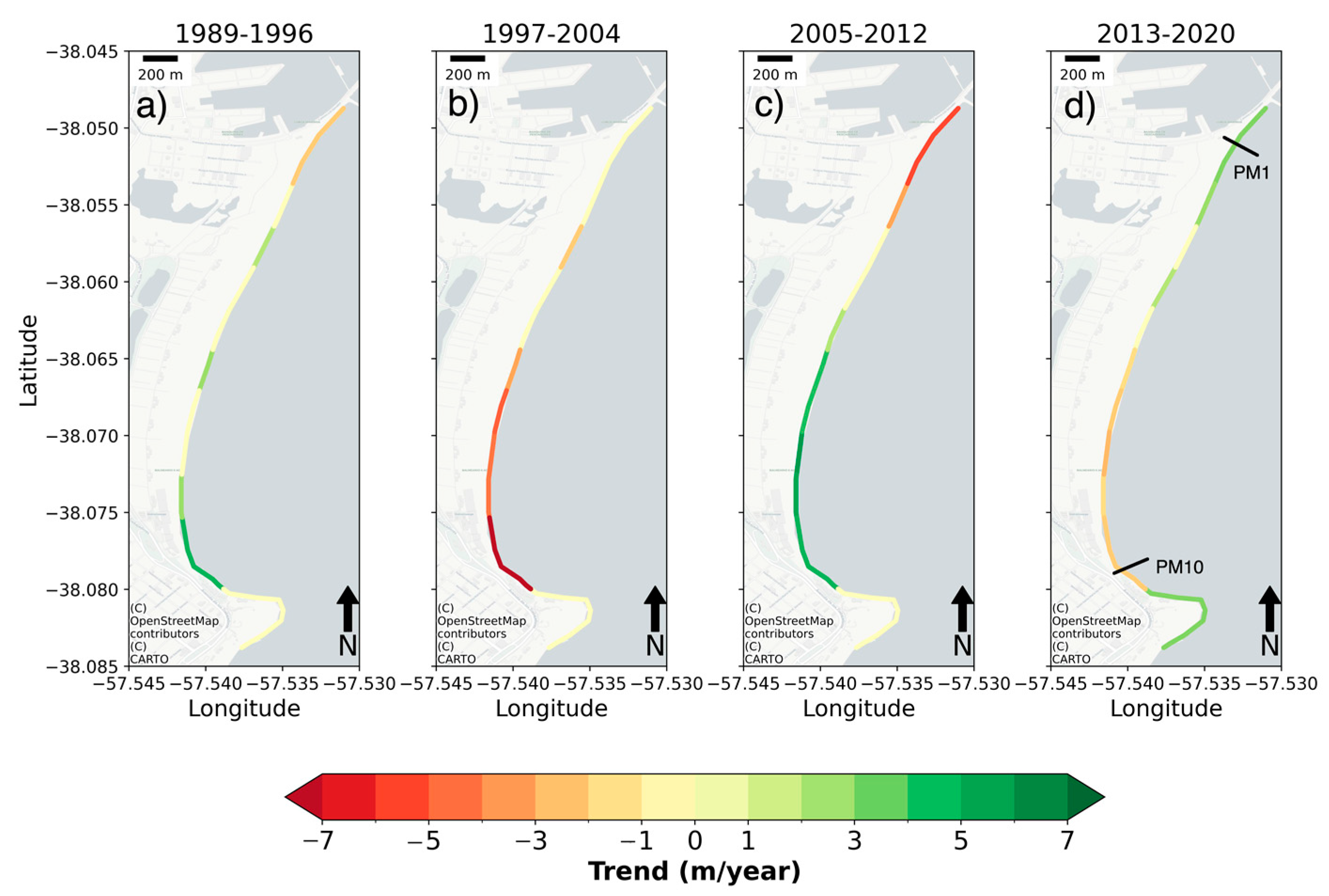
3.3. Long-Term Trends
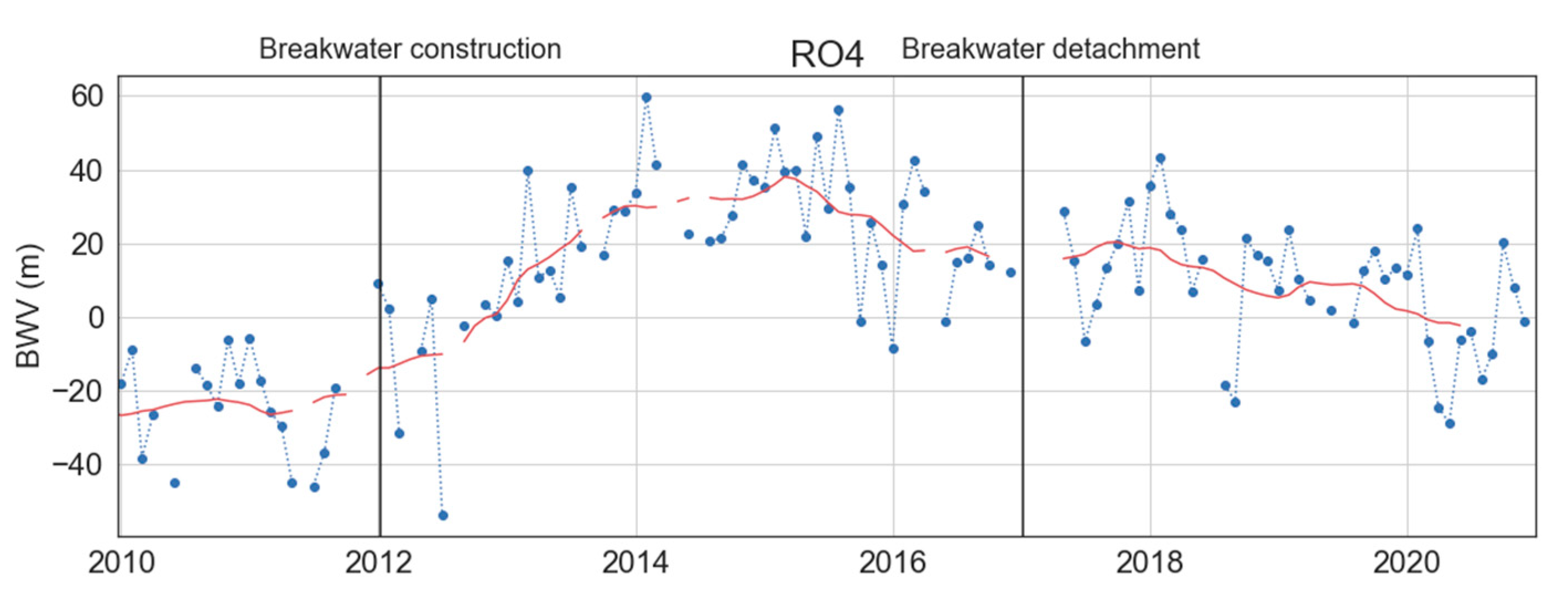
3.4. Anthropic Interventions
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Senechal, N.; de Alegría-Arzaburu, A.R. Seasonal imprint on beach morphodynamics. In Sandy Beach Morphodynamics; Elsevier: Amsterdam, The Netherlands, 2020; pp. 461–486. [Google Scholar] [CrossRef]
- Castelle, B.; Guillot, B.; Marieu, V.; Chaumillon, E.; Hanquiez, V.; Bujan, S.; Poppeschi, C. Spatial and temporal patterns of shoreline change of a 280-km high-energy disrupted sandy coast from 1950 to 2014: SW France. Estuar. Coast. Shelf Sci. 2018, 200, 212–223. [Google Scholar] [CrossRef]
- Harley, M. Coastal storm definition. In Coastal Storms: Processes and Impacts; Wiley-Blackwell: Hoboken, NJ, USA, 2017; pp. 1–21. [Google Scholar] [CrossRef]
- Castelle, B.; Masselink, G.; Scott, T.; Stokes, C.; Konstantinou, A.; Marieu, V.; Bujan, S. Satellite-derived shoreline detection at a high-energy meso-macrotidal beach. Geomorphology 2021, 383, 107707. [Google Scholar] [CrossRef]
- Merkens, J.L.; Reimann, L.; Hinkel, J.; Vafeidis, A.T. Gridded population projections for the coastal zone under the Shared Socioeconomic Pathways. Glob. Planet. Chang. 2016, 145, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Ranasinghe, R. Assessing climate change impacts on open sandy coasts: A review. Earth Sci. Rev. 2016, 160, 320–332. [Google Scholar] [CrossRef] [Green Version]
- Vitousek, S.; Barnard, P.L.; Limber, P. Can beaches survive climate change? J. Geophys. Res. Earth Surf. 2017, 122, 1060–1067. [Google Scholar] [CrossRef]
- Vousdoukas, M.I.; Ranasinghe, R.; Mentaschi, L.; Plomaritis, T.A.; Athanasiou, P.; Luijendijk, A.; Feyen, L. Sandy coastlines under threat of erosion. Nat. Clim. Chang. 2020, 10, 260–263. [Google Scholar] [CrossRef]
- Antonioli, F.; Anzidei, M.; Amorosi, A.; Lo Presti, V.; Mastronuzzi, G.; Deiana, G.; De Falco, G.; Fontana, A.; Fontolan, G.; Lisco, S.; et al. Sea-level rise and potential drowning of the Italian coastal plains: Flooding risk scenarios for 2100. Quat. Sci. Rev. 2017, 158, 29–43. [Google Scholar] [CrossRef] [Green Version]
- Marsico, A.; Lisco, S.; Lo Presti, V.; Antonioli, F.; Amorosi, A.; Anzidei, M.; Deiana, G.; De Falco, G.; Fontana, A.; Fontolan, G.; et al. Flooding scenario for four Italian coastal plains using three relative sea level rise models. J. Maps 2017, 13, 961–967. [Google Scholar] [CrossRef] [Green Version]
- Barnard, P.L.; Short, A.D.; Harley, M.D.; Splinter, K.D.; Vitousek, S.; Turner, I.L.; Allan, J.; Banno, M.; Bryan, K.R.; Doria, A.; et al. Coastal vulnerability across the Pacific dominated by El Niño/Southern oscillation. Nat. Geosci. 2015, 8, 801–807. [Google Scholar] [CrossRef]
- Turner, I.L.; Harley, M.D.; Short, A.D.; Simmons, J.A.; Bracs, M.A.; Phillips, M.S.; Splinter, K.D. A multi-decade dataset of monthly beach profile surveys and inshore wave forcing at Narrabeen, Australia. Sci. Data 2016, 3, 160024. [Google Scholar] [CrossRef] [Green Version]
- Banno, M.; Nakamura, S.; Kosako, T.; Nakagawa, Y.; Yanagishima, S.I.; Kuriyama, Y. Long-term observations of beach variability at Hasaki, Japan. J. Mar. Sci. Eng. 2020, 8, 871. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Toure, S.; Diop, O.; Kpalma, K.; Maiga, A.S. Shoreline detection using optical remote sensing: A review. ISPRS Int. J. Geo-Inf. 2019, 8, 75. [Google Scholar] [CrossRef] [Green Version]
- Almonacid-Caballer, J.; Sánchez-García, E.; Pardo-Pascual, J.E.; Balaguer-Beser, A.A.; Palomar-Vázquez, J. Evaluation of annual mean shoreline position deduced from Landsat imagery as a mid-term coastal evolution indicator. Mar. Geol. 2016, 372, 79–88. [Google Scholar] [CrossRef]
- Liu, Q.; Trinder, J.; Turner, I.L. Automatic super-resolution shoreline changes monitoring using Landsat archival data: A case study at Narrabeen–Collaroy Beach, Australia. J. Appl. Remote Sens. 2017, 11, 016036. [Google Scholar] [CrossRef]
- Hagenaars, G.; de Vries, S.; Luijendijk, A.P.; de Boer, W.P.; Reniers, A.J.H.M. On the accuracy of automated shoreline detection derived from satellite imagery: A case study of the sand motor mega-scale nourishment. Coast. Eng. 2018, 133, 113–125. [Google Scholar] [CrossRef]
- Vos, K.; Harley, M.D.; Splinter, K.D.; Simmons, J.A.; Turner, I.L. Sub-annual to multi-decadal shoreline variability from publicly available satellite imagery. Coast. Eng. 2019, 150, 160–174. [Google Scholar] [CrossRef]
- Bishop-Taylor, R.; Nanson, R.; Sagar, S.; Lymburner, L. Mapping Australia’s dynamic coastline at mean sea level using three decades of Landsat imagery. Remote Sens. Environ. 2021, 267, 112734. [Google Scholar] [CrossRef]
- Pardo-Pascual, J.E.; Sánchez-García, E.; Almonacid-Caballer, J.; Palomar-Vázquez, J.M.; Priego De Los Santos, E.; Fernández-Sarría, A.; Balaguer-Beser, Á. Assessing the accuracy of automatically extracted shorelines on microtidal beaches from Landsat 7, Landsat 8 and Sentinel-2 imagery. Remote Sens. 2018, 10, 326. [Google Scholar] [CrossRef] [Green Version]
- Douglas, B.C.; Crowell, M. Long-term shoreline position prediction and error propagation. J. Coast. Res. 2000, 16, 145–152. [Google Scholar]
- Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef] [Green Version]
- Genz, A.S.; Fletcher, C.H.; Dunn, R.A.; Frazer, L.N.; Rooney, J.J. The Predictive Accuracy of Shoreline Change Rate Methods and Alongshore Beach Variation on Maui, Hawaii. J. Coast. Res. 2007, 231, 87–105. [Google Scholar] [CrossRef] [Green Version]
- Hapke, C.J.; Himmelstoss, E.; A Kratzmann, M.; List, J.H.; Thieler, E.R. National Assessment of Shoreline Change: Historical Shoreline Change along the New England and Mid-Atlantic Coasts Open-File Report 2010—1118; U.S. Geological Survey: Reston, VA, USA, 2010; Volume 57. [CrossRef] [Green Version]
- Bacino, G.L.; Dragani, W.C.; Codignotto, J.O.; Pescio, A.E.; Farenga, M.O. Shoreline change rates along Samborombón Bay, Río de la Plata estuary, Argentina. Estuar. Coast. Shelf Sci. 2020, 237, 106659. [Google Scholar] [CrossRef]
- Indiveri, A.; Marsico, A.; Pennetta, L. Erosion hazard assessment along the Capitolo coast (Monopoli, southern Italy). J. Maps 2013, 9, 274–278. [Google Scholar] [CrossRef]
- De Santis, V.; Caldara, M.; Marsico, A.; Capolongo, D.; Pennetta, L. Evolution of the Ofanto River delta from the ‘Little Ice Age’to modern times: Implications of large-scale synoptic patterns. Holocene 2018, 28, 1948–1967. [Google Scholar] [CrossRef]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The state of the world’s beaches. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef]
- Vos, K.; Splinter, K.D.; Harley, M.D.; Simmons, J.A.; Turner, I.L. CoastSat: A Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Model. Softw. 2019, 122, 104528. [Google Scholar] [CrossRef]
- Sánchez-García, E.; Palomar-Vázquez, J.M.; Pardo-Pascual, J.E.; Almonacid-Caballer, J.; Cabezas-Rabadán, C.; Gómez-Pujol, L. An efficient protocol for accurate and massive shoreline definition from mid-resolution satellite imagery. Coast. Eng. 2020, 160, 103732. [Google Scholar] [CrossRef]
- Pucino, N.; Kennedy, D.M.; Young, M.; Ierodiaconou, D. Assessing the accuracy of Sentinel-2 instantaneous subpixel shorelines using synchronous UAV ground truth surveys. Remote Sens. Environ. 2022, 282, 113293. [Google Scholar] [CrossRef]
- Merlotto, A.; Verón, E.M. Evaluación de los servicios culturales de recreación y turismo del ecosistema playa en la ciudad de Mar del Plata, Argentina. Rev. Univ. Georg. 2019, 28, 35–56. [Google Scholar]
- Isla, F.I.; Cortizo, L.; Merlotto, A.; Bértola, G.; Albisetti, M.P.; Finocchietti, C. Erosion in Buenos Aires province: Coastal-management policy revisited. Ocean Coast. Manag. 2018, 156, 107–116. [Google Scholar] [CrossRef]
- Marcomini, S.C.; López, R.A. Alteración de la dinámica costera por efecto de la explotación de arena de playa, partidos de General Alvarado y Lobería, Provincia de Buenos Aires. Rev. Asoc. Argent. Sedimentol. 1991, 6, 1–18. [Google Scholar]
- Bértola, G.R. Morfodinamica de playas del sudeste de la provincia de Buenos Aires (1983 a 2004). Lat. Am. J. Sedimentol. Basin Anal. 2006, 13, 31–57. [Google Scholar]
- Bértola, G.R.; del Río, J.L.; Farenga, M.O. Relleno de playa en Honu Beach (Mar del Plata, Argentina. Rev. Geol. Apl. Ing. Ambiente 2016, 37, 1–11. [Google Scholar]
- Veneziano, M.F.; García, M.C. Protección costera y regeneración de playas en el sur de municipio de Gral. Pueyrredón, Pcia. de Buenos Aires. In Proceedings of the II Jornadas Nacionales de Ambiente, Buenos Aires, Argentina, 19–21 November 2014. [Google Scholar]
- Pousa, J.L.; D’Onofrio, E.E.; Fiore, M.M.; Kruse, E.E. Environmental impacts and simultaneity of positive and negative storm surges on the coast of the Province of Buenos Aires, Argentina. Environ. Earth Sci. 2013, 68, 2325–2335. [Google Scholar] [CrossRef]
- Fiore, M.M.; D’Onofrio, E.E.; Pousa, J.L.; Schnack, E.J.; Bértola, G.R. Storm surges and coastal impacts at Mar del Plata, Argentina. Cont. Shelf Res. 2009, 29, 1643–1649. [Google Scholar] [CrossRef]
- Isla, F.I. Variaciones espaciales y temporales de la deriva litoral, SE de la Provincia de Buenos Aires, Argentina. Rev. Geo. Sur. 2015, 5, 24–41. [Google Scholar]
- Prario, B.; Dragani, W. Estimación del clima de olas en dos sitios costeros de Mar del Plata para el aprovechamiento de energía undimotriz. In Technical Report SHN 01/19-DC, Servicio de Hidrografía Naval, Ministerio de Defensa; Servicio de Hidrografía Naval: Ciudad Autónoma de Buenos Aires, Argentina, 2019; 11p. [Google Scholar]
- Law-Chune, S.; Aouf, L.; Dalphinet, A.; Levier, B.; Drillet, Y.; Drevillon, M. Waverys: A CMEMS global wave reanalysis during the altimetry period. Ocean Dyn. 2021, 71, 357–378. [Google Scholar] [CrossRef]
- Caviglia, F.J.; Pousa, J.L.; Lanfredi, N.W. A determination of the energy flux constant from dredge records. J. Coast. Res. 1991, 543–549. [Google Scholar]
- Isla, F.I.; Cortizo, L.C. Sediment input from fluvial sources and cliff erosion to the continental shelf of Argentina. Rev. Gestão Costeira Integr. -J. Integr. Coast. Zone Manag. 2014, 14, 541–552. [Google Scholar] [CrossRef] [Green Version]
- Hernández, F.M. Entre el Estado, la playa y la pared: Tramas y conflictos de la política de cemento en los complejos balnearios de Punta Mogotes y La Perla, Mar del Plata. In Proceedings of the I Jornadas Platenses de Geografía, La Plata, Argentina, 17–19 October 2019. [Google Scholar]
- Bértola, G.; Cortizo, L.C. Transporte de arena en médanos litorales activos y colgados del sudeste de Buenos Aires. Rev. Asoc. Geol. Argent. 2005, 60, 174–184. [Google Scholar]
- Wijedasa, L.S.; Sloan, S.; Michelakis, D.G.; Clements, G.R. Overcoming limitations with Landsat imagery for mapping of peat swamp forests in Sundaland. Remote Sens. 2012, 4, 2595. [Google Scholar] [CrossRef] [Green Version]
- Davis, J.C.; Sampson, R.J. Statistics and Data Analysis in Geology; Wiley: New York, NY, USA, 1986; Volume 646. [Google Scholar]
- Swales, A. Geostatistical estimation of short-term changes in beach morphology and sand budget. J. Coast. Res. 2002, 18, 338–351. [Google Scholar]
- Harley, M.D.; Turner, I.L.; Short, A.D.; Ranasinghe, R. Assessment and integration of conventional, RTK-GPS and image-derived beach survey methods for daily to decadal coastal monitoring. Coast. Eng. 2011, 58, 194–205. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Sciarrone, R.; Melendez, R.; Loschacoff, S.Y. Rompeolas Aislados como Estructuras de Proteccion Costera, Recuperacion de Playas. Asociación Argentina de Ingenieros Portuarios. 2012. Available online: http://www.aadip.org.ar/pdf/papers/seccion1/Sciarrone-Loschacoff.pdf (accessed on 29 July 2022).
- Ceccon, P.E.S.; Armaroli, C. Performance of remote sensing algorithms for shoreline mapping under different beach morphodynamic conditions (No. EGU21-13028). In Proceedings of the 23rd EGU General Assembly, Online, 19–30 April 2021. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H., Jr. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- McAllister, E.; Payo, A.; Novellino, A.; Dolphin, T.; Medina-Lopez, E. Multispectral satellite imagery and machine learning for the extraction of shoreline indicators. Coast. Eng. 2022, 174, 104102. [Google Scholar] [CrossRef]
- Mao, Y.; Harris, D.L.; Xie, Z.; Phinn, S. Efficient measurement of large-scale decadal shoreline change with increased accuracy in tide-dominated coastal environments with Google Earth Engine. ISPRS J. Photogramm. Remote Sens. 2021, 181, 385–399. [Google Scholar] [CrossRef]
- Ding, Y.; Yang, X.; Jin, H.; Wang, Z.; Liu, Y.; Liu, B.; Zhang, J.; Liu, X.; Gao, K.; Meng, D. Monitoring coastline changes of the malay islands based on google earth engine and dense time-series remote sensing images. Remote Sens. 2021, 13, 3842. [Google Scholar] [CrossRef]
- Isla, F.I.; Bértola, G.; Farenga, M.; Cortizo, L. Variaciones antropogénicas de las playas del sudeste de Buenos Aires, Argentina. Pesqui. Geociênc. 2001, 28, 27–35. [Google Scholar] [CrossRef] [Green Version]
- Farenga, M.O.; Adamini, R.; Isla, F.I. Recuperación de playas de intensa extracción de arena: Ensenada de Mogotes, Mar del Plata, Argentina, 1987–1990. Thalassas Int. J. Mar. Sci. 1992, 10, 41–47. [Google Scholar]
- Lamarchina, S.; Maenza, R.A.; Isla, F.I. Mixed sand and gravel beaches of Buenos Aires, Argentina. Morphodynamics and stability. J. Coast. Conserv. 2021, 25, 1–11. [Google Scholar] [CrossRef]
- Masselink, G.; Pattiaratchi, C.B. Seasonal changes in beach morphology along the sheltered coastline of Perth, Western Australia. Mar. Geol. 2001, 172, 243–263. [Google Scholar] [CrossRef]
- Orlando, L.; Ortega, L.; Defeo, O. Multi-decadal variability in sandy beach area and the role of climate forcing. Estuar. Coast. Shelf Sci. 2019, 218, 197–203. [Google Scholar] [CrossRef]
- Young, I.R.; Ribal, A. Multiplatform evaluation of global trends in wind speed and wave height. Science 2019, 80, eaav9527. [Google Scholar] [CrossRef]
- Talavera, L.; Río, L.D.; Benavente, J.; Barbero, L.; López-Ramírez, J.A. UAS & SfM-based approach to monitor overwash dynamics and beach evolution in a sandy spit. J. Coast. Res. 2018, 85, 221–225. [Google Scholar] [CrossRef]
- Guisado-Pintado, E.; Jackson, D.W. Coastal impact from high-energy events and the importance of concurrent forcing parameters: The cases of storm Ophelia (2017) and storm Hector (2018) in NW Ireland. Front. Earth Sci. 2019, 7, 190. [Google Scholar] [CrossRef] [Green Version]
- Schnack, E.J.; Pousa, J.L.; Isla, F.I. Erosive processes on the sandy coastline of Argentina. Vechta. Stud. Zur Angew. Geogr. Und Reg. 1998, 20, 133–136. [Google Scholar]
- Lee, G.; Nichols, R.J.; Birkemeier, W. Storm-driven variability of the beach-nearshore profile at Duck, North Carolina. Mar. Geol. 1998, 148, 163–177. [Google Scholar] [CrossRef]
- Carvalho, B.C.; Dalbosco, A.L.P.; Guerra, J.V. Shoreline position change and the relationship to annual and interannual meteo-oceanographic conditions in Southeastern Brazil. Estuar. Coast. Shelf Sci. 2020, 235, 106582. [Google Scholar] [CrossRef]
- Gutiérrez, O.; Panario, D.; Nagy, G.J.; Bidegain, M.; Montes, C. Climate teleconnections and indicators of coastal systems response. Ocean Coast. Manag. 2016, 122, 64–76. [Google Scholar] [CrossRef] [Green Version]
- Cáceres, R.A.; Zyserman, J.A.; Perillo, G.M.E. Analysis of Sedimentation Problems at the Entrance to Mar del Plata Harbor. J. Coast. Res. 2016, 318, 301–314. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Billet, C.; Bacino, G.; Alonso, G.; Dragani, W. Shoreline Temporal Variability Inferred from Satellite Images at Mar del Plata, Argentina. Water 2023, 15, 1299. https://doi.org/10.3390/w15071299
Billet C, Bacino G, Alonso G, Dragani W. Shoreline Temporal Variability Inferred from Satellite Images at Mar del Plata, Argentina. Water. 2023; 15(7):1299. https://doi.org/10.3390/w15071299
Chicago/Turabian StyleBillet, Carolina, Guido Bacino, Guadalupe Alonso, and Walter Dragani. 2023. "Shoreline Temporal Variability Inferred from Satellite Images at Mar del Plata, Argentina" Water 15, no. 7: 1299. https://doi.org/10.3390/w15071299




