Uncertainty Assessment of WinSRFR Furrow Irrigation Simulation Model Using the GLUE Framework under Variability in Geometry Cross Section, Infiltration, and Roughness Parameters
Abstract
:1. Introduction
- Evaluating the outputs uncertainty of the WinSRFR model in an innovative way, including advance curve, flow depth hydrograph, and runoff hydrograph, using the GLUE framework in response to Kostiakov–Lewis infiltration equation, Manning’s roughness coefficient, and cross-sectional parameters sets based on the experimental data of a furrow irrigation system.
- Assessing the reliability predictions of WinSRFR model for two open- and closed-ended of furrow irrigating systems.
- Investigating the effects of three likelihood functions, the coefficient of determination (R2), Nash–Sutcliffe efficiency (NSE), and percentage bias (PBIAS), on the parameter set performance and uncertainty analysis of the WinSRFR model.
2. Materials and Methods
2.1. Description of WinSRFR Model
2.2. Description of Important Input Parameters of WinSRFR Model
2.2.1. Geometry Cross Section
2.2.2. Kostiakov–Lewis Infiltration Function
2.2.3. Manning’s Roughness Coefficient
2.3. Generalized Likelihood Uncertainty Estimation (GLUE)
2.4. Data Sets
2.5. Evaluation Criteria
3. Results and Discussion
3.1. Creating Random Sample Sets Using Monte Carlo Simulation
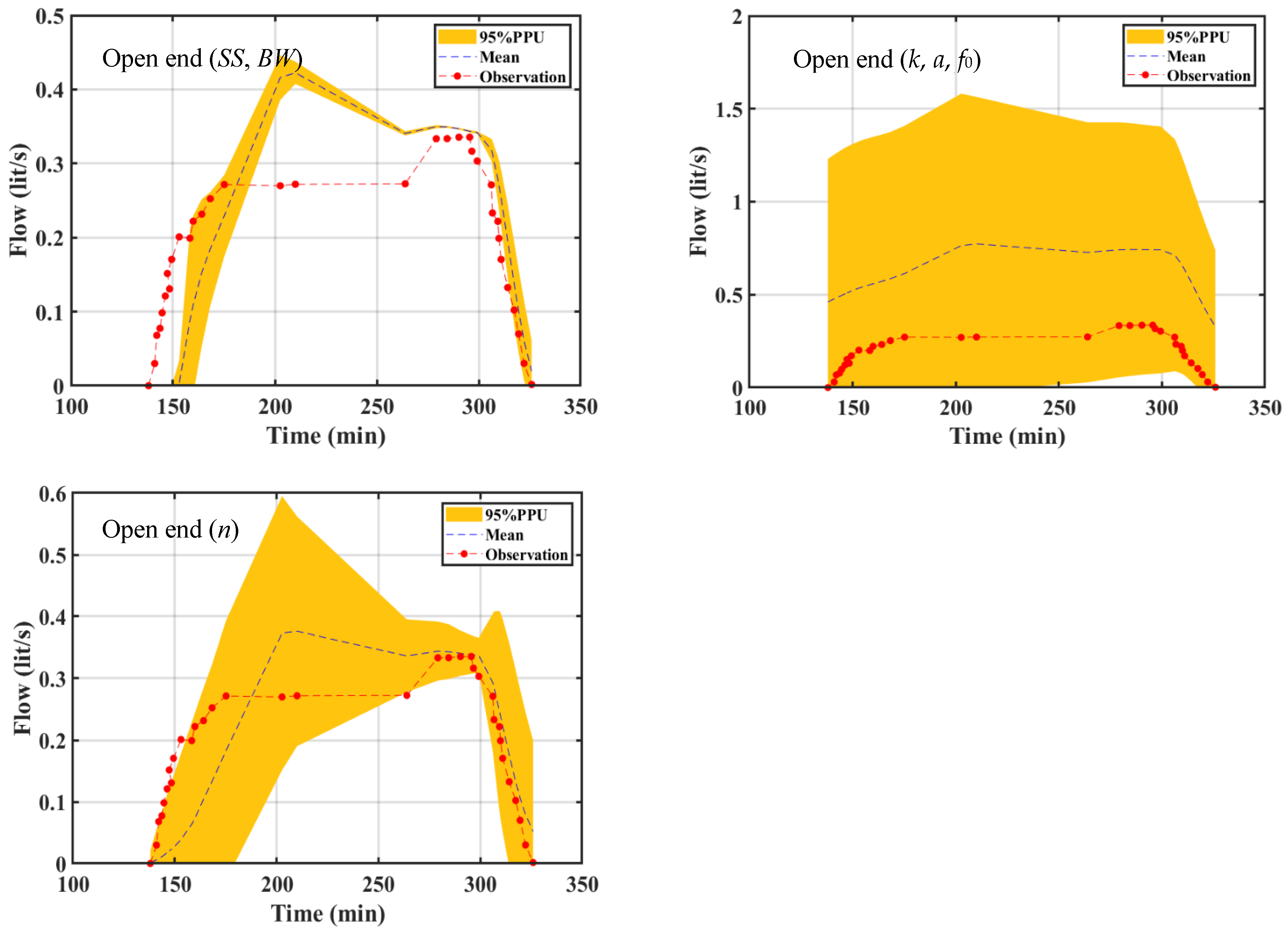
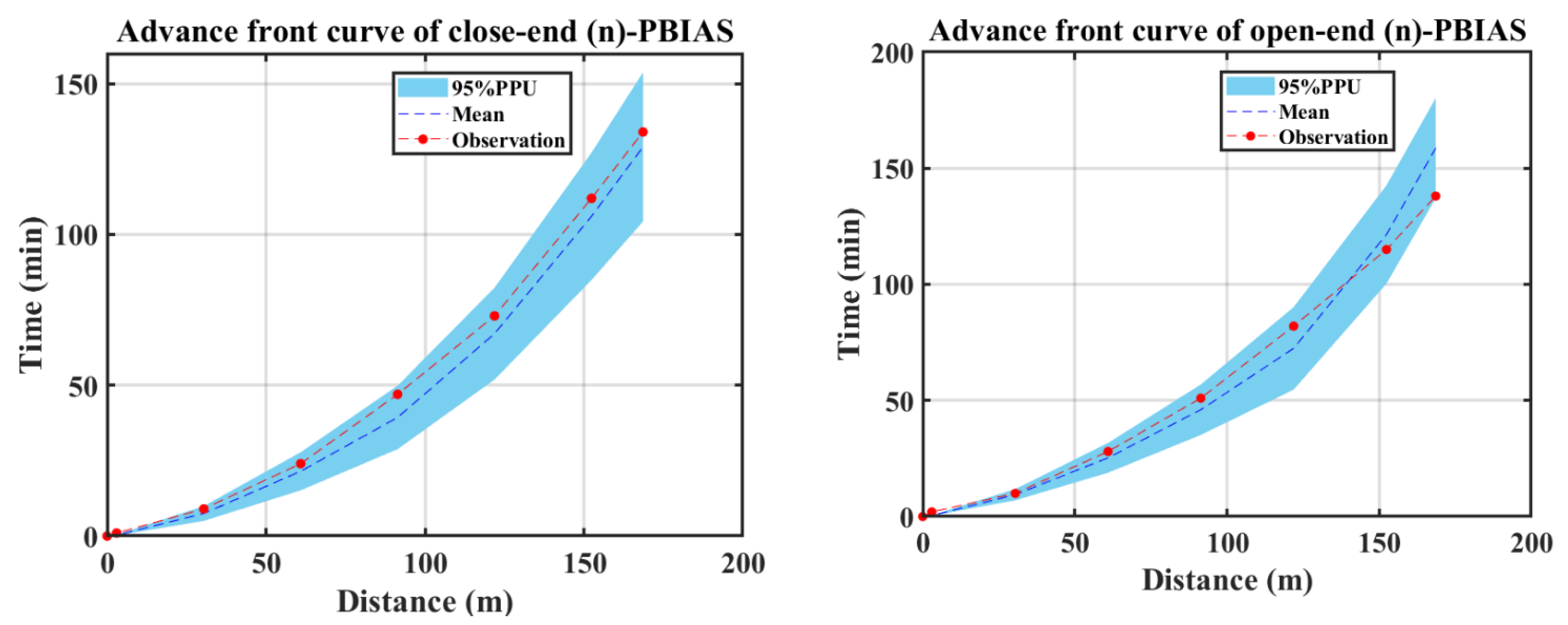
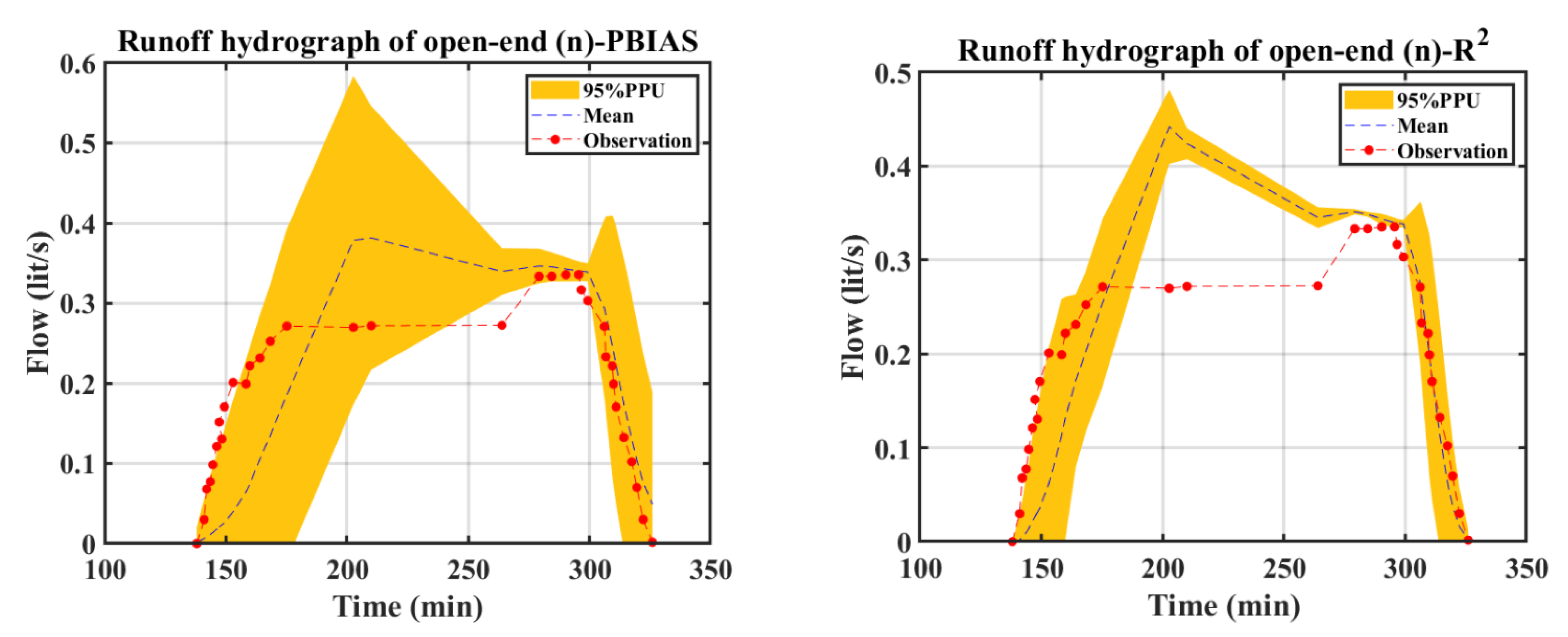
3.2. Simulation Using WinSRFR Furrow Irrigation Model and Uncertainty Analysis
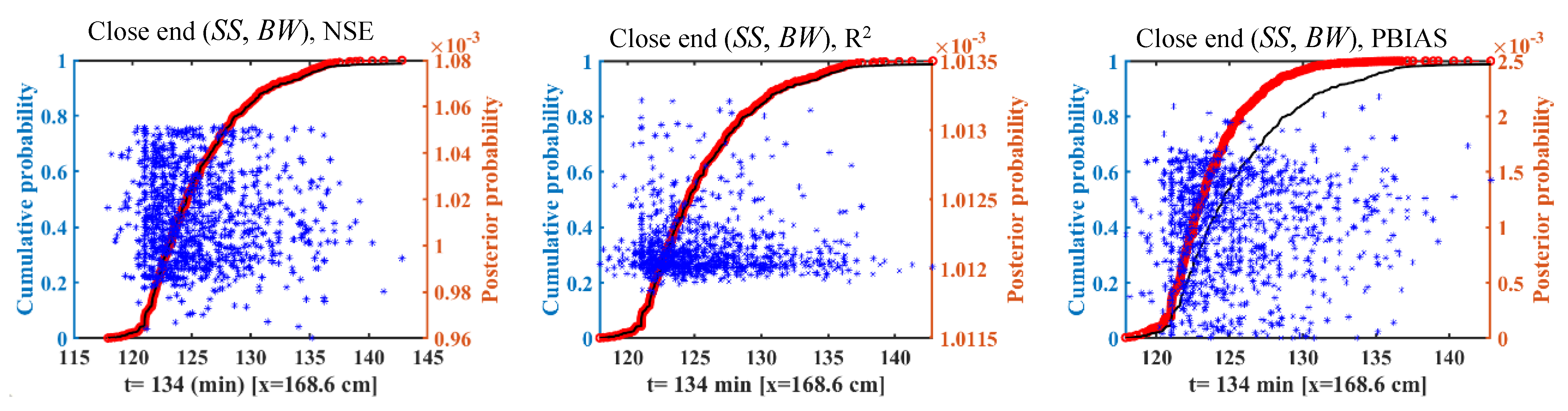
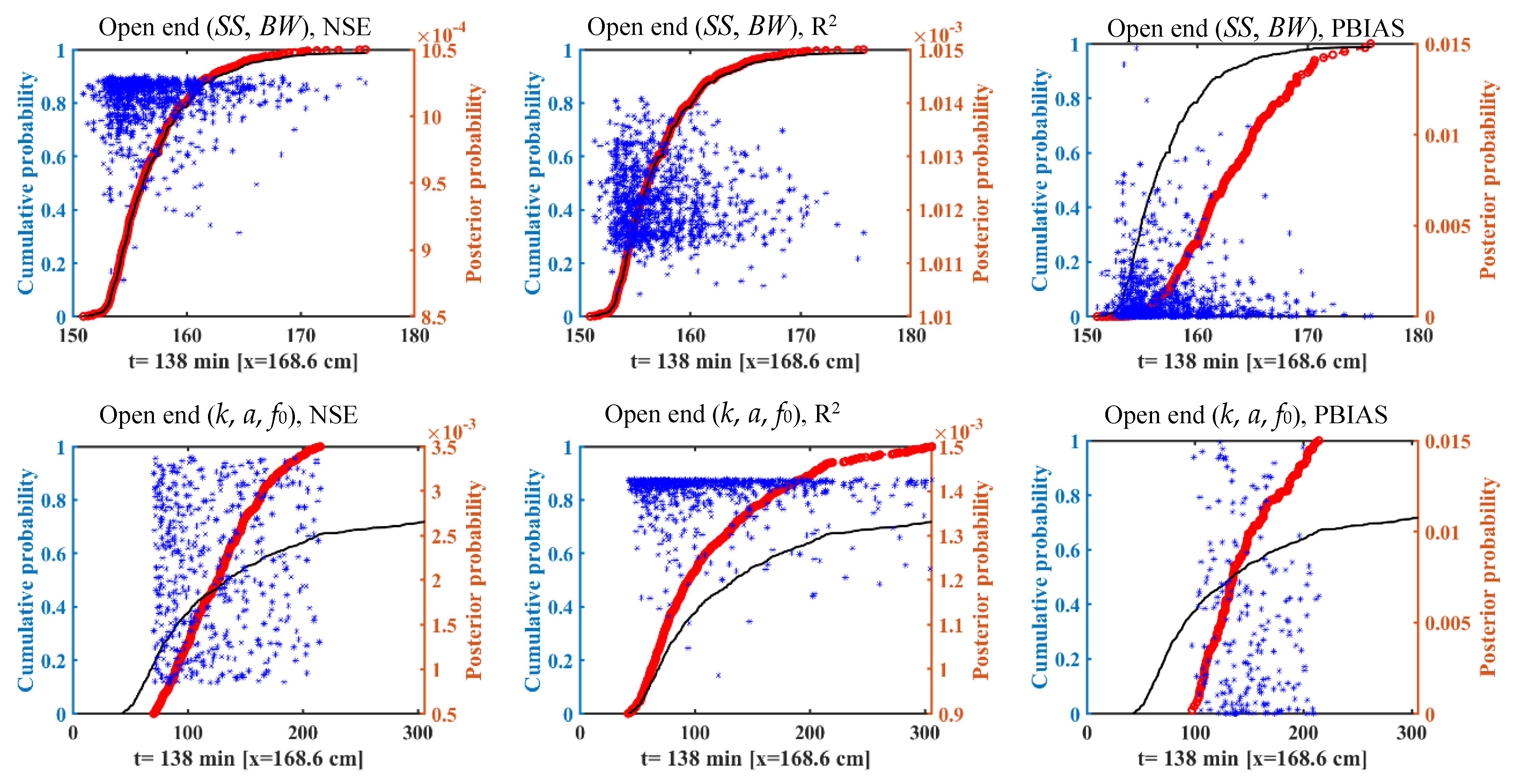
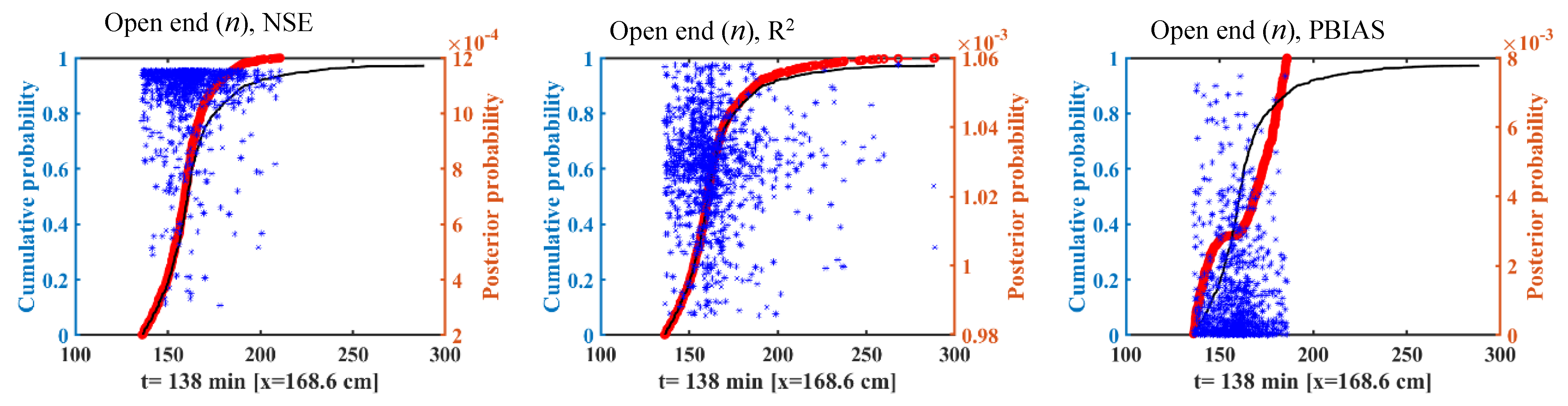
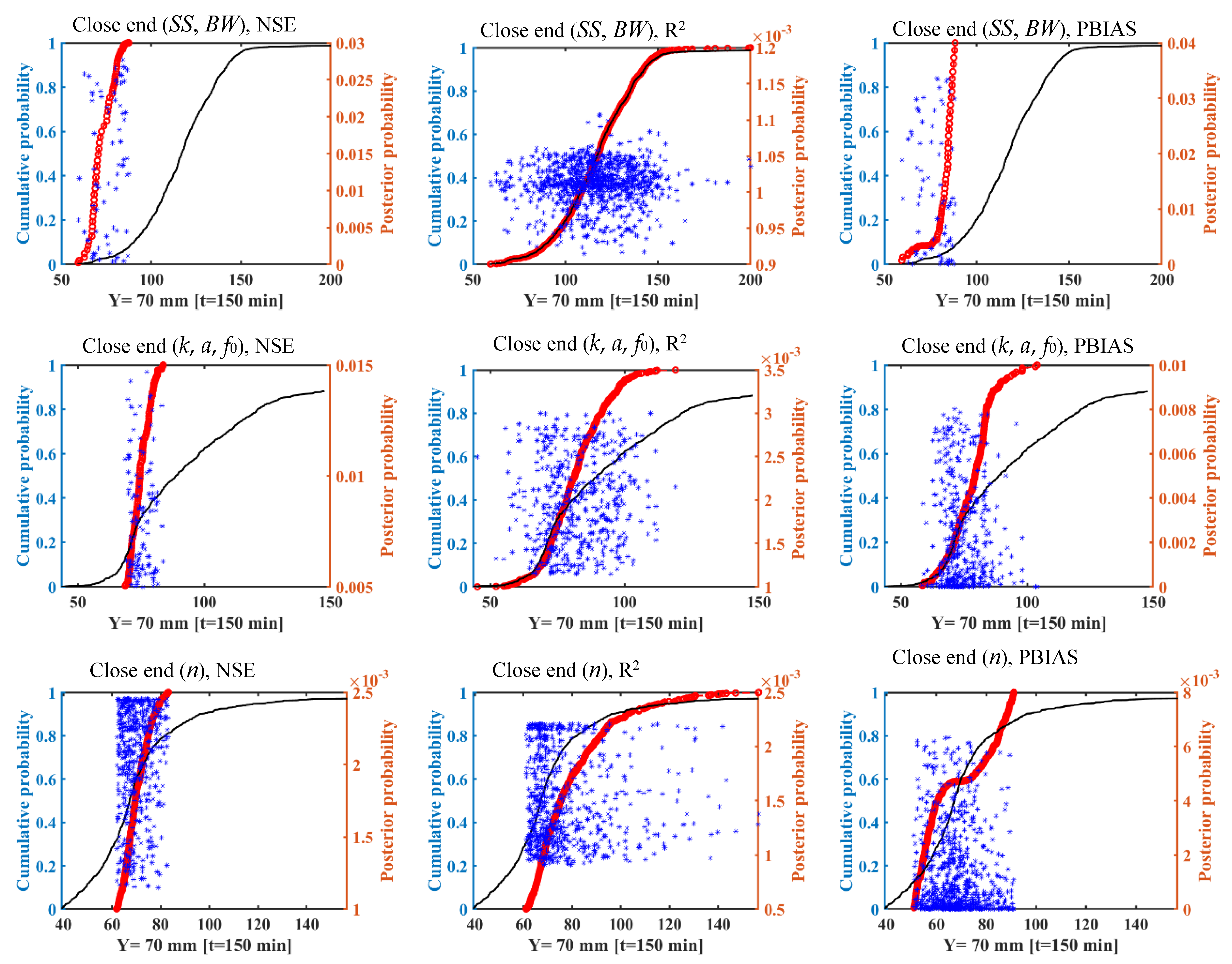
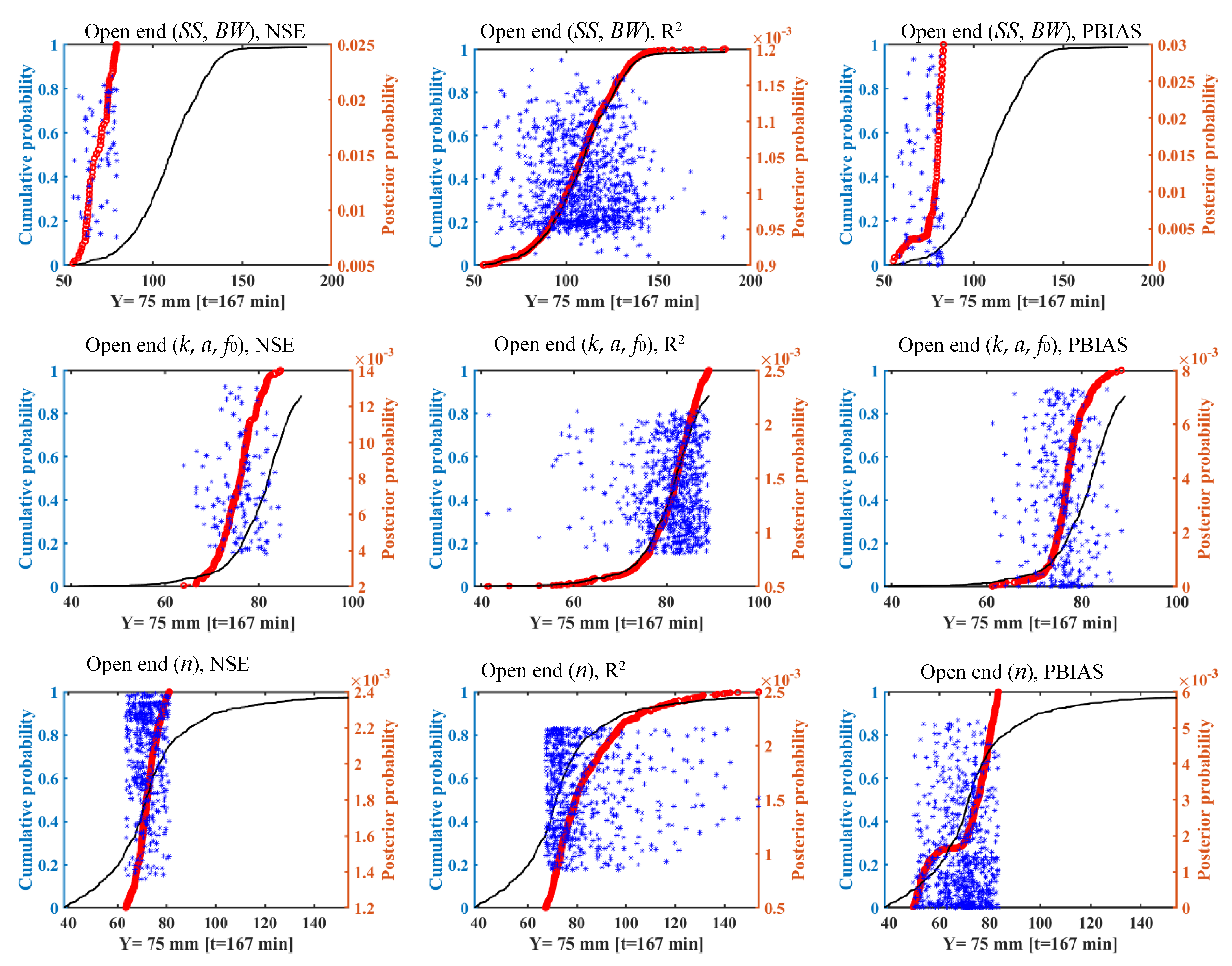
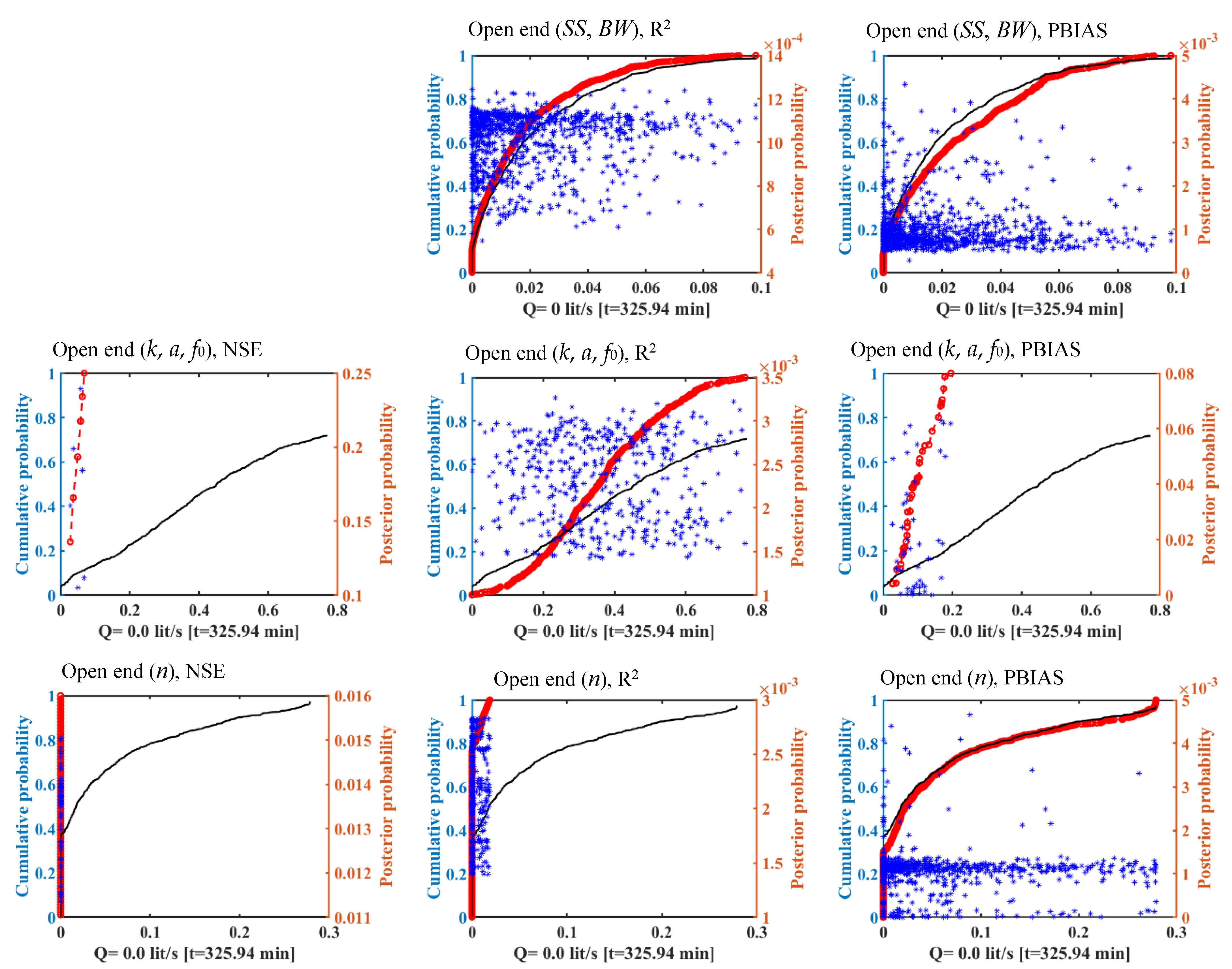
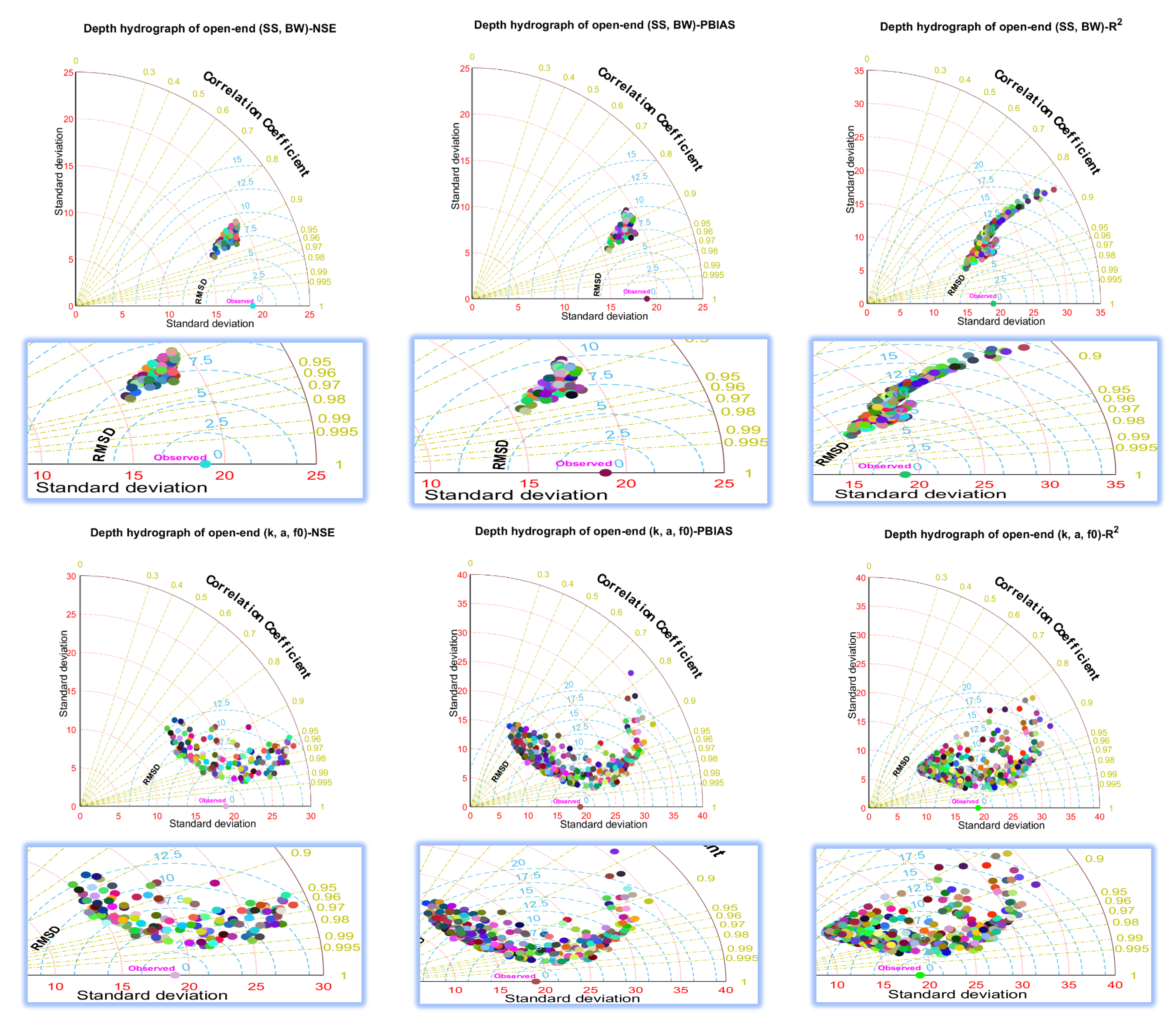
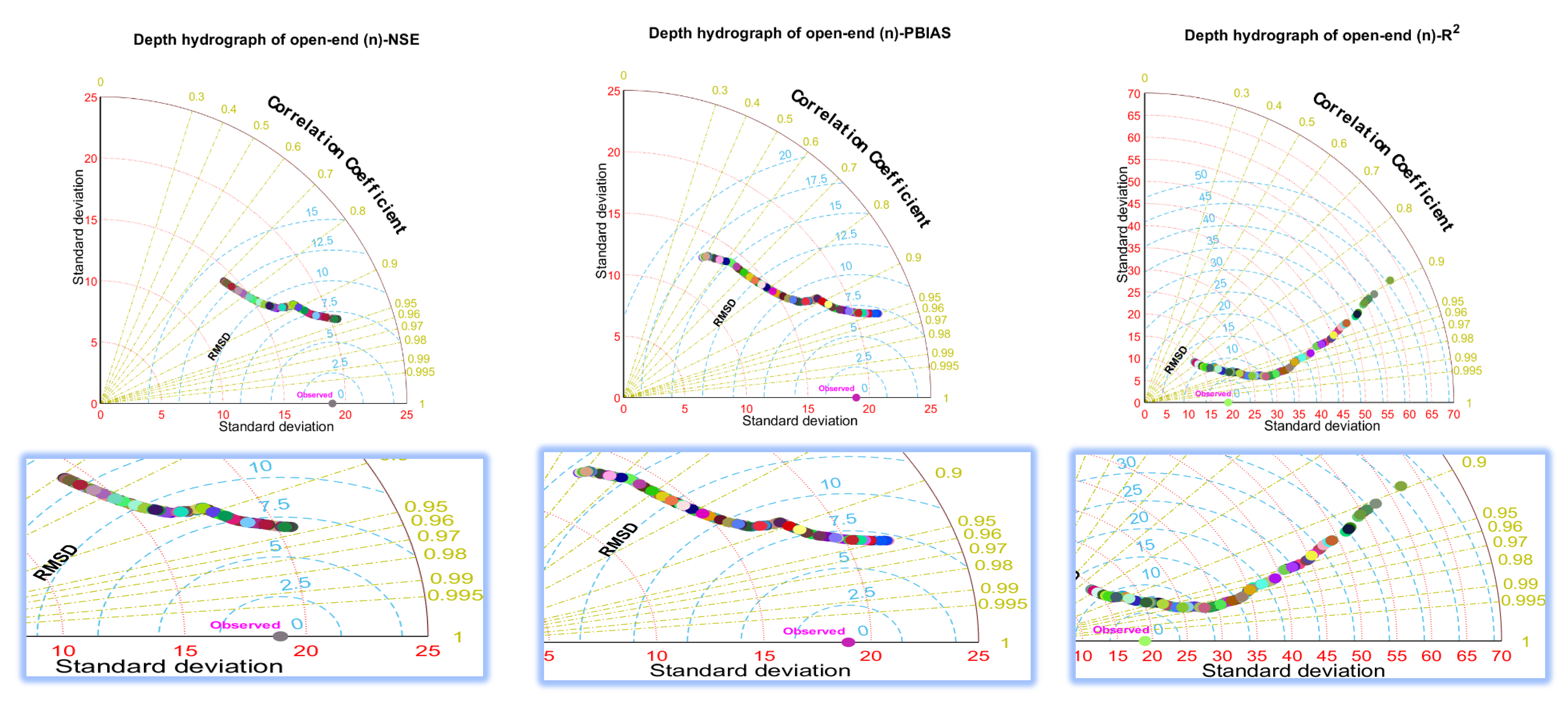
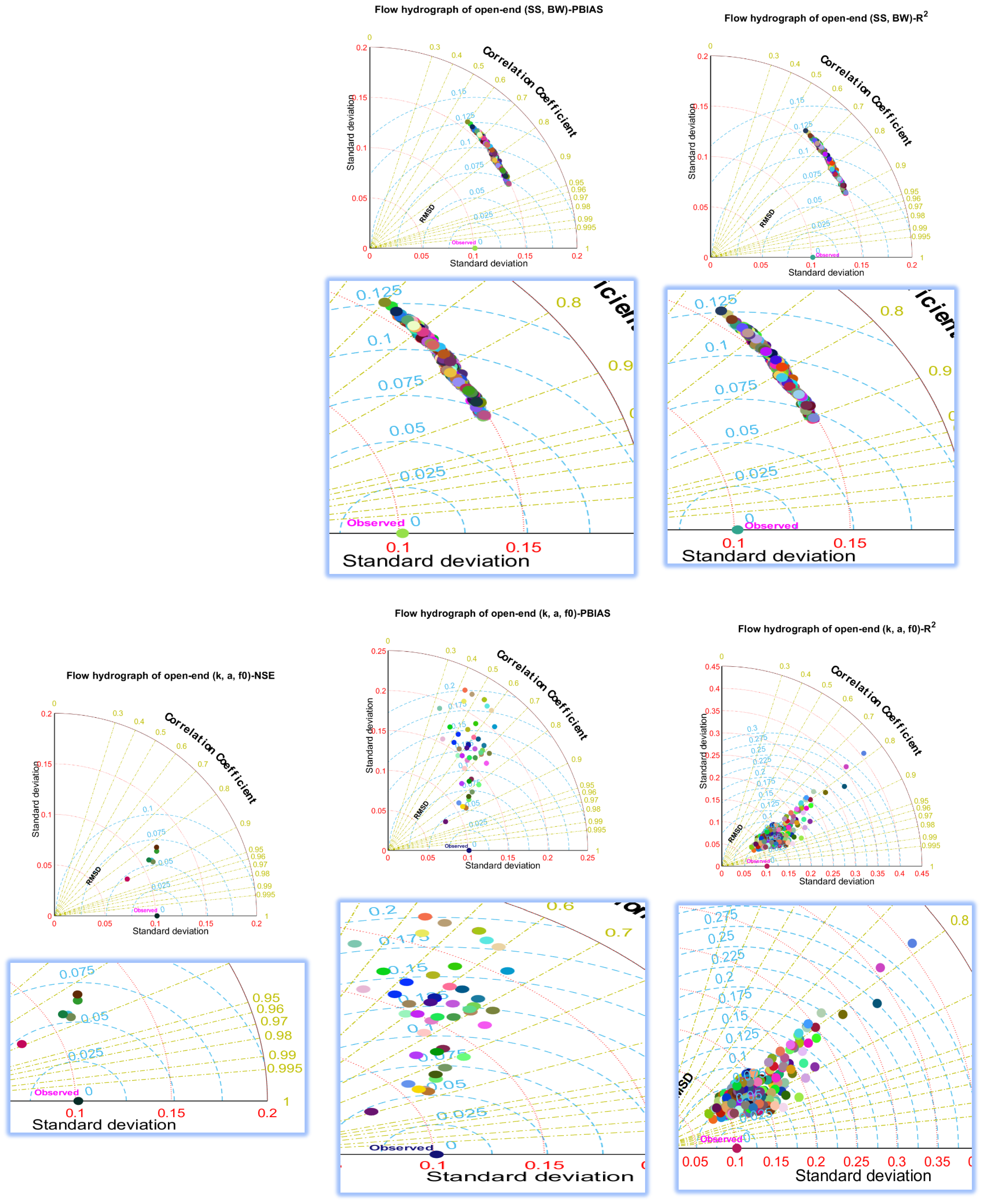
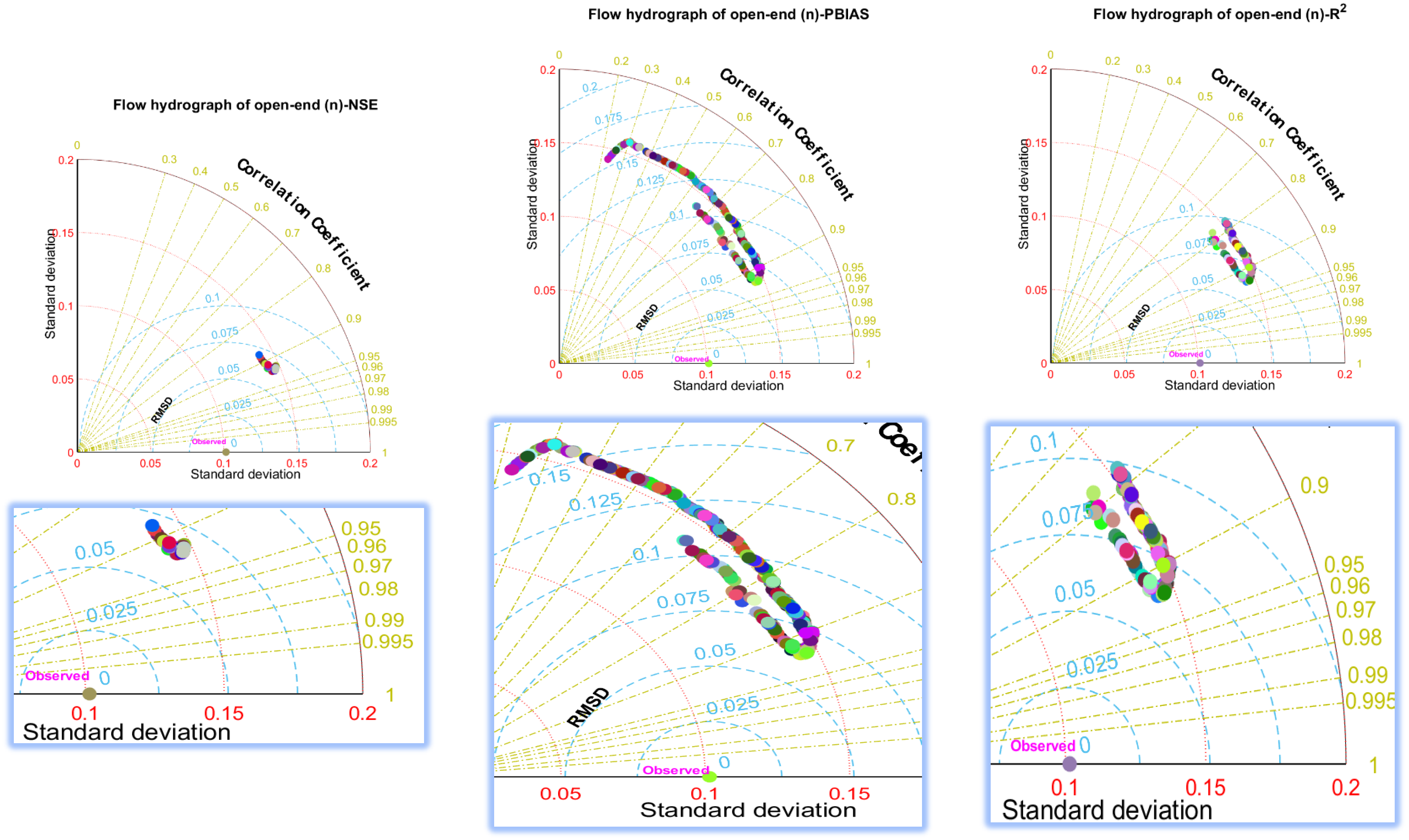
3.3. Effect of Likelihood Measures on Uncertainty
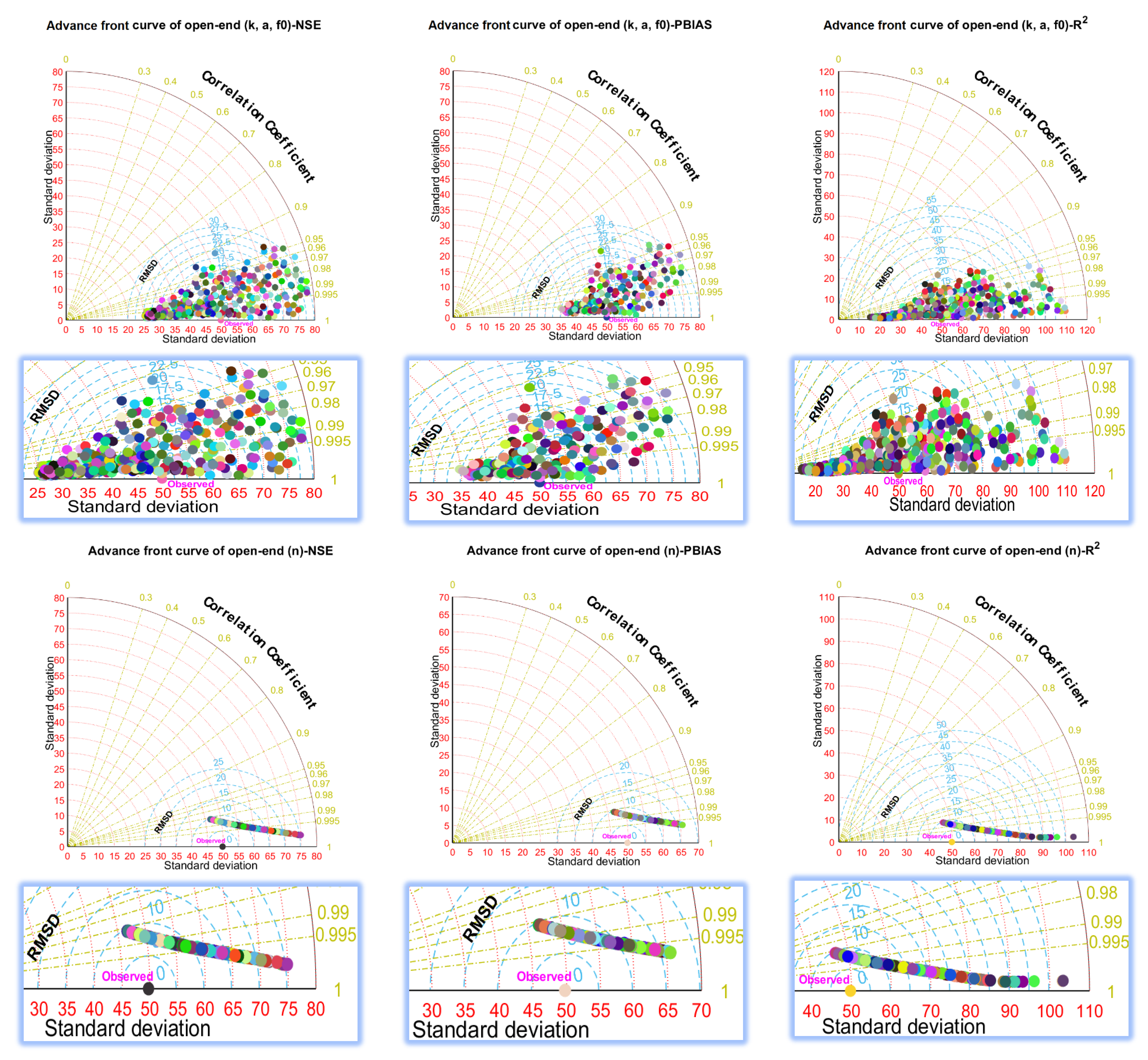
3.4. Analysis of Accuracy and Uncertainty Associated with Different Parameters
4. Conclusions
- -
- The initial evaluation without filtering non-behavioral estimations showed that the model outputs have high uncertainties in regard to the input parameter of geometry cross section. The value width range of uncertainty bound could be reduced by employing Kostiakov–Lewis infiltration and Manning’s roughness parameters.
- -
- Likelihood measures greatly affect the uncertainty bounds, especially with respect to the Kostiakov–Lewis infiltration and Manning’s roughness parameters. The confidence interval and uncertainty bound of the advance front curve and runoff hydrograph did not change in response to employing likelihood functions for geometry cross section parameters.
- -
- There is a higher level of instability in the model outputs related to soil infiltration parameters than those related to the roughness coefficient. This result is related to the higher level of sensitivity of the WinSRFR model in inaccurate measurements, methods, and equipment to monitor the soil infiltration than that which is considering for the optimum roughness coefficient.
- -
- The PBIAS likelihood function played a critical role in the uncertainty results for the estimated advance front curve and runoff hydrograph. In contrast, the NSE likelihood function was more important to implicitly determine the flow depth hydrograph estimation uncertainty. These functions reduced the uncertainty of model outputs by avoiding the parameter sets that produced outputs there were very different from the observations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Nazemi, A.; Wheater, H.S. On inclusion of water resource management in Earth system models—Part 1: Problem definition and representation of water demand. Hydrol. Earth Syst. Sci. 2015, 19, 33–61. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimian, H.; Liaghat, A. Field evaluation of various mathematical models for furrow and border irrigation systems. Soil Water Res. 2011, 6, 91–101. [Google Scholar] [CrossRef] [Green Version]
- Mazarei, R.; Mohammadi, A.S.; Ebrahimian, H.; Naseri, A.A. Temporal variability of infiltration and roughness coefficients and furrow irrigation performance under different inflow rates. Agric. Water Manag. 2021, 245, 106465. [Google Scholar] [CrossRef]
- Koech, R.K.; Smith, R.J.; Gillies, M.H. A real-time optimisation system for automation of furrow irrigation. Irrig. Sci. 2014, 32, 319–327. [Google Scholar] [CrossRef]
- Brunetti, G.; Šimůnek, J.; Bautista, E. A hybrid finite volume-finite element model for the numerical analysis of furrow irrigation and fertigation. Comput. Electron. Agric. 2018, 150, 312–327. [Google Scholar] [CrossRef] [Green Version]
- Lalehzari, R.E.Z.A.; Ansari Samani, F.A.R.I.D.E.; Boroomand-nasab, S.A.E.E.D. Analysis of evaluation indicators for furrow irrigation using opportunity time. Irrig. Drain. 2015, 64, 85–92. [Google Scholar] [CrossRef]
- Bautista, E.; Clemmens, A.J.; Strelkoff, T.S.; Schlegel, J. Modern analysis of surface irrigation systems with WinSRFR. Agric. Water Manag. 2009, 96, 1146–1154. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, X.; Huo, Z.; Feng, S.; Huang, G.; Mao, X. Uncertainty and sensitivity assessments of an agricultural–hydrological model (RZWQM2) using the GLUE method. J. Hydrol. 2016, 534, 19–30. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Mun, S.; Sassenrath, G.F.; Schmidt, A.M.; Lee, N.; Wadsworth, M.C.; Rice, B.; Corbitt, J.Q.; Schneider, J.M.; Tagret, M.L.; Pote, J.; et al. Uncertainty analysis of an irrigation scheduling model for water management in crop production. Agric. Water Manag. 2015, 155, 100–112. [Google Scholar] [CrossRef] [Green Version]
- Choliz, J.S.; Sarasa, C. Uncertainty in irrigation technology: Insights from a CGE approach. Water 2019, 11, 617. [Google Scholar] [CrossRef] [Green Version]
- Kisekka, I.; Kandelous, M.M.; Sanden, B.; Hopmans, J.W. Uncertainties in leaching assessment in micro-irrigated fields using water balance approach. Agric. Water Manag. 2019, 213, 107–115. [Google Scholar] [CrossRef] [Green Version]
- Mondaca-Duarte, F.D.; van Mourik, S.; Balendonck, J.; Voogt, W.; Heinen, M.; van Henten, E.J. Irrigation, crop stress and drainage reduction under uncertainty: A scenario study. Agric. Water Manag. 2020, 230, 105990. [Google Scholar] [CrossRef]
- Gillies, M.H.; Smith, R.J.; Raine, S.R. Accounting for temporal inflow variation in the inverse solution for infiltration in surface irrigation. Irrig. Sci. 2007, 25, 87–97. [Google Scholar] [CrossRef] [Green Version]
- Strelkoff, T.S.; Clemmens, A.J.; Bautista, E. Estimation of soil and crop hydraulic properties. J. Irrig. Drain. Eng. 2009, 135, 537–555. [Google Scholar] [CrossRef] [Green Version]
- Esfandiari, M.; Maheshwari, B.L. Application of the optimization method for estimating infiltration characteristics in furrow irrigation and its comparison with other methods. Agric. Water Manag. 1997, 34, 169–185. [Google Scholar] [CrossRef]
- Nie, W.; Ma, X.; Fei, L. Evaluation of infiltration models and variability of soil infiltration properties at multiple scales. Irrig. Drain. 2017, 66, 589–599. [Google Scholar] [CrossRef]
- Kamali, P.; Ebrahimian, H.; Parsinejad, M. Estimation of manning roughness coefficient for vegetated furrows. Irrig. Sci. 2018, 36, 339–348. [Google Scholar] [CrossRef]
- Oyonarte, N.A.; Mateos, L.; Palomo, M.J. Infiltration variability in furrow irrigation. J. Irrig. Drain. Eng. 2002, 128, 26–33. [Google Scholar] [CrossRef]
- Bai, M.; Xu, D.; Li, Y.; Pereira, L.S. Stochastic modeling of basins microtopography: Analysis of spatial variability and model testing. Irrig. Sci. 2010, 28, 157–172. [Google Scholar] [CrossRef]
- Sepaskhah, A.R.; Bondar, H. Sw—Soil and water: Estimation of manning roughness coefficient for bare and vegetated furrow irrigation. Biosyst. Eng. 2002, 82, 351–357. [Google Scholar] [CrossRef]
- Mailapalli, D.R.; Raghuwanshi, N.S.; Singh, R.; Schmitz, G.H.; Lennartz, F. Spatial and temporal variation of manning’s roughness coefficient in furrow irrigation. J. Irrig. Drain. Eng. 2008, 134, 185–192. [Google Scholar] [CrossRef]
- Xu, J.; Cai, H.; Saddique, Q.; Wang, X.; Li, L.; Ma, C.; Lu, Y. Evaluation and optimization of border irrigation in different irrigation seasons based on temporal variation of infiltration and roughness. Agric. Water Manag. 2019, 214, 64–77. [Google Scholar] [CrossRef]
- Walker, W.R.; Skogerboe, G.V. Surface Irrigation: Theory and Practice; Pearson College Div: Logan, UT, USA, 1987; pp. 81–87. [Google Scholar]
- Clemmens, A.J.; El-Haddad, Z.; Strelkoff, T.S. Assessing the potential for modern surface irrigation in Egypt. Trans. ASAE 1999, 42, 995. [Google Scholar] [CrossRef]
- Bo, C.; Zhu, O.; Shaohui, Z. Evaluation of hydraulic process and performance of border irrigation with different regular bottom configurations. J. Resour. Ecol. 2012, 3, 151–160. [Google Scholar] [CrossRef]
- Strelkoff, T.S.; Clemmens, A.J. Approximating wetted perimeter in power-law cross section. J. Irrig. Drain. Eng. 2000, 126, 98–109. [Google Scholar] [CrossRef]
- Eldeiry, A.A.; Garsia, L.A.; El-Zaher, A.S.A.; El-Sherbini Kiwan, M. Furrow irrigation system design for clay soils in arid regions. Appl. Eng. Agric. 2005, 21, 411–420. [Google Scholar] [CrossRef] [Green Version]
- Navabian, M.; Liaghat, A.M.; Smith, R.J.; Abbasi, F. Empirical functions for dependent variables in cutback furrow irrigation. Irrig. Sci. 2009, 27, 215–222. [Google Scholar] [CrossRef]
- Salahou, M.K.; Jiao, X.; Lü, H. Border irrigation performance with distance-based cut-off. Agric. Water Manag. 2018, 201, 27–37. [Google Scholar] [CrossRef]
- Tung, Y.; Yen, B. Hydrosystem Engineering Uncertainty Analysis; McGraw-Hill Book Company: New York, NY, USA, 2006. [Google Scholar]
- Setegn, S.G.; Srinivasan, R.; Melesse, A.M.; Dargahi, B. SWAT model application and prediction uncertainty analysis in the Lake Tana Basin, Ethiopia. Hydrol. Process. Int. J. 2010, 24, 357–367. [Google Scholar] [CrossRef]
- He, J.; Dukes, M.D.; Hochmuth, G.J.; Jones, J.W.; Graham, W.D. Evaluation of sweet corn yield and nitrogen leaching with CERES-Maize considering input parameter uncertainties. Trans. ASABE 2011, 54, 1257–1268. [Google Scholar] [CrossRef]
- Shafiei, M.; Ghahraman, B.; Saghafian, B.; Davary, K.; Pande, S.; Vazifedoust, M. Uncertainty assessment of the agro-hydrological SWAP model application at field scale: A case study in a dry region. Agric. Water Manag. 2014, 146, 324–334. [Google Scholar] [CrossRef]
- Tan, J.; Cao, J.; Cui, Y.; Duan, Q.; Gong, W. Comparison of the generalized likelihood uncertainty estimation and Markov Chain Monte Carlo methods for uncertainty analysis of the ORYZA_V3 model. Agron. J. 2019, 111, 555–564. [Google Scholar] [CrossRef]
- Yan, L.; Jin, J.; Wu, P. Impact of parameter uncertainty and water stress parameterization on wheat growth simulations using CERES-Wheat with GLUE. Agric. Syst. 2020, 181, 102823. [Google Scholar] [CrossRef]
- Zhang, Y.; Arabi, M.; Paustian, K. Analysis of parameter uncertainty in model simulations of irrigated and rainfed agroecosystems. Environ. Model. Softw. 2020, 126, 104642. [Google Scholar] [CrossRef]
- Martínez-Ruiz, A.; López-Cruz, I.L.; Ruiz-García, A.; Pineda-Pineda, J.; Sánchez-García, P.; Mendoza-Pérez, C. Uncertainty analysis of the HORTSYST model applied to fertigated tomatoes cultivated in a hydroponic greenhouse system. Span. J. Agric. Res. 2021, 19, e0802. [Google Scholar] [CrossRef]
- Strelkoff, T.S.; Clemmens, A.J. Hydraulics of Surface Systems Design Operation of Farm Irrigation Systems; Hoffman, G., Evans, R.G., Eds.; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2007. [Google Scholar]
- Bautista, E.; Clemmens, A.J.; Strelkoff, T.S.; Niblack, M. Analysis of surface irrigation systems with WinSRFR-Example application. Agric. Water Manag. 2009, 96, 1162–1169. [Google Scholar] [CrossRef]
- Gillies, M.H. Managing the Effect of Infiltration Variability on Surface Irrigation. Ph.D. Thesis, University of Southern Queensland, Toowoomba, Australia, 2008. [Google Scholar]
- Bautista, E.; Schlegel, J.L.; Strelkoff, T.S. WinSRFR 4.1-User Manual; USDA-ARS Arid Land Agricultural Research Center: Maricopa, AZ, USA, 2012. [Google Scholar]
- Seifi, A.; Ehteram, M.; Nayebloei, F.; Soroush, F.; Gharabaghi, B.; Torabi Haghighi, A. GLUE uncertainty analysis of hybrid models for predicting hourly soil temperature and application wavelet coherence analysis for correlation with meteorological variables. Soft Comput. 2021, 25, 10723–10748. [Google Scholar] [CrossRef]
- Ahmadisharaf, E.; Benham, B.L. Risk-based decision making to evaluate pollutant reduction scenarios. Sci. Total Environ. 2020, 702, 135022. [Google Scholar] [CrossRef]
- Perea, H. Development, Verification, and Evaluation of a Solute Transport Model in Surface Irrigation. Ph.D. Dissertation, Department of Agricultural and Biosystems Engineering, University of Arizona, Tucson, AZ, USA, 2005. [Google Scholar]
- Seifi, A.; Ehteram, M.; Soroush, F. Uncertainties of instantaneous influent flow predictions by intelligence models hybridized with multi-objective shark smell optimization algorithm. J. Hydrol. 2020, 587, 124977. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Seifi, A.; Dehghani, M.; Singh, V.P. Uncertainty analysis of water quality index (WQI) for groundwater quality evaluation: Application of Monte-Carlo method for weight allocation. Ecol. Indic. 2020, 117, 106653. [Google Scholar] [CrossRef]
- Logez, M.; Maire, A.; Argillier, C. Monte-Carlo methods to assess the uncertainty related to the use of predictive multimetric indices. Ecol. Indic. 2019, 96, 52–58. [Google Scholar] [CrossRef]
- Perea, H.; Bautista, E.; Hunsaker, D.J.; Strelkoff, T.S.; Williams, C.; Adamsen, F.J. Nonuniform and unsteady solute transport in furrow irrigation. II: Description of field experiments and calibration of infiltration and roughness coefficients. J. Irrig. Drain. Eng. 2011, 137, 315–326. [Google Scholar] [CrossRef]
- Seifi, A.; Ehteram, M.; Dehghani, M. A robust integrated Bayesian multi-model uncertainty estimation framework (IBMUEF) for quantifying the uncertainty of hybrid meta-heuristic in global horizontal irradiation predictions. Energy Convers. Manag. 2021, 241, 114292. [Google Scholar] [CrossRef]
- Cahoon, J. Kostiakov infiltration parameters from kinematic wave model. J. Irrig. Drain. Eng. 1998, 124, 127–130. [Google Scholar] [CrossRef]
- Gillies, M.H.; Smith, R.J. Infiltration parameters from surface irrigation advance and run-off data. Irrig. Sci. 2005, 24, 25–35. [Google Scholar] [CrossRef] [Green Version]
- Khoi, D.N.; Thom, V.T. Parameter uncertainty analysis for simulating streamflow in a river catchment of Vietnam. Glob. Ecol. Conserv. 2015, 4, 538–548. [Google Scholar] [CrossRef] [Green Version]
- Nie, W.; Fei, L.; Ma, X. Impact of infiltration parameters and Manning roughness on the advance trajectory and irrigation performance for closed-end furrows. Span. J. Agric. Res. 2014, 12, 1180–1191. [Google Scholar] [CrossRef] [Green Version]
- Khorami, M.; Ghahraman, B. Uncertainty analysis of soil parameters in soil moisture profile uncertainty using fuzzy set theory. Iran-Water Resour. Res. 2017, 13, 126–138. [Google Scholar]
- Nie, W.B.; Li, Y.B.; Zhang, F.; Ma, X.Y. Optimal discharge for closed-end border irrigation under soil infiltration variability. Agric. Water Manag. 2019, 221, 58–65. [Google Scholar] [CrossRef]
- Moravejalahkami, B.; Mostafazadeh-Fard, B.; Heidarpour, M.; Abbasi, F. Furrow infiltration and roughness prediction for different furrow inflow hydrographs using a zero-inertia model with a multilevel calibration approach. Biosyst. Eng. 2009, 103, 374–381. [Google Scholar] [CrossRef]
- Bai, M.; Xu, D.; Li, Y.; Zhang, S.; Liu, S. Coupled impact of spatial variability of infiltration and microtopography on basin irrigation performances. Irrig. Sci. 2017, 35, 437–449. [Google Scholar] [CrossRef]
- Viola, F.; Noto, L.V.; Cannarozzo, M.; La Loggia, G. Daily streamflow prediction with uncertainty in ephemeral catchments using the GLUE methodology. Phys. Chem. Earth 2009, 34, 701–706. [Google Scholar] [CrossRef]
- Hantush, M.M.; Zhang, H.X.; Camacho-Rincon, R.A.; Ahmadisharaf, E.; Mohamoud, Y.M. Model Uncertainty Analysis and the Margin of Safety. In Total Maximum Daily Load Development and Implementation: Models, Methods, and Resources; American Society of Civil Engineers: Reston, VA, USA, 2022; pp. 271–306. [Google Scholar]
- Candela, A.N.G.E.L.A.; Noto, L.V.; Aronica, G. Influence of surface roughness in hydrological response of semiarid catchments. J. Hydrol. 2005, 313, 119–131. [Google Scholar] [CrossRef]







| Geometry and Field Characteristics | Furrow 1 | Furrow 2 |
|---|---|---|
| Length (m) | 168.60 | 168.60 |
| Downstream condition | Open ended | Closed ended |
| Average slope | 2.40 × 10−4 | 2.60 × 10−4 |
| Bottom width (m) | 0.16 | 0.27 |
| Side slope | 2.00 | 1.56 |
| Manning coefficient | 0.05 | 0.05 |
| 1.50 × 10−3 | 1.70 × 10−3 |
| Parameter | Distribution | p-Value | Coefficients | Formulation |
|---|---|---|---|---|
| BW | Wakeby | 0.13 | ||
| SS | Wakeby | 0.13 | ||
| k | Log-Logistic | 0.12 | ||
| a | Wakeby | 0.12 | ||
| f0 | Wakeby | 0.12 | ||
| n | Wakeby | 0.19 |
| Conditions | Uncertainty Criteria | Advance Front | Depth Hydrograph | Flow Hydrograph |
|---|---|---|---|---|
| Close end (SS, BW) | p-factor | 12.50 | 34.38 | |
| r-factor | 0.11 | 4.40 | ||
| Open end (SS, BW) | p-factor | 50 | 52.78 | 14.71 |
| r-factor | 0.11 | 3.44 | 0.48 | |
| Close end (k, a, f0) | p-factor | 100 | 100 | |
| r-factor | 1.14 | 3.99 | ||
| Open end (k, a, f0) | p-factor | 87.50 | 100 | 100 |
| r-factor | 2.07 | 2.32 | 11.49 | |
| Close end (n) | p-factor | 87.50 | 100 | |
| r-factor | 0.64 | 3.92 | ||
| Open end (n) | p-factor | 87.50 | 100 | 97.06 |
| r-factor | 0.75 | 3.52 | 2.07 |
| Conditions | Likelihood Criteria | Advance Front | Depth Hydrograph | Flow Hydrograph |
|---|---|---|---|---|
| Close end (SS, BW) | NSE | 100 | 4.76 | |
| R2 | 100 | 100 | ||
| PBIAS | 100 | 7.69 | ||
| Open end (SS, BW) | NSE | 100 | 6.58 | 0 |
| R2 | 100 | 100 | 100 | |
| PBIAS | 100 | 9.01 | 100 | |
| Close end (k, a, f0) | NSE | 56.35 | 14.06 | |
| R2 | 76.08 | 57.37 | ||
| PBIAS | 21.54 | 48.75 | ||
| Open end (k, a, f0) | NSE | 53.40 | 15.76 | 0.84 |
| R2 | 81.41 | 81.41 | 59.75 | |
| PBIAS | 23.36 | 35.71 | 6.41 | |
| Close end (n) | NSE | 96.61 | 50.67 | |
| R2 | 96.61 | 68.40 | ||
| PBIAS | 86.64 | 76.10 | ||
| Open end (n) | NSE | 96.20 | 50.05 | 7.61 |
| R2 | 100 | 64.75 | 47.58 | |
| PBIAS | 89.41 | 72.05 | 98.56 |
| Conditions | Criteria | Advance Front | Depth Hydrograph | Flow Hydrograph | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NSE | PBIAS | R2 | NSE | PBIAS | R2 | NSE | PBIAS | R2 | ||
| Close end (SS, BW) | p-factor | 12.5 | 12.5 | 12.5 | 87.5 | 90.6 | 34.38 | |||
| r-factor | 0.11 | 0.11 | 0.11 | 0.99 | 1.42 | 4.40 | ||||
| Open end (SS, BW) | p-factor | 50 | 50 | 50 | 77.8 | 80.56 | 52.78 | 0 | 14.71 | 14.71 |
| r-factor | 0.11 | 0.11 | 0.11 | 1.05 | 1.21 | 3.44 | 0 | 0.48 | 0.48 | |
| Close end (k, a, f0) | p-factor | 87.5 | 87.5 | 87.5 | 62.5 | 100 | 100 | |||
| r-factor | 0.63 | 0.51 | 0.70 | 1.06 | 2.09 | 3.06 | ||||
| Open end (k, a, f0) | p-factor | 87.5 | 87.5 | 87.5 | 94.45 | 100 | 100 | 32.37 | 41.18 | 44.12 |
| r-factor | 0.88 | 0.66 | 1.44 | 1.32 | 1.85 | 2.24 | 0.47 | 1.89 | 8.98 | |
| Close end (n) | p-factor | 87.5 | 87.5 | 87.5 | 71.87 | 90.63 | 90.63 | |||
| r-factor | 0.51 | 0.40 | 0.51 | 0.93 | 1.75 | 3.10 | ||||
| Open end (n) | p-factor | 87.5 | 87.5 | 87.5 | 52.78 | 72.22 | 61.11 | 29.41 | 91.18 | 70.59 |
| r-factor | 0.52 | 0.39 | 0.75 | 0.76 | 1.37 | 2.69 | 0.37 | 2.01 | 1.06 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seifi, A.; Golestani Kermani, S.; Mosavi, A.; Soroush, F. Uncertainty Assessment of WinSRFR Furrow Irrigation Simulation Model Using the GLUE Framework under Variability in Geometry Cross Section, Infiltration, and Roughness Parameters. Water 2023, 15, 1250. https://doi.org/10.3390/w15061250
Seifi A, Golestani Kermani S, Mosavi A, Soroush F. Uncertainty Assessment of WinSRFR Furrow Irrigation Simulation Model Using the GLUE Framework under Variability in Geometry Cross Section, Infiltration, and Roughness Parameters. Water. 2023; 15(6):1250. https://doi.org/10.3390/w15061250
Chicago/Turabian StyleSeifi, Akram, Soudabeh Golestani Kermani, Amir Mosavi, and Fatemeh Soroush. 2023. "Uncertainty Assessment of WinSRFR Furrow Irrigation Simulation Model Using the GLUE Framework under Variability in Geometry Cross Section, Infiltration, and Roughness Parameters" Water 15, no. 6: 1250. https://doi.org/10.3390/w15061250







