Improving Groundwater Imputation through Iterative Refinement Using Spatial and Temporal Correlations from In Situ Data with Machine Learning
Abstract
:1. Introduction
1.1. Motivation
1.2. Research Overview
2. Methods
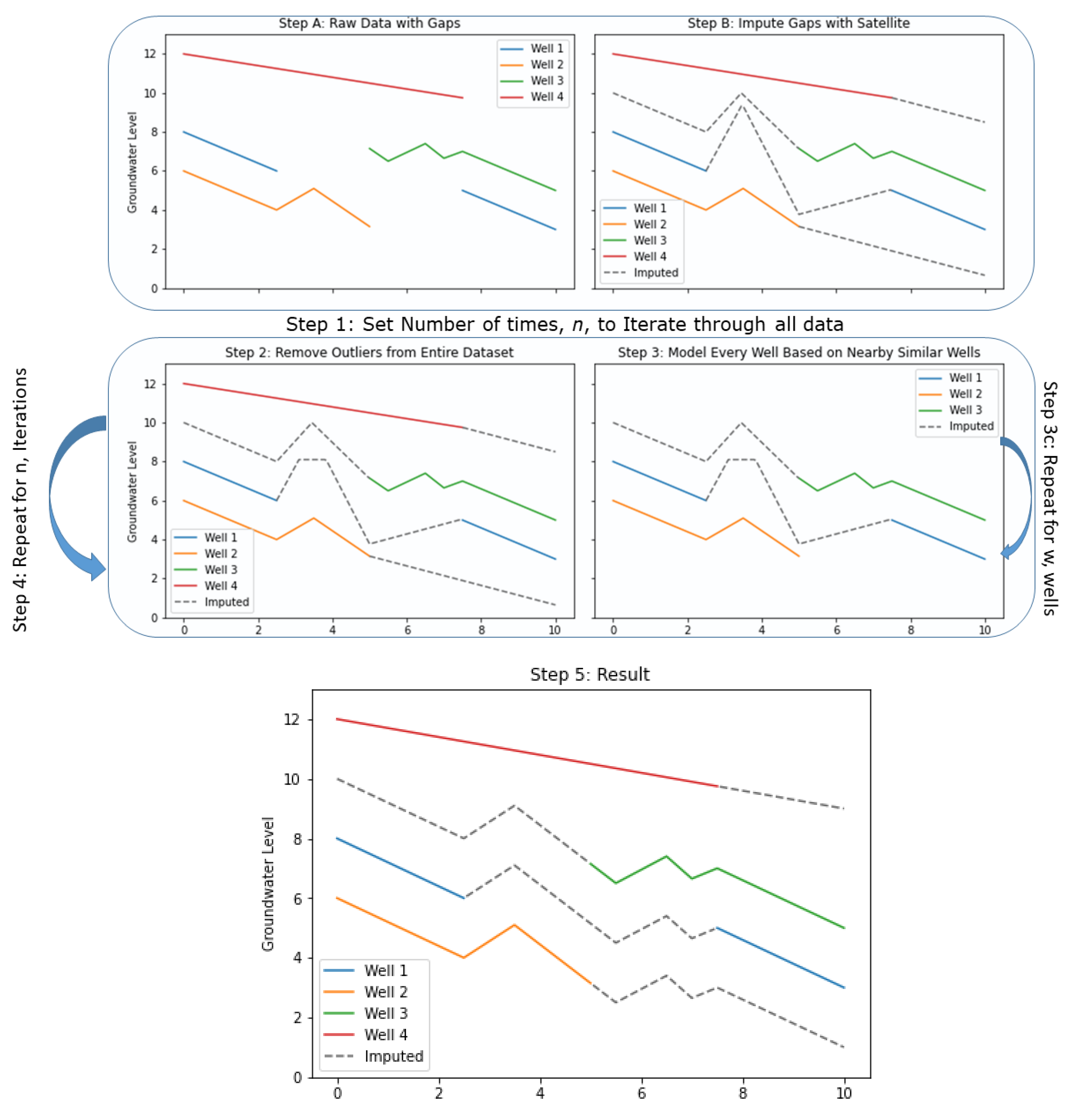
2.1. Methods Overview
- Step A: Obtain the raw groundwater data with gaps and preprocess each dataset so that the datasets at each well have the same time steps.
- Step B: Perform an initial imputation to generate a complete time series dataset for each well. This means that every discretized time step will have an associated value. After imputation, replace any imputed value that has an observed measurement with the original data. The imputation step only fills gaps (i.e., imputation).
- Step 1: Select the number of iterations, n, to pass through the entire data set.
- Step 2: Use a Hampel filter, described in Section 2.2, to smooth synthetic data spikes or model predictions that are unrealistic for groundwater data. This process removes outliers from the initially imputed dataset. Before each iteration step, apply this filter to remove outliers. The Hampel filter is used so that any anomalies do not propagate errors.
- Step 3: Iterate through each well, w, in the aquifer. For each well:
- ○
- Step 3a: Select a small set of imputed time series datasets from the wells correlated to the target well. We selected wells based on linear correlation and spatial distance; both ideas are explained in Section 2.3.
- ○
- Step 3b: Develop a model for the target well using the time series data selected in Step 3a.
- ○
- Step 3c: Run the target well model to generate a complete time series. Replace any predictions that have an observed value with the in situ measurement. The results of every model are updated synchronously at the end of the iteration. This means that an updated representation will not be available as a feature until the next iteration; if a particular well is selected multiple times as a feature, each model will see the same version of the data. Once every well has been visited, the model output is used as the input for the next iteration.
- Step 4: Repeat Steps 2 and 3 for n iterations.
- Step 5: Examine the results.
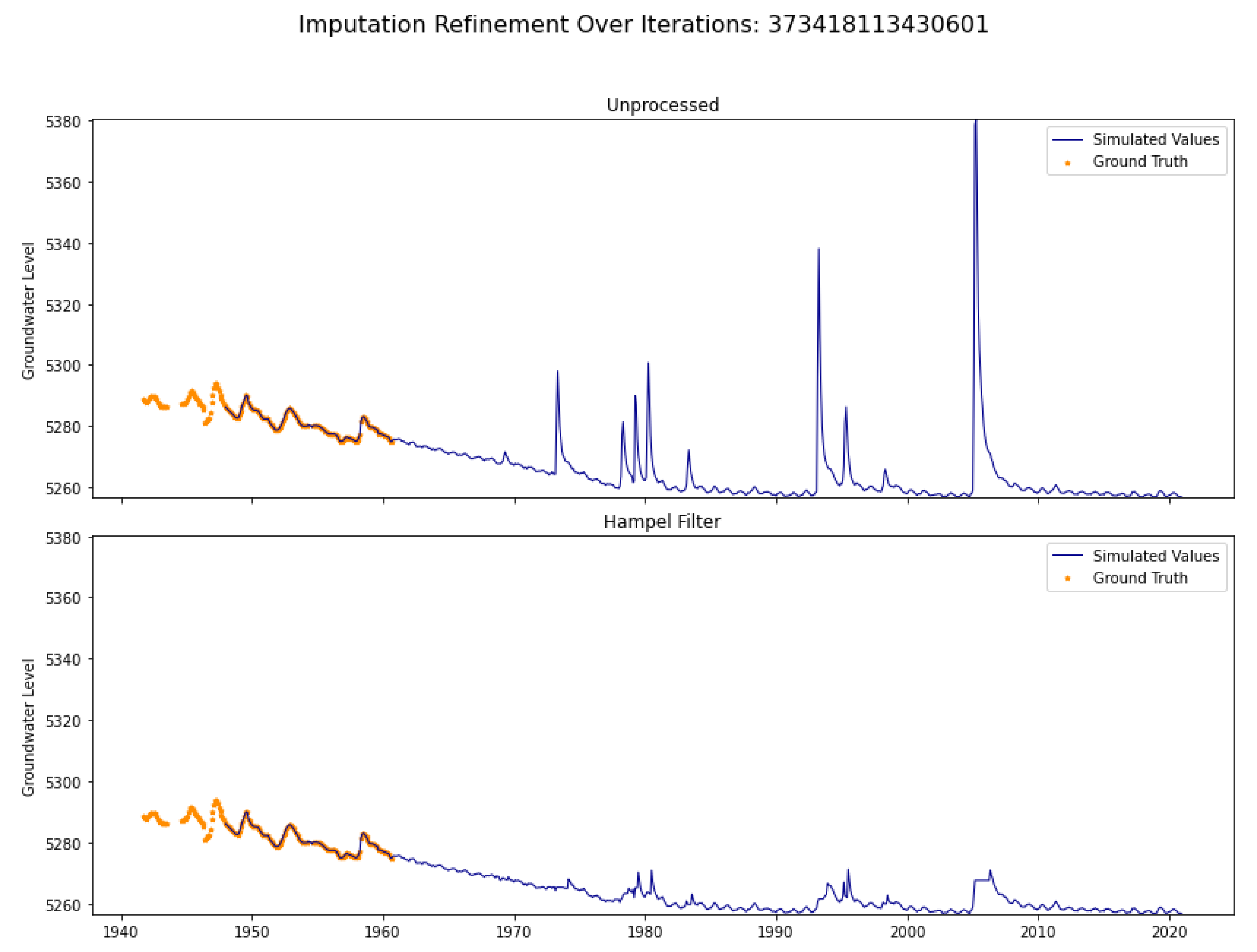
2.2. Hampel Filter
2.3. Well Modeling
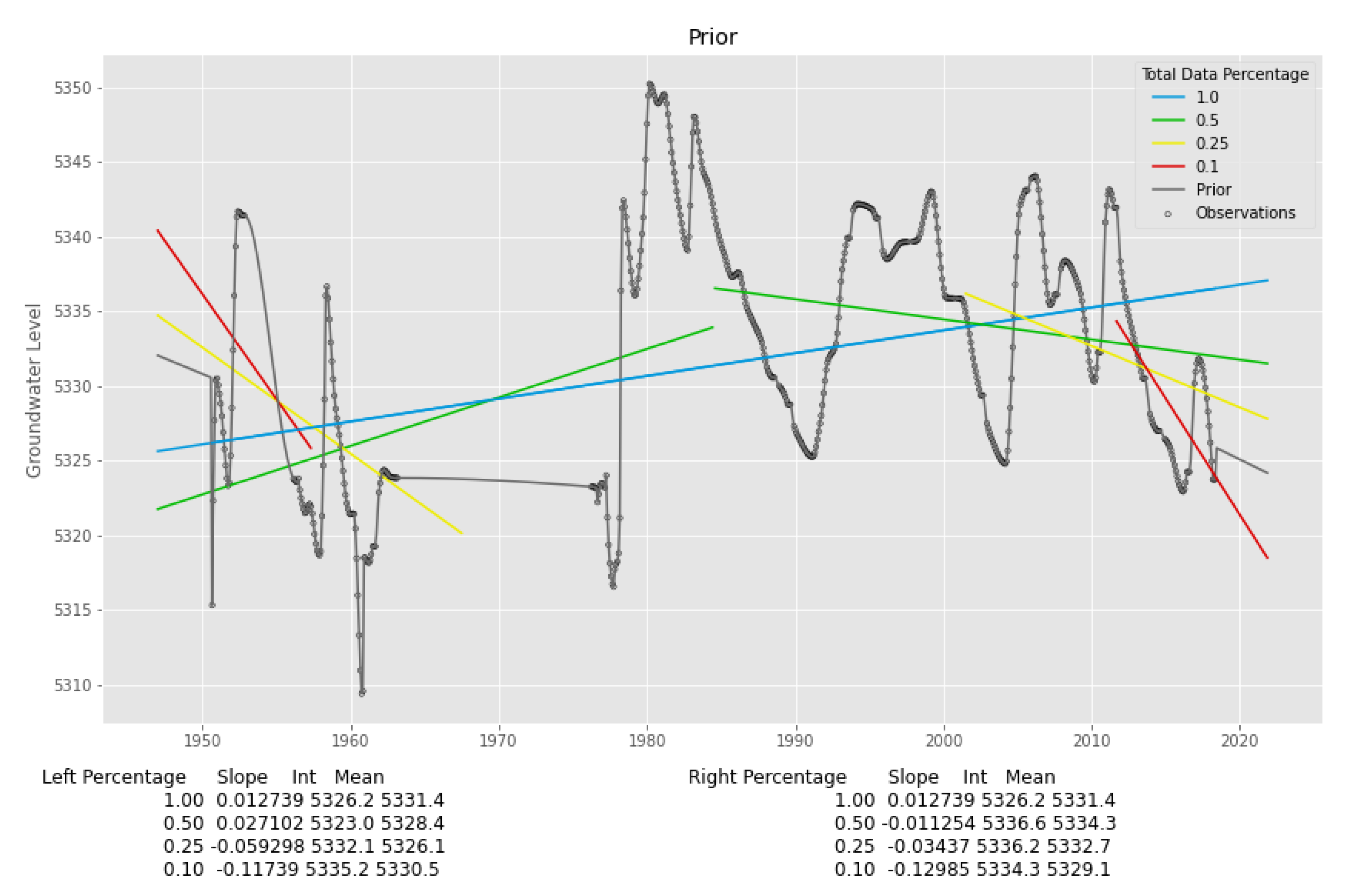
2.3.1. Well Feature Selection
2.3.2. Prior Features
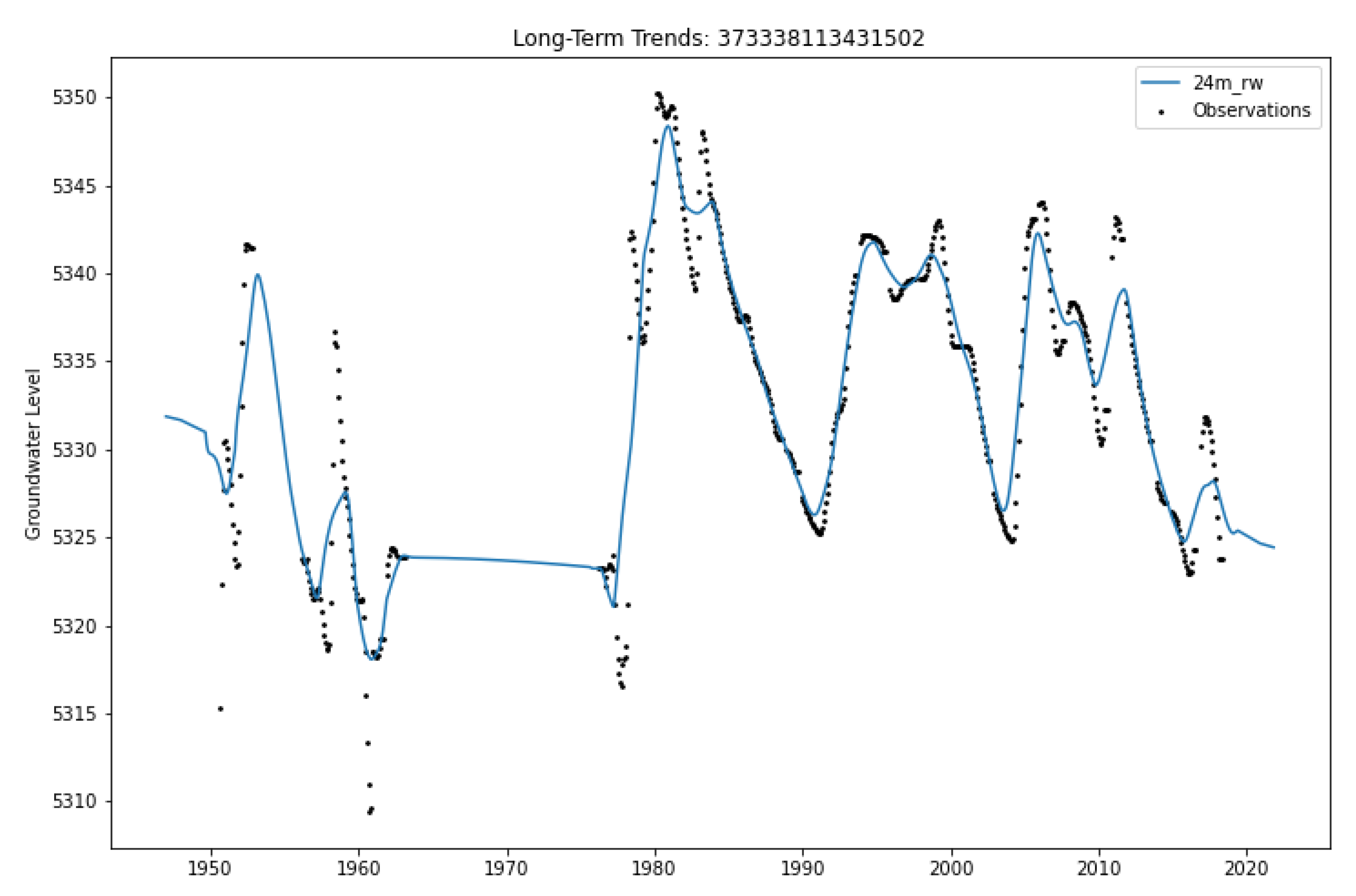
2.3.3. Temporal Features
2.4. Iterative Refinement
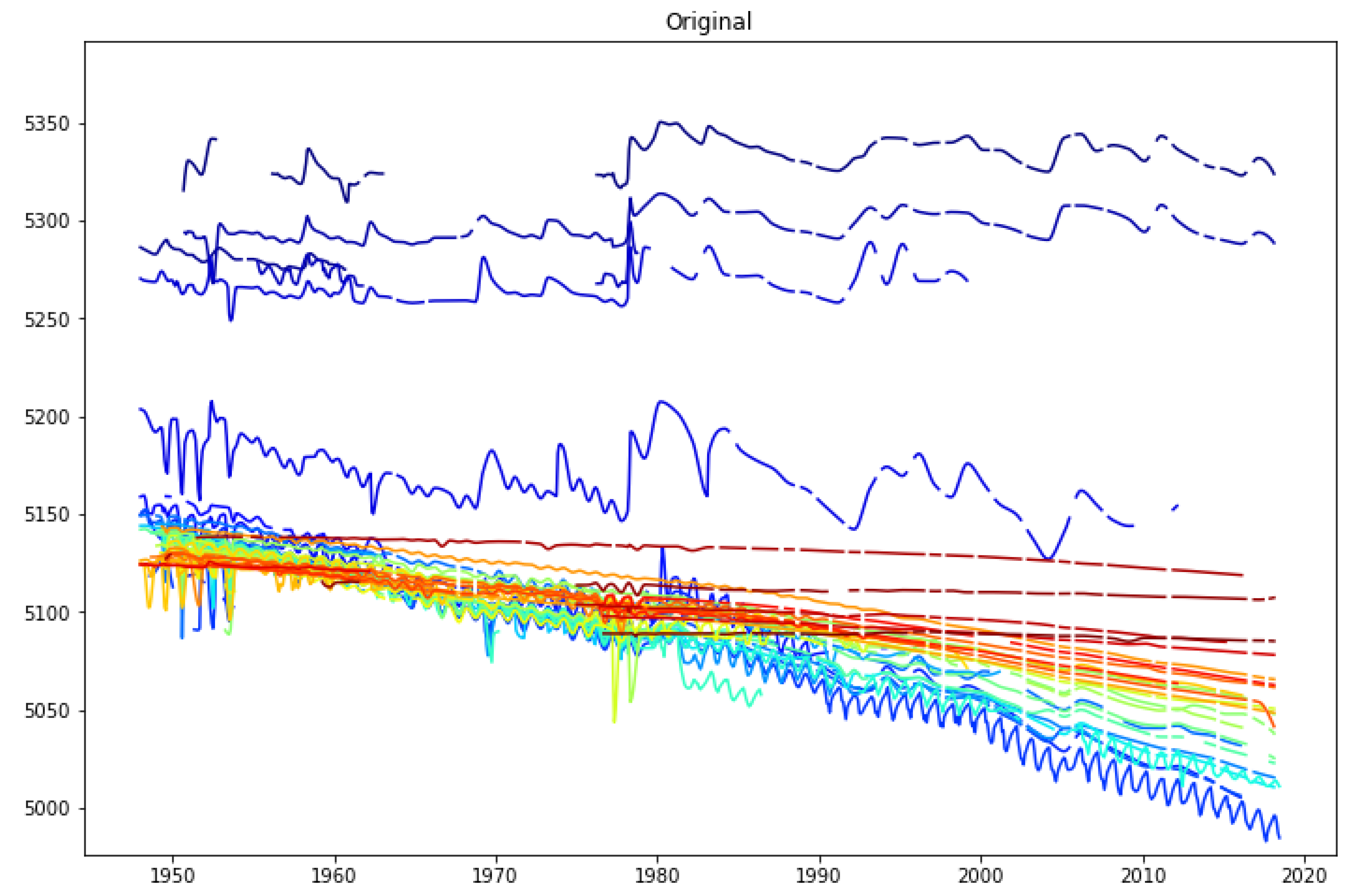
3. Results
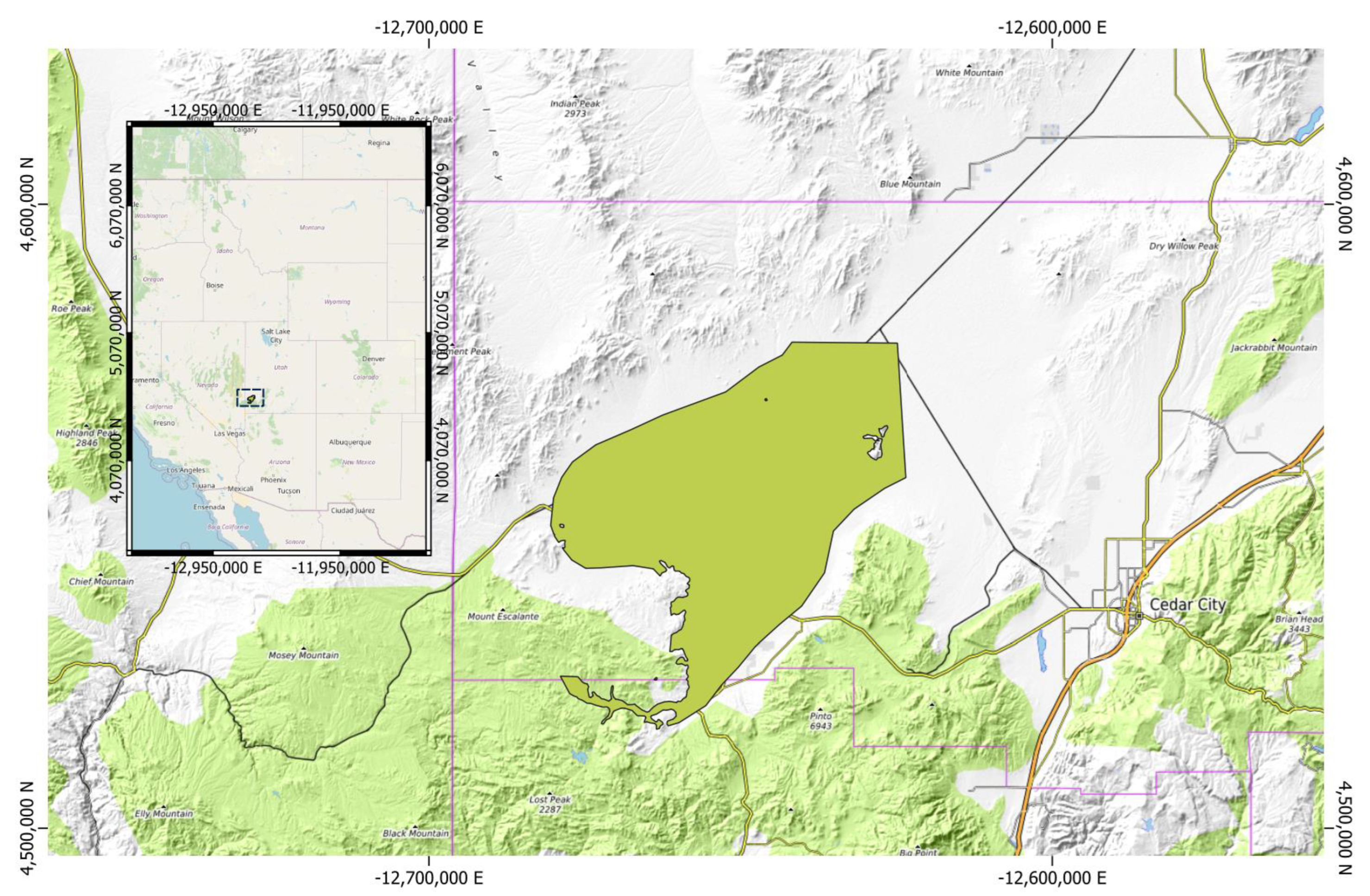
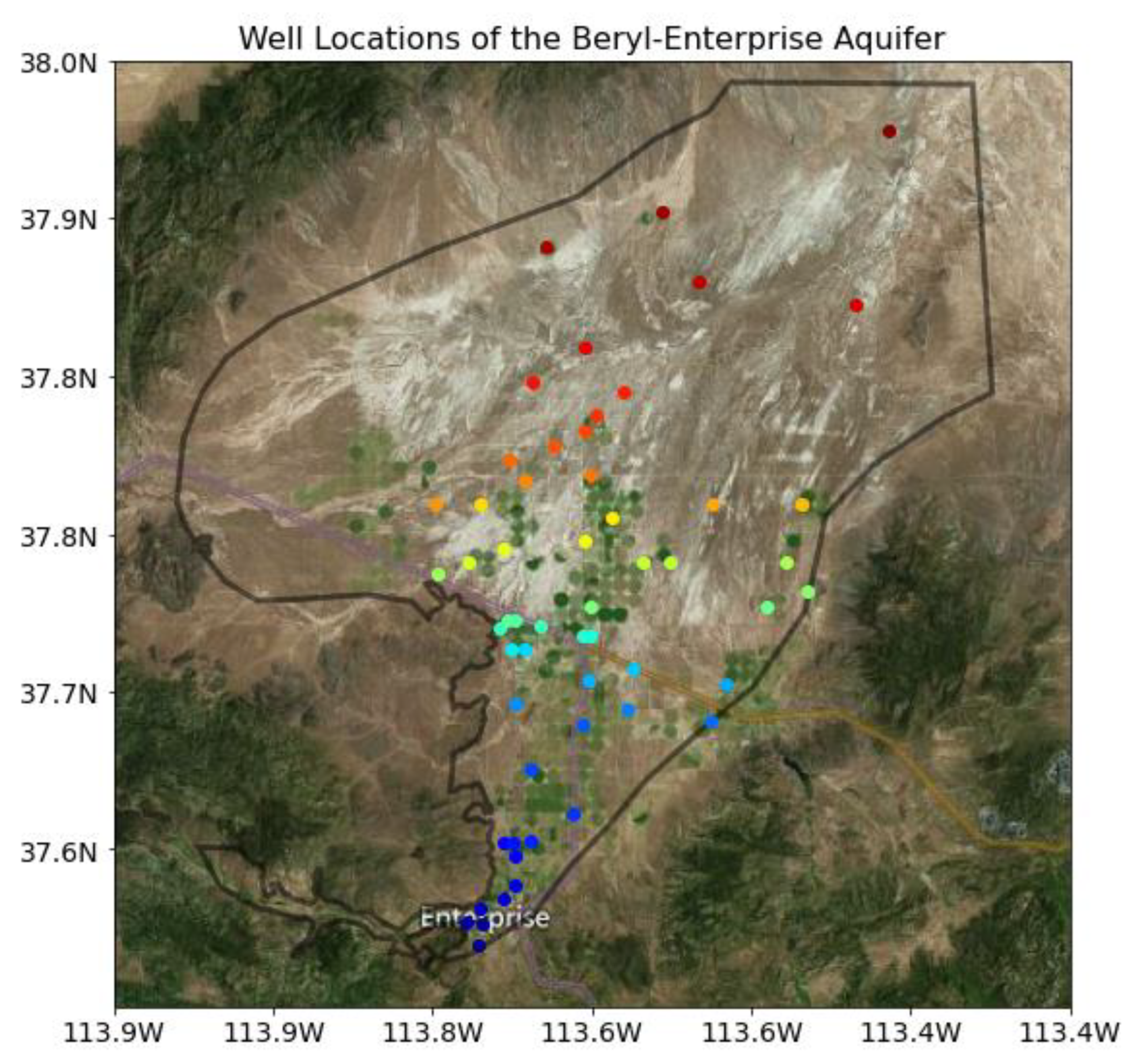
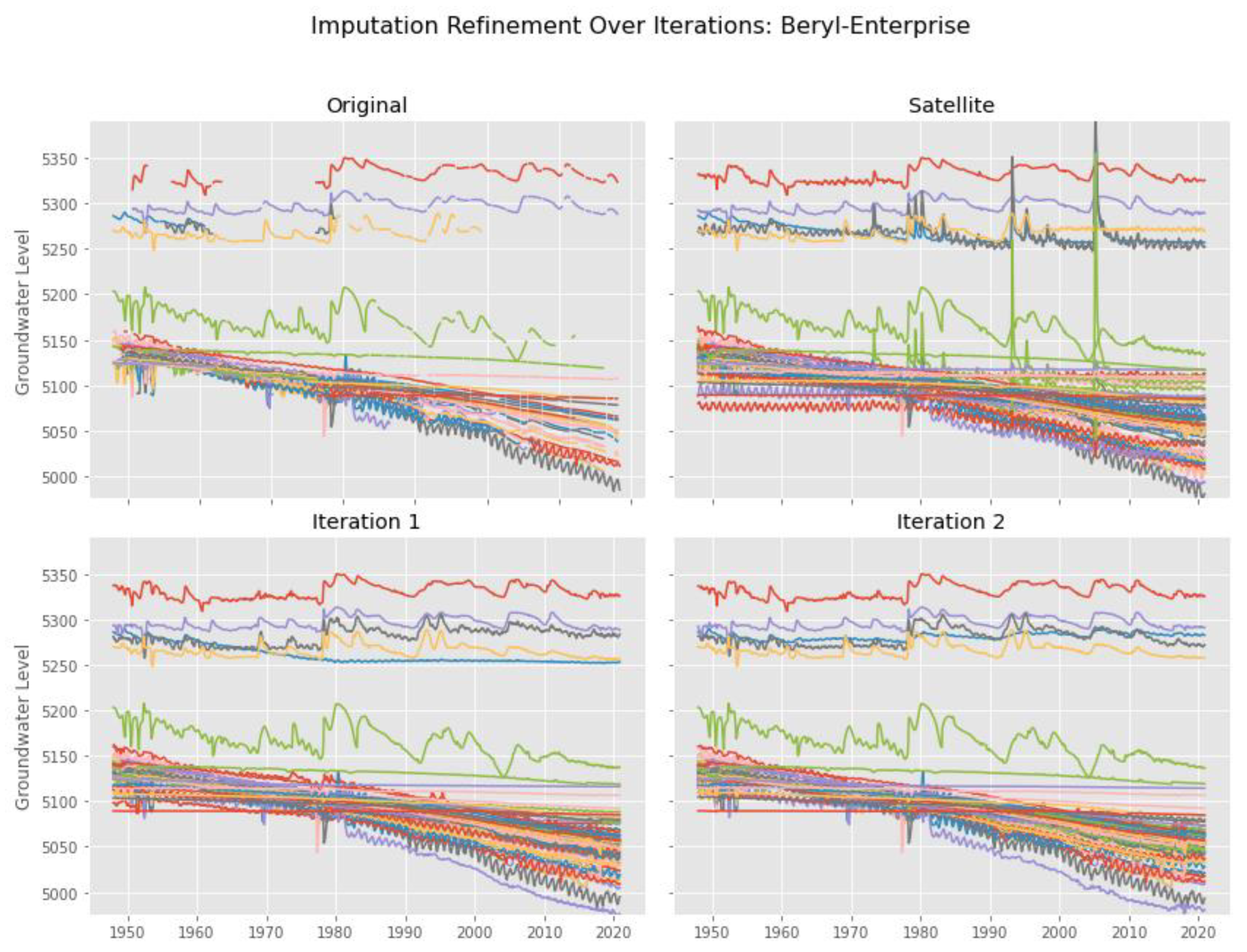
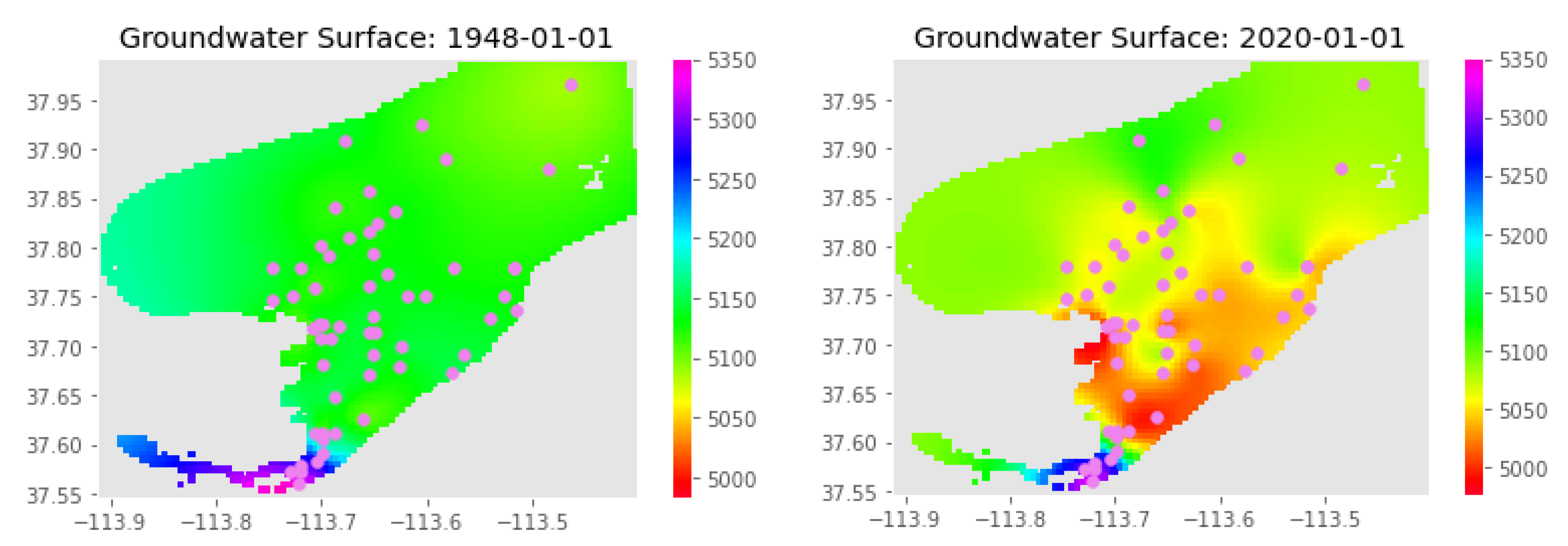
3.1. Case Study: Beryl-Enterprise Utah Aquifer
3.2. Aquifer Results
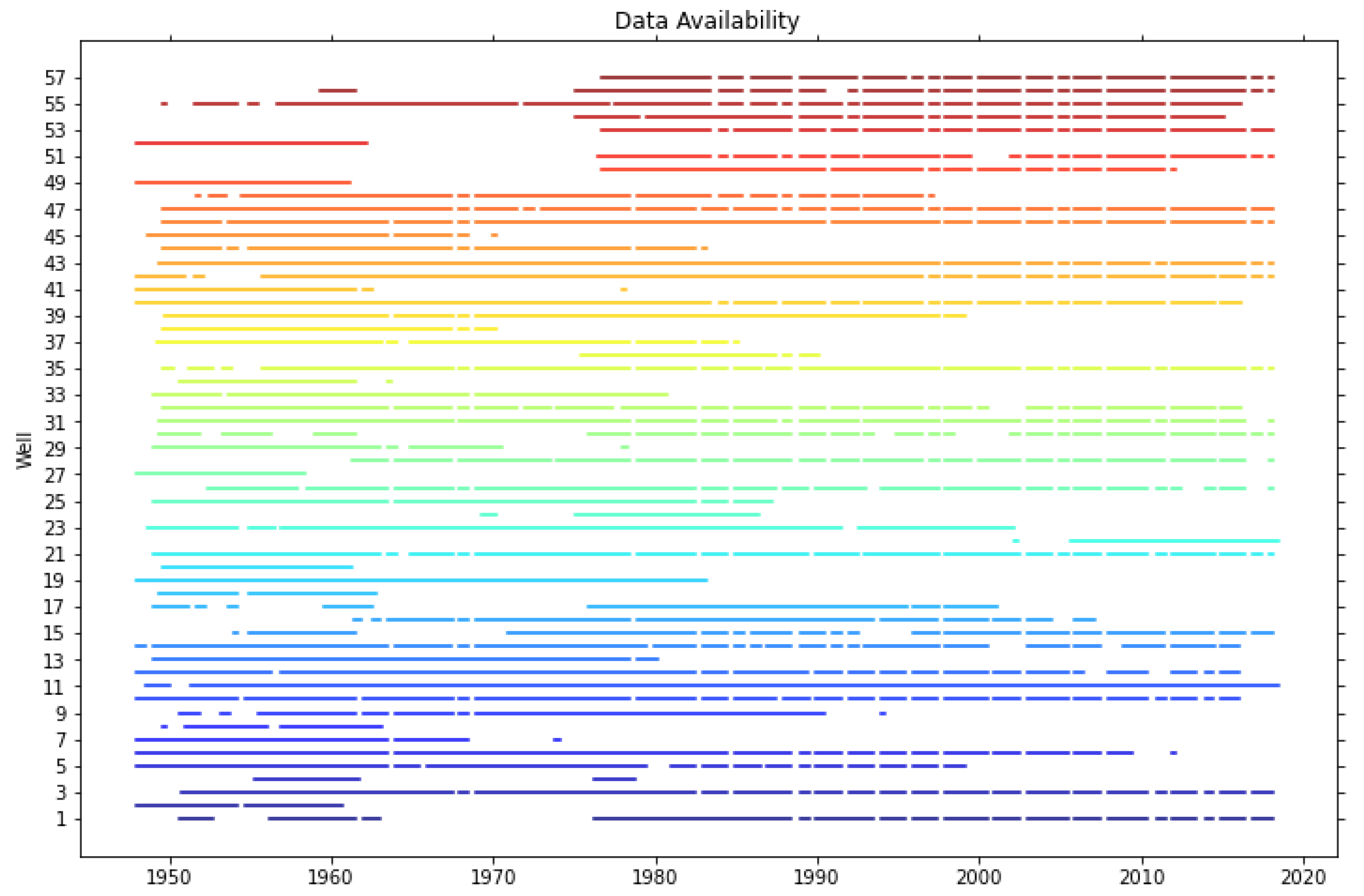
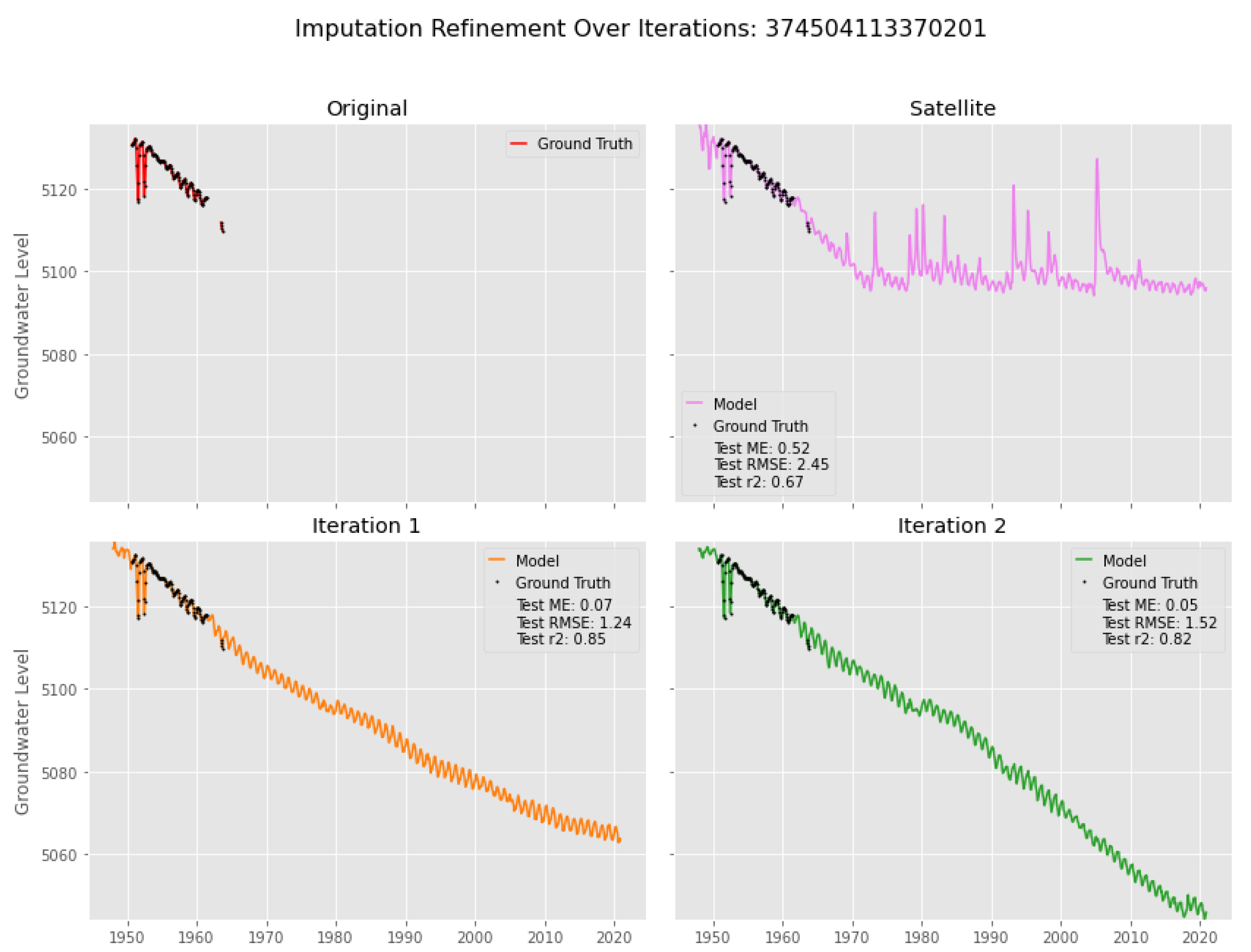
3.3. Well Details
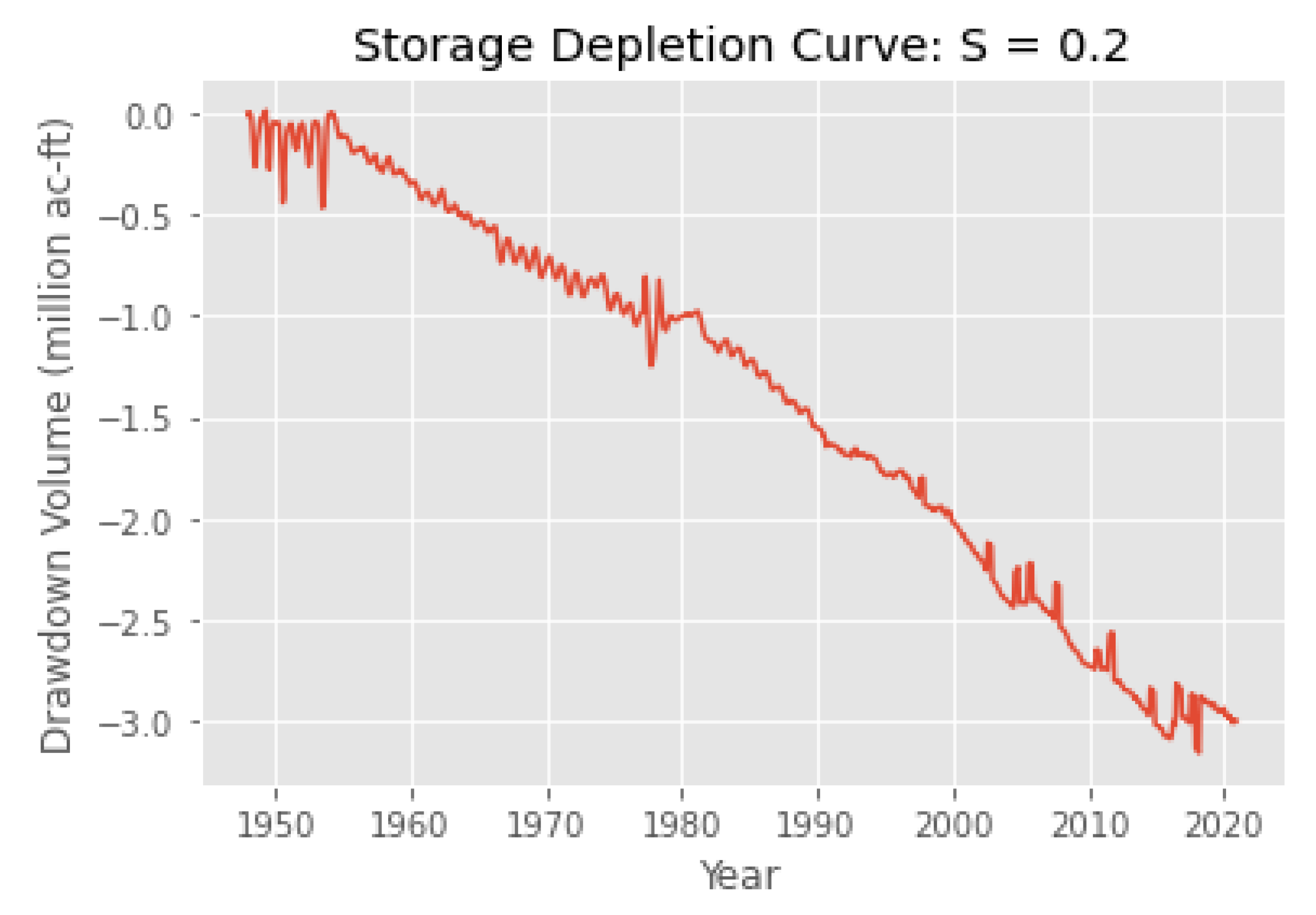
3.4. Validation through Water Storage Analysis
4. Discussion
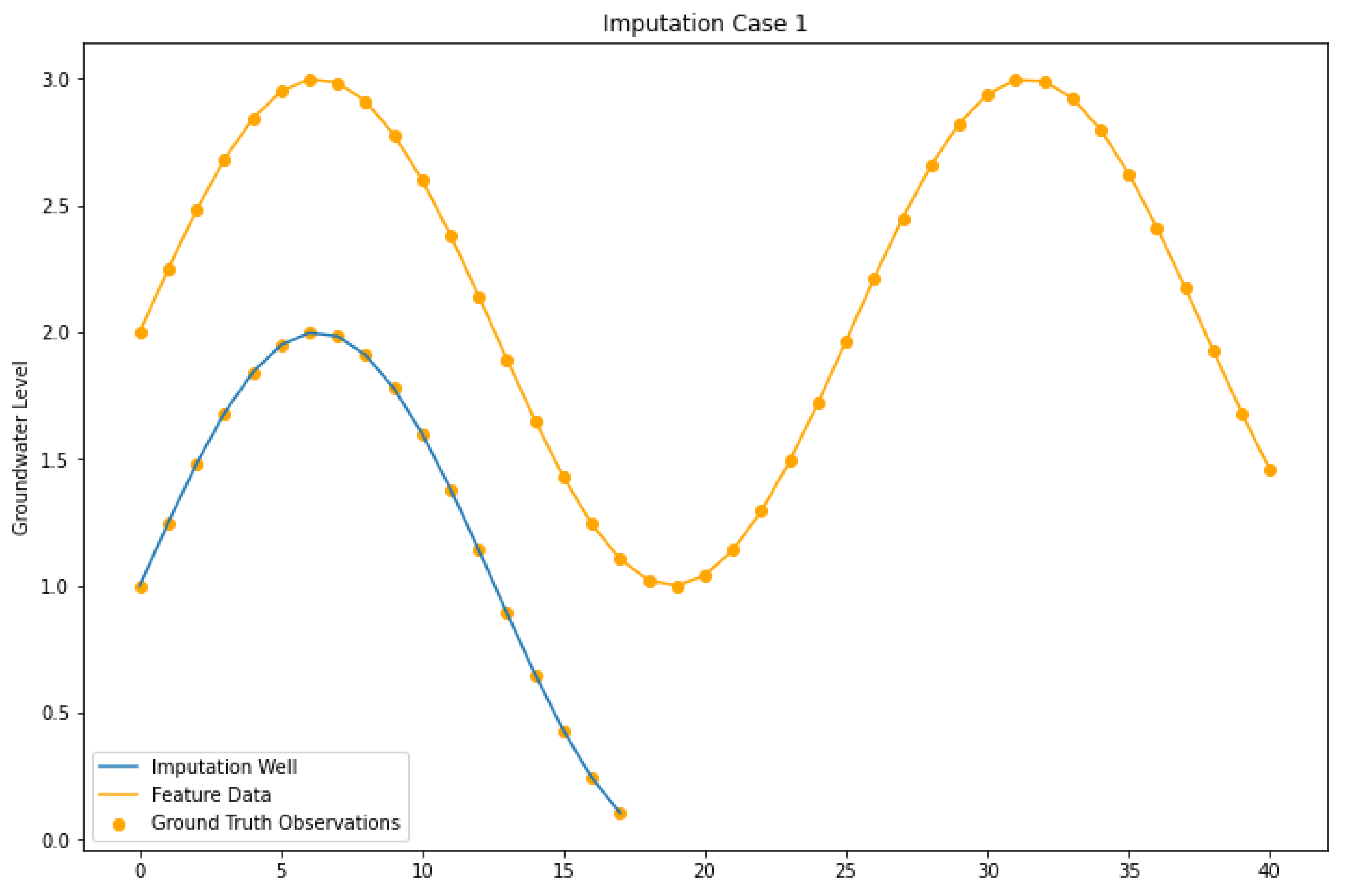
4.1. Imputation Case I
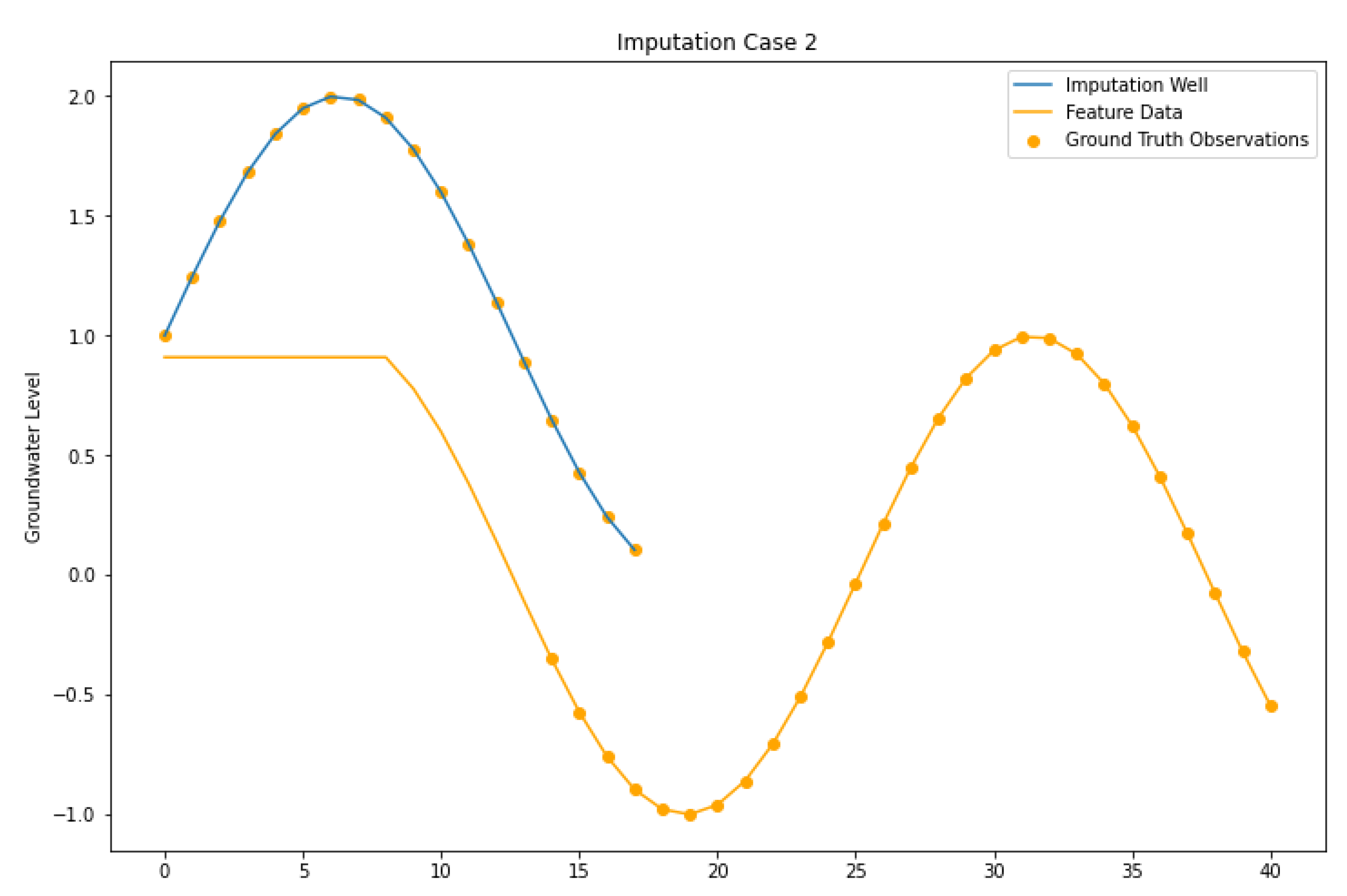
4.2. Imputation Case II
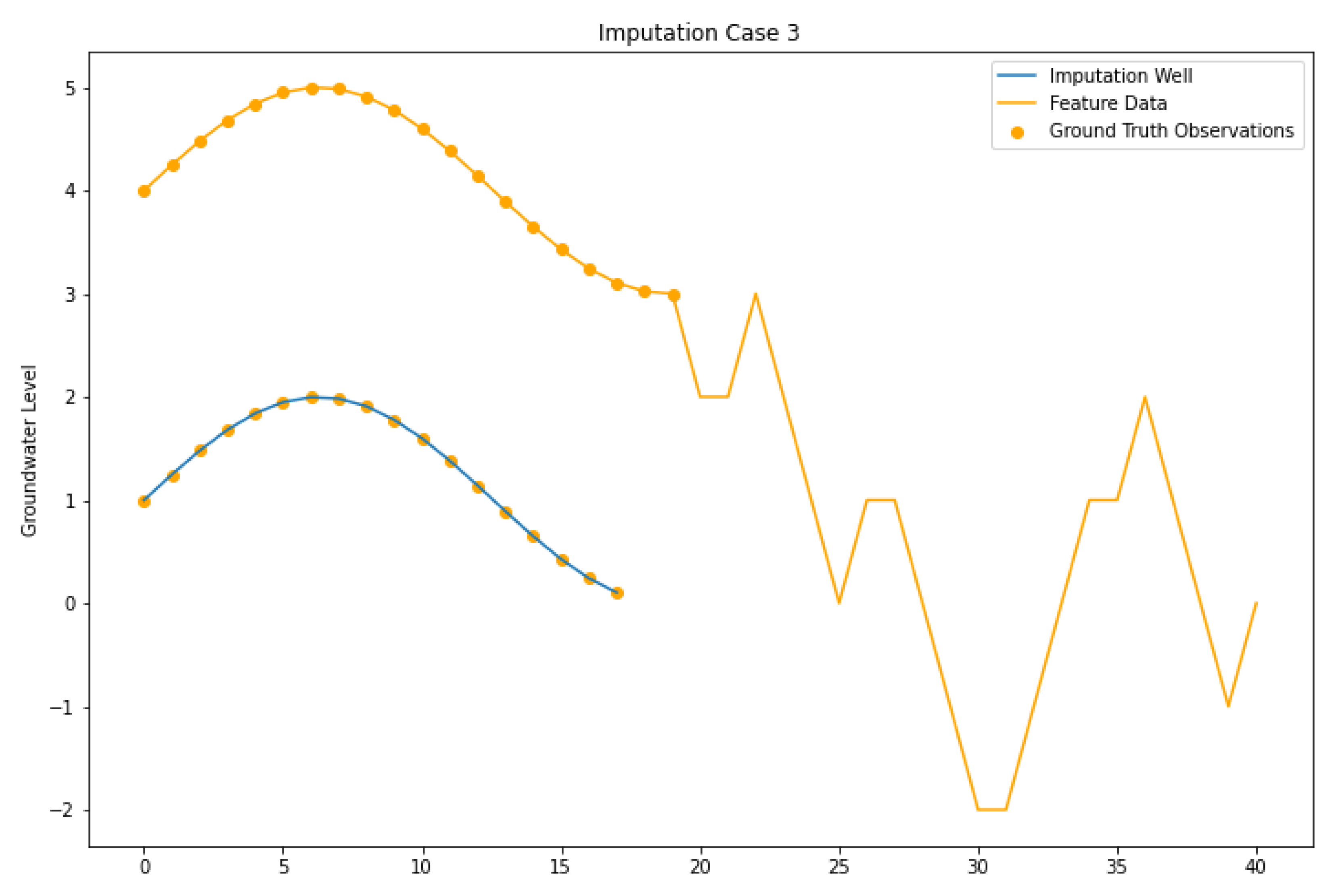
4.3. Imputation Case III
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barber, N.L. Summary of Estimated Water Use in the United States in 2005; U.S. Geological Survey: Reston, VA, USA, 2009.
- Giordano, M.; Villholth, K.G. The Agricultural Groundwater Revolution: Opportunities and Threats to Development; CABI: Long Beach, CA, USA, 2007; ISBN 978-1-84593-173-5. [Google Scholar]
- Konikow, L.F.; Kendy, E. Groundwater Depletion: A Global Problem. Hydrogeol. J. 2005, 13, 317–320. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between Groundwater and Surface Water: The State of the Science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Fogg, G.E.; LaBolle, E.M. Motivation of Synthesis, with an Example on Groundwater Quality Sustainability. Water Resour. Res. 2006, 42, W03S05. [Google Scholar] [CrossRef]
- Famiglietti, J.S. The Global Groundwater Crisis. Nat. Clim Change 2014, 4, 945–948. [Google Scholar] [CrossRef] [Green Version]
- Beran, B.; Piasecki, M. Availability and Coverage of Hydrologic Data in the US Geological Survey National Water Information System (NWIS) and US Environmental Protection Agency Storage and Retrieval System (STORET). Earth Sci. Inform. 2008, 1, 119–129. [Google Scholar] [CrossRef] [Green Version]
- Barbosa, S.A.; Pulla, S.T.; Williams, G.P.; Jones, N.L.; Mamane, B.; Sanchez, J.L. Evaluating Groundwater Storage Change and Recharge Using GRACE Data: A Case Study of Aquifers in Niger, West Africa. Remote Sens. 2022, 14, 1532. [Google Scholar] [CrossRef]
- Mower, R.W.; Sandberg, G.W. Hydrology of the Beryl-Enterprise Area, Escalante Desert, Utah, with Emphasis on Ground Water; with a Section on Surface Water; Technical Publication; Utah Department of Natural Resources, Division of Water Rights: Salt Lake City, UT, USA, 1982; Volume 73, p. 86. [Google Scholar]
- Evans, S.W.; Jones, N.L.; Williams, G.P.; Ames, D.P.; Nelson, E.J. Groundwater Level Mapping Tool: An Open Source Web Application for Assessing Groundwater Sustainability. Environ. Model. Softw. 2020, 131, 104782. [Google Scholar] [CrossRef]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Hoboken, NJ, USA, 1979; ISBN 978-0-13-365312-0. [Google Scholar]
- Alley, W.M.; Healy, R.W.; LaBaugh, J.W.; Reilly, T.E. Flow and Storage in Groundwater Systems. Science 2002, 296, 1985–1990. [Google Scholar] [CrossRef] [Green Version]
- Becker, M.W. Potential for Satellite Remote Sensing of Ground Water. Groundwater 2006, 44, 306–318. [Google Scholar] [CrossRef]
- McStraw, T.C.; Pulla, S.T.; Jones, N.L.; Williams, G.P.; David, C.H.; Nelson, J.E.; Ames, D.P. An Open-Source Web Application for Regional Analysis of GRACE Groundwater Data and Engaging Stakeholders in Groundwater Management. JAWRA J. Am. Water Resour. Assoc. 2021, 58, 1002–1016. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating Groundwater Storage Changes in the Mississippi River Basin (USA) Using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef] [Green Version]
- Sun, A.Y. Predicting Groundwater Level Changes Using GRACE Data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’adi, Z.; Mehr, A.D.; et al. Groundwater Level Prediction Using Machine Learning Models: A Comprehensive Review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Ahmadi, A.; Olyaei, M.; Heydari, Z.; Emami, M.; Zeynolabedin, A.; Ghomlaghi, A.; Daccache, A.; Fogg, G.E.; Sadegh, M. Groundwater Level Modeling with Machine Learning: A Systematic Review and Meta-Analysis. Water 2022, 14, 949. [Google Scholar] [CrossRef]
- Vu, M.T.; Jardani, A.; Massei, N.; Fournier, M. Reconstruction of Missing Groundwater Level Data by Using Long Short-Term Memory (LSTM) Deep Neural Network. J. Hydrol. 2021, 597, 125776. [Google Scholar] [CrossRef]
- Bowes, B.D.; Sadler, J.M.; Morsy, M.M.; Behl, M.; Goodall, J.L. Forecasting Groundwater Table in a Flood Prone Coastal City with Long Short-Term Memory and Recurrent Neural Networks. Water 2019, 11, 1098. [Google Scholar] [CrossRef] [Green Version]
- Evans, S.; Williams, G.P.; Jones, N.L.; Ames, D.P.; Nelson, E.J. Exploiting Earth Observation Data to Impute Groundwater Level Measurements with an Extreme Learning Machine. Remote Sens. 2020, 12, 2044. [Google Scholar] [CrossRef]
- Ramirez, S.G.; Williams, G.P.; Jones, N.L. Groundwater Level Data Imputation Using Machine Learning and Remote Earth Observations Using Inductive Bias. Remote Sens. 2022, 14, 5509. [Google Scholar] [CrossRef]
- Motevalli, A.; Naghibi, S.A.; Hashemi, H.; Berndtsson, R.; Pradhan, B.; Gholami, V. Inverse Method Using Boosted Regression Tree and K-Nearest Neighbor to Quantify Effects of Point and Non-Point Source Nitrate Pollution in Groundwater. J. Clean. Prod. 2019, 228, 1248–1263. [Google Scholar] [CrossRef]
- Gundogdu, K.S.; Guney, I. Spatial Analyses of Groundwater Levels Using Universal Kriging. J. Earth Syst. Sci. 2007, 116, 49–55. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, S.H.; Sedghamiz, A. Application and Evaluation of Kriging and Cokriging Methods on Groundwater Depth Mapping. Environ. Monit. Assess. 2008, 138, 357–368. [Google Scholar] [CrossRef] [PubMed]
- Sener, E.; Davraz, A.; Ozcelik, M. An Integration of GIS and Remote Sensing in Groundwater Investigations: A Case Study in Burdur, Turkey. Hydrogeol. J. 2005, 13, 826–834. [Google Scholar] [CrossRef]
- Tapoglou, E.; Karatzas, G.P.; Trichakis, I.C.; Varouchakis, E.A. A Spatio-Temporal Hybrid Neural Network-Kriging Model for Groundwater Level Simulation. J. Hydrol. 2014, 519, 3193–3203. [Google Scholar] [CrossRef]
- Ramirez, S.G.; Hales, R.C.; Williams, G.P.; Jones, N.L. Extending SC-PDSI-PM with Neural Network Regression Using GLDAS Data and Permutation Feature Importance. Environ. Model. Softw. 2022, 157, 105475. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Hampel, F.R. The Influence Curve and Its Role in Robust Estimation. J. Am. Stat. Assoc. 1974, 69, 383–393. [Google Scholar] [CrossRef]
- Liu, H.; Shah, S.; Jiang, W. On-Line Outlier Detection and Data Cleaning. Comput. Chem. Eng. 2004, 28, 1635–1647. [Google Scholar] [CrossRef]
- Outlier Removal Using Hampel Identifier—MATLAB Hampel. Available online: https://www.mathworks.com/help/signal/ref/hampel.html (accessed on 18 January 2023).
- Ruppert, D.; Matteson, D.S. Statistics and Data Analysis for Financial Engineering: With R Examples; Springer Texts in Statistics; Springer New York: New York, NY, USA, 2015; ISBN 978-1-4939-2613-8. [Google Scholar]
- EmilienDupont Interactive Visualization of Optimization Algorithms in Deep Learning. Available online: https://emiliendupont.github.io/2018/01/24/optimization-visualization/ (accessed on 1 February 2021).
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd ed.; O’Reilly Media, Incorporated: Sebastopol, CA, USA, 2019. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. Oper. Syst. Des. Implement. 2016, 101, 582–598. [Google Scholar]
- Chollet, F. Deep Learning with Python; Manning Publications Co.: Shelter Island, NY, USA, 2018; ISBN 978-1-61729-443-3. [Google Scholar]
- USGS Water Data for the Nation. Available online: https://waterdata.usgs.gov/nwis (accessed on 22 May 2022).
- Jones, K.L. Beryl Enterprise Ground Water Management Plan. Available online: https://waterrights.utah.gov/groundwater/ManagementReports/BerylEnt/berylEnterprise.asp (accessed on 28 January 2023).
- Mower, R.W. Ground-Water Data for the Beryl-Enterprise Area, Escalante Desert, Utah; Open-File Report; U.S. Geological Survey: Reston, VA, USA, 1981; Volume 81–340.



| Value | Feature Wells Used | Value | Feature Wells Used |
|---|---|---|---|
| < 0.1 | 11 | < 0.6 | 6 |
| < 0.2 | 10 | < 0.7 | |
| < 0.3 | 9 | < 0.8 | 5 |
| < 0.4 | 8 | < 0.9 | |
| < 0.5 | 7 | < 1.0 |
| Date | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Decimal Time |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 January 1948 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0000 |
| 1 February 1948 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0012 |
| 1 March 1948 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0023 |
| 1 April 1948 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0035 |
| 1 May 1948 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0046 |
| 1 June 1948 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0058 |
| 1 July 2020 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0.9942 |
| 1 August 2020 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0.9954 |
| 1 September 2020 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0.9965 |
| 1 October 2020 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0.9977 |
| 1 November 2020 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0.9988 |
| 1 December 2020 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1.0000 |
| Imputation Case I | Target and feature wells have measured data over the same intervals and the feature well has measured data over the gaps. |
| Imputation Case II | Target and feature wells do not necessarily have measured data over the same intervals. Much of the correlation between the two is conducted through previous imputation results. The feature well have measured data within the gaps of the target well. |
| Imputation Case III | Target and feature wells have measured data over the same interval, but only imputed values exist over the gap periods. The feature wells do not have any measured data in the gaps. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramirez, S.G.; Williams, G.P.; Jones, N.L.; Ames, D.P.; Radebaugh, J. Improving Groundwater Imputation through Iterative Refinement Using Spatial and Temporal Correlations from In Situ Data with Machine Learning. Water 2023, 15, 1236. https://doi.org/10.3390/w15061236
Ramirez SG, Williams GP, Jones NL, Ames DP, Radebaugh J. Improving Groundwater Imputation through Iterative Refinement Using Spatial and Temporal Correlations from In Situ Data with Machine Learning. Water. 2023; 15(6):1236. https://doi.org/10.3390/w15061236
Chicago/Turabian StyleRamirez, Saul G., Gustavious Paul Williams, Norman L. Jones, Daniel P. Ames, and Jani Radebaugh. 2023. "Improving Groundwater Imputation through Iterative Refinement Using Spatial and Temporal Correlations from In Situ Data with Machine Learning" Water 15, no. 6: 1236. https://doi.org/10.3390/w15061236






