1. Introduction
The issue of stability analysis of geotechnical slopes is a major challenge in the fields of geotechnics and geological hazards. Most landslide hazards are caused by the soil becoming nearly saturated due to heavy rainfall, resulting in a rapid decrease in cohesion and an internal friction angle. The varying mechanical properties of different soils also limit the accuracy of conventional finite element numerical analysis in solving slope stability problems, often leading to mismatches with actual conditions or inaccurate predictions of instability.
Since Fellenius introduced the circular slide method for addressing soil slope instability in 1927, several techniques for analyzing the stability of slopes have already been created. Using the frictional circular approach [
1], for exclusively frictional, cohesive, two dimensional soil slopes, Taylor [
2] developed stability graphs to determine the factor of safety. The limit equilibrium method and numerical simulation method are commonly used analysis techniques in the study of geological hazards, such as landslides and debris flows. Available numerical simulation analysis approaches encompass a range of techniques, including the rigid body element method, equivalent continuous model, block theory, discontinuous deformation analysis (DDA), discrete element method (DEM), and finite element method (FEM). Among these, the most popular numerical simulation technique in slope engineering is the FE method, which plays a crucial role. The FE method addresses the limitations of limit equilibrium theory, such as the requirement to divide soil into strips and assume rigidity. The application of FE numerical simulation in slope stability analysis involves utilizing classical geotechnical elastic-plasticity theory. This method calculates stress and displacement values at each node within each minimum solid element, followed by deriving the macroscopic stress and deformation values of the geotechnical body. The reduction of the strength parameters of the geotechnical body is then implemented to determine geotechnical instability and solve the slope safety factor.
Recent years have seen a surge in research by Chinese and international scholars on various slope stability analysis methods, inspired by Zienkiewicz’s classic strength reduction method (SRM) [
3]. The most widely cited example of the application of SRM in finite element numerical simulation is demonstrated in Dawson’s article [
4], which has been replicated by multiple scholars using various numerical software. Overall, the strength reduction method (SRM) is the most applicable method for slope stability analysis at present.
Slope failure criteria have been the subject of studies by Ugai [
5], Matsui [
6], Griffiths [
7], and others. These studies determined safety factors by gradually increasing the reduced factor until the slope became unstable. Wei [
8] explored the application of finite element SRM in dam failure criteria. Zheng [
9] and Liu [
10] investigated the viability of various criteria, including numerical computation convergence, abrupt displacement or deformation, and equivalent plastic connection zone. Wu et al. [
11] described a novel approach that determines slope stability using the acceleration value. First, Taylor [
2] suggested using various reduction factors for friction angle and cohesion and emphasized that the frictional resistance on the sliding surface is primarily responsible for slope stability, with cohesion serving as supplementary support. This theoretical formulation became known as the Double Strength Reduction Method (DRM). Water content was shown to be the primary factor impacting the slope mass characteristics by Liu [
10] and Tang [
12,
13,
14] in their study of the shear strength decrease procedures for clay and sand. Xue et al. [
15] established a nonlinear correlation faction between the reduction coefficients of friction angle and cohesion and then validated this conclusion utilizing FE software ABAQUS. The proportionate relation between reduction factors for various slopes was examined by Yuan et al. [
16]. Then, they proposed two methods for defining the comprehensive safety factor. A non-proportional relationship between the reduction coefficients of cohesion and internal friction angle was observed by Xue et al. [
17] when assuming linear attenuation of strength parameters. The DRM reduction coefficients were determined using a method established by Xu [
18] based on the impact of water content fluctuation. Using the shortest path of stress reduction, Zhao [
19] and Isakov et al. [
20] provided a formula for computing the minimal slope complete safety coefficient. Lastly, Bai et al. [
21] modified the concept of DRM and solved for the final slope safety factor using a maximum Mohr stress circle tangent. Various scholars [
22,
23,
24] have explored the anchoring mechanism of soil and the stability of different types of soil slopes using the strength-reduction method of analysis.
Wang [
25] and Cai [
26] investigated the impact of rainfall on the stability of unsaturated soil slopes using the conventional finite element strength reduction method. However, they did not enhance or optimize the strength reduction method and continued to employ the conventional finite strength reduction method. This paper addresses this issue by introducing a new method for the simultaneous reduction of both strength coefficients, taking into account the impact of changing water content on soil strength values. The proposed method is realized through the implementation of a user-defined subroutine (USDFLD) in the FE software ABAQUS. The validity of the proposed method is confirmed through both theoretical analysis and numerical simulation.
A numerical simulation study of Azhuoluo slope stability was performed by employing the USDFLD user-defined subroutine in the FE software ABAQUS 2019. The Azhuoluo slope is located in the Chinese province of Guizhou, Shuicheng county. On 23 July 2019, a large geological landslide disaster occurred in this area. The simulation results revealed that the friction angle and cohesion of the red soil, which was a result of the residual accumulation of basalt weathering, exhibited a non-synchronized decline as the water content increased. This new numerical simulation method, which takes into account the impact of water content on slope stability analysis, successfully demonstrated the intrinsic mechanism of slope instability and its clear physical meaning, making it a valuable tool for engineering applications.
2. Fundamental Concepts of SRM
2.1. Description of the Traditional Strength Reduction Coefficient
Bishop [
1] introduced the idea of a slope stability safety factor for the first time in the limit equilibrium approach. Later, Zienkiewicz [
3] put forth the idea of a shear strength reduction coefficient, which serves a similar purpose, in his research on elastic-plastic FE numerical study of soil. The reduction factor for shear strength is calculated as the maximum shear strength ratio within the slope to the actual stress, given that the external load remains constant. The maximum shear stress is obtained by applying a reduction coefficient F to the rock–soil material parameters of friction angle
and cohesion
. These modified values
and
are then inputted into the FE software ABAQUS 2019 for simulation. The procedure is repeated until the slope reaches a critical stress condition, which is indicated by a ratio of 1 between the predicted shear strength and actual shear stress. Then, the reduction coefficient serves as the slope’s safety factor, as described by Equations (1) and (2).
2.2. Double Strength Reduction Method
The conventional Strength Reduction Method (SRM) involves reducing both the cohesion and friction angle equally. Taylor [
2] found that the slope stability effects of cohesion and friction angle, as well as their relative reduction intensities, were not the same. As a result, when carrying out slope safety factor reduction, it is necessary to reduce the two parameters to varying degrees based on the actual circumstances, and this is what is known as the Double Strength Reduction Method (DRM). The following are the details of the calculations:
The expressions in Equations (3) and (4) outline the relationship between the natural cohesion and friction angle of the soil slope, and the cohesion and friction angle of the soil slope under critical stress.
The safety factor for cohesion and the safety factor for friction angle, respectively, indicate the reduction coefficients
Fc and
Fφ for cohesion and friction angle. When it comes to analyzing and evaluating slope stability, it is common to only obtain a single comprehensive safety factor value rather than separate values for cohesion and friction angle. The different approaches currently used to calculate the double-strength reduction factor
F are listed in
Table 1.
The destabilization of the soil slopes is caused by the degradation of the internal friction angle and cohesion of the geotechnical material. Most landslides happen as a result of a sudden increase in soil water content brought on by intense rainfall, which leads to the saturation of the soil and a rapid decline in the soil’s strength parameters.
It is evident that the instability of slopes is influenced by the soil’s water content , which acts as the independent variable, and the internal friction angle and cohesion , which act as the dependent variables. Hence, the alteration in soil water content can be utilized to adjust the values of internal friction angle and cohesion , providing a clearer representation of the intrinsic slope instability mechanisms resulting from changes in water content .
In this study, the third method for determining the composite safety factor, listed in
Table 1, was employed to adjust the values of
and
based on the variations in soil water content
. This adjustment of
and
was accomplished by utilizing
as a function of their respective relationships, which allowed for an asynchronous calculation process. The task of calculating the double strength reduction coefficient in a non-linear manner was simplified by only taking into account the water content of the soil in its critical state on the slope once the relationship between the cohesion and internal friction angle of the soil and its water content was established.
In this study, the reduction in cohesive force and internal friction angle caused by changes in soil water content was analyzed. The critical water content
was used to determine the cohesive force and internal friction angle under these conditions. These values were then compared to their natural states to determine the reduction factors for each. Lastly, a weighting of the reduction coefficients for cohesive force and internal friction angle was performed to obtain the overall slope stability, represented as the integrated safety factor. This approach is a finite element method that accounts for the effect of changing water content on soil strength parameters.
and represent the reduction degree of cohesion and the internal friction angle of soil slope in the critical state relative to the initial state, respectively.
The weighting coefficients for the reduction in cohesion and the internal friction angle are represented by
and
, respectively. The slope’s safety factor
F can be represented as follows, as stated in the fourth method for calculating the double strength reduction coefficient shown in
Table 1:
The slope safety factor value
F can eventually be derived by substituting Equations (5)–(8) into Equation (9) and performing rearrangement.
In Equation (10), the reduction coefficient of cohesion is denoted as , and the reduction coefficient of the internal friction angle is denoted as . They, respectively, represent the decline in soil strength at the critical state of instability due to changes in water content. These coefficients can be derived by utilizing Equations (3) and (4).
2.3. Performing the FE Strength Reduction Method Based on ABAQUS
The double-strength reduction method relies on changes in soil properties caused by fluctuations in water content. This method involves reducing the strength parameters of the soil, while considering the variations in water content to determine the slope safety factor and analyze slope stability.
To implement this method, field sampling and testing must be conducted to determine the relationship between soil cohesiveness, friction angle, and water content. Using the finite element method, the and values for each water content are calculated iteratively until the slope’s critical stress state is reached. This stress state is identified through non-convergent calculations.
In this work, the USDFLD user material subroutine of the ABAQUS FE software was used to execute non-synchronous finite element reduction computations of
and
values depending on changes in water content.
Figure 1 shows the calculation method.
2.4. Slope Instability Criteria and Numerical Simulation Constitutive Model
The classical limit equilibrium approach for determining the slope stability safety factor makes the assumption that the rock and soil mass act like a rigid-plastic body. However, natural rock and soil materials exhibit elastic, plastic, and viscous characteristics that are not consistent with this assumption.
When using ABAQUS 2019 software for numerical simulation of geotechnical engineering, one can choose between elastoplastic, viscoelastic, or elastoplastic viscoelastic constitutive models, depending on the specific situation. The ABAQUS software also allows for the customization of the constitutive relationship through the redevelopment function of its user-defined subroutines.
In slope engineering, various geotechnical constitutive relationships have been developed to analyze the failure of the mechanical properties of geotechnical materials, such as the Drucker-Prager criterion and Mohr–Coulomb criterion. Because of its simplicity, clarity of the parameters, and capacity to represent the characteristics of rocks and soils, the Mohr–Coulomb criteria is frequently employed. However, the sharp corners in the principal stress plane of the Mohr–Coulomb criteria can cause uncertainty in plastic flow direction.
ABAQUS software incorporates the modified Mohr-Coulomb criteria, which changes the yield surface into a smooth and continuous elliptical function. According to the modified Mohr–Coulomb criteria, yield happens when every integration point in a material experiences shear stress that linearly relies on normal stress in the same plane. The modified M-C model is based on Mohr’s circle plotted in the plane of the highest and least primary stresses for states of stress at yield. The M-C surface, which represents a shear criterion, and the Rankine surface, which models an optional tension cutoff criterion, together form the yield surface of the modified M-C model.
In the simulation process, there are three ways to determine whether a slope has failed: (1) during the simulation, the numerical model does not converge, and the calculation is aborted; (2) by observing the abrupt transition value of the displacement at a characteristic point on the slope; and (3) by seeing if the slope forms a clearly defined roughly equivalent plastic strain band. It is concluded that to obtain a reasonable safety factor value, all three methods should be used in combination and applied based on the natural geological conditions of the slope.
3. Example Analysis
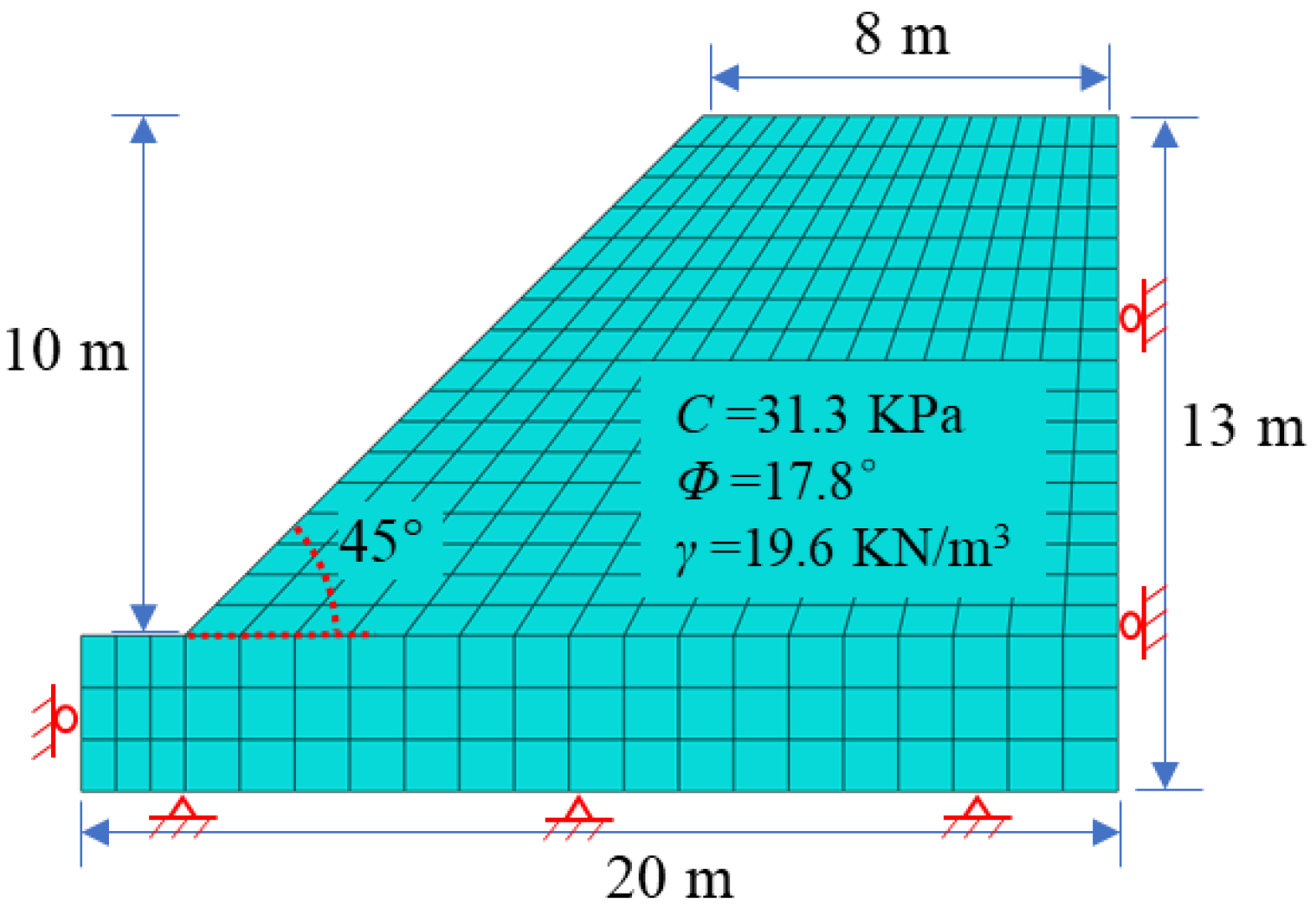
In this study, the slope model proposed by Dawson [
4] was utilized. The dimensional representation of the model is shown in
Figure 2. Additionally, the mechanical parameters of the red clay soil, as given by Zhang [
27], were employed. Young’s modulus of the soil was determined to be 100 MPa, with a Poisson’s ratio of 0.35. The cohesive force
was found to be 31.3 KPa, and the internal friction angle
was 17.8°. Lastly, the unit weight of soil was calculated to be 19.6 KN/mm
3.
According to the direct shear test results on red clay with varying water content, as reported in the literature [
27], the cohesive force
and internal friction angle
can be represented as functions of water content, as demonstrated in Equations (11) and (12).
The boundary conditions of the model were established with fixed horizontal and vertical displacements at the bottom and fixed horizontal displacements at the sides. The finite element type used was a plane strain quadrilateral element (CPE4) with a mesh size of 0.5 m at the top of the slope model and 1.0 m at the bottom. The modified Mohr–Coulomb criteria were used in the numerical simulation method. The analysis was performed in two steps. First, a geostatic analysis was conducted to calculate the ground stress of the slope under the influence of gravity and bring the model to an equilibrium state of ground stress, followed by a static general analysis to perform a static calculation of the slope with double strength parameter reduction.
The parameters and settings mentioned above were inputted into the FE software ABAQUS, and the USDFLD user-defined subroutine was utilized to conduct numerical calculations until the model calculation was terminated due to a lack of convergence.
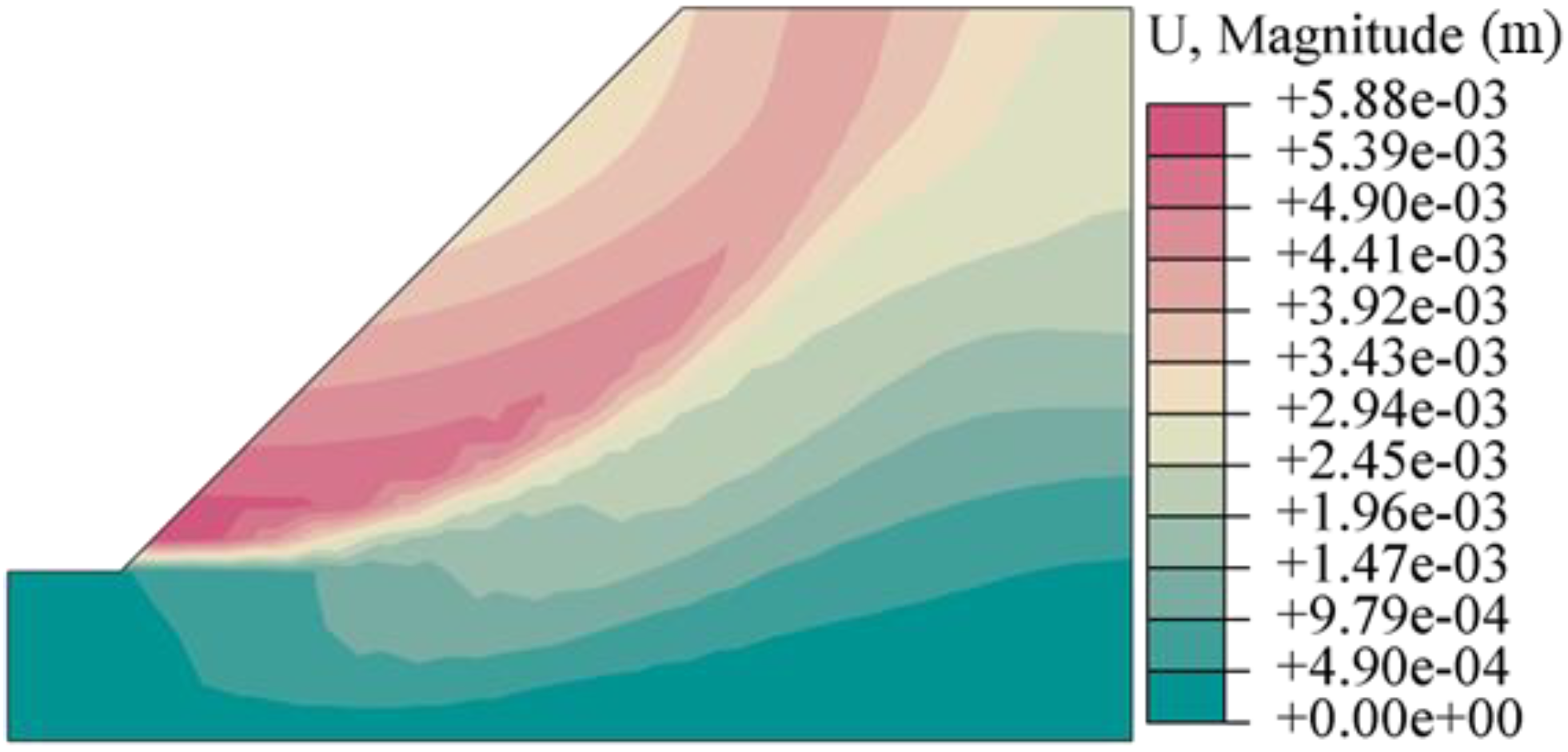
Figure 3 displays the equivalent displacement distributions calculated when the slope reaches its critical instability point, following the simultaneous decrease of the cohesive force
and internal friction angle
values.
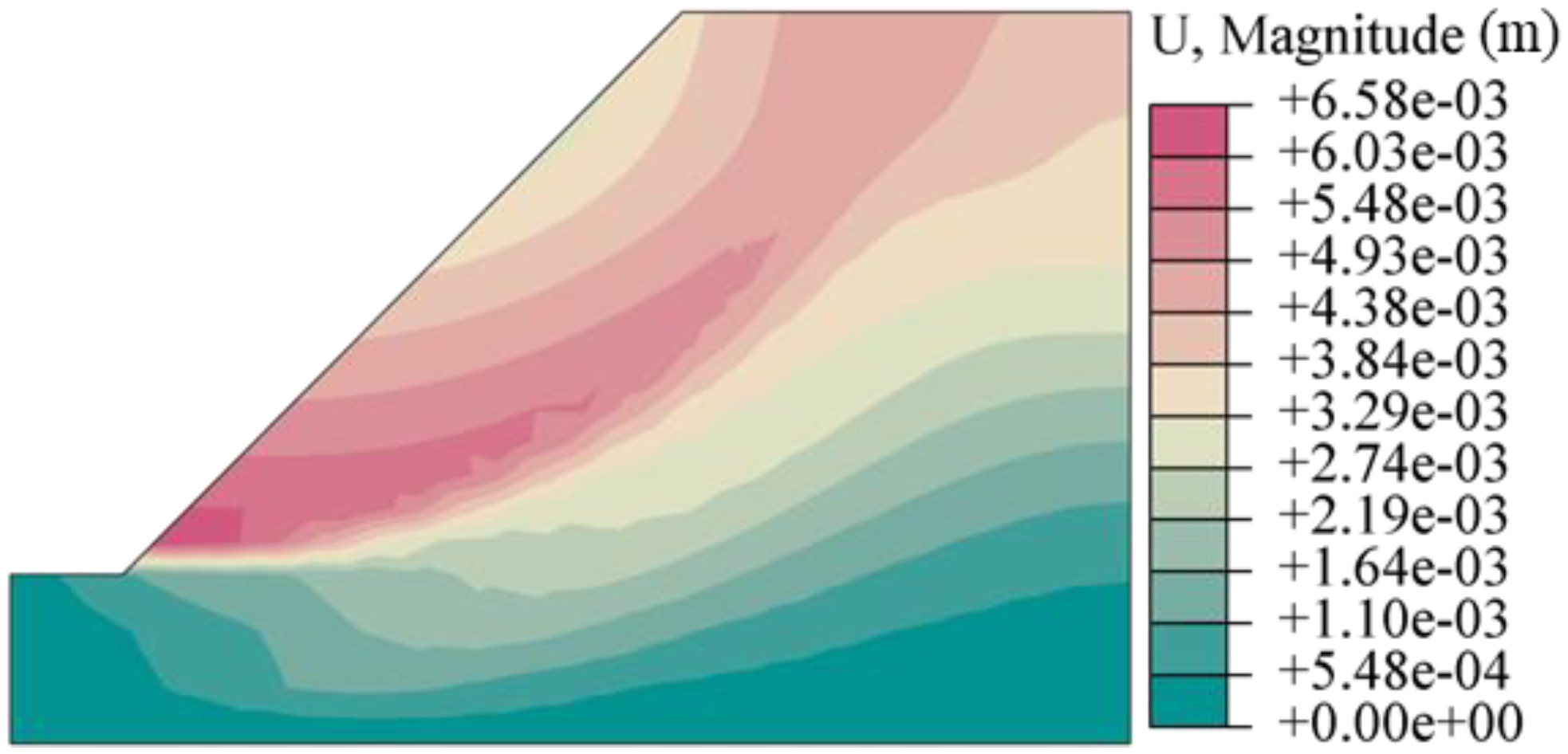
Figure 4, on the other hand, presents the equivalent displacement distributions that result from invoking the USDFLD user-defined subroutine and decrementing the values of
and
in an asynchronous manner. The comparison revealed that the equivalent displacement distributions and slip surface locations derived from both methods were largely congruent; however, the equivalent displacement values computed with the new algorithm tended to be greater in magnitude.
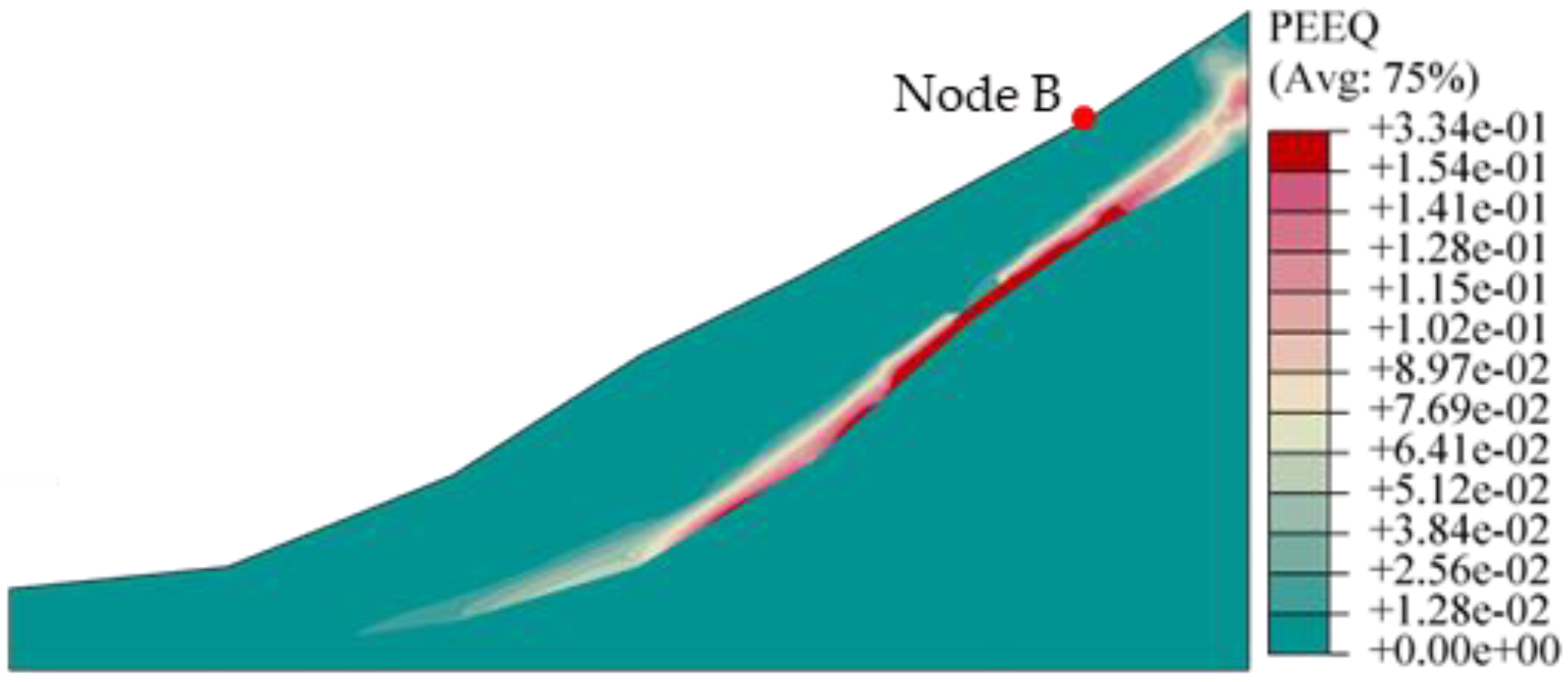
Figure 5 and
Figure 6 depict the plastic strain contour plot of a slope at its critical instability, calculated using the conventional strength reduction method and the novel method presented in this paper, respectively. The locations of the equivalent plastic zones appeared to be largely similar; however, the equivalent plastic strain calculated by the conventional method (with a maximum of 0.0303) surpassed that of the novel method (with a maximum of 0.0144). Moreover, the conventional method resulted in a plastic zone with better penetration, whereas the equivalent plastic band produced by the reduction of the two plastic strength parameters in this paper did not penetrate as far up the slope.
This slope model was integrated into the Slope module of the GeoStudio software, and the limit equilibrium approach was used to calculate the slope’s safety factor, specifically the Morgenstern–Price strip division method.
Figure 7 displays the outcome of the crucial sliding surface calculation.
To verify the accuracy of the numerical results, the safety factor of this slope was calculated using various methods and compared, as demonstrated in
Table 2.
Table 2 compares the slope’s safety factor between different slopes, which was calculated using different methods. The results revealed that the safety factor calculated using the limit equilibrium method was 1.586, whereas the traditional strength reduction method yielded a value of 1.58. Additionally, the safety coefficient determined by the novel method, which considered soil moisture content and utilized the USDFLD user-defined subroutine, was 1.532. It was evident from the calculated safety factors that the DSRM resulted in a lower safety factor compared to the others. Among all the safety factors computed by the double-strength reduction method, the safety factor estimated using the approach proposed in this paper was the most consistent with the value calculated by the limit equilibrium method.
In conclusion, the results of the various methods used to calculate the safety factors of slopes were relatively comparable. The limit equilibrium method yielded the highest safety factor, while Yuan W’s method produced the lowest value. The new method introduced in this paper provided a moderate safety factor value.
4. Engineering Example
The research site is situated in the Chinese provinces of Guizhou, Shuicheng County, and Jichang Town, an area characterized by its complex distribution of potential and historical landslides. In particular, the area was impacted by a devastating landslide event on 23 July 2019, which claimed the lives of 52 individuals.
The slope is 500 m from Jichang Town’s southwest side and has a height difference of over 500 m from its peak to the base, where the Pingdi reservoir is situated. A county road is located at the summit of the incline. The landslide measured over 1.3 km in length, with a slide bed length of 1.1 km, a back edge width of 180 m, and a leading-edge width of 370 m, with a general sliding direction toward the NNE. The total affected area was 374,000 square meters.
Figure 8 shows a landslide with an estimated volume of around 2 million cubic meters.
Consequently, in order to forestall the repetition of similar geologically-triggered landslides, it is imperative to conduct a thorough examination of the stability of the local slopes.
4.1. Engineering Geological Characteristics of the Study Area
Therefore, with the large landslide in Jichang Town on 23 July 2019, serving as a backdrop, the slope located 300 m to the east of the landslide site in Azhuoluo Village was selected as the focus of the study.
The research area is located on the western side of the upper sections of the Beipan River and is characterized by large elevational differences in the mountainous terrain. The highest point in the region reaches an altitude of +2870 m, while the lowest point is at +631 m, making it a mid-mountain landscape. This region experiences high annual rainfall due to its location in the temperate monsoon climate zone, with an average precipitation of around 1100 mm per year.
The region’s geology is significant for being at the southeastern edge of the South China Block and Qinghai-Tibetan Plateau, and the geological and topographic conditions of the slope in question are depicted in
Figure 8 and
Figure 9.
The slope is characterized by two main rock formations: the Longtan Formation coal-bearing strata (P
2l), and the Emeishan Basalt strata (P
2β). Quaternary red soil strata (Q), formed from the weathering of Emeishan basalt strata (P
2β), covers the surface. Pyroclastic rocks, basaltic lava, and tuffs make up the majority of the basalt, which has noticeable columnar joints. A clear division between the basalt and soil layers is visible (
Figure 10), with the rock strata trending northeast and a slope inclination of approximately 30°. The soil layer on the slope is inconsistent, being thicker in the valleys and thinner near the crest and waist, where the basalt may be directly exposed.
Measuring the slope’s weathered-basalt slope soil’s precise thickness is challenging due to the steep and steep mountain.
Figure 11, however, offers a broad approximation based on a few data sites. The clay layer is thinner at the slope’s top and waist than at its bottom, where it is thicker by a significant amount. These clays are naturally weathered from hard basalt.
4.2. Numerical Modeling of Azhuoluo Slope
Figure 11 shows how the chosen A’-A profile in the research area has been determined to have a hazardous tendency to slide.
The Azhuoluo slope, measuring 85 m in height and 160 m horizontally from the slope base, is coated in residual red soil ranging from several meters to over ten meters at its crest. The Azhuoluo slope consists of a residual soil layer on the top and a basalt layer at the bottom, and their respective mechanical properties in their natural states are displayed in
Table 3.
The research team of this paper conducted several site visits to assess the geological hazards of landslides. During these visits, it was determined that, of the various potential landslide areas, it was not the hard basalt bedrock but rather the residual soil layer on top that was causing slope instability. This soil, formed through the weathering of the basaltic surface, experiences rapid decay in its cohesive force and internal friction angle during strong rainfall, leading to instability. Previous research studies have confirmed this finding, with the intersection of the rock and soil layers identified as the primary source of instability due to loss of bearing capacity and scraping along this boundary after heavy rain.
The study team [
28] performed laboratory tests on soil samples collected from the site of landslide geological hazards. The samples were dried, ground, and sieved through a 2 mm standard to obtain a uniform texture. The soil samples were then remolded to mimic different moisture contents, ranging from 5% to 50% in increments of 5%. The samples were put through direct shear tests to ascertain the cohesiveness
and friction angle
under various moisture conditions. The results of these tests are presented in
Figure 12.
The water content, represented as
, was modeled as a function of the cohesion
and friction angle
values based on the experimental data. The functional relationships are shown in Equations (13) and (14) in the data.
The procedure for setting up the numerical simulation involves modeling the slope based on its actual dimensions.
The present paper’s numerical model of slope stability featured specific boundary conditions whereby the model’s bottom constrained both horizontal and vertical displacements, while horizontal displacements were constrained on either side of the model.
The finite element type used is a plane strain quadrilateral element (CPE4). The finite element mesh size was established at 1.0 m at the top of the slope model and at 1.5 m at the bottom. The Mohr–Coulomb criteria were used as the strength criterion for the numerical simulation process.
The simulation began with a geostatic analysis, which calculated the geostress of the slope under the influence of gravity, bringing the model to an equilibrium state of in situ stress. The second step was a static general analysis that accounted for the slope’s double-strength parameters.
These options and parameters were entered into the FE program ABAQUS, and the USDFLD user-defined subroutine was utilized for numerical calculations until convergence was achieved or the calculation was terminated.
Table 3 displays the strength parameters of the geotechnical body in its natural state.
4.3. Numerical Simulation Results
Figure 13 shows the equivalent plastic strain cloud of the critical instability stage of the Azhuoluo slope, while
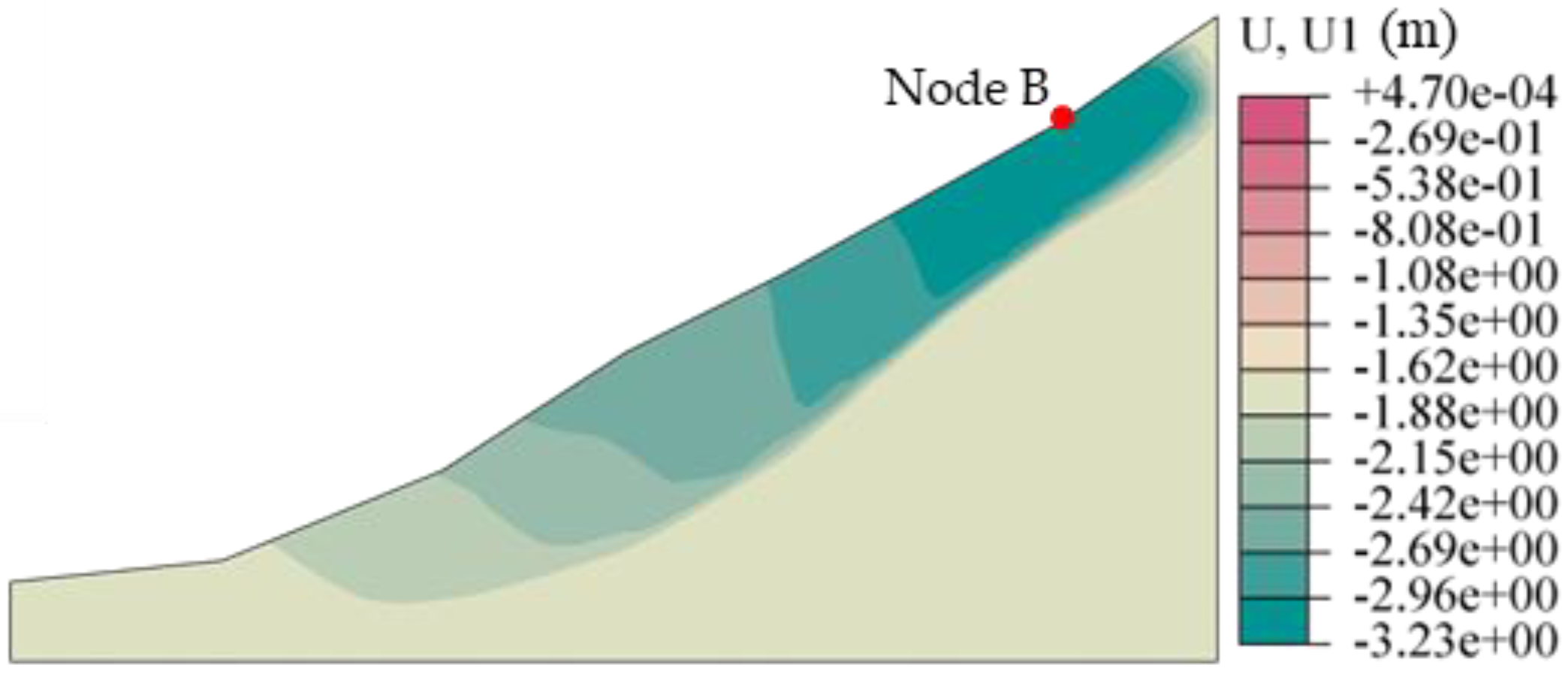
Figure 14 showcases the displacement cloud in the horizontal U1 direction at this state.
The figures indicate that the failure of the slope takes place at the junction of soil and rock layers within the slope. This was further corroborated by the horizontal displacement cloud, which displayed the maximum horizontal displacement of 3.23 m at the crest of the slope and confirmed that the slope slip was located at the interface between the soil and rock layers.
As a result of prolonged exposure to heavy rain, the bearing capacity of the basalt-weathered soil layer covered by the surface layer of the slope gradually deteriorates, resulting in slope instability. The zone of plastic deformation is located at the interface between the soil and rock layers.
Based on the evaluation of the outcomes of the numerical simulation, it appeared that the Azhuoluo slope reaches a critical state of instability when the water content reaches 32.0%.
The basis for determining that the Azhuoluo slope is in a critical instability state was determined by a sudden change in horizontal displacement at a point on the top of the slope or by the formation of a plastic penetration zone on the slope.
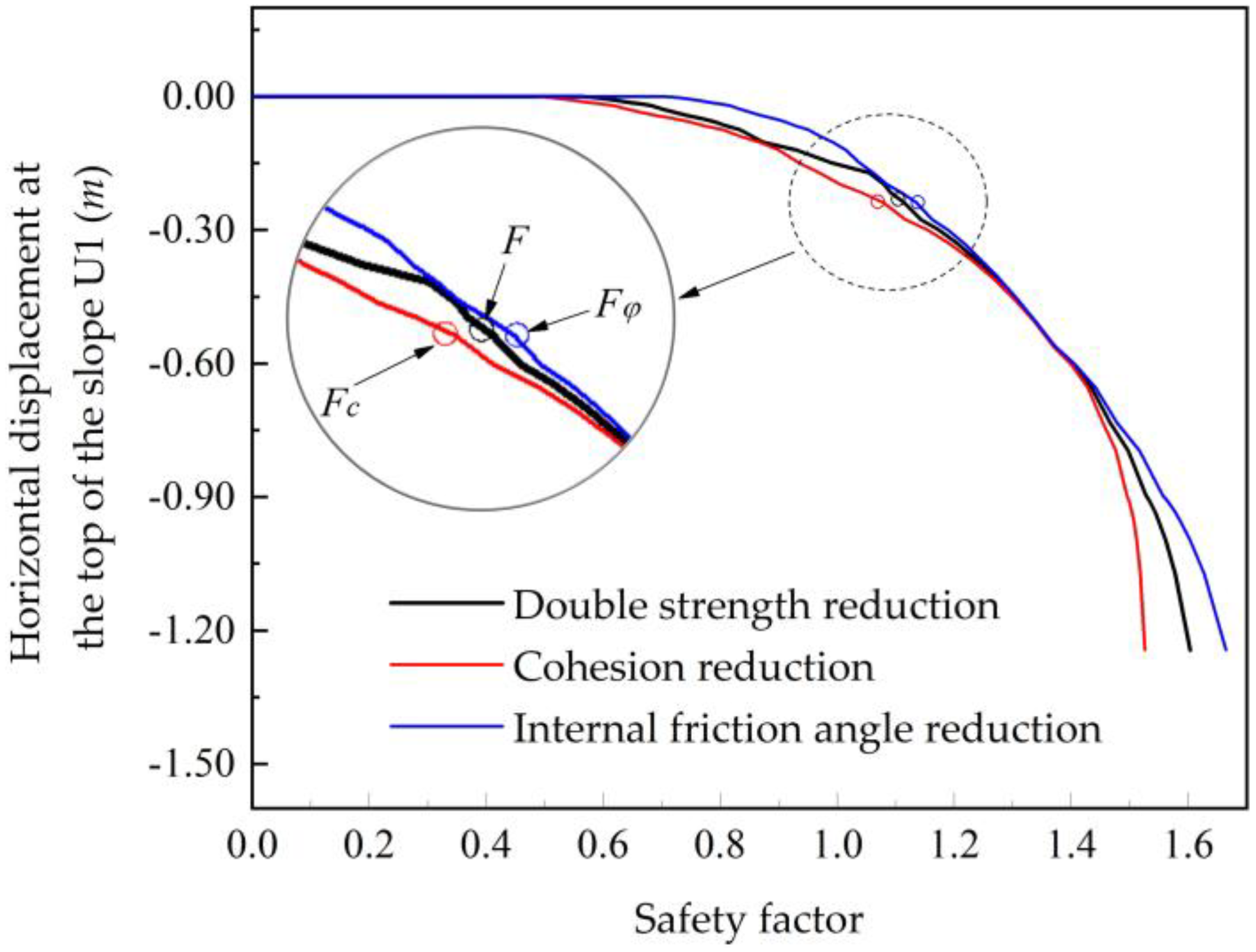
At this stage, the soil exhibited a cohesive strength of 31.0 kPa and an internal friction angle of 30.9°. Using these values, the discount factors for cohesion
and friction angle
were calculated as 1.079 and 1.137, respectively. Substituting these factors into equation 10, we determined the synthesized safety factor of the slope to be 1.114, as shown in
Figure 15.
As shown in
Figure 15, as the value of horizontal displacement at the slope’s summit was determined for a certain moment in the numerical simulation, the reduction coefficient for the friction angle was greater than that for cohesion, and the comprehensive reduction coefficient was between the two. This indicates that as the water content
increases, the rate of decay for the internal friction angle is faster than that of cohesion. It was evident that the cohesion
and the friction angle
of the residual soil layer, which is formed by local basalt weathering, exhibited unsynchronized decay as the water content increased. Consequently, the traditional method of simultaneous decay of
and
values in the FE method is unrealistic, and this new method of double-strength unsynchronized decay based on water content change, presented in this paper, is more practical and better suited for resolving the above-mentioned engineering problems.
5. Conclusions
(1) Based on a discussion of existing slope stability analysis methods, this paper proposes a novel numerical method for the asynchronous discounting of double strength parameters based on the variation of water content. Using the secondary development module provided in the FE program ABAQUS, the USDFLD user-defined material subroutine was written to enable numerical calculation of the non-simultaneous reduction of cohesion and internal friction angle. This approach provided a more realistic representation of the soil strength reduction process. The validity of the theoretical and numerical methodologies presented in this paper was confirmed through comparisons with the limit equilibrium method and alternative double-strength reduction methods.
(2) The stability of the Azhuoluo slope located in Shuicheng county, Guizhou Province, China, was evaluated using a numerical simulation in the context of the mega landslide that occurred in the area. The results showed that the slope is a soil–rock mixture, with a residual soil layer formed from the weathering of basalt on top of a hard basalt layer, and the soil–rock interface is well-defined. Upon analyzing the numerical simulation results, it was discovered that the Azhuoluo slope experiences a state of critical instability upon an increase in soil water content to 32%. The slope’s synthesized safety factor was determined to be 1.114. The numerical results suggest that the slope’s potential slip surface occurred along the soil–rock interface, leading to the formation of a high-speed debris flow landslide.
(3) With rising water content, the residual soil layer formed by basalt weathering displays asynchronous decay in its internal friction angle and cohesion, with a faster rate of decline in the internal friction angle compared to cohesion.