A Coupled Seepage–Deformation Model for Simulating the Effect of Fracture Seepage on Rock Slope Stability Using the Numerical Manifold Method
Abstract
:1. Introduction
2. Coupled Seepage–Deformation Model for the NMM
2.1. Fundamentals of the NMM
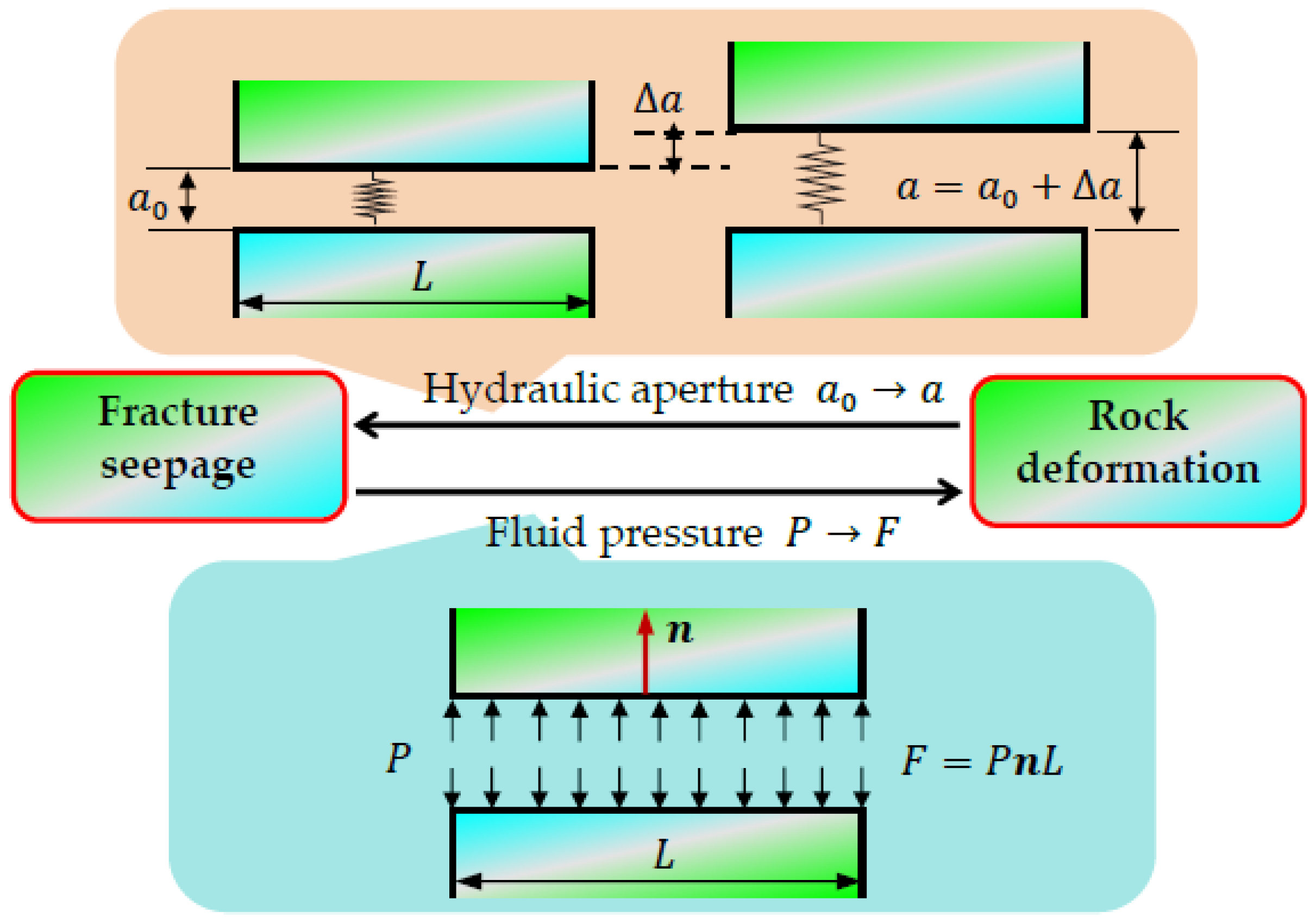
2.2. Basic Formulas of Seepage–Deformation Coupling Model
- The rock matrix is impermeable, and only fracture seepage is considered.
- The fluid flow is assumed to be laminar, steady, viscous, and incompressible, and the fluid pressure is always positive.
- The fluid flow has no effect on the strength of the material, and no hydraulic fractures initialize and propagate in the model.
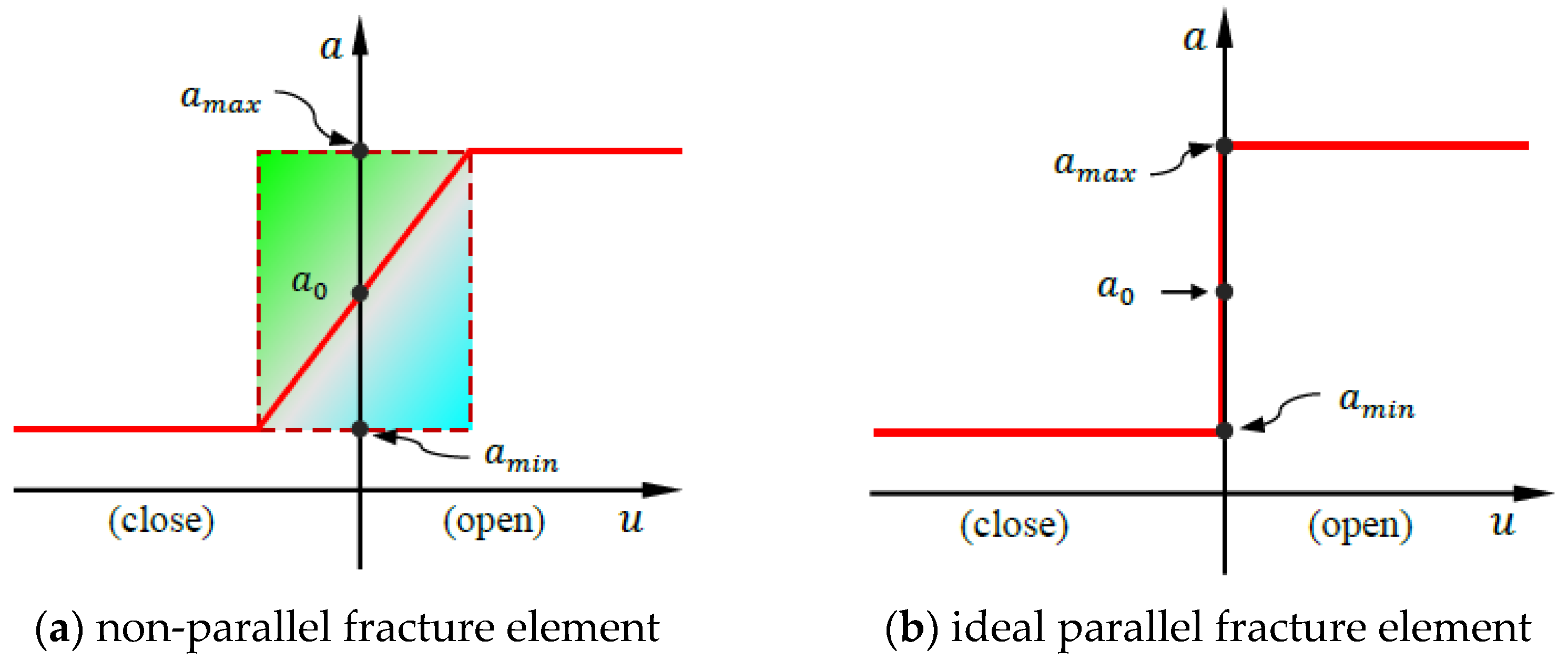
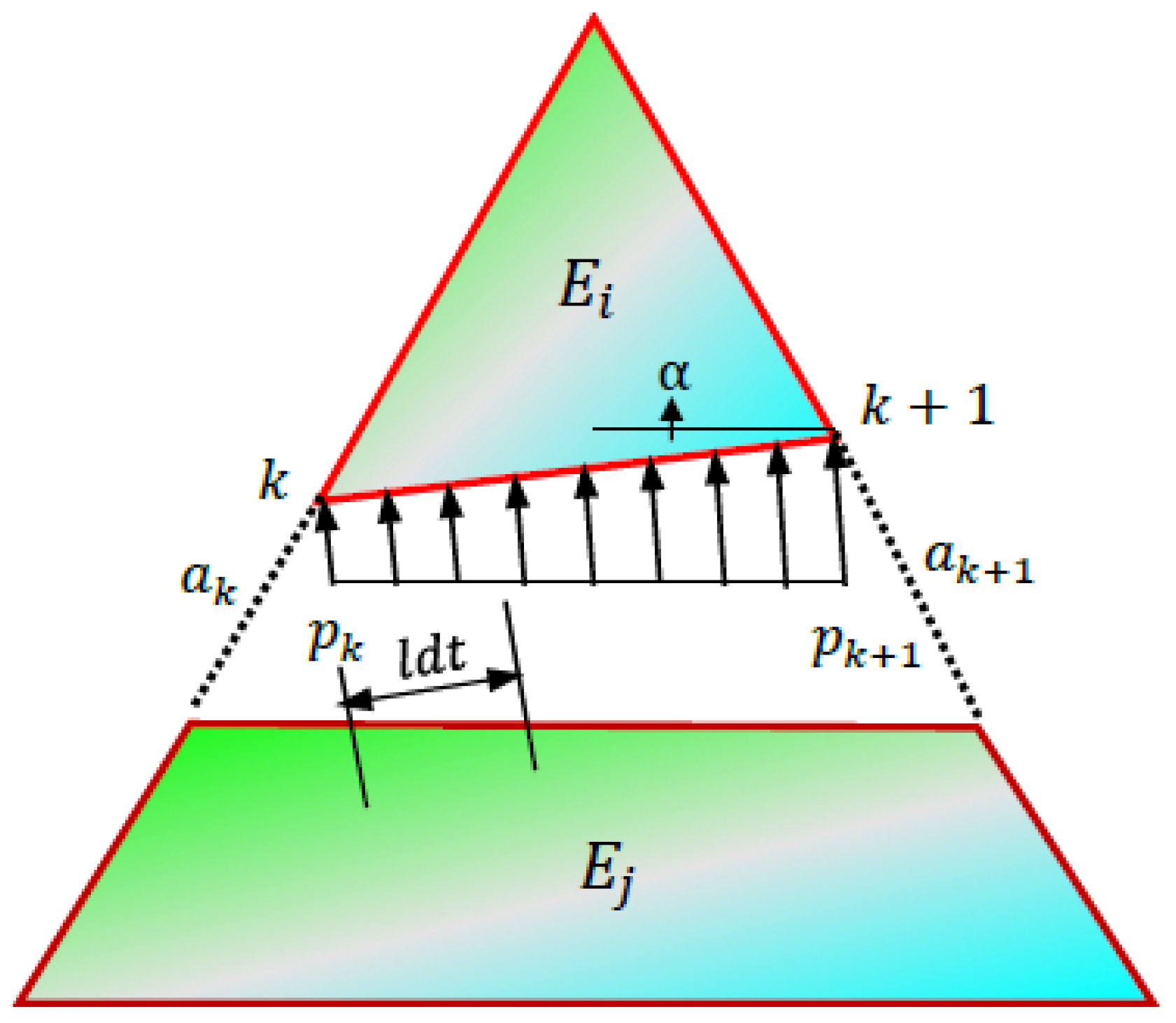
2.3. Fluid Pressure on Manifold Element Boundaries
3. Modeling of Seepage along Fractured Network by the NMM
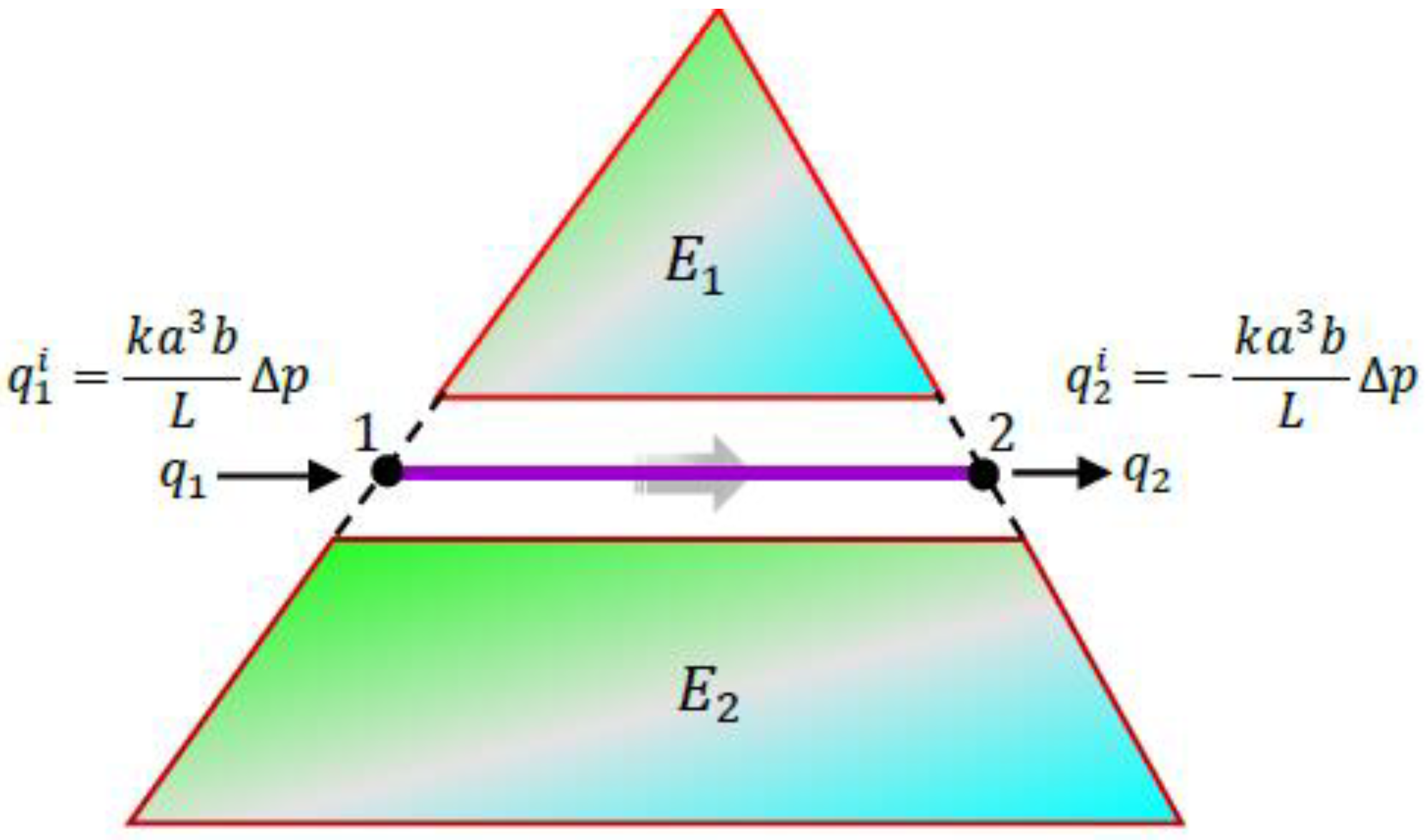
3.1. Calculation of Fluid Pressure along the Fracture Network
3.2. Calculation of Factor of Safety (FoS) along Rock Fractures
4. Numerical Examples
4.1. Verification of the Coupled Seepage–Deformation Model
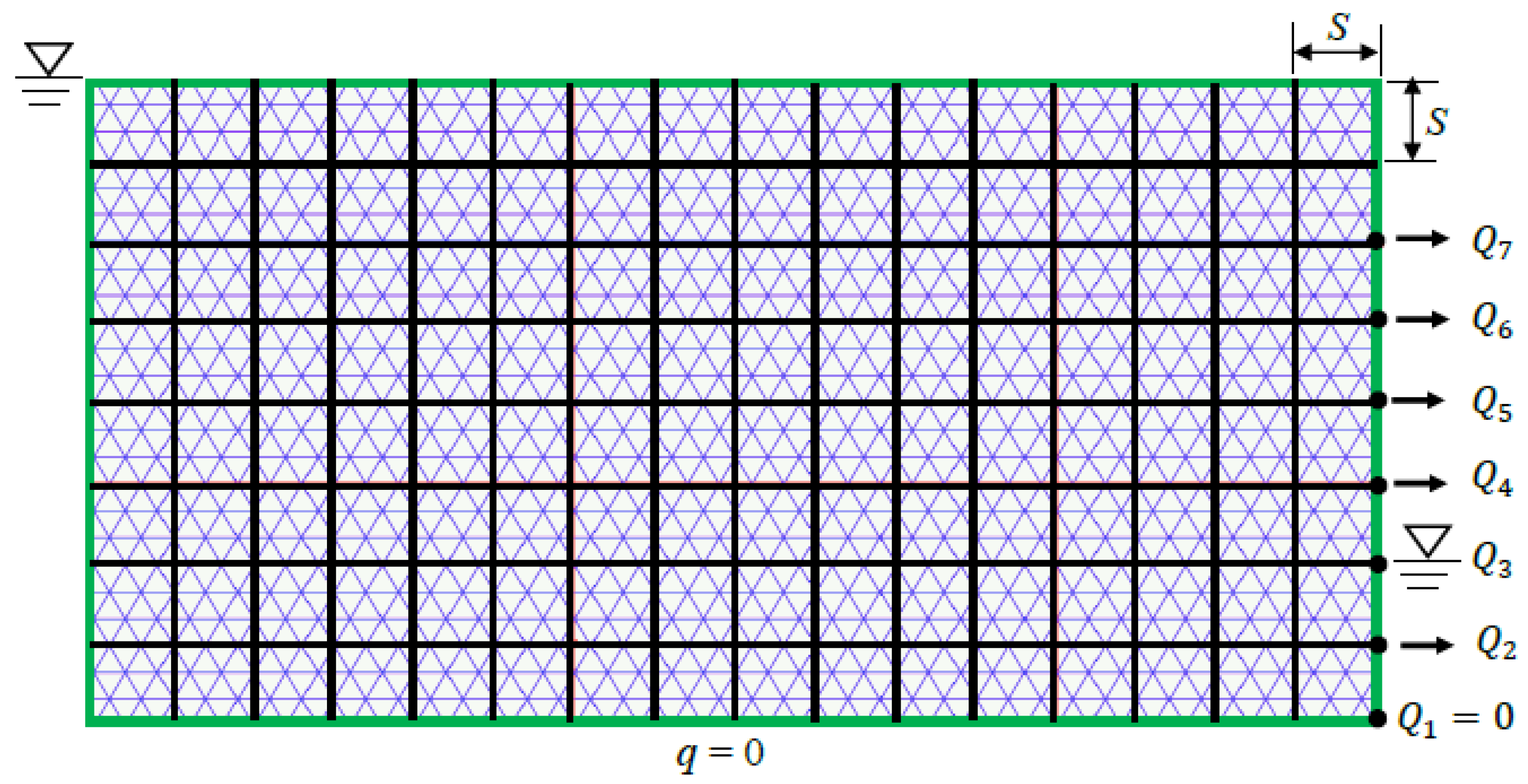
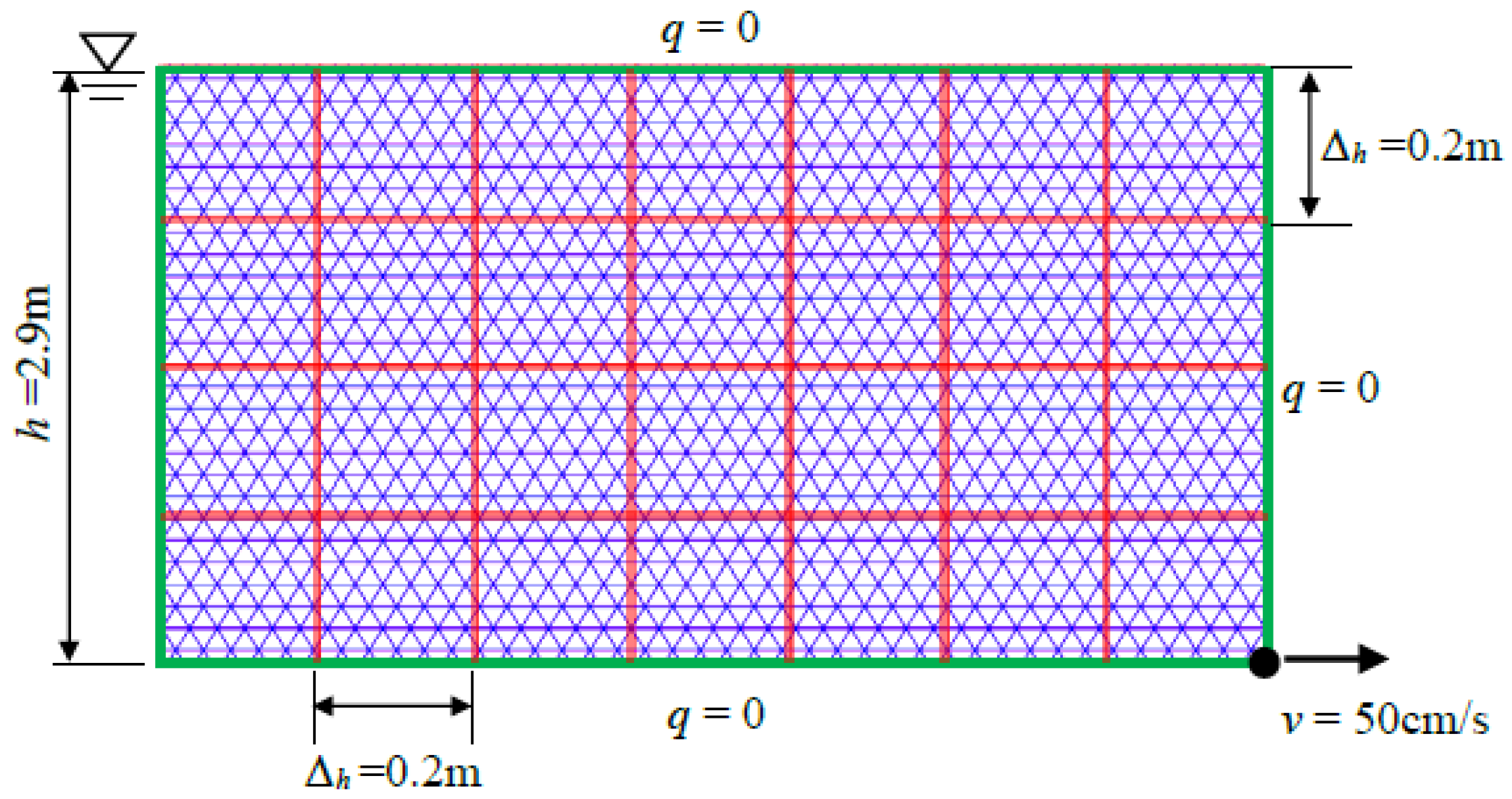
4.2. Fracture Seepage of Fluid Flow through a Regular Fracture Network
- h0 = 0.8 m is prescribed at the left side of the model, and except for the impermeable base, the other boundaries are free surfaces;
- h0 = 0.8 m is prescribed at the left side of the model, but the right side has a water head of h = 0.4 m.
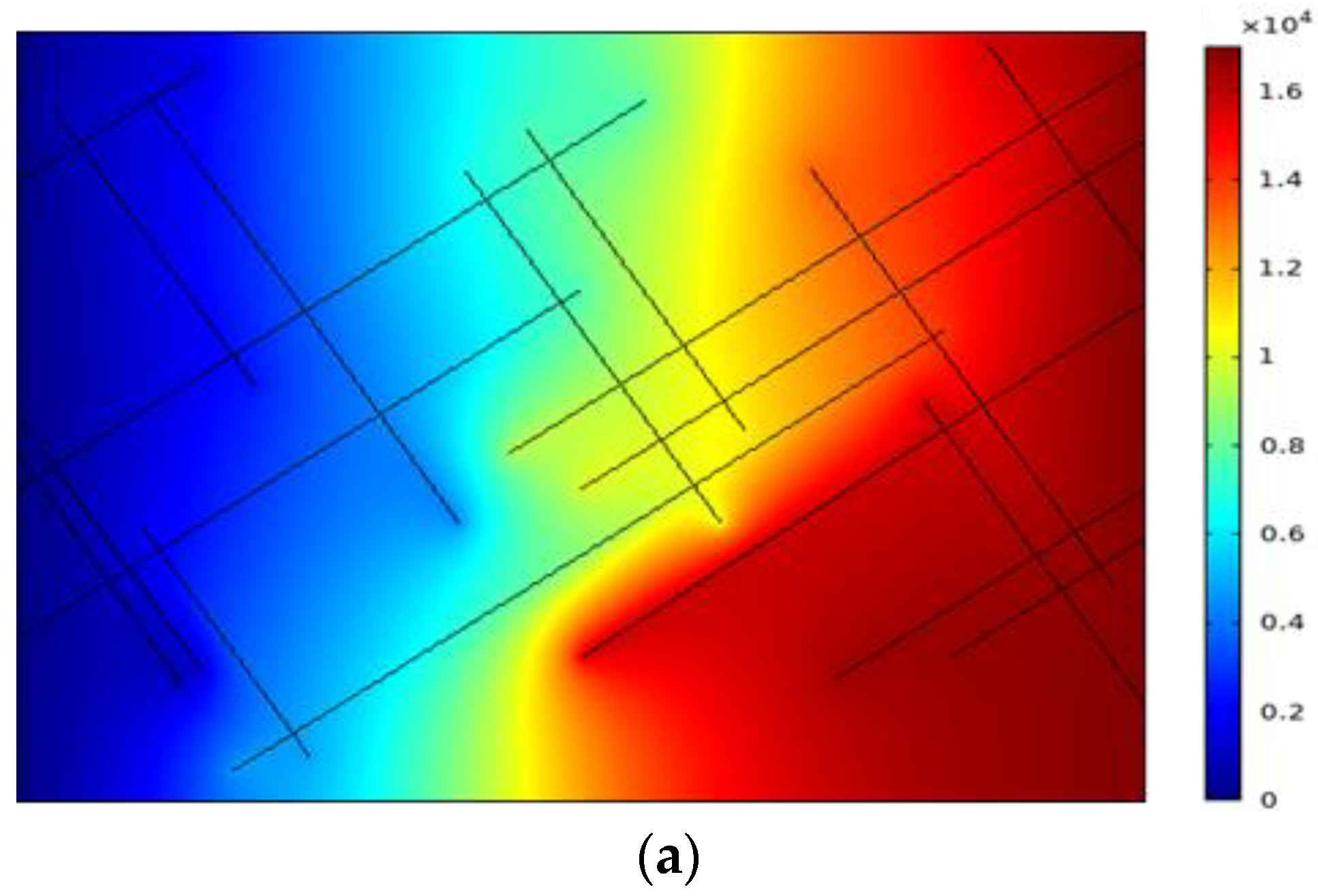
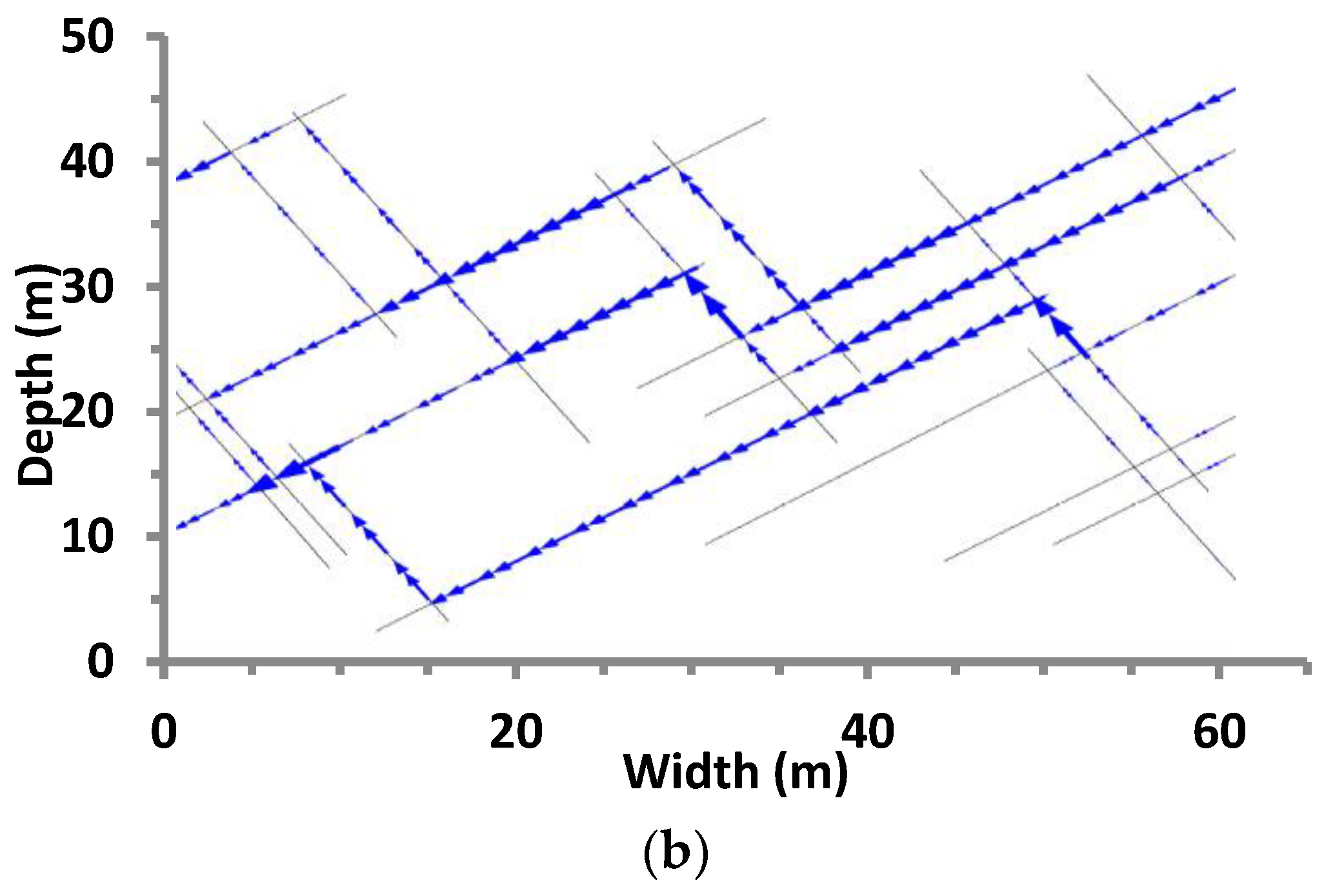
4.3. Joint Seepage in an Arbitrary Complex Rock Fracture Network
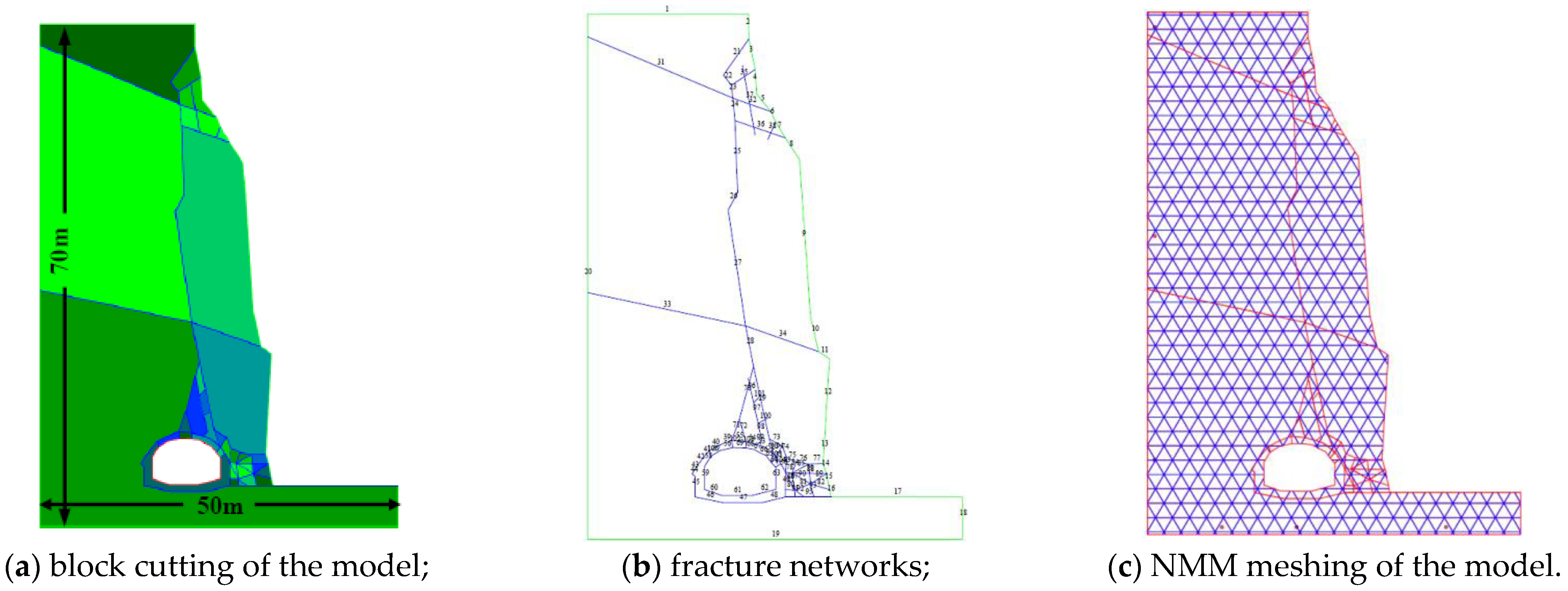
4.4. Rock Slope Stability Analysis Using the Coupled Seepage–Deformation Model
- The effect of groundwater is ignored, and only the self-weight of the rock mass is considered (i.e., Condition 1);
- The effect of groundwater is not ignored, the highest groundwater head is located at the top of the slope (see Figure 15), and the bottom of the slope is taken as an outlet for the water flow (i.e., Condition 2);
- The highest groundwater head is the same as Condition 2, but considering the condition under a frozen state of the rock slope surface, the groundwater outlet is blocked (i.e., Condition 3).
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Neuman, S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeol. J. 2005, 13, 124–147. [Google Scholar] [CrossRef]
- An, X.M.; Ning, Y.J.; Ma, G.W.; He, L. Modeling progressive failures in rock slopes with non-persistent joints using the numerical manifold method. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 679–701. [Google Scholar] [CrossRef]
- Kim, Y.I.; Amadei, B.; Pan, E. Modeling the effect of water, excavation sequence and rock reinforcement with discontinuous deformation analysis. Int. J. Rock Mech. Min. Sci. 1999, 36, 949–970. [Google Scholar] [CrossRef]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. 1985, 22, 121–140. [Google Scholar] [CrossRef]
- Louis, C.A. A study of groundwater flow in jointed rock and its influence on the stability of rock mass. Rock Mech. Res. Rep. 1969, 10, 10–15. [Google Scholar]
- Japan Society of Civil Engineering. Report of Stability Analysis and Field Measurements for Rock Slope in Japan; Japan Society of Civil Engineering: Tokyo, Japan, 1994. [Google Scholar]
- Pal, S.; Kaynia, A.M.; Bhasin, R.K.; Paul, D.K. Earthquake stability analysis of rock slopes: A case study. Rock Mech. Rock Eng. 2012, 45, 205–215. [Google Scholar] [CrossRef]
- Biot, M.A. General solutions of the equations of elasticity and consolidation for a porous material. J. Appl. Mech. 1956, 78, 91–96. [Google Scholar] [CrossRef]
- Rice, J.R.; Cleary, M.P. Some basic stress diffusion solutions for fluid-saturated elastic porous-media with compressible constituents. Rev. Geophys. 1976, 14, 227–241. [Google Scholar] [CrossRef]
- Curran, J.H.; Carvalho, J.L. A Displacement Discontinuity Model for Fluid-saturated Porous Media. In Proceedings of the 6th ISRM Congress, Montreal, QC, Canada, 30 August–3 September 1987. [Google Scholar]
- Carvalho, J.L. Poroelastic Effects and Influence of Material Interfaces on Hydraulic Fracturing. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1990. [Google Scholar]
- Long, J.C.; Pemer, J.S.; Wilson, C.R. Porous media equivalents for networks of discontinuous fractures. Water Resour. Res. 1982, 18, 645–658. [Google Scholar] [CrossRef] [Green Version]
- Nouri, A.; Panah, A.K.; Pak, A.; Vaziri, H.; Islam, M.R. Evaluation of hydraulic fracturing pressure in a porous medium by using the finite element method. Energy Resour. 2002, 24, 715–724. [Google Scholar] [CrossRef]
- Wang, F.T.; Liu, Y. A mechanism-based simulation algorithm for crack propagation in non-uniform geomaterials. Comput. Geotech. 2022, 151, 104994. [Google Scholar] [CrossRef]
- Santillán, D.; Juanes, R.; Cueto-Felgueroso, L. Phase field model of fluid-driven fracture in elastic media: Immersed-fracture formulation and validation with analytical solutions. J. Geophys. Res. Solid Earth 2017, 122, 2565–2589. [Google Scholar] [CrossRef] [Green Version]
- Santillán, D.; Juanes, R.; Cueto-Felgueroso, L. Phase Field Model of Hydraulic Fracturing in Poroelastic Media: Fracture Propagation, Arrest, and Branching Under Fluid Injection and Extraction. J. Geophys. Res. Solid Earth 2018, 123, 2127–2155. [Google Scholar] [CrossRef] [Green Version]
- Jing, L.R.; Hudson, J.A. Numerical methods in rock mechanics. Int. J. Rock Mech. Min. Sci. 2002, 39, 409–427. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Shimizu, H.; Murata, S.; Ishida, T. The distinct element analysis for hydraulic fracturing in hard rock considering fluid viscosity and particle size distribution. Int. J. Rock Mech. Min. Sci. 2011, 48, 712–727. [Google Scholar] [CrossRef]
- Shi, G.H. Discontinuous Deformation Analysis: A New Numerical Model for the Statics and Dynamics of Block Systems. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1988. [Google Scholar]
- Jing, L.R.; Ma, Y.; Fang, Z.L. Modeling of fluid flow and solid deformation for fractured rocks with discontinuous deformation analysis (DDA) method. Int. J. Rock Mech. Min. Sci. 2001, 38, 343–355. [Google Scholar] [CrossRef]
- Al-Busaidi, A.; Hazzard, J.F.; Young, R.P. Distinct element modeling of hydraulically fractured Lac du Bonnet granite. J. Geophys. Res. Solid Earth 2005, 110, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Y.Y.; Zhang, H.Q.; Zhang, X.L.; Li, H.B.; Jiang, Q.H. A two-dimensional coupled hydro-mechanical discontinuum model for simulating rock hydraulic fracturing. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 457–481. [Google Scholar] [CrossRef]
- Shi, G.H. Manifold method of material analysis. In Proceedings of the Transcations of the Ninth Army Confernece on Applied Mathematics and Computing, Minneapolis, NM, USA, 18–21 June 1991; pp. 57–76. [Google Scholar]
- Shi, G.H. Modeling rock joints and blocks by manifold method. In Proceedings of the 33th US Rock Mechanics Symposium, Santa Fe, NM, USA, 3–5 June 1992; pp. 639–648. [Google Scholar]
- Jiang, Q.H.; Deng, S.S.; Zhou, C.B.; Lu, W.B. Modeling unconfined seepage flow using three-dimensional numerical manifold method. J. Hydrodyn. 2010, 22, 554–561. [Google Scholar] [CrossRef]
- Wu, Z.J.; Wong, L.N.Y. Extension of numerical manifold method for coupled fluid flow and fracturing problems. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1990–2008. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, F.; Li, C.G. Primal mixed solution to unconfined seepage flow in porous media with numerical manifold method. Appl. Math. Model. 2015, 39, 794–808. [Google Scholar] [CrossRef]
- Zhang, G.X.; Li, X.; Li, H.F. Simulation of hydraulic fracture utilizing numerical manifold method. Sci. China-Technol. Sci. 2015, 58, 1542–1557. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Lin, S.Z.; Xie, Z.Q. Fractured porous medium flow analysis using numerical manifold method with independent covers. J. Hydrolic. 2016, 542, 790–808. [Google Scholar] [CrossRef]
- Ma, G.W.; Wang, H.D.; Fan, L.F.; Chen, Y. Segmented two-phase flow analysis in fractured geological medium based on the numerical manifold method. Adv. Water Resour. 2018, 121, 112–129. [Google Scholar] [CrossRef]
- Hu, M.S.; Rutqvist, J.; Wang, Y. A practical model for fluid flow in discrete-fracture porous media by using the numerical manifold method. Adv. Water Resour. 2016, 97, 38–51. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.S.; Wang, Y.; Rutqvist, J. Fully coupled hydro-mechanical numerical manifold modeling of porous rock with dominant fractures. Acta Geotech. 2017, 12, 231–252. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.S.; Rutqvist, J.; Wang, Y. A numerical manifold method model for analyzing fully coupled hydro-mechanical processes in porous rock masses with discrete fractures. Adv. Water Resour. 2017, 102, 111–126. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.T.; Tang, X.H.; Zheng, H.; Liu, Q.S.; Liu, Z.J. Hydraulic fracturing modeling using the enriched numerical manifold method. Appl. Math. Model. 2018, 53, 462–486. [Google Scholar] [CrossRef]
- Wang, Y.H.; Yang, Y.T.; Zheng, H. On the implementation of a hydro-mechanical coupling model in the numerical manifold method. Eng. Anal. Bound. Elem. 2019, 109, 161–175. [Google Scholar] [CrossRef]
- Antelmi, M.; Mazzon, P.; Höhener, P.; Marchesi, M.; Alberti, L. Evaluation of MNA in a Chlorinated Solvents-Contaminated Aquifer using Reactive Transport Modeling coupled with Isotopic Fractionation Analysis. Water 2021, 13, 2945. [Google Scholar] [CrossRef]
- Alberti, L.; Antelmi, M.; Oberto, G.; La Licata, I.; Mazzon, P. Evaluation of fresh groundwater Lens Volume and its possible use in Nauru island. Water 2022, 14, 3201. [Google Scholar] [CrossRef]
- Babuška, I.; Melenk, J.M. The partition of unity method. Int. J. Numer. Methods Eng. 1997, 40, 727–758. [Google Scholar] [CrossRef]
- An, X.M.; Li, L.X.; Ma, G.W.; Zhang, H.H. Prediction of rank deficiency in partition of unity-based methods with plane triangular or quadrilateral meshes. Comput. Methods Appl. Mech. Eng. 2011, 200, 665–674. [Google Scholar] [CrossRef]
- Zheng, H.; Yang, Y.T. On generation of lumped mass matrices in partition of unity based methods. Int. J. Numer. Methods Eng. 2017, 112, 1040–1069. [Google Scholar] [CrossRef]
- Lin, H.I.; Lee, C.H. An approach to assessing the hydraulic conductivity disturbance in fractured rocks around the Syueshan tunnel, Taiwan. Tunn. Undergr. Space Technol. 2009, 24, 222–230. [Google Scholar] [CrossRef]
- Yan, C.; Zheng, H.; Sun, G.; Ge, X. Combined finite-discrete element method for simulation of hydraulic fracturing. Rock Mech. Rock Eng. 2016, 49, 1389–1410. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Wang, J.S.Y.; Iwai, K. Validity of cubic law for fluid flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef] [Green Version]
- She, C.X.; Guo, Y.Y.; Wang, W.M. Numerical method for seepage in blocky rock mass. Chin. J. Rock Mech. Eng. 2001, 20, 359–364. [Google Scholar]
- Kristinof, R.; Ranjith, P.G.; Choi, S.K. Finite element simulation of fluid flow in fractured rock media. Environ. Earth Sci. 2010, 60, 765–773. [Google Scholar] [CrossRef]
- Harr, M.E. Groundwater and Seepage; McGraw-Hill Book Company: New York, NY, USA, 1962. [Google Scholar]
- Gao, H.Y. Research on Flow Field and Its Coupling with Stress Field in Fractured Rocks. Ph.D. Thesis, Heihai University, Nanjing, China, 1994. [Google Scholar]
- Grenoble, B.A. Influence of Geology on Seepage and Uplift in Concrete Gravity Dam Foundations. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 1989. [Google Scholar]
- Lamas, L.N. An experimental study of the hydro-mechanical properties of granite joints. In Proceedings of the 8th International Congress on Rock Mechanics, Tokyo, Japan, 25–29 September 1995; pp. 733–738. [Google Scholar]
- Zhang, G.X.; Wu, X.F. Influence of seepage on the stability of rock slope—Coupling of seepage and deformation by DDA method. Chin. J. Rock Mech. Eng. 2003, 22, 1269–1275. [Google Scholar]










| Work No. | T1–7 | T1–8 | T1–9 | T1–10 |
|---|---|---|---|---|
| (cm) | 115.70 | 134.37 | 151.38 | 227.20 |
| (cm) | 71.37 | 71.37 | 72.01 | 54.36 |
| (cm) | 44.33 | 63.00 | 79.37 | 172.84 |
| 0.727 | 1.033 | 1.302 | 2.835 |
| Port No. | T1–7 | T1–8 | T1–9 | T1–10 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 112.74 | 112.65 | −0.20 | 130.06 | 130.56 | 0.79 | 146.18 | 147.45 | 1.60 | 215.36 | 217.81 | 1.42 |
| 2 | 113.06 | 113.16 | 0.23 | 129.97 | 131.19 | 1.94 | 146.63 | 147.70 | 1.35 | 217.03 | 218.57 | 0.89 |
| 3 | 109.44 | 109.22 | −0.50 | 124.51 | 126.37 | 2.95 | 140.17 | 142.49 | 2.92 | 201.45 | 201.93 | 0.28 |
| 4 | 112.95 | 112.52 | −0.97 | 130.32 | 130.56 | 0.38 | 146.53 | 146.94 | 0.52 | 216.78 | 217.04 | 0.15 |
| 5 | 113.28 | 113.54 | 0.59 | 130.78 | 131.32 | 0.86 | 147.16 | 148.08 | 1.16 | 217.15 | 218.06 | 0.53 |
| 6 | 114.36 | 114.68 | 0.72 | 133.19 | 133.10 | −0.14 | 150.27 | 150.11 | −0.20 | 223.86 | 224.03 | 0.10 |
| 7 | 107.89 | 108.20 | 0.70 | 123.58 | 124.84 | 2.00 | 138.22 | 140.97 | 3.46 | 193.95 | 200.79 | 3.96 |
| 8 | 108.12 | 108.46 | 0.77 | 124.26 | 125.10 | 1.33 | 138.49 | 141.35 | 3.60 | 194.88 | 201.17 | 3.64 |
| 9 | 90.27 | 91.19 | 2.08 | 102.43 | 102.11 | −0.51 | 111.75 | 114.81 | 3.86 | 141.72 | 141.61 | −0.06 |
| 10 | 88.32 | 89.41 | 2.46 | 97.83 | 98.55 | 1.14 | 105.38 | 111.00 | 7.08 | 134.37 | 133.86 | −0.30 |
| 11 | 91.95 | 91.82 | −0.29 | 101.35 | 103.51 | 3.43 | 110.73 | 116.33 | 7.06 | 139.26 | 144.40 | 2.97 |
| 12 | 97.68 | 97.79 | 0.25 | 109.37 | 111.38 | 3.19 | 121.64 | 125.60 | 4.99 | 154.32 | 165.10 | 6.24 |
| 13 | 98.48 | 98.68 | 0.45 | 110.69 | 112.40 | 2.71 | 124.38 | 127.00 | 3.30 | 156.87 | 167.39 | 6.09 |
| 14 | 95.88 | 95.63 | −0.56 | 107.41 | 107.32 | −0.14 | 119.59 | 120.90 | 1.65 | 148.37 | 157.99 | 5.57 |
| 15 | 97.06 | 96.52 | −1.22 | 108.14 | 109.73 | 2.52 | 120.15 | 123.44 | 4.15 | 152.64 | 163.20 | 6.11 |
| 16 | 96.97 | 97.28 | 0.70 | 108.66 | 110.36 | 2.70 | 120.63 | 123.95 | 4.18 | 153.33 | 163.96 | 6.15 |
| 17 | 76.75 | 77.72 | 2.19 | 81.06 | 82.30 | 1.97 | 83.47 | 89.41 | 7.48 | 81.06 | 86.49 | 3.14 |
| 18 | 75.22 | 76.45 | 2.77 | 77.98 | 78.99 | 1.60 | 81.46 | 85.09 | 4.57 | 75.12 | 77.98 | 1.65 |
| 19 | 80.17 | 81.79 | 3.65 | 89.16 | 88.65 | −0.81 | 90.16 | 96.14 | 7.53 | 94.75 | 100.46 | 3.30 |
| 20 | 77.28 | 78.74 | 3.29 | 82.57 | 83.31 | 1.17 | 91.07 | 90.68 | −0.49 | 83.16 | 89.66 | 3.76 |
| 21 | 83.43 | 84.33 | 2.03 | 93.08 | 92.96 | −0.19 | 97.32 | 100.46 | 3.96 | 105.47 | 113.67 | 4.74 |
| 22 | 76.45 | 77.34 | 2.01 | 83.78 | 83.06 | −1.14 | 87.95 | 87.63 | −0.40 | 76.04 | 87.76 | 6.78 |
| 23 | 75.56 | 75.82 | 0.59 | 78.64 | 79.50 | 1.37 | 81.26 | 83.82 | 3.23 | 70.73 | 78.11 | 4.27 |
| 24 | 74.34 | 74.17 | −0.38 | 76.86 | 77.09 | 0.37 | 79.34 | 80.39 | 1.32 | 66.18 | 71.63 | 3.15 |
| Material | Young’s Modulus (GPa) | Poisson’s Ratio | Tensile Strength (MPa) | Cohesion (kPa) | Internal Friction Angle (°) | Density (kN/m3) |
|---|---|---|---|---|---|---|
| Rock mass | 5 | 0.25 | 1.0 | 1.5 | 45 | 24 |
| Tunnel lining | 20 | 0.2 | 1.5 | 2.0 | 45 | 25 |
| Fracture | / | / | / | 0.0 | 30 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, X.; Zhang, Y.; Chen, Y.; Chen, Y.; Qi, C.; Pasternak, E.; Dyskin, A. A Coupled Seepage–Deformation Model for Simulating the Effect of Fracture Seepage on Rock Slope Stability Using the Numerical Manifold Method. Water 2023, 15, 1163. https://doi.org/10.3390/w15061163
Qu X, Zhang Y, Chen Y, Chen Y, Qi C, Pasternak E, Dyskin A. A Coupled Seepage–Deformation Model for Simulating the Effect of Fracture Seepage on Rock Slope Stability Using the Numerical Manifold Method. Water. 2023; 15(6):1163. https://doi.org/10.3390/w15061163
Chicago/Turabian StyleQu, Xiaolei, Yunkai Zhang, Youran Chen, Youyang Chen, Chengzhi Qi, Elena Pasternak, and Arcady Dyskin. 2023. "A Coupled Seepage–Deformation Model for Simulating the Effect of Fracture Seepage on Rock Slope Stability Using the Numerical Manifold Method" Water 15, no. 6: 1163. https://doi.org/10.3390/w15061163
APA StyleQu, X., Zhang, Y., Chen, Y., Chen, Y., Qi, C., Pasternak, E., & Dyskin, A. (2023). A Coupled Seepage–Deformation Model for Simulating the Effect of Fracture Seepage on Rock Slope Stability Using the Numerical Manifold Method. Water, 15(6), 1163. https://doi.org/10.3390/w15061163













