Quantification of Groundwater Hazards Related to Fluvial Floods via Groundwater Flow Modelling: A Review
Abstract
:1. Introduction
2. Methods
2.1. Rationale
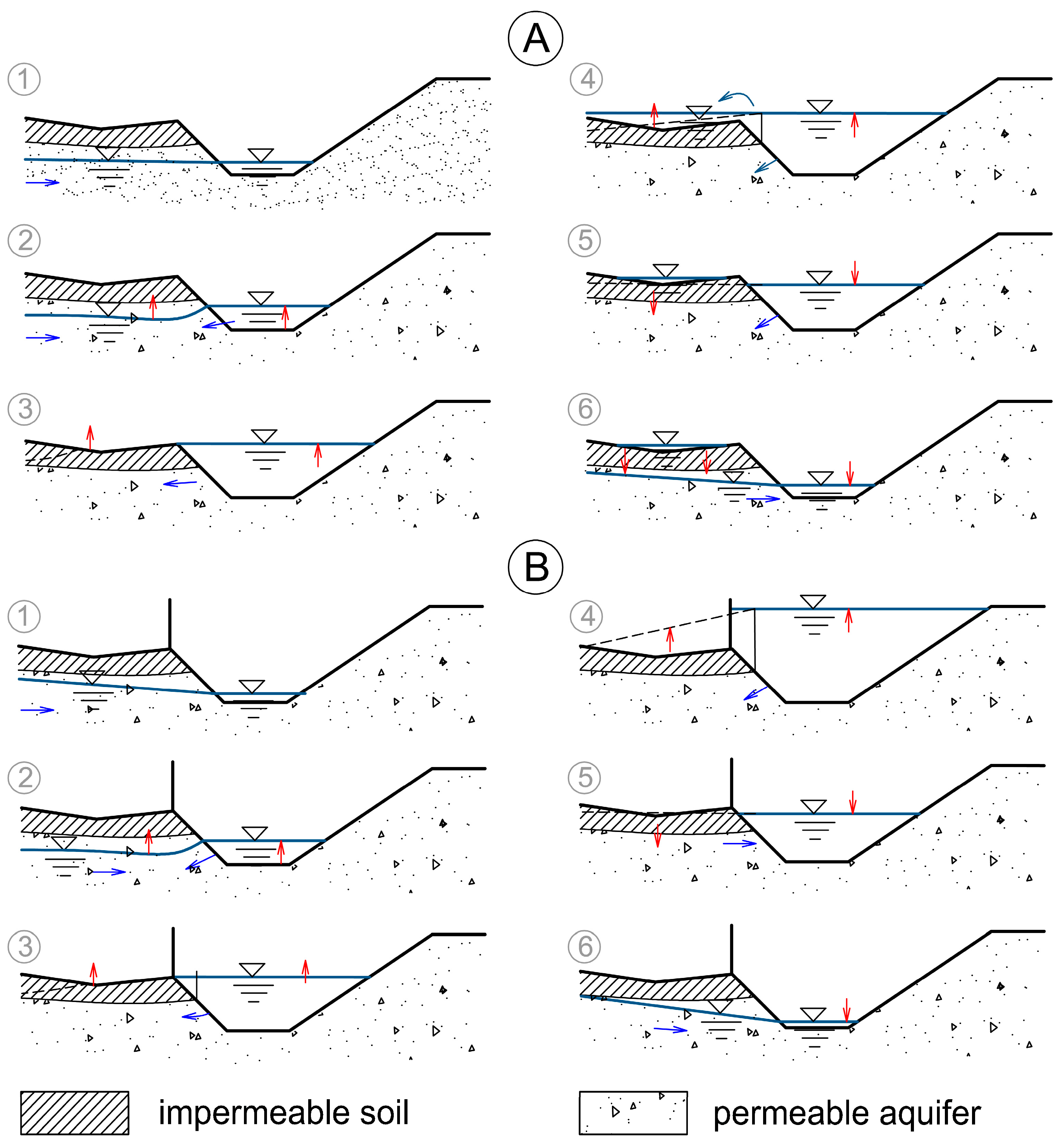
2.2. Hazardous Situations
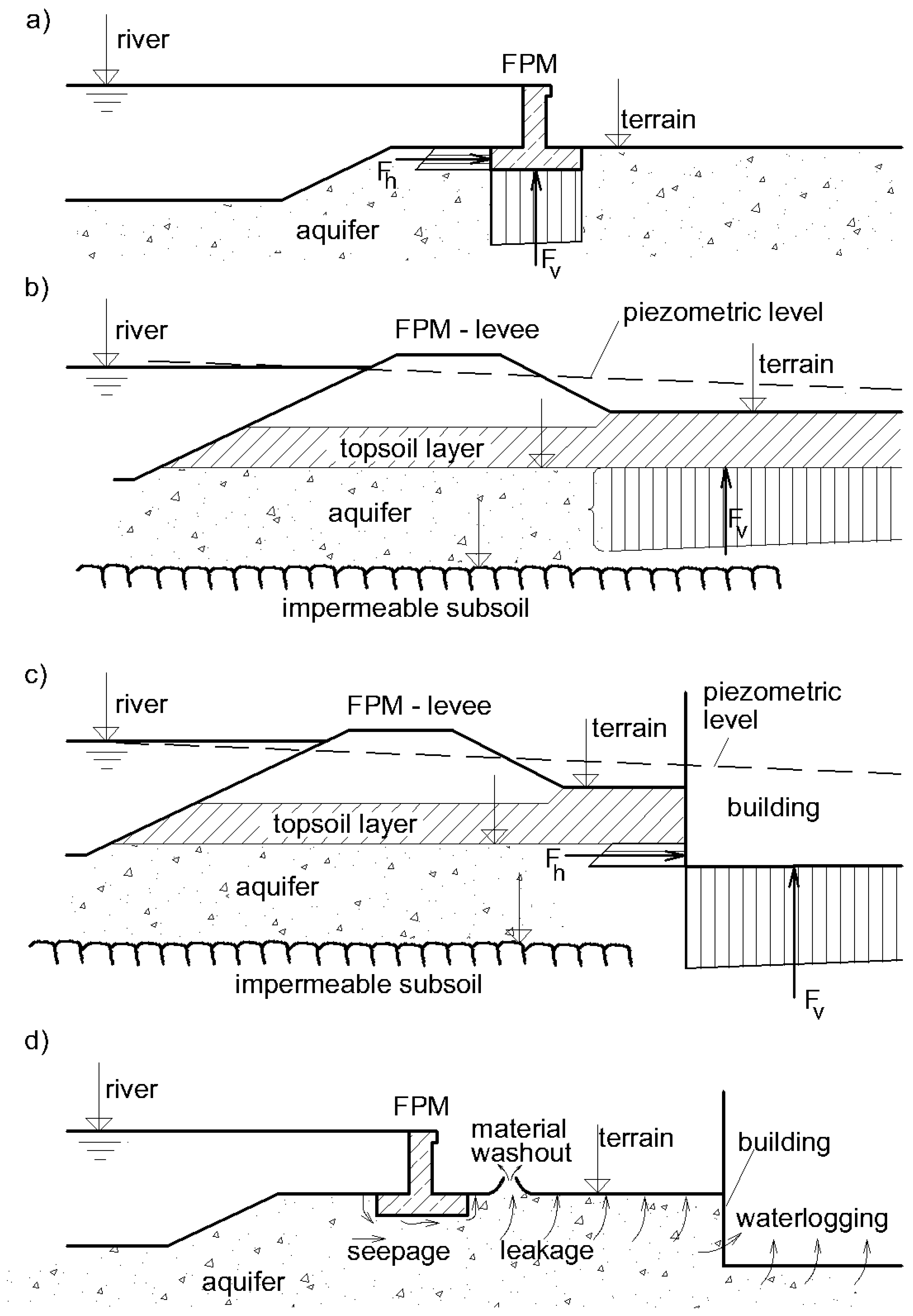
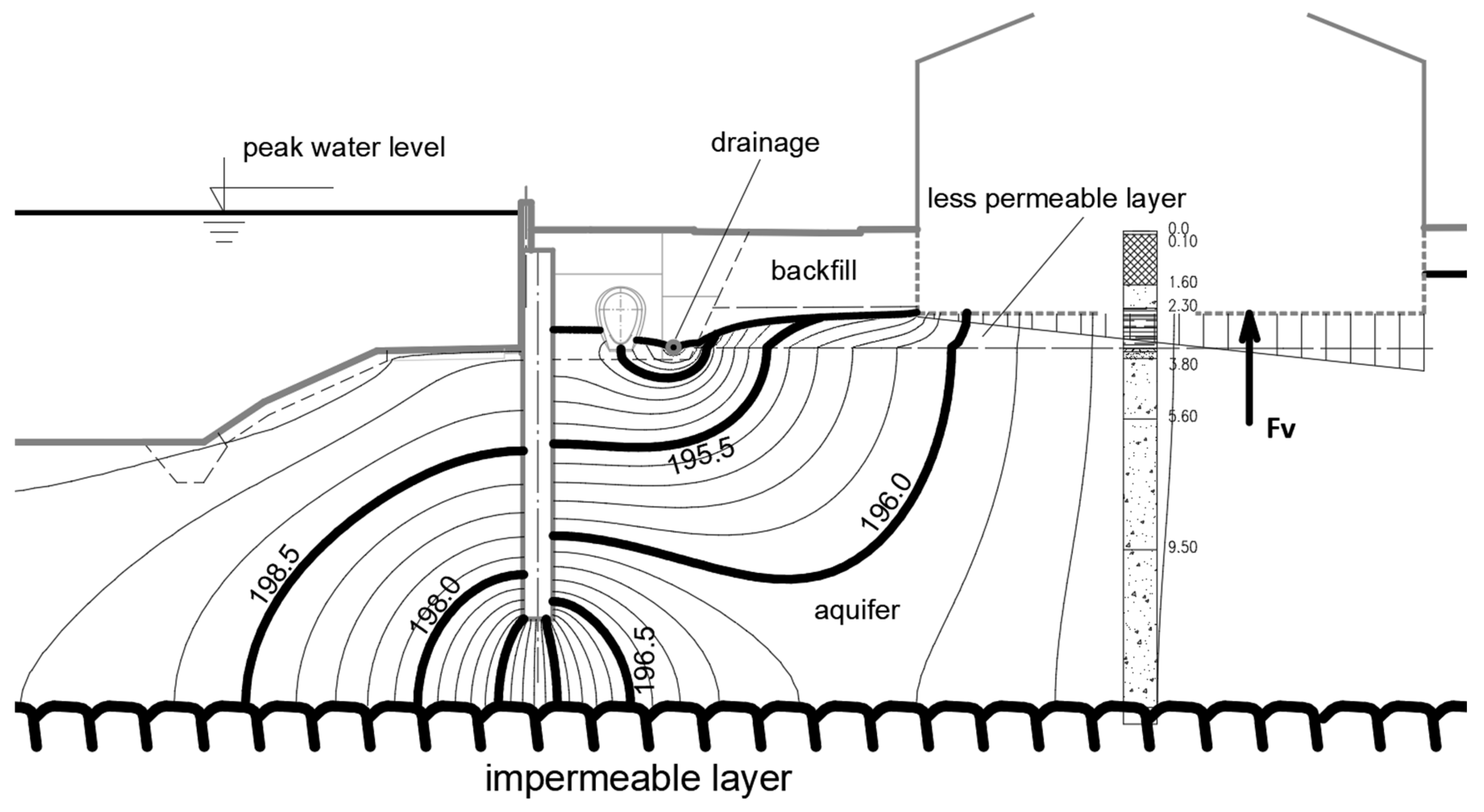
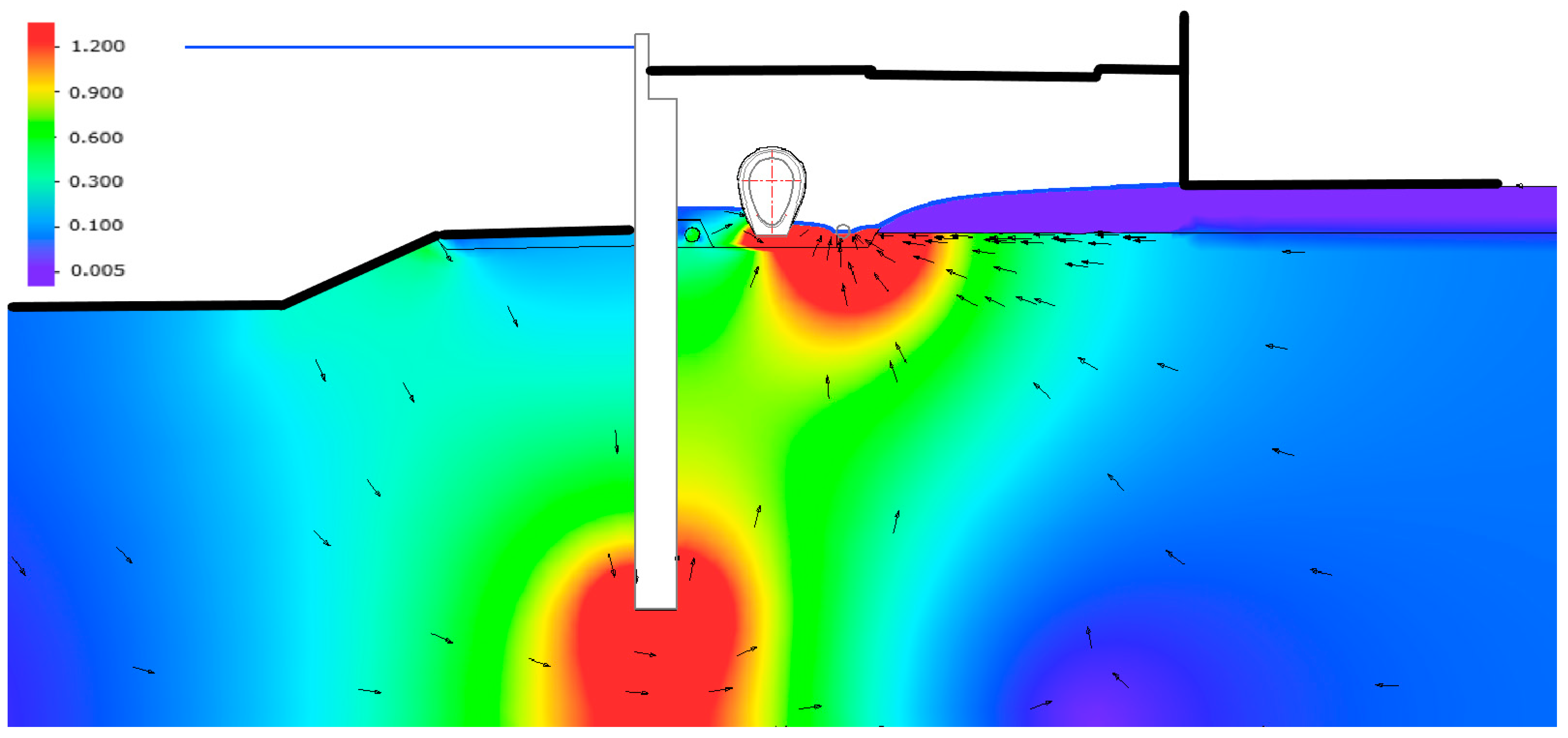
- Flood protection structures are subjected to forces acting on their subsurface parts. In addition to earth pressure, forces caused by the groundwater underflowing the foundations must be taken into account. The most critical horizontal (Fh) and vertical (Fv) water pressure forces are shown in Figure 2a.
- An increase in the piezometric head in the confined aquifer behind the FPM may result in uplift acting on impervious fluvial topsoil (Figure 2b). Similarly, pressure due to the increase of the groundwater level (piezometric head) may affect the subsurface parts of the buildings with deep foundations (Figure 2c). Such uplift can cause ruptures in the topsoil and buildings, resulting in localized concentrated leakage, significant deformation of foundation slabs, or even global structural instability. This may also initiate waterlogging of the objects (Figure 2d).
- In cases when permeable soils crop out to the terrain, seepage may occur behind the FPM. This causes loading of soils by a pressure gradient, which may result in the internal erosion of susceptible soils (Figure 2d) in the form of external suffusion or boiling. These processes in the progression phase may often endanger the stability of the FPM.
- In case of long-term floods, in combination with the permeable aquifer, waterlogging of the area behind the FPM may occur due to seepage onto the terrain (Figure 2d).
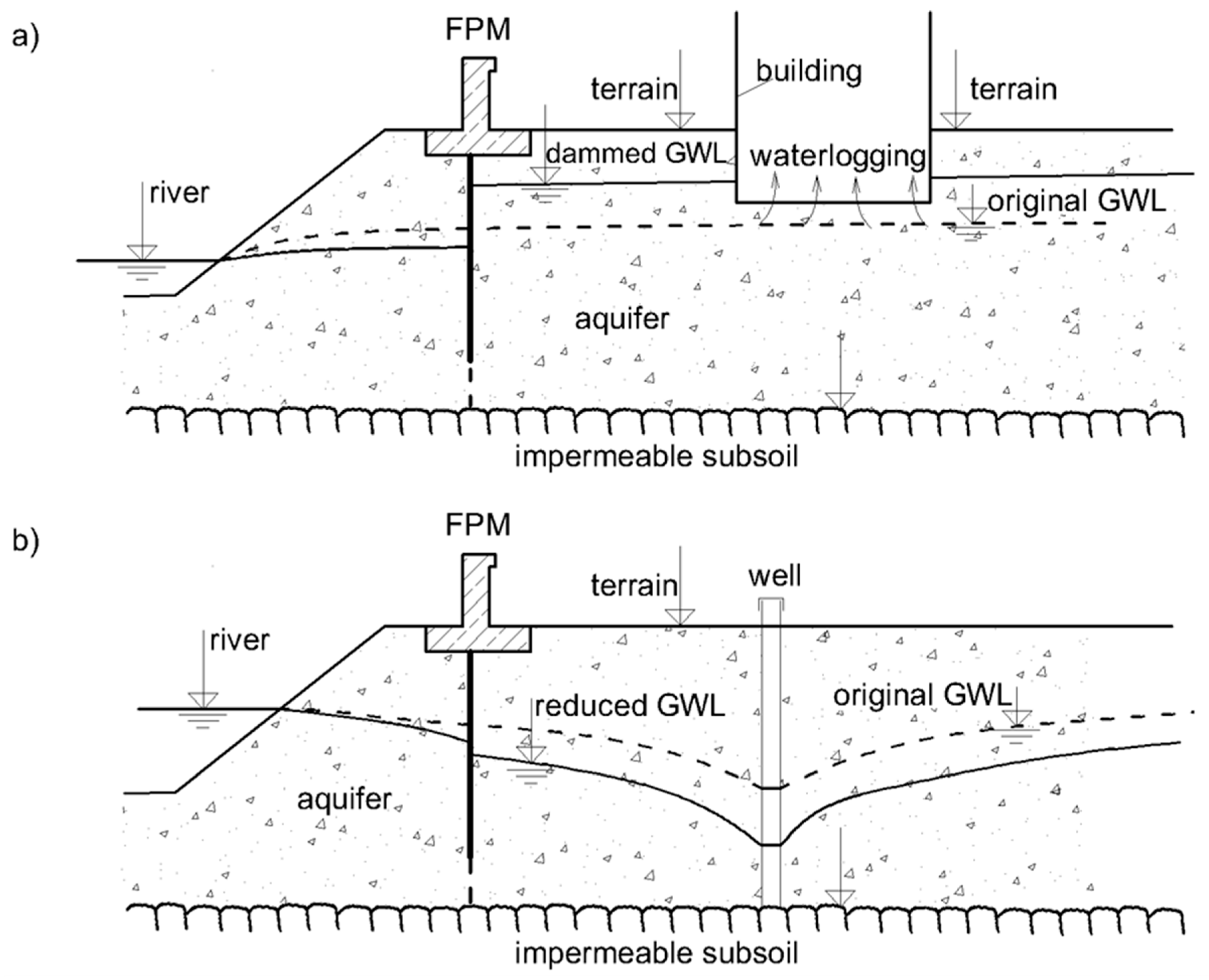
- Damming of the groundwater level (GWL) in an aquifer behind the FPM (Figure 3a) may cause a significant permanent rise of groundwater levels, resulting in waterlogging of subsurface parts of buildings in the area.
- If groundwater resources occur behind the FPM, impervious subsurface elements may block the natural bank infiltration from a river and thus deteriorate the water source, respective to a decrease the yield of wells (Figure 3b). This may also result in a significant decrease of GWL in the protected area and cause unacceptable overloading of wells.
2.3. Hazard Quantification
- piezometric head h;
- water pressure p, horizontal (Fh) and vertical (Fv) water pressure forces acting on the surface of subsurface structures, topsoil layer, and the FPM;
- pressure, or hydraulic gradient (grad p, grad h), which acts on the soil as a volumetric force and may cause its internal instability;
- waterlogging of the area is quantified by the affected area A, where water seeps onto terrain;
- seepage amount Q when dealing with pumped water from wells.
2.4. Data Acquisition
3. Groundwater Flow Modelling
3.1. Modelling Procedure and Types of Models
- The description of a real system where the area of interest is identified, and management problems and potential hazards are formulated.
- The objectives of modelling have to be carefully defined together with expected outcomes (see Section 2). This involves the analysis of both flood and non-flood situations.
- The conceptual model consists of a set of assumptions related to the geometry, shape, and boundaries of the domain, as well as aquifer materials and their properties (homogeneity, isotropy, porosity, hydraulic conductivity, compressibility, etc.). According to the expected character of the flow, the dimension and time regime (steady, transient) of the model are defined (Table 2).
- The mathematical formulation (model) is represented by a set of governing equations, plus initial and boundary conditions.
- The computer code appropriate for the problem solution has to be selected [47,48,49]. Pre- and post- processing are necessary parts of the data analysis, preparation, and presentation. To this end, engineering approaches are combined with efficient post-processing methods which enable the display of spatial and temporal data using CAD systems and thematic maps within GIS tools.
- The numerical model should be subject to calibration and verification based on data from groundwater level observations and pumping amount measurements. The calibrated and verified model may be used for the simulation of scenarios that answer posed questions and achieve defined objectives.
- one-dimensional (1D) groundwater flow model for cases where parallel seepage in a flat aquifer with small hydraulic gradients is expected (Dupuit assumption)—this model may be used for both confined and unconfined aquifers;
- two-dimensional model in the horizontal plane (2Dh) applicable for large and complex aquifers with small hydraulic gradients (Dupuit assumption)—this model may be used for both confined and unconfined aquifers;
- two-dimensional model in the vertical plane (2Dv), which can be used for parallel flow with significant variation in flow direction in the vertical plane, both for confined flow and flow with a phreatic surface;
- three-dimensional model (3D) for flow both in confined and unconfined conditions.
- preliminary analysis is carried out using a 1D model;
- complex analysis of flood propagation to the aquifer using a transient 2Dh model;
- modelling of the conditions during a non-flood period using a steady state 2Dh model;
- detailed analysis of conditions at the FPM using a steady state 2Dv model;
- if necessary, the detailed steady state 3D modelling of singularities, where no dimensional approximations exist, may be considered.
3.2. One-Dimensional Model
3.3. 2Dh Model of Flow in a Horizontal Plane
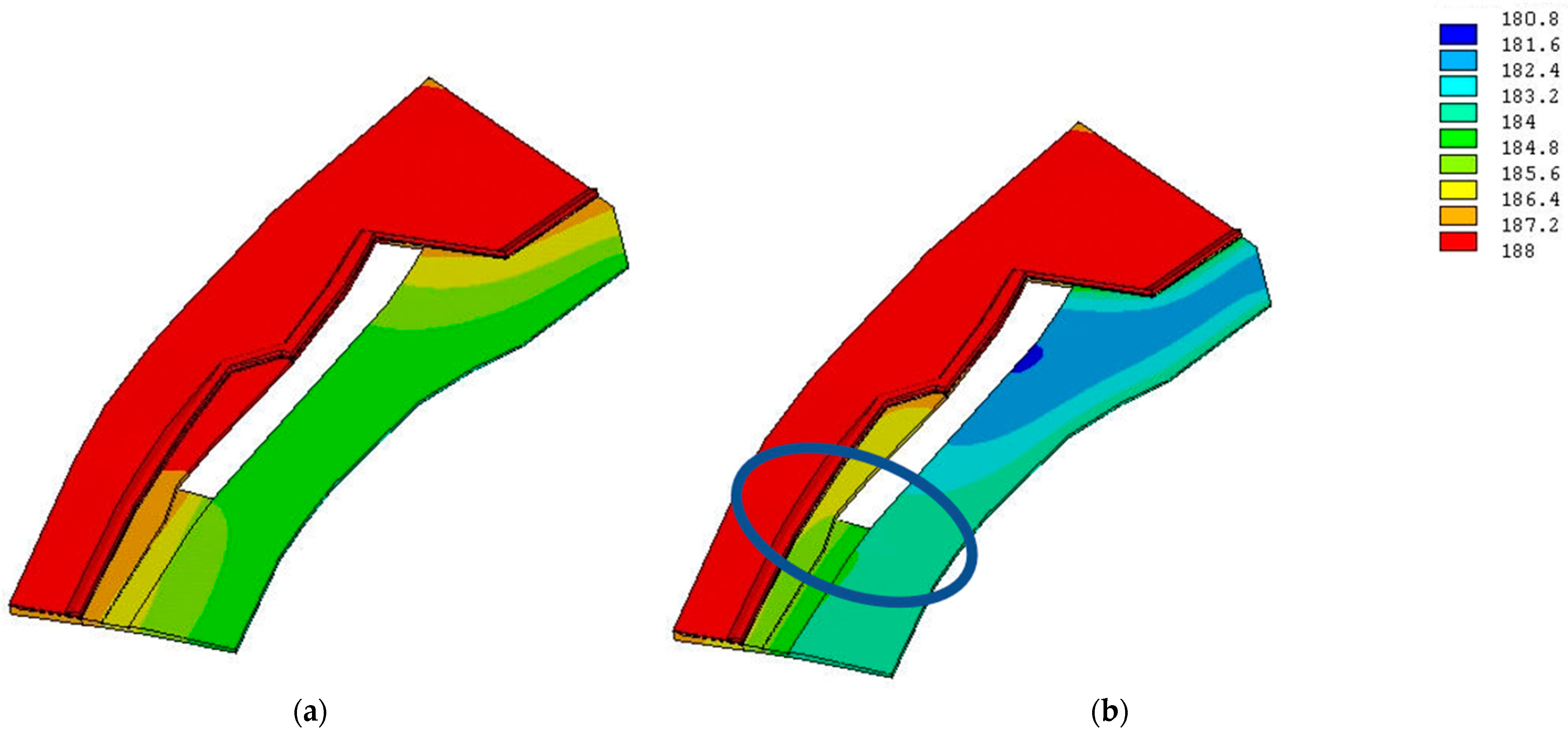
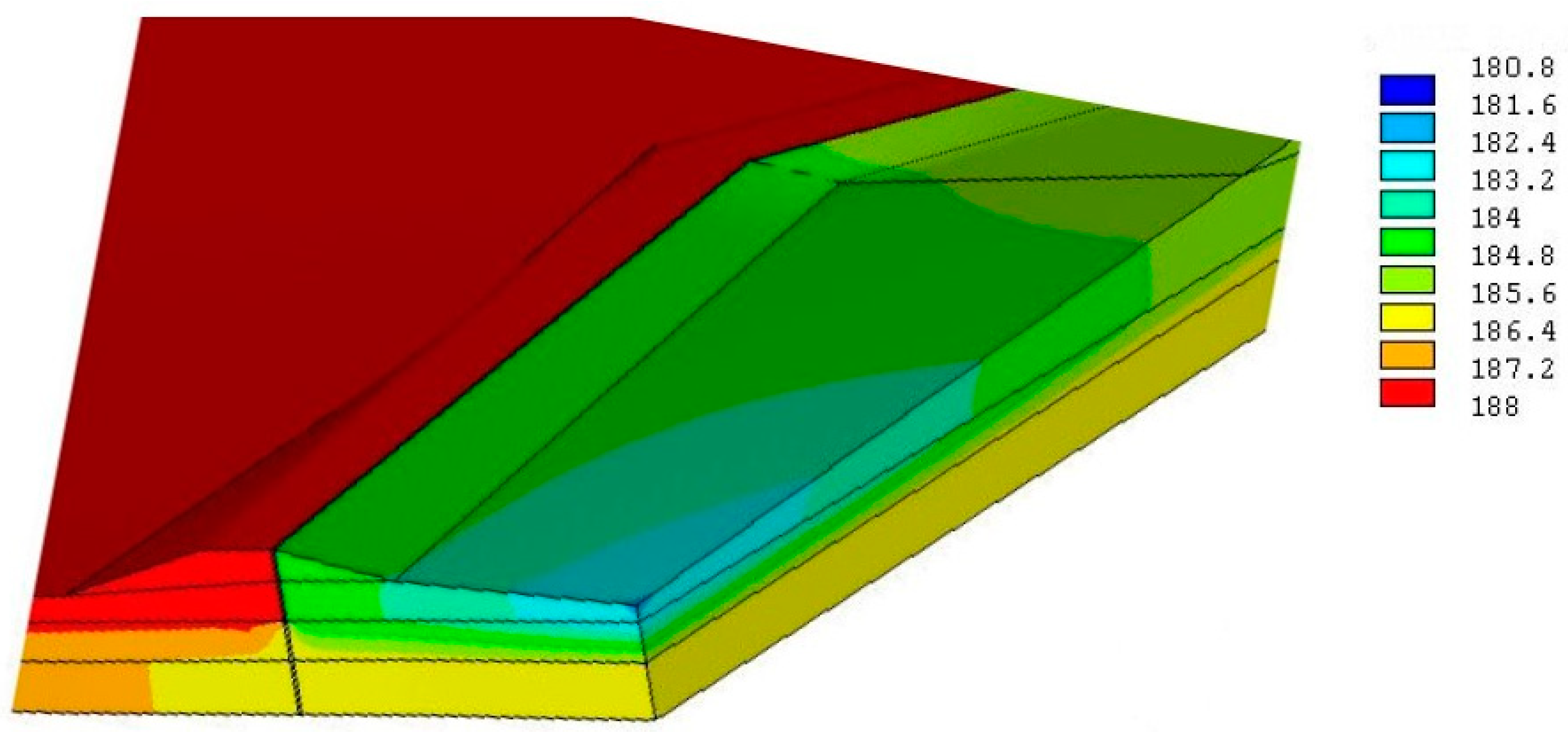
- Subsurface elements of the FPM may unacceptably increase the water level in the aquifer behind the FPM (Figure 3a), increase the water pressure on the floors and walls of cellars, and cause dampness of walls and even waterlogging of the terrain. The situation may be crucial in case of the infiltration of rainwater in urban areas behind the FPM.
- If riverbank infiltration supports the water supply provided by wells close to the riverbank, subsurface elements of the FPM may reduce the yield of affected water sources (Figure 3b).
3.4. 2Dv Model of Flow in a Vertical Plane
3.5. 3D Model
3.6. Discussion of Uncertainties
- The geological composition of the area, such as the thickness of individual layers (aquifer, topsoil, etc.), which is usually derived from a limited number of boreholes or pits;
- limited understanding about overall hydrogeological and hydrological conditions, i.e., time-dependent groundwater flow regime, the direction and amount of groundwater flow, inflows and infiltration to an aquifer—the uncertainties are governed by the extent of monitoring network and frequency of readings;
- the knowledge about geological and hydrogeological properties of topsoil and aquifer soils, namely granulometry, porosity, hydraulic conductivity, and storativity, which are derived from laboratory and field testing, but in many cases only use empirical formulae supplemented by single hydraulic tests (pumping tests);
- the rate of interaction between the river and aquifer, which may be influenced by local clogging;
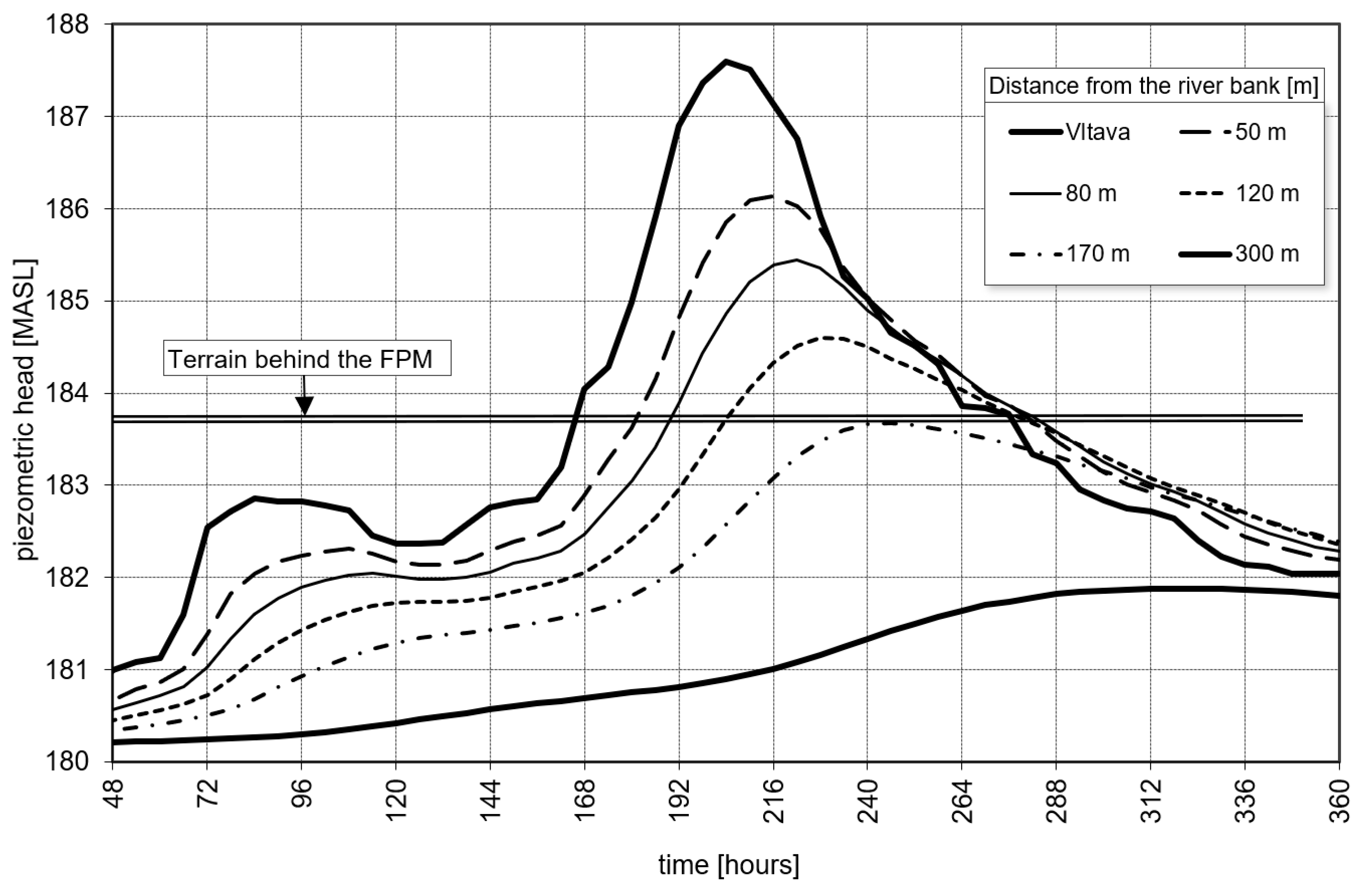
- boundary conditions, both at the riverside and behind the FPM, are derived from flood hydrographs which are not routinely statistically assessed in terms of their shape and flood volume;
- infiltration rates during the simulated event.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Robins, N.S.; Finch, J.W. Groundwater flood or groundwater-induced flood? Q. J. Eng. Geol. Hydrogeol. 2012, 45, 119–121. [Google Scholar] [CrossRef] [Green Version]
- CIRIA. The International Levee Handbook; U.S. Army. Corps of Engineers: Washington, DC, USA, 2013; 1332p.
- Miroslaw-Swiatek, D.; Popielski, P.; Sliwinski, P.; Cwalina, T.; Skutnik, Z. Analysis of factors influencing levee safety using the DEMATEL method. PLoS ONE 2021, 16, e0255755. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, D.; Dixon, A.; Newell, A.; Hallaways, A. Groundwater flooding within an urbanised flood plain. J. Flood Risk Manag. 2012, 5, 68–80. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Li, W. A review of regional groundwater flow modelling. J. Geosci. Front. 2011, 2, 205–214. [Google Scholar] [CrossRef] [Green Version]
- MacDonald, D.M.J.; Bloomfield, J.P.; Hughes, A.G.; MacDonald, A.M.; Adams, B.; McKenzie, A.A. Improving the understanding of the risk from groundwater flooding in the UK. In Proceedings of the Floodrisk 2008, European Conference on Flood Risk Management, Oxford, UK, 30 September–2 October 2008; CRC Press: Leiden, The Netherlands. [Google Scholar]
- Environment Agency. Making Space for Water, Groundwater Flood Records Collation, Monitoring and Risk Assessment; Extended Report (Chalk Aquifers), Jacobs, Report to Environment Agency; Environment Agency: Bristol, UK, 2006; 187p. [Google Scholar]
- Adams, B.; Bloomfield, J.P.; Gallagher, A.J.; Jackson, C.R.; Rutter, H.K.; Williams, A.T. An early warning system for groundwater flooding in the Chalk. Q. J. Eng. Geol. Hydrogeol. 2010, 43, 185–193. [Google Scholar] [CrossRef]
- Chromá, K.; Brázdil, R.; Dolák, L.; Řehoř, J.; Řezníčková, L. Documentary data in the study of fatalities caused by meteorological and hydrological events: The Czech Republic, 1964–2019. In Proceedings of the EGU General Assembly 2020, Virtual, 4–8 May 2020. [Google Scholar] [CrossRef]
- Müller, M.; Kašpar, M.; Valeriánová, A.; Crhová, L.; Holtanová, E.; Gvoždíková, B. Novel indices for the comparison of precipitation extremes and floods: An example from the Czech territory. Hydrol. Earth Syst. Sci. 2015, 19, 4641–4652. [Google Scholar] [CrossRef] [Green Version]
- Fetter, C.W. Applied Hydrogeology, 4th ed.; Prentice Hall, Inc.: Upper Saddle River, NJ, USA, 2001; 598p. [Google Scholar]
- Directive. Directive 2006/118/EC of the European Parliament and of the Council. Directive on the protection of groundwater against pollution and deterioration. Off. J. Eur. Communities 2006, 372, 13. [Google Scholar]
- Joseph, N.; Preetha, P.P.; Narasimhan, B. Assessment of environmental flow requirements using a coupled surface water-groundwater model and a flow health tool: A case study of Son River in the Ganga Basin. Ecol. Indic. 2020, 121, 107110. [Google Scholar] [CrossRef]
- Čubanová, L.; Šoltész, A.; Bednárová, E.; Baroková, D.; Orfanus, M. Complex Proposal of Flood Protection Measures for Small Municipalities in the Area of Small Carpathians. In Proceedings of the 5th World Multidisciplinary Civil Engineering-Architecture-Urban Planning Symposium (WMCAUS), Prague, Czech Republic, 15–19 June 2020. [Google Scholar] [CrossRef]
- Bear, J.; Verruijt, A. Modeling Groundwater Flow and Pollution; Springer: Dordrecht, Netherlands, 1992. [Google Scholar]
- Peralta, R.C. Groundwater Optimization Handbook: Flow, Contaminant Transport, and Conjunctive Management; CRC Press: Roca Baton, FL, USA, 2012. [Google Scholar]
- Thomas, A.; Eldho, T.I.; Rastogi, A.K.; Majumder, P. A comparative study in aquifer parameter estimation using MFree point collocation method with evolutionary algorithms. J. Hydroinform. 2019, 21, 455–473. [Google Scholar] [CrossRef]
- Ghafoori, Y.; Vidmar, A.; Riha, J.; Kryzanowski, A. A Review of Measurement Calibration and Interpretation for Seepage Monitoring by Optical Fiber Distributed Temperature Sensors. J. Sens. 2020, 20, 5696. [Google Scholar] [CrossRef]
- Ackerer, P.; Carrera, J.; Delay, F. Identification of aquifer heterogeneity through inverse methods. In Special Issue: Geo-Hydrological Data & Models; Institute de France, Académie des Sciences: Paris, France, 2022. [Google Scholar] [CrossRef]
- Swathi, B.; Eldho, T.I. Aquifer parameter and zonation structure estimation using meshless local Petrov–Galerkin method and particle swarm optimization. J. Hydroinform. 2018, 20, 457–467. [Google Scholar] [CrossRef] [Green Version]
- Koltsida, E.; Kallioras, A. Groundwater flow simulation through the application of the FREEWAT modeling platform. IWA Publishing. J. Hydroinform. 2019, 21, 812–833. [Google Scholar] [CrossRef]
- Eryiğit, M. Estimation of parameters in groundwater modelling by modified Clonalg. J. Hydroinform. 2021, 23, 298–306. [Google Scholar] [CrossRef]
- Evans, S.W.; Jones, N.L.; Williams, G.P.; Ames, D.P.; Nelson, E.J. Groundwater Level Mapping Tool: An open source web application for assessing groundwater sustainability. Environ. Model. Softw. 2020, 131, 104782. [Google Scholar] [CrossRef]
- Hoffmann, J.; Sander, P. Remote sensing and GIS in hydrogeology. Hydrogeol. J. 2007, 15, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Senthilkumar, M.; Gnanasundar, D.; Arumugam, R. Identifying groundwater recharge zones using remote sensing & GIS techniques in Amaravathi aquifer system, Tamil Nadu, South India. Sustain. Environ. Res. 2019, 29, 15. [Google Scholar] [CrossRef] [Green Version]
- Oyedele, A.A. Use of remote sensing and GIS techniques for groundwater exploration in the basement complex terrain of Ado-Ekiti, SW Nigeria. Appl. Water Sci. 2019, 9, 51. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Hyun, Y.; Lee, S.; Lee, M.-J. Groundwater potential mapping using remote sensing and GIS-based machine learning techniques. Remote Sens. 2020, 12, 1200. [Google Scholar] [CrossRef] [Green Version]
- Al-Bahrani, H.; Al-Rammahi, A.; Al-Mamoori, S.; Almaliki, L.; Al-Ansari, N. Groundwater detection and classification using remote sensing and GIS in Najaf, Iraq. Groundw. Sustain. Dev. 2022, 19, 100838. [Google Scholar] [CrossRef]
- Swain, N.R.; Christensen, S.D.; Snow, A.D.; Dolder, H.; Espinoza-Dávalos, G.; Goharian, E.; Jones, N.L.; Nelson, E.J.; Ames, D.P.; Burian, S.J. A new open source platform for lowering the barrier for environmental web app development. Environ. Model. Softw. 2016, 85, 11–26. [Google Scholar] [CrossRef] [Green Version]
- Sege, J.; Ghanem, M.; Ahmad, W.; Bader, H.; Rubin, Y. Distributed data collection and web-based integration for more efficient and informative groundwater pollution risk assessment. Environ. Model. Softw. 2018, 100, 278–290. [Google Scholar] [CrossRef]
- Sit, M.; Langel, R.J.; Thompson, D.; Cwiertny, D.M.; Demir, I. Web-based data analytics framework for well forecasting and groundwater quality. Sci. Total Environ. 2020, 761, 144121. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.; Jones, N.; Greer, J.; Nelson, J. A cloud-based MODFLOW service for aquifer management decision support. Comput. Geosci. 2015, 78, 81–87. [Google Scholar] [CrossRef]
- Glass, J.; Junghanns, R.; Schlick, R.; Stefan, C. The INOWAS platform: A web-based numerical groundwater modelling approach for groundwater management applications. Environ. Model. Softw. 2022, 155, 105452. [Google Scholar] [CrossRef]
- Collins, S.L.; Christelis, V.; Jackson, C.R.; Mansour, M.M.; Macdonald, D.M.J.; Barkwith, A.K.A.P. Towards integrated flood inundation modelling in groundwater-dominated catchments. J. Hydrol. 2020, 591, 125755. [Google Scholar] [CrossRef]
- Merchán-Rivera, P.; Geist, A.; Disse, M.; Huang, J.; Chiogna, G. A Bayesian framework to assess and create risk maps of groundwater flooding. J. Hydrol. 2022, 610, 127797. [Google Scholar] [CrossRef]
- Julínek, T.; Duchan, D.; Říha, J. Mapping of uplift hazard due to rising groundwater level during floods. J. Flood Risk Manag. 2020, 13, e12601. [Google Scholar] [CrossRef]
- Kumar, R.; Yazdan, M.S. Evaluating Preventive Measures for Flooding from Groundwater: A Case Study. J. Multidiscip. Sci. J. 2023, 6, 1–16. [Google Scholar] [CrossRef]
- Yu, X.; Moraetis, D.; Nikolaidisc, N.P.; Lid, B.; Duffye, C.; Liu, B. A coupled surface-subsurface hydrologic model to assess groundwater flood risk spatially and temporally. Environ. Model. Softw. 2019, 114, 129–139. [Google Scholar] [CrossRef]
- Joo, J.; Tian, Y. Impact of Stream-Groundwater Interactions on Peak Streamflow in the Floods. Hydrology 2021, 8, 141. [Google Scholar] [CrossRef]
- Peña, F.; Nardi, F.; Melesse, A.; Obeysekera, J.; Castelli, F.; Price, R.M.; Crowl, T.; Gonzalez-Ramirez, N. Compound flood modeling framework for surface–subsurface water interactions. J. Nat. Hazards Earth Syst. Sci. 2022, 22, 775–793. [Google Scholar] [CrossRef]
- Ferraz, G.; Krámer, T. Surface Water–Groundwater Interactions and Bank Storage during Flooding: A Review. Period. Polytech. Civ. Eng. 2022, 66, 149–163. [Google Scholar] [CrossRef]
- Wei, S.; Zheng, Y.; Liang, X.; Xu, P.; Tian, Y.; Frame, J.M.; Zhang, Y. A distributed domain model coupling open channel flow and groundwater flow to quantify the impact of lateral hydrologic exchange on hydrograph. J. Hydrol. 2022, 611, 128010. [Google Scholar] [CrossRef]
- Naughton, O.; McCormack, T.; Gill, L.; Johnston, P. Groundwater flood hazards and mechanisms in lowland karst terrains. In Advances in Karst Research: Theory, Fieldwork and Applications; Parise, M., Gabrovsek, F., Kaufmann, G., Ravbar, N., Eds.; Geological Society, London, Special Publications: London, UK, 2018; Volume 466, pp. 397–410. [Google Scholar]
- Fell, R.; Fry, J.J. The state of the art of assessing the likelihood of internal erosion of embankment dams, water retaining structures and their foundations. In Internal Erosion of Dams and their Foundations; Taylor and Francis: London, UK, 2007; pp. 1–23. [Google Scholar]
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change. 2012. Available online: https://www.ipcc.ch/pdf/special-reports/srex/SREX_Full_Report.pdf (accessed on 20 January 2023).
- Pinder, G.F.; Gray, W.G. Finite Element Simulation in Surface and Subsurface Hydrology; Academic Press: New York, NY, USA; San Francisco, CA, USA; London, UK, 1977; 295p. [Google Scholar]
- Galavi, V. Groundwater Flow, Fully Coupled Flow Deformation and Undrained Analyses in PLAXIS 2D and 3D; PLAXIS BV. Research Department: Delft, NL, USA, 2010; 285p. [Google Scholar]
- GMS. Groundwater Modeling System GMS 10.7. Aquaveo, Provo, USA. 2021. Available online: https://www.aquaveo.com/software/gms-groundwater-modeling-system-introduction (accessed on 2 February 2023).
- ANSYS. Engineering Simulation Software. 2023. Available online: https://www.ansys.com/ (accessed on 2 February 2023).
- Hálek, V.; Švec, J. Groundwater Hydraulics; Academia: Prague, Czech Republic, 1979; 620p. [Google Scholar]
- Moghadam, Z.; Jahanshahi, R.; Asadi, N.; Behzadifar, V. Factors affecting on the groundwater uplift in the Mashhad city, Iran. Iran. Water Res. J. 2019, 14, 13. [Google Scholar]
- EN1997-1:2004; Eurocode 7: Geotechnical Design. European Committee for Standardisation: Brussels, Belgium, 2004; 105p.
- De Caro, M.; Crosta, G.B.; Previati, A. Modelling the interference of underground structures with groundwater flow and remedial solutions in Milan. J. Eng. Geol. 2020, 272, 105652. [Google Scholar] [CrossRef]
- Frick, M.; Scheck-Wenderoth, M.; Schneider, M.; Cacace, M. Surface to Groundwater Interactions beneath the City of Berlin: Results from 3D Models. J. Geofluids 2019, Volume 2019, 4129016. [Google Scholar] [CrossRef] [Green Version]
- Jandora, J.; Říha, J. Groundwater flow modelling of the flood protection measures in Prague-Troja. Water Manag. 2008, 58, 68–73. [Google Scholar]
- Dagan, G. An overview of stochastic modeling of groundwater flow and transport: From theory to applications. Eos Trans. Am. Geophys. Union 2002, 83, 621–625. [Google Scholar] [CrossRef]
- Rwanga, S.; Ndambuki, J. Solving groundwater problems fraught with uncertain recharge: An application to Central Limpopo, South Africa. Groundw. Sustain. Dev. 2020, 10, 100305. [Google Scholar] [CrossRef]
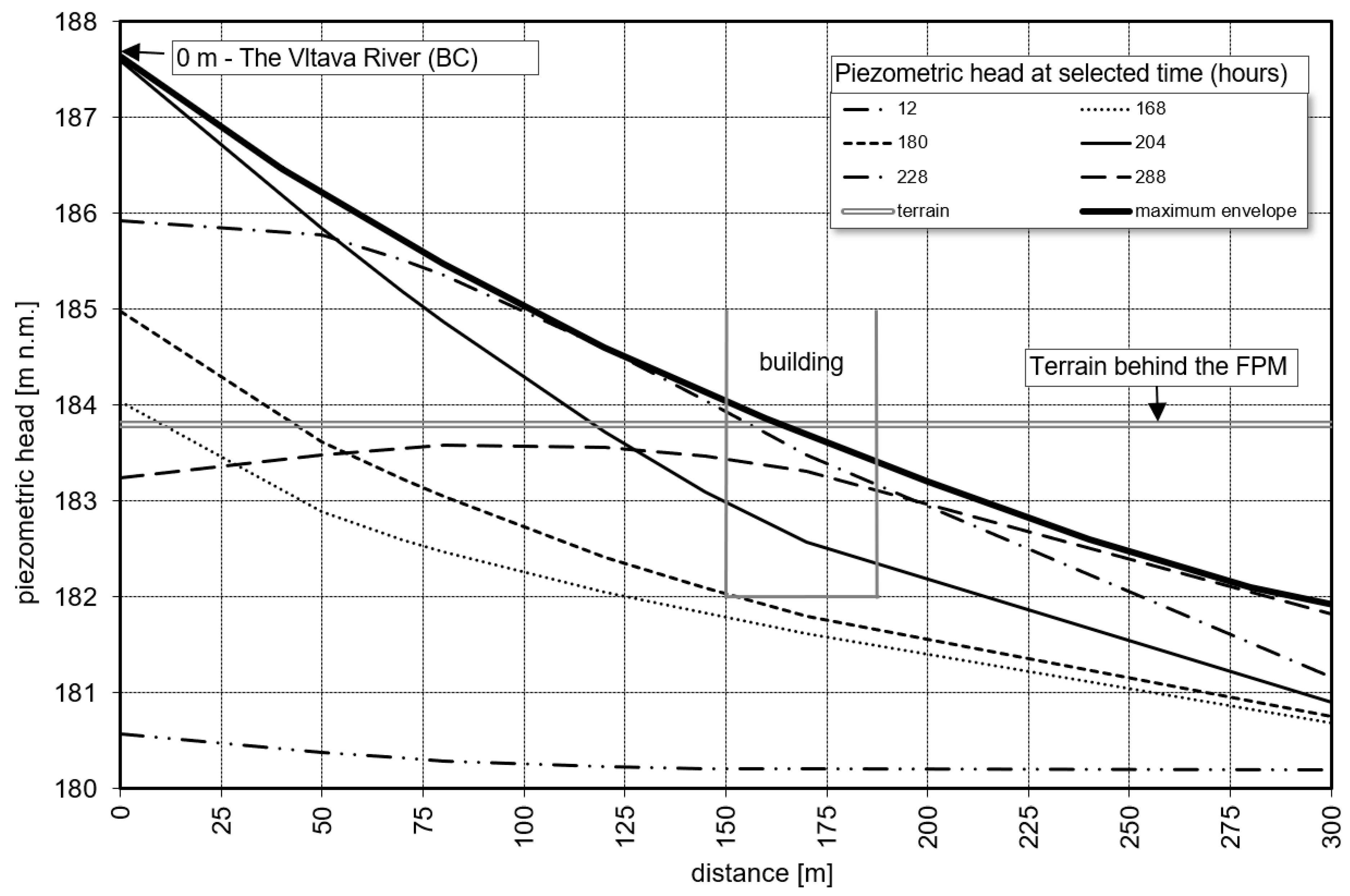
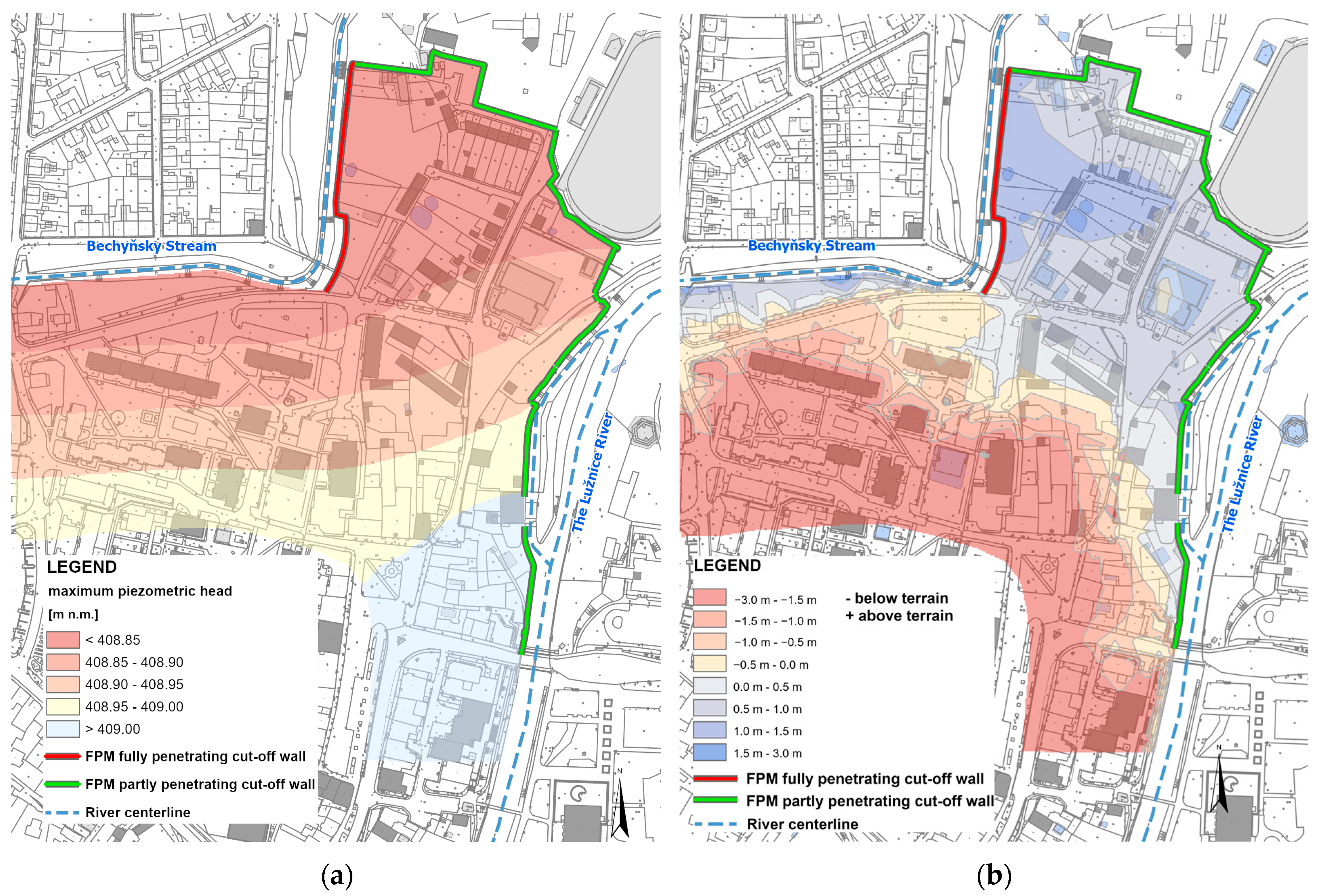
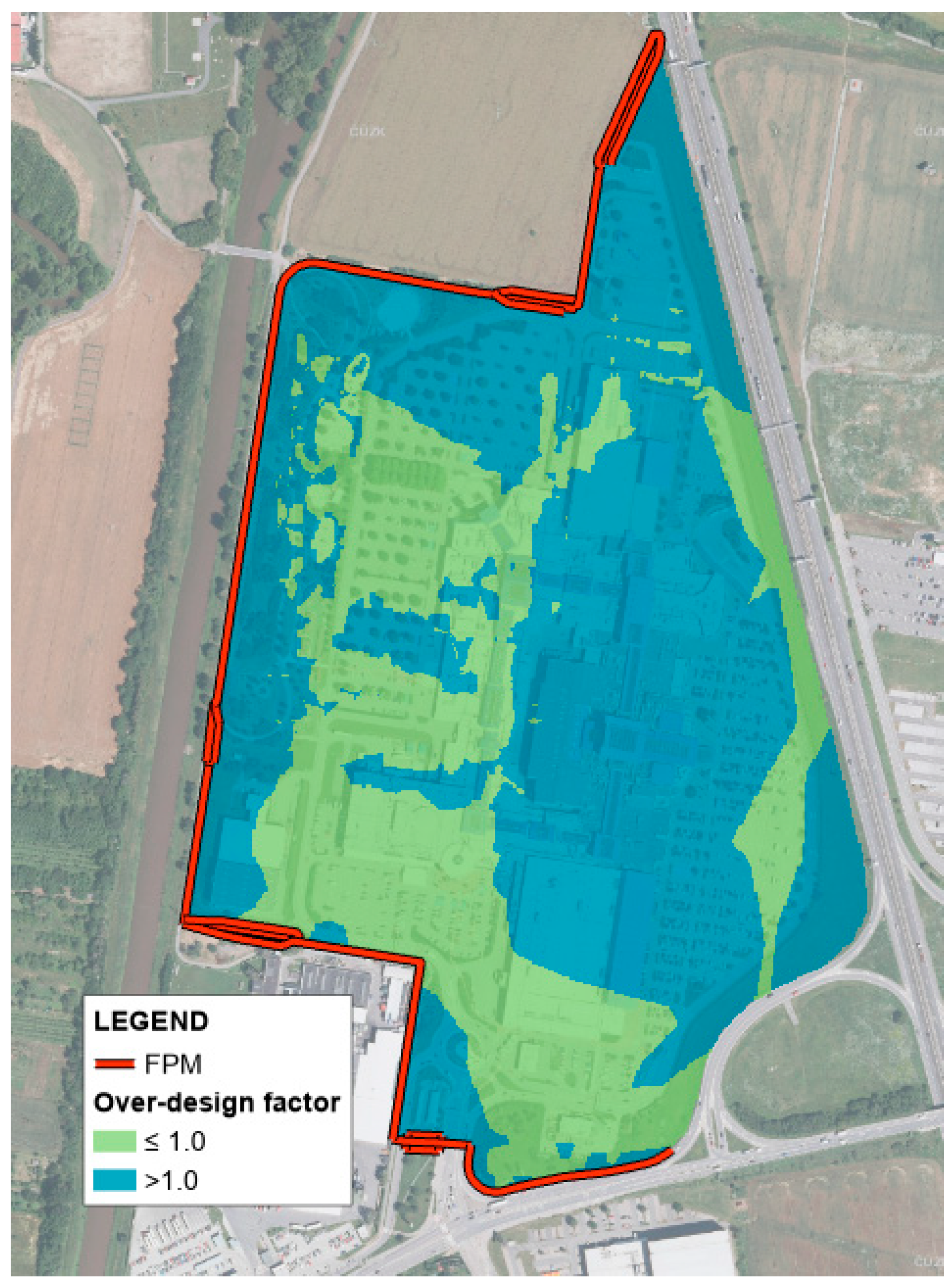

| Period | Hazard | Potential Consequences |
|---|---|---|
| Flood | Temporary increased water pressure on subsurface parts of FPM | Loss of stability of FPM, flooding of protected area |
| Temporary increased water pressure on aquifer topsoil behind FPM | Collapse of topsoil layer, internal erosion of subbase soil, collapse of FPM | |
| Temporary rise of water table/piezometric head in protected territory, seepage behind FPM on terrain, increased hydraulic gradients below FPM | Soil instability due to seepage, internal erosion, loss of stability of FPM | |
| Temporary rise of water table in protected territory | Temporary waterlogging of terrain behind FPM | |
| No flood | Permanent rise of groundwater table/piezometric head, damming due to subsurface elements of FPM | Permanent waterlogging of terrain and structures behind FPM, increased pressure on underground parts of structures |
| Permanent reduction of bank infiltration due to impermeable subsurface parts of FPM | Reduction of water extracted from groundwater resources, groundwater level drawdown, overloading of wells |
| Problem | Type of Model | Solution Method |
|---|---|---|
| preliminary assessment of the propagation of a flood wave into an aquifer | 1D—transient | analytical methods for simplified boundary and initial conditions, numerical methods |
| complex spatial assessment of flood wave propagation into a larger aquifer, assessment of piezometric head and pressure in the aquifer, assessment of local stability of the topsoil and structures behind FPM, delimitation of waterlogged areas | 2Dh—transient | numerical methods |
| assessment of the effect of subsurface elements of FPM during non-flood periods, changes in the yield of affected water sources, piezometric head and pressure in an aquifer, assessment of the stability of structures behind FPM, hazard of waterlogging | 2Dh—steady state | numerical methods |
| detailed assessment of the local conditions in the vicinity of FPM, stability of FPM and other structures for the peak flood water level scenario, assessment of non-flood scenarios | 2Dv—steady state | numerical methods |
| solutions at places with complex geometrical conditions and a general flow direction, such as FPM that cross subsurface conduits, tunnels, etc. | 3D—steady state | numerical methods |
| Period | Hazard | Interpretation | Figure |
|---|---|---|---|
| Flood | Increased water pressure on subsurface parts of FPM and structures behind FPM, detailed analysis | Map of pressure head, safety factor, cross sections with piezometric contours, pressure diagrams | Figure 2a,c, Figure 5, Figure 8 and Figure 9 |
| Increased water pressure on aquifer topsoil behind FPM | Flood wave propagation diagrams, maps of piezometric head, uplift pressures, safety factor | Figure 2b, Figure 4, Figure 5, Figure 6, Figure 7a, Figure 8, Figure 12 and Figure 13 | |
| Rise of piezometric head in protected area, seepage on terrain | Flood wave propagation diagrams, cross section with piezometric contours and hydraulic gradients | Figure 4, Figure 5, Figure 9 and Figure 10 | |
| Temporary rise of water table in protected territory | Flood wave propagation diagrams, map of maximum piezometric head differences, map of waterlogged area | Figure 4, Figure 5 and Figure 6a | |
| No flood | Rise of groundwater table/piezometric head, damming due to subsurface parts of FPM | Map of piezometric head differences and terrain, differences before and after construction of FPM | Figure 6b and Figure 7 |
| Permanent reduction of bank infiltration due to impermeable/semipermeable subsurface parts of FPM | Map of differences in phreatic/piezometric surface, cross section through wells, drop in yield | Figure 3, Figure 6b, and Figure 7b,c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Říha, J.; Julínek, T.; Duchan, D. Quantification of Groundwater Hazards Related to Fluvial Floods via Groundwater Flow Modelling: A Review. Water 2023, 15, 1145. https://doi.org/10.3390/w15061145
Říha J, Julínek T, Duchan D. Quantification of Groundwater Hazards Related to Fluvial Floods via Groundwater Flow Modelling: A Review. Water. 2023; 15(6):1145. https://doi.org/10.3390/w15061145
Chicago/Turabian StyleŘíha, Jaromír, Tomáš Julínek, and David Duchan. 2023. "Quantification of Groundwater Hazards Related to Fluvial Floods via Groundwater Flow Modelling: A Review" Water 15, no. 6: 1145. https://doi.org/10.3390/w15061145





