An Effective Standalone Solar Air Gap Membrane Distillation Plant for Saline Water Desalination: Mathematical Model, Optimization
Abstract
:1. Introduction
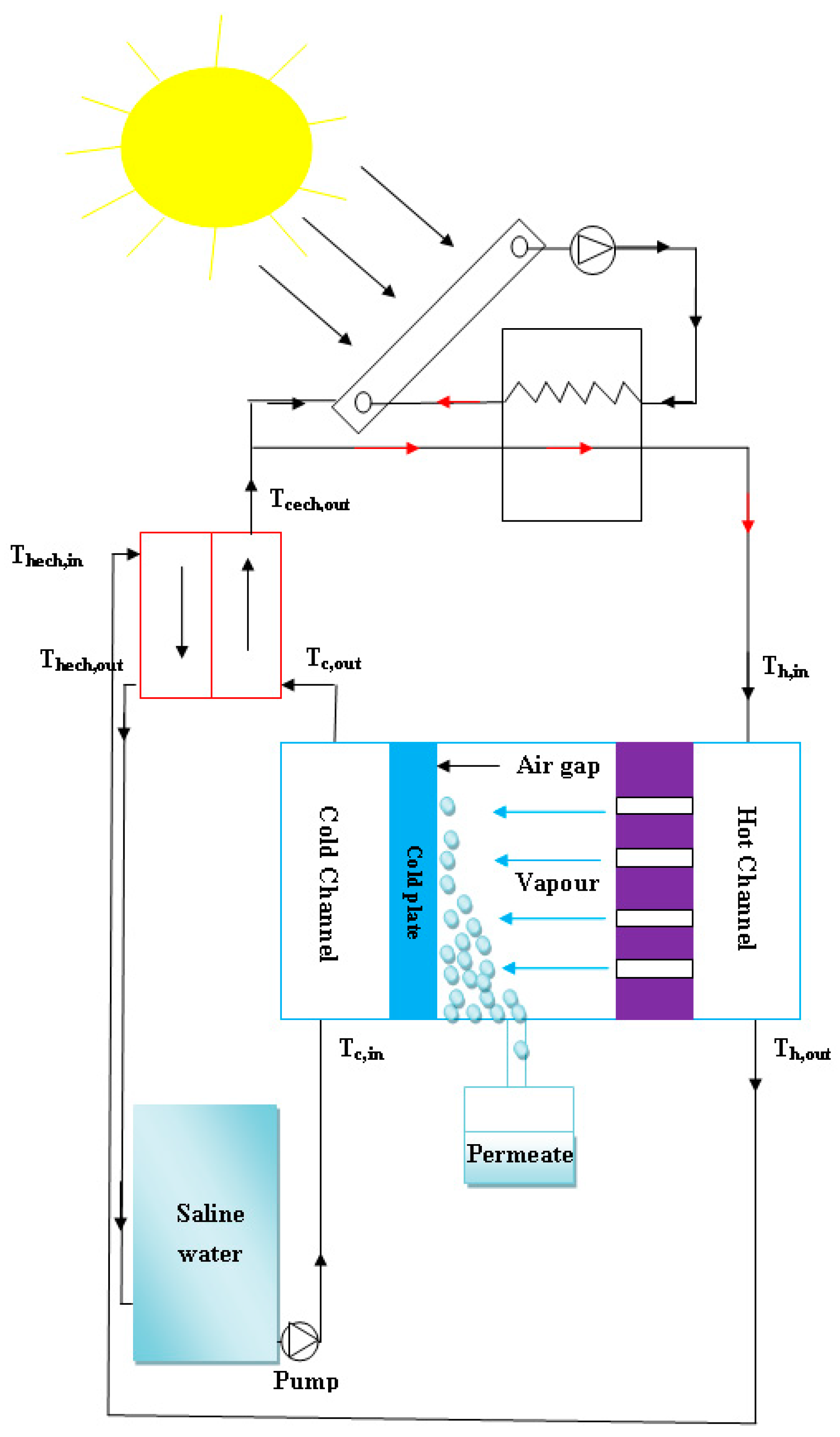
2. System Description
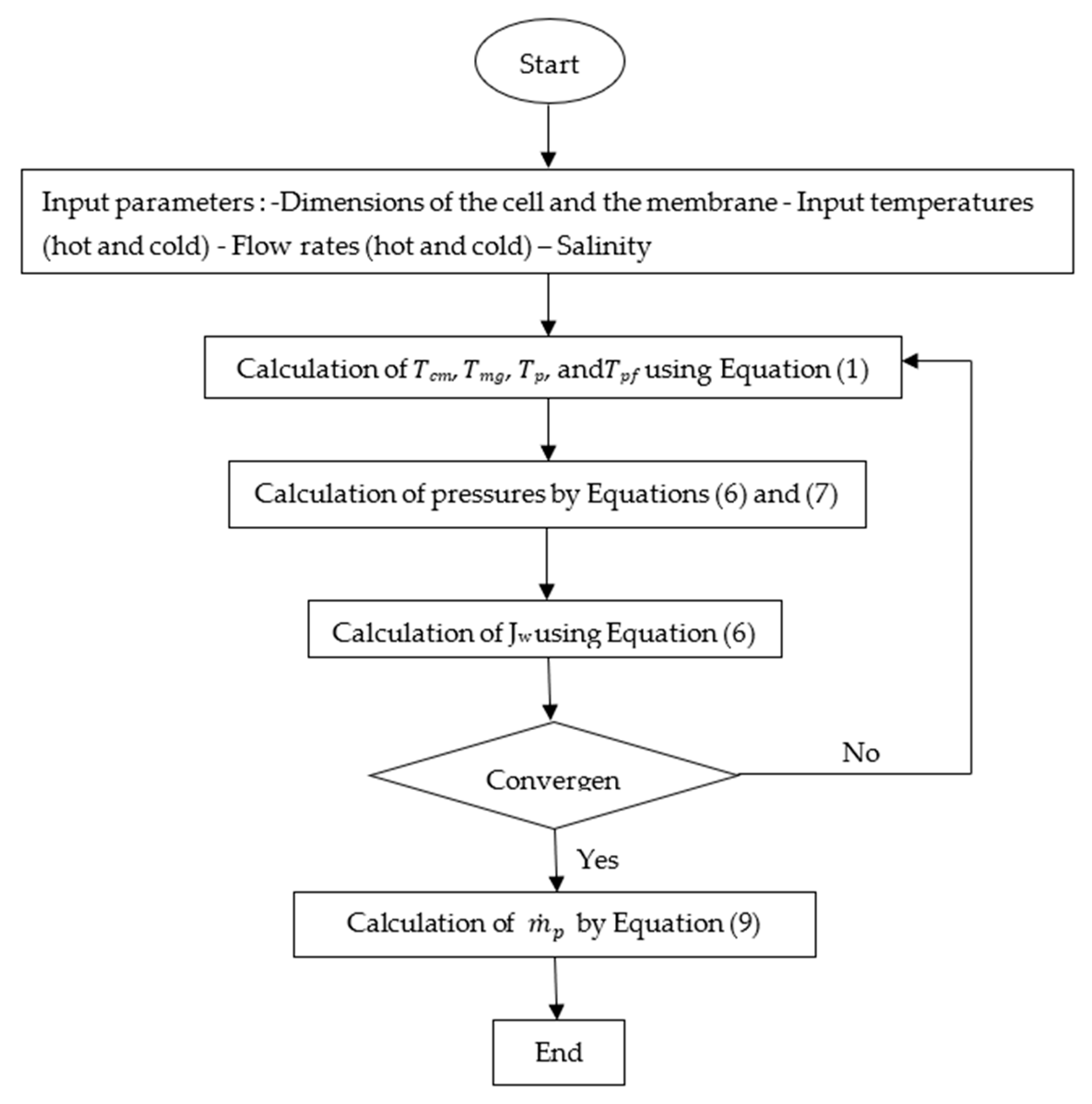
3. Numerical Modeling and Proposed Method
3.1. AGMD Unit
3.1.1. Heat Transfer
3.1.2. Mass Transfer
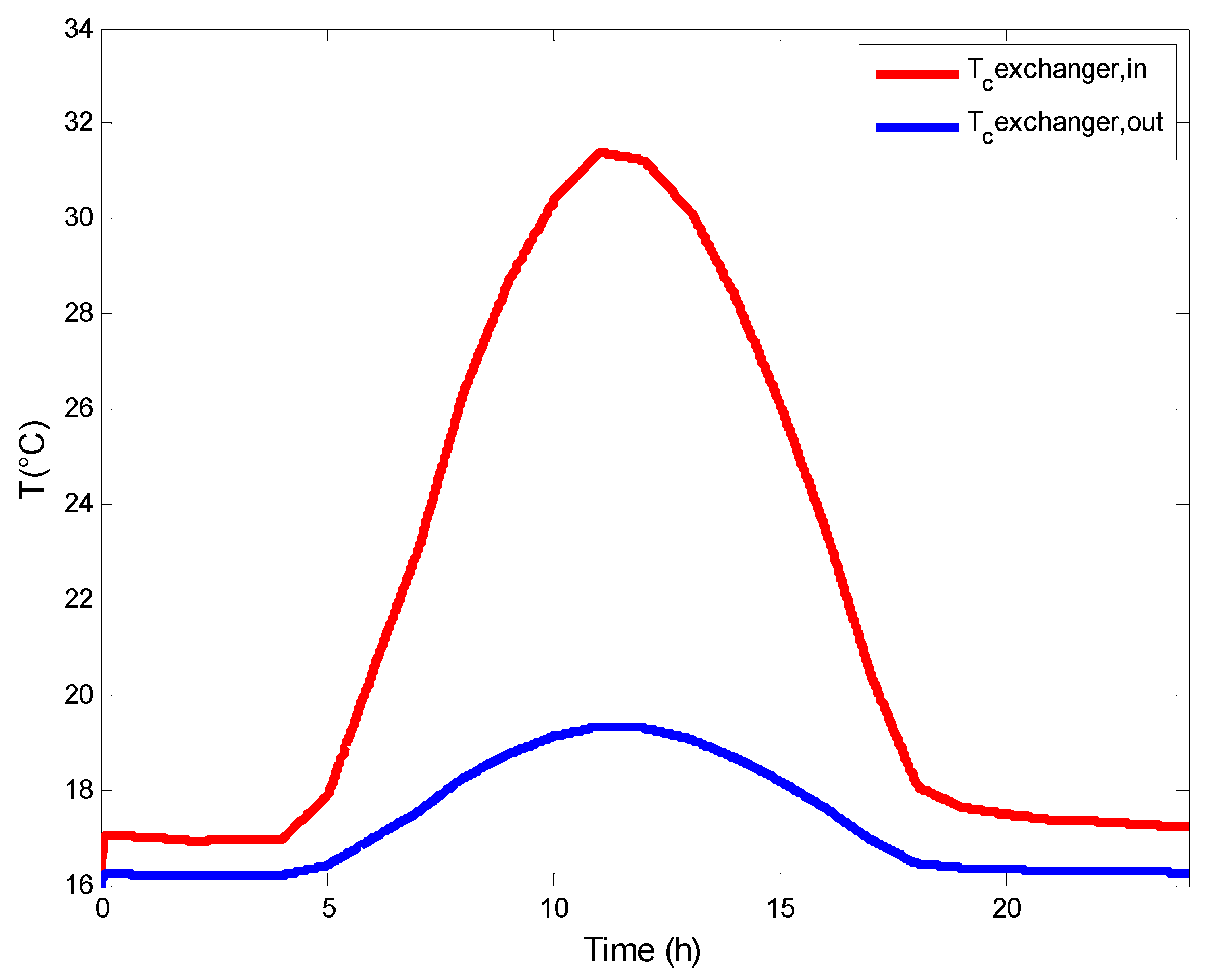
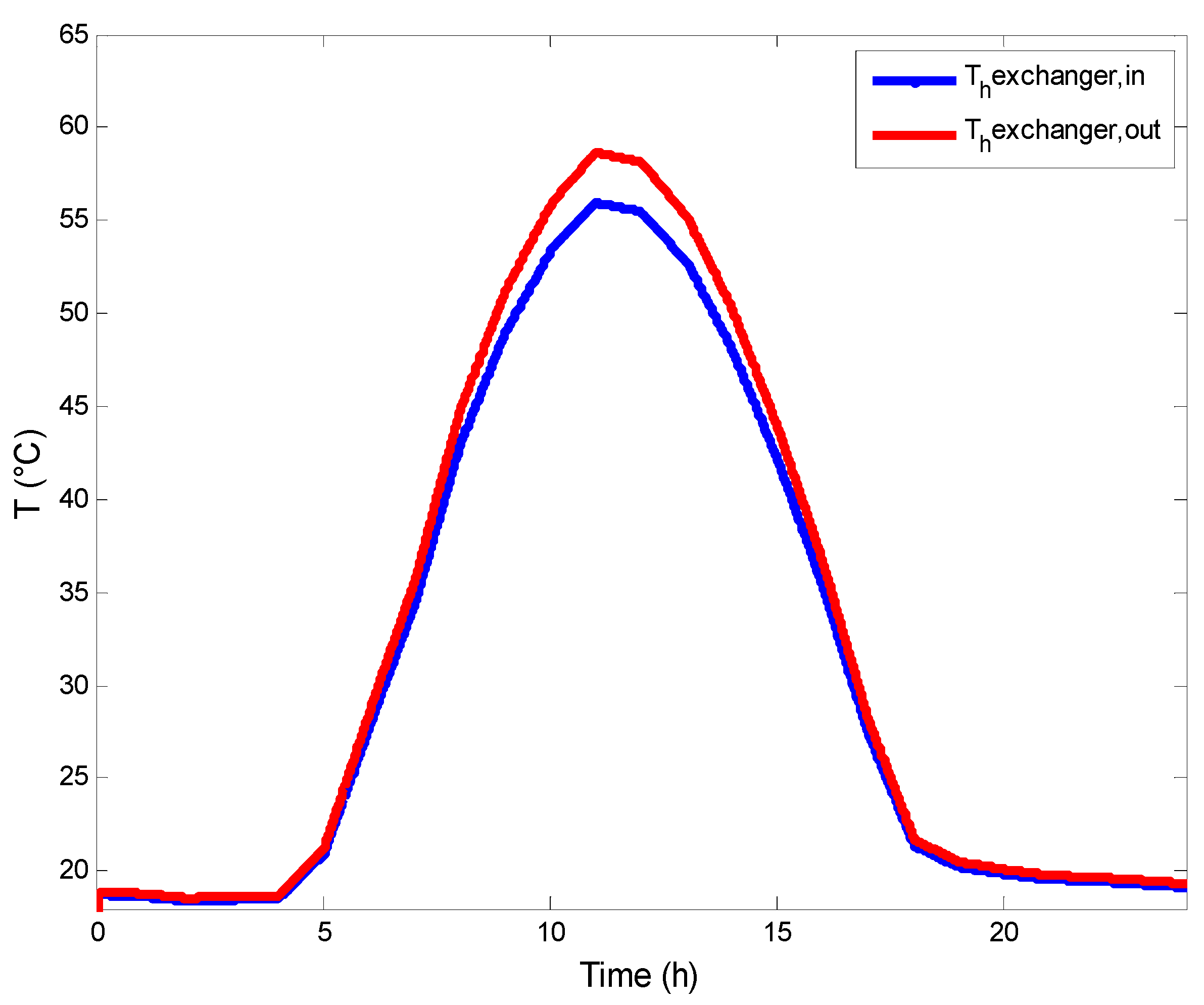
3.2. Heat Exchangers Model
3.3. Solar Flat Plate Collector
3.4. System Performance Assessment
4. Results and Discussion
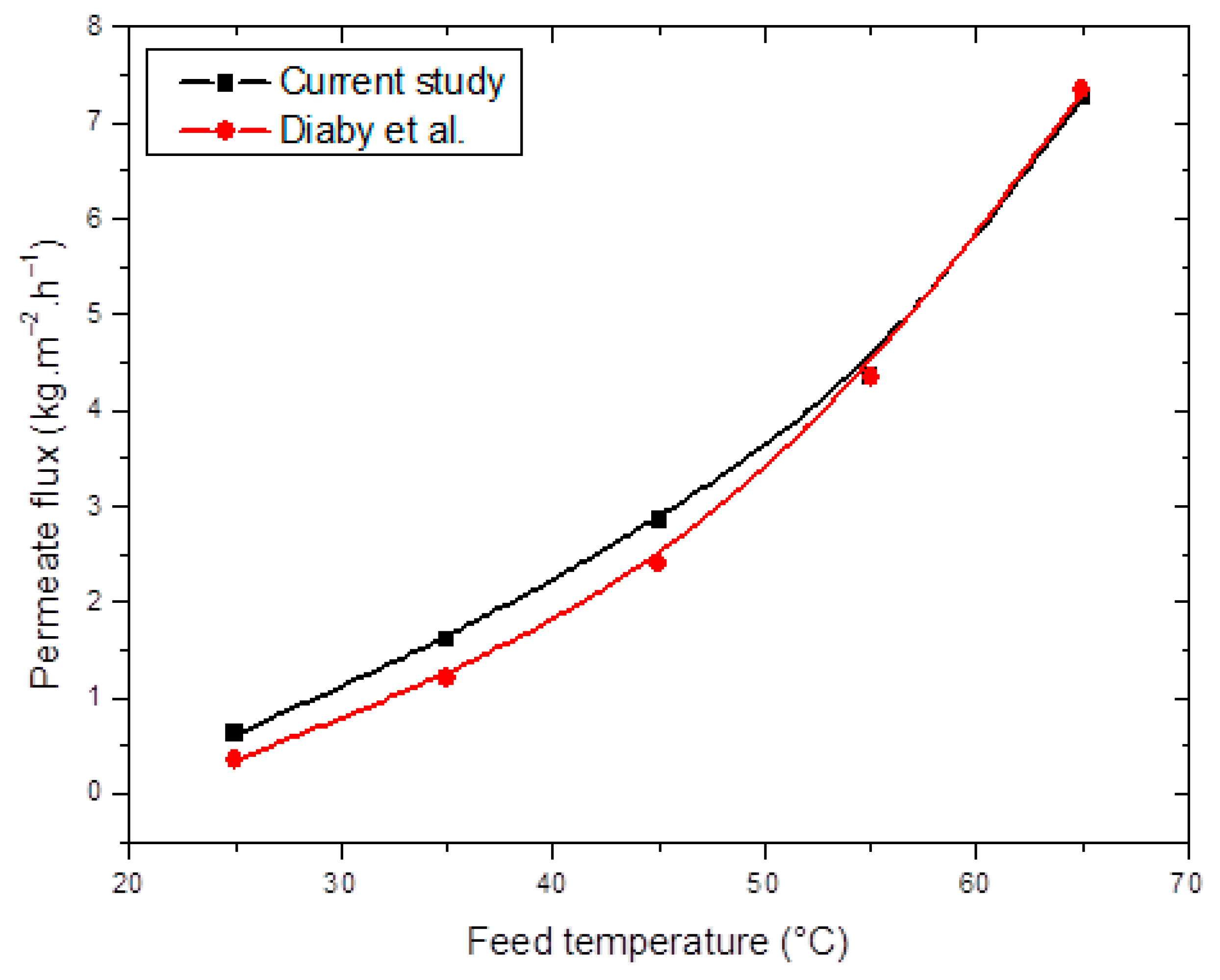
4.1. Validation of the AGMD Model
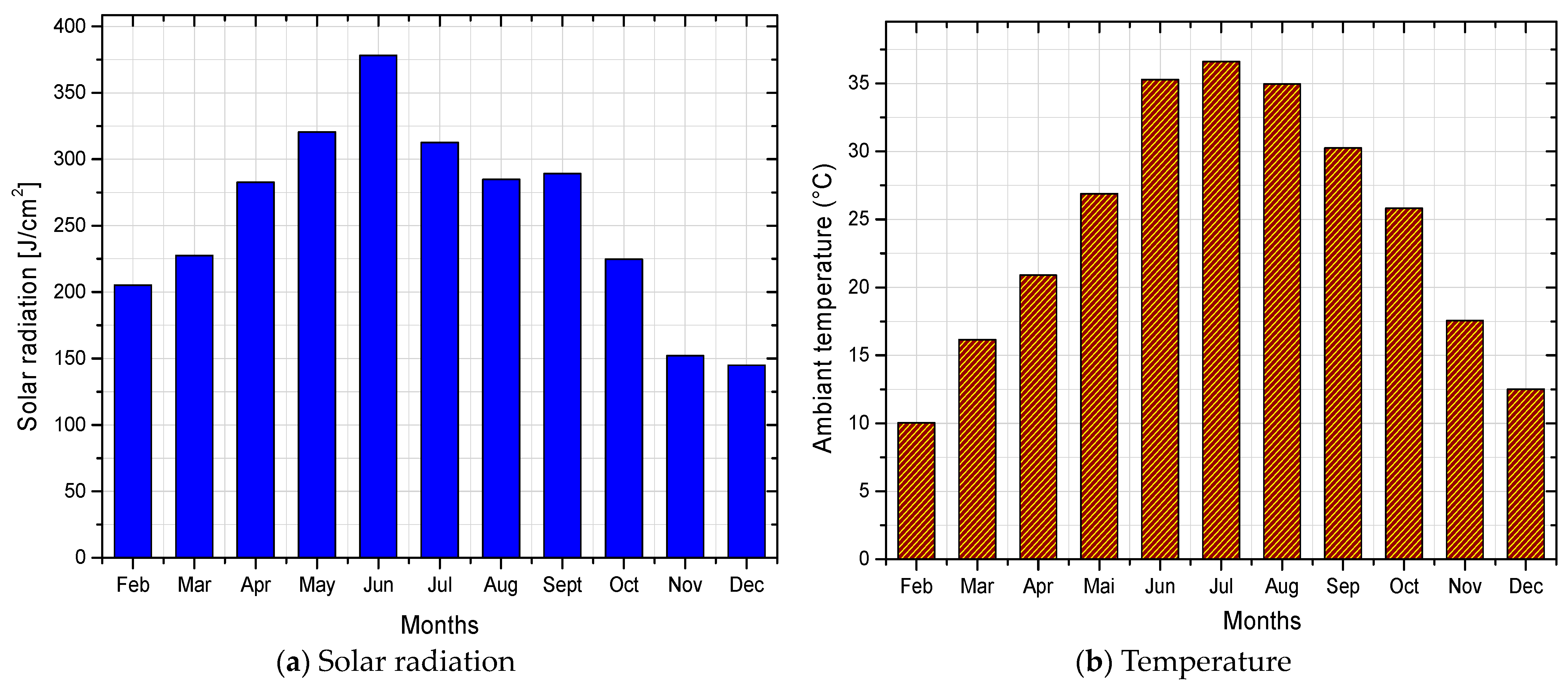
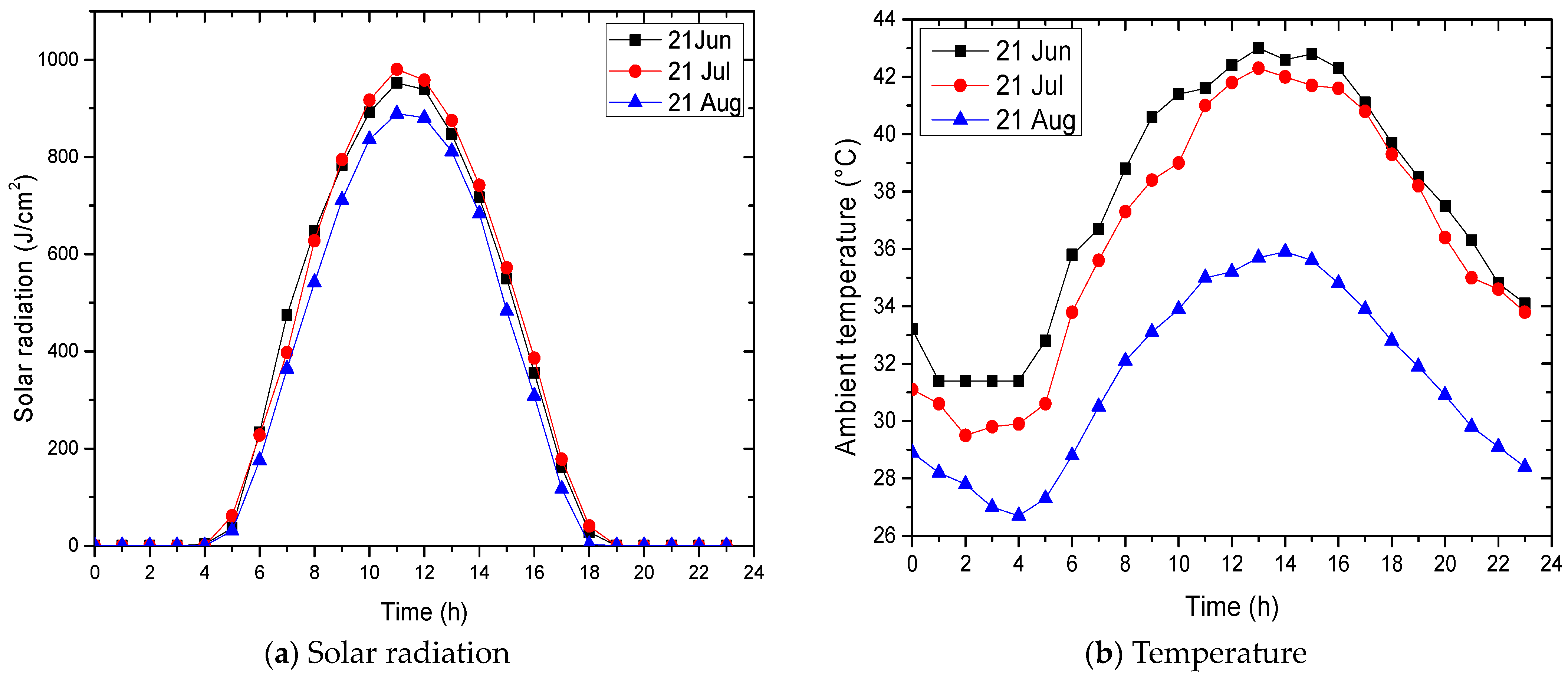
4.2. Evaluation of Solar Potential
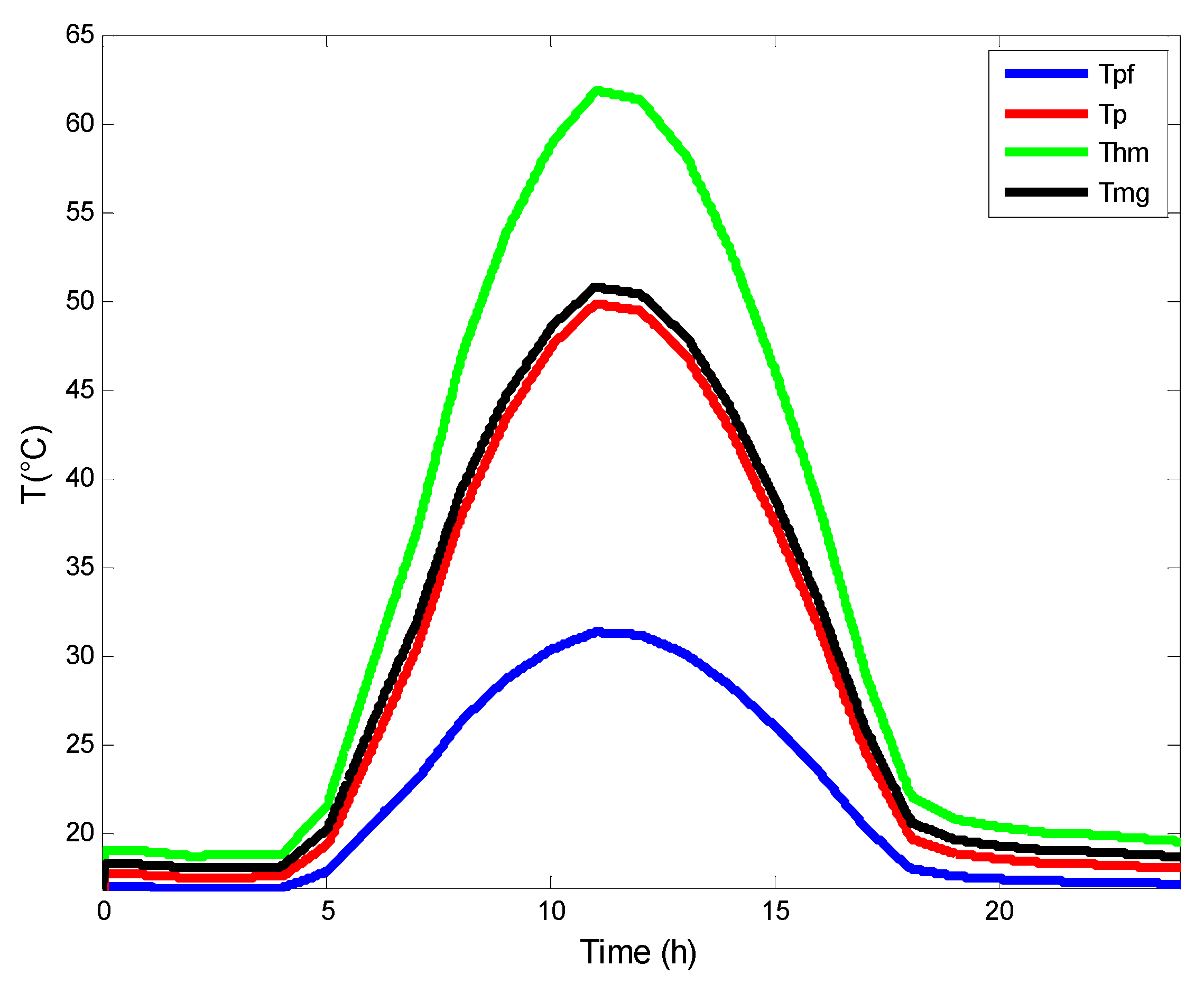
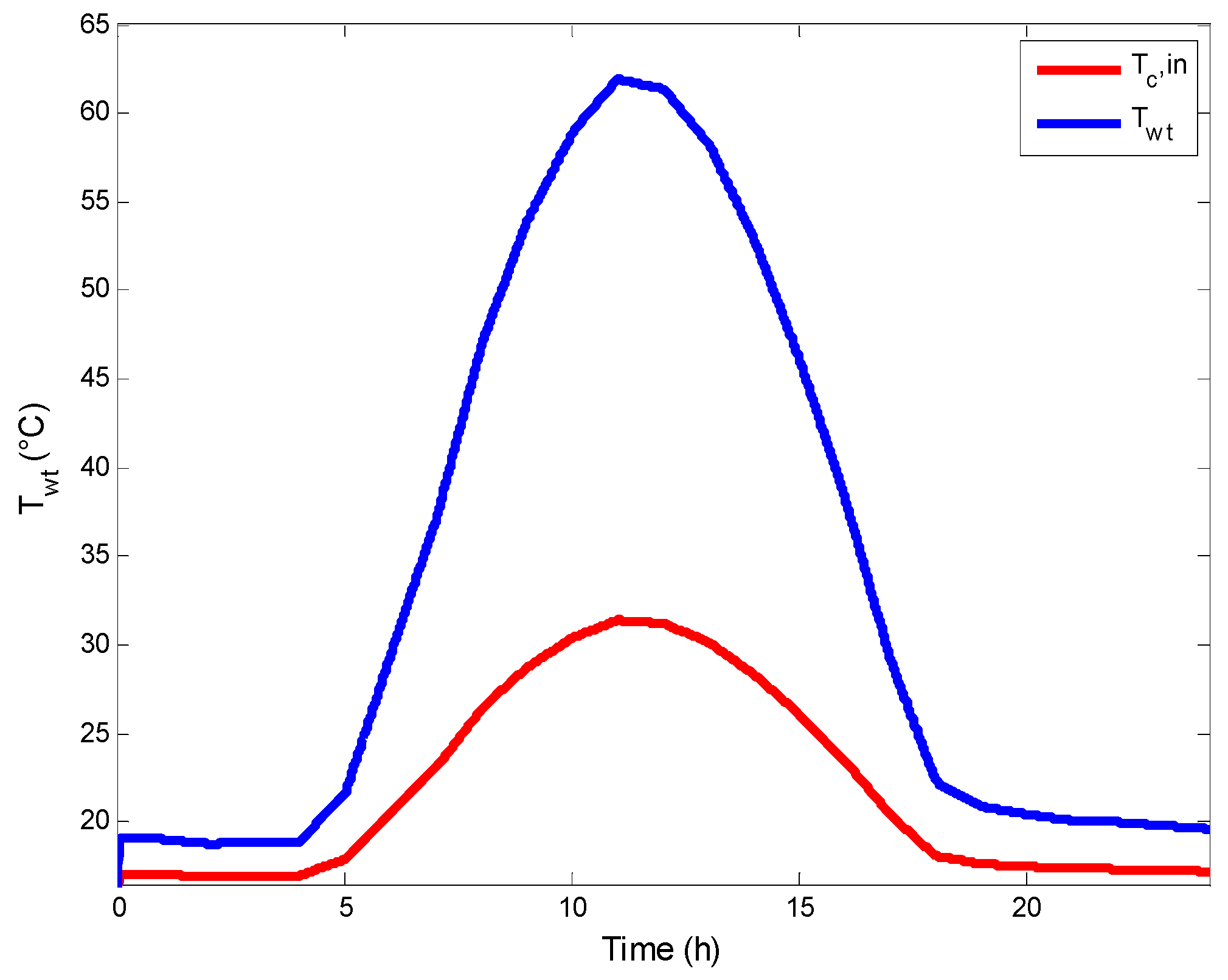
4.3. Variation of the Temperature in AGMD Unit
4.4. Variation of the Saline Water Temperature in Flat Plate Collector
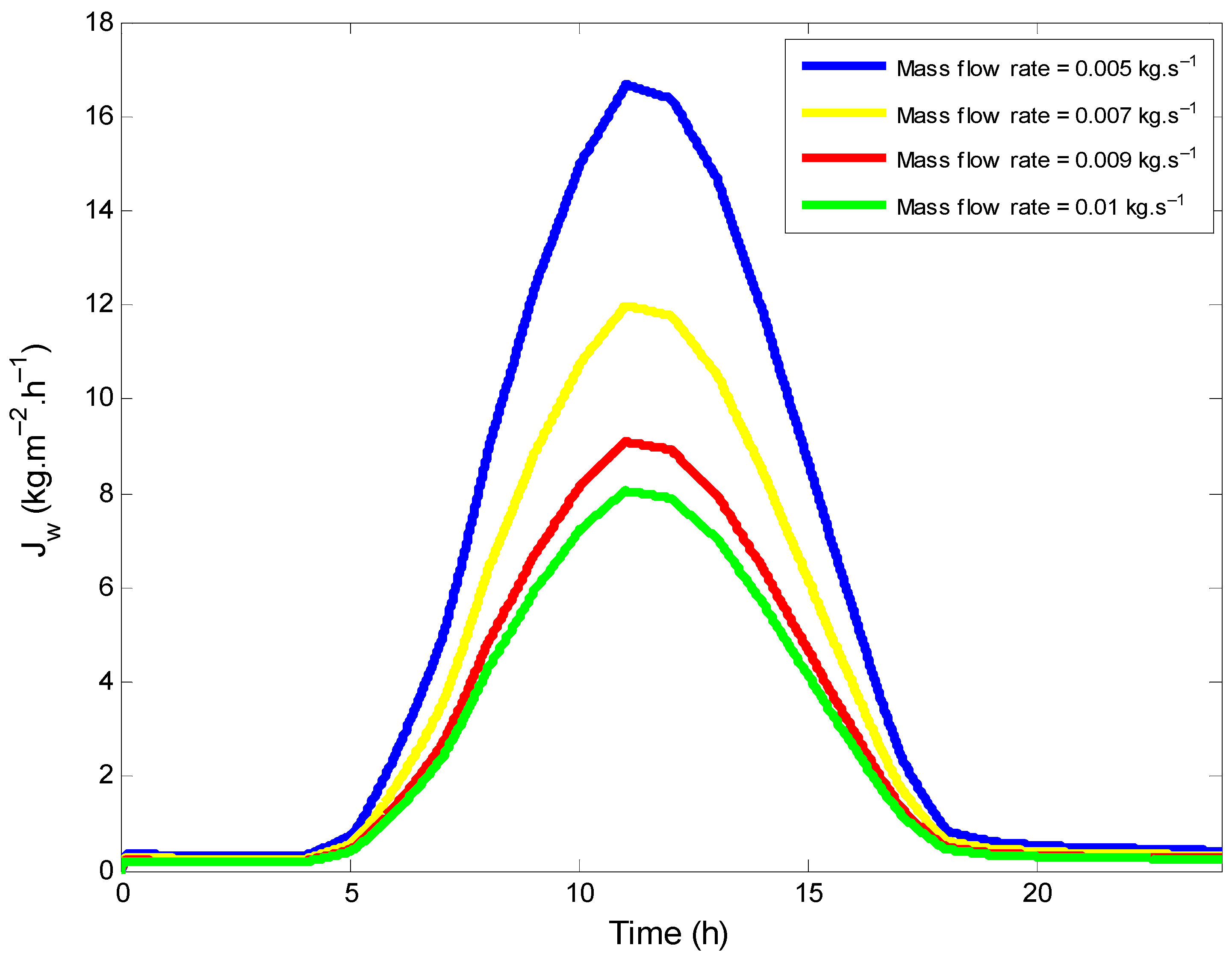
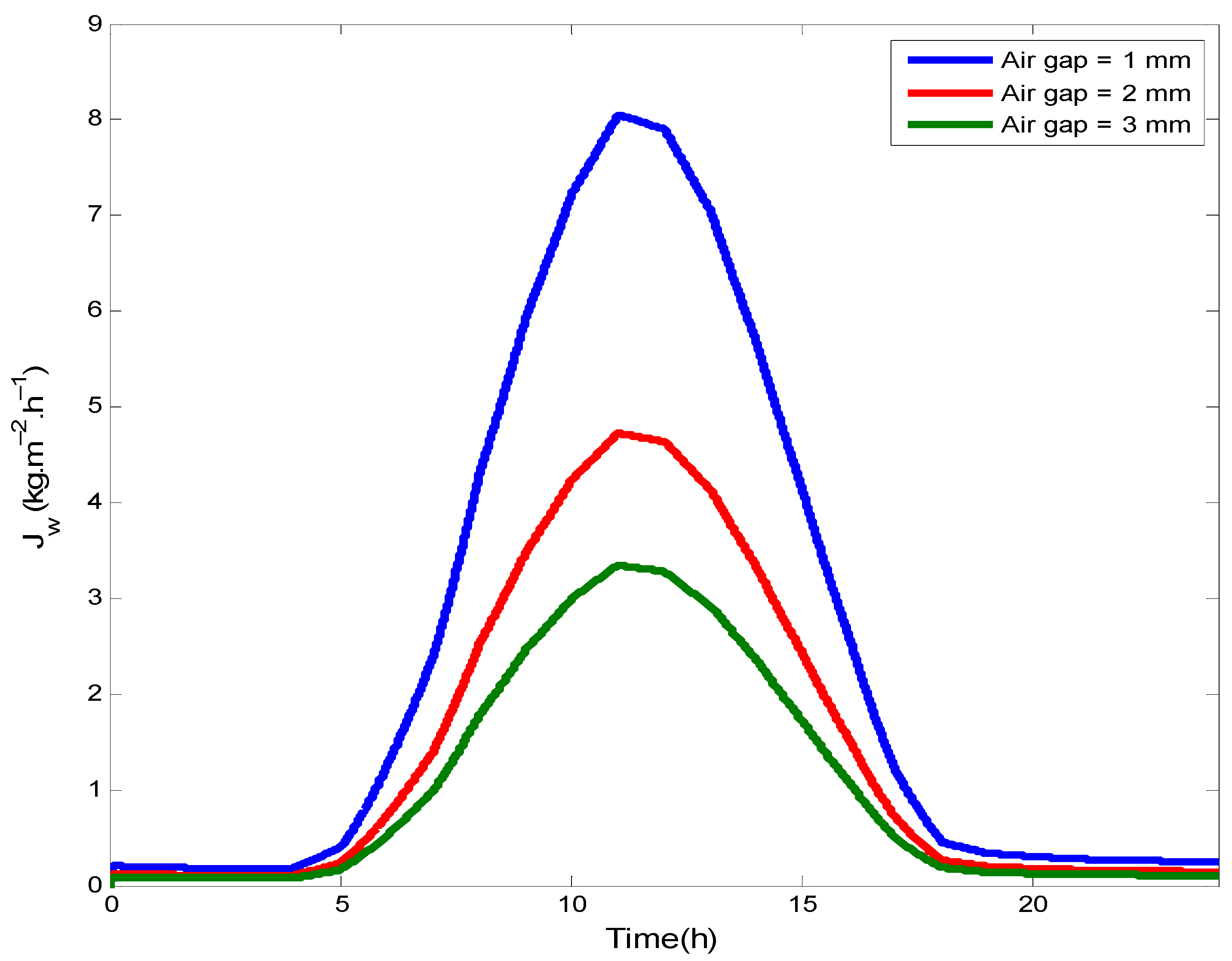
4.5. Variation of the Permeate Flux
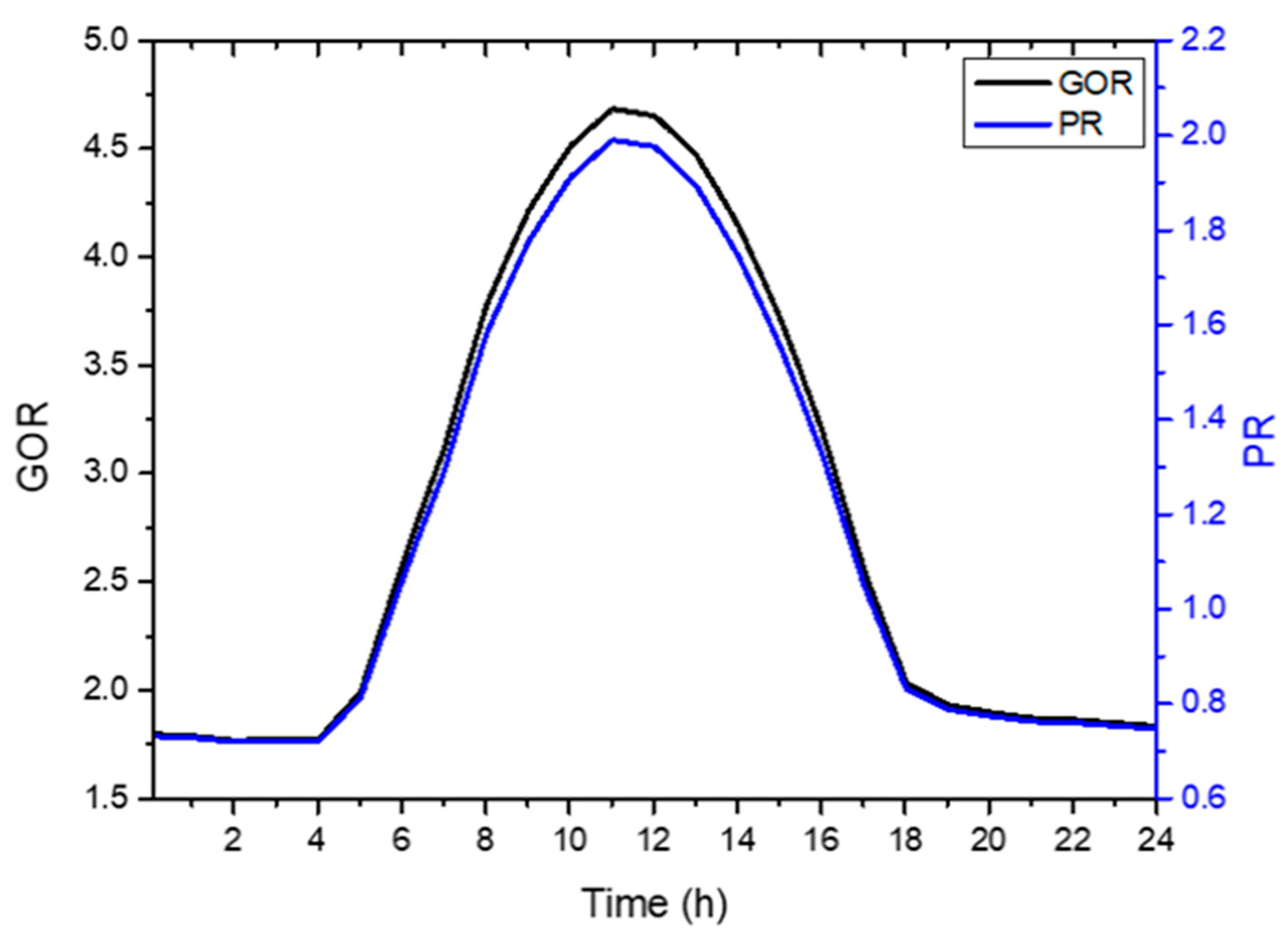
4.6. System Performance
5. Conclusions
- The variation of the temperature of the heat transfer fluid at the outlet of the solar SFPC increases gradually to reach 50 °C, which is the most used value in the literature for the AGMD process and the collector’s safety.
- An average distillate water production of 8 kg·m−2·h−1 could be achieved at 68 °C for a feed temperature and a flow rate of 1 L·min−1.
- Enhanced air gap thickness will be conducted to thermal and mass resistance, and thus a decrease in the mass flux and the thermal efficiency of the AGMD.
- The maximum GOR and PR values of 4.6 and 2, respectively, can be reached at 12:00 h corresponding to the minimum irreversible loss of the overall desalination system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | surface area [m2] | VMD | vacuum membrane distillation |
| Bw | mass transfer coefficient [kg·m−2·h−1·Pa−1] | Greek letters | |
| Cp | thermal capacity [J·kg−1·K−1] | α | activity coefficient [−] |
| Dva | thermal diffusivity of water vapour in air [m2·s−1] | β | water fraction [−] |
| dh | hydraulic diameter [m] | δ | thickness [m] |
| F | correction factor [−] | ε | porosity [−] |
| FR | heat removal factor [−] | μ | dynamic viscosity [kg·m−1·s−1] |
| GOR | gained output ratio [−] | ρ | density [kg·m−3] |
| hcc | heat transfer coefficient [W·m−2·K−1] | φ | thermal flux [W·m−2] |
| hch | convective heat transfer coefficient [W·m−2·K−1] | τ | tortuosity [−] |
| hv | enthalpy [kJ·kg−1] | Subscripts | |
| Jw | permeate flux [kg·m−2·s−1] | 0 | reference state |
| k | thermal conductivity [W·m−1·K−1] | a | air |
| L | module length [m] | ag | air gap |
| LMDT | logarithmic mean temperature difference [K] | c | cold |
| Mw | Molar mass of water [kg·mol−1] | f | feed |
| mass flow rate [kg·s−1] | h | hot | |
| MED | multiple-effect distillation | hm | hot fluid—membrane interface |
| MD | membrane distillation | in | inlet |
| MSF | multi-stage flash distillation | m | membrane |
| P | pressure [Pa] | mg | membrane—air gap interface |
| PR | Performance Ratio [−] | out | outlet |
| useful energy delivered by the solar collector [kW] | p | plate | |
| thermal flux [W·m−2] | mg | membrane—air gap interface | |
| R | thermal resistance [m2·K·W−1] | pc | cold fluid—plate interface |
| RO | reverse osmosis | r | receiver |
| s | salinity [g·kg−1] | so | source |
| T | temperature [°C] | sw | seawater |
| t | time [s] | th | thermal |
| U | heat transfer coefficient [W·m−2·K−1] | v | vapour |
References
- Kumar, A.; Saini, R.P.; Saini, J.S. A Review of Thermohydraulic Performance of Artificially Roughened Solar Air Heaters. Renew. Sustain. Energy Rev. 2014, 37, 100–122. [Google Scholar] [CrossRef]
- Bayrak, F.; Oztop, H.F.; Hepbasli, A. Energy and Exergy Analyses of Porous Baffles Inserted Solar Air Heaters for Building Applications. Energy Build. 2013, 57, 338–345. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Q.; Xiu, D.; Zhao, Z.; Sun, Q. A Building Integrated Solar Collector: All-Ceramic Solar Collector. Energy Build. 2013, 62, 15–17. [Google Scholar] [CrossRef]
- Zhai, X.Q.; Wang, R.Z.; Dai, Y.J.; Wu, J.Y.; Xu, Y.X.; Ma, Q. Solar Integrated Energy System for a Green Building. Energy Build. 2007, 39, 985–993. [Google Scholar] [CrossRef]
- Djellouli-Tabet, Y. Common Scarcity, Diverse Responses in the Maghreb Region. In Water and Sustainability in Arid Regions: Bridging the Gap Between Physical and Social Sciences; Springer: Heidelberg, Germany, 2010; pp. 87–102. [Google Scholar]
- Rabehi, A.; Guermoui, M.; Djafer, D.; Zaiani, M. Radial Basis Function Neural Networks Model to Estimate Global Solar Radiation in Semi-Arid Area. Leonardo Electron. J. Pract. Technol. 2015, 27, 177–184. [Google Scholar]
- Al-Obaidani, S.; Curcio, E.; Macedonio, F.; Di Profio, G.; Al-Hinai, H.; Drioli, E. Potential of Membrane Distillation in Seawater Desalination: Thermal Efficiency, Sensitivity Study and Cost Estimation. J. Membr. Sci. 2008, 323, 85–98. [Google Scholar] [CrossRef]
- Diaby, A.T.; Byrne, P.; Loulergue, P.; Balannec, B.; Szymczyk, A.; Maré, T.; Sow, O. Design Study of the Coupling of an Air Gap Membrane Distillation Unit to an Air Conditioner. Desalination 2017, 420, 308–317. [Google Scholar] [CrossRef]
- Banat, F.; Jwaied, N.; Rommel, M.; Koschikowski, J.; Wieghaus, M. Desalination by a “Compact SMADES” Autonomous Solarpowered Membrane Distillation Unit. Desalination 2007, 217, 29–37. [Google Scholar] [CrossRef]
- Banat, F.; Jwaied, N.; Rommel, M.; Koschikowski, J.; Wieghaus, M. Performance Evaluation of the “Large SMADES” Autonomous Desalination Solar-Driven Membrane Distillation Plant in Aqaba, Jordan. Desalination 2007, 217, 17–28. [Google Scholar] [CrossRef]
- Chafidz, A.; Al-Zahrani, S.; Al-Otaibi, M.N.; Hoong, C.F.; Lai, T.F.; Prabu, M. Portable and Integrated Solar-Driven Desalination System Using Membrane Distillation for Arid Remote Areas in Saudi Arabia. Desalination 2014, 345, 36–49. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Z.; Lior, N.; Zeng, H. An Experimental Study of Solar Thermal Vacuum Membrane Distillation Desalination. Desalin. Water Treat. 2015, 53, 887–897. [Google Scholar] [CrossRef]
- Guillén-Burrieza, E.; Zaragoza, G.; Miralles-Cuevas, S.; Blanco, J. Experimental Evaluation of Two Pilot-Scale Membrane Distillation Modules Used for Solar Desalination. J. Membr. Sci. 2012, 409, 264–275. [Google Scholar] [CrossRef]
- Suárez, F.; Tyler, S.W.; Childress, A.E. A Theoretical Study of a Direct Contact Membrane Distillation System Coupled to a Salt-Gradient Solar Pond for Terminal Lakes Reclamation. Water Res. 2010, 44, 4601–4615. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, L.; Yang, H.; Chen, H. Feasibility Research of Potable Water Production via Solar-Heated Hollow Fiber Membrane Distillation System. Desalination 2009, 247, 403–411. [Google Scholar] [CrossRef]
- Banat, F.; Jumah, R.; Garaibeh, M. Exploitation of Solar Energy Collected by Solar Stills for Desalination by Membrane Distillation. Renew. Energy 2002, 25, 293–305. [Google Scholar] [CrossRef]
- Shafieian, A.; Azhar, M.R.; Khiadani, M.; Sen, T.K. Performance improvement of thermal-driven membrane-based solar desalination systems using nanofluid in the feed stream. Sustain. Energy Technol. Assess. 2020, 39, 100715. [Google Scholar] [CrossRef]
- Qtaishat, M.R.; Banat, F. Desalination by Solar Powered Membrane Distillation Systems. Desalination 2013, 308, 186–197. [Google Scholar] [CrossRef]
- Banat, F.; Jwaied, N. Economic Evaluation of Desalination by Small-Scale Autonomous Solar-Powered Membrane Distillation Units. Desalination 2008, 220, 566–573. [Google Scholar] [CrossRef]
- Guillén-Burrieza, E.; Blanco, J.; Zaragoza, G.; Alarcón, D.-C.; Palenzuela, P.; Ibarra, M.; Gernjak, W. Experimental Analysis of an Air Gap Membrane Distillation Solar Desalination Pilot System. J. Membr. Sci. 2011, 379, 386–396. [Google Scholar] [CrossRef]
- Kubota, S.; Ohta, K.; Hayano, I.; Hirai, M.; Kikuchi, K.; Murayama, Y. Experiments on Seawater Desalination by Membrane Distillation. Desalination 1988, 69, 19–26. [Google Scholar] [CrossRef]
- Summers, E.K.; Lienhard, V.J.H. A Novel Solar-Driven Air Gap Membrane Distillation System. Desalin. Water Treat. 2013, 51, 1344–1351. [Google Scholar] [CrossRef]
- Moudjeber, D.-E.; Ruiz-Aguirre, A.; Ugarte-Judge, D.; Mahmoudi, H.; Zaragoza, G. Solar Desalination by Air-Gap Membrane Distillation: A Case Study from Algeria. Desalin. Water Treat. 2016, 57, 22718–22725. [Google Scholar] [CrossRef]
- Kumar, N.U.; Martin, A. Experimental Modeling of an Air-Gap Membrane Distillation Module and Simulation of a Solar Thermal Integrated System for Water Purification. Water Treat. 2017, 84, 123–134. [Google Scholar]
- Shirsath, G.B.; Muralidhar, K.; Pala, R.G.S. Variable Air Gap Membrane Distillation for Hybrid Solar Desalination. J. Environ. Chem. Eng. 2020, 8, 103751. [Google Scholar] [CrossRef]
- SANDİD, A.; Nehari, D.; Elmeriah, A.; Remlaoui, A. Dynamic Simulation of an Air-Gap Membrane Distillation (AGMD) Process Using Photovoltaic Panels System and Flat Plate Collectors. J. Therm. Eng. 2021, 7, 117–133. [Google Scholar] [CrossRef]
- Sandida, A.M.; Neharia, T.; Neharia, D. Simulation Study of an Air-Gap Membrane Distillation System for Seawater Desalination Using Solar Energy. Desalin. Water Treat. 2021, 229, 40–51. [Google Scholar] [CrossRef]
- Sandid, A.M.; Bassyouni, M.; Nehari, D.; Elhenawy, Y. Experimental and Simulation Study of Multichannel Air Gap Membrane Distillation Process with Two Types of Solar Collectors. Energy Convers. Manag. 2021, 243, 114431. [Google Scholar] [CrossRef]
- Thai Huynh, N.V.T.; Nguyen, T.; Manh Nguyen, Q. Optimum Design for the Magnification Mechanisms Employing Fuzzy Logic–ANFIS. Comput. Mater. Contin. 2022, 73, 5961–5983. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Nguyen, Q.M.; Huynh, N.T.; Huynh, T.T. Optimal Design for Compliant Mechanism Flexure Hinges: Bridge-Type. Micromachines 2021, 12, 1304. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Vo, N.T.M. CFD Analysis and Optimum Design for a Centrifugal Pump Using an Effectively Artificial Intelligent Algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef]
- Khalifa, A.E.; Lawal, D.U. Performance and Optimization of Air Gap Membrane Distillation System for Water Desalination. Arab. J. Sci. Eng. 2015, 40, 3627–3639. [Google Scholar] [CrossRef]
- Dudchenko, A.V.; Bartholomew, T.V.; Mauter, M.S. Cost Optimization of Multi-Stage Gap Membrane Distillation. J. Membr. Sci. 2021, 627, 119228. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Li, Y.-W.; Chang, H. Optimal Design and Control of Solar Driven Air Gap Membrane Distillation Desalination Systems. Appl. Energy 2012, 100, 193–204. [Google Scholar] [CrossRef]
- Khayet, M.; Cojocaru, C. Air Gap Membrane Distillation: Desalination, Modeling and Optimization. Desalination 2012, 287, 138–145. [Google Scholar] [CrossRef]
- Khayet, M.; Cojocaru, C. Artificial Neural Network Modeling and Optimization of Desalination by Air Gap Membrane Distillation. Sep. Purif. Technol. 2012, 86, 171–182. [Google Scholar] [CrossRef]
- He, Q.; Li, P.; Geng, H.; Zhang, C.; Wang, J.; Chang, H. Modeling and Optimization of Air Gap Membrane Distillation System for Desalination. Desalination 2014, 354, 68–75. [Google Scholar] [CrossRef]
- Diaby, A.T.; Byrne, P.; Loulergue, P.; Sow, O.; Maré, T. Experimental Study of a Heat Pump for Simultaneous Cooling and Desalination by Membrane Distillation. Membranes 2021, 11, 725. [Google Scholar] [CrossRef]
- Khalifa, A.; Ahmad, H.; Antar, M.; Laoui, T.; Khayet, M. Experimental and Theoretical Investigations on Water Desalination Using Direct Contact Membrane Distillation. Desalination 2017, 404, 22–34. [Google Scholar] [CrossRef]
- Boubakri, A.; Hafiane, A.; Al Tahar Bouguecha, S. Nitrate Removal from Aqueous Solution by Direct Contact Membrane Distillation Using Two Different Commercial Membranes. Desalin. Water Treat. 2015, 56, 2723–2730. [Google Scholar] [CrossRef]
- Irshad, M.; Yadav, A.; Singh, R.; Kumar, A. Mathematical Modelling and Performance Analysis of Single Pass Flat Plate Solar Collector. IOP Conf. Ser. Mater. Sci. Eng. 2018, 404, 012051. [Google Scholar] [CrossRef]
- Ismail, T. Study, Realization and Simulation of a Solar Collector. Ph.D. Thesis, Universite Des FreresMentouri, Constantine, Algeria, 2016. [Google Scholar]
- Terfai, A.; Chiba, Y.; Zirari, M.; Bouaziz, M.N. Numerical Simulation of a Flat-Plate Solar Collector Operating Under Open Cycle Mode of Heat Extraction. In Proceedings of the Advances in Green Energies and Materials Technology: Selected Articles from the Algerian Symposium on Renewable Energy and Materials (ASREM-2020); Springer: Heidelberg, Germany, 2021; pp. 153–158. [Google Scholar]
- Zelzouli, K.; Guizani, A.; Sebai, R.; Kerkeni, C. Solar Thermal Systems Performances versus Flat Plate Solar Collectors Connected in Series. Engineering 2012, 4, 881–893. [Google Scholar] [CrossRef]
- Koschikowski, J.; Wieghaus, M.; Rommel, M. Solar Thermal-Driven Desalination Plants Based on Membrane Distillation. Desalination 2003, 156, 295–304. [Google Scholar] [CrossRef]
- Fane, A.G.; Schofield, R.W.; Fell, C.J.D. The Efficient Use of Energy in Membrane Distillation. Desalination 1987, 64, 231–243. [Google Scholar] [CrossRef]
- Alsaadi, A.S.; Ghaffour, N.; Li, J.-D.; Gray, S.; Francis, L.; Maab, H.; Amy, G.L. Modeling of Air-Gap Membrane Distillation Process: A Theoretical and Experimental Study. J. Membr. Sci. 2013, 445, 53–65. [Google Scholar] [CrossRef]
- Banat, F.A. Membrane Distillation for Desalination and Removal of Volatile Organic Compounds from Water. Ph.D. Thesis, McGill University, Montreal, QC, Canada, 1994. [Google Scholar]
- Garci-Payo, M.C. MA Lzquierdo-Gill and C. Fernandez-Pineda. J. Membr. Sci 2000, 169, 61. [Google Scholar]
- Safavi, M.; Mohammadi, T. High-Salinity Water Desalination Using VMD. Chem. Eng. J. 2009, 149, 191–195. [Google Scholar] [CrossRef]
- Martinez-Diez, L.; Florido-Diaz, F.J.; Vazquez-Gonzalez, M.I. Study of Evaporation Efficiency in Membrane Distillation. Desalination 1999, 126, 193–198. [Google Scholar] [CrossRef]
- Schofield, R.W.; Fane, A.G.; Fell, C.J.D.; Macoun, R. Factors Affecting Flux in Membrane Distillation. Desalination 1990, 77, 279–294. [Google Scholar] [CrossRef]
- Yun, Y.; Ma, R.; Zhang, W.; Fane, A.G.; Li, J. Direct Contact Membrane Distillation Mechanism for High Concentration NaCl Solutions. Desalination 2006, 188, 251–262. [Google Scholar] [CrossRef]
- Gairaa, K.; Bakelli, Y. Solar Energy Potential Assessment in the Algerian South Area: Case of Ghardaïa Region. J. Renew. Energy 2013, 2013, 496348. [Google Scholar] [CrossRef]
- Al-Zoubi, H.; Al-Amri, F.; Khalifa, A.E.; Al-Zoubi, A.; Muhammad, A.; Ebtehal, Y.; Mallick, T.K. A Comprehensive Review of Air Gap Membrane Distillation Process. Desalin. Water Treat. 2018, 110, 27–64. [Google Scholar] [CrossRef]
- Rahimi-Ahar, Z.; Hatamipour, M.S.; Ahar, L.R. Air Humidification-Dehumidification Process for Desalination: A Review. Prog. Energy Combust. Sci. 2020, 80, 100850. [Google Scholar] [CrossRef]
- Zheng, H. Solar Energy Desalination Technology; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 0-12-809422-2. [Google Scholar]
- De Andrés, M.C.; Doria, J.; Khayet, M.; Peña, L.; Mengual, J.I. Coupling of a Membrane Distillation Module to a Multieffect Distiller for Pure Water Production. Desalination 1998, 115, 71–81. [Google Scholar] [CrossRef]
- Camacho, L.M.; Dumée, L.; Zhang, J.; Li, J.; Duke, M.; Gomez, J.; Gray, S. Advances in Membrane Distillation for Water Desalination and Purification Applications. Water 2013, 5, 94–196. [Google Scholar] [CrossRef]
- Alquraish, M.M.; Mejbri, S.; Abuhasel, K.A.; Zhani, K. Experimental Investigation of a Pilot Solar-Assisted Permeate Gap Membrane Distillation. Membranes 2021, 11, 336. [Google Scholar] [CrossRef]



| MD Type | Membrane Type | Pore Size | Solution | Feed Teperature (°C) | Jw (kg·m−2·h−1) | Reference |
|---|---|---|---|---|---|---|
| AGMD | PVDF | 0.22 | Methanol/water | 50 | ≈3.9–4.6 | [49] |
| AGMD | PTFE | 0.2 | NaCl | 65 | ≈7 | [8] |
| AGMD | PTFE | 0.2 | NaCl | 80 | ≈6.5 | [47] |
| VMD | PP | 0.2 | NaCl | 55 | ≈10.7–7.0 | [50] |
| DCMD | PTFE | 0.2 | NaCl | 31 | ≈32.4–25.2 | [51] |
| DCMD | PVDF | 0.4 | NaCl | 81 | ≈44–63 | [52] |
| DCMD | PVDF | 0.22 | NaCl | 68 | ≈36–28.8 | [53] |
| AGMD | PTFE | 0.2 | NaCl | 65 | 7.03 | Current study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mibarki, N.; Triki, Z.; Belhadj, A.-E.; Tahraoui, H.; Zamouche, M.; Kebir, M.; Amrane, A.; Zhang, J.; Mouni, L. An Effective Standalone Solar Air Gap Membrane Distillation Plant for Saline Water Desalination: Mathematical Model, Optimization. Water 2023, 15, 1141. https://doi.org/10.3390/w15061141
Mibarki N, Triki Z, Belhadj A-E, Tahraoui H, Zamouche M, Kebir M, Amrane A, Zhang J, Mouni L. An Effective Standalone Solar Air Gap Membrane Distillation Plant for Saline Water Desalination: Mathematical Model, Optimization. Water. 2023; 15(6):1141. https://doi.org/10.3390/w15061141
Chicago/Turabian StyleMibarki, Nawel, Zakaria Triki, Abd-Elmouneïm Belhadj, Hichem Tahraoui, Meriem Zamouche, Mohammed Kebir, Abdeltif Amrane, Jie Zhang, and Lotfi Mouni. 2023. "An Effective Standalone Solar Air Gap Membrane Distillation Plant for Saline Water Desalination: Mathematical Model, Optimization" Water 15, no. 6: 1141. https://doi.org/10.3390/w15061141
APA StyleMibarki, N., Triki, Z., Belhadj, A.-E., Tahraoui, H., Zamouche, M., Kebir, M., Amrane, A., Zhang, J., & Mouni, L. (2023). An Effective Standalone Solar Air Gap Membrane Distillation Plant for Saline Water Desalination: Mathematical Model, Optimization. Water, 15(6), 1141. https://doi.org/10.3390/w15061141








