Simulation of an Oxic-Settling-Anaerobic Pilot Plant Operated under Real Conditions Using the Activated Sludge Model No.2d
Abstract
:1. Introduction
2. Materials and Methods
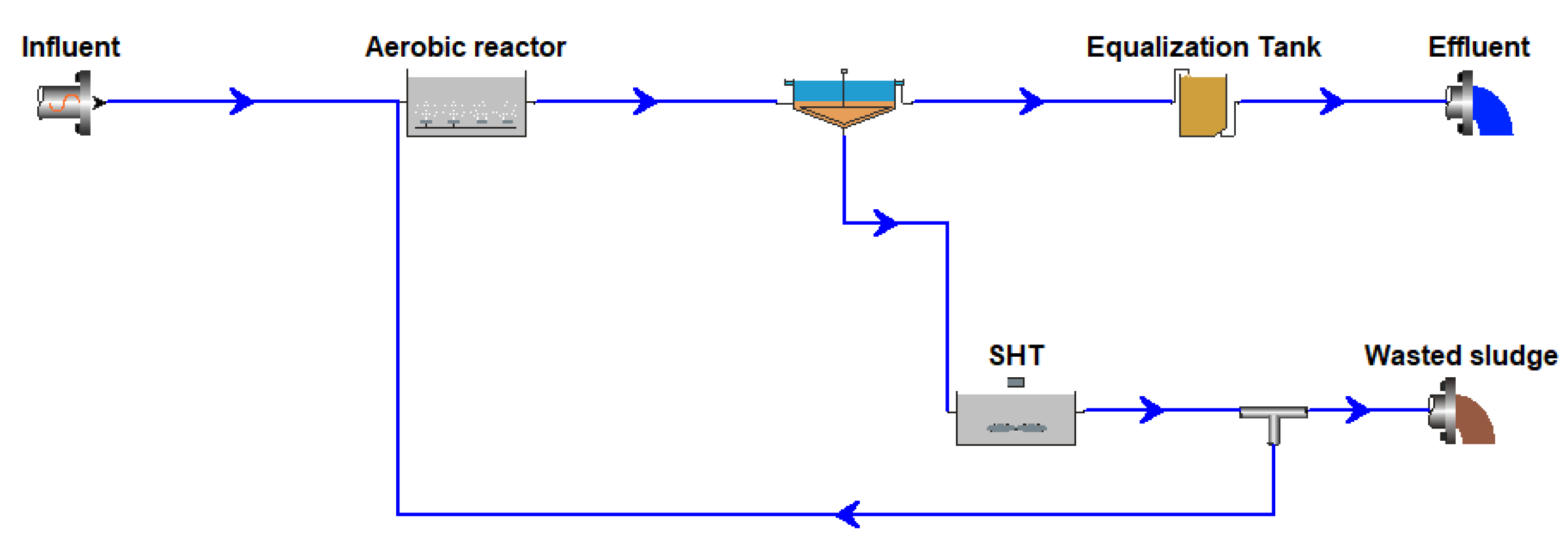
2.1. OSA Pilot Plant Operation
- -
- An aerobic reactor, with a variable volume of 0.5–1.08 m3. In the aerobic reactor, the aeration and the mixing were provided by four air diffusers. It was continuously fed by gravity from an influent reservoir with a volume of 0.373 m3;
- -
- A settling tank with a volume of 0.8 m3; and
- -
- An anoxic/anaerobic sludge holding tank (SHT) of 2.0 m3, where the total sludge flowrate from the settler was recirculated. The SHT was equipped of a mechanical stirrer to maintain the sludge suspended with homogeneous composition.
2.2. Mathematical Modeling Using the Activated Sludge Model No.2d
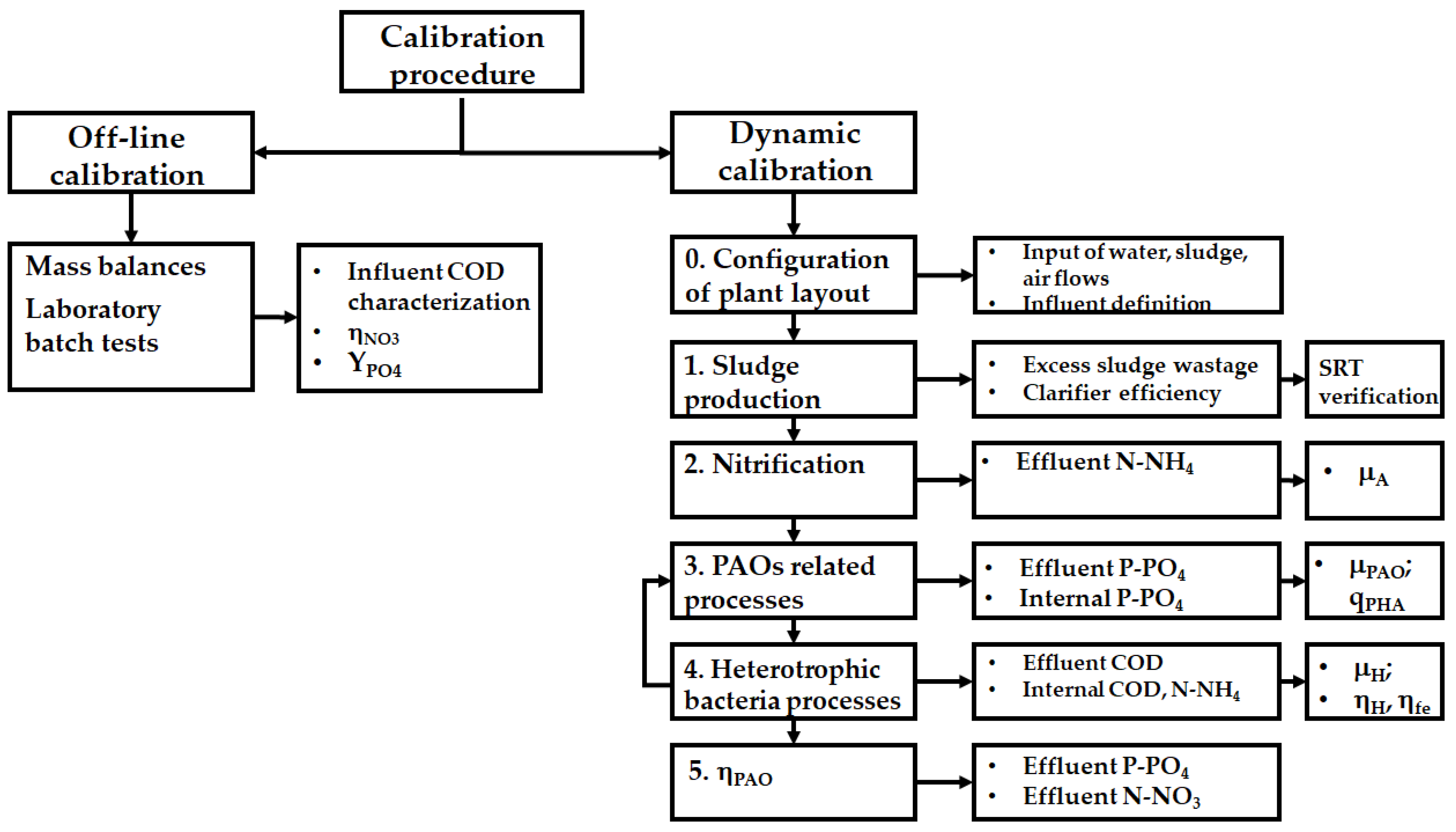
2.3. System Calibration Methodology
- The COD fractions;
- The reduction factor for heterotrophic denitrification, ηNO3; and
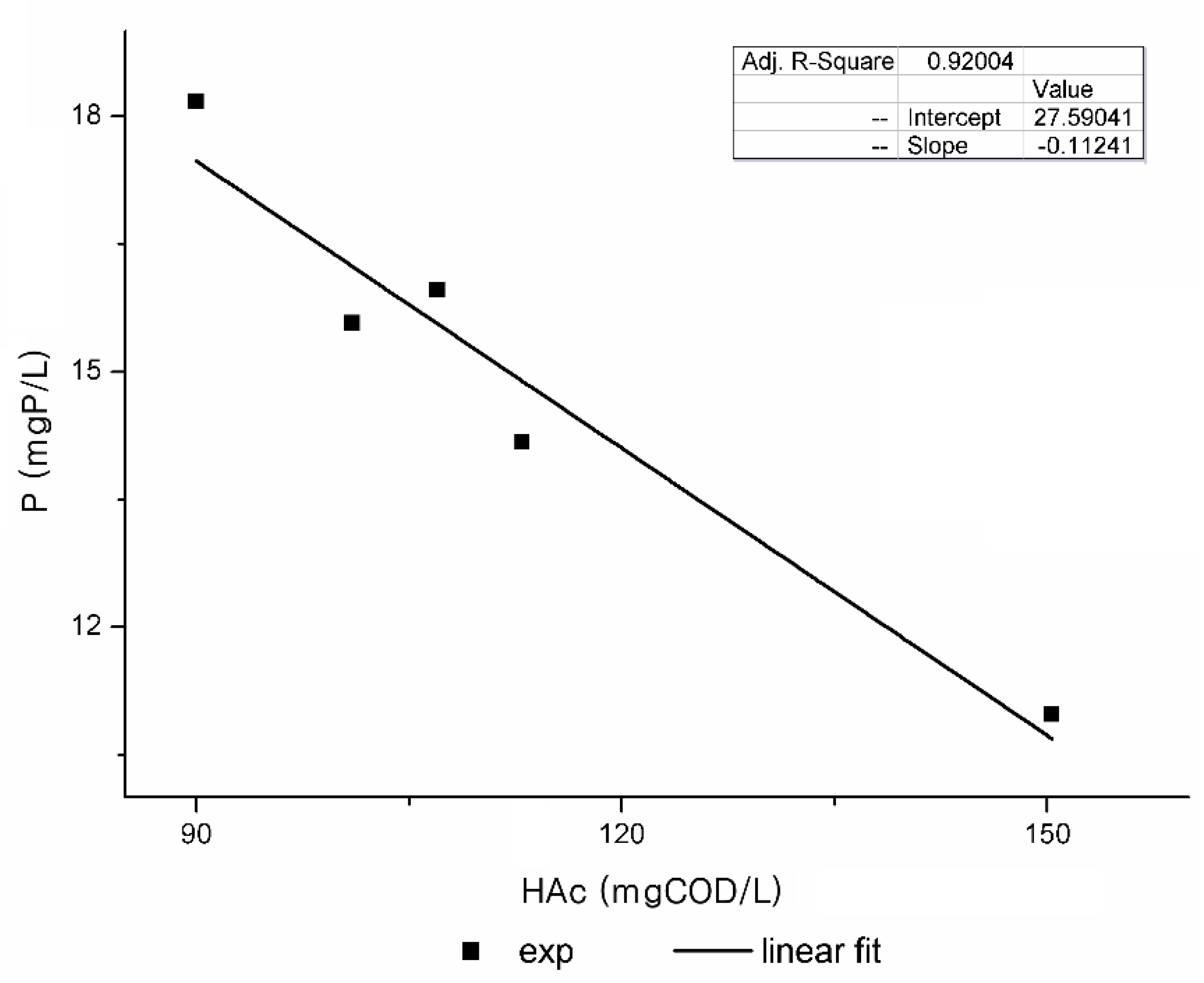
- The amount of P released per g of PHA stored, YPO4 (g P/g COD).
- The maximum growth rate of autotrophic organisms μA (d−1);
- The rate constant for storage of XPHA (base XPP) qPHA (d−1);
- The maximum growth rate of PAOs, μPAO (d−1), and the reduction factor for PAOs anoxic activity, ηPAO;
- The anoxic hydrolysis reduction factor, ηH, and the anaerobic hydrolysis reduction factor, ηfe; and
- The maximum heterotrophic growth rate μH (d−1).
2.3.1. Off-Line Calibration
- SA, represents the fermentation products (while it is assumed to be acetate, it encompasses a whole range of other fermentation products);
- SF is the fermentable readily biodegradable organic substrates;
- SI stands for the inert soluble organic material;
- XS represents the slowly biodegradable organic substrates (particulate); and
- XI represents the inert particulate organic substrates.
- The total COD (tCOD) was determined analyzing the un-filtrated samples with HACH test cuvettes according with the Reactor Digestion Method approved by USEPA [20];
- The soluble COD (sCOD) was determined in the same manner of tCOD, but analyzing samples filtrated at 0.45 μm;
- The particulate COD was calculated by the difference between the total and the soluble COD;
- The biodegradable COD was determined by mass balances in respirometric tests performed with real wastewater;
- The non-biodegradable COD was found by the difference between tCOD and bioCOD;
- The inert soluble SI was esteemed by a respirometric test performed with real filtered wastewater and addition of allylthiourea (ATU) to avoid nitrification. Although the SI fraction is usually assumed being equal to effluent soluble COD (or at least as a fraction of it), in this work, it was established to not consider the effluent soluble COD concentration since its value could be influenced by the hydrolysis processes occurring into SHT;
- The inert particulate XI fraction was obtained by the Equation (5); and
- The soluble biodegradable fraction, given by the sum of SF and SA, was obtained by the Equation (2).
2.3.2. BioWin Dynamic Calibration
- mi is the measured value of the given pollutant effluent concentration;
- pi is the correspondent BioWin simulated value; and
- N is the number of observations.
3. Results and Discussion
4. Conclusions
- The values of reduction factor accounting for processes accomplished in anoxic and anaerobic conditions—ηNO3, ηPAO, ηH, and ηfe—were found lower than those proposed by ASM2d, indicating that in the sludge holding tank, the reactions proceeded generally with slower kinetics.
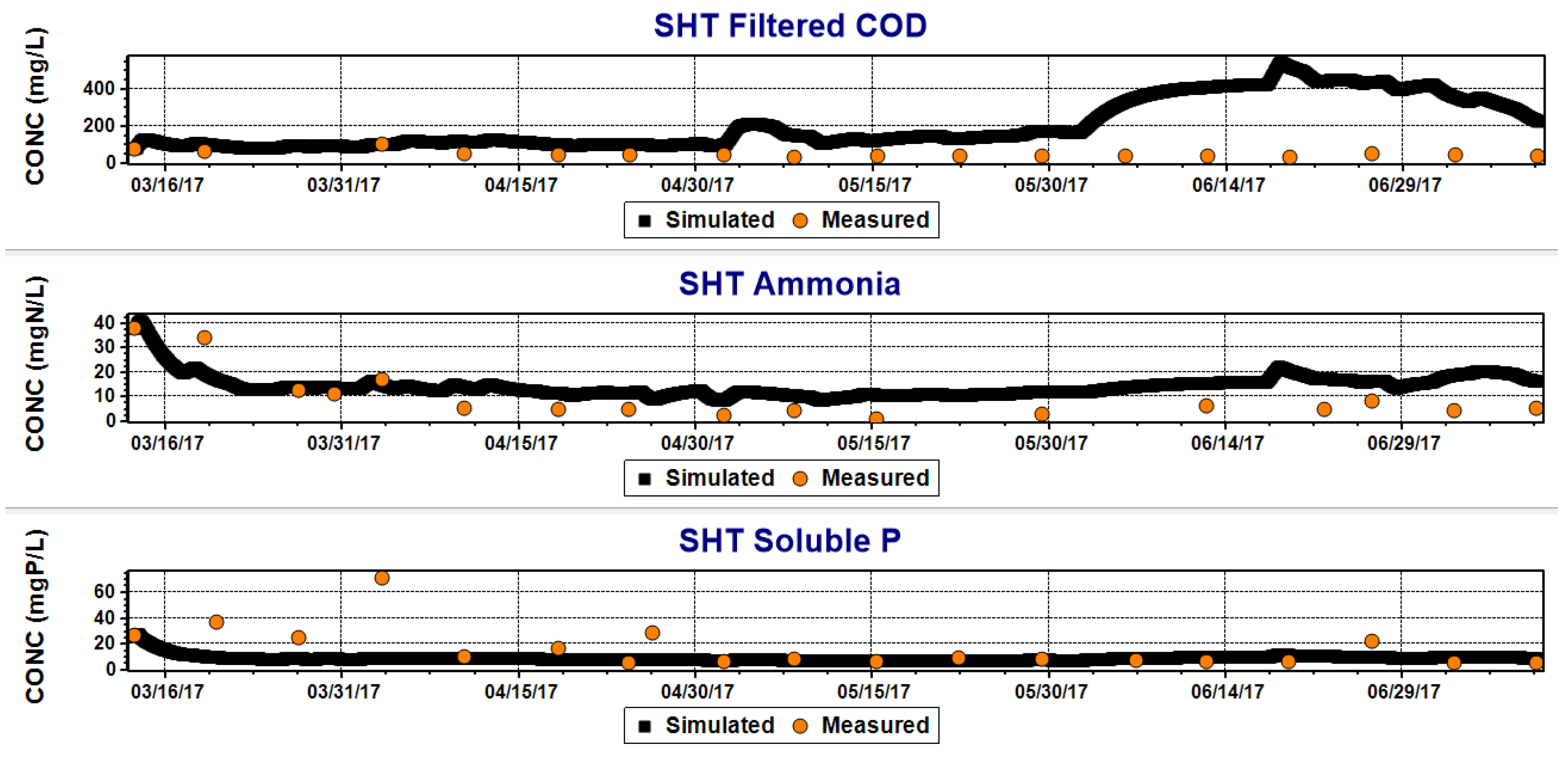
- Good reproducibility of soluble P concentrations was obtained with adjusted parameters of Activated Sludge Model No.2d as regards both the effluent and the trend inside the SHT.
- The simulation of the ammonia concentrations was satisfying except for period III of operations when a relevant ammonia accumulation was noticed in the system. On that occasion, the simulated values diverged from the measured one, showing a failure of the simulation.
- Some issues were observed in COD simulation, but it is unclear whether they are due to a failure in simulating the hydrolysis into the SHT or in simulating the effects of single peaks in influent concentration.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Description |
| ASM | Activated sludge model |
| CAS | Conventional activated sludge |
| COD | Chemical oxygen demand |
| EPS | Extracellular polymeric substances |
| HRT | Hydraulic retention time |
| MLSS | Mixed liquor suspended solids |
| MLVSS | Mixed liquor volatile suspended solids |
| ORP | Oxidation reduction potential |
| OSA | Oxic settling anaerobic |
| PAO | Polyphosphate accumulating organism |
| PHA | Polyhydroxyalkanoates |
| QIN | Influent flowrate |
| QOUT | Effluent flowrate |
| QR | Return flowrate |
| sCOD | Soluble chemical oxygen demand |
| SRT | Solids retention time |
| SS | Suspended solids |
| SVI | Sludge volume index |
| T | Temperature |
| VAER | Volume of the aerobic reactor |
| WWTP | Wastewater treatment plant |
| Yobs | Observed yield |
References
- Vitanza, R.; Cortesi, A.; De Arana-Sarabia, M.E.; Gallo, V.; Vasiliadou, I.A. Oxic settling anaerobic (OSA) process for excess sludge reduction: 16 months of management of a pilot plant fed with real wastewater. J. Water Process. Eng. 2019, 32, 100902. [Google Scholar] [CrossRef]
- Chudoba, P.; Morel, A.; Capdeville, B. The case of both energetic uncoupling and metabolic selection of microorganisms in the OSA activated sludge system. Environ. Technol. 1992, 13, 761–770. [Google Scholar] [CrossRef]
- Martins, C.L.; Velho, V.F.; Magnus, B.S.; Xavier, J.A.; Guimarães, L.B.; Leite, W.R.; Costa, R.H.R. Assessment of sludge reduction and microbial dynamics in an OSA process with short anaerobic retention time. Environ. Technol. Innov. 2020, 19, 101025. [Google Scholar] [CrossRef]
- Demir, Ö.; Filibeli, A. The investigation of the sludge reduction efficiency mechanisms in oxic–settling–anaerobic (OSA) process. Water Sci. Technol. 2017, 73, 2311–2323. [Google Scholar] [CrossRef] [PubMed]
- Velho, V.F.; Foladori, P.; Andreottola, G.; Costa, R.H.R. Anaerobic side-stream reactor for excess sludge reduction: 5-year management of a full-scale plant. J. Environ. Manag. 2016, 177, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhao, Q.; Jin, W.; Lin, J. Mechanism on minimization of excess sludge in oxic-settling anaerobic (OSA) process. Front. Environ. Sci. Eng. China 2008, 2, 36–43. [Google Scholar] [CrossRef]
- Corsino, S.F.; Capodici, M.; Di Trapani, D.; Torregrossa, M.; Viviani, G. Combination of the OSA process with thermal treatment at moderate temperature for excess sludge minimization. Bioresour. Technol. 2020, 300, 122679. [Google Scholar] [CrossRef] [PubMed]
- Nazif, S.; Mehrdadi, N.; Zare, S.; Mosavari, S. Improvement and prediction of OSA system performance in sludge reduction through integration with thermal and mechanical treatment. Water Sci. Technol. 2016, 74, 2087–2096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Romero-Pareja, P.M.; Aragon-Cruz, C.A.; Quiroga-Alonso, J.M.; Coello-Oviedo, M.D. Incorporating the Oxic-Settling-Anaerobic (OSA) process into an anoxic–oxic-system for sewage sludge reduction and nutrient removal. Environ. Prog. Sustain. Energy 2017, 37, 1068–1074. [Google Scholar] [CrossRef]
- Saby, S.; Djafer, M.; Chen, G.H. Effect of low ORP in anoxic sludge zone on excess sludge production in oxic-settling-anoxic activated sludge process. Water Res. 2003, 37, 11–20. [Google Scholar] [CrossRef]
- Semblante, G.U.; Hai, F.I.; Ngo, H.H.; Guo, W.; You, S.J.; Price, W.E.; Nghiem, L.D. Sludge cycling between aerobic, anoxic and anaerobic regimes to reduce sludge production during wastewater treatment: Performance, mechanisms, and implications. Bioresour. Technol. 2014, 155, 395–409. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Foladori, P.; Velho, V.F.; Costa, R.H.R.; Bruni, L.; Quaranta, A.; Andreottola, G. Concerning the role of cell lysis-cryptic growth in anaerobic side-stream reactors: The single-cell analysis of viable, dead and lysed bacteria. Water Res. 2015, 74, 132–142. [Google Scholar] [CrossRef] [PubMed]
- Yağci, N.; Pala-Özkök, Í.; Sarialioğlu, F.; Alli, B.; Artan, N.; Orhon, D.; Sözen, S. Respirometric anatomy of the OSA process: Microbial basis of enhanced sludge reduction mechanism. J. Chem. Technol. Biotechnol. 2018, 93, 3462–3471. [Google Scholar] [CrossRef]
- Henze, M.; Grady, C.P.L., Jr.; Gujer, W.; Marais, G.v.R.; Matsuo, T. Activated Sludge Model No. 1., IAWPRC Scientific and Technical Report No. 1; IAWPRC: London, UK, 1987. [Google Scholar]
- Ferrentino, R.; Langone, M.; Villa, R.; Andreottola, G. Strict anaerobic side-stream reactor: Effect of the sludge interchange ratio on sludge reduction in a biological nutrient removal process. Environ. Sci. Pollut. Res. 2018, 25, 1243–1256. [Google Scholar] [CrossRef] [PubMed]
- Henze, M.; Gujer, W.; Mino, T.; Matsuo, T.; Wentzel, M.C.; Marais, G.v.R. Activated Sludge Model No. 2., IAWQ Scientific and Technical Report No. 3; IAWQ: London, UK, 1995. [Google Scholar]
- Henze, M.; Gujer, W.; Mino, T.; Matsuo, T.; Wentzel, M.C.; Marais, G.v.R.; van Loosdrecht, M.C.M. Activated Sludge Model No.2d. Water Sci. Technol. 1999, 39, 165–182. [Google Scholar] [CrossRef]
- Henze, M.; Gujer, W.; Mino, T.; van Loosdrecht, M. Activated Sludge Models, ASM1, ASM2, ASM2d and ASM3. Scientific and Technical Report (Volume 5); IWA Publishing: London, UK, 2000. [Google Scholar] [CrossRef]
- Garcıa-Usach, F.; Ribes, J.; Ferrer, J.; Seco, A. Calibration of denitrifying activity of polyphosphate accumulating organisms in an extended ASM2d model. Water Res. 2010, 44, 5284–5297. [Google Scholar] [CrossRef] [PubMed]
- HACH DR/2010 Spectrophotometer Handbook; Hach Company: Loveland, CO, USA, 1999.
- van Veldhuizen, H.M.; van Loosdrecht, M.C.M.; Heijnen, J.J. Modelling biological phosphorus and nitrogen removal in a full scale activated sludge process. Water Res. 1999, 33, 3459–3468. [Google Scholar] [CrossRef]
- Drewnowski, J.; Makinia, J.; Szaja, A.; Łagód, G.; Kopeć, Ł. Comparative Study of Balancing SRT by Using Modified ASM2d in Control and Operation Strategy at Full-Scale WWTP. Water 2019, 11, 485. [Google Scholar] [CrossRef] [Green Version]
- Vanrolleghem, P.A.; Insel, G.; Petersen, B.; Sin, G.; De Pauw, D.; Nopens, I.; Weijers, S.; Gernaey, K. A comprehensive model calibration procedure for activated sludge models. In Proceedings of the 76th Annual WEF Technical Exhibition and Conference (WEFTEC2003), Los Angeles, CA, USA, 11–15 October 2003. [Google Scholar]
- Larrea, L.; Irizar, I.; Hidalgo, M.E. Improving the predictions of ASM2d through modelling in practice. Water Sci. Technol. 2002, 45, 199–208. [Google Scholar] [CrossRef]

| I | II | III | IV | V | VI | ||
|---|---|---|---|---|---|---|---|
| QIN | (m3/d) | 1.44 | 1.47 | 1.47 | 1.47 | 1.47 | 1.44 |
| QR | (m3/d) | 3.02 | 3.02 | 3.02 | 2.04 | 2.04 | 2.04 |
| VAER | (m3) | 0.50 | 0.50 | 0.50 | 0.88 | 0.88 | 0.88 |
| SRT | (d) | 201 | 37 | 81 | 92 | 65 | 406 |
| SS | (mg SS/L) | 111.0 ± 79.1 | 178.0 ± 70.7 | 114.4 ± 136.6 | 137.5 ± 108.8 | 70.7 ± 77.9 | 143.3 ± 167.1 |
| COD | (mg COD/L) | 260.0 ± 94.0 | 293.0 ± 59.1 | 228.0 ± 81.6 | 340.0 ± 289.8 | 213.0 ± 149.0 | 332.4 ± 235.0 |
| sCOD | (mg COD/L) | 106.0 ± 37.5 | 131.0 ± 27.7 | 109.0 ± 62.0 | 105.0 ± 28.1 | 83.6 ± 90.9 | 106.4 ± 17.7 |
| N-NH4 | (mg N/L) | 27.3 ± 9.8 | 36.7 ± 5.7 | 32.3 ± 15.2 | 26.6 ± 12.2 | 20.1 ± 3.6 | 19.7 ± 9.2 |
| N-NO3 | (mg N/L) | 2.2 ± 0.7 | 5.4 ± 1.4 | 3.2 ± 1.3 | 2.0 ± 1.4 | 0.8 ± 0.8 | 0.4 ± 0.5 |
| P-PO4 | (mg P/L) | 2.5 ± 1.7 | 4.3 ± 0.9 | 4.0 ± 1.5 | 4.0 ± 1.4 | 3.7 ± 2.1 | 2.4 ± 1.2 |
| MLSS | (mg SS/L) | 3198 ± 476 | 3120 ± 659 | 3016 ± 262 | 2452 ± 700 | 1432 ± 208 | 1720 ± 833 |
| MLVSS | (mg VSS/L) | 2279 ± 374 | 2423 ± 434 | 2492 ± 224 | 1968 ± 583 | 1048 ± 259 | 1553 ± 648 |
| ORP | (mV) | +73 | +53 | +7 | +133 | +148 | +153 |
| T | (°C) | 20.5 | 10.3 | 12.8 | 18.0 | 27.7 | 20.1 |
| SS | (mg SS/L) | 4461 ± 813 | 3427 ± 587 | 3748 ± 395 | 3808 ± 487 | 2128 ± 420 | 2563 ± 1294 |
| VSS | (mg VSS/L) | 3032 ± 561 | 2733 ± 379 | 3172 ± 364 | 2992 ± 479 | 1604 ± 289 | 2002 ± 857 |
| pH | - | 7.2 | 7.2 | 6.9 | 7.1 | 7.4 | 6.9 |
| ORP | (mV) | −227 | −331 | −411 | −323 | −56 | −140 |
| T | (°C) | 22.3 | 11.1 | 14.5 | 20.0 | 30.3 | 22.1 |
| Yobs | (g TSS/g COD) | 0.465 | 0.366 | 0.457 | 0.246 | 0.112 | 0.318 |
| SVI | (mL/g TSS) | 97 | 126 | 217 | 198 | 73 | 85 |
| Parameter | Unit | Calibrated | Default ASM2d |
|---|---|---|---|
| ηNO3 | - | 0.46 (a) | 0.80 |
| YPO4 | gP/gCOD | 0.112 (a) | 0.40 |
| μA | d−1 | 1.40 (b) | 1.00 |
| μH | d−1 | 1.88 (b) | 6.00 |
| μPAO | d−1 | 1.23 (b) | 1.00 |
| qPHA | d−1 | 0.57 (b) | 3.00 |
| ηh | - | 0.30 (b) | 0.60 |
| ηfe | - | 0.20 (b) | 0.40 |
| ηPAO * | - | 0.07–0.16 | 0.60 |
| RSME (Effluent Concentrations) | RSME (SHT Concentrations) | |||||||
|---|---|---|---|---|---|---|---|---|
| Period | SRT Calculated | COD | N-NH4 | N-NO3 | P-PO4 | COD | N-NH4 | P-PO4 |
| I | 218 | 16.8 | 2.3 | 4.5 | 2.3 | 20.6 | 5.6 | 5.5 |
| II | 38 | 14.1 | 16.9 | 7.2 | 2.1 | 21.2 | 15.3 | 3.0 |
| III | 78 | 24.7 | 29.2 | 9.7 | 4.2 | 47.1 | 30.4 | 16.0 |
| IV | 91 | 157.8 | 6.7 | 3.9 | 3.0 | 227.0 | 9.0 | 17.6 |
| V | 67 | 60.9 | 5.2 | 3.5 | 2.0 | 93.5 | 9.4 | 3.2 |
| VI | 464 | 165.0 | 7.5 | 4.0 | 2.3 | 222.0 | 10.9 | 4.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vitanza, R.; Cortesi, A.; Gallo, V.; De Arana, M.E.; Vasiliadou, I.A. Simulation of an Oxic-Settling-Anaerobic Pilot Plant Operated under Real Conditions Using the Activated Sludge Model No.2d. Water 2021, 13, 3383. https://doi.org/10.3390/w13233383
Vitanza R, Cortesi A, Gallo V, De Arana ME, Vasiliadou IA. Simulation of an Oxic-Settling-Anaerobic Pilot Plant Operated under Real Conditions Using the Activated Sludge Model No.2d. Water. 2021; 13(23):3383. https://doi.org/10.3390/w13233383
Chicago/Turabian StyleVitanza, Rosa, Angelo Cortesi, Vittorino Gallo, Maria E. De Arana, and Ioanna A. Vasiliadou. 2021. "Simulation of an Oxic-Settling-Anaerobic Pilot Plant Operated under Real Conditions Using the Activated Sludge Model No.2d" Water 13, no. 23: 3383. https://doi.org/10.3390/w13233383
APA StyleVitanza, R., Cortesi, A., Gallo, V., De Arana, M. E., & Vasiliadou, I. A. (2021). Simulation of an Oxic-Settling-Anaerobic Pilot Plant Operated under Real Conditions Using the Activated Sludge Model No.2d. Water, 13(23), 3383. https://doi.org/10.3390/w13233383







