1. Introduction
With the increase in extreme weather events induced by climate change, understanding the response mechanism of groundwater systems to precipitation is of critical importance [
1,
2,
3,
4]. To date, two valuable correlation methods including the auto-correlation and cross-correlation function have been typically applied to assess the responses of aquifers to precipitation [
5,
6,
7]. The auto-correlation analysis characterizes the degree of “inertia” [
8,
9], or “persistence” [
3], or “memory effect” [
10] of an individual time series. The cross-correlation analysis can provide the response time between rainfall and groundwater levels (GWLs). In addition, the correlation methods are usually combined with spectral analysis, such as Fourier analysis, to detect the periodicity of a signal.
Jenkins and Watts [
11] and Box and Jenkins [
12] explained the basic principles of correlation and spectral analyses. Mangin [
13] applied these methods to three karstic systems in the Pyrenean Mountains (France–Spain), and their work indicated that these analyses provide an excellent method for the investigation of a hydrological system. After that, correlation and spectral analyses have been widely used in different aquifer systems, including karstic systems [
14,
15,
16], alluvial aquifers [
3,
5], and coastal aquifers [
17,
18], etc.
Although correlation and spectral analysis have been widely used in hydrology and hydrogeology, these methods cannot describe how the frequency of a signal changes with time. Instead, the wavelet transform method is an effective tool for detecting the periodicity of a nonlinear system and can provide localized intermittent periodicities [
19,
20,
21]. Based on the cross wavelet and wavelet coherence methods, Yu and Lin [
22] found that the temporal lag from rainfall to groundwater was about 3.71–72.07 days for the Pingtung Plain in Taiwan. Zhang et al. [
23] found that the time lag of groundwater depth to precipitation in the Yellow River Delta during 2006–2010 ranged from 35. 51 to 178. 36 days, and the relationship between groundwater depth and precipitation is largely affected by land use types, soil texture, and micro-geomorphic types. Cai et al. [
24] show that the response time of groundwater levels to rainfall during 2006–2018 extended from 80 to ~190 days in Puyang, Henan, China, and that it increases with the burial depth of groundwater. Although there are many studies investigating the relationship between rainfall and aquifers, seldom does research focus on areas facing severe water shortage such as the Heilonggang region, China.
The Heilonggang region is located in the southeast of Hebei Province (
Figure 1), a part of the North China Plain, and serves as an important agricultural planting area for the nation. Agricultural water accounts for 76% of water resource consumption in this area, and more than 80% of agricultural irrigation water comes from groundwater [
25]. The increasing demand for groundwater resources has led to the decline in GWLs and caused a series of ecological problems such as land subsidence, etc. Previous studies of this area mainly focus on the optimization of irrigation and planting regimes [
26,
27,
28], and few researchers have paid attention to the long-term groundwater dynamics and associated responses to rainfall in this region. Clarifying the relationship between groundwater and precipitation can help us better understand the local groundwater circulation, provide references for groundwater resource management, and be conducive to ecological protection [
29,
30]. Therefore, in this study, we aim to (1) estimate the persistence of aquifers and their responses to rainfall through the auto-correlation and cross-correlation functions, (2) identify groundwater periodicity through spectral analyses, (3) determine the groundwater response time through cross-correlation and cross spectral analyses, and (4) explore the influences of rainfall intensity, humidity index, and groundwater pumping on the response time.
2. Materials and Methods
2.1. Study Site
The Heilonggang region covers an area of 34,700 km2. The terrain in this region is gentle and inclines slightly from southwest to northeast with a topographic slope of 0.2~0.1‰. From west to east, the geomorphic type is dominated by the mountain alluvial-diluvial plain, the central alluvial-lacustrine plain and the coastal plain, respectively. Accordingly, from west to east, sediments change from gravel in front of the mountain, to medium coarse and medium fine sand in the middle, then to fine sand in the coastal area.
The study site is mainly affected by the warm temperate semi-arid and semi-humid continental monsoon with four distinct seasons. The annual average precipitation is 500~600 mm, mostly concentrated in July and August. The river system in the Heilonggang area comprises the Zhangweinan Canal system, the Heilonggang Canal system, and the Ziya River system. All rivers finally drain into the Bohai Sea (
Figure 1). Reservoirs have been built at the upper reaches of almost all rivers, and more than 80% of the surface runoff is detained by the reservoirs, resulting in long-term drying of the rivers flowing through the area and greatly reducing the amount of river leakage.
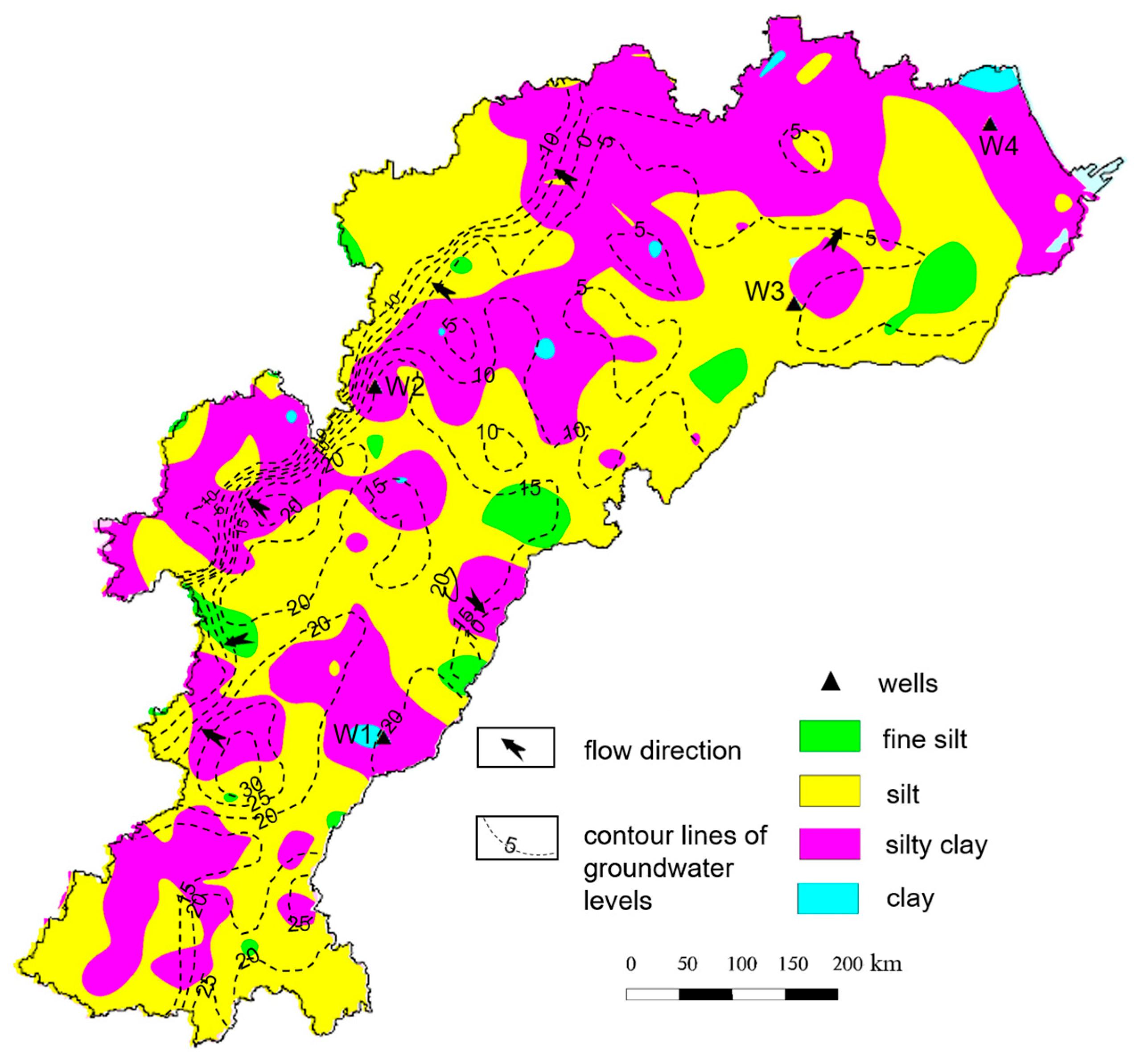
Aquifers in the Heilonggang area are mainly composed of Quaternary strata. The Quaternary aquifer system can be divided into four aquifer groups from top to bottom (
Figure S1). Among them, the first aquifer group is the aquifer we focused on in this study. It is composed of Holocene and Upper Pleistocene loose sediments, with a bottom depth of 20~50 m [
31]. The vadose zone lithology in this area is mainly composed of silt and silty clay (
Figure 2).
In the 1950s, the degree of groundwater exploitation in this area was very low, and the whole groundwater flow system was in a natural state. Shallow groundwater generally flows from southwest to northeast (
Figure S2a). Under the influence of human activities, local groundwater depression cones have formed in the north part of the region (
Figure S2b). At present, the groundwater depression cones have further expanded towards the west (
Figure 2), and the southwest–northeast hydraulic gradient has decreased greatly compared to the natural state.
Shallow fresh groundwater mainly occurs in the west and north of the research area, and shallow brackish water mainly occurs in the east of the region. The distribution area of the shallow fresh groundwater accounts for 51.6% of the total Heilonggang area [
32]. Rainfall serves as the main source for the river and shallow groundwater.
2.2. Datasets
The groundwater data were obtained from the “Groundwater Almanacs of Geological Environment Monitoring in China”. Four boreholes monitoring a substantial length of shallow groundwater were selected in this study, as shown in
Figure 1. Detail characteristics of each monitoring well are presented in
Table 1. The rainfall data before 2018 was extracted daily from the “China meteorological forcing dataset (1979–2018)” [
33], and the data after 2018 was collected from China Meteorological Administration (
http://data.cma.cn/, accessed on 1 June 2022).
2.3. Mann–Kendall Trend Analysis
The Mann–Kendall trend test is a nonparametric statistical test [
34,
35]. It is not necessary to assume that samples obey a certain distribution and are not disturbed by a few outliers.
The trend of time series is determined using
Z values:
where
S is the testing statistic, and
n is the sample size. A positive value of
S indicates an increasing trend, and vice versa. If |
Z| ≥ 1.96, it indicates the time series passes the significance test with 95% confidence.
2.4. Auto-Correlation and Cross-Correlation Functions
The auto-correlation functions were used to depict the persistence degree of the time series. The auto-correlation coefficient
rxx(
k) is expressed as [
12]:
where
N is the length of the series;
k is the time lag; and
is the arithmetic mean of the series.
The cross-correlation coefficient between series
x and
y is defined as [
12]:
where
N is the length of the series;
k is the time lag; and
σx and
σy are the standard deviations.
The cross-correlation functions characterize the relationships between the input and output signals. Here, we take the rainfall as input signals and the GWLs as output signals. If the rainfall can be considered random, the cross-correlation functions give the impulse response of the aquifer.
The sliding-window cross-correlation method followed by Delbart et al. [
2] was also carried out to investigate the influences of rainfall intensity on the response time. The sliding-window cross-correlation method consists of slicing the
x (precipitation) and
y (GWLs) series with partially superposed windows. For each window, the
rxy values between rainfall and GWLs are computed, and the corresponding response time is identified. Then, a time series of response times is obtained for different windows. In this study, the window length is 6 months, and the sliding interval is 1.5 months. Note that the correlation coefficients should be not lower than the standard error of ~
, where
N is the sample size, and “2” is the critical value for the 0.95 probability of the normal distribution. That is, values for which the
rxy peak was not significant at a 95% confidence level were left out.
2.5. Wavelet Transform
Hydrologic time series are usually nonstationary with temporal variations in both frequency and amplitude. Through the continuous wavelet transform, a complete time-scale representation of localized and transient phenomena occurring at different time scales can be obtained [
36]. The wavelet spectrum is defined as the modulus of wavelet coefficients. This wavelet spectrum can also be averaged in time, known as the global averaged wavelet spectrum [
20], which helps to identify the characteristic periods within a single time series. Here, the Morlet wavelet serves as the wavelet mother function [
37].
After the continuous wavelet transform, the cross wavelet transform (XWT) is used to determine the cross wavelet spectrum of two time series, and to examine relationships between the two series. The XWT is defined as:
where
is the wavelet transform of time series
xt (rainfall) at frequency scale
s; and
is the complex conjugate of wavelet transform
for
yt (GWLs). The XWT can be represented using polar coordinates:
where
is the power of the cross wavelet; and
φt(
s) is the phase angle, which denotes the delay between the two series at time
t and scale
s.
The time lag Δ
T at a scale
s between the two signals is calculated by:
where
T(
s) is the period relative to the scale
s.
The distribution of the cross wavelet power is:
where
and
are Fourier background spectra of the two series
xt and
yt; and
Zν(
p) is the confidence level associated with the probability
p, and
. The 5% significance level is determined using
Z2(95%) = 3.999.
This study performed XWT on the original time series of rainfall and GWLs to understand their relationships. To exclude the edge effects, the cone of influence is introduced for all wavelet transforms. Codes used for wavelet analyses were based on those originally written by Grinsted et al. [
19] and finished by Matlab 2014b (MathWorks, Natick, MA, USA).
3. Results
3.1. Observed Time Series and Trend Analysis
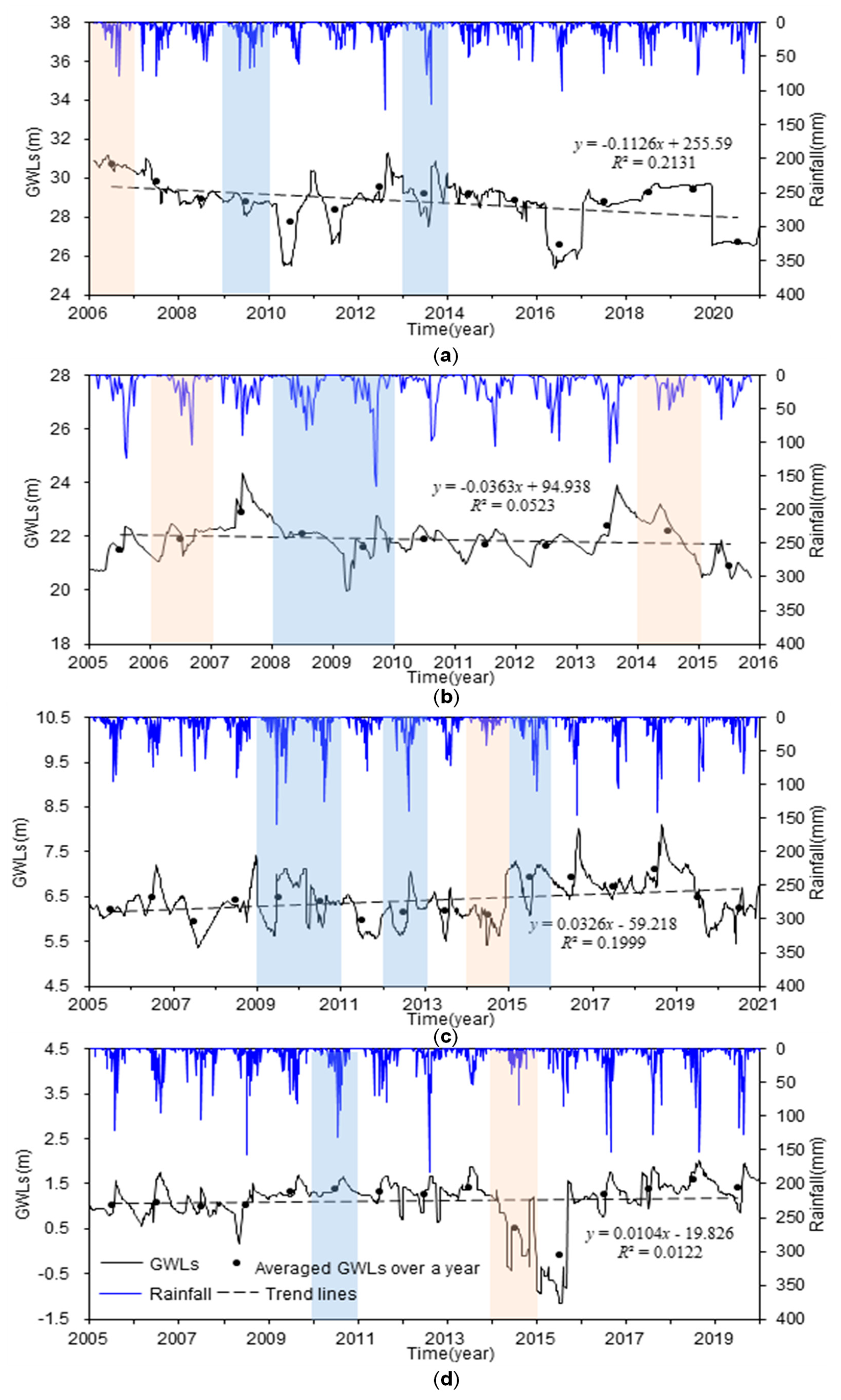
Piezometric levels of all boreholes shown in
Figure 3 characterize the behavior of unconfined aquifers. The average GWLs decrease from upstream to downstream, i.e., from 28.77 m at W1, to 21.90 m at W2, to 6.42 m at W3, and to 1.09 m at W4. The standard deviation of the GWLs also declines from 1.25 m at W1 in the west, to 0.70 m at W2 in the middle, and to ~0.5 m for the other two wells in the east of the region. According to the Pearson Type-III distribution curve, the wet year and dry year are identified and denoted by the blue and orange bands, respectively. For example, in
Figure 3d, the years 2010 and 2014 are identified as the wet year and dry year, respectively.
According to the Mann–Kendall statistics (
Table 2), the GWLs at W1 and W2 present a downward trend while the GWLs at W3 and W4 show an upward trend (all at the 95% confidence level). For the annual averaged GWLs, piezometric levels of W1 and W2 decrease at a rate of 0.11 m/y and 0.04 m/y, respectively. Annual averaged GWLs of W3 and W4 increase at a rate of 0.03 m/y and 0.01 m/y, respectively. Both W3 and W4 are located in Cangzhou City. In 2008, Cangzhou City was listed as a national pilot area for groundwater protection, and the amount of exploitation decreased rapidly. Yan et al. [
38] also reported that after 2008, the amount of artificial mining decreased and the depth of groundwater decreased. Our study result is in line with them.
3.2. Auto-Correlation and Cross-Correlation Analyses
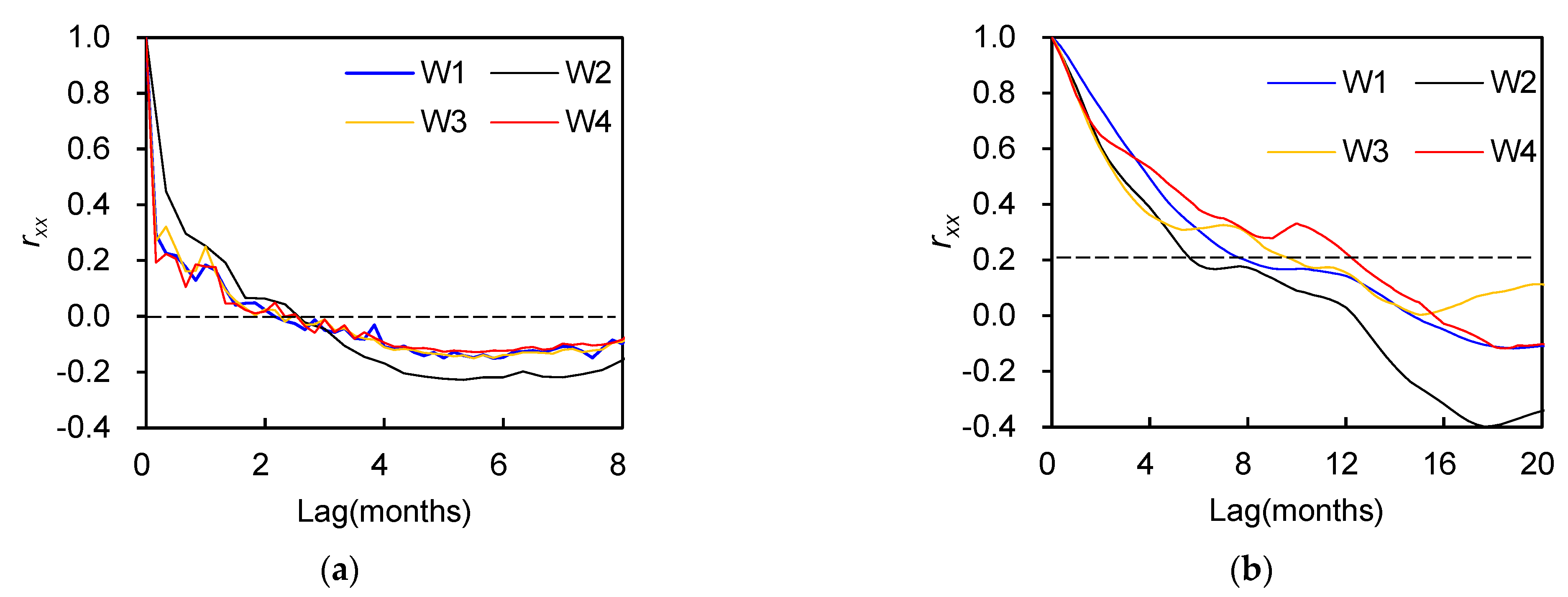
Figure 4a shows that the auto-correlation coefficients of rainfall decay quickly close to zero, and all of the correlograms become null within 3 months, implying that the rainfall is relatively random. By comparison, GWLs present a long memory effect relative to rainfall (
Figure 4b). The auto-correlation functions of GWLs show that the order of increasing inertia ranks as follows: W2→W1→W3→W4. For example, the auto-correlation slope (the slope of the auto-correlation coefficient before the curve becomes flat) increases from −12.7 × 10
−2 month
−1 at W2 to −5.0 × 10
−2 month
−1 at W4 (
Table 3), and the time lag required for auto-correlation coefficients to reach 0.2 (
k0.2 values) also rises from W2 (5.7 months) to W4 (12.3 months). Note that without considering W2, there is an upward trend in persistence from upstream to downstream, which has also been identified by Duvert et al. [
3] in a subtropical agricultural catchment dominated by alluvial aquifers in southeast Queensland, Australia.
Figure 5 shows that the peak value of
rxy between precipitation and GWLs is the maximum of 0.52 at W2, followed by 0.45 at W1, 0.41 at W3, and 0.40 at W4. It is interesting that this order is consistent with the above ranking result from the auto-correlation functions of GWLs. That is, the shorter the memory time, the greater the correlation coefficient. The time lags corresponding to the peak values are 0.67 months at W2and W3, and 1.33 months at W1 and W4.
3.3. Continuous Wavelet Spectra
Wavelet power spectra for rainfall and GWLs were plotted in
Figure 6. Warmer colors denote higher power. It is statistically significant that the rainfall spectrum has a clear annual periodicity throughout the study period, which is mainly caused by the annual wet/dry cycle. For groundwater, this annual periodicity was identified during 2009–2014 and 2015–2017 for W1, 2008–2015 for W2, 2006–2011 and 2014–2016 for W3, and 2014–2016 for W4.
It can be seen that high-power frequencies in the rainfall spectra are absorbed and filtered by the aquifer to produce the groundwater signals. Therefore, aquifers serve as low-pass filters, which is consistent with the research of Imagawa et al. [
5] and Duvert et al. [
3]. It is interesting that the period when the maximum value in the global wavelet spectrum is achieved increases gradually from 2.1 years at W1 (upstream) to 3.7 years at W4 (downstream). Gómez et al. [
39] also identified “longer aquifer regulation times in larger basins”. The increasing time period from upstream to downstream we observed here further demonstrates the impacts of regional water circulation.
3.4. Cross Wavelet Spectral Analysis
Cross wavelet spectra are given in
Figure 7. The averaged phase angles are 2.40 rad, 0.40 rad, 2.50 rad, and 1.02 rad for W1, W2, W3, and W4, respectively. That is, the groundwater lags behind precipitation by 139.14 days at W1, 23.27 days at W2, 145.01 days at W3, and 59.22 days at W4, respectively (
Table 4).
The temporal lags for the wet years are also calculated. The time lags for the wet years at W1, W3, and W4 have been shortened by 12 days, 13 days, and 10 days, respectively. This further strengthens the conclusion that high rainfall shortens aquifer response time [
2,
3]. However, the time lags for wet years at W2 have been prolonged by 16 days. This is mainly caused by human pumping activities, which will be further discussed in
Section 4.2.
Compared to the results of other studies shown in
Table 5, the response times of W1 and W3 are comparable to those of most wells located in the Yellow River Basin [
6,
23,
40,
41]. The response time of W2 is close to the minimum value observed in the Yellow River Delta [
23]. The response time of W4 is close to the shortest lags of Jinan Baiquan Spring Watershed and the largest ones of Pingtung Plain. There are many factors that can affect the groundwater response time. Here, we only considered the effects of rainfall intensity, pumping activities, and humidity index in the next section.
4. Discussion
4.1. Rainfall Intensity
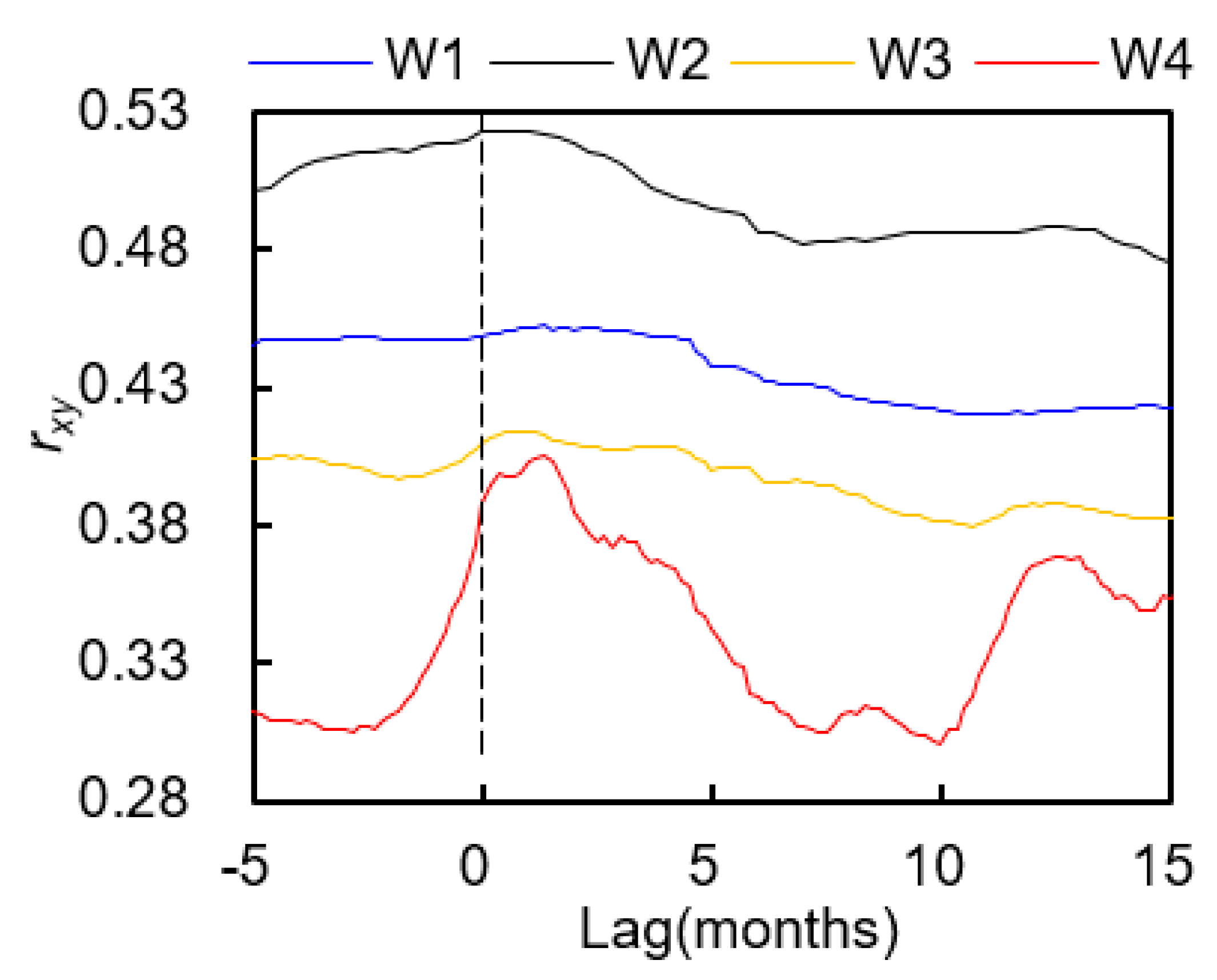
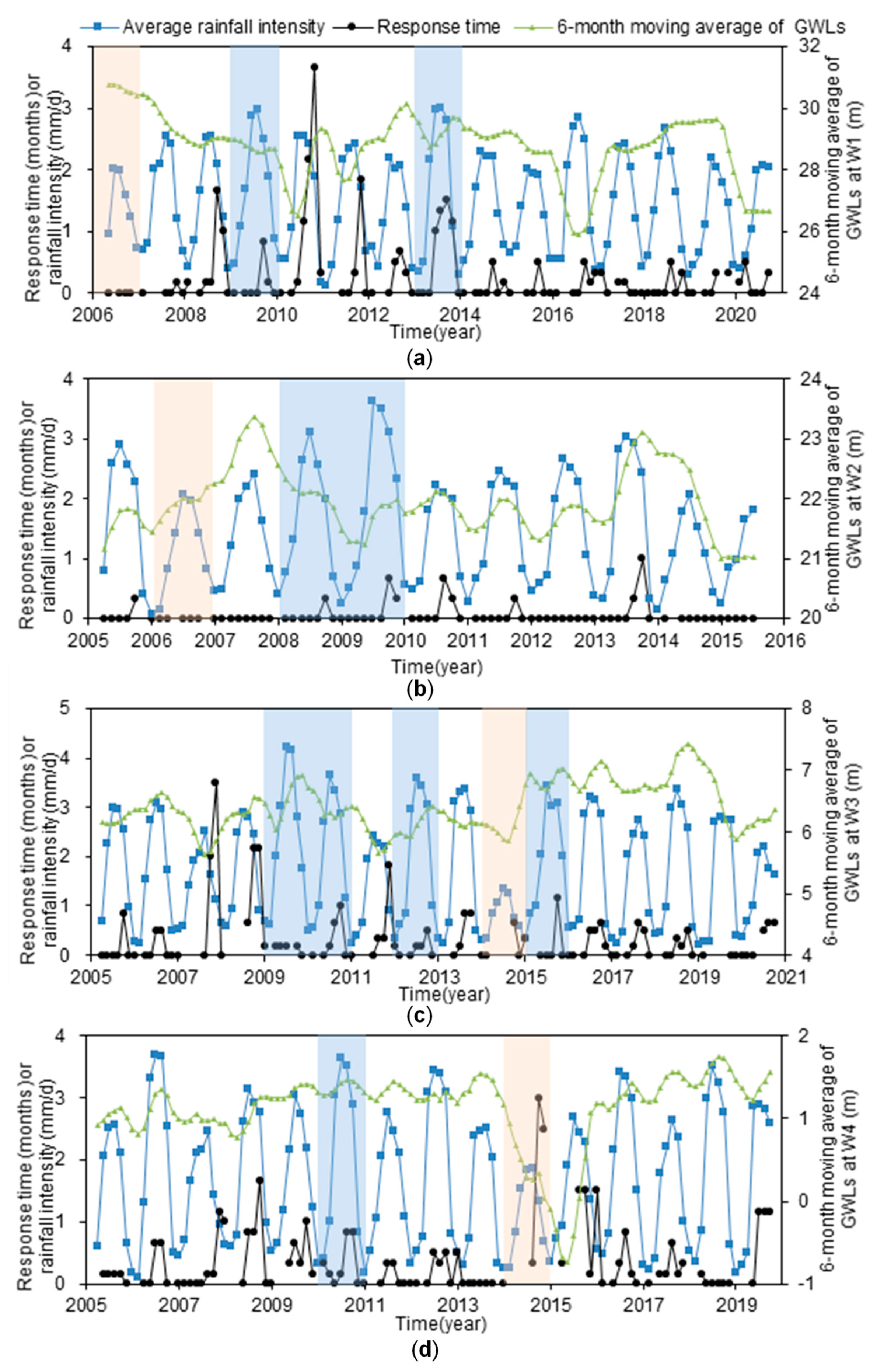
The time series of response times obtained from the sliding-window cross-correlation method is shown in
Figure 7. It can be seen that the fluctuation of groundwater at W2 is almost consistent with that of precipitation: when the rainfall intensity becomes smaller, the GWLs become lower, and vice versa. The fast response leads to a short response time, which is within one month through the year. The same is true for W4 under wet and normal conditions, during which the response time is no more than 1.7 months. However, under dry conditions such as the year of 2014, the response time becomes larger, reaching up to 3 months. Generally speaking, aquifers at W2 and W4 react quickly to local rainfall. In contrast, wells one and three respond slowly to the rainfall with visible time lags as shown in
Figure 7a,c. The variation range of the response time is 0~3.7 months for W1 and 0~3.5 months for W3. These values further verified the time lags as shown in
Table 4.
4.2. Pumping
As we have mentioned above, agricultural development in this area relies heavily on groundwater. To ensure the winter wheat production, groundwater has to be extracted from March to June if there is not sufficient rainwater. For W2, we can see a significant decline in the water level from 2008 to 2009 despite the wet year, during which the maximum time lag could reach 45 days. This phenomenon is also observed at W4: the maximum response time over the drought period of 2014–2015 was prolonged to 113 days, which was very close to the response time obtained from the sliding-window cross-correlation method as shown in
Figure 8.
To further explore the effect of pumping on the time lags, we counted the lags in the years of pumping and those in the years of no or little pumping for each well (
Table 4). The results show that the temporal lags for the pumping years are 1.3~2.0 times those during the years without pumping. Pumping can lead to a dropdown of the GWLs, with an increasing unsaturated zone thickness, and thus a longer time is needed for the aquifer to receive the infiltrated rainfall signal. Therefore, the time lags between groundwater and precipitation will be enlarged by groundwater pumping activities.
4.3. Humidity Index
The potential evapotranspiration (PET) data were obtained from the “1 km monthly potential evapotranspiration dataset in China (1990–2021)” [
42], based on the Hargreaves method [
43]. The annual average PET at the four stations did not vary greatly, and ranges from 1190 mm at W1, to 1214 mm at W2, to 1187 mm at W3, and 1069 mm at W4. Seasonal variations in PET have also been observed (
Figure S3). Generally, the variation pattern of PET is consistent with that of precipitation, though sometimes the peak of PET arrives ~1 month before the precipitation.
The humidity index (the aridity index in UNEP, [
44]) can be used to assess the surface-water stress or the arid degree at a given location [
45]. It is defined as the ratio of precipitation P to the PET:
The results from the cross wavelet spectra between HI and GWLs are given in
Table 6 and
Figure S4. Compared to the time lags between P and GWLs as shown in
Table 4, the lags between HI and GWLs are shortened by 14% at W1, 36% at W2, 28.5% at W3, and 19.6% at W4, respectively. This can be understood since not all rainfall can recharge aquifers. Only the effective rainfall can produce surface runoff or infiltrate into the subsurface. Compared to the precipitation, the humidity index reflects comprehensive influences of both P and PET, and to some extent the effective rainfall. Therefore, the GWLs response more quickly to the HI index than to the rainfall.
4.4. Comprehensive Analysis
To further investigate the controlling factors of the time lags between aquifers and rainfall identified using the XWT method, changes in lags induced by different factors are given in
Table 7. It can be seen that variations in the time lags at W2 and W4 are most sensitive to pumping. In fact,
Figure 3 and
Table 4 indicate that compared to W1 and W3, W2 and W4 are in areas less affected by human activities with few pumping years. Therefore, they are very sensitive to the pumping under the regional background of groundwater level recession. The large percentage change in time lags induced by pumping at these areas highlights the fragility of local aquifer systems.
On the other hand, variations in the time lags at W1 and W3 are less affected by pumping, but most sensitive to HI. They are not sensitive to pumping because things could hardly become worse at these areas that have suffered from pumping to a certain extent. These unhealthy aquifers that have been affected by pumping, or these somewhat thirsty aquifers, will try to recover as long as they are replenished by rainfall. Therefore, they are most sensitive to HI. This highlights the resilience of local aquifers.
Assuming that all rises in water level are due to recharge from precipitation, the water table fluctuation (WTF) method [
46,
47] tell us the recharge ratio (
α) can be estimated as:
where
Sy is the specific yield; Σ
h is cumulative rise in water-level; and Σ
P is the total precipitation in the period corresponding to the water level rise.
Here, the hydrologic year during which the water table rose most significantly is chosen, and the maximum empirical values of
Sy provided by [
48] are also used. As a result, the recharge ratio we estimated as shown in
Table 8 is larger than or close to the maximum value of the empirical values. As a whole, the recharge ratio decreases from upstream to downstream. Specially, it decreases from W2 to W4, which is in line with the inertia ranks as shown in
Figure 4. Meanwhile, considering the smallest time lags indicated by the cross wavelet spectra, the site of W2 has a good potentiality for groundwater recharge.
4.5. Limitations
There are many factors affecting the groundwater response time. Here, we only discussed the influences of rainfall intensity, evaporation, and groundwater pumping. Other factors, such as river water, were not taken into account. In fact, these factors are not isolated, but interact in various geological and geographical contexts. It is reported that the partial wavelet coherency method can detect localized and scale-specific bivariate relationships between predictor and response variables after removing the impact of other variables [
30,
49,
50]. Therefore, in future research, the partial wavelet coherence method can be further implemented to distinguish the impacts of climate change and human activities on the GWLs, for better understanding their impacts on the groundwater flow system.
5. Conclusions
This research provides analyses of the long-term dynamics, the persistence, and the periodicity of shallow groundwater located in the Heilonggang region, China. The interrelation between precipitation and groundwater levels is also examined based on correlation and spectral analyses. The results of this research provide a more complete understanding of the local groundwater circulation system. The major conclusions are as follows.
Firstly, trend analysis shows that the GWLs at W1 and W2 present a downward trend while the GWLs at W3 and W4 show an upward trend over the observation period. Therefore, more attention should be paid to the upstream of the aquifer system.
Secondly, auto-correlation analysis indicates a rising trend in the memory time for aquifers from upstream to downstream. The cross-correlation analysis stresses that the shorter the memory time, the greater the correlation coefficient between rainfall and GWLs. The continuous wavelet spectra shows that the dominant period increases gradually from 2.1 years at W1 to 3.7 years at W4, further demonstrating longer regulation times from upstream to downstream.
Thirdly, both the cross wavelet spectra and the sliding-window cross-correlation method display that wells two and four respond quickly while wells one and three respond slowly to the local rainfall. The time lags between aquifers and rainfall at W1, W2, W3, and W4 are 139.14 ± 59.76 days (2008–2020), 23.27 ± 12.03 days (2005–2014), 145.01 ± 68.00 days (2007–2020), and 59.22 ± 26.14 days (2005–2019), respectively. The temporal lags of groundwater to precipitation are shortened by 10~13 days during the wet year conditions, and the lags during the pumping years are 1.3~2.0 times those during the years without pumping. The time lags between HI and GWLs are reduced by 14~36%, compared to those between rainfall and GWLs.
Further analysis shows that variations in the time lags at W2 and W4 are most sensitive to pumping, while variations in the time lags at W1 and W3 are less affected by pumping, but most sensitive to HI. The overestimated recharge ratio decreases from 0.32 at W2 to 0.17 at W4, suggesting that the site of W2 has a good potentiality for groundwater recharge.
Finally, although this research provides a new insight into relations between precipitation and groundwater in the study area, there are still some other factors, such as river water, which were not considered. Future researchers could possibly use the partial wavelet coherence method to distinguish the effects of human activities and climate change on the GWLs.
Supplementary Materials
The following supporting information can be downloaded at:
https://www.mdpi.com/article/10.3390/w15061100/s1, Figure S1. Aquifer groups in the Heilonggang region. Figure S2. Shallow groundwater flow field in (a) 1959 and (b) 2005. Figure S3. Monthly precipitation (P) and monthly potential evapotranspiration (PET) at (a) W1, (b) W2, (c) W3 and (d) W4. Figure S4. Cross wavelet spectra between HI and GWLs at (a) W1, (b) W2 (c) W3 and (d) W4.
Author Contributions
Methodology, C.W.; formal analysis, C.W.; investigation, H.L.; data curation, Y.L.; writing—original draft preparation, C.W. and W.Q.; Writing—Review & Editing, W.Q.; funding acquisition, F.D.; visualization, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the S&T Program of Hebei (No: 22373601D), the Water Conservancy Science and Technology Project of Hebei Province, China (2021-39), the Open Fund for Hebei Province Collaborative Innovation Center for Sustainable Utilization of Water Resources and Optimization of Industrial Structure (XTZX202111), the Scientific Research Projects of the Higher University in Hebei (BJK2022007), the Natural Science funds Project in Hebei Province (D2020403022, E2021403001), National Pre-research Funds of Hebei GEO University in 2023 (KY202314), the Youth Project of Hebei GEO University (QN202118 and QN202141).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are contained within the article.
Acknowledgments
We are very grateful to the three anonymous reviewers for their constructive comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Taylor, R.G.; Scanlon, B.; Doll, P.; Rodell, M.; van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Change 2013, 3, 322–329. [Google Scholar] [CrossRef] [Green Version]
- Delbart, C.; Valdes, D.; Barbecot, F.; Tognelli, A.; Richon, P.; Couchoux, L. Temporal variability of karst aquifer response time established by the sliding-windows cross-correlation method. J. Hydrol. 2014, 511, 580–588. [Google Scholar] [CrossRef]
- Duvert, C.; Jourde, H.; Raiber, M.; Cox, M.E. Correlation and spectral analyses to assess the response of a shallow aquifer to low and high frequency rainfall fluctuations. J. Hydrol. 2015, 527, 894–907. [Google Scholar] [CrossRef]
- Cuthbert, M.O.; Gleeson, T.; Moosdorf, N.; Befus, K.M.; Schneider, A.; Hartmann, J.; Lehner, B. Global patterns and dynamics of climate–groundwater interactions. Nat. Clim. Change 2019, 9, 137–141. [Google Scholar] [CrossRef]
- Imagawa, C.; Takeuchi, J.; Kawachi, T.; Chono, S.; Ishida, K. Statistical analyses and modeling approaches to hydrodynamic characteristics in alluvial aquifer. Hydrol. Process. 2013, 27, 4017–4027. [Google Scholar] [CrossRef]
- Cai, Z.; Ofterdinger, U. Analysis of groundwater-level response to rainfall and estimation of annual recharge in fractured hard rock aquifers, NW Ireland. J. Hydrol. 2016, 535, 71–84. [Google Scholar] [CrossRef] [Green Version]
- Meng, Q.; Xing, L.; Liu, L.; Xing, X.; Zhao, Z.; Zhang, F.; Li, C. Time-lag characteristics of the response of karst springs to precipitation in the northern China. Environ. Earth Sci. 2021, 80, 348. [Google Scholar] [CrossRef]
- Delbart, C.; Valdés, D.; Barbecot, F.; Tognelli, A.; Couchoux, L. Spatial organization of the impulse response in a karst aquifer. J. Hydrol. 2016, 537, 18–26. [Google Scholar] [CrossRef]
- Geng, X.; Boufadel, M.C. Spectral responses of gravel beaches to tidal signals. Sci. Rep. 2017, 7, 40770. [Google Scholar] [CrossRef] [Green Version]
- Duy, N.L.; Nguyen, T.V.K.; Nguyen, D.V.; Tran, A.T.; Nguyen, H.T.; Heidbüchel, I.; Merz, B.; Apel, H. Groundwater dynamics in the Vietnamese Mekong Delta: Trends, memory effects, and response times. J. Hydrol. Reg. Stud. 2021, 33, 100746. [Google Scholar] [CrossRef]
- Jenkins, G.M.; Watts, D.G. Spectral Analysis and Its Applications; Holden Day Inc.: San Francisco, CA, USA, 1968; p. 525. [Google Scholar]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Prentice Hall: Upper Saddle River, NJ, USA, 1976; p. 575. [Google Scholar]
- Mangin, A. Pour une meilleure connaissance des systèmes hydrologiques à partir des analyses corrélatoire et spectrale. J. Hydrol. 1984, 67, 25–43. [Google Scholar] [CrossRef]
- Larocque, M.; Mangin, A.; Razack, M.; Banton, O. Contribution of correlation and spectral analyses to the regional study of a large karst aquifer (Charente, France). J. Hydrol. 1998, 205, 217–231. [Google Scholar] [CrossRef]
- Labat, D.; Ababou, R.; Mangin, A. Rainfall-runoff relations for karstic springs. Part II: Continuous wavelet and discrete orthogonal multiresolution analyses. J. Hydrol. 2000, 238, 149–178. [Google Scholar] [CrossRef]
- Massei, N.; Dupont, J.; Mahler, B.; Laignel, B.; Fournier, M.; Valdes, D.; Ogier, S. Investigating transport properties and turbidity dynamics of a karst aquifer using correlation, spectral, and wavelet analyses. J. Hydrol. 2006, 329, 244–257. [Google Scholar] [CrossRef]
- Shi, D.C.; Lin, G. Application of spectral analysis to determine hydraulic diffusivity of a sandy aquifer (Pingtung County, Taiwan). Hydrol. Process. 2004, 18, 1655–1669. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Cheong, T.; Kim, R.; Koh, D.; Ryu, J.; Chang, H. Use of time series analysis for the identification of tidal effect on groundwater in the coastal area of Kimje, Korea. J. Hydrol. 2005, 300, 188–198. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Proc. Geoph. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Labat, D. Cross wavelet analyses of annual continental freshwater discharge and selected climate indices. J. Hydrol. 2010, 385, 269–278. [Google Scholar] [CrossRef]
- Li, J.; Pu, J.; Zhang, T.; Wang, S.; Huo, W.; Yuan, D. Investigation of transport properties and characteristics of a large karst aquifer system in southern China using correlation, spectral, and wavelet analyses. Environ. Earth Sci. 2021, 80, 84. [Google Scholar] [CrossRef]
- Yu, H.; Lin, Y. Analysis of space–time non-stationary patterns of rainfall–groundwater interactions by integrating empirical orthogonal function and cross wavelet transform methods. J. Hydrol. 2015, 525, 585–597. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, C.; He, Y.; Liu, Q.; Li, H.; Wu, C.; Liu, G. An analysis of the space-time patterns of precipitation-shallow groundwater depth interactions in the Yellow River Delta. Hydrogeol. Eng. Geol. 2020, 47, 21–30. (In Chinese) [Google Scholar]
- Cai, Y.; Huang, R.; Xu, J.; Xing, J.; Yi, D. Dynamic Response Characteristics of Shallow Groundwater Level to Hydro-Meteorological Factors and Well Irrigation Water Withdrawals under Different Conditions of Groundwater Buried Depth. Water 2022, 14, 3937. [Google Scholar] [CrossRef]
- Yang, M. Current Situation Research on Groundwater Irrigation Management in Heilonggang Region. Master’s Thesis, Hebei Agriculture University, Baoding, China, 2018. (In Chinese). [Google Scholar]
- Jin, M.; Zhang, R.; Sun, L.; Gao, Y. Temporal and spatial soil water management: A case study in the Heilonggang region, PR China. Agr. Water Manag. 1999, 42, 173–187. [Google Scholar] [CrossRef]
- Pan, D.; Ren, L.; Liu, Y. Application of distributed hydrological model for optimizing irrigation regime in Heilong-gang and Yundong plain II. Water production function and irrigation regime optimization. J. Hydraul. Eng. 2012, 43, 777–784. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, X.; Ren, L. Simulating and assessing the effects of seasonal fallow schemes on the water-food-energy nexus in a shallow groundwater-fed plain of the Haihe River basin of China. J. Hydrol. 2021, 595, 125992. [Google Scholar] [CrossRef]
- Alfio, M.R.; Balacco, G.; Rose, M.D.; Fidelibus, C.; Martano, P. A Hydrometeorological Study of Groundwater Level Changes during the COVID-19 Lockdown Year (Salento Peninsula, Italy). Sustainability 2022, 14, 1710. [Google Scholar] [CrossRef]
- Gu, X.; Sun, H.; Zhang, Y.; Zhang, S.; Lu, C. Partial Wavelet Coherence to Evaluate Scale-dependent Relationships Between Precipitation/Surface Water and Groundwater Levels in a Groundwater System. Water Resour. Manag. 2022, 36, 2509–2522. [Google Scholar] [CrossRef]
- Bai, G. Analysis of Groundwater Regulation and Storage Conditions in Heilonggang Region, Hebei. Master’s Thesis, Shijiazhuang University of Economics, Shijiazhuang, China, 2015. (In Chinese). [Google Scholar]
- Wang, B. Study on Comprehensive Quality Assessment and Coupling-Coordination Relationsihp of Water-Land Resources in Heilonggang District. Ph.D. Thesis, Chinese Academy of Geological Sciences, Beijing, China, 2011. (In Chinese). [Google Scholar]
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef] [Green Version]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Griffin, C., Ed.; Bucks: London, UK, 1975. [Google Scholar]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Morlet, J.; Arens, G.; Fourgeau, E.; Giard, D. Wave propagation and sampling theory-Part II, Sampling theory and complex waves. Geophysics 1982, 47, 222–236. [Google Scholar] [CrossRef] [Green Version]
- Yan, B.; Li, X.; Hou, J.; Bi, P. Study on the dynamic characteristics of shallow groundwater level under the influence of climate change and human activities in Cangzhou, China. Water Supply 2020, 21, 797–814. [Google Scholar] [CrossRef]
- Gómez, D.; Melo, D.C.D.; Rodrigues, D.B.B.; Xavier, A.C.; Guido, R.C.; Wendland, E. Aquifer Responses to Rainfall through Spectral and Correlation Analysis. J. Am. Water Resour. Assoc. 2018, 54, 1341–1354. [Google Scholar] [CrossRef]
- Qi, X.; Li, W.; Yang, L.; Shang, H.; Yi, F. The Lag Analysis of Groundwater Level Anomaliesto Precipitation Anomaly of Jinan Baiquan Springs Watershed. Earth Environ. 2015, 43, 619–627. (In Chinese) [Google Scholar]
- Feng, W.; Qi, X.; Li, H.; Li, W.; Yin, X. Wavelet analysis between groundwater level regimes and precipitation, North Pacific Index in the Xiongan New Area. Hydrogeol. Eng. Geol. 2017, 44, 1–8. (In Chinese) [Google Scholar]
- Peng, S.Z.; Ding, Y.X.; Wen, Z.M.; Chen, Y.M.; Cao, Y.; Ren, J.Y. Spatiotemporal change and trend analysis of potential evapotranspiration over the Loess Plateau of China during 2011–2100. Agr. Forest Meteorol. 2017, 233, 183–194. [Google Scholar] [CrossRef] [Green Version]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- United Nations Environment Programme. World Atlas of Desertification, 2nd ed.; Arnold, Hodder Headline, PLC: London, UK, 1997. [Google Scholar]
- Hirata, A.; Kominami, Y.; Ohashi, H.; Tsuyama, I.; Tanaka, N.; Nakao, K.; Hijioka, Y.; Matsui, T. Global estimates of stress-reflecting indices reveal key climatic drivers of climate-induced forest range shifts. Sci. Total Environ. 2022, 824, 153697. [Google Scholar] [CrossRef]
- Healy, R.W.; Cook, P.G. Using groundwater levels to estimate recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Moon, S.K.; Woo, N.C.; Lee, K.S. Statistical analysis of hydrographs and water-table fluctuation to estimate groundwater recharge. J. Hydrol. 2004, 292, 198–209. [Google Scholar] [CrossRef]
- Research Group of “57-01-03”. National Key Science and Technology Project during the Seventh Five-Year Plan Period. Assessment of groundwater resources in north China. Bull. Inst. Hydrogeol. Eng. Geol. CAGS 1993, 9, 33–53. (In Chinese) [Google Scholar]
- Hu, W.; Si, B. Technical note: Improved partial wavelet coherency for understanding scale-specific and localized bivariate relationships in geosciences. Hydrol. Earth Syst. Sci. 2021, 25, 321–331. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, S.; Ding, Y.; Fu, Q.; Wang, Y.; Cai, H.; Shi, H. Assessing the responses of vegetation to meteorological drought and its influencing factors with partial wavelet coherence analysis. J. Environ. Manag. 2022, 311, 114879. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Location of the study area.
Figure 1.
Location of the study area.
Figure 2.
Vadose zone lithology and the flow direction map (2020).
Figure 2.
Vadose zone lithology and the flow direction map (2020).
Figure 3.
Observed time series of rainfall and GWLs at (a) W1, (b) W2, (c) W3, and (d) W4. The blue and orange bands indicate the wet year and dry year, respectively.
Figure 3.
Observed time series of rainfall and GWLs at (a) W1, (b) W2, (c) W3, and (d) W4. The blue and orange bands indicate the wet year and dry year, respectively.
Figure 4.
Auto-correlation functions for (a) rainfall, and (b) GWLs.
Figure 4.
Auto-correlation functions for (a) rainfall, and (b) GWLs.
Figure 5.
Cross-correlation diagrams between rainfall and GWLs.
Figure 5.
Cross-correlation diagrams between rainfall and GWLs.
Figure 6.
Continuous wavelet spectra for both precipitation and GWLs at (a) W1, (b) W2, (c) W3, and (d) W4, with the global wavelet spectrum right side of each subplot. Zones surrounded by black lines have significant wavelet power at the 95% confidence level. White lines denote the cone of influence.
Figure 6.
Continuous wavelet spectra for both precipitation and GWLs at (a) W1, (b) W2, (c) W3, and (d) W4, with the global wavelet spectrum right side of each subplot. Zones surrounded by black lines have significant wavelet power at the 95% confidence level. White lines denote the cone of influence.
Figure 7.
Cross wavelet spectra (left) with global wavelet spectra (right) between rainfall and GWLs at (a) W1, (b) W2, (c) W3, and (d) W4. Zones surrounded by black lines have significant wavelet power at the 95% confidence level. White lines denote the cone of influence. The phase angles are indicated by the black arrows.
Figure 7.
Cross wavelet spectra (left) with global wavelet spectra (right) between rainfall and GWLs at (a) W1, (b) W2, (c) W3, and (d) W4. Zones surrounded by black lines have significant wavelet power at the 95% confidence level. White lines denote the cone of influence. The phase angles are indicated by the black arrows.
Figure 8.
Time series of rainfall intensity, response time, and 6-month moving average of GWLs at (a) W1, (b) W2, (c) W3, and (d) W4. The blue and orange bands indicate the wet and dry years, respectively.
Figure 8.
Time series of rainfall intensity, response time, and 6-month moving average of GWLs at (a) W1, (b) W2, (c) W3, and (d) W4. The blue and orange bands indicate the wet and dry years, respectively.
Table 1.
Detail information of the monitoring wells. The thickness of unsaturated zones was calculated as the average depth over the observation period.
Table 1.
Detail information of the monitoring wells. The thickness of unsaturated zones was calculated as the average depth over the observation period.
| Well Number | Surface Elevation (m a.s.l.) | Monitoring Depth (m) | Unsaturated Zone Thickness (m) | Observation Period (dd-mm-yyyy) | Frequency (Day−1) |
|---|
| W1 | 34.44 | 11~48 | 5.6 | 5 February 2006—30 December 2020 | 5 |
| W2 | 25.23 | 0~10 | 3.3 | 10 January 2005—30 October 2015 | 10 |
| W3 | 8.51 | 0.5~4.33 | 2.2 | 5 January 2005—30 December 2020 | 5 |
| W4 | 2.16 | 6.4~8.1 | 1.1 | 5 January 2005—30 December 2019 | 5 |
Table 2.
Test results of the Mann–Kendall trend analysis.
Table 2.
Test results of the Mann–Kendall trend analysis.
| | W1 | W2 | W3 | W4 |
|---|
| S | −114,083 | −7903 | 124,953 | 127,118 |
| Z | −9.7 | −3.1 | 9.6 | 10.7 |
Table 3.
Parameters of the auto-correlation functions.
Table 3.
Parameters of the auto-correlation functions.
| | W1 | W2 | W3 | W4 |
|---|
| Slope (×10−2 month−1) | −9.3 | −12.7 | −5.0 | −5.0 |
| k0.2 (months) | 7.8 | 5.7 | 9.8 | 12.3 |
Table 4.
Time lags from the cross wavelet spectra between rainfall and GWLs (period of 365 days band).
Table 4.
Time lags from the cross wavelet spectra between rainfall and GWLs (period of 365 days band).
| Title 1 | W1 | W2 | W3 | W4 |
|---|
| All significant periods Lags (days) | 2008–2020 | 2005–2014 | 2007–2020 | 2005–2019 |
| 139.14 ± 59.76 | 23.27 ± 12.03 | 145.01 ± 68.00 | 59.22 ± 26.14 |
| Wet years | 2009, 2013 | 2008–2009 | 2009–2010, 2012, 2015 | 2010 |
| Lags (days) | 126.77 ± 11.07 | 39.07 ± 5.97 | 132.48 ± 20.30 | 49.40 ± 2.37 |
| Years of pumping | 2009–2011, 2013–2017, 2020 | 2006, 2008–2009
2014 | 2007, 2010–2020 | 2008,
2014–2016,
2019 |
| Lags (days) | 156.10 ± 38.79 | 39.07 ± 6.05 | 159.19 ± 74.44 | 88.74 ± 18.25 |
| Years of no or little pumping | 2008, 2012, 2018–2019 | 2005, 2007, 2010–2013 | 2008, 2009 | 2005–2007, 2009–2013, 2017–2018 |
| Lags (days) | 112.06 ± 50.74 | 23.31 ± 8.68 | 123.38 ± 23.85 | 44.46 ± 14.29 |
Table 5.
Time lags of groundwater to rainfall at different study areas.
Table 5.
Time lags of groundwater to rainfall at different study areas.
| References | Study Sites | Study Periods | Depth(m) | Time Lags (Days) |
|---|
| Yu and Lin [22] | Pingtung Plain, Tainwan | 2005–2010 | - | 3.71–72.07 |
| Zhang et al. [23] | Yellow River Delta | 2006–2010 | 1.2–2.2 | 35.51–178.36 |
| Qi et al. [40] | Baiquan Spring Watershed, Jinan | 1990–2011 | ~20–70 | 80.8–185.37 |
| Cai et al. [6] | Puyang area, Henan | 2006–2018 | 1–35.1 | 128–175 |
| Feng et al. [41] | Xiongan New Area, China | 1991–2016 | 30–152 | 147.56–177.20 |
Table 6.
Time lags from the cross wavelet spectra between HI and GWLs (period of 365 days band).
Table 6.
Time lags from the cross wavelet spectra between HI and GWLs (period of 365 days band).
| | W1 | W2 | W3 | W4 |
|---|
| All significant periods | 2009–2017 | 2005–2014 | 2008–2012, 2014–2018 | 2005–2007, 2014–2019 |
| Lags (days) | 119.11 ± 39.41 | 14.85 ± 10.07 | 103.65 ± 40.20 | 47.60 ± 22.61 |
Table 7.
Variation in time lags due to different factors.
Table 7.
Variation in time lags due to different factors.
| Factors | Variation | W1 | W2 | W3 | W4 |
|---|
| Wet years | Absolute changes (days) | −12.37 | | −12.53 | −9.82 |
| Percentage change | −8.89% | | −8.64% | −16.58% |
| Pumping | Absolute changes (days) | 16.96 | 15.8 | 14.18 | 29.52 |
| Percentage change | 12.19% | 67.90% | 9.78% | 49.85% |
| HI | Absolute changes (days) | −20.03 | −8.42 | −41.36 | −11.62 |
| Percentage change | −14.40% | −36.18% | −28.52% | −19.62% |
Table 8.
Recharge ratio calculated using the WTF method.
Table 8.
Recharge ratio calculated using the WTF method.
| | W1 | W2 | W3 | W4 |
|---|
| hydrologic year | 2018 | 2013 | 2009 | 2018 |
| Vadose zone lithology | Silty clay | Silty clay | Silt | Silty clay |
| Sy | 0.05 | 0.05 | 0.074 | 0.05 |
| Recharge ratio α | 0.27 | 0.32 | 0.25 | 0.17 |
| Empirical values of α | 0.18–0.26 | 0.15–0.26 | 0.20–0.28 | 0.12–0.19 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).