A Prediction Model and Factor Importance Analysis of Multiple Measuring Points for Concrete Face Rockfill Dam during the Operation Period
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Multi-Factor and Multi-Monitoring Point Statistical Model
2.1.1. The Water Level Component δH
2.1.2. The Temperature Component δS
2.1.3. The Time Effect Component δT
2.1.4. The Rheological Component δε
2.1.5. The Material Component δm
2.2. XGBoost Model for Multiple Monitoring Points Model
2.3. Hyperparameter Optimization and Performance Measures
2.4. Factor Importance Analysis Based on SHAP
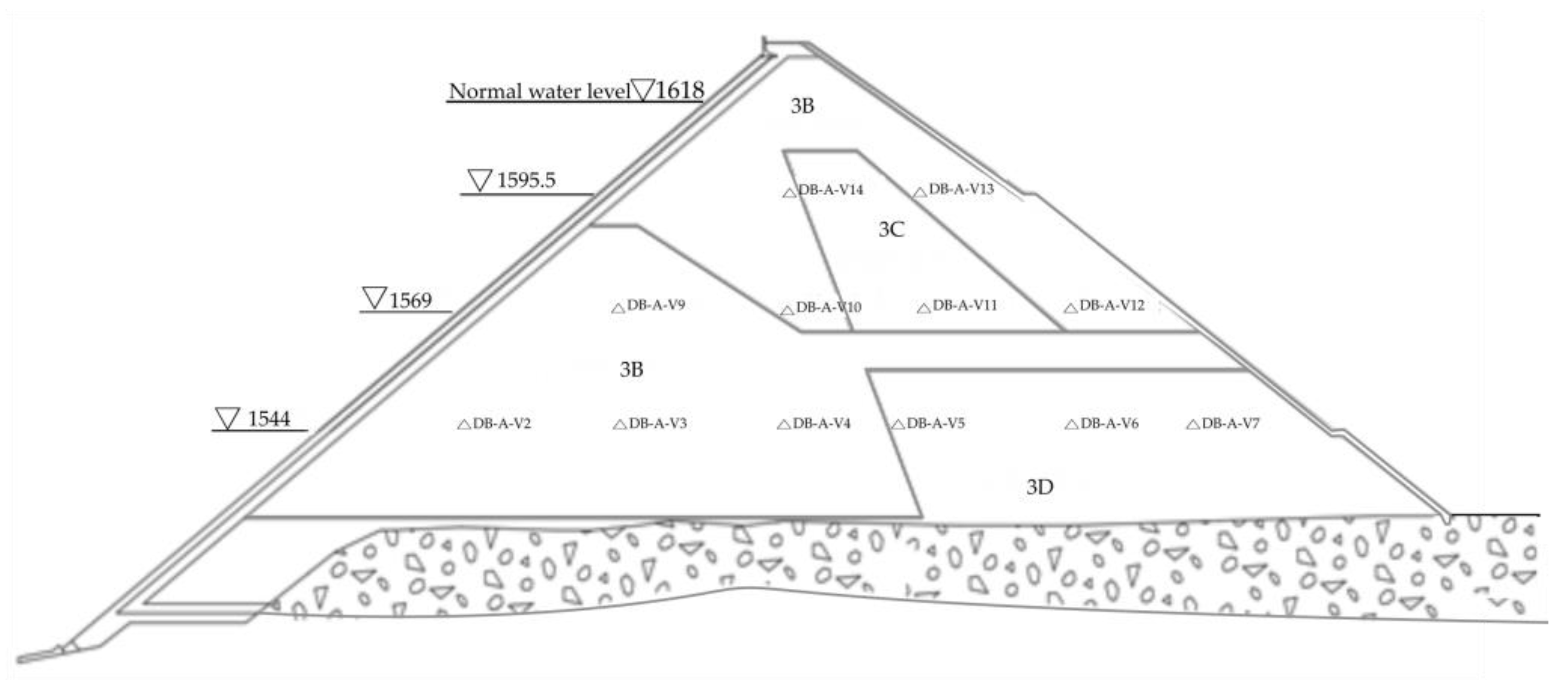
3. Case Study
4. Results
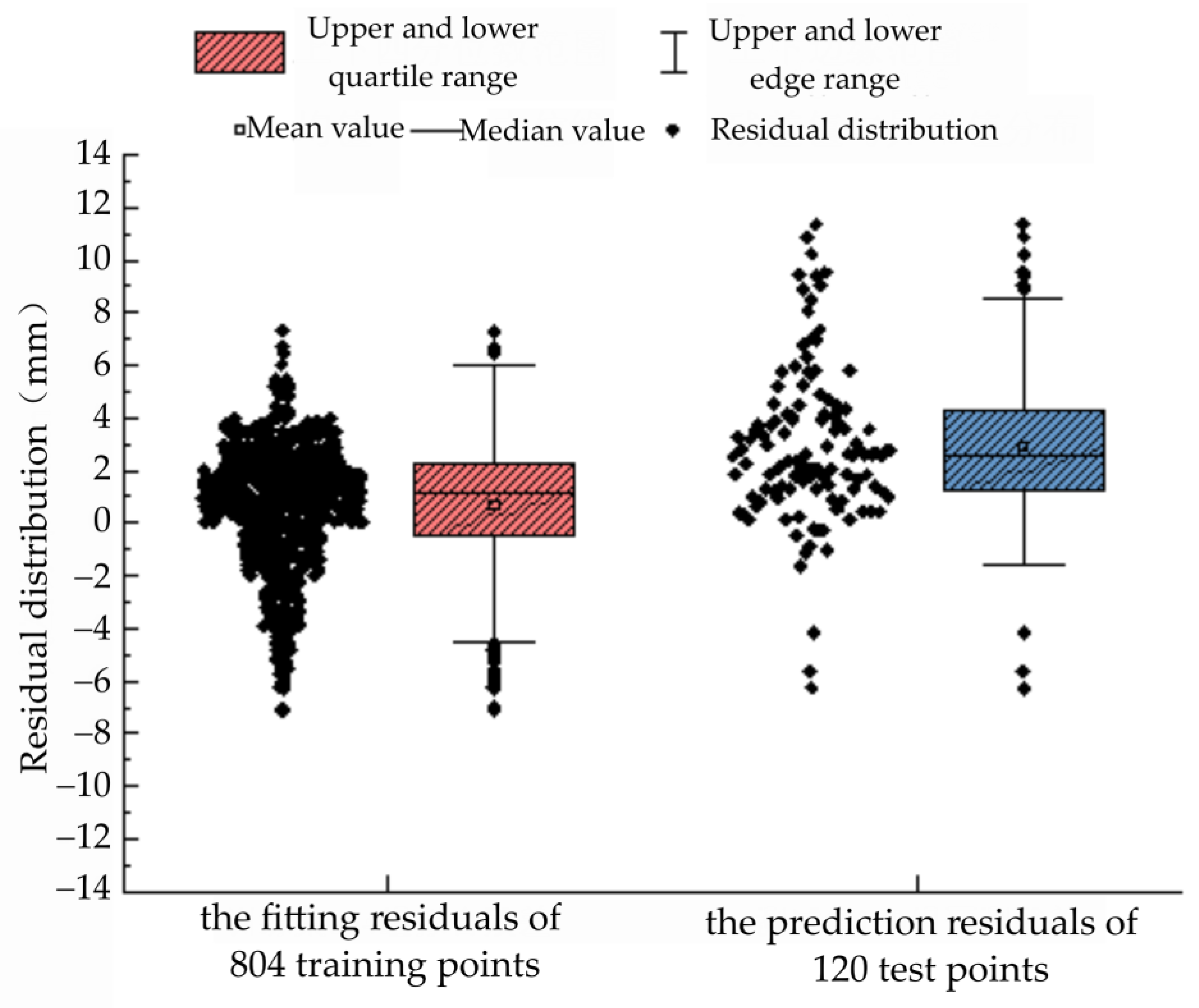
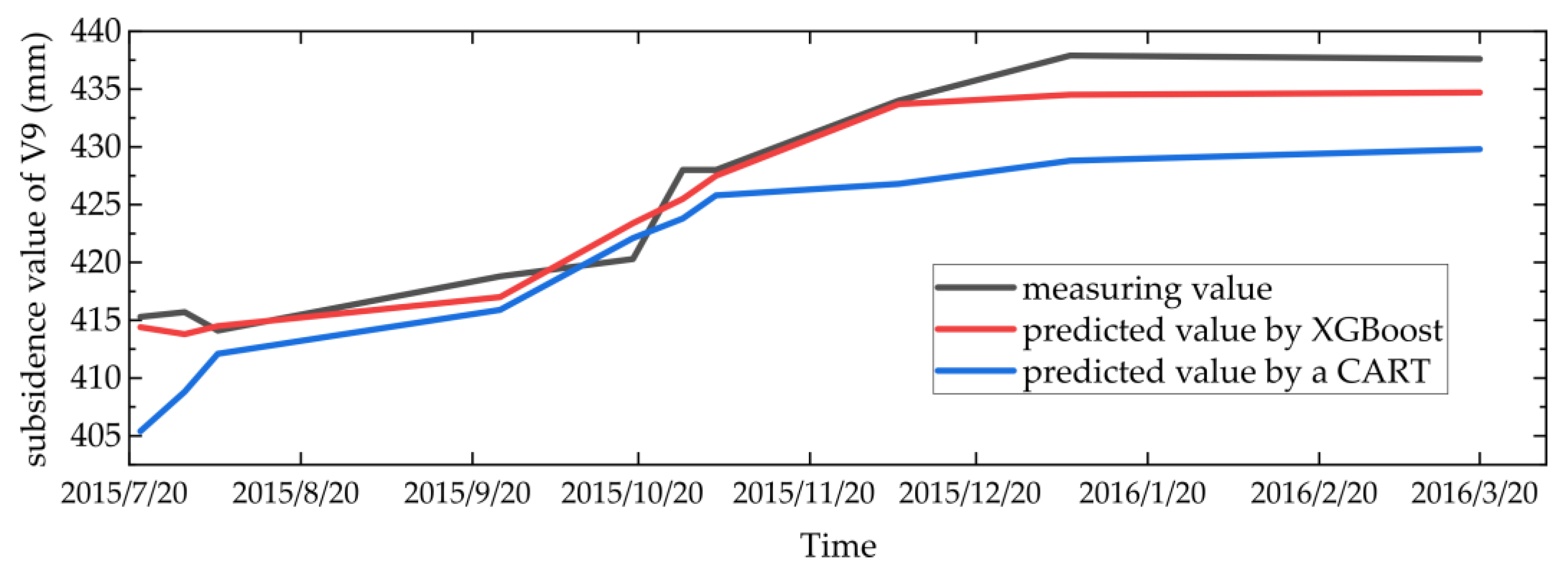
4.1. Prediction Accuracy of the New MMP Model
4.2. Orders of Importance of Factors by SHAP
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tatin, M.; Briffaut, M.; Dufour, F.; Simon, A.; Fabre, J.-P. Thermal displacements of concrete dams: Accounting for water temperature in statistical models. Eng. Struct. 2015, 91, 26–39. [Google Scholar] [CrossRef]
- Hu, Y.; Shao, C.; Gu, C.; Meng, Z. Concrete Dam Displacement Prediction Based on an ISODATA-GMM Clustering and Random Coefficient Model. Water 2019, 11, 714. [Google Scholar] [CrossRef] [Green Version]
- Min, K.; Li, Y.; Yin, Q.; Wen, L. Research on prediction performance of multiple monitoring points model based on support vector machine. IOP Conf. Ser. Mater. Sci. Eng. 2020, 794, 012038. [Google Scholar] [CrossRef]
- He, J.-P.; Tu, Y.-Y.; Shi, Y.-Q. Fusion Model of Multi Monitoring Points on Dam Based on Bayes Theory. Procedia Eng. 2011, 15, 2133–2138. [Google Scholar] [CrossRef] [Green Version]
- Cheng, L.; Zheng, D. Two online dam safety monitoring models based on the process of extracting environmental effect. Adv. Eng. Softw. 2013, 57, 48–56. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.; Toledo, M.Á.; Oñate, E. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Arch. Comput. Methods Eng. 2017, 24, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Statist. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Sun, X.; Zheng, D.; Zhou, M. Spatiotemporal Prediction Model for Settlement Value of Face Rockfill Dam During Operation Period. J. China Three Gorges Univ. Nat. Sci. 2019, 41, 5–8. [Google Scholar]
- Huang, D.; Liu, B.; Dai, W. Building multiple-point displacement model of Wuqiangxi dam based on BP neural network. Geotech. Investig. Surv. 2017, 45, 62–64. [Google Scholar]
- Chai, L.; Qi, D.; Wu, H. Application of multi-point and multidirectional BP Network Model in Dam deformation monitoring. Water Resour. Power 2014, 32, 94–97. [Google Scholar]
- Li, Y.; Min, K.; Zhang, Y.; Wen, L. Prediction of the failure point settlement in rockfill dams based on spatial-temporal data and multiple-monitoring-point models. Eng. Struct. 2021, 243, 112658. [Google Scholar] [CrossRef]
- Lu, X.; Wu, Z.; Zhou, Z.; Chen, J. Research on the Prediction Model of Deformation of High Core Rockfill Dam During Construction Period. Adv. Eng. Sci. 2017, 49, 61–69. [Google Scholar] [CrossRef]
- Kang, F.; Liu, J.; Li, J.; Li, S. Concrete dam deformation prediction model for health monitoring based on extreme learning machine. Struct. Control Health Monit. 2017, 24, e1997. [Google Scholar] [CrossRef]
- Wei, B.; Yuan, D.; Xu, Z.; Li, L. Modified hybrid forecast model considering chaotic residual errors for dam deformation. Struct. Control Health Monit. 2018, 25, e2188. [Google Scholar] [CrossRef]
- Taffese, W.Z.; Sistonen, E. Machine learning for durability and service-life assessment of reinforced concrete structures: Recent advances and future directions. Autom. Constr. 2017, 77, 1–14. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Kim, B.-T. Prediction of relative crest settlement of concrete-faced rockfill dams analyzed using an artificial neural network model. Comput. Geotech. 2008, 35, 313–322. [Google Scholar] [CrossRef]
- Su, H.; Chen, Z.; Wen, Z. Performance improvement method of support vector machine-based model monitoring dam safety: Performance Improvement Method of Monitoring Model of Dam Safety. Struct. Control Health Monit. 2016, 23, 252–266. [Google Scholar] [CrossRef]
- Marandi, S.M.; VaeziNejad, S.M.; Khavari, E. Prediction of Concrete Faced Rock Fill Dams Settlements Using Genetic Programming Algorithm. IJG 2012, 3, 601–609. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Nguyen, L.T.K.; Chung, H.-H.; Tuliao, K.V.; Lin, T.M.Y. Using XGBoost and Skip-Gram Model to Predict Online Review Popularity. SAGE Open 2020, 10, 215824402098331. [Google Scholar] [CrossRef]
- Lim, S.; Chi, S. Xgboost application on bridge management systems for proactive damage estimation. Adv. Eng. Inform. 2019, 41, 100922. [Google Scholar] [CrossRef]
- Shi, N.; Li, Y.; Wen, L.; Zhang, Y. Rapid prediction of landslide dam stability considering the missing data using XGBoost algorithm. Landslides 2022, 19, 2951–2963. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Rahmzadeh, A.; Alam, M.S.; Tremblay, R. Explainable machine learning based efficient prediction tool for lateral cyclic response of post-tensioned base rocking steel bridge piers. Structures 2022, 44, 947–964. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Ibrahim, M.; Ebead, U.; Alam, M.S. Explainable machine learning model and reliability analysis for flexural capacity prediction of RC beams strengthened in flexure with FRCM. Eng. Struct. 2022, 255, 113903. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Truong, G.T.; Shin, M. Development of extreme gradient boosting model for prediction of punching shear resistance of r/c interior slabs. Eng. Struct. 2021, 235, 112067. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Tang, L.; Zhang, W.; Lacasse, S.; Liu, H.; Gao, L. Efficient reliability analysis of earth dam slope stability using extreme gradient boosting method. Acta Geotech. 2020, 15, 3135–3150. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Ebead, U.; Alam, M.S. Machine learning-based shear capacity prediction and reliability analysis of shear-critical RC beams strengthened with inorganic composites. Case Stud. Constr. Mater. 2022, 16, e01008. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Abushanab, A.; Ebead, U.; Alnahhal, W. FAI: Fast, accurate, and intelligent approach and prediction tool for flexural capacity of FRP-RC beams based on super-learner machine learning model. Mater. Today Commun. 2022, 33, 104461. [Google Scholar] [CrossRef]
- AlKhereibi, A.H.; Wakjira, T.G.; Kucukvar, M.; Onat, N.C. Predictive Machine Learning Algorithms for Metro Ridership Based on Urban Land Use Policies in Support of Transit-Oriented Development. Sustainability 2023, 15, 1718. [Google Scholar] [CrossRef]
- Al-Hamrani, A.; Wakjira, T.G.; Alnahhal, W.; Ebead, U. Sensitivity analysis and genetic algorithm-based shear capacity model for basalt FRC one-way slabs reinforced with BFRP bars. Compos. Struct. 2023, 305, 116473. [Google Scholar] [CrossRef]
- Ishfaque, M.; Salman, S.; Jadoon, K.Z.; Danish, A.A.K.; Bangash, K.U.; Qianwei, D. Understanding the Effect of Hydro-Climatological Parameters on Dam Seepage Using Shapley Additive Explanation (SHAP): A Case Study of Earth-Fill Tarbela Dam, Pakistan. Water 2022, 14, 2598. [Google Scholar] [CrossRef]
- Sigtryggsdóttir, F.G.; Snæbjörnsson, J.T.; Grande, L. Statistical Model for Dam-Settlement Prediction and Structural-Health Assessment. J. Geotech. Geoenviron. Eng. 2018, 144, 04018059. [Google Scholar] [CrossRef]
- Liashchynskyi, P.; Liashchynskyi, P. Grid search, random search, genetic algorithm: A big comparison for NAS. arXiv 2019, arXiv:1912.06059. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2960–2968. [Google Scholar]
- Dong, W.; Huang, Y.; Lehane, B.; Ma, G. An artificial intelligence-based conductivity prediction and feature analysis of carbon fiber reinforced cementitious composite for non-destructive structural health monitoring. Eng. Struct. 2022, 266, 114578. [Google Scholar] [CrossRef]
- Panda, C.; Mishra, A.K.; Dash, A.K.; Nawab, H. Predicting and explaining severity of road accident using artificial intelligence techniques, SHAP and feature analysis. Int. J. Crashworthiness 2022. [Google Scholar] [CrossRef]
- Štrumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Shapley, L.S. A Value for N-Person Games. In Classics in Game Theory; Princeton University Press: Princeton, NJ, USA, 1997; Volume 69. [Google Scholar]




| Water Level Component (δH) | Rheology–Soil Weight Component (δε) | Time Effect Component (δT) | Material Component (δm) | |
|---|---|---|---|---|
| Factors |
| Parameters | Value | Range | Note |
|---|---|---|---|
| eta | 0.2 | [0.01, 0.3] | the shrinkage step size |
| max_depth | 5 | [3, 10] | the maximum depth of the decision tree |
| learning_rate | 0.1 | [0.05, 0.3] | the learning rate |
| N | 160 | / | the maximum number of iterations |
| Components from the MMP Model | NO. | Factors | Components from the Traditional Model | NO. | Factors |
|---|---|---|---|---|---|
| Water level component | X1 | Water level component | Y1 | ||
| X2 | Y2 | ||||
| X3 | Y3 | ||||
| Rheology–soil weight component | X4 | Temperaturecomponent | Y4 | ||
| X5 | Y5 | ||||
| X6 | Y6 | ||||
| X7 | Y7 | ||||
| X8 | Location component | Y8 | |||
| Time effect component | X9 | Y9 | |||
| X10 | Time effect component | Y10 | |||
| Material component | X11 | Y11 | |||
| X12 | Note: Time effect components are same in the two models; X5(d2) and Y9(y) are the same. | ||||
| X13 | r | ||||
| Measuring Point | Training Set | Test Set by XGboost | Test Set by CART | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE /mm | RMSE /mm | MAPE/% | R2 | MAE /mm | RMSE /mm | MAPE/% | R2 | MAE /mm | RMSE /mm | MAPE/% | R2 | |
| V2 | 3.41 | 4.18 | 1.54 | 0.88 | 7.31 | 7.74 | 2.65 | 0.85 | 9.54 | 8.65 | 5.88 | 0.49 |
| V3 | 1.34 | 1.57 | 0.34 | 0.97 | 1.95 | 2.18 | 0.47 | 0.94 | 6.87 | 8.64 | 3.76 | 0.56 |
| V4 | 2.24 | 2.58 | 0.54 | 0.95 | 4.00 | 4.19 | 0.88 | 0.93 | 5.88 | 6.00 | 1.56 | 0.58 |
| V5 | 1.49 | 1.92 | 0.24 | 0.98 | 3.17 | 3.54 | 0.50 | 0.92 | 4.67 | 4.99 | 1.09 | 0.58 |
| V6 | 0.93 | 1.37 | 0.17 | 0.99 | 1.35 | 2.05 | 0.24 | 0.96 | 4.56 | 3.77 | 1.88 | 0.64 |
| V7 | 1.27 | 2.02 | 0.39 | 0.94 | 1.97 | 2.49 | 0.55 | 0.92 | 3.64 | 5.85 | 1.55 | 0.56 |
| V9 | 2.39 | 2.86 | 0.62 | 0.95 | 1.77 | 2.09 | 0.41 | 0.93 | 5.47 | 6.16 | 1.2 | 0.59 |
| V10 | 1.80 | 2.23 | 0.26 | 0.98 | 1.67 | 2.23 | 0.24 | 0.95 | 2.67 | 4.73 | 0.89 | 0.65 |
| V11 | 2.44 | 2.68 | 0.49 | 0.96 | 2.14 | 2.48 | 0.42 | 0.93 | 4.34 | 4.53 | 1.14 | 0.67 |
| V12 | 0.68 | 2.04 | 0.22 | 0.97 | 1.22 | 3.15 | 0.34 | 0.94 | 1.54 | 3.86 | 0.39 | 0.73 |
| V14 | 1.23 | 2.22 | 0.34 | 0.94 | 4.12 | 4.79 | 1.00 | 0.90 | 8.12 | 8.42 | 3.55 | 0.62 |
| V15 | 0.61 | 2.46 | 0.23 | 0.95 | 7.08 | 7.55 | 2.03 | 0.85 | 10.57 | 10.05 | 7.89 | 0.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, L.; Wang, T.; Wang, Y.; Wang, Z.; Min, K. A Prediction Model and Factor Importance Analysis of Multiple Measuring Points for Concrete Face Rockfill Dam during the Operation Period. Water 2023, 15, 1081. https://doi.org/10.3390/w15061081
Shao L, Wang T, Wang Y, Wang Z, Min K. A Prediction Model and Factor Importance Analysis of Multiple Measuring Points for Concrete Face Rockfill Dam during the Operation Period. Water. 2023; 15(6):1081. https://doi.org/10.3390/w15061081
Chicago/Turabian StyleShao, Lei, Ting Wang, Youde Wang, Zilong Wang, and Kaiyi Min. 2023. "A Prediction Model and Factor Importance Analysis of Multiple Measuring Points for Concrete Face Rockfill Dam during the Operation Period" Water 15, no. 6: 1081. https://doi.org/10.3390/w15061081
APA StyleShao, L., Wang, T., Wang, Y., Wang, Z., & Min, K. (2023). A Prediction Model and Factor Importance Analysis of Multiple Measuring Points for Concrete Face Rockfill Dam during the Operation Period. Water, 15(6), 1081. https://doi.org/10.3390/w15061081





