Evaluating the Feasibility of the Liuxihe Model for Forecasting Inflow Flood to the Fengshuba Reservoir
Abstract
:1. Introduction
2. Data and Methods
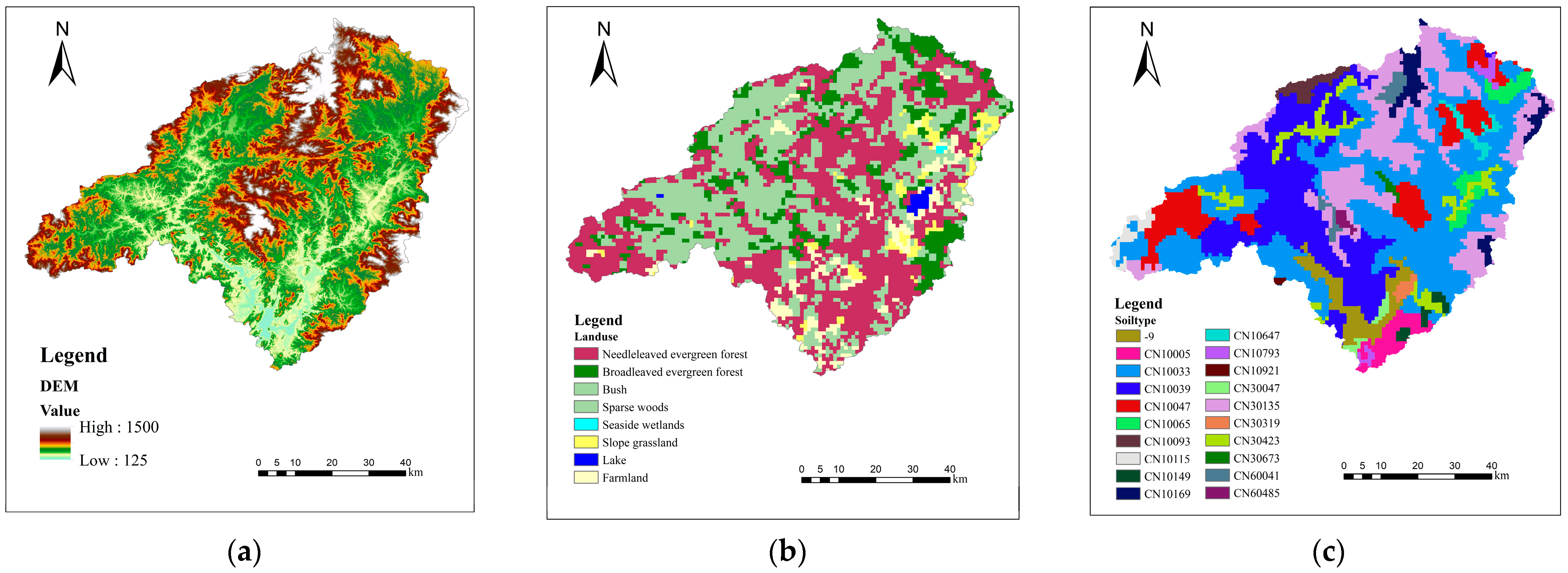
2.1. Watershed Physical Characteristics
2.2. Hydrological Data
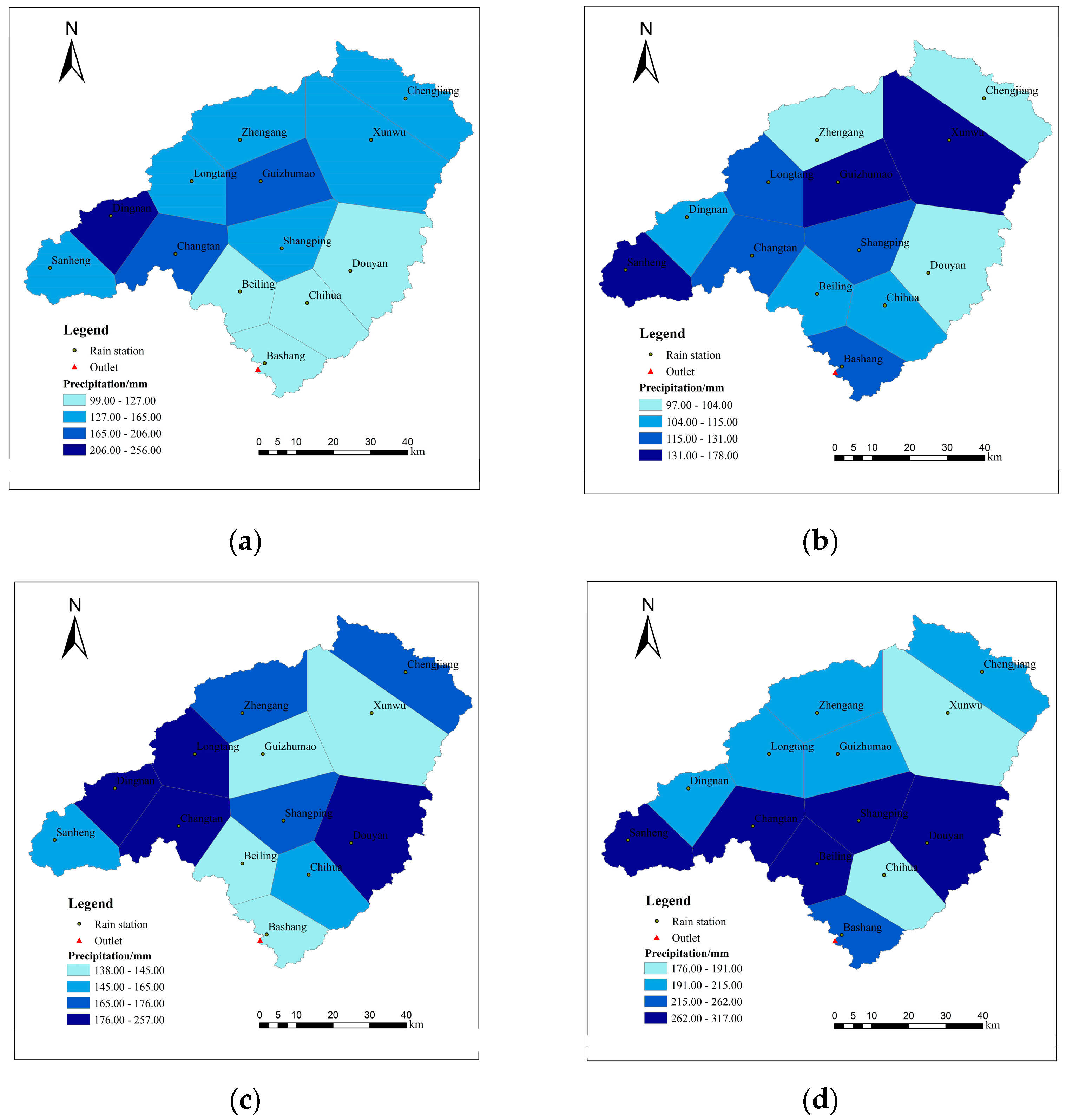
2.3. Temporal and Spatial Distribution of Rainfall
3. Model Construction
3.1. Liuxihe Model Setup
3.2. Derivation of Initial Parameters
- Topographic parameters include the flow direction and slope and are obtained from the DEM data;
- The main meteorological parameter is evaporation capacity. Based on experience, the evaporation capacity of all units was set at 5 mm/d [17];
- The land use parameters include the slope roughness and evaporation coefficient, among which the evaporation coefficient is an insensitive parameter [17]. According to the parameterization experience of the Liuxihe model, the evaporation coefficient was uniformly set at 0.7 [17]. The slope roughness is a sensitive parameter, and the value in the recommended relevant literature was adopted [43,44], as shown in Table 2;
- 4.
- Soil parameters include the saturated water content, saturated hydraulic conductivity, field water holding rate, wilting water content, soil thickness, and soil properties. The value of soil properties was set uniformly to 2.5 [17], and the other parameters were calculated using the soil hydraulic characteristic calculator proposed by Arya et al. [45]. The results are shown in Table 3.
3.3. Parameter Optimization Method
3.4. Model Valiadtion
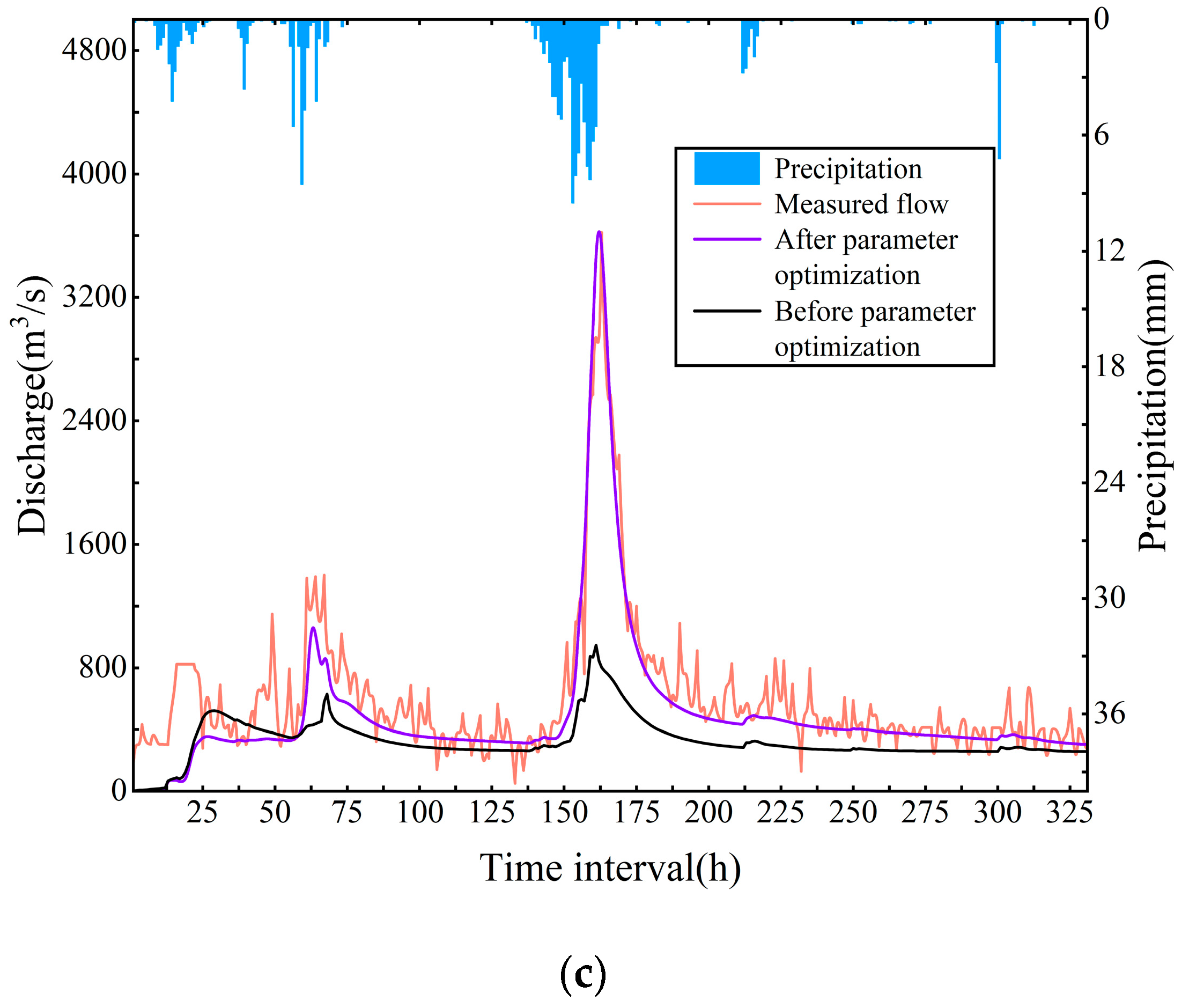
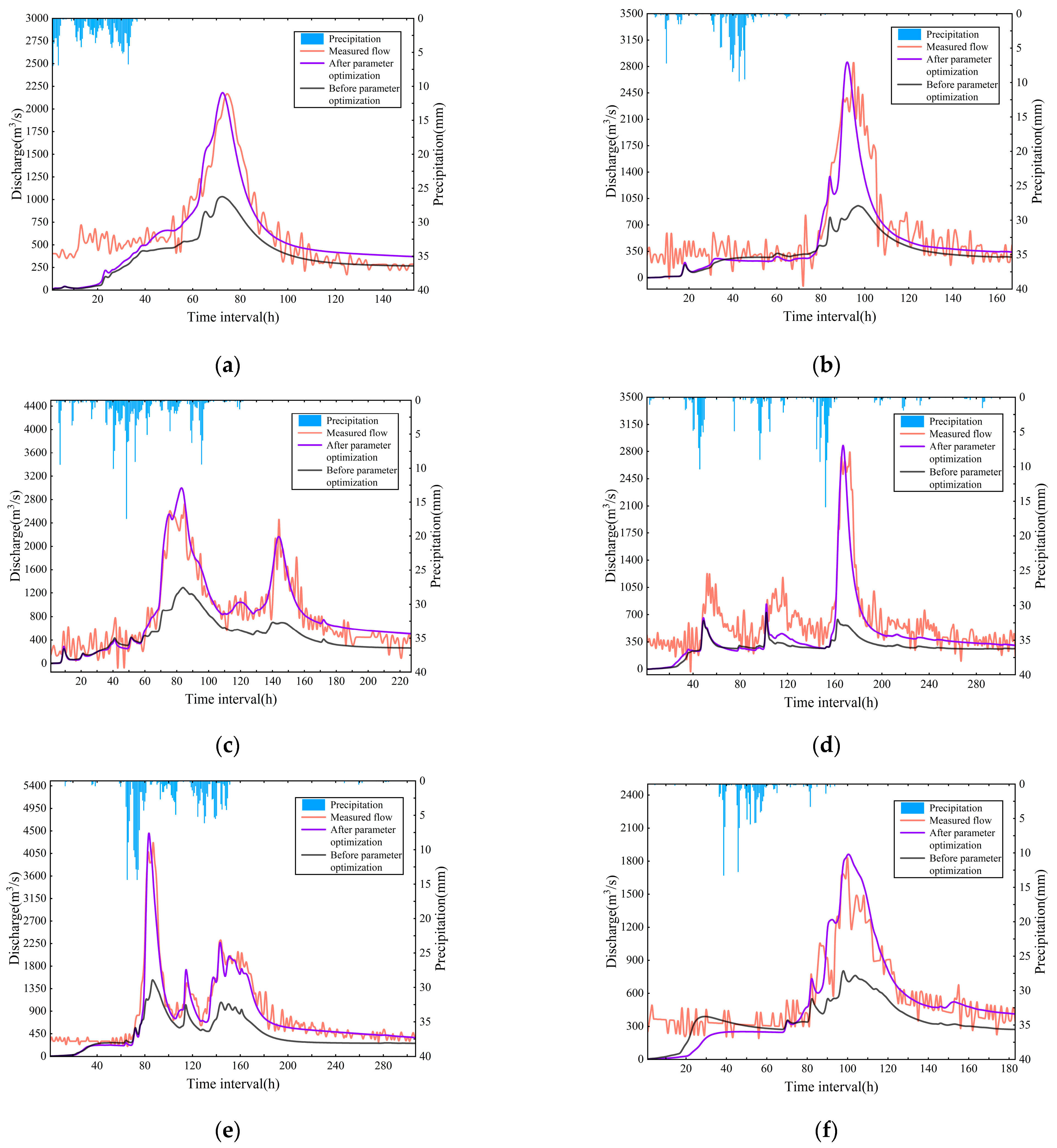
4. Results
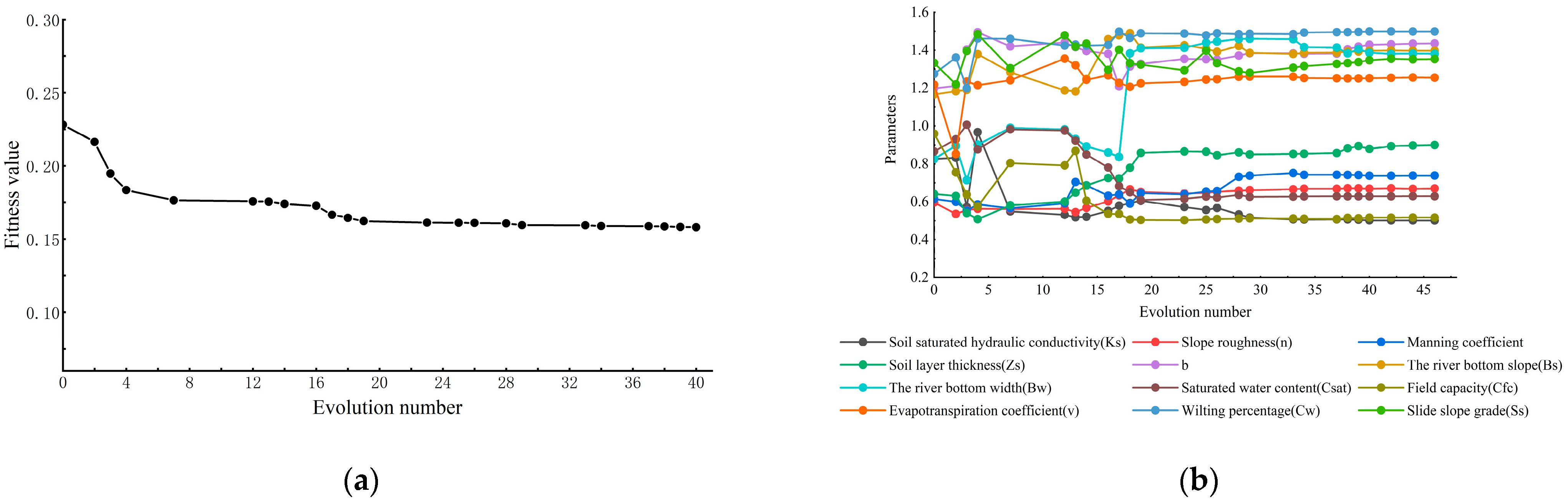
4.1. Parameter Optimization of the Liuxihe Model
4.2. Model Performance Evaluation
4.3. Influence of Parameter Optimization
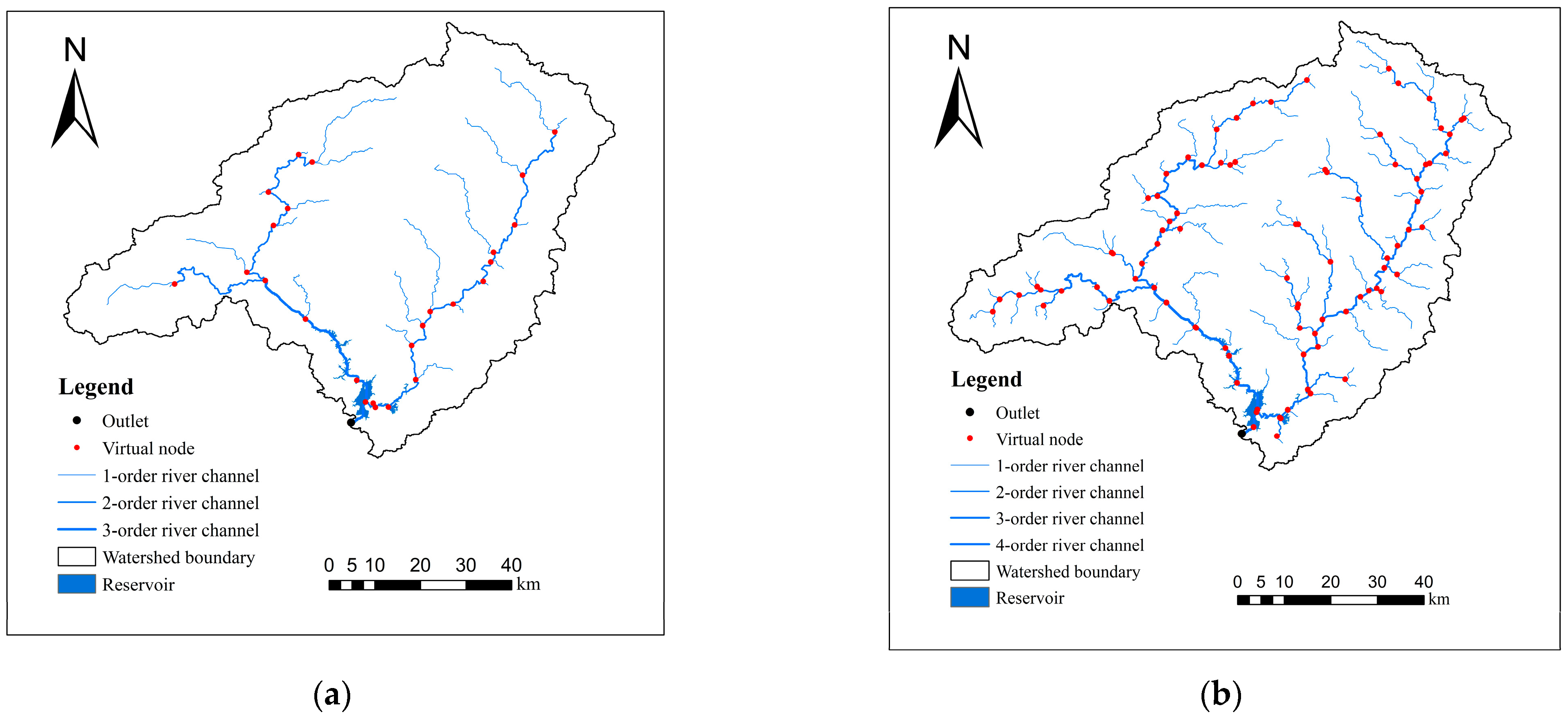
4.4. Influence of River Classification on Simulation Results
5. Discussion
- Rainfall is a key factor in the formation of floods, and the quality of rainfall interpolation methods can affect the amount of precipitation on the surface of the basin. The Liuxihe model uses the most widely used and common rainfall data interpolation technique (Thiessen polygons). Therefore, in order to approach the true precipitation situation on the surface of the basin, improvements are needed in the rainfall interpolation method.
- We performed a simulation analysis without considering the operation of the upstream watershed of the Fengshuba Reservoir. The reservoir flow simulation modeled the natural runoff and confluence within the basin, which eventually reaches Fengshuba Reservoir without factoring in the reservoir’s impact, but the reality is that it will be affected by the operation of the reservoir.
6. Conclusions
- The Liuxihe model showed good simulation accuracy for reservoir inflow floods. The average error of the flood peak was <0.02, and the average error of the flood peak time was <3 h. The Liuxihe model was found to be suitable for flood forecasting in the Fengshuba Reservoir Basin. The statistical index values of some simulations were low because the measured flood flow was highly irregular; fluctuations and outliers existed.
- The initial parameters of the model were uncertain, but the simulation performance of the Liuxihe model was improved significantly through parameter optimization. After parameter optimization, the average Nash–Sutcliffe coefficient was 31% higher, the average peak flow error was 46% lower, the average correlation coefficient was 9% higher, and the average peak flow time error was reduced.
- The influence of different river classifications on the model was examined. Compared with that of a third-class river, the simulation performance of the Liuxihe model constructed using a fourth-class river was better: there was an increase in the average value of the Nash–Sutcliffe coefficient by 6.5% and the average value of the correlation coefficient by 5.7% as well as a decrease in the process relative error by 4.8% and the average peak error by 1%.
- The distribution of precipitation in the watershed is uneven in time and space. However, the Liuxihe model can still simulate the uneven distribution of precipitation with high accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- El Alfy, M. Assessing the Impact of Arid Area Urbanization on Flash Floods Using GIS, Remote Sensing, and HEC-HMS Rainfall–Runoff Modeling. Hydrol. Res. 2016, 47, 1142–1160. [Google Scholar] [CrossRef] [Green Version]
- Jie, M.-X.; Chen, H.; Xu, C.-Y.; Zeng, Q.; Tao, X. A Comparative Study of Different Objective Functions to Improve the Flood Forecasting Accuracy. Hydrol. Res. 2016, 47, 718–735. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Yuan, D.; Liu, J.; Jiang, Y.; Chen, Y.; Hsu, K.L.; Sorooshian, S. Predicting Floods in a Large Karst River Basin by Coupling PERSIANN-CCS QPEs with a Physically Based Distributed Hydrological Model. Hydrol. Earth Syst. Sci. 2019, 23, 1505–1532. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Li, J.; Wang, H.; Qin, J.; Dong, L. Large-Watershed Flood Forecasting with High-Resolution Distributed Hydrological Model. Hydrol. Earth Syst. Sci. 2017, 21, 735–749. [Google Scholar] [CrossRef] [Green Version]
- Crawford, N.H.; Linsley, R.K. Digital Simulation in Hydrology: Stanford Watershed Model IV; Technical Report, No. 39; Department of Civil Engineering, Stanford University: Stanford, CA, USA, 1966. [Google Scholar]
- Todini, E. The ARNO Rainfall—Runoff Model. J. Hydrol. 1996, 175, 339–382. [Google Scholar] [CrossRef]
- Lu, M. Review and Prospect of Xin’anjiang Model Research. J. Water Resour. 2021, 52, 432–441. [Google Scholar] [CrossRef]
- Chen, Y.; Tan, J.; Wang, H.; Dong, L.; Chen, H. Flood forecasting method for small and medium rivers based on the Liuxihe model. Water Conserv. Hydropower Technol. 2017, 48, 12–19, 27. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, Y.; Wang, L.; Wu, S.; Shao, G. Flood Forecasting Scheme of Nanshui Reservoir Based on Liuxihe Model. Trop. Cyclone Res. Rev. 2021, 10, 106–115. [Google Scholar] [CrossRef]
- Xu, S.; Chen, Y.; Xing, L.; Li, C. Baipenzhu Reservoir Inflow Flood Forecasting Based on a Distributed Hydrological Model. Water 2021, 13, 272. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An Introduction to the European Hydrological System—Systeme Hydrologique Europeen, “SHE”, 1: History and Philosophy of a Physically-Based, Distributed Modelling System. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burges, S.J. A Simple Hydrologically Based Model of Land Surface Water and Energy Fluxes for General Circulation Models. J. Geophys. Res. 1994, 99, 14415. [Google Scholar] [CrossRef]
- Vieux, B.E. Distributed Hydrologic Modeling. In Encyclopedia of GIS; Shekhar, S., Xiong, H., Eds.; Springer: Boston, MA, USA, 2008; pp. 250–254. ISBN 978-0-387-35973-1. [Google Scholar]
- Beven, K.J.; Kirkby, M.J.; Freer, J.E.; Lamb, R. A History of TOPMODEL. Hydrol. Earth Syst. Sci. 2021, 25, 527–549. [Google Scholar] [CrossRef]
- Weber, T.; McPhee, M.J.; Anderssen, R.S. (Eds.) Agricultural Flood and Drought Risk Reduction by a Proposed Multi-Purpose Dam: A Case Study of the Malwathoya River Basin, Sri Lanka. In Proceedings of the 21st International Congress on Modelling and Simulation MODSIM2015, Broadbeach, Australia, 29 November–4 December 2015. [Google Scholar]
- Okazumi, T.; Miyamoto, M.; Shrestha, B.; Gusyev, M. Uncertainty Estimation During the Process of Flood Risk Assessment in Developing Countries—Case Study in the Pampanga River Basin. J. Disaster Res. 2014, 9, 69–77. [Google Scholar] [CrossRef]
- Chen, Y.; Ren, Q.; Huang, F.; Xu, H.; Cluckie, I. Liuxihe Model and Its Modeling to River Basin Flood. J. Hydrol. Eng. 2011, 16, 33–50. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Tan, J.; Li, M.; Dong, L. Research on Flood Forecasting of Meijiang River Basin Based on Liuxihe Model. China Rural Water Conserv. Hydropower 2017, 11, 124–128, 133. [Google Scholar]
- Chen, Y.; Xu, H.; Huang, F. Preliminary Study on Inflow Flood Simulation of Small and Medium Reservoirs Based on the Liuxihe Model. In River Development, Protection and Sustainable Utilization of Water Resources, Proceedings of the Sixth China Water Forum; Water Conservancy and Hydropower Press: Bejing, China, 2008; pp. 242–245. [Google Scholar]
- Huang, H.; Chen, Y.; Jiang, H. A Preliminary Study on the Flood Forecasting Scheme of the Wujiang River Basin Based on the Liuxihe Model. In Proceedings of the Fourth Youth Science and Technology Forum of the Chinese Water Conservancy Society; Water Conservancy and Hydropower Press: Bejing, China, 2008; pp. 265–270. [Google Scholar]
- Hutting, R.J.M. Hydrological Modelling of the Liuxihe River Basin to Contribute to the Development of Flood Management. Available online: https://essay.utwente.nl/687/ (accessed on 9 February 2023).
- Liu, L.; Ao, T.; Zhou, L.; Takeuchi, K.; Gusyev, M.; Zhang, X.; Wang, W.; Ren, Y. Comprehensive Evaluation of Parameter Importance and Optimization Based on the Integrated Sensitivity Analysis System: A Case Study of the BTOP Model in the Upper Min River Basin, China. J. Hydrol. 2022, 610, 127819. [Google Scholar] [CrossRef]
- Yang, X.; Jomaa, S.; Zink, M.; Fleckenstein, J.H.; Borchardt, D.; Rode, M. A New Fully Distributed Model of Nitrate Transport and Removal at Catchment Scale. Water Resour. Res. 2018, 54, 5856–5877. [Google Scholar] [CrossRef]
- Xu, H.; Chen, Y.; Zeng, B.; He, J.; Liao, Z. Application of SCE-UA algorithm in parameter optimization of Liuxihe model. Trop. Geogr. 2012, 32, 32–37. [Google Scholar] [CrossRef]
- Xing, L.; Chen, Y.; Feng, Y.; Huang, X.; Huang, Z. Research on Forecasting Model of Xinfengjiang Reservoir Inflow Flood Based on Liuxihe Model. Hydrology 2022, 42, 47–53. [Google Scholar] [CrossRef]
- Duan, W.; Guo, S.; Wang, J.; Liu, D. Impact of Cascaded Reservoirs Group on Flow Regime in the Middle and Lower Reaches of the Yangtze River. Water 2016, 8, 218. [Google Scholar] [CrossRef] [Green Version]
- Tan, J.; Chen, Y.; Li, M.; Wang, H. Influence of river course data on Liuxihe model for forecasting floods in small and medium rivers. People’s Yangtze River 2018, 49, 23–29. [Google Scholar] [CrossRef]
- Tan, J.; Chen, Y.; Wang, H.; Zhang, J.; Li, M. Influence of Digital Water System Classification on Flood Forecasting of Small Rivers in Liuxihe Model. J. Yangtze River Acad. Sci. 2018, 35, 57–63. [Google Scholar]
- Tan, J.; Chen, Y.; Wang, H. Application of Thiessen polygon rainfall interpolation method in flood forecasting of Liuxi River model. China Rural Water Conserv. Hydropower 2017, 1, 88–93. [Google Scholar]
- Chen, Y.; Li, J.; Xu, H. Improving Flood Forecasting Capability of Physically Based Distributed Hydrological Models by Parameter Optimization. Hydrol. Earth Syst. Sci. 2016, 20, 375–392. [Google Scholar] [CrossRef] [Green Version]
- Liao, Z.; Chen, Y.; Xu, H.; Yan, W.; Ren, Q. Sensitivity Analysis of Liuxihe Model Parameters Based on E-FAST. Trop. Geogr. 2012, 32, 606–612+632. [Google Scholar] [CrossRef]
- Fan, Z.; Hao, Z.; Chen, Y.; Wang, J.; Huang, F. Application and research of Liuxihe model in flood simulation of Baipenzhu Reservoir. J. Sun Yat-Sen Univ. (Nat. Sci. Ed.) 2012, 51, 113–118. [Google Scholar]
- Zhu, D.; Das, S.; Ren, Q. Hydrological Appraisal of Climate Change Impacts on the Water Resources of the Xijiang Basin, South China. Water 2017, 9, 793. [Google Scholar] [CrossRef] [Green Version]
- Zhu, D.; Wang, G.; Ren, Q.; Ilyas, A.M. Hydrological Evaluation of Hourly Merged Satellite–Station Precipitation Product in the Mountainous Basin of China Using a Distributed Hydrological Model. Meteorol. Appl. 2020, 27, e1909. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, Y.; Sun, H.; Liu, J. Remote Sensing-Supported Flood Forecasting of Urbanized Watersheds—A Case Study in Southern China. Remote Sens. 2022, 14, 6129. [Google Scholar] [CrossRef]
- Kumar, B.; Lakshmi, V.; Patra, K.C. Evaluating the Uncertainties in the SWAT Model Outputs Due to DEM Grid Size and Resampling Techniques in a Large Himalayan River Basin. J. Hydrol. Eng. 2017, 22, 04017039. [Google Scholar] [CrossRef]
- Wei, Z.; Chen, Y.; Liu, Y.; Dong, L.; Xu, Z.; Wang, H. Research on Distributed Model of Baiguishan Reservoir Flood Forecasting. China Rura. Water Conserv. Hydropower 2017, 2, 57–62, 66. [Google Scholar]
- Li, C.; Chen, Y.; Ye, S.; Wang, C.; Chen, W. Study on the Liuxihe Model for Incoming Flood Forecast of Shangyoujiang Reservoir. J. Hydroelectr. Eng. 2021, 40, 1–12. [Google Scholar]
- Wang, H.; Chen, Y. Identifying Key Hydrological Processes in Highly Urbanized Watersheds for Flood Forecasting with a Distributed Hydrological Model. Water 2019, 11, 1641. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Xu, H.; Li, J. Automatic optimization of parameters of distributed model for flood forecasting in river basins. J. Sun Yat-Sen Univ. (Nat. Sci. Ed.) 2017, 56, 125–133. [Google Scholar] [CrossRef]
- Quantitative Analysis of Watershed Geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [CrossRef] [Green Version]
- Liao, Z.; Chen, Y.; Xu, H.; He, J. Liuxihe Model Research on Rainstorm Flood Forecasting in Tiantoushui Basin. People’s Yangtze River 2012, 43, 12–16. [Google Scholar] [CrossRef]
- Wang, Z.-M.; Batelaan, O.; De Smedt, F. A Distributed Model for Water and Energy Transfer between Soil, Plants and Atmosphere (WetSpa). Phys. Chem. Earth 1996, 21, 189–193. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The Extraction of Drainage Networks from Digital Elevation Data. Comput. Vis. Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Arya, L.M.; Paris, J.F. A Physicoempirical Model to Predict the Soil Moisture Characteristic from Particle-Size Distribution and Bulk Density Data. Soil Sci. Soc. Am. J. 1981, 45, 1023–1030. [Google Scholar] [CrossRef]

| Flood Event No. | Start Time | End Time | Duration (h) | Total Rainfall (mm) | Peak Flow (m3/s) |
|---|---|---|---|---|---|
| 2010052211 | 22 May 2010 | 25 May 2010 | 62 | 775 | 1460 |
| 2011051315 | 13 May 2011 | 19 May 2011 | 153 | 2033 | 2170 |
| 2013051811 | 18 May 2013 | 24 May 2013 | 145 | 1503 | 1570 |
| 2014051901 | 19 May 2014 | 25 May 2014 | 167 | 1661 | 2850 |
| 2015052419 | 24 May 2015 | 28 May 2015 | 91 | 1037 | 1420 |
| 2016012613 | 26 Jan. 2016 | 4 Feb. 2016 | 204 | 2093.6 | 3030 |
| 2016031715 | 17 Mar. 2016 | 27 Mar. 2016 | 227 | 3094 | 3010 |
| 2016041006 | 10 April 2016 | 24 April 2016 | 337 | 2469 | 2990 |
| 2016042408 | 24 April 2016 | 8 May 2016 | 331 | 2322 | 3620 |
| 2016052003 | 20 May 2016 | 25 May 2016 | 118 | 1201 | 1490 |
| 2016101923 | 19 Oct. 2016 | 25 Oct. 2016 | 139 | 1334 | 1820 |
| 2016112501 | 25 Nov. 2016 | 30 Nov. 2016 | 126 | 782 | 1310 |
| 2017061201 | 12 June 2017 | 25 June 2017 | 326 | 2886 | 1480 |
| 2019041710 | 17 Apr. 2019 | 21 Apr. 2019 | 90 | 1052 | 1270 |
| 2019050417 | 4 May 2019 | 10 May 2019 | 135 | 1232 | 1060 |
| 2019060702 | 7 June 2019 | 19 June 2019 | 307 | 3149 | 4460 |
| 2019062012 | 20 June 2019 | 28 June 2019 | 183 | 1491.5 | 1830 |
| 2020060703 | 7 June 2020 | 12 June 2020 | 135 | 1326 | 1490 |
| Land Use Type | Evaporation Coefficient | Slope Roughness Coefficient |
|---|---|---|
| Evergreen needle-leaf forest | 0.7 | 0.4 |
| Evergreen broadleaf forest | 0.7 | 0.6 |
| Bush | 0.7 | 0.4 |
| Sparse woods | 0.7 | 0.3 |
| Coastal wetland | 0.7 | 0.2 |
| Slope grassland | 0.7 | 0.1 |
| Lake | 0.7 | 0.2 |
| Farmland | 0.7 | 0.15 |
| Soil Type | Thickness of Soil Layer (mm) | Saturated Water Content | Field Moisture Retention | Saturated Hydraulic Conductivity (mm·h−1) | Soil Characteristic Coefficient | Wilting Moisture Content |
|---|---|---|---|---|---|---|
| CN-9 | 0.0001 | 0.0001 | 0.0001 | 0.0001 | 2.5 | 0.0001 |
| CN10005 | 1000 | 0.502 | 0.355 | 9.82 | 2.5 | 0.136 |
| CN10033 | 1000 | 0.451 | 0.3 | 8.64 | 2.5 | 0.176 |
| CN10039 | 600 | 0.515 | 0.422 | 1.95 | 2.5 | 0.296 |
| CN10047 | 1000 | 0.455 | 0.319 | 6.34 | 2.5 | 0.192 |
| CN10065 | 1000 | 0.491 | 0.433 | 0.47 | 2.5 | 0.315 |
| CN10093 | 1000 | 0.454 | 0.144 | 74.49 | 2.5 | 0.063 |
| CN10115 | 700 | 0.500 | 0.377 | 4.89 | 2.5 | 0.221 |
| CN10149 | 1000 | 0.481 | 0.390 | 1.86 | 2.5 | 0.262 |
| CN10169 | 1000 | 0.458 | 0.252 | 23.82 | 2.5 | 0.110 |
| CN10647 | 1000 | 0.454 | 0.337 | 3.99 | 2.5 | 0.214 |
| CN10793 | 1110 | 0.436 | 0.249 | 15.76 | 2.5 | 0.149 |
| CN10921 | 1000 | 0.495 | 0.391 | 2.78 | 2.5 | 0.255 |
| CN30047 | 1500 | 0.461 | 0.265 | 20.78 | 2.5 | 0.115 |
| CN30135 | 1000 | 0.435 | 0.207 | 28.33 | 2.5 | 0.121 |
| CN30319 | 800 | 0.453 | 0.239 | 26.07 | 2.5 | 0.109 |
| CN30423 | 670 | 0.446 | 0.240 | 21.87 | 2.5 | 0.126 |
| CN30673 | 1000 | 0.443 | 0.201 | 29.31 | 2.5 | 0.121 |
| CN60041 | 870 | 0.438 | 0.260 | 13.86 | 2.5 | 0.154 |
| CN60485 | 250 | 0.470 | 0.323 | 8.38 | 2.5 | 0.175 |
| Parameter | Average Nash–Sutcliffe Coefficient | Average Correlation Coefficient | Average Process Relative Error | Average Peak Error | Average Water Balance Coefficient | Average Peak Time Error |
|---|---|---|---|---|---|---|
| Optimized | 0.58 | 0.85 | 0.65 | 0.03 | 0.98 | 2.8 |
| Parameter | Average Nash–Sutcliffe Coefficient | Average Correlation Coefficient | Average Process Relative Error | Average Peak Error | Average Water Balance Coefficient | Average Peak Time Error |
|---|---|---|---|---|---|---|
| Optimized | 0.58 | 0.85 | 0.65 | 0.03 | 0.98 | 2.8 |
| Initial | 0.27 | 0.76 | 0.64 | 0.49 | 0.69 | −3.33 |
| Parameters | Saturated Water Content (Csat) | Slope Roughness (n) | Manning Coefficient | Evaporation Coefficient (v) | River Bottom Slope (Bs) | River Bottom Width (Bw) |
|---|---|---|---|---|---|---|
| 2016042408 (4-level) | 0.629 | 0.67 | 0.738 | 1.255 | 1.397 | 1.381 |
| 2016042408 (3-level) | 1.343 | 1.232 | 1.496 | 0.542 | 0.5 | 0.771 |
| Flood Event Number | NSE | R | PRE | E | WBC | ∆H (h) |
|---|---|---|---|---|---|---|
| 2010052211 | 0.593 | 0.837 | 0.399 | 0.016 | 0.922 | 0 |
| 0.572 | 0.814 | 0.393 | 0.061 | 0.864 | −1 | |
| 2011051315 | 0.705 | 0.864 | 0.569 | 0.008 | 0.91 | −1 |
| 0.62 | 0.808 | 0.655 | 0.021 | 0.886 | −4 | |
| 2013051811 | 0.482 | 0.776 | 0.338 | 0.061 | 0.892 | 20 |
| 0.497 | 0.778 | 0.327 | 0.072 | 0.898 | 12 | |
| 2014051901 | 0.784 | 0.908 | 0.432 | 0.016 | 0.803 | −3 |
| 0.84 | 0.924 | 0.432 | 0.003 | 0.932 | −3 | |
| 2015052419 | 0.334 | 0.816 | 0.487 | 0.012 | 0.691 | −2 |
| 0.484 | 0.805 | 0.425 | 0.002 | 0.809 | 2 | |
| 2016012613 | 0.298 | 0.765 | 1.542 | 0.022 | 1.391 | −1 |
| 0.484 | 0.762 | 0.968 | 0.065 | 1.248 | −3 | |
| 2016031715 | 0.768 | 0.889 | 0.968 | 0.002 | 1.043 | −2 |
| 0.683 | 0.837 | 1.204 | 0.132 | 1.081 | −6 | |
| 2016041006 | 0.569 | 0.847 | 0.644 | 0.025 | 0.697 | −6 |
| 0.522 | 0.776 | 0.777 | 0.056 | 0.845 | −9 | |
| 2016042408 | 0.715 | 0.876 | 0.667 | 0.013 | 0.844 | −1 |
| 0.572 | 0.82 | 0.742 | 0.016 | 0.759 | −2 | |
| 2016052003 | 0.593 | 0.88 | 0.476 | 0.024 | 0.876 | 2 |
| 0.406 | 0.771 | 0.524 | 0.023 | 0.849 | −3 | |
| 2016101923 | 0.465 | 0.789 | 0.634 | 0.068 | 1.154 | −2 |
| 0.423 | 0.751 | 0.731 | 0.057 | 1.225 | −4 | |
| 2016112501 | 0.11 | 0.714 | 0.906 | 0.019 | 1.25 | 3 |
| 0 | 0.699 | 1.037 | 0.014 | 1.377 | 3 | |
| 2017061201 | 0.5 | 0.74 | 2.002 | 0.091 | 0.961 | 44 |
| 0.259 | 0.574 | 2.411 | 0.077 | 0.943 | 42 | |
| 2019041710 | 0.763 | 0.92 | 0.464 | 0.047 | 1.026 | 5 |
| 0.632 | 0.812 | 0.573 | 0.01 | 0.991 | 2 | |
| 2019050417 | 0.487 | 0.859 | 0.312 | 0.06 | 1.305 | 3 |
| 0.467 | 0.799 | 0.38 | 0.003 | 1.116 | 0 | |
| 2019060702 | 0.913 | 0.964 | 0.254 | 0.01 | 0.887 | −4 |
| 0.83 | 0.92 | 0.343 | 0.03 | 1.05 | −1 | |
| 2019062012 | 0.679 | 0.918 | 0.32 | 0.02 | 0.944 | 0 |
| 0.629 | 0.869 | 0.317 | 0.022 | 0.783 | −3 | |
| 2020060703 | 0.659 | 0.87 | 0.333 | 0.023 | 0.987 | −3 |
| 0.335 | 0.689 | 0.37 | 0.03 | 0.798 | −4 | |
| Average indicator | 0.579 | 0.846 | 0.652 | 0.029 | 0.976 | 2.8 |
| 0.514 | 0.789 | 0.7 | 0.039 | 0.97 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Chen, Y.; Zhu, Y.; Xu, S. Evaluating the Feasibility of the Liuxihe Model for Forecasting Inflow Flood to the Fengshuba Reservoir. Water 2023, 15, 1048. https://doi.org/10.3390/w15061048
Zhao Y, Chen Y, Zhu Y, Xu S. Evaluating the Feasibility of the Liuxihe Model for Forecasting Inflow Flood to the Fengshuba Reservoir. Water. 2023; 15(6):1048. https://doi.org/10.3390/w15061048
Chicago/Turabian StyleZhao, Yanjun, Yangbo Chen, Yanzheng Zhu, and Shichao Xu. 2023. "Evaluating the Feasibility of the Liuxihe Model for Forecasting Inflow Flood to the Fengshuba Reservoir" Water 15, no. 6: 1048. https://doi.org/10.3390/w15061048





