Recent Advances and Challenges in the Inverse Identification of Thermal Diffusivity of Natural Ice in China

Abstract

The ice thermal parameters are the key to reasonably simulating ice phenology, distribution, and thickness, but they have always been a “vulnerable group” in ice research. Technically, it may seem simple to obtain accurate ice thermal property parameters, but in reality, there are numerous impact factors, requiring a rigorous research process. In the 1980s, the thermal conductivity of ice was explored in the field and laboratory, after which there has been no significant progress in China. In this century, mathematics is introduced, after which the inversion identification and analysis with the time-series data of the vertical temperature profiles of ice layers by in situ testing are carried out. The in situ thermal diffusivities of different natural ices were obtained and cross-validated with the inversion identification results. Both natural freshwater ice and sea ice exhibited differences in the thermal diffusivity of the pure ice chosen for the current simulations due to impurities within the unfrozen water among the ice crystals, but the trends are consistent with the results of a small number of laboratory tests on different types of saltwater frozen ice. In this paper, the inversion identification results of the thermal diffusivity of typical ice were selected, and the factors constraining the thermal diffusivities were analyzed. The importance of parameterizing the thermal diffusivity in the phase transition zone of ice under the trend of global warming was illustrated. Future research ideas on the physical mechanism, application value, and parameterization scheme of the thermal diffusivity of natural ice were envisaged.

1. Introduction

Thermal conductivity indicates the thermal conduction properties of materials, while thermal diffusivity not only reflects their thermal conduction properties but also takes into account the effects of specific heat and density. In steady-state heat conduction, the thermal conductivity determines the capacity of heat transmission because the inner temperature of the materials does not change with time. Conversely, in unsteady state conduction, the temperature of the materials changes with time, so the thermal diffusivity determines the temperature distribution. The temperature in natural ice changes constantly due to unsteady heat conduction [1,2], so the thermal diffusivity of ice plays an important role. The accuracy of the ice thermal diffusivity improves the water-ice-air coupling model. In most previous studies, especially when simulating large-scale fresh ice, the thermal conductivity, specific heat, and density of pure and clear ice were set as constants [3,4]. For sea ice, only the thermal conductivity is parameterized, while specific heat and density are considered constants [5,6]. These methods are feasible for simulating the evolution of large-scale ice, but there will be a bias for small-scale ice. First of all, the unfrozen water in fresh ice contains trace impurities, and the freshwater ice can be regarded as a three-phase composite material composed of pure ice bubbles and low salinity unfrozen water. Due to the low ice temperature, most of the unfrozen water around the ice crystal is frozen, and a two-phase composite material of pure ice bubbles can be seen. However, if freshwater ice contains sediment (e.g., the Yellow River ice), a four-phase composition of pure ice bubbles unfrozen water sediment depending on the amount of sediment that appears in the ice [7]. Sea ice is recognized as a four-phase composite material composed of pure ice brine cells, bubbles, and solid salt. The distribution, size, shape, and total volume ratio of each phase component control the various properties of the ice for both freshwater ice and sea ice. Secondly, ice-unfrozen water is sensitive to temperature within the temperature range of phase transition, and small temperature changes will alter the ratio of phase components. Research has focused on “low-temperature” ice, where the volume ratios of phases in the ice are stable, particularly the low bubble ratio, and the brine volume ratio has become a key physical indicator for evaluating the properties of sea ice [8]. However, the sea ice temperature in the Bohai Sea is higher than that in the polar regions, with a large bubble ratio in the ice, and it was found in the 1980s and 1990s that the only use of the brine volume ratio would limit the correct evaluation of the mechanical properties of sea ice during the spring ice-melt period [9]. Therefore, porosity, the sum of the brine bubble volume ratio, is a perfect indicator for evaluating its properties [10]. It is also applied in the evaluation of the thermal and mechanical properties of high-latitude ice at present [11,12], but the brine volume ratio is still used as an indicator for evaluating thermal and mechanical properties [13,14]. Finally, as the climate warms, natural ice has increased in temperature in addition to the macroscopic phenomena of thinner ice thickness and shorter ice ages, leading to an increase in the spatial and temporal ratio of ice temperatures in the phase transition zone relative to high temperatures, including polar ice [15]. It may be ineffective to continue to simulate current conditions of ice using the thermal properties of ice as a constant or in a relationship where the relatively low-temperature zone varies only with ice temperature. In particular, the bias will be greater when simulating ice conditions during ice-melting periods.

There are basic models for the thermal conductivity of porous materials in simple structural forms. If the natural ice is viewed as a two-phase composite material, the distribution relationship between the two materials can be normalized and assumed to provide a thermal conductivity model of the two-phase composite material. A report on the application to natural ice and a comparative analysis of different models are shown in the literature [16]. In fact, the composition of other composite materials can be solids containing gases or static or dynamic liquids, but their solid components generally do not undergo a phase transition. Natural ice, however, has a temperature-dependent variation in the volume ratios of the solid, gaseous, and liquid phases, with a significant variation in the phase transition temperature zone. In addition, since the chemical molecular formula of ice is the same as that of water, the total mass of the two remains basically unchanged during the phase transition process, but the volume ratios change, suggesting that natural ice with phase transition is much more complicated than composite materials without phase transition. Although there are few research results on natural ice, the research ideas on the thermal properties of solution-containing composite materials and soil can be used as references [17,18,19]. In particular, research results on thermal property parameters of frozen soil or ice-containing composite materials with ice phase transition, such as testing technology [20,21], composite material modeling [22], and the evolution process and mechanism of the frozen soil temperature field [23], are presented. For time-series survey data of on-site ice temperature, mathematical inversion identification of the corresponding thermal diffusivity based on the measured temperature field data under ideal conditions is also a basic method for research in similar fields [24,25,26].

As to the establishment of an accurate thermal property evaluation model of natural ice, the support of measured ice thermal property parameters is needed first. Huang et al. (2013) studied the thermal conductivity of natural freshwater ice using laboratory conditions. Based on the measurements of ice crystals and bubbles, the structure of bubbles in ice is found to be quite complex. At present, a single basic model and empirical equations are difficult to achieve the desired precision, so simple structural models can be improved to form empirical and semi-empirical models [16]. Besides, using the time-series data of the vertical temperature profile within ice layers of the measured natural ice, the inversion identification of the thermal diffusivity of natural ice can be conducted with the finite difference method [27]. Specifically, a one-dimensional ice thermodynamic non-linear distributed parameter system is constructed to identify the thermal diffusivity of ice based on the one-dimensional heat conduction equation of ice. With the theoretical trend and ranges of thermal diffusivity of natural ice as constraints and the bias between the simulated and observed ice temperature as the objective function, an inversion identification model of a discontinuous or non-linear distributed parameter system is established via the small interval refinement stratification of the studied ice layers. Then, the statistical relationship between the inversion-identified thermal diffusivity of ice and freshwater ice temperature or sea ice porosity is established to express the effects of ice temperature, density, and salinity on the thermal diffusivity of natural ice. In this paper, the research results are summarized, especially the problems in the interpretation of physical mechanisms, and the direction of future efforts is reflected.

2. Fundamentals of Physics and Mathematics

2.1. Physical Background of the Thermal Diffusivity of Ice

Ice physics is essential to controlling the thermal diffusivity of ice, and the type of ice crystals only determines which one to choose when applying the composite material model. For freshwater ice, ice temperature and density are necessary, and for sea ice, ice salinity should be added. These physical parameters can describe the thermal conductivity of ice, specific heat, latent heat, etc. [5,28], Thermal diffusivity is the function of thermal conductivity, density, and specific heat. In physical essence, the thermal diffusivity is determined by the ice temperature, density, and salinity as well, i.e.,

$$\lambda =\frac{k}{\rho \cdot c},$$

(1)

where λ is the thermal diffusivity of ice, m² s⁻¹, k is the thermal conductivity of ice, W m⁻¹ °C⁻¹, ρ is the ice density, kg m⁻³, and c is the ice specific heat, J g⁻¹ °C⁻¹.

The relationships among the thermal conductivity of pure ice, specific heat, and ice temperature, proposed by Yen (1981). Then researchers achieved similar or further development results based on Yen (1981) [29].

$$k_{pi}(T)=2.0733e^{-0.0057T},$$

(2)

$$c_{pi}(T)=2096.806+7.122T,$$

(3)

Equation (4) can be used when the density of pure ice changes with the ice temperature [30].

$${\rho }_{pi}(T)=\frac{916.8}{1+(158T+0.54T^2)\times {10}^{-6}},$$

(4)

where k_pi is the thermal conductivity of pure ice, W m⁻¹ °C⁻¹, T is the ice temperature, °C, c_pi is the specific heat of pure ice, J kg⁻¹ °C⁻¹, and ρ_pi is the density of pure ice, kg m⁻³.

Schewerdtfecer (1963) assumed that the bubbles in the sea ice were spherical and applied the thermal conductivity model of classic Maxwell composite materials to derive the equations for the specific heat and thermal diffusivity of sea ice [28], where the effective specific heat of sea ice is Equation (5).

$$c_{si,eff}(z)=\frac{S_{si}(z)}{\alpha T{(z)}^2}L+\frac{S_{si}(z)}{\alpha T(z)}(c_w-c_{pi})+c_{pi},$$

(5)

where factor α = −0.0182°C⁻¹, z is the sea ice layer depth, m, and S_si(z) and T(z) are sea ice salinity (‰) and temperature (°C). L means latent heat of ice freezing, J g⁻¹, and it is L_pi = 334 J g⁻¹, and when S_si = 8 ‰, L_pi = 264 J g⁻¹. c_w = 4.19 J g⁻¹ °C⁻¹, which is the specific heat of pure water. Equation (3) was not used to calculate the specific heat of pure ice, and c_pi = 2.09 J g⁻¹ °C⁻¹ was taken directly.

The corresponding effective thermal conductivity of sea ice is given by Equation (6).

$$k_{si,eff}(z)=k_{pi}-(k_{pi}-k_b)\frac{S_{si}(z){\rho }_{si}}{\alpha {\rho }_{w}T(z)},$$

(6)

where ρ_si is the density of sea ice, kg m⁻³, k_b is the thermal conductivity of brine, W m⁻¹ °C⁻¹, k_b(T) = 0.52 + 0.023T², and ρ_w = 1000 kg m⁻³, which is the density of pure water. The thermal conductivity of pure ice was not calculated by Equation (2), and k_pi = 2.1 W m⁻¹ °C⁻¹ was taken.

Therefore, the calculation of freshwater ice is simpler than that of sea ice. However, the thermal diffusivity of pure ice calculated by Equations (1)–(4) is a far cry from that in the phase transition zone of natural ice. According to Chen et al. (2005), the thermal diffusivity of KCl and NaCl saltwater frozen ice in the ice temperature zone of −3 °C to 0 °C varies non-linearly and is the same as the thermal diffusivity of water near the freezing point [31]. Physically, pure ice completes the phase transition at 0°C, with the thermal diffusivity varying directly between 10.0 × 10⁻⁷ m² s⁻¹ and 1.35 × 10⁻⁷ m² s⁻¹ [32], while all others are transitioning in the phase transition zone. This reflects the significant variation in the pure ice, water, and bubble volume ratios in the ice in the phase transition zone, and the thermal diffusivity of ice is mainly determined by the volume ratio of pure ice and water. Only in the low-temperature zone without phase transition, the ice’s thermal diffusivity is mainly determined by the volume ratio of pure ice and bubbles. For a unified representation of the effect of the water and bubble volume ratio in the ice, the porosity v is introduced, which is the sum of the bubble volume ratio in the ice and the unfrozen water (brine) volume ratio, expressed as a thousand (‰). As for sea ice, Cox and Weeks (1983) fitted the statistical equation of sea ice porosity in the temperature range of −2 °C to −22.9 °C according to the sea ice phase diagram with the required sea ice physical parameters of temperature, density, and salinity [33]. Later, Leppäranta and Manninen (1988) supplemented the equation for calculating the porosity of low-salinity sea ice at temperatures higher than −2 °C [34]. If the salinity is 0 for freshwater ice, the porosity is the bubble volume ratio of natural freshwater ice, which is only a function of ice density.

2.2. Non-Linearly Distributed Parameter System

The heat transfer in the ice layers is expressed by the classical one-dimensional heat conduction equation [35], as shown in Equation (7).

$$\rho c\frac{\partial }{\partial t}T(z,t)=\frac{\partial }{\partial z}\left(k\frac{\partial T(z,t)}{\partial z}-I(z,t)\right),$$

(7)

where z is the vertical coordinate of the ice layer depth, m, with the downward direction defined as the positive direction; t is the time; and I denotes the heat source item, W·m⁻², which is equivalent to the radiation component reaching the depth z.

In the inversion identification, the part of the ice surface greatly affected by solar radiation and the bottom layer greatly affected by heat flux from water were removed, or the nighttime data without solar radiation were selected, and the identified ice layer system can be regarded as an ideal situation without external heat sources. In addition, the values of the time and space step lengths used were very small, and interpolation processing was required for the time and space intervals of measured data.

For freshwater ice, its thermal diffusivity decreases with the increase of ice temperature over a range [21]. When the ice temperature changes very little, the change in thermal diffusivity is also small. In the inversion identification, it was assumed that there is a linear relationship between the thermal diffusivity and ice temperature, i.e., λ(T) = a_i + b_iT, and the heat conduction equation describing the thermal diffusivity of freshwater ice for a small range of ice temperature changes and the corresponding initial-boundary conditions can be expressed as Equation (8).

$$\left\{\begin{array}{l}\frac{\partial }{\partial t}T(z,t)=\lambda (T;a_i,b_i)\frac{{\partial }^2}{\partial z^2}T(z,t)\hspace{1em}\hspace{1em}\hspace{1em}(z,t)\in \Omega \times I\\ T(z,0)\left|{}_{t=0}\right.=T_0(z)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}z\in \Omega \\ T(z,t)\left|{}_{z=z_1}\right.=T_1(t)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}t\in I\\ T(z,t)\left|{}_{z=z_2}\right.=T_2(t)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}t\in I\end{array}\right.,$$

(8)

where λ(T; a_i, b_i) represents the thermal diffusivity of ice, which is a function of the ice temperature T as determined by the parameters a_i and b_i. The position of the first temperature probe near the ice surface was taken as the origin of the coordinates, and vertically downward was taken as the positive direction of the oz axis. The starting position of the inversion identified ice temperature range was set as z₁, and the end as z₂, i.e., the inversion identification zone Ω = [z₁, z₂], time variable t ∈ I = (0, t_m], and 0 < tm < +∞ is the observation time.

The thermal diffusivity of sea ice decreases with increasing porosity. Similarly, after a variety of simple function calculations [36], in the inversion identification, a simple function $\lambda (v)=a_{si}{(1+v)}^{b_{si}}$ was used to describe the relation between the thermal diffusivity of sea ice and porosity over a small range of temperature variations, so that the heat conduction equation describing the thermal diffusivity of sea ice and the corresponding initial boundary conditions can be expressed as Equation (9).

$$\left\{\begin{array}{l}\frac{\partial }{\partial t}T(z,t)=\lambda (v;a_{si},b_{si})\frac{{\partial }^2}{\partial z^2}T(z,t)\hspace{1em}\hspace{1em}\hspace{1em}(z,t)\in \Omega \times I\\ T(z,t)\left|{}_{t=0}\right.=T_0(z)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}z\in \Omega \\ T(z,t)\left|{}_{z=z_1}\right.=T_1(t)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}t\in I\\ T(z,t)\left|{}_{z=z_2}\right.=T_2(t)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}t\in I\end{array}\right.,$$

(9)

where v is the ice porosity, ‰, and λ (v; a_si, b_si) represent the thermal diffusivity of sea ice, which is a function of the porosity v determined by the parameters a_si and b_si.

Based on the research results on the ice thermal diffusivity [4,29,31], the inversion identification model of the non-linear system for the ice thermal diffusivity is Equation (10).

$$\begin{array}{ll}\min & f(z,t;a,b)={\displaystyle {\int }_{t\in I}{\displaystyle {\int }_{z\in \Omega }{(T(z,t;a,b)-\overline{T}(z,t))}^{2}dzdt}}\\ s.t.& T(z,t;a,b)\in S_{U_{ad}}\end{array}$$

(10)

where f (z, t; a, b) is the objective function calculating the absolute deviation between calculated and measured ice temperatures, which tries to make the calculated ice temperature close to the measured ice temperature. T(z, t; a, b) is the fitting function for the temperature calculation obtained by the numerical calculation method through Equations (8) or (9), and T(z, t) refers to the fitting function of the measured temperature. U_ad denotes the allowable set of parameters (a, b), which was obtained from the analysis of relevant research [27,37], and S_Uad is the set of solutions T(z, t; a, b) of Equations (8) or (9) depending on parameters (a, b) ∈ U_ad. Applying the parameter identification theory of the distributed parameter system, the optimal parameters a and b were obtained by computer programming with an improved genetic algorithm. The relevant theoretical analysis of the parameter identification model is detailed in the literature [27,37].

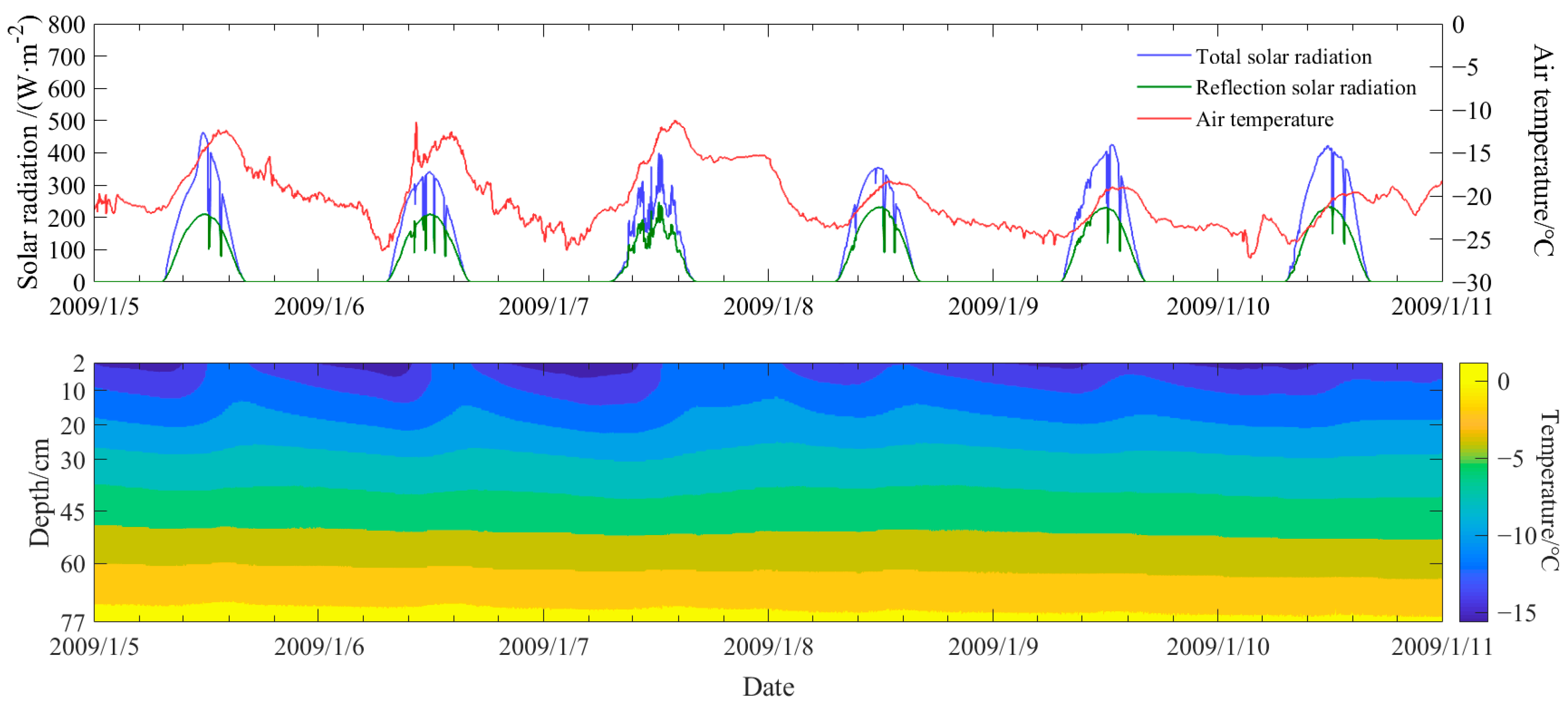
3. Field Survey of the Vertical Temperature Profile of Natural Ice

Since the 1980s, fixed-point temperature vertical profile surveys of natural freshwater ice and sea ice have been carried out, and the survey sites in China are shown in Figure 1. The inversion identification of thermal diffusivity had been conducted for some of the survey data, while some were yet to be carried out. In some of these surveys, both ice crystals and density were measured, while in others, the thermal conductivity was measured. Research of the ice thermal properties was performed in Hongqipao Reservoir, the Thermakarst Lake of Beiluhe on the Qinghai-Tibet Plateau, the estuary of the Yellow River, the Fen River Reservoir II, Bayuquan in the Bohai Sea, and Zhongshan Station in Antarctica, the survey sites shown in Table 1. In addition, the inversion identification of the thermal diffusivity of ice has not yet been carried out at the following sites: Hanzhang Lake, Wuliangsu Lake, Qinghai Lake, Ngoring Lake, and Shisifenzi of the Yellow River.

From January to February 2004, a survey of the temperature vertical profile of river ice and the formation and dissipation processes of ice was carried out in a shady place on the Fen River Reservoir II. Specifically, the air temperature at a height of 1.5 m from the ice surface, the ice temperature every 5 cm within 0.55 m vertically downward from the ice surface, and the water temperature at 100 cm and 150 cm below the ice surface were measured. Temperature data were automatically collected every 15 min [38,39]. The PT100 (JUMO, Germany) was used as the temperature probe, with a precision of ±0.1°C and a resolution of 0.01°C.

From December 2008 to April 2009 and from October 2009 to April 2010, a field survey on the formation and dissipation process of ice was carried out in Hongqipao Reservoir [40,41,42] to obtain the air temperature, ice temperature, and water temperature at 150 cm above the ice surface. The ice or water temperature probes were placed at 2, 7, 12, 17, 32, 47, 62, 77, 92, 107, 122, 152, 182, 212, and 242 cm below the ice surface. Besides solar radiation, wind speed, wind direction, ice thickness, ice crystals, bubbles in ice, and ice density were measured. The PT100 (JUMO, Germany) was adopted as the temperature probe, and the TRM-ZS1 polar wind direction and wind speed gradient monitoring recorder was used for radiation measurement, with a resolution of 1 W m⁻² and each sampling interval of 1 min.

From October 2010 to July 2011, a set of temperature chains was installed in the Thermakarst Lake of Beiluhe on the Qinghai-Tibet Plateau [16,42], and the PT100 system (Campbell CR10) developed by the State Key Laboratory of Frozen Soil Engineering, Cold and Arid Region Environment and Engineering Research Institute, Chinese Academy of Sciences, was used, with a resolution of 0.1 °C. The temperature sensor probes installed every 5 cm automatically recorded the temperature every 30 min. An array of data, such as air temperature, ice temperature, and water temperature under the ice, was obtained.

From April to October 2006, a field survey of overwintering sea ice physics was carried out near the Zhongshan Station in Prydz Bay, Antarctica. A series of ice core salinity, density vertical profiles, and continuous ice temperature vertical profiles were measured, as well as time-series data on ice thickness. The temperature probe PT100 (JUMO, Germany) was placed every 6 cm, and the sampling interval was 30 min [43].

In the 1980s, the ice thermodynamic properties in Bayuquan in the Bohai Sea and the Yellow River estuary were studied [44]. The ice temperature vertical distribution profile was measured in the Bayuquan harbor basin from 5 to 23 January 1987. There are two sections formed at five temperature measurement points that are parallel and perpendicular to the harbor basin wall, respectively. A total of 12 layers of temperature measurement probes with a copper-composite thermocouple were buried vertically at each temperature measurement position at the depths of 3, 8, 13, 18, 23, 28, 33, 38, 43, 53, 78, and 103 cm below the ice surface. The temperature value was converted based on the thermal potential measured with an UJ33a potentiometer with a precision of 1 microvolt. The precision was ±0.1 °C within the measured temperature range of 0 to −25 °C, calibrated by a secondary standard thermometer [45]. Two CN-9L heat flux sensors (prod. Japan) were inserted at 8 cm and 23 cm, which are highly responsive and allow instantaneous dynamic changes to be measured. The heat flux passing through the heat flux sensor was converted based on the potential values measured at the two poles of the sheet, after which the thermal conductivity was calculated from the calibration coefficient of the heat flux sensor [44]. Meanwhile, samples were taken to measure the salinity (3.2‰), density (876 kg m⁻³), and crystal (grain size of 2.1–32 mm) vertical profiles of the ice. On January 28, 1988, the ice slabs were collected at the No. 3 Drainage and Irrigation Station of Gudong Oilfield on the north side of the Yellow River estuary, about 1500 m from the shore. Its thickness was 11 cm, the mean salinity of the sea ice was 0.400‰, and the sea ice density was 961 kg m⁻³. The upper and lower incubators were prepared in the laboratory, and the thermal conductivity of ice samples in the low-temperature zone was tested [44].

Generally, there is less snow accumulation on the ice surface in arid and semi-arid areas of China. Even if some snow falls, it is difficult to remain on the ice surface due to the strong winds. Therefore, snow accumulation has little effect on the ice and the water temperature under the ice. Among the survey sites, only the Hongqipao Reservoir had continuous snow accumulation, which can reduce the effect of radiation on ice and water temperature, but the snow accumulation is not enough to cause changes in ice and water temperature characteristics. The air temperature, some ice temperature, and radiation values of Hongqipao Reservoir from 5 to 10 January 2009 were taken as an example (Figure 2) [46], and the lake ice evolution was analyzed. The ice temperature increases with depth, and the variation decreases and stabilizes in Figure 2. In other words, the influence of ice temperature on air temperature reduces with increasing depth, and the restriction of the water temperature under the ice is generally reflected. Furthermore, the temperature characteristics of river ice and sea ice measured in situ are basically the same as those of lake ice [39,40,42,43,45]. The total solar radiation and reflected solar radiation flux in northern China typically start to increase around 6:30 each day, reach a peak near 12:30, and then start to decrease. There is no total solar radiation or reflected solar radiation between 17:00 each day and 6:30 the next day. In addition, the moment of air temperature/ice temperature peaks shows a certain lag with the radiation peak [40,41].

The sites selected for the field survey are all flat and stable ice layers with growth caused by thermodynamic processes, so the crystal structure is relatively simple no matter if it is lake ice, river ice, or sea ice. Generally, granular ice is found near the ice surface, followed by columnar ice. If snow falls during the initial freezing period, the granular ice will account for more [42]. A sample of ice crystals from surface to bottom is shown in Figure 3. In the arid area of the Qinghai-Tibet Plateau, granular ice on the ice surface disappears due to sublimation [47]. Granular ice appears crosswise only at the Zhongshan Station, Antarctica, where sea ice is highly dynamic [36].

Table 1. Basic information about the site for the survey and research on ice thermal properties.

Information	Hongqipao Reservoir	Thermakarst Lake, Beiluhe	Estuary, Yellow River	Fen River Reservoir II	Bayuquan, Bohai Sea	Zhongshan Station, Antarctica
Latitude and longitude/°	112.27° E, 37.60° N	92.92° E, 34.83° N	119.12° E, 37.88° N	112.38° E, 37.98° N	122.07° E, 40.28° N	76.37° E, 69.37° S
Elevation/m	140	4640	2	800–1400	2	11
Duration of freezing period/d	150–180	150–210	80–100	80–100	110–120	300
Ice thickness at severe ice period/m	1.0–1.2	0.7–1.0	0.1–0.2	0.4–0.5	0.3–0.4	1.6–1.8
Mode of Ice Formation	Thermodynamics	Thermodynamics	Thermodynamics	Thermodynamics	Thermodynamics	Thermodynamics
Ice classification	Lake Ice	Lake Ice	Saltwater ice	River ice	Sea ice	Sea ice
Ice crystals	Granular/columnar	Columnar	Columnar		Granular/columnar	Granular/columnar mixture
Ice physical indicators	Density	Density, bubbles	Salinity, density		Salinity, Density	Salinity, density
Ice thermal indicators	Laboratory thermal conductivity, identified thermal diffusivity	Laboratory thermal conductivity, identified thermal diffusivity	Laboratory thermal conductivity	Identified thermal diffusivity	Thermal conductivity in situ	Identified thermal diffusivity
Literatures	[40,41]	[16]	[44]	[38,39]	[44]	[43]

Table 1. Basic information about the site for the survey and research on ice thermal properties.

Information	Hongqipao Reservoir	Thermakarst Lake, Beiluhe	Estuary, Yellow River	Fen River Reservoir II	Bayuquan, Bohai Sea	Zhongshan Station, Antarctica
Latitude and longitude/°	112.27° E, 37.60° N	92.92° E, 34.83° N	119.12° E, 37.88° N	112.38° E, 37.98° N	122.07° E, 40.28° N	76.37° E, 69.37° S
Elevation/m	140	4640	2	800–1400	2	11
Duration of freezing period/d	150–180	150–210	80–100	80–100	110–120	300
Ice thickness at severe ice period/m	1.0–1.2	0.7–1.0	0.1–0.2	0.4–0.5	0.3–0.4	1.6–1.8
Mode of Ice Formation	Thermodynamics	Thermodynamics	Thermodynamics	Thermodynamics	Thermodynamics	Thermodynamics
Ice classification	Lake Ice	Lake Ice	Saltwater ice	River ice	Sea ice	Sea ice
Ice crystals	Granular/columnar	Columnar	Columnar		Granular/columnar	Granular/columnar mixture
Ice physical indicators	Density	Density, bubbles	Salinity, density		Salinity, Density	Salinity, density
Ice thermal indicators	Laboratory thermal conductivity, identified thermal diffusivity	Laboratory thermal conductivity, identified thermal diffusivity	Laboratory thermal conductivity	Identified thermal diffusivity	Thermal conductivity in situ	Identified thermal diffusivity
Literatures	[40,41]	[16]	[44]	[38,39]	[44]	[43]

Low-temperature ice samples, especially those frozen after sampling, have a low ratio of unfrozen water in the ice. The density of low-temperature ice samples can reflect the bubble volume ratio in natural ice. Bubbles in natural freshwater ice are generally visible but are relatively rare, such as the sword-headed bubbles in Hongqipao Reservoir (Figure 4a) [42]. The lake ice of Beiluhe on the Qinghai-Tibet Plateau has a higher porosity and larger bubbles [47]. Figure 4b,c show spine-shaped and linear granular bubbles in the lake ice of Beiluhe, respectively. The spine-shaped bubbles are larger in size, pancake-like, approximately 1 cm to 5 cm in diameter horizontally, and up to 1 cm to 2 cm thick vertically, with a flat top and bottom and an irregular spherical shape. In contrast, the linear granular bubbles are smaller, generally 0.3–2.5 mm in diameter, with individual bubbles appearing to be spherical, but with some connected in series to form a cylindrical-like shape, and the slenderness ratio (ratio of the width and height of the longitudinal section of the bubble) is 100–200 [47].

4. Thermal Diffusivity Characteristics of Natural Freshwater Ice and Sea Ice

4.1. Thermal Diffusivity Characteristics of Freshwater Ice

The time-series data of the ice temperature vertical profile of Fen River Reservoir II, measured from 0:00 on 23 January to 0:00 on 5 February 2004, were grouped into daily mean temperatures −6 °C, which were recorded −6 to −3 °C and −3 to 0 °C, and then the inversion identification of thermal diffusivity was calculated, respectively. During the inversion identification, the high-temperature section of the river ice was cryptographically divided into several small temperature sections and periods to explore the fine relationship between the thermal diffusivity and temperature near the freezing point. The inversion-identified thermal diffusivity of ice in Fen River Reservoir II is shown in Figure 5a [39].

According to Figure 5a, when the temperature of natural river ice ranges from 0 °C to −0.76 °C, its thermal diffusivity increases sharply from a small value in a non-linear manner. When the temperature is lower than −0.76 °C, the thermal diffusivity of natural ice is close to the thermal diffusivity of pure ice proposed by Yen (1981) [29]. When the temperature is lower than −2.12 °C, the error between the thermal diffusivity of natural ice and the experimental results of Koubyshkin and Sazonov (1988) [30] is less than 0.035. Therefore, the inversion-identified thermal diffusivity characteristics of freshwater ice in Fen River Reservoir II were summarized as follows: (1) When the temperature of the entire ice layer is low, especially when the ice surface temperature is significantly lower than the melting point, i.e., no phase transition occurs at the ice surface, the results are all closer to the previous experimental ones. (2) When the air and ice surface temperatures are high (above or reach 0 °C), the inversion identification results are smaller than the thermal diffusivity of pure ice calculated by Yen (1981) [29] or Koubyshkin and Sazonov (1988) [30].

Based on the measured ice temperature from the Hongqipao Reservoir, the time and space step length used in the inversion identification were interpolation data of 10 s and 0.5 cm, respectively, and the inversion identification was calculated by layers. The inversion-identified thermal diffusivity of reservoir ice and temperature in the winter of 2008–2009 are shown in Figure 5b, and all the data from the two winters of 2008–2009 and 2009–2010, the thermal diffusivity of ice obtained by inversion identification, are shown in Figure 5c. In the low ice temperature range (−15 °C to −3 °C), the inversion-identified thermal diffusivity of reservoir ice is similar to the results reported in the literature, i.e., the thermal diffusivity reduces slowly with increasing ice temperature. In the high ice temperature range (−3 °C to 0 °C), the inversion-identified thermal diffusivity of reservoir ice decreases significantly with the increasing ice temperature and approaches the thermal diffusivity of water. It suggests that the ice is in the phase transition stage; the ratio of pure ice crystals in the ice decreases and the ratio of unfrozen water increases, ensuring that the thermal diffusivity of ice converges with the thermal diffusivity of water due to the increased water volume ratio [46,48]. On the other hand, the high thermal diffusivity of bubbles cannot be manifested at this stage due to their small ratio.

Based on the measurements of the ice temperature vertical profile in the Thermakarst Lake of Beiluhe on the Qinghai-Tibet Plateau, the inversion identification was calculated by layers with an interpolated time and space step length of 10 s and 0.5 cm, respectively, to obtain the scatter diagram of thermal diffusivity changing with ice temperature, as shown in Figure 5d. In the relatively low ice temperature range (−15 °C to −3 °C), the thermal diffusivity varies slowly with ice temperature. Similarly, in the relatively high ice temperature range (−3 °C to 0 °C), the thermal diffusivity changes drastically, dropping rapidly with the increasing ice temperature and converging to the thermal diffusivity value of fresh water [27].

Researchers have adopted different non-linear fitting methods when establishing the relationship between the inversion identification results and ice temperature in Figure 5. The results of the low-temperature section of the Fen River Reservoir II in Figure 5a are similar to those of previous studies. Bai (2006) suggested using previous results based on actual conditions but introduced a statistical Equation (11) for the high-temperature section [38]. The results supported the inversion-identified thermal diffusivity of other freshwater ice in China [27,36].

$$\lambda (T)=(12.6+\frac{2.7}{T-0.12})\times {10}^{-7}\hspace{1em}\hspace{1em}\hspace{1em}T\in [-0.19,-2.12],$$

(11)

Figure 5b shows the inversion identification results of Hongqipao Reservoir in the winter of 2008–2009 without the fitting expression of scattered points (93 points). Figure 5c presents the inversion identification results of Hongqipao Reservoir in the two winters of 2008–2009 and 2009–2010 [46]. The results were used for the ice temperature evaluation in Kanas Lake, Xinjiang, China [49]. The adjustment of the calculation method used in this identification results in 204 identification results for 87 identification temperature intervals. Despite the scattered results, a new piecewise Equation (12) of thermal diffusivity with temperature is given on this basis [48].

$$\lambda (T)=\left\{\begin{array}{cc}\left(\frac{T}{0.08T-0.01}\right)\times {10}^{-7}\hfill & -0.85\le T<-0.1\\ 10.83\times {10}^{-7}\cdot e^{-0.009T}& -15\le T<-0.85\end{array}\right.,$$

(12)

The thermal diffusivity of lake ice in the Thermakarst Lake of Beiluhe on the Qinghai-Tibet Plateau varies with ice temperature (Figure 5d) and is calculated as Equation (13) [27]. It was part of a contribution to one of the Norway-China collaboration projects [50].

$$\lambda (T)=[2.61\times \ln (-T+0.11)+6.35]\times {10}^{-7}\hspace{1em}\hspace{1em}\hspace{1em}T\in [-15,0),$$

(13)

The symbols in Equations (11)–(13) are the same as the above ones.

To compare the difference between the inversion identification results of freshwater and the thermal diffusivity calculated from pure ice, the results of Yen (1981) [29], Koubyshkin, and Sazonov (1988) [30] were plotted in Figure 5. These results for pure ice are consistent with those for the thermal diffusivity of pure ice in the laboratory [21]. However, the phase transition of natural freshwater ice is not complete at 0 °C, and there is a phase transition temperature range. The thermal conductivity of any impure ice decreases rapidly from a high value in the phase transition zone as the ice temperature approaches the freezing point [41,44,51]. Chen (2005) used KCl and NaCl saltwater freezing to measure the process of thermal diffusivity change in the phase transition zone (−3 °C to 0 °C) by temperature wave analysis (TWA) and to obtain the thermal diffusivity that rapidly decreases in value for water as it approaches the freezing point [31]. However, the results from the piecewise function are also marked in Figure 5. In comparison, the results of Chen (2005) confirmed the correctness of the inversion identification results of natural ice.

In addition, according to Figure 5d, when the ice temperature ranges from −15 °C to −5 °C, the inversion-identified thermal diffusivity value of lake ice in Beiluhe is significantly higher than other inversion identification results of lake ice and literature reports [31]. While the temperature is higher than −5 °C, the inversion identification results are almost the same as the experimental results [31]. It indicates that when the temperature of a large number of spine-shaped bubbles in the lake ice of Beiluhe (Figure 4b) is lower than −5 °C and the phase transition is stable, the bubbles begin to contribute. Since the thermal diffusivity of gas is much greater than that of pure ice, ice with more bubbles has a greater thermal diffusivity. In most cases, as the size and content of bubbles in river ice and reservoir ice are smaller [42], their impact on thermodynamic properties is often neglected. However, such bubbles in ice as in the Beiluhe cannot be overlooked, and even the combined effects of bubble content, size, and shape on the thermal diffusivity of ice may need to be considered [16].

4.2. Thermal Diffusivity Characteristics of Sea Ice

Sea ice is distinguished from freshwater ice by the presence of salt. The unfrozen water among ice crystals, known as brine, is both saltier and denser than seawater. When the sea ice temperature is high, the edges of the crystalline grains begin to melt, the brine channel widens, and the brine in the ice drains downward by gravity, after which it may be left to fill with gas. It results in both liquids and gases of complex chemical compositions in the ice, and their volume ratios vary with temperature, causing a more complex mathematical expression of the change in the thermal diffusivity of sea ice. Theoretically, instead of establishing a relationship with ice temperature, the thermal diffusivity of sea ice has to be introduced as a function of density and salinity. The porosity of sea ice is a function of temperature, density, and salinity, but when the porosity is introduced and there is a lack of salinity and density vertical profiles for online monitoring, sampling tests will be conducted at different times, resulting in no corresponding porosity even though the inversion-identified thermal diffusivity of sea ice is obtained using ice temperature.

In 2006, during the continuous survey of the formation and dissipation of sea ice and the ice temperature vertical profile at Zhongshan Station, Antarctica, seven ice cores were sampled to test the ice density and salinity. Assuming that the porosity of the ice core did not change for 24 h on the day of sampling [37], the inversion-identified thermal diffusivity of the ice and the porosity at the corresponding location during this period were plotted as a scatter diagram (Figure 6) [36,37] to obtain a statistical relationship Equation (14) between the thermal diffusivity and porosity of Antarctic sea ice. Figure 6 also shows that the thermal diffusivity of each ice core varies significantly.

$$\lambda (v)=10.8\times {10}^{-7}{(1+v)}^{-0.302}\hspace{1em}\hspace{1em}\hspace{1em}v\in (0,275],$$

(14)

5. Future Working Directions and Considerations on the Relation between Thermal Conductivity and Ice Physical Parameters

Both in freshwater lake (or reservoir) ice and in river ice and sea ice, the thermal diffusivities of ice are all dominated by three physical parameters that can be quantified: the ice temperature, ice density, and salinity. With regard to pure ice frozen from pure water, its freezing point and melting point are the same, which are 0 °C. Thus, the phase transition is also finished at 0 °C. However, natural water usually contains a certain amount of dissolved chemicals, which will result in a concentration of the unfrozen water’s salinity and a lower freezing point. Especially when there are different chemicals at different levels, the freezing and melting points are also diversified [31,52]. This leads to an irreversible phenomenon in the thermodynamics of natural ice as well as in saline frozen soil [53]. In fact, these small changes usually bring deviations from the accurate thermodynamic processes on a small scale. Therefore, researchers must reflect on what exactly the determinants describing the thermal diffusion in ice are and build a parameterization program for the thermal diffusivity of natural freshwater ice or sea ice. Some considerations open for discussion are as follows:

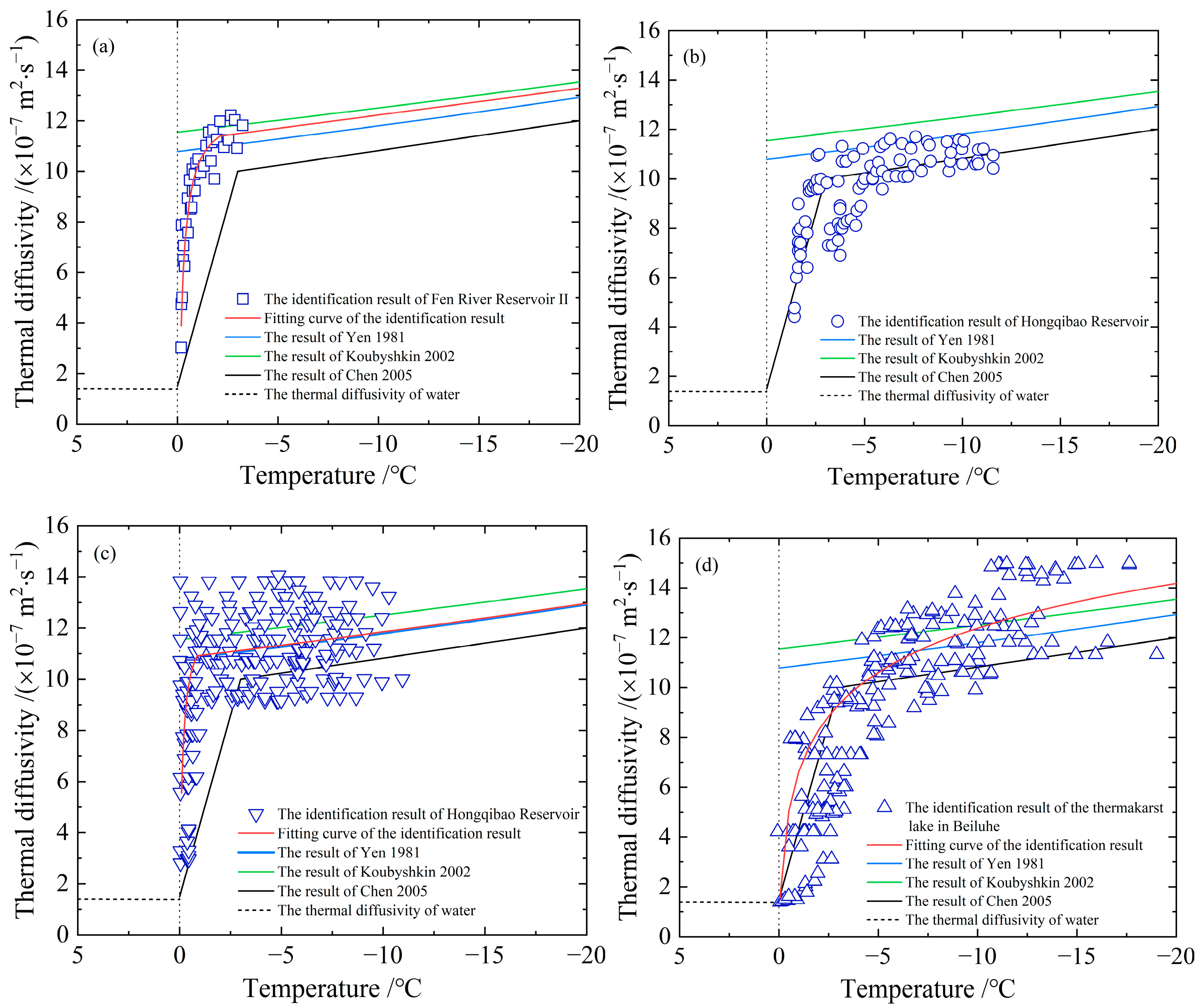
• The thermal diffusivities in Figure 5 are obtained based on measured data of ice temperature from different fields. The heat conduction equation was solved for numerical solutions during the inversion identification process, which relies on the initial boundary value conditions. Hence, different schemes and the initial conditions will generate various results of thermal diffusivity. The optimal parameters of the inversion identification model of the non-linearly distributed parameter system are not absolutely the best solution. However, comprehending from the measured data’s precision, on which the study is based, it will not make a difference in the identified thermal diffusivity. Figure 5a shows the results of a segmented discontinuous approach, which is to divide the temperature into multiple small ranges according to the measured ice temperature. It deems that the thermal diffusivity of ice varies as a linear variation or a power function variation with temperature within small temperature ranges, and the thermal diffusivity was recalculated again in the next temperature range. Although the results of these two calculations have the same function, their thermal diffusivities are different. Compared with other approaches, this method requires a lot of computation, but the resulting thermal diffusivities perform well in the sensitive high-temperature zone of phase transition, and even the smaller the temperature ranges, the better the results. Consequently, the points in the resulting scatter plot in Figure 5a are rather more concentrated, while the results in Figure 5b–d are relatively dispersed for the expansion of the selected temperature range in identification. Moreover, factors such as the time and space step length, interpolation method, and programming algorithm adopted in the identification calculation process can also influence the identification results in varying degrees. Figure 5b,c show the results from different scholars on account of the measurements taken at the same test site in different years, especially the data in Figure 5c covering the measured temperature data applied in Figure 5b. Nevertheless, the dispersion of the two identification results is apparently different because of the different methods. The steps, including how to unify the step length, interpolation, algorithm, etc., also need to be explored to acquire optimal results;
• As the global warming develops, lake ice, river ice, and sea ice are all reducing. In the Arctic area, except for the shortening of the freezing period on a macro level, thinner ice thickness, and a decline in the proportion of multi-year ice, there are also phenomena including an increase in ice temperature, a decrease in ice salinity, a reduction in ice density, and a widening of the varying range of ice density [15]. Likewise, the ice conditions in the Bohai Sea and inland China are also decreasing [54,55]. As the spatial and temporal proportions of comparatively “high-temperature” ice are growing worldwide, the simulation effects will be reduced in reality if the previous data on the relation between the thermal diffusivity of ice and temperature with no regard to the phase transition or constants are adopted for numerical simulations. If the thermal diffusivity of ice reduces, the heat storage capacity of the ice body will be strengthened, and it will cause an increase in entropy in the phase transition process from ice to water or from water to ice, which can moderate the melting or freezing rate of ice. In other words, despite the fact that the thermal conductivity of ice in the phase transition zone of the sea ice in the Bohai Sea was also relatively small in the 1980s [44], the ice in the Bohai Sea covers a comparatively small percentage of the global situation of sea ice, so that it is covered by a large amount of other low-temperature ice. However, the spatial and temporal proportions of ice within the phase transition zone have increased. In this case, previously adopted methods may still be fairly feasible on large-scale issues, but they may no longer be proper to describe the thermodynamic behavior of ice on a finite microscale;
• In the inversion identification of thermal diffusivity, only the time-series data of ice temperature vertical profiles are used, without counting the types of ice crystals at the temperature measurement positions since these types cannot be expressed by numerical values directly. The crystals of ice frozen in calm waters (e.g., reservoir and lake ice) have a pattern of granular ice on the surface and then columnar ice [42]. While this is more complicated in the crystals of ice frozen from rivers and oceans. Granular ice’s properties are basically isotropic, while columnar ice exhibits anisotropy. This can result in a difference between the mathematical models and the calculated results, such as the spread velocity of radar waves in the ice as determined by permittivity [7,56]. Research shows that the thermal conductivities of natural columnar lake ice range from 1.60 W·m⁻¹·°C⁻¹ to 2.20 W·m⁻¹·°C⁻¹ in both the vertical and parallel long axes and are slightly higher (about 5%) in the vertical long axis, showing that the thermal conductivity of ice crystals only has weak anisotropy [16]. From the perspective of the dispersion of inversion-identified ice thermal diffusivities, the differences among the fitted curves and the data points are over 5%. The uncertainty in inversion-identified is larger than the difference in the anisotropy of ice crystals. If 5–10% of the error caused by thermal diffusivity can be accepted on the large scale simulated, the influence of ice crystals can be ignored. In the cases of transformation of ice crystals and overlapping or mixing of granular ice and columnar ice due to dynamics and thermodynamics, the differences of ice crystals can also be neglected. Otherwise, thermal diffusivity models of ice corresponding to various crystal structures should be selected. The ice crystal in the inversion identification of the thermal diffusivity is basically the columnar ice in China;
• If unfrozen water among ice crystals undergoes a phase transition, its mass will remain the same, but its volume ratio will be different, which is the same as the study of frozen soil [53]. If unfrozen water discharges under gravity, it is likely that the partial space originally occupied by unfrozen water will be replaced by gas. In general, the higher the content of bubbles, the lower the ice density. Therefore, ice density can reveal the content of bubbles [56,57] and is an ideal indicator reflecting the effect of bubbles on the thermal diffusivity of ice. If the content of bubbles is less than 3%, the laboratory-tested thermal conductivity of freshwater ice is close to the value [16] calculated by Hamilton and Crosser’s (1962) model [58]. When the content of bubbles is over 16%, any model of the porous medium’s thermal conductivity cannot accurately compute the thermal conductivity [16]. A joint computing model of the thermal diffusivity of lake ice must be built by introducing a shape factor that includes the content and shape of bubbles in the ice. In future ice investigations, promoting the ice density test is indispensable for all models. Meanwhile, focusing on ice density can also reflect two potential scientific issues: First, the ice temperature in the phase transition zone is relatively high, and the bubble content is high because of the discharge of unfrozen water. Secondly, as global warming develops, the plants under shallow lakes in mid-latitudes have higher activity, releasing gases under the ice in winter, and greenhouse gases contained in lake bottoms at high latitudes or high altitudes may be released, such as in the thermokarst lake ice of the Qinghai-Tibet Plateau. Since the thermal diffusivity of bubbles is much higher than that of pure ice, the thermal diffusivity of lake ice with bubbles is larger than the theoretical thermal diffusivity of pure ice. Particularly, the thermal diffusivity of bubble-containing lake ice with a relatively low temperature is more obviously higher than the value of pure ice because the content of unfrozen water reduces;
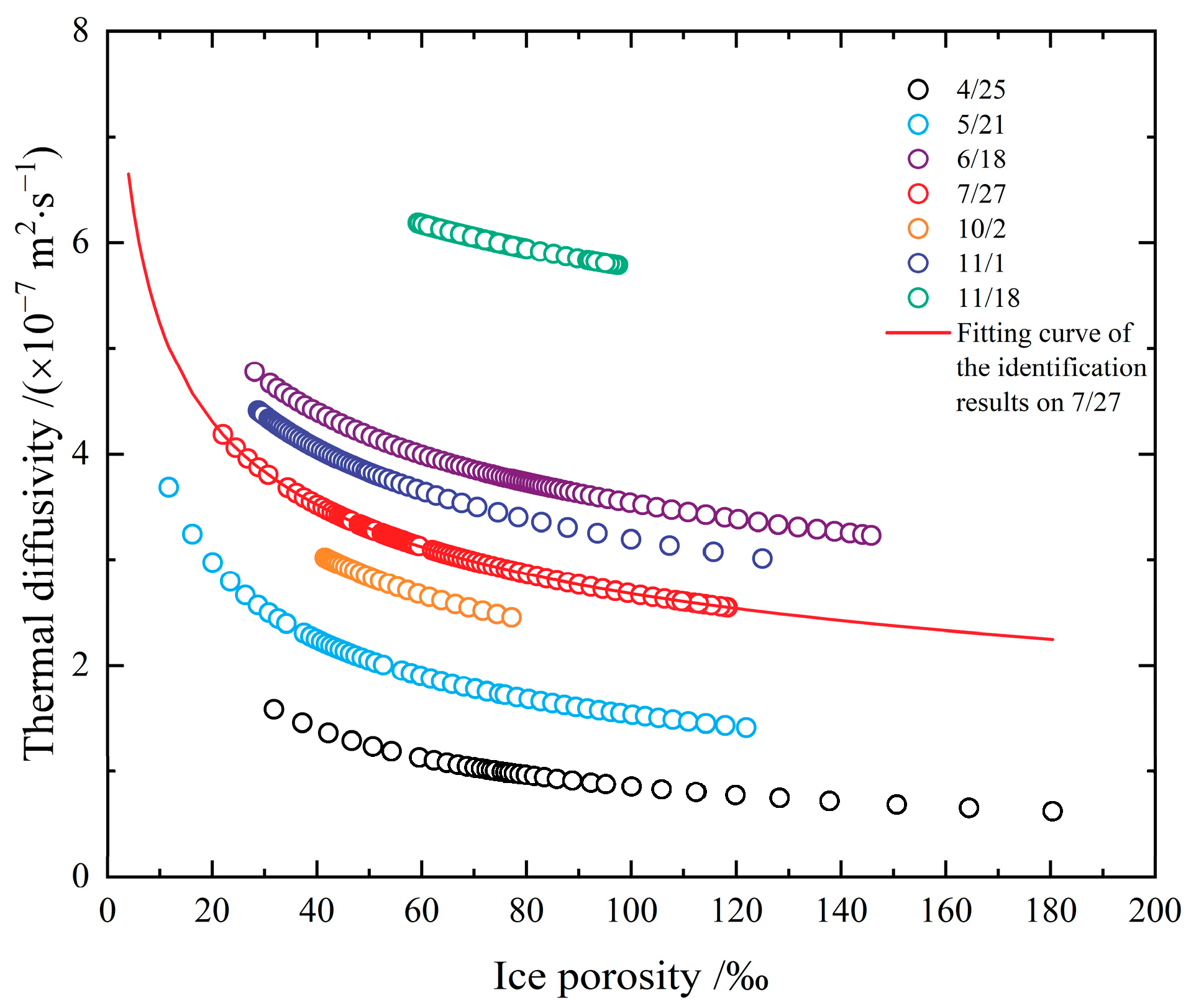
• Natural freshwater ice contains impurities, and the freezing temperature of unfrozen water is dynamic [31]. Meanwhile, the freezing and melting temperatures of ice with saline water. This shows an irreversible phenomenon in thermodynamics [31,59]. The salinity of sea ice is much higher than that of freshwater ice, and its influence is unmissable. When it comes to freshwater ice, the thermal diffusivity of ice can also be described as the relation between temperature and density if the influence of salinity is ignored, while this is impossible for sea ice because it might need to be an expression of the volume ratio of brine (temperature, salinity, density) and the volume ratio of bubbles (temperature, density). However, the inversion identification result for the thermal diffusivity of Antarctic sea ice (Figure 6) indicates that it is not that simple. It suggests that the refinement of the parameterization for the thermal diffusivity of sea ice is relatively difficult if the thermodynamic irreversible phenomenon is neglected, especially for sea ice in the melting period;
• The previous results of experimental [31] and inversion identification [48] are expressed as segmented functions instead of continuous functions for ice temperature. Since the thermal diffusivity of natural ice is mainly controlled by the thermal diffusivity of pure ice, bubbles, and saline or pure unfrozen water, with the thermal diffusivity of unfrozen water as the lower limit and the thermal diffusivity of bubbles as the upper limit. It is suggested that future development should be based on the logistic functional form, and the suggested Equation (15) form is as follows:

  $$\lambda =\frac{C}{1+A{e}^{BT+D}}+E,$$

  (15)

  where E is the lower limit of Equation (15), and it is close to the thermal diffusivity of unfrozen water (λ_w), which is 1.38 × 10⁻⁷ m²·s⁻¹ at 0 °C. C + E is the upper limit of Equation (15), and it is close to the thermal diffusivity of bubbles (λ_a). Since the bubble volume ratio is related to the ice density, its expression is Equation (16) [56,57].

  $$v_a=\frac{{\rho }_{pi}-\rho }{{\rho }_{pi}}\times 1000‰,$$

  (16)

  where ρ_pi is the density of pure ice, 916.8 kg·m⁻³, and ρ is the density of natural ice. C is a nonlinear relation because the shape factor should be introduced when the bubble in ice is high in content and large in size. According to the model reported in the literature [17], the form of the power function (17) is suggested as follows.

  $$C=\alpha (1+\beta v_a{}^{\gamma }),$$

  (17)
  In (15) to (17), B is the maximum growth rate of the thermal diffusivity of natural ice at a certain temperature, A is also related to salinity, D/B is the ice-water phase transition temperature, which is also relatively complicated for unfrozen saline water not closed in the freezing and melting process, α, β, γ are fitting coefficients.
• This consideration is not proved by examples yet because of the sparse density data obtained from natural ice in the field. However, there were measured thermal conductivities at different temperatures (−5, −10, −15, −20, and −25 °C) and different densities (300, 350, 400, and 450 kg.m⁻³) of snow samples in the laboratory. Hence, this consideration was utilized to make a fitting (R² = 0.906) analysis of 152 groups of data for the thermal conductivity of snow, indirectly proving the feasibility of this consideration. We look forward to continuing to accumulate field density test data on freshwater ice to confirm the validity of this research orientation;
• The expression of the relation between the thermal diffusivity and porosity of sea ice in Figure 6 is simple, but it exhibits great differences among ice cores. It is hard to explain the physical origin of these differences, either from the aspect of ice ages or bubble volume ratio. Maybe it is incorrect to use temperature and porosity to evaluate the thermal diffusivity of sea ice. The thermal diffusivity probably needs to be expressed as a multi-relation of ice temperature and the volume ratios of brine and bubbles. If this orientation is correct, it will be necessary to collect data on both salinity and density of sea ice. Here, the salinity is computed with electrical conductivity rather than being decided by a chemical analysis of specific substance composition. The laboratory measurements have found that the substance composition also influences thermal diffusivity [31]. The density of sea ice has been an indispensable factor in contemporary physical investigations of sea ice. In the future, we will be developing online measurement technologies for ice salinity and density and discovering refined expressions of the relation between the thermal diffusivity and physical indicators (e.g., temperature, salinity, and density of sea ice).