Improving the Resolution of GRACE/InSAR Groundwater Storage Estimations Using a New Subsidence Feature Weighted Combination Scheme
Abstract
:1. Introduction
2. Materials and Methods
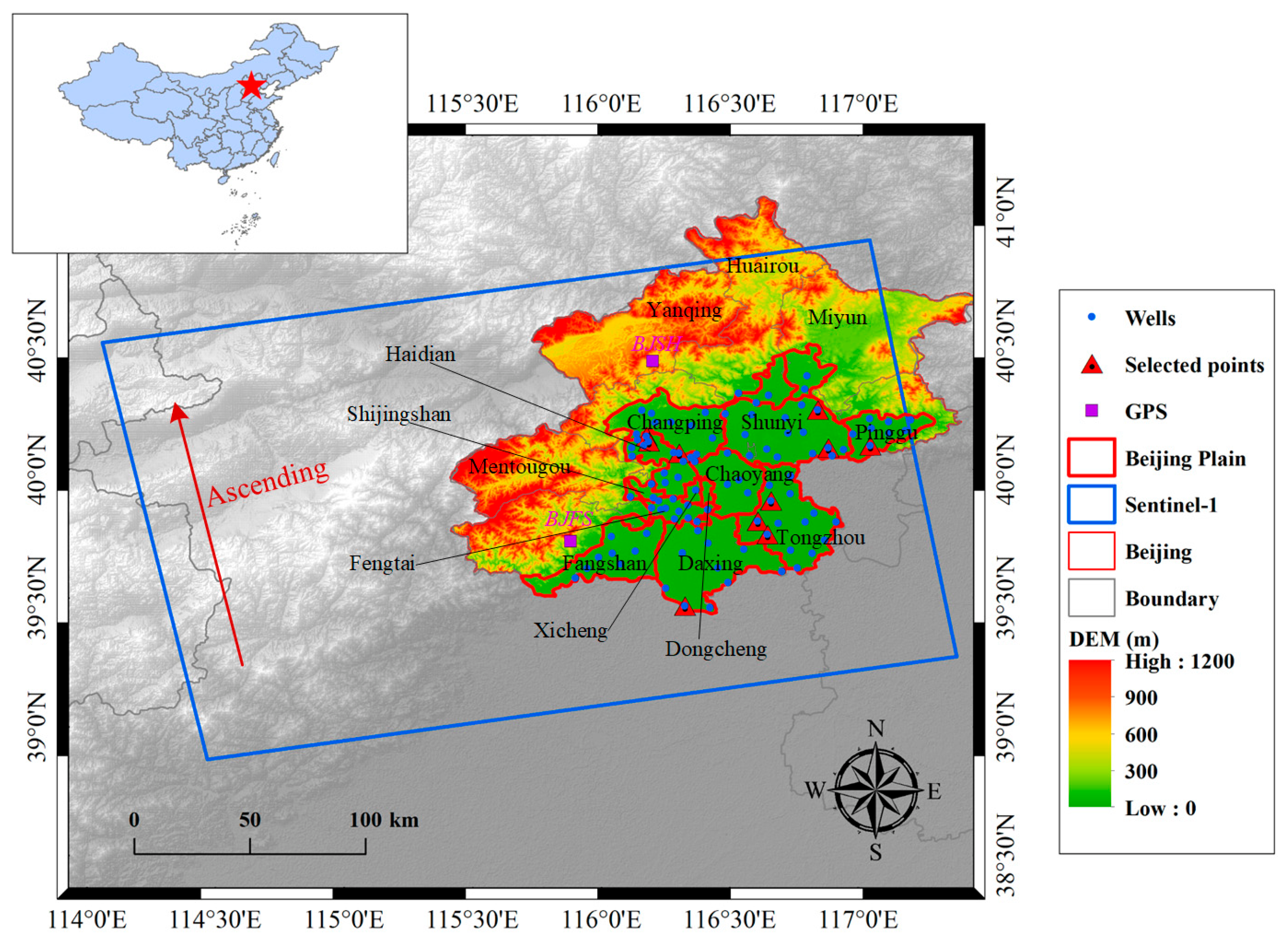
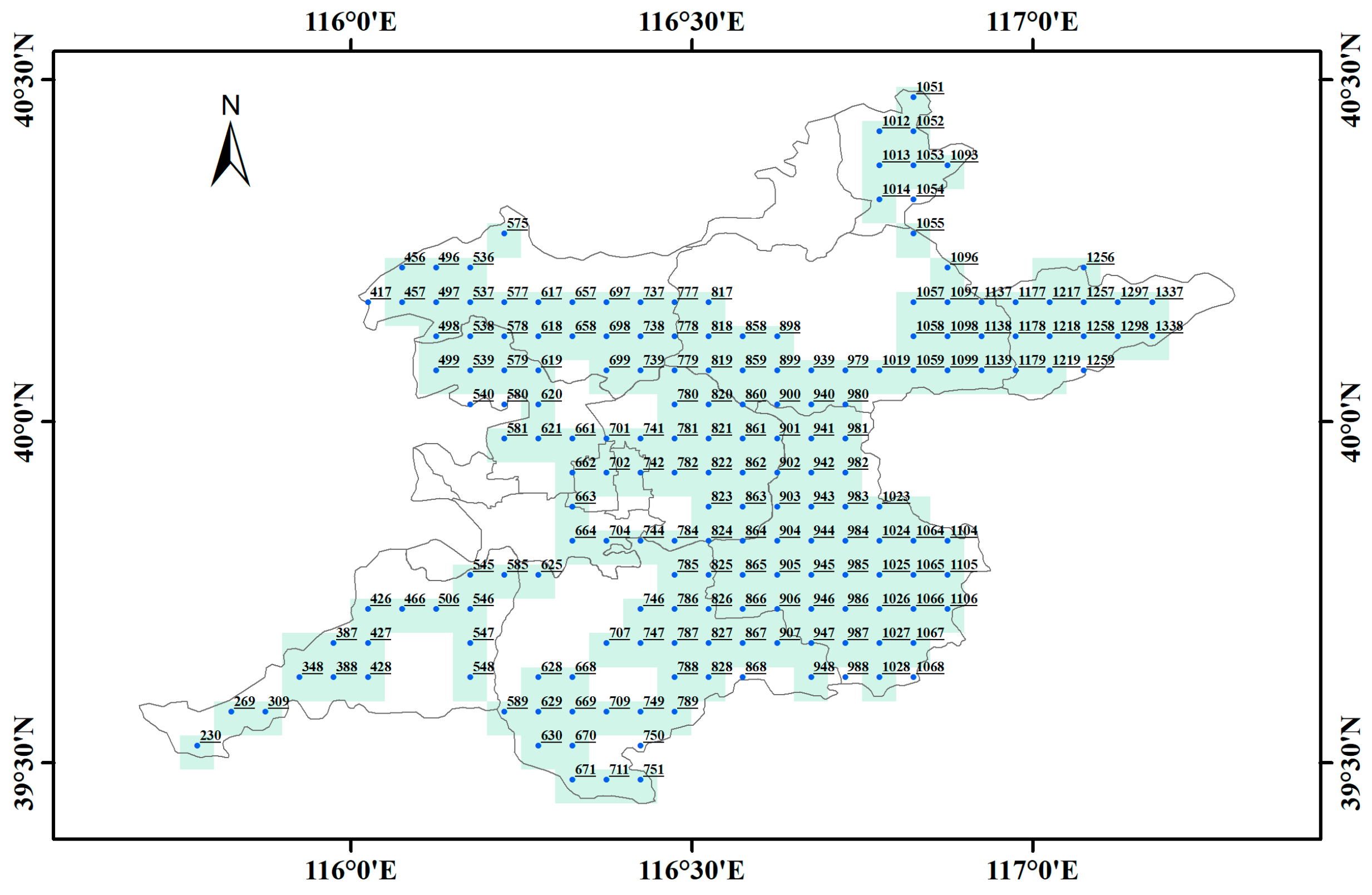
2.1. Study Area
2.2. Materials
2.2.1. SAR Data
2.2.2. GRACE and GLDAS Data
2.2.3. Validation Data
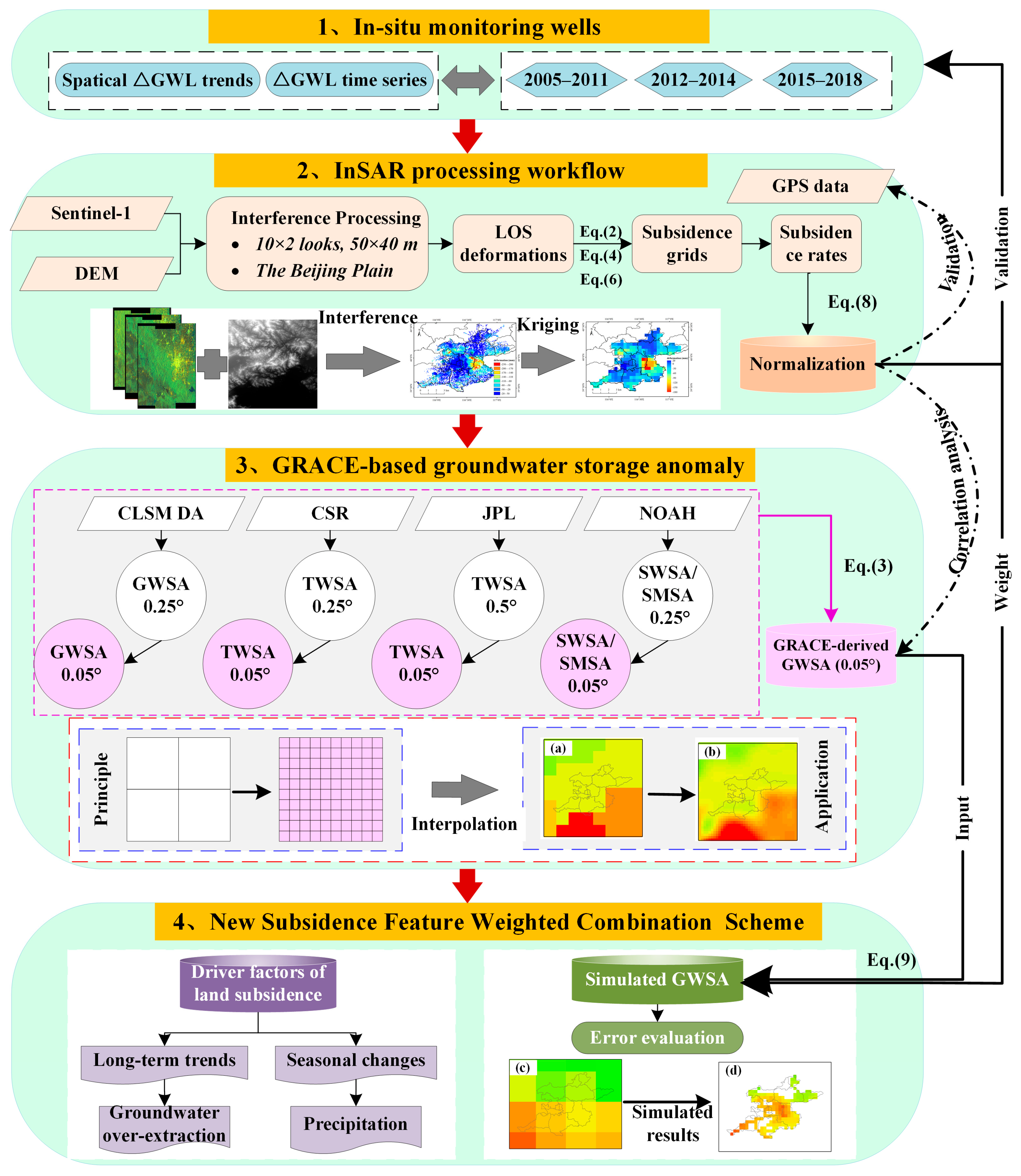
2.3. Method
2.3.1. InSAR Measurements
2.3.2. GRACE Solutions
2.3.3. New Subsidence Feature Weighted Combination Scheme
3. Results
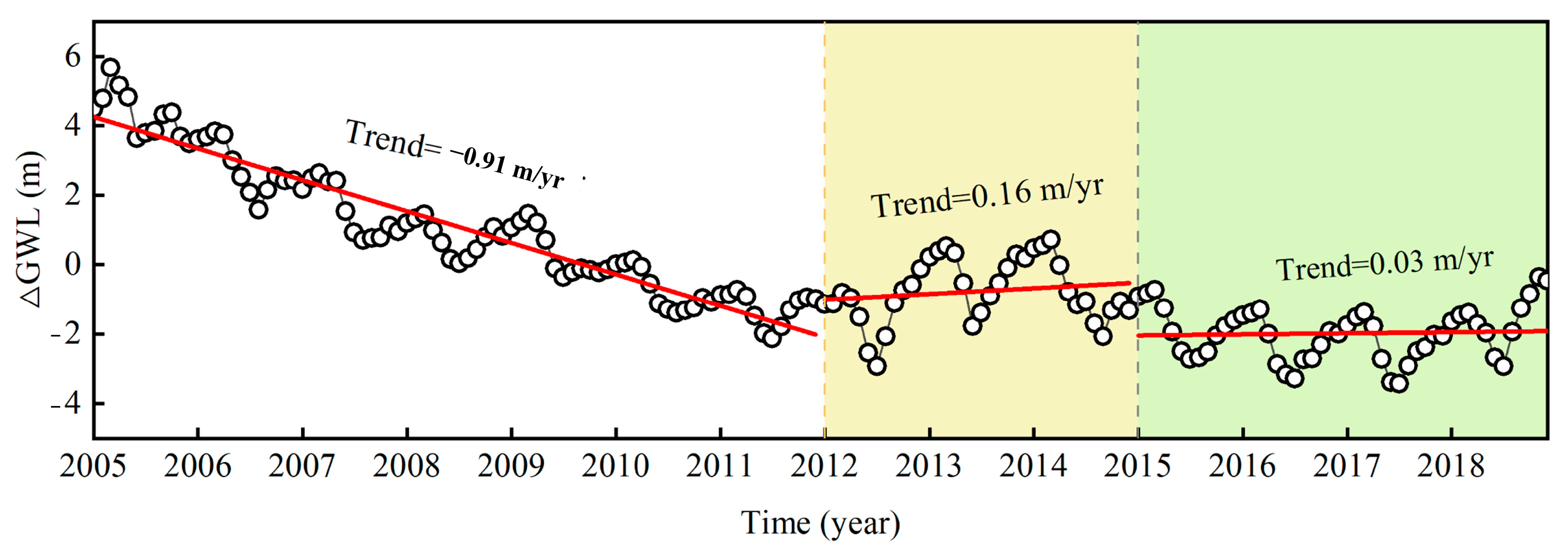
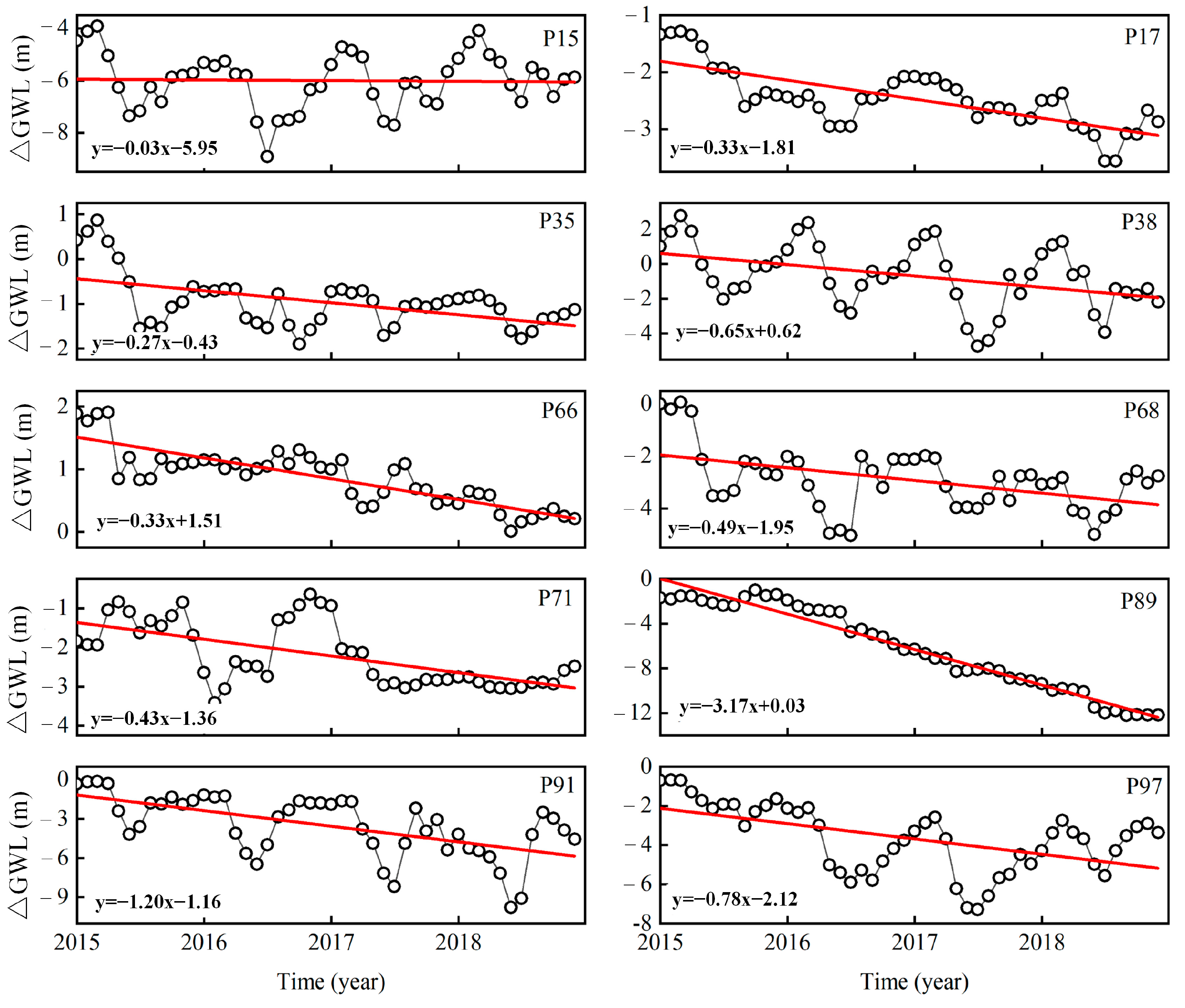
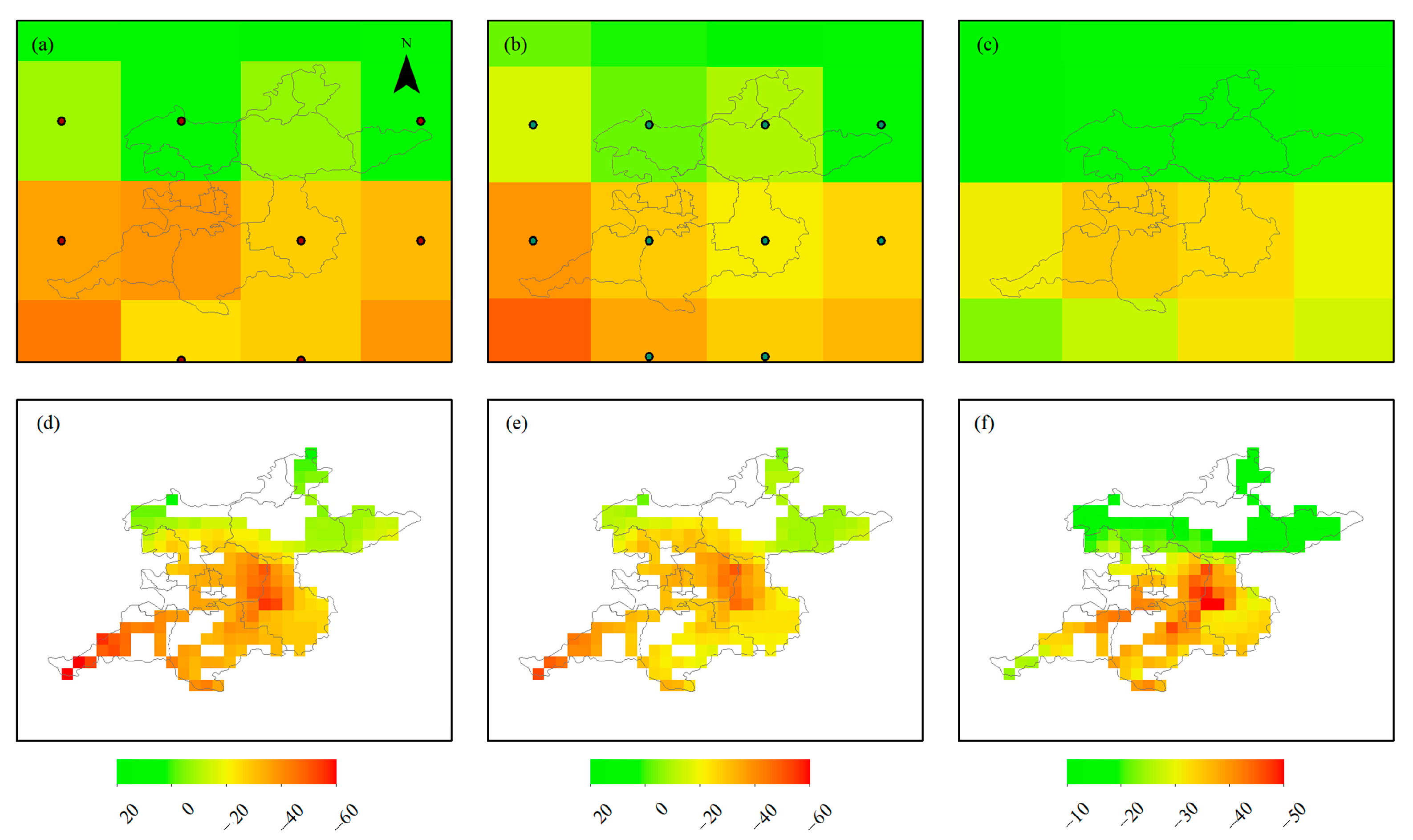
3.1. Groundwater Level Changes
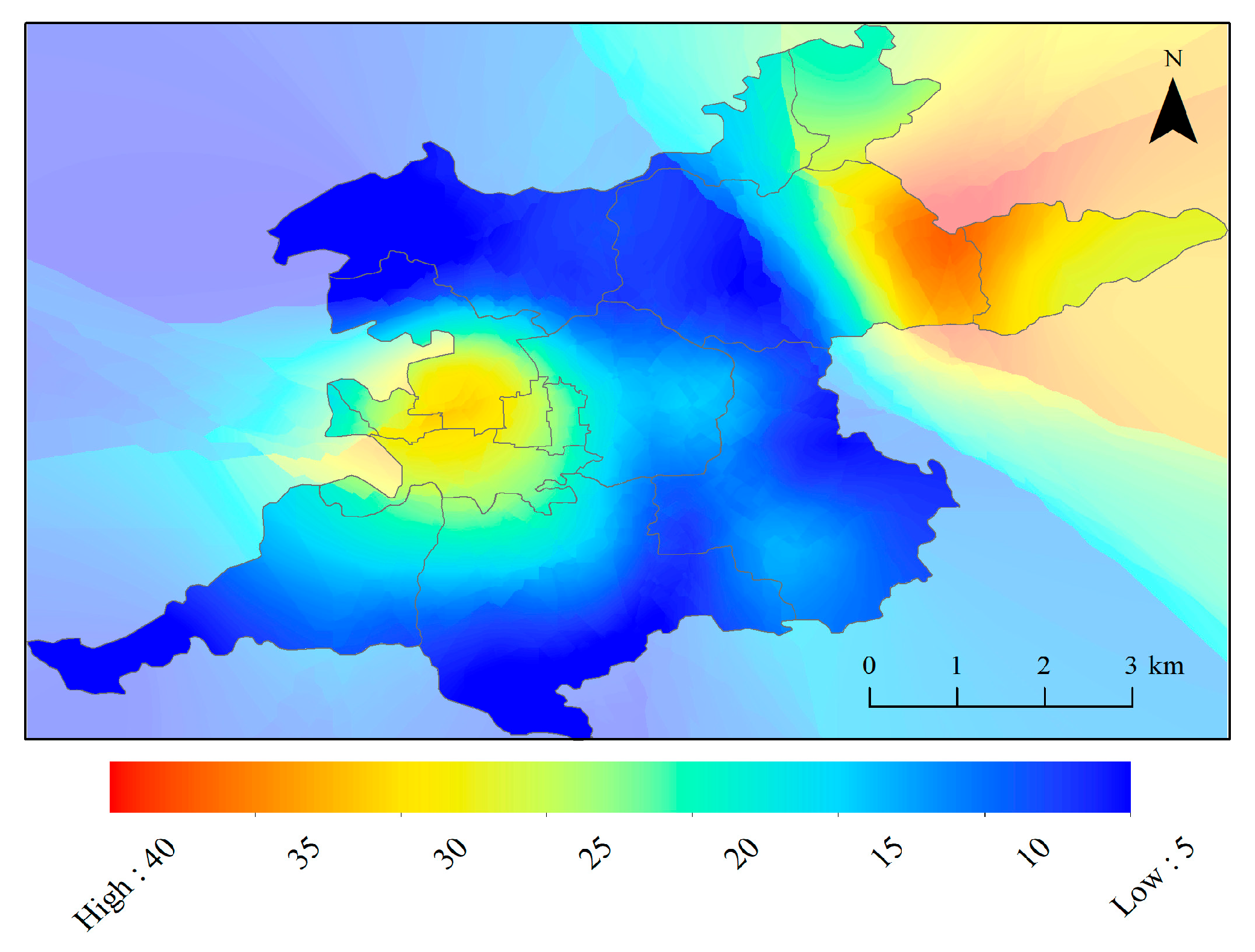
3.2. InSAR-Derived Land Deformation
3.3. Reliability of InSAR Results
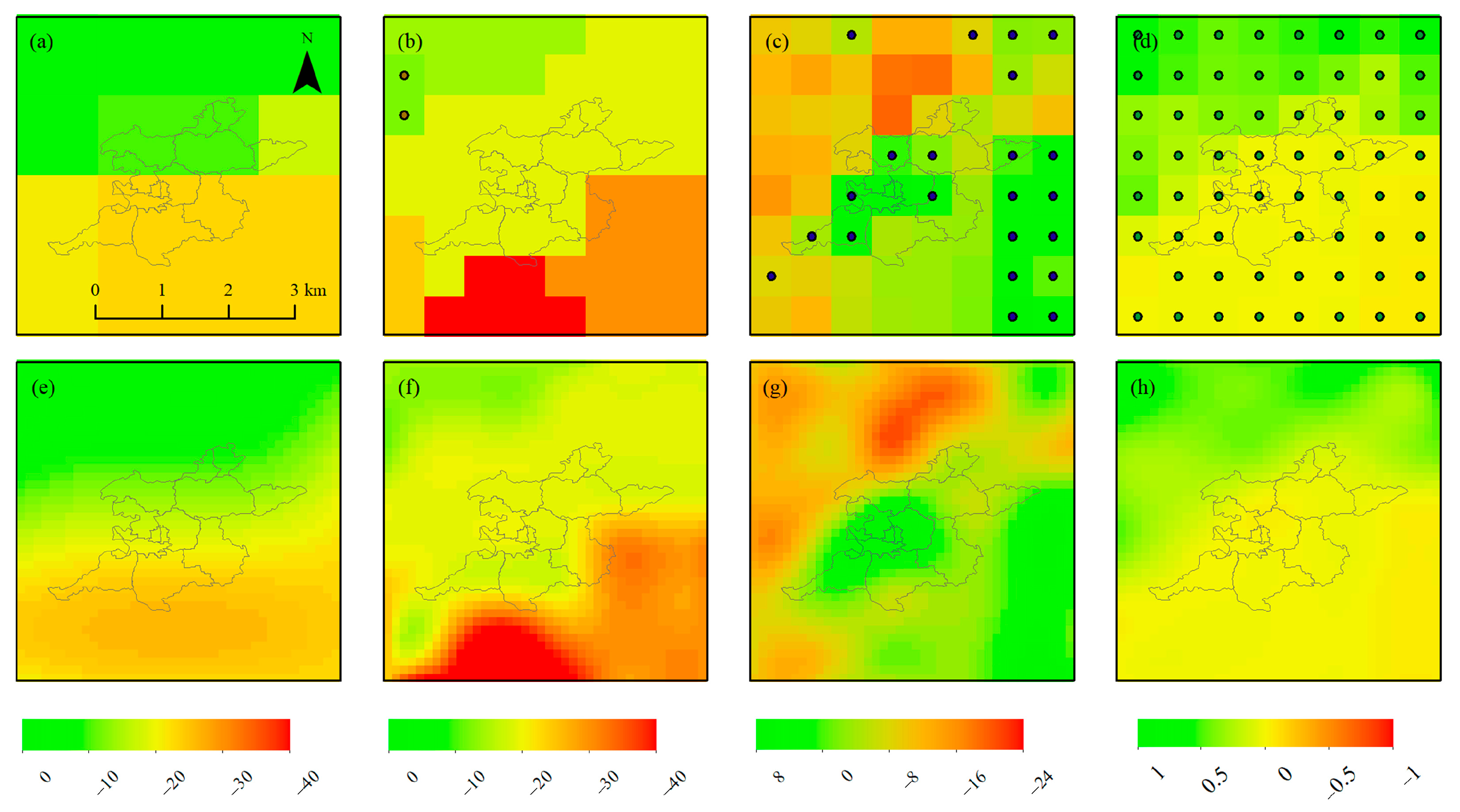
3.4. GWSA Derived by NSFWC Scheme
4. Discussion
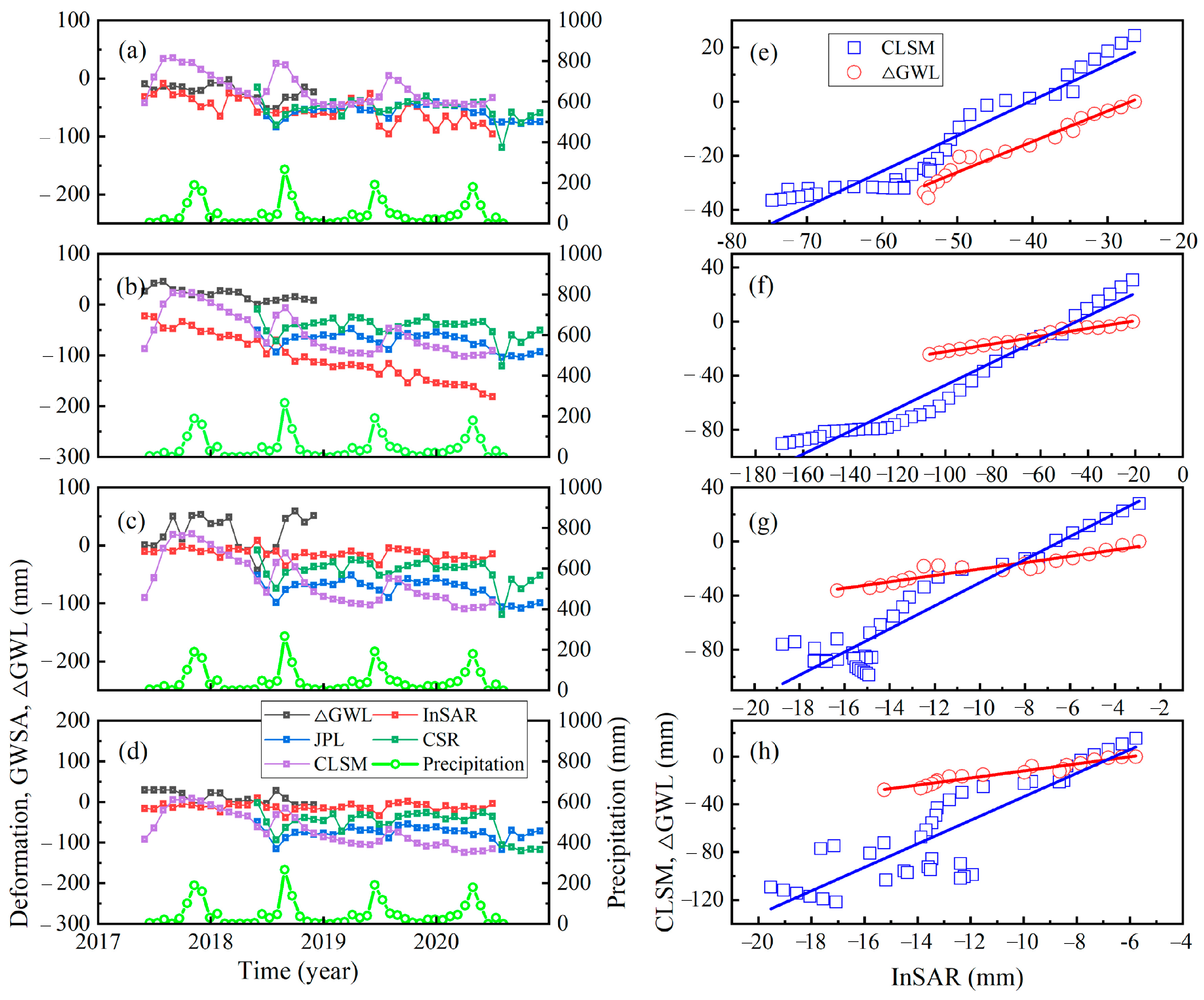
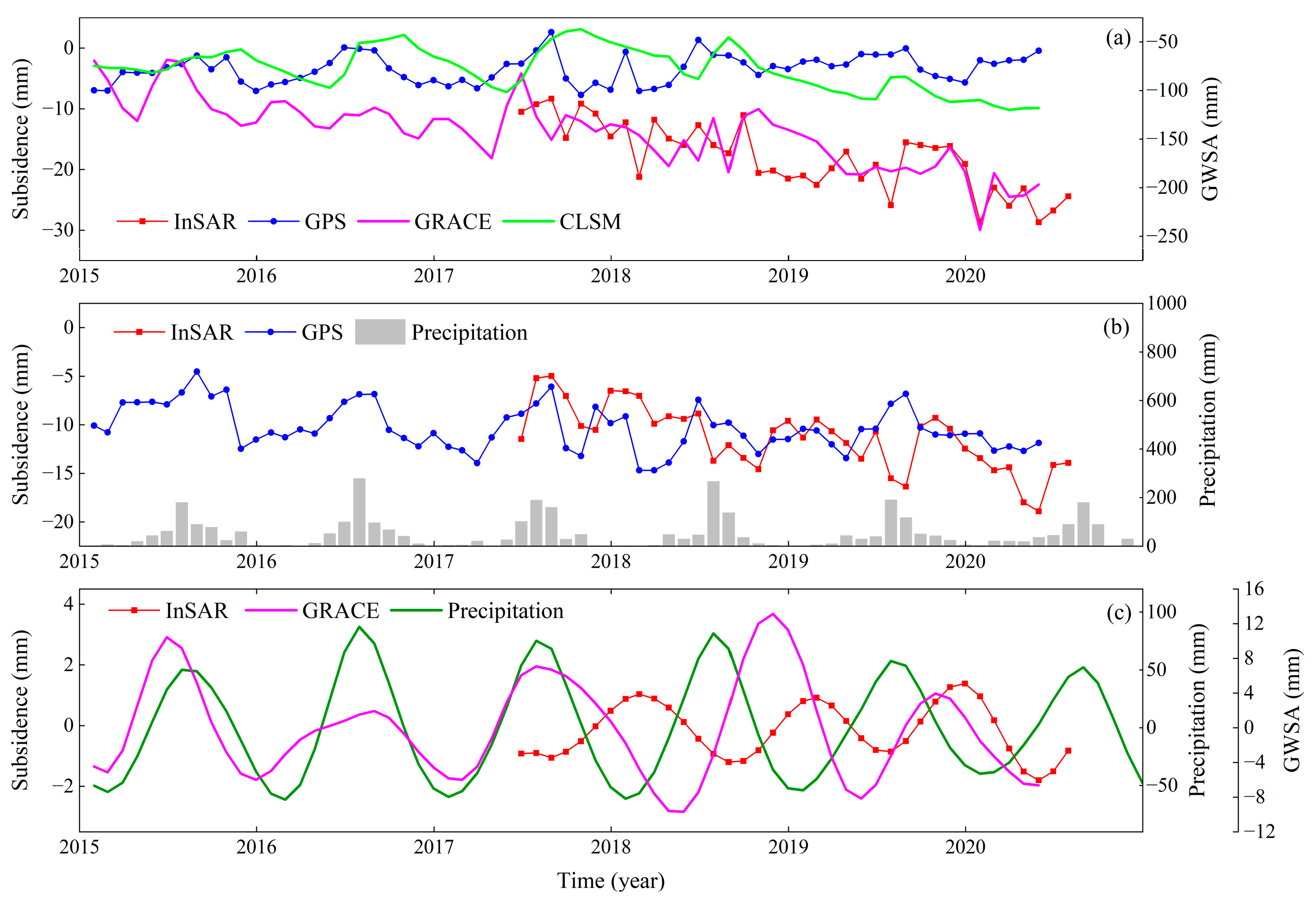
4.1. Comparison of GWSA, Land Subsidence, and Precipitation
4.2. Impact of Land Subsidence
4.3. Uncertainty of Simulated GWSA
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Sun, Q.; Fourie, A.; Ju, F.; Dong, X. Risk assessment and prevention of surface subsidence in deep multiple coal seam mining under dense above-ground buildings: Case study. Hum. Ecol. Risk Assess. 2019, 25, 1579–1593. [Google Scholar] [CrossRef]
- Smith, R.G.; Knight, R.; Chen, J.; Reeves, J.A.; Zebker, H.A.; Farr, T.; Liu, Z. Estimating the permanent loss of groundwater storage in the southern San Joaquin Valley, California. Water Resour. Res. 2017, 53, 2133–2148. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Wang, M.; Wang, Z.; Zhang, H. Surface deformation monitoring in Zhengzhou city from 2014 to 2016 using time-series InSAR. Remote Sens. 2018, 10, 1731. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Gong, H.; Lei, K.; Li, J.; Zhou, C.; Gao, M.; Guan, H.; Lv, W. Land subsidence lagging quantification in the main exploration aquifer layers in Beijing plain, China. Int. J. Appl. Earth Obs. 2019, 75, 54–67. [Google Scholar] [CrossRef]
- Zhu, Z.; Ren, C.; Zhou, L.; Shi, X.; Li, X.; Zhang, D. Monitoring Tianjin land subsidence by SBAS-InSAR based on Sentinel-1A SAR images. ISPRS J. Photogramm. 2020, 3, 315–331. [Google Scholar] [CrossRef] [Green Version]
- Hao, R.; Wang, X.W.; Xu, Y.S. Analysis of the factors resulting in the acceleration of land subsidence in the central area of Dezhou city, China. Environ. Earth Sci. 2022, 81, 400. [Google Scholar] [CrossRef]
- Bai, L.; Jiang, L.; Zhao, Y.; Li, Z.; Cao, G.; Zhao, C.; Liu, R.; Wang, H. Quantifying the influence of long-term overexploitation on deep groundwater resources across Cangzhou in the North China Plain using InSAR measurements. J. Hydrol. 2022, 605, 127368. [Google Scholar] [CrossRef]
- Liu, B.; Zou, X.; Yi, S.; Sneeuw, N.; Li, J.; Cai, J. Reconstructing GRACE-like time series of high mountain glacier mass anomalies. Remote Sens. Environ. 2022, 280, 113177. [Google Scholar] [CrossRef]
- Alshehri, F.; Mohamed, A. Analysis of Groundwater Storage Fluctuations Using GRACE and Remote Sensing Data in Wadi As-Sirhan, Northern Saudi Arabia. Water 2023, 15, 282. [Google Scholar] [CrossRef]
- Mohamed, A.; Abdelrady, A.; Alarifi, S.S.; Othman, A. Geophysical and Remote Sensing Assessment of Chad’s Groundwater Resources. Remote Sens. 2023, 15, 560. [Google Scholar] [CrossRef]
- Chaussard, E.; Burgmann, R.; Shirzaei, M.; Fielding, E.J.; Baker, B. Predictability of hydraulic head changes and characterization of aquifer system and fault properties from InSAR-derived ground deformation. J. Geophys. Res. Solid Earth 2014, 119, 6572–6590. [Google Scholar] [CrossRef]
- Ojha, C.; Shirzaei, M.; Werth, S.; Argus, D.F.; Farr, T.G. Sustained groundwater loss in California’s Central Valley exacerbated by intense drought periods. Water Resour. Res. 2018, 54, 4449–4460. [Google Scholar] [CrossRef]
- Castellazzi, P.; Martel, R.; Galloway, D.L. Assessing groundwater depletion and dynamics using GRACE and InSAR: Potential and limitations. Groundwater 2016, 54, 768. [Google Scholar] [CrossRef] [Green Version]
- Béjar-Pizarro, M.; Ezquerro, P.; Herrera, G.; Tomás, R.; Guardiola-Albert, C.; Hernández, J.; Merodo, J.; Marchamalo, M.; Martínez, M. Mapping groundwater level and aquifer storage variations from InSAR measurements in the Madrid aquifer, Central Spain. J. Hydrol. 2017, 547, 678–689. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.; Bai, L.; Zhao, Y.; Cao, G.; Wang, H.; Sun, Q. Combining InSAR and hydraulic head measurements to estimate aquifer parameters and storage variations of confined aquifer system in Cangzhou, North China Plain. Water Resour. Res. 2018, 54, 8234–8252. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Huang, Q.; Guo, J.; Jiang, J.; Wang, Q.; Nishyirimbere, N. Displacement monitoring and modeling of Qinghai–Tibet Railway in permafrost area using Sentinel-1A data. Arab. J. Geosci. 2019, 12, 204. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Longuevergne, L.; Long, D. Ground referencing GRACE satellite estimates of groundwater storage changes in the California Central Valley, USA. Water Resour. Res. 2012, 48, W04520. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.; Zhong, M.; Feng, W.; Zhang, Z.; Shen, Y.; Wu, D. Groundwater depletion in the west Liaohe river basin, china and its implications revealed by GRACE and in situ measurements. Remote Sens. 2018, 10, 493. [Google Scholar] [CrossRef] [Green Version]
- Yin, W.; Hu, L.; Zheng, W.; Jiao, J.; Han, S.; Zhang, M. Assessing underground water exchange between regions using GRACE data. J. Geophys. Res. Atmos. 2020, 125, e2020JD032570. [Google Scholar] [CrossRef]
- Farinotti, D.; Longuevergne, L.; Moholdt, G.; Duethmann, D.; Molg, T.; Bolch, T.; Vorogushyn, S.; Guntner, A. Substantial glacier mass loss in the Tien Shan over the past 50 years. Nat. Geosci. 2015, 8, 716–722. [Google Scholar] [CrossRef]
- Yin, W.; Hu, L.; Zhang, M.; Wang, J.; Han, S. Statistical downscaling of GRACE-derived groundwater storage using ET data in the North China Plain. J. Geophys. Res. Atmos. 2018, 123, 5973–5987. [Google Scholar] [CrossRef]
- Vishwakarma, B.; Zhang, J.; Sneeuw, N. Downscaling GRACE total water storage change using partial least squares regression. Sci. Data 2021, 8, 95. [Google Scholar] [CrossRef]
- Long, D.; Chen, X.; Scanlon, B.R.; Wada, Y.; Hong, Y.; Singh, V.P.; Chen, Y.; Wang, C.; Han, Z.; Yang, W. Have GRACE satellites overestimated groundwater depletion in the Northwest India Aquifer? Sci. Rep. 2016, 6, 24398. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Liu, P.; Massoud, E.; Farr, T.; Lundgren, P.; Famiglietti, J. Monitoring Groundwater change in California’s central valley using Sentinel-1 and GRACE observations. Geosciences 2019, 9, 436. [Google Scholar] [CrossRef] [Green Version]
- Milewski, A.; Thomas, M.; Seyoum, W.; Rasmussen, T. Spatial downscaling of grace TWSA data to identify spatiotemporal groundwater level trends in the upper Floridian aquifer, Georgia, USA. Remote Sens. 2019, 11, 2756. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Zheng, W.; Yin, W.; Li, X.; Zhang, G.; Zhang, J. Improving the Spatial Resolution of GRACE-Derived Terrestrial Water Storage Changes in Small Areas Using the Machine Learning Spatial Downscaling Method. Remote Sens. 2021, 13, 4760. [Google Scholar] [CrossRef]
- Zhong, D.; Wang, S.; Li, J. A self-calibration variance-component model for spatial downscaling of grace observations using land surface model outputs. Water Resour. Res. 2020, 11, 376–382. [Google Scholar] [CrossRef]
- Arshad, A.; Zhang, W.; Zhang, Z.; Wang, S.; Shalamzari, M.J. Reconstructing high-resolution gridded precipitation data using an improved downscaling approach over the high altitude mountain regions of Upper Indus Basin (UIB). Sci. Total Environ. 2021, 784, 147140. [Google Scholar] [CrossRef]
- Arshad, A.; Ali, M.; Maryam, S.; Ahmad, B. Combining downscaled-GRACE data with SWAT to improve the estimation of groundwater storage and depletion variations in the Irrigated Indus Basin (IIB). Sci. Total Environ. 2022, 838, 156044. [Google Scholar] [CrossRef]
- Ali, S.; Liu, D.; Fu, Q.; Cheema, M.; Pal, S.; Arshad, A.; Pham, Q.; Zhang, L. Constructing high-resolution groundwater drought at spatio-temporal scale using GRACE satellite data based on machine learning in the Indus Basin. J. Hydrol. 2022, 612, 128295. [Google Scholar] [CrossRef]
- Ali, S.; Khorrami, B.; Jehanzaib, M.; Tariq, A.; Ajmal, M.; Arshad, A.; Shafeeque, M.; Dilawar, A.; Basit, I.; Zhang, L.; et al. Spatial Downscaling of GRACE Data Based on XGBoost Model for Improved Understanding of Hydrological Droughts in the Indus Basin Irrigation System (IBIS). Remote Sens. 2023, 15, 873. [Google Scholar] [CrossRef]
- Noor, R.; Arshad, A.; Shafeeque, M.; Liu, J.; Baig, A.; Ali, S.; Maqsood, A.; Pham, Q.B.; Dilawar, A.; Khan, S.N.; et al. Combining APHRODITE Rain Gauges-Based Precipitation with Downscaled-TRMM Data to Translate High-Resolution Precipitation Estimates in the Indus Basin. Remote Sens. 2023, 15, 318. [Google Scholar] [CrossRef]
- Pranjal, P.; Kadiyan, N.; Chatterjee, R.S. Interpreting land subsidence impacts due to groundwater depletion using remote sensing-based GRACE gravity anomaly and D-InSAR technique: A study on north-western parts of India. Environ. Earth Sci. 2021, 80, 596. [Google Scholar] [CrossRef]
- Castellazzi, P.; Longuevergne, L.; Martel, M.; Rivera, A.; Brouard, C.; Chaussard, E. Quantitative mapping of groundwater depletion at the water management scale using a combined GRACE/InSAR approach. Remote Sens. Environ. 2018, 205, 408–418. [Google Scholar] [CrossRef]
- Shang, Q.; Liu, X.; Deng, X.; Zhang, B. Downscaling of GRACE datasets based on relevance vector machine using InSAR time series to generate maps of groundwater storage changes at local scale. J. Appl. Rem. Sens. 2019, 13, 048503. [Google Scholar] [CrossRef]
- Massoud, E.C.; Liu, Z.; Shaban, A.; Hage, M.E. Groundwater depletion signals in the Beqaa Plain, Lebanon: Evidence from GRACE and Sentinel-1 data. Remote Sens. 2021, 13, 915. [Google Scholar] [CrossRef]
- Castellazzi, P.; Garfias, J.; Martel, R.; Brouard, C.; Rivera, A. InSAR to support sustainable urbanization over compacting aquifers: The case of Toluca Valley, Mexico. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 33–44. [Google Scholar] [CrossRef]
- He, Q. Temporal InSAR Monitoring of Surface Deformation and Its Relationship with Groundwater Level in Beijing. Master’s Thesis, China University of Geosciences, Beijing, China, 2020. (In Chinese). [Google Scholar]
- Liu, Y.; Ye, C.; Jia, S. Division of water-bearing rock group and compressible layer in subsidence area of Beijing Plain. Urban Geol. 2007, 4, 10–15. (In Chinese) [Google Scholar]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 MASCONs. J. Geophys. Res. Solid. Earth. 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Shen, Y.; Zheng, W.; Yin, W.; Xu, A.; Zhu, H.; Yang, S.; Su, K. Inverted Algorithm of Terrestrial Water-Storage Anomalies Based on Machine Learning Combined with Load Model and Its Application in Southwest China. Remote Sens. 2021, 13, 3358. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-Gonz´alez, M.; Devanth´ery, N.; Crippa, B. Persistent scatterer interferometry: A review. ISPRS J. Photogramm. 2016, 115, 78–89. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.H.; Monserrat, O.; Crosetto, M.; Crippa, B.; Wang, Y.A.; Jiang, J.F.; Ding, Y. Displacement monitoring and health evaluation of two bridges using Sentinel-1 SAR images. Remote Sens. 2018, 10, 1714. [Google Scholar] [CrossRef] [Green Version]
- He, X.; He, M. InSAR Earth Observation Data Processing Method and Comprehensive Survey; Science Press: Beijing, China, 2012; pp. 54–56. [Google Scholar]
- Wang, Q.Q.; Huang, Q.H.; He, N.; He, B.; Wang, Z.C.; Wang, Y.A. Displacement monitoring of Upper Atbara Dam based on time series InSAR. Surv. Rev. 2019, 52, 485–496. [Google Scholar] [CrossRef]
- Han, P. Status quo of groundwater development and utilization in Haihe River basin and its management. Haihe Water Resour. 2015, 39, 1–5. (In Chinese) [Google Scholar]
- Ren, Y.; Pan, Y.; Gong, H. Haihe Basin groundwater reserves space trend analysis. J. Cap. Norm. Univ. 2014, 35, 89–98. (In Chinese) [Google Scholar]
- Zhong, Y.; Feng, W.; Humphrey, V.; Zhong, M. Human-induced and climate-driven contributions to water storage variations in the haihe river basin, china. Remote Sens. 2019, 11, 3050. [Google Scholar] [CrossRef] [Green Version]
- Mohamad, N.; Ahmad, A.; Din, A. Monitoring groundwater depletion due to drought using satellite gravimetry: A review. IOP Conf. Ser. Earth Environ. Sci. 2020, 540, 012054. [Google Scholar] [CrossRef]
- Yang, X.; Tian, S.; Feng, W.; Ran, J.; You, W.; Jiang, Z.; Gong, X. Spatiotemporal evaluation of water storage trends from hydrological models over Australia using GRACE Mascon solutions. Remote Sens. 2020, 12, 3578. [Google Scholar] [CrossRef]
- Vautard, R.; Ghil, M. Singular spectrum analysis in nonlinear dynamics with applications paleoclimate time series. Physica D 1989, 35, 399–424. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, X.; Xiong, P.; You, H.; Zhang, H.; Yang, F.; Zhao, Y.; Yang, Y.; Liu, Y. Deformation monitoring and analysis of Kunyang phosphate mine fusion with InSAR and GPS measurements. Adv. Space Res. 2022, 69, 2637–2658. [Google Scholar] [CrossRef]
- Li, Q. Numerical Analysis; Tsinghua University Press: Beijing, China, 2008; pp. 34–35. (In Chinese) [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 448–456. [Google Scholar]
- Zheng, L.Q.; Pan, Y.; Gong, H.L. Comparing groundwater storage changes in two main grain producing areas in china: Implications for sustainable agricultural water resources management. Remote Sens. 2020, 12, 21–43. [Google Scholar] [CrossRef]
- Mohamed, A.; Gonçalvès, J. Hydro-geophysical monitoring of the North Western Sahara Aquifer System’s groundwater resources using gravity data. J. Afr. Earth Sci. 2021, 178, 104188. [Google Scholar] [CrossRef]
- Rodgers, J.L.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model. Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Hu, L.; Zhang, M.; Liu, X. Evaluation of groundwater withdrawals in Tongzhou district, Beijing, China. Hum. Ecol. Risk Assess. 2019, 27, 1441–1457. [Google Scholar] [CrossRef]
- Dong, J.; Lai, S.; Wang, N.; Wang, Y.; Zhang, L.; Liao, M. Multi-scale deformation monitoring with Sentinel-1 InSAR analyses along the Middle Route of the South-North Water Diversion Project in China. Int. J. Appl. Earth Obs. 2021, 100, 102324. [Google Scholar] [CrossRef]
- Ge, D.Q. Study on Key Techniques of InSAR Monitoring of Regional Land Subsidence. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2013. (In Chinese). [Google Scholar]
- Zhang, T.; He, Q.; Jing, C.; Liu, L. Dynamic monitoring of groundwater in Beijing Plain area based on InSAR. Sci. Technol. Eng. 2019, 19, 16–22. (In Chinese) [Google Scholar]
- Jiang, Y.; Tian, F.; Luo, Y. Relationship between stratified land subsidence and groundwater level variation in typical areas of Beijing. South--North Water Transf. Water Sci. Technol. 2015, 13, 95–99. (In Chinese) [Google Scholar]
- Hoffmann, J.; Galloway, D.L.; Zebker, H.A. Inverse modeling of interbred storage parameters using land subsidence observations, Antelope Valley, California. Water Resour. Res. 2003, 39, 1031. [Google Scholar] [CrossRef]
- Hu, X.; Lu, Z.; Wang, T. Characterization of hydrogeological properties in Salt Lake Valley, Utah using InSAR. J. Geophys. Res. 2018, 123, 1257–1271. [Google Scholar] [CrossRef] [Green Version]
- Galloway, D.L.; Hoffmann, J. The application of satellite differential SAR interferometry-derived ground displacements in hydrogeology. Hydrgeol. J. 2007, 15, 133–154. [Google Scholar] [CrossRef] [Green Version]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science and Business Media: New York, NY, USA, 2001; pp. 120–121. [Google Scholar]
- Ghil, M.; Allen, M.; Dettinger, M. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 1003. [Google Scholar] [CrossRef] [Green Version]
- Pool, D.R. The utility of gravity and water-level monitoring at alluvial aquifer wells in southern Arizona. Geophysics 2008, 73, 49–59. [Google Scholar] [CrossRef]





| Sentinel-1A | Parameter | Dataset | Parameter |
|---|---|---|---|
| Launch time | 2014.4.3 | Sensing period | 20 May 2017–15 July 2020 |
| Band | C-band (~5.6 cm) | Image number | 39 |
| Coverage width | 250 km | Orbit number | 142 |
| Spatial resolution | 5 m × 20 m | Multi-look | 10 × 2 |
| Track height | 700 km | Order | Ascending |
| Revisit time | 12 day | Sensor mode | IW |
| Sensor mode | SM, IW, EW, WV | Polarisation | VV |
| Polarisation | VV, HH, VV+VH, HH+HV | Time baseline | 24/36 days |
| Space baseline | <180 m |
| ID | P17 | P66 | P68 | P86 |
|---|---|---|---|---|
| r1 (InSAR/△GWL) | 0.97 | 0.98 | 0.94 | 0.97 |
| r2 (InSAR/CLSM) | 0.95 | 0.97 | 0.94 | 0.86 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Zheng, W.; Yin, W.; Kang, G.; Huang, Q.; Shen, Y. Improving the Resolution of GRACE/InSAR Groundwater Storage Estimations Using a New Subsidence Feature Weighted Combination Scheme. Water 2023, 15, 1017. https://doi.org/10.3390/w15061017
Wang Q, Zheng W, Yin W, Kang G, Huang Q, Shen Y. Improving the Resolution of GRACE/InSAR Groundwater Storage Estimations Using a New Subsidence Feature Weighted Combination Scheme. Water. 2023; 15(6):1017. https://doi.org/10.3390/w15061017
Chicago/Turabian StyleWang, Qingqing, Wei Zheng, Wenjie Yin, Guohua Kang, Qihuan Huang, and Yifan Shen. 2023. "Improving the Resolution of GRACE/InSAR Groundwater Storage Estimations Using a New Subsidence Feature Weighted Combination Scheme" Water 15, no. 6: 1017. https://doi.org/10.3390/w15061017






