Water Quality Analysis of a Tropical Reservoir Based on Temperature and Dissolved Oxygen Modeling by CE-QUAL-W2
Abstract
:1. Introduction
2. Methods and Materials
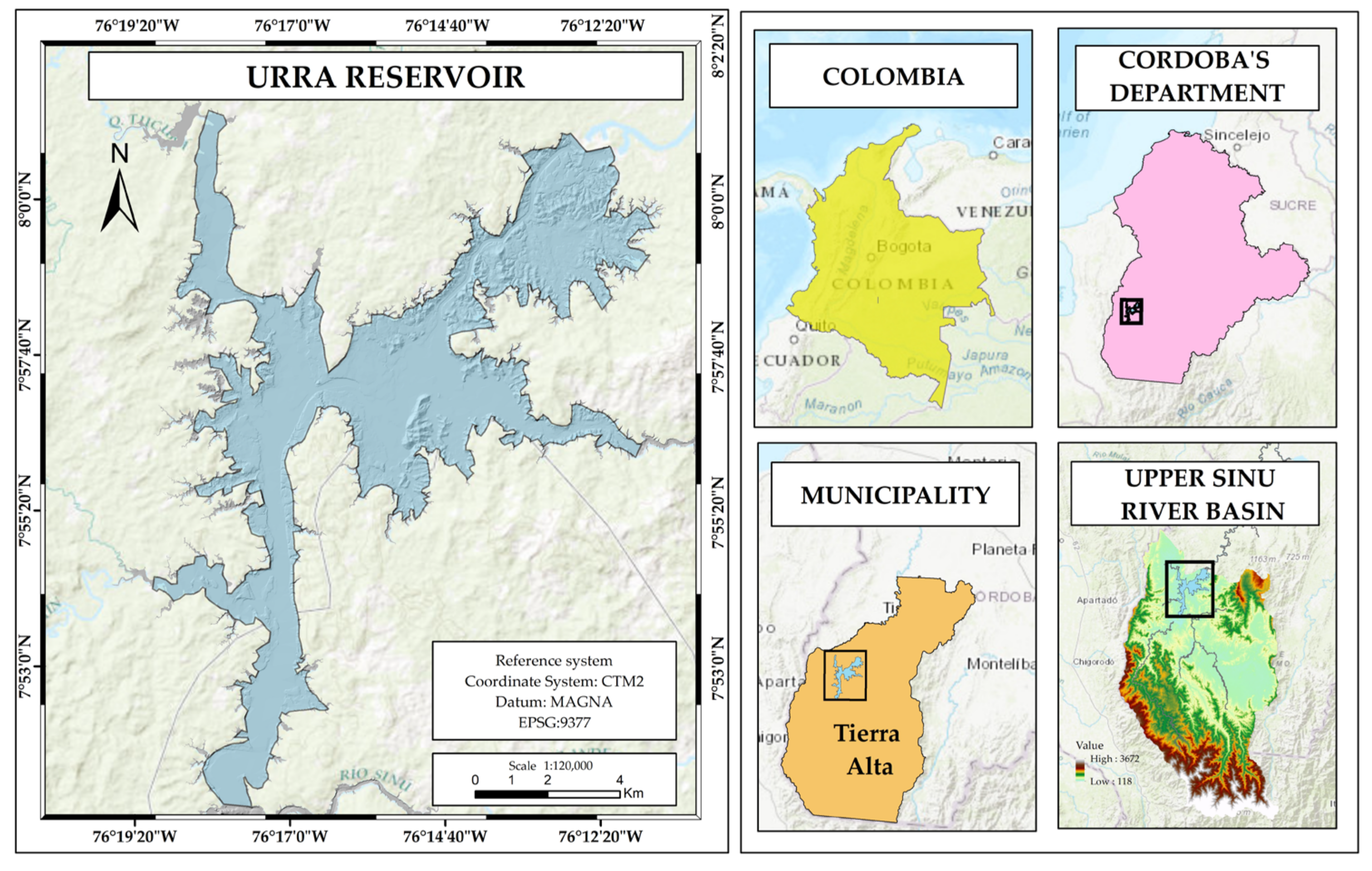
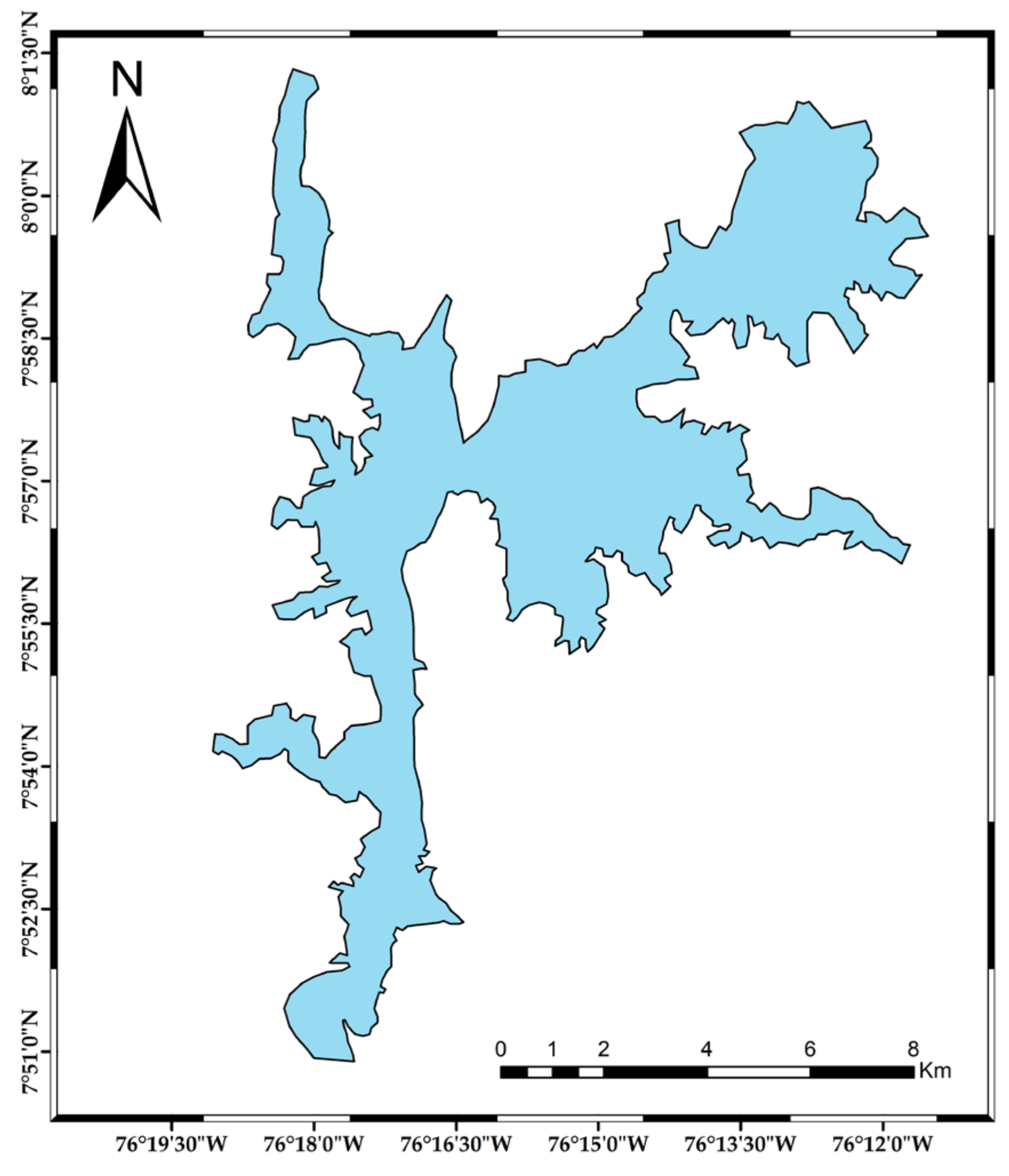
2.1. Study Area
2.2. Model Description
2.2.1. Initial and Boundary Conditions of the CE-QUAL-W2 Model
- Depth: the average depth and spatial distribution of depth in the reservoir. These values were assigned using the CSV file described in the input and processing data Section 2.2.4.
- Temperature: the average temperature and spatial temperature distribution in the reservoir water. This input was manually assigned as described in the input and processing data Section 2.2.4.
- Salinity: the average and spatial distribution of salinity in the reservoir water.
- Nutrient concentration: This condition describes the concentration of nutrients such as nitrogen and phosphorus and their spatial distribution in the reservoir. Dissolved oxygen concentrations were defined by the modelers.
- Suspended matter concentration: This input defines the suspended matter concentration in the reservoir water and its spatial distribution.
- Flow velocity and direction: The velocity and direction of flow in the reservoir or impoundment.
- Water inflow and outflow: the amount of water entering and leaving the reservoir or impoundment, including flow to and from rivers or aquifers and evapotranspiration. These values were assigned through a CSV file described in the input and processing data Section 2.2.4.
- Nutrient inflow and outflow: the amount of nutrients entering and leaving the reservoir, including wastewater discharge and agriculture.
- Precipitation: the amount of precipitation falling in the reservoir or impoundment.
- Evapotranspiration: the amount of water that evaporates and transpires in the reservoir or impoundment.
- Heat transfer with air: the amount of heat transferred from the air to the water in the reservoir, which affects water temperature.
- Conditions in the river or aquifer feeding the reservoir: this condition refers to the hydrochemical characteristics in the river or aquifer feeding the reservoir, including depth, temperature, salinity, velocity, and direction, among others.
2.2.2. Equations
2.2.3. Generalities
2.2.4. Input and Processing Data
2.2.5. Calibration and Sensitivity Analysis
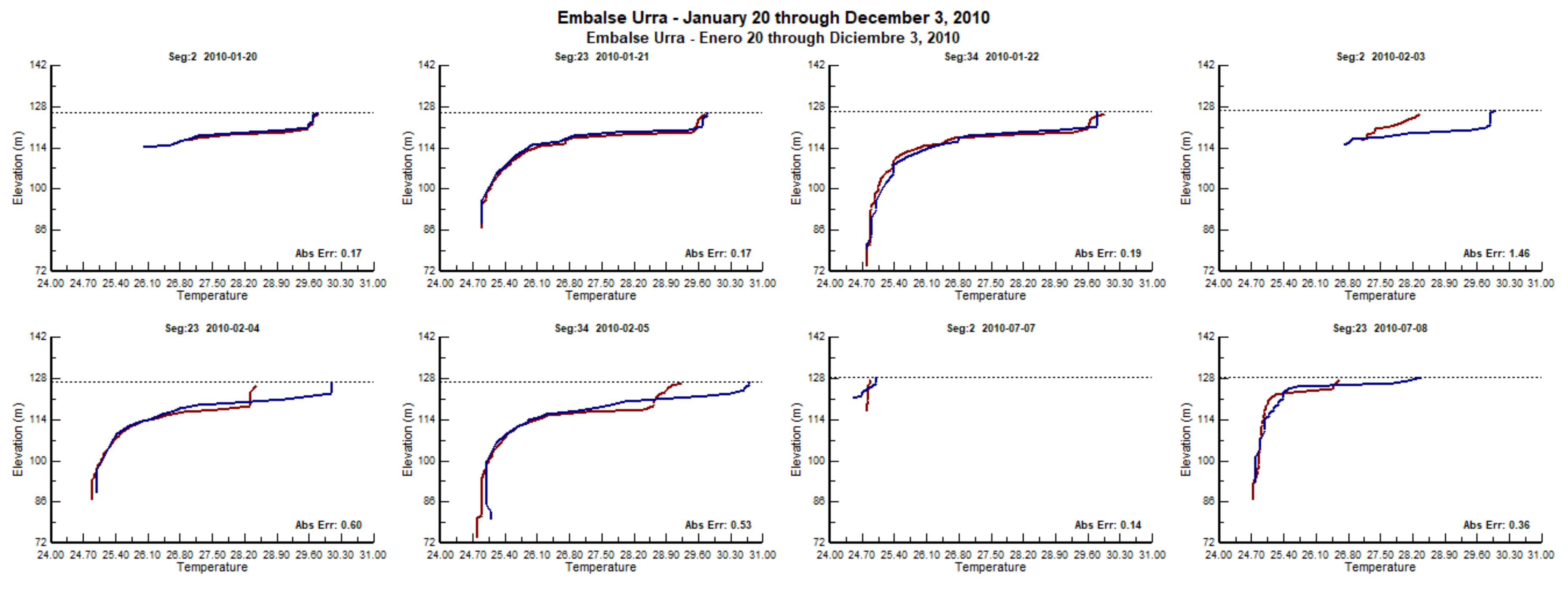
2.2.6. Source of Errors
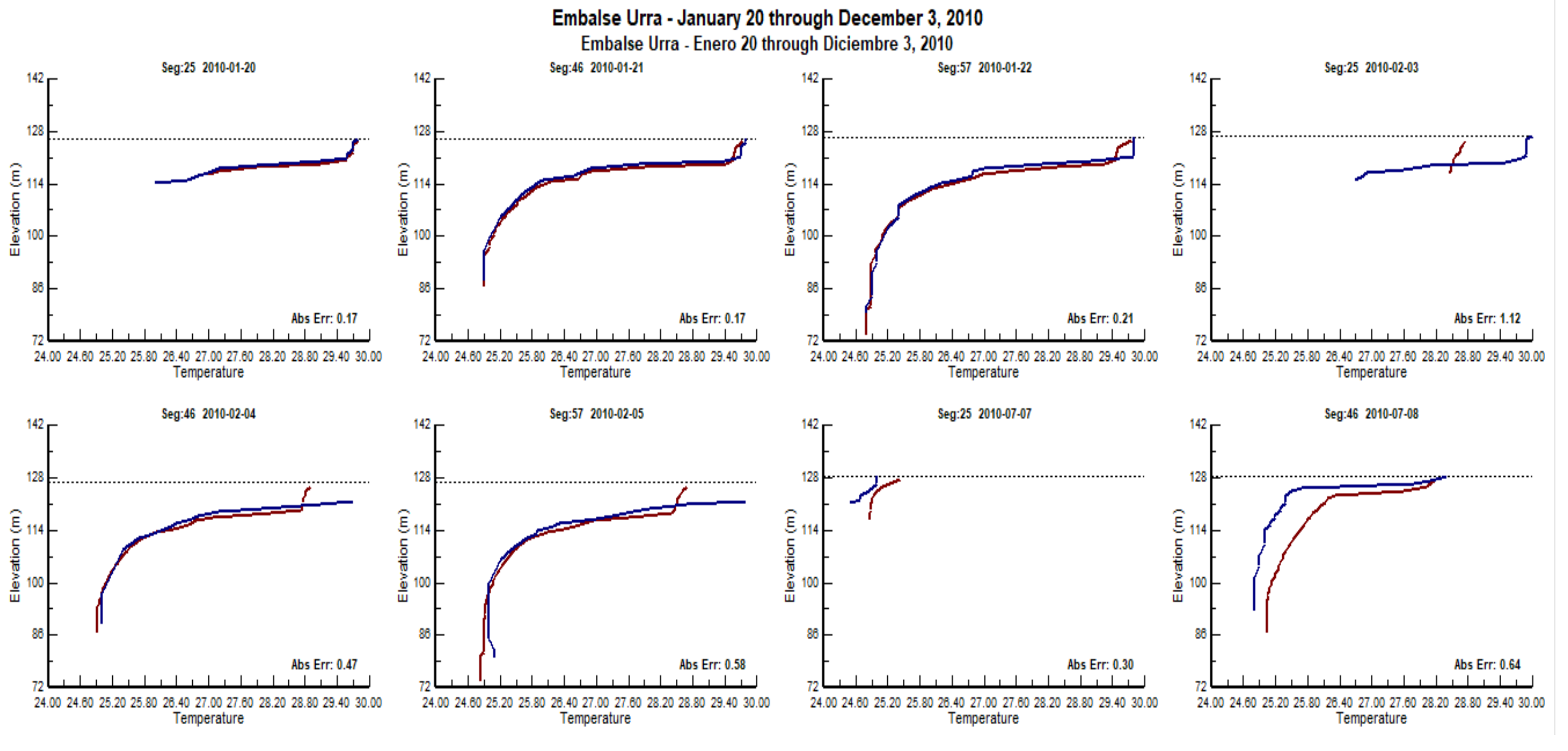
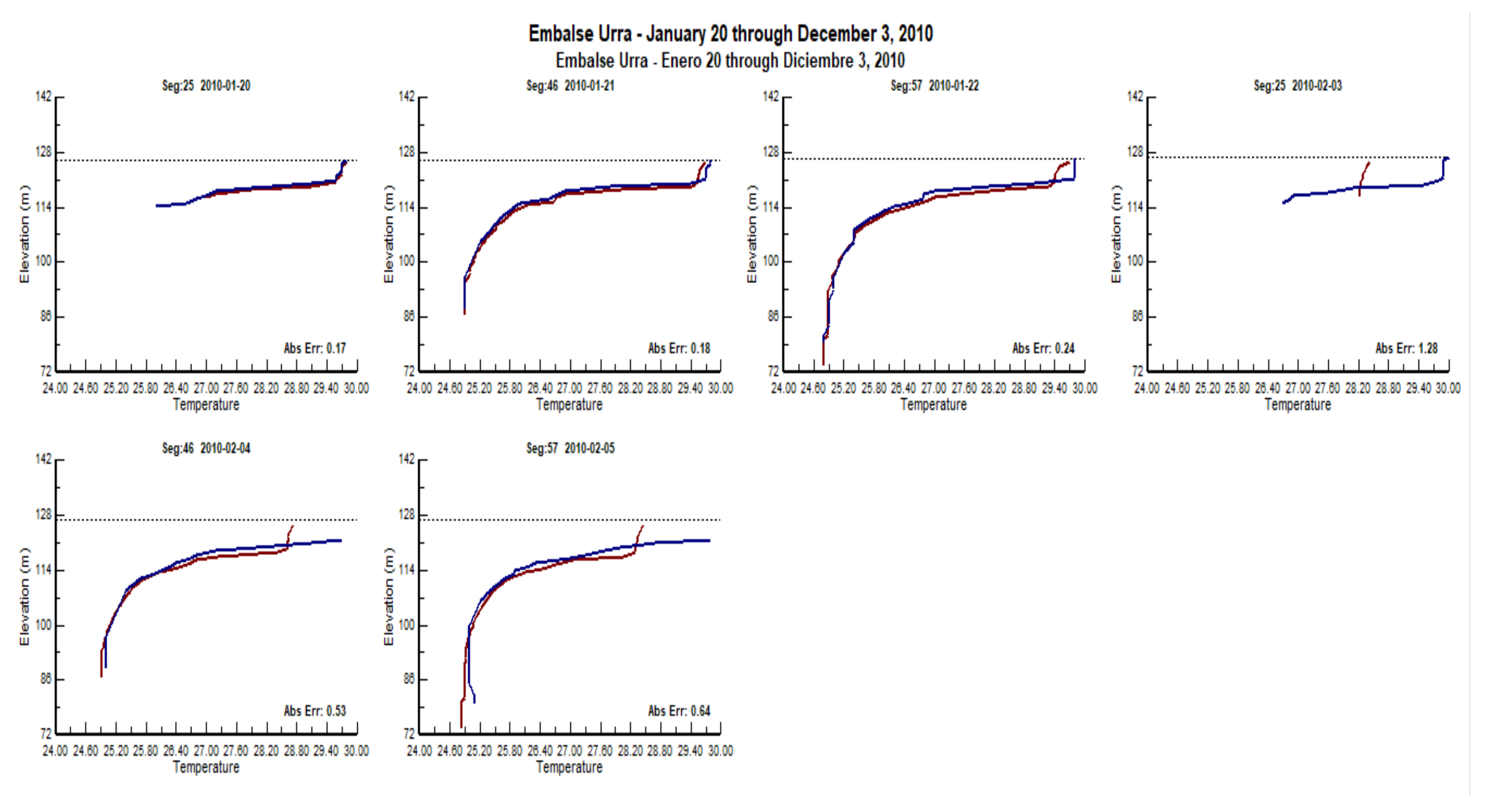
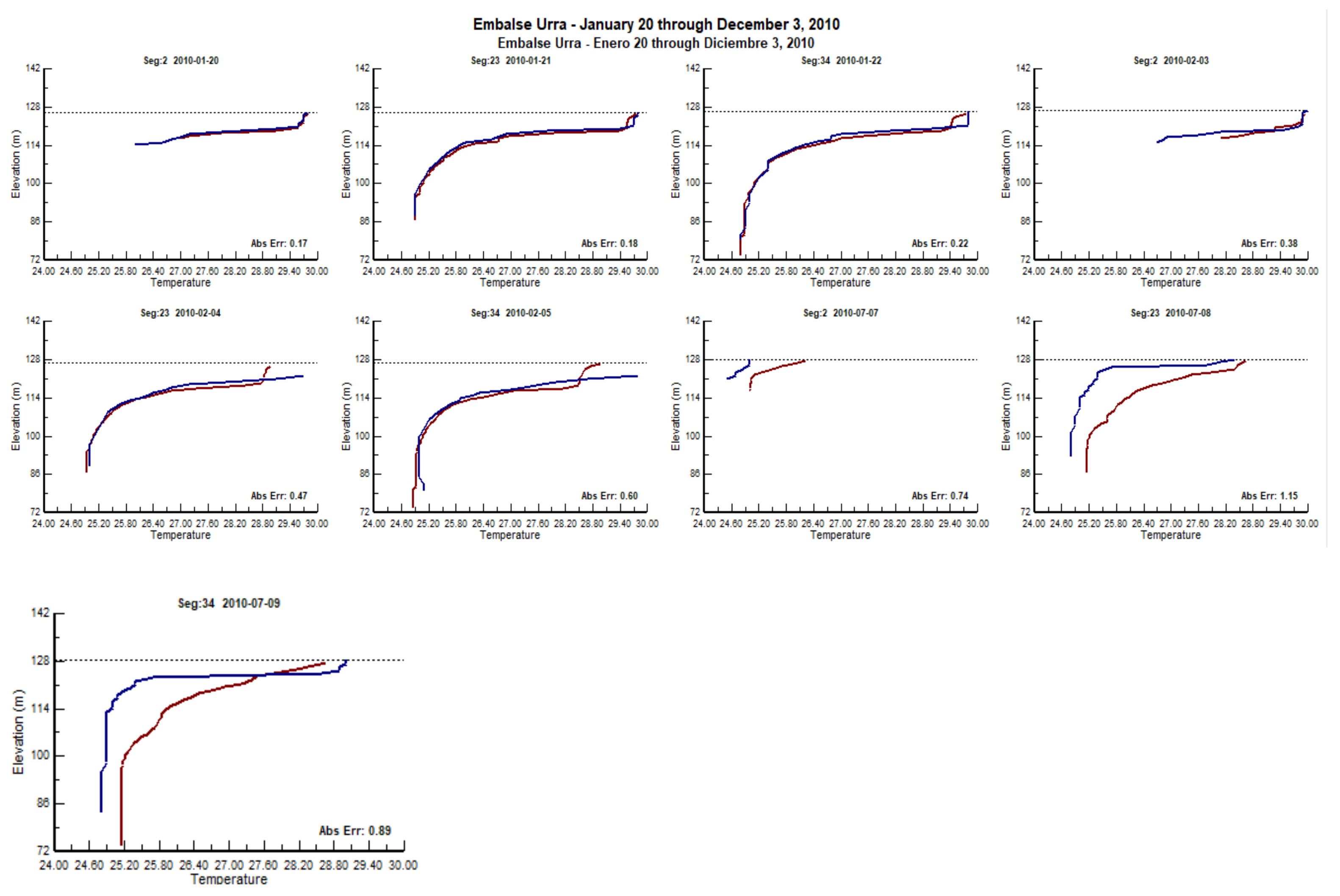
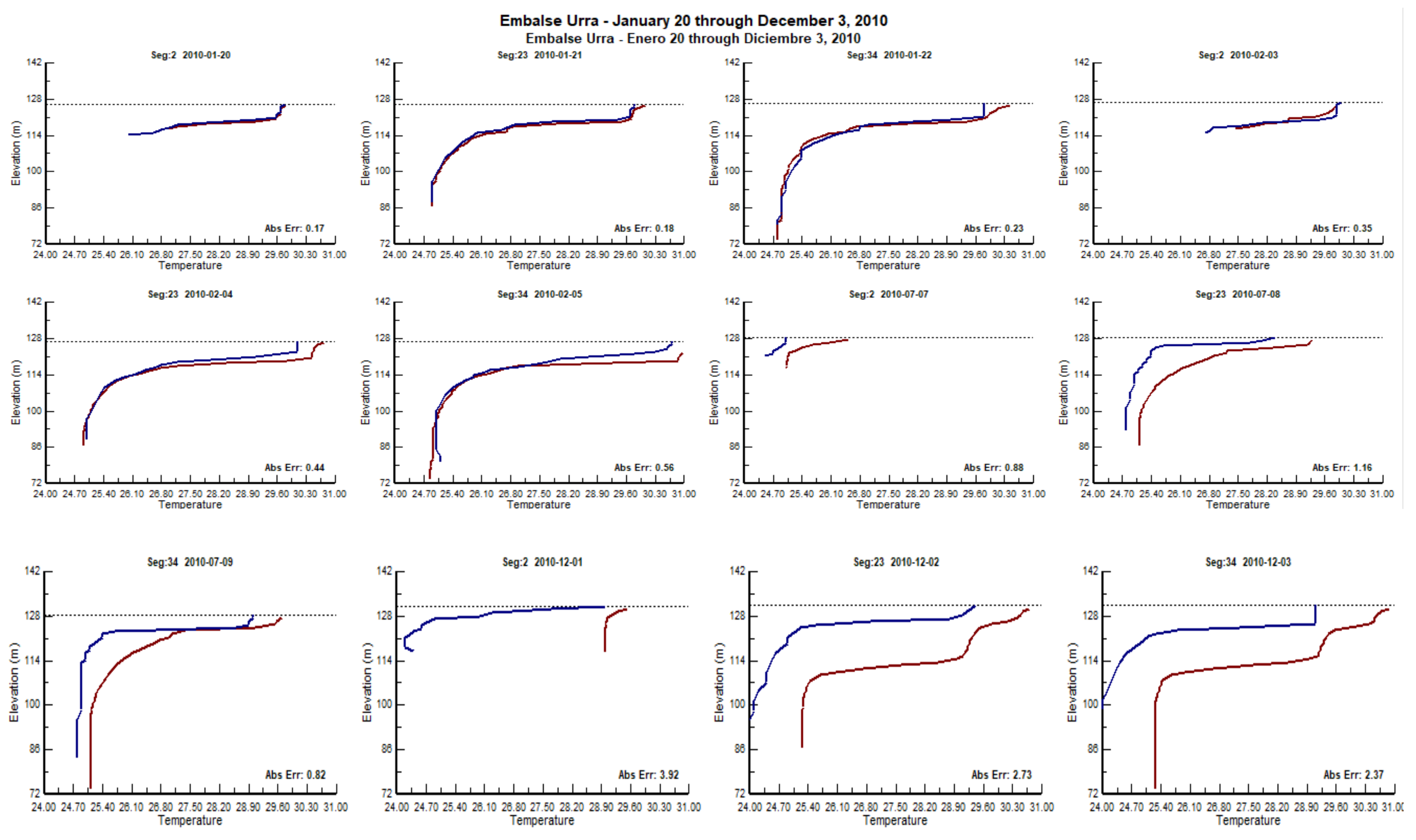
3. Results and Discussion
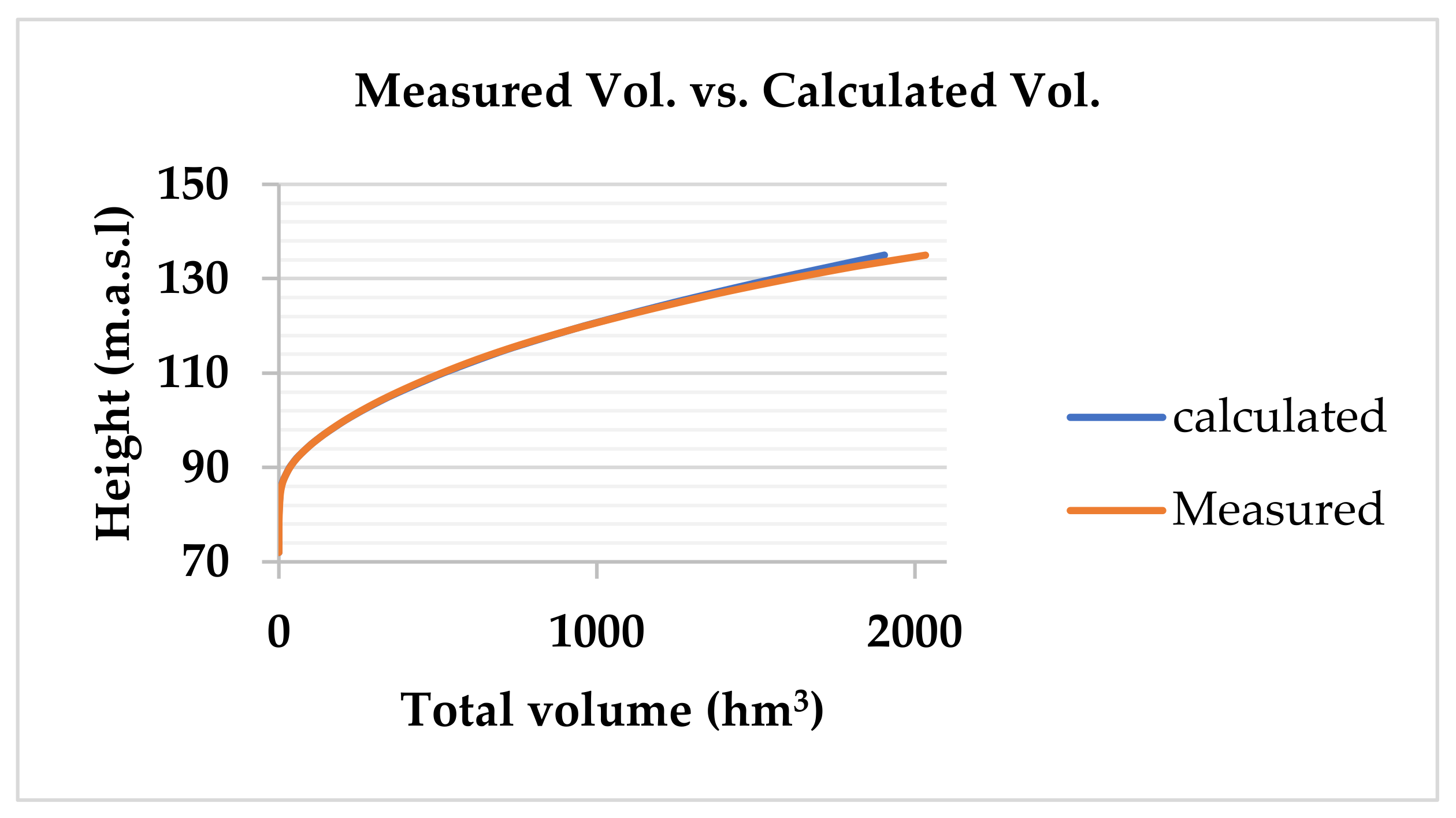
3.1. Analysis of the Bathymetry Results
3.2. Water Quality Simulation
Calibration
3.3. Results with Adjusted Meteorology (Applying the Vertical Turbulence Method W2)
3.4. Model Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stelzer, C.; Nestmann, F. The importance of reservoirs for water supply and power generation—An overview. In Global Change: Enough Water for All?: Scientific Facts; Verlag Wissenschaftliche Auswertungen: Hamburg, Germany, 2007; Volume 5, pp. 117–121. [Google Scholar] [CrossRef]
- Branche, E. The multipurpose water uses of hydropower reservoir: The SHARE concept. C. R. Phys. 2017, 18, 469–478. [Google Scholar] [CrossRef]
- Li, J.; Zhong, P.-A.; Wang, Y.; Yang, M.; Fu, J.; Liu, W.; Xu, B. Risk analysis for the multi-reservoir flood control operation considering model structure and hydrological uncertainties. J. Hydrol. 2022, 612, 128263. [Google Scholar] [CrossRef]
- Boretti, A.; Rosa, L. Reassessing the projections of the World Water Development Report. Npj Clean Water 2019, 2, 15. [Google Scholar] [CrossRef] [Green Version]
- United Nations, U.W. Wastewater Management A UN-Water Analytical Brief; WHO: Geneva, Switzerland, 2015. [Google Scholar]
- Khodabandeh, F.; Dehghani Darmian, M.; Azhdary Moghaddam, M.; Hashemi Monfared, S.A. Reservoir quality management with CE-QUAL-W2/ANN surrogate model and PSO algorithm (case study: Pishin Dam, Iran). Arab. J. Geosci. 2021, 14, 401. [Google Scholar] [CrossRef]
- Noori, R.; Yeh, H.-D.; Ashrafi, K.; Rezazadeh, N.; Bateni, S.M.; Karbassi, A.; Kachoosangi, F.T.; Moazami, S. A reduced-order based CE-QUAL-W2 model for simulation of nitrate concentration in dam reservoirs. J. Hydrol. 2015, 530, 645–656. [Google Scholar] [CrossRef]
- Winton, R.S.; López-Casas, S.; Valencia-Rodríguez, D.; Bernal-Forero, C.; Delgado, J.; Wehrli, B.; Jiménez-Segura, L. Patterns and drivers of water quality changes associated with dams in the Tropical Andes. EGUsphere 2022, 403, 1–21. [Google Scholar] [CrossRef]
- Song, Y.; You, L.; Chen, M.; Li, J.; Zhang, L.; Peng, T. Key hydrodynamic principles for controlling algal blooms using emergency reservoir operation strategies. J. Environ. Manag. 2023, 325, 116470. [Google Scholar] [CrossRef]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High-resolution mapping of the world’s reservoirs and dams for sustainable river-flow management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef] [Green Version]
- Afshar, A.; Shojaei, N.; Sagharjooghifarahani, M. Multiobjective Calibration of Reservoir Water Quality Modeling Using Multiobjective Particle Swarm Optimization (MOPSO). Water Resour. Manag. 2013, 27, 1931–1947. [Google Scholar] [CrossRef]
- Chanudet, V.; Fabre, V.; van der Kaaij, T. Application of a three-dimensional hydrodynamic model to the Nam Theun 2 Reservoir (Lao PDR). J. Great Lakes Res. 2012, 38, 260–269. [Google Scholar] [CrossRef]
- Neitsch, S.; Arnold, J.; Kiniry, J.; Williams, J.; King, K. Soil and Water Assessment Tool (SWAT) User’s Manual Version 2000; Technical Report for Texas Water Resources Institute: College Station, TX, USA, 2002. [Google Scholar]
- Ma, L.; He, C.; Bian, H.; Sheng, L. MIKE SHE modeling of ecohydrological processes: Merits, applications, and challenges. Ecol. Eng. 2016, 96, 137–149. [Google Scholar] [CrossRef]
- Xingpo, L.; Muzi, L.; Yaozhi, C.; Jue, T.; Jinyan, G. A comprehensive framework for HSPF hydrological parameter sensitivity, optimization and uncertainty evaluation based on SVM surrogate model—A case study in Qinglong River watershed, China. Environ. Model. Softw. 2021, 143, 105126. [Google Scholar] [CrossRef]
- Dehdari, V.; Oliver, D.S.; Deutsch, C.V. Comparison of optimization algorithms for reservoir management with constraints—A case study. J. Pet. Sci. Eng. 2012, 100, 41–49. [Google Scholar] [CrossRef]
- Diogo, P.A.; Fonseca, M.; Coelho, P.S.; Mateus, N.S.; Almeida, M.C.; Rodrigues, A.C. Reservoir phosphorous sources evaluation and water quality modeling in a transboundary watershed. Desalination 2008, 226, 200–214. [Google Scholar] [CrossRef]
- Hamilton, D.P.; Hocking, G.C.; Patterson, J.C. Criteria for selection of spatial dimension in the application of one- and two-dimensional water quality models. Math. Comput. Simul. 1997, 43, 387–393. [Google Scholar] [CrossRef]
- Ochoa, S.; Reyna, T.; Reyna, S.; García, M.; Labaque, M.; Manuel Díaz, J. Modelación Hidrodinámica Del Tramo Medio Del Río Ctalamochita, Provincia de Córdoba. Rev. Fac. Cienc. Exactas Fís. Nat. 2016, 3, 95–101. [Google Scholar]
- Ostfeld, A.; Salomons, S. A hybrid genetic—Instance based learning algorithm for CE-QUAL-W2 calibration. J. Hydrol. 2004, 310, 122–142. [Google Scholar] [CrossRef]
- Wells, S.A. CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 4.2.2. User Manual: Part 1 Introduction, Model Download Package, How to Run the Model; Technical Report for Department of Civil and Environmental Engineering Portland State University: Portland, OR, USA, 2020. [Google Scholar]
- Bonalumi, M.; Anselmetti, F.S.; Wüest, A.; Schmid, M. Modeling of temperature and turbidity in a natural lake and a reservoir connected by pumped-storage operations. Water Resour. Res. 2012, 48, W08508. [Google Scholar] [CrossRef] [Green Version]
- Noori, R.; Tian, F.; Ni, G.; Bhattarai, R.; Hooshyaripor, F.; Klöve, B. ThSSim: A novel tool for simulation of reservoir thermal stratification. Sci. Rep. 2019, 9, 18524. [Google Scholar] [CrossRef] [Green Version]
- Noori, R.; Asadi, N.; Deng, Z. A simple model for simulation of reservoir stratification. J. Hydraul. Res. 2019, 57, 561–572. [Google Scholar] [CrossRef]
- Tavoosi, N.; Hooshyaripor, F.; Noori, R.; Farokhnia, A.; Maghrebi, M.; Kløve, B.; Haghighi, A.T. Experimental-numerical simulation of soluble formations in reservoirs. Adv. Water Resour. 2022, 160, 104109. [Google Scholar] [CrossRef]
- Chuo, M.; Ma, J.; Liu, D.; Yang, Z. Effects of the impounding process during the flood season on algal blooms in Xiangxi Bay in the Three Gorges Reservoir, China. Ecol. Model. 2018, 392, 236–249. [Google Scholar] [CrossRef]
- Kurup, R.G.; Hamilton, D.P.; Phillips, R.L. Comparison of two 2-dimensional, laterally averaged hydrodynamic model applications to the Swan River Estuary. Math. Comput. Simul. 2000, 51, 627–638. [Google Scholar] [CrossRef]
- Larabi, S.; Schnorbus, M.A.; Zwiers, F. A coupled streamflow and water temperature (VIC-RBM-CE-QUAL-W2) model for the Nechako Reservoir. J. Hydrol. Reg. Stud. 2022, 44, 101237. [Google Scholar] [CrossRef]
- Shojaei, N.; Wells, S. Automatic Calibration of Water Quality Models for Reservoirs and Lakes. In Proceedings of the World Environmental and Water Resources Congress 2014, Portland, OR, USA, 1–5 June 2014; Volume 2014, pp. 1020–1029. [Google Scholar] [CrossRef]
- American Society of Civil Engineers Task Committee on Turbulence Models in Hydraulic Computation. Turbulence Modeling of Surface Water Flow and Transport: Part I. J. Hydraul. Eng. 1988, 114, 970–991. [Google Scholar] [CrossRef]
- Afshar, A.; Feizi, F.; Yousefi Moghadam, A.; Saadatpour, M. Enhanced CE-QUAL-W2 model to predict the fate and transport of volatile organic compounds in water body: Gheshlagh reservoir as case study. Environ. Earth Sci. 2017, 76, 803. [Google Scholar] [CrossRef]
- Bartholow, J.; Hanna, R.B.; Saito, L.; Lieberman, D.; Horn, M. Simulated Limnological Effects of the Shasta Lake Temperature Control Device. Environ. Manag. 2001, 27, 609–626. [Google Scholar] [CrossRef]
- Chung, S.; Oh, J. Calibration of CE-QUAL-W2 for a monomictic reservoir in a monsoon climate area. Water Sci. Technol. 2006, 54, 29–37. [Google Scholar] [CrossRef]
- Deliman, P.N.; Gerald, J.A. Application of the Two-Dimensional Hydrothermal and Water Quality Model, CE-QUAL-W2, to the Chesapeake Bay–Conowingo Reservoir. Lake Reserv. Manag. 2002, 18, 10–19. [Google Scholar] [CrossRef] [Green Version]
- Azadi, F.; Ashofteh, P.-S.; Loáiciga, H.A. Reservoir Water-Quality Projections under Climate-Change Conditions. Water Resour. Manag. 2018, 33, 401–421. [Google Scholar] [CrossRef]
- Xie, Q.; Liu, Z.; Fang, X.; Chen, Y.; Li, C.; MacIntyre, S. Understanding the Temperature Variations and Thermal Structure of a Subtropical Deep River-Run Reservoir before and after Impoundment. Water 2017, 9, 603. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Cheng, S.; Sun, Y.; Zou, R.; Ma, W.; Zhou, Q.; Liu, Y. Thermal mixing of Lake Erhai (Southwest China) induced by bottom heat transfer: Evidence based on observations and CE-QUAL-W2 model simulations. J. Hydrol. 2021, 603, 126973. [Google Scholar] [CrossRef]
- Yu, S.J.; Lee, J.Y.; Ha, S.R. Effect of a seasonal diffuse pollution migration on natural organic matter behavior in a stratified dam reservoir. J. Environ. Sci. 2010, 22, 908–914. [Google Scholar] [CrossRef] [PubMed]
- Torres, E.; Galván, L.; Cánovas Ruiz, C.; Soria-Píriz, S.; Arbat-Bofill, M.; Nardi, A.; Papaspyrou, S.; Ayora, C. Oxycline formation induced by Fe(II) oxidation in a water reservoir affected by acid mine drainage modeled using a 2D hydrodynamic and water quality model—CE-QUAL-W2. Sci. Total. Environ. 2016, 562, 1–12. [Google Scholar] [CrossRef]
- Parra-Cuadros, M.; Villegas-Jiménez, N.E.; Hernández-Atilano, E.; Aguirre-Ramírez, N.J.; de Vélez-Macías, F.J. Aplicación del modelo CE QUAL-W2: Una aproximación a la estructura térmica en el embalse Miguel Martínez Isaza, Concordia, Antioquia, Colombia. Tecnológicas 2019, 22, 99–113. [Google Scholar] [CrossRef] [Green Version]
- Clavijo-Bernal, O.F. El agua y la participación como ejes articuladores del territorio. Consideraciones a partir de URRÁ y su incidencia sobre la cuenca del río Sinú. Gestión Ambiente 2021, 24, 51–74. [Google Scholar] [CrossRef]
- URRÁ S.A. E.S. Reporte técnico de monitoreo ambiental. Printed document. 2021. [Google Scholar]
- Hernández Camacho, J.; Walschburger, T.; Ortiz Quijano, R.; Hurtado Guerra, A. Origen y Distribución de La Biota Su-ramericana y Colombiana. Acta Zool. Mex. 1992, 55–104. [Google Scholar]
- Palencia Severiche, G.; Mercado-Fernandez, T.; Combath Caballero, E. Estudio Agroclimático de Córdoba; Technical Report for Facultad de Ciencias Agrícolas; Universidad de Córdoba: Córdoba, Spain, 2006. [Google Scholar]
- URRÁ S.A. E.S. Incremento del volumen del embalse de URRÁ. Reporte técnico. 2010. [Google Scholar]
- Vélez Flórez, A.J. Propuesta Metodológica Para La Evaluación y Cuantificación de La Alteración Del Régimen de Caudales de Corrientes Alteradas Antrópicamente, Caso URRÁ I. Master’s Thesis, Universidad Nacional de Colombia, Bogotá, Colombia, 2009. [Google Scholar]
- Wells, S.A. CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 4.5, User Manual Part 2, Hydrodynamic and Water Quality Model Theory; Technical Report for Department of Civil and Environmental Engineering, Portland State University: Portland, OR, USA, 2021. [Google Scholar]
- Kuo, J.-T.; Lung, W.-S.; Yang, C.-P.; Liu, W.-C.; Yang, M.-D.; Tang, T.-S. Eutrophication modelling of reservoirs in Taiwan. Environ. Model. Softw. 2006, 21, 829–844. [Google Scholar] [CrossRef]
- Yang, Y.; Deng, Y.; Tuo, Y.; Li, J.; He, T.; Chen, M. Study of the thermal regime of a reservoir on the Qinghai-Tibetan Plateau, China. PLoS ONE 2020, 15, e0243198. [Google Scholar] [CrossRef]
- Debele, B.; Srinivasan, R.; Parlange, J.-Y. Coupling upland watershed and downstream waterbody hydrodynamic and water quality models (SWAT and CE-QUAL-W2) for better water resources management in complex river basins. Environ. Model. Assess. 2006, 13, 135–153. [Google Scholar] [CrossRef]
- Dolz, J.; Armengol, J.; Roura, M.; De Pourcq, K.; Arbat, M.; López, P. Estudio de La Dinámica Sedimentaria y Batimetría de Precisión Del Embalse de Ribarroja. 2009.
- Chakraborty, S.; Chowdhury, R. A hybrid approach for global sensitivity analysis. Reliab. Eng. Syst. Saf. 2016, 158, 50–57. [Google Scholar] [CrossRef]
- Almansa, C.; Masaló, I.; Reig, L.; Piedrahita, R.; Oca, J. Influence of tank hydrodynamics on vertical oxygen stratification in flatfish tanks. Aquac. Eng. 2014, 63, 1–8. [Google Scholar] [CrossRef]
- Barrut, B.; Blancheton, J.-P.; Champagne, J.-Y.; Grasmick, A. Mass transfer efficiency of a vacuum airlift—Application to water recycling in aquaculture systems. Aquac. Eng. 2012, 46, 18–26. [Google Scholar] [CrossRef] [Green Version]
- Null, S.E.; Mouzon, N.R.; Elmore, L.R. Dissolved oxygen, stream temperature, and fish habitat response to environmental water purchases. J. Environ. Manag. 2017, 197, 559–570. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Z.; Liu, M.; He, J.; Shi, K.; Zhou, Y.; Wang, M.; Liu, X. Dissolved oxygen stratification and response to thermal structure and long-term climate change in a large and deep subtropical reservoir (Lake Qiandaohu, China). Water Res. 2015, 75, 249–258. [Google Scholar] [CrossRef]
- Liu, W.-C.; Chen, W.-B.; Kimura, N. Impact of phosphorus load reduction on water quality in a stratified reservoir-eutrophication modeling study. Environ. Monit. Assess. 2008, 159, 393–406. [Google Scholar] [CrossRef]
- Shabani, A.; Zhang, X.; Chu, X.; Zheng, H. Automatic Calibration for CE-QUAL-W2 Model Using Improved Global-Best Harmony Search Algorithm. Water 2021, 13, 2308. [Google Scholar] [CrossRef]
- Kim, S.K.; Choi, S.-U. Assessment of the impact of selective withdrawal on downstream fish habitats using a coupled hydrodynamic and habitat modeling. J. Hydrol. 2021, 593, 125665. [Google Scholar] [CrossRef]
- Azadi, F.; Ashofteh, P.-S.; Chu, X. Evaluation of the effects of climate change on thermal stratification of reservoirs. Sustain. Cities Soc. 2021, 66, 102531. [Google Scholar] [CrossRef]
- Boehrer, B.; Schultze, M. Stratification of Lakes. Rev. Geophys. 2008, 46, RG2005. [Google Scholar] [CrossRef] [Green Version]
- Prats, J.; Reynaud, N.; Rebière, D.; Peroux, T.; Tormos, T.; Danis, P.-A. LakeSST: Lake Skin Surface Temperature in French inland water bodies for 1999–2016 from Landsat archives. Earth Syst. Sci. Data 2018, 10, 727–743. [Google Scholar] [CrossRef] [Green Version]
- Koparan, C.; Koc, A.B.; Sawyer, C.; Privette, C. Temperature Profiling of Waterbodies with a UAV-Integrated Sensor Subsystem. Drones 2020, 4, 35. [Google Scholar] [CrossRef]
- Owen, L.; Dávalos Lind, L. An Introduction to the Limnology of Lake Chapala, Jalisco, Mexico. In The Lerma-Chapala Watershed; Springer: Boston, MA, USA, 2001. [Google Scholar]
- Simons, T.J. Effect of Outflow Diversion on Circulation and Water Quality of Lake Chapala; National Water Research Institute: Fountain Valley, CA, USA, 1984. [Google Scholar]
- Arbat Bofill, M.; Bladé, E.; Sánchez Juny, M.; Cea, L.; Niñerola, D.; Dolz, J. Modelación Numérica 3d Hidrodinámica y Térmica En El Entorno de La Confluencia Ebro-Segre. In Proceedings of the Libro Artículos XXVII Congreso Latinoamericano de Hidráulica, Lima, Peru, 26–30 September 2016; pp. 3888–3897. [Google Scholar]
- Kim, Y.; Kim, B. Application of a 2-Dimensional Water Quality Model (CE-QUAL-W2) to the Turbidity Interflow in a Deep Reservoir (Lake Soyang, Republic of Korea). Lake Reserv. Manag. 2006, 22, 213–222. [Google Scholar] [CrossRef]
- Cole, T. Reservoir Thermal Modeling Using CE-QUALW2. In Development and Application of Computer Techniques to Environmental Studies VIII; WIT Press: Southampton, UK, 2000; pp. 238–246. [Google Scholar]
- Vega-Durán, J.; Escalante-Castro, B.; Canales, F.A.; Acuña, G.J.; Kaźmierczak, B. Evaluation of Areal Monthly Average Precipitation Estimates from MERRA2 and ERA5 Reanalysis in a Colombian Caribbean Basin. Atmosphere 2021, 12, 1430. [Google Scholar] [CrossRef]
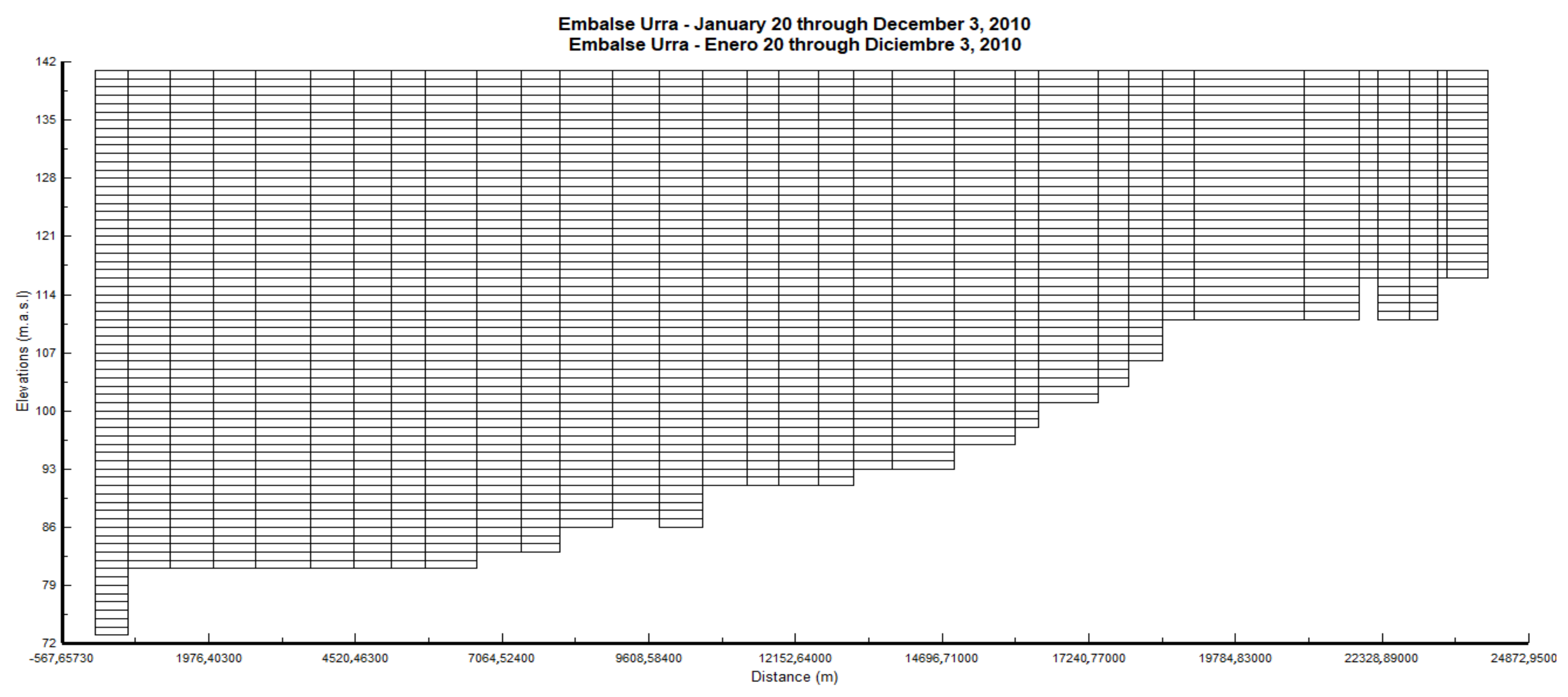
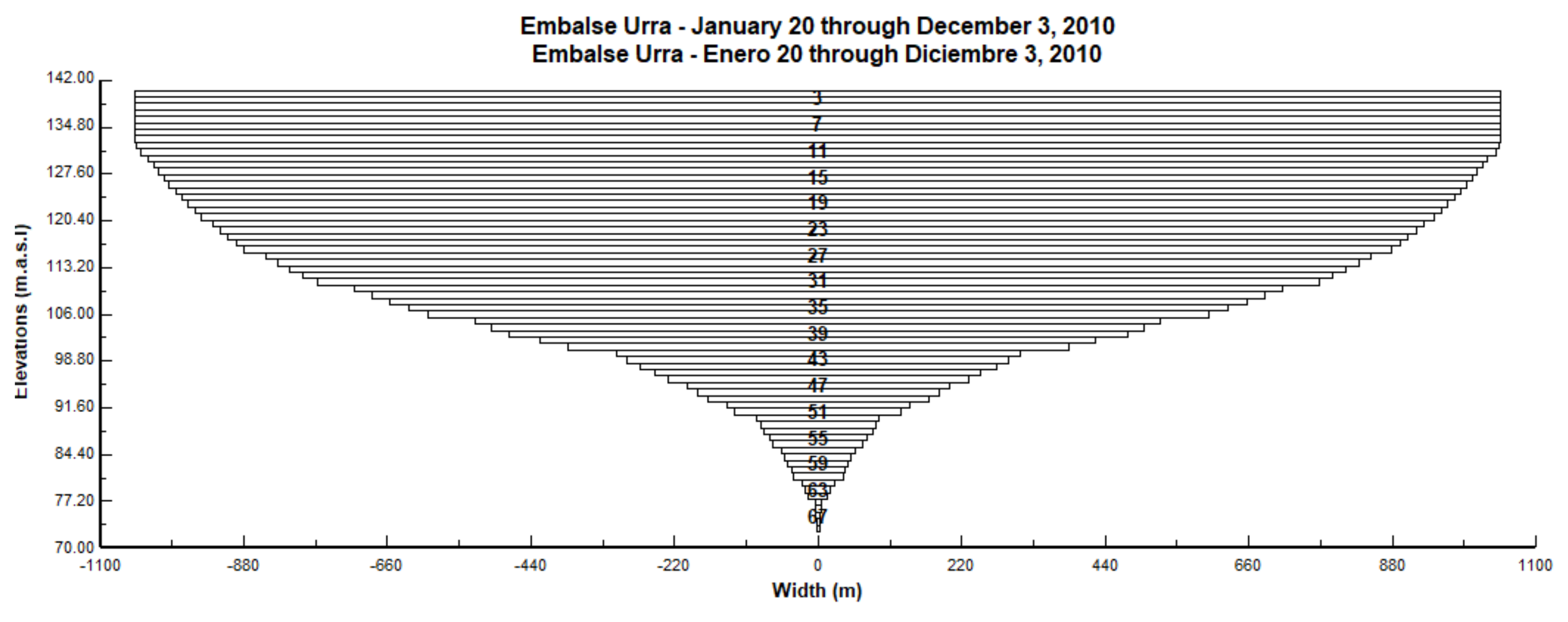
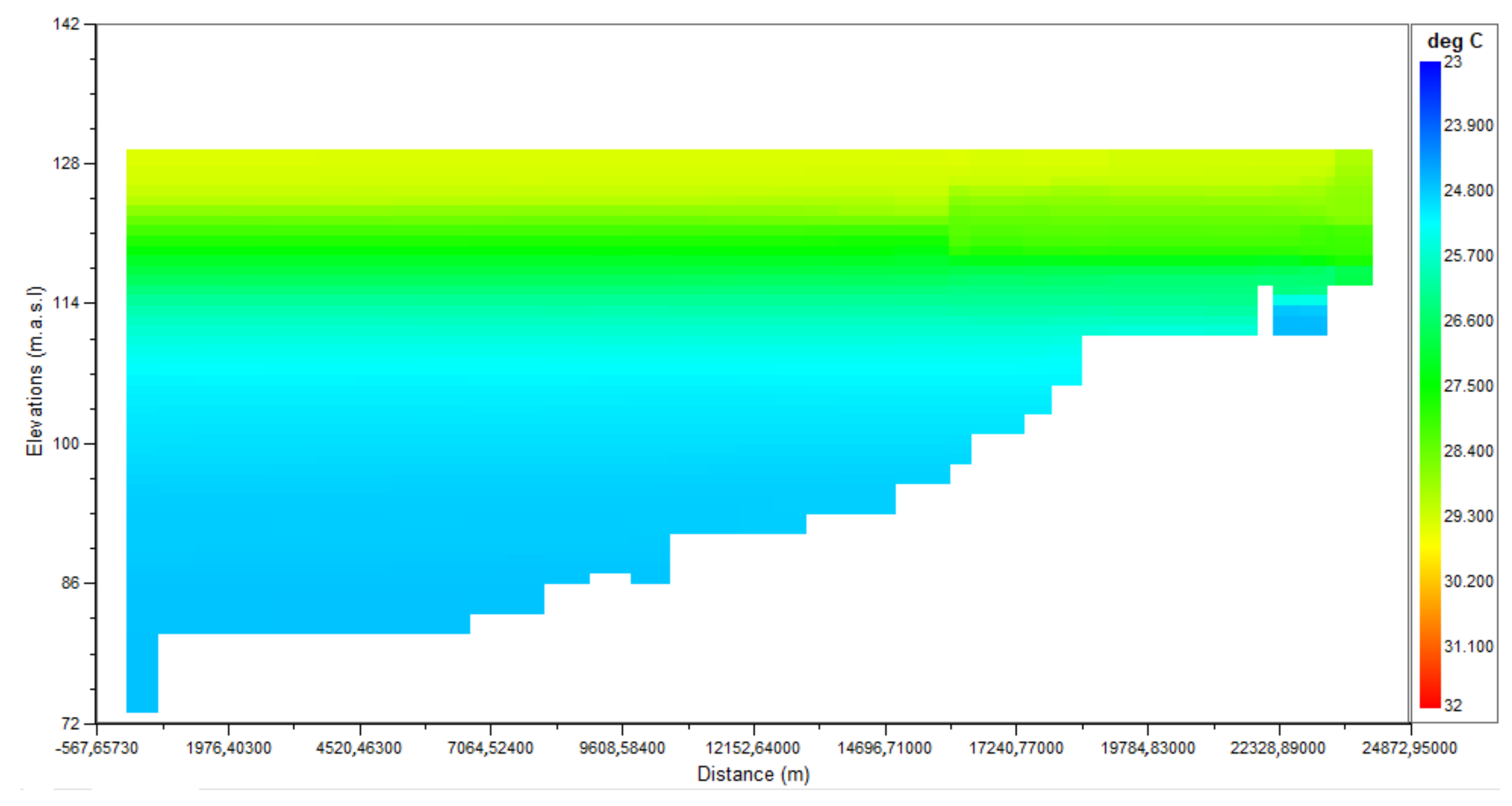
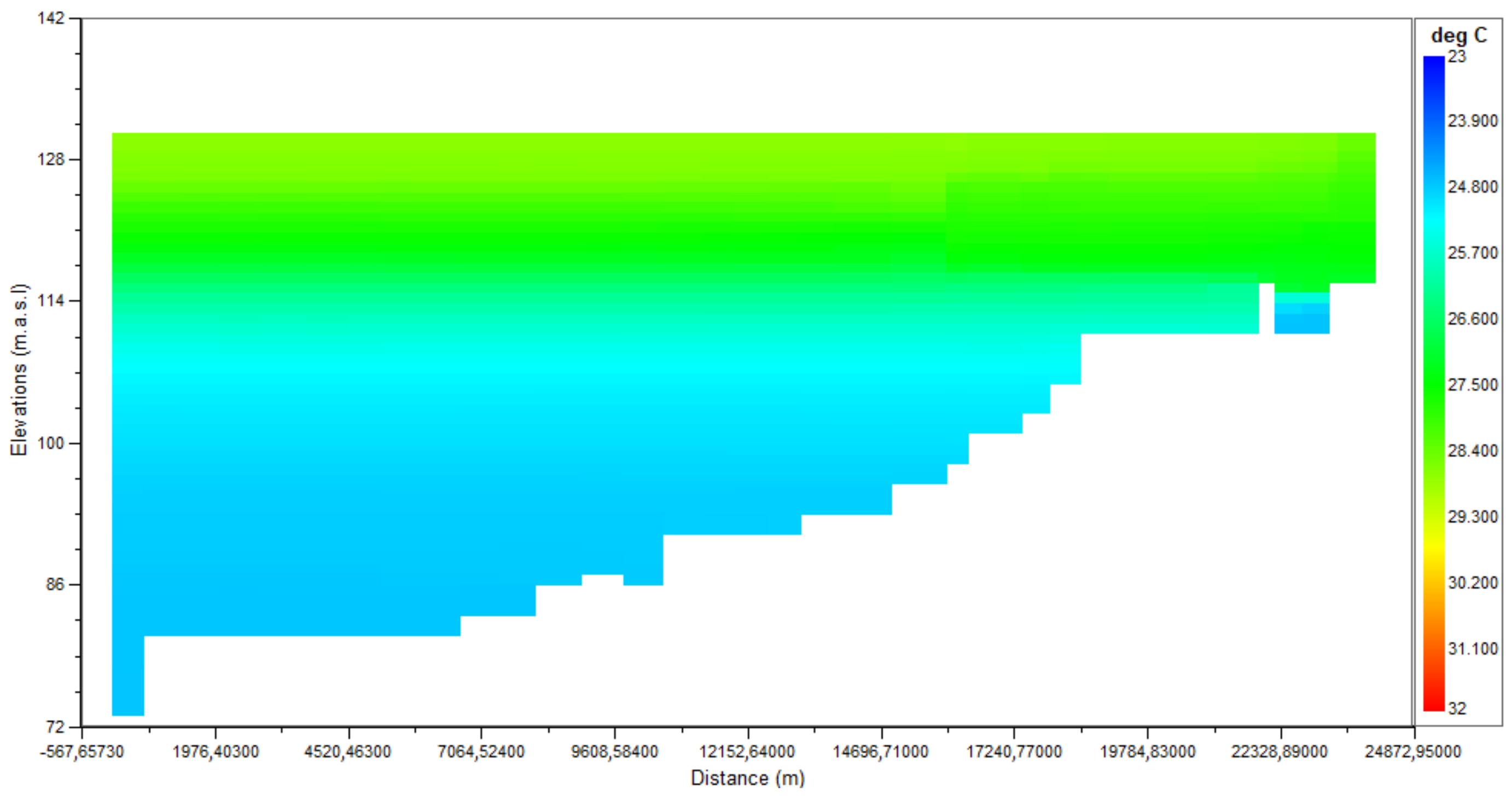




| Zone | Segmentation |
|---|---|
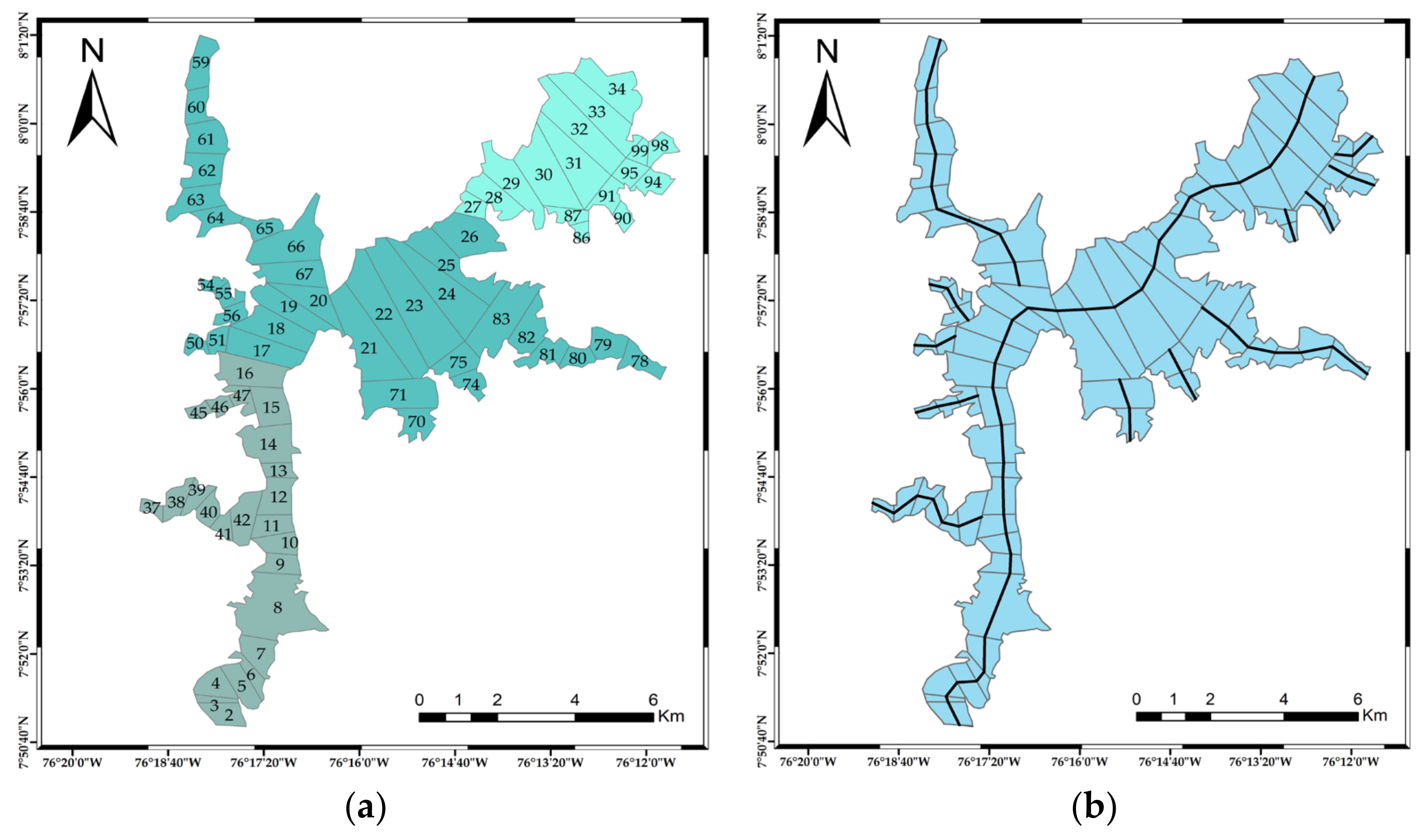
| Zone 1: the confluence of the Verde River/Sinú River | Branch 1 segments 1 to 16. Branches 2 and 3. |
| Zone 2: middle zone of the reservoir | Branch 1 segments 17 to 26. Branches from 4 to 9. |
| Zone 3: near the dam | Branch 1 segments 27 to 35. Branches from 10 to 13. |
| Parameter | Unit |
|---|---|
| Temperature | (°C) |
| Dissolved oxygen | (mg/L) |
| Description | Parameters | Unity | −50% | −20% | Calibration Range | 20% | 50% |
|---|---|---|---|---|---|---|---|
| Eddy longitudinal viscosity | AX | m2s−1 | 0.5 | 0.8 | 1.0 | 1.2 | 1.5 |
| Eddy longitudinal diffusivity | DX | m2s−1 | 0.5 | 0.8 | 1.0 | 1.2 | 1.5 |
| Manning’s coefficient | FRICT | m2s−1 | 0.015 | 0.024 | 0.030 | 0.036 | 0.045 |
| Wind shelter coefficient | WSC | - | 0.2 | 0.32 | 0.4 | 0.48 | 0.6 |
| Absorbed solar radiation at the surface | BETA | - | 0.21 | 0.33 | 0.45 | 0.50 | 0.63 |
| Absorption coefficient for pure water | EXH2O | m−1 | 0.375 | 0.6 | 0.75 | 0.9 | 1.125 |
| Heat exchange coefficient in the sediment | CBHE | W m−2s−1 | 0.25 | 0.4 | 0.5 | 0.6 | 0.75 |
| HEAT EXCHANGE | WB1 |
|---|---|
| H SLHTC—Heat computations/Equilibrium (ET) or Term-by-term (TERM) | TERM |
| SROC—Read in short wave solar radiation ON or OFF | OFF |
| RHEVAP—Use Ryan-Harleman evap model—for cooling ponds ON or OFF | OFF |
| METIC—Interpolate meteorological data ON or OFF | OFF |
| FETCHC—Heinz Stefan lake fetch correction—there is already an internal OFF | OFF |
| AFW—Evaporation coefficient | 9.2 |
| BFW—Evaporation coefficient | 0.46 |
| CFW—Evaporation coefficient | 2 |
| WINDH—Wind height measurement above the ground surface, m | 10 |
| TRANSPORT SCHEME | WB1 |
| SLTRC—UPWIND, QUICKEST, ULTIMATE—use ULTIMATE | ULTIMATE |
| THETA—degree of implicitness—use 0.55—Time-weighting for vertical adv | 0.55 |
| HYD COEFFICIENTS | WB1 |
| AX—Longitudinal eddy viscosity, m2/s | 1 |
| DX—Longitudinal eddy diffusivity/conductivity, m2/s | 1 |
| CBHE—Coefficient of bottom heat exchange, W m−1 oC−1 | 0.5 |
| TSED—Temperature of sediment, C, average year-round air temperature | 25 |
| Fl—Interfacial friction factor | 0 |
| TSEDF—Sediment temperature coefficient (0–1) heat lost to sediments th | 0.8 |
| FRICC—Bottom friction factor type: CHEZY or MANN | MANN |
| ZO—water surface roughness height, m, for wind shear | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tavera-Quiroz, H.; Rosso-Pinto, M.; Hernández, G.; Pinto, S.; Canales, F.A. Water Quality Analysis of a Tropical Reservoir Based on Temperature and Dissolved Oxygen Modeling by CE-QUAL-W2. Water 2023, 15, 1013. https://doi.org/10.3390/w15061013
Tavera-Quiroz H, Rosso-Pinto M, Hernández G, Pinto S, Canales FA. Water Quality Analysis of a Tropical Reservoir Based on Temperature and Dissolved Oxygen Modeling by CE-QUAL-W2. Water. 2023; 15(6):1013. https://doi.org/10.3390/w15061013
Chicago/Turabian StyleTavera-Quiroz, Humberto, Mauricio Rosso-Pinto, Gerardo Hernández, Samuel Pinto, and Fausto A. Canales. 2023. "Water Quality Analysis of a Tropical Reservoir Based on Temperature and Dissolved Oxygen Modeling by CE-QUAL-W2" Water 15, no. 6: 1013. https://doi.org/10.3390/w15061013
APA StyleTavera-Quiroz, H., Rosso-Pinto, M., Hernández, G., Pinto, S., & Canales, F. A. (2023). Water Quality Analysis of a Tropical Reservoir Based on Temperature and Dissolved Oxygen Modeling by CE-QUAL-W2. Water, 15(6), 1013. https://doi.org/10.3390/w15061013








