A Case Study: Groundwater Level Forecasting of the Gyorae Area in Actual Practice on Jeju Island Using Deep-Learning Technique
Abstract
:1. Introduction
2. Theoretical Background
2.1. Study Material
2.2. Test Statistics: Cross-Wavelet and Granger Causality
2.3. LSTM Technique
3. Application and Proposed New Method
3.1. Predictor Selection for Groundwater Level Forecasting
3.2. Construction of the LSTM Model and Result
3.3. Proposed New Method to Forecast Groundwater Levels
4. Result and Discussion
5. Conclusions
- The study analyzed the correlation between JH Gyorae-1′s GWLs and 12 kinds of hydro-meteorological data (maximum temperature, daily minimum temperature, daily mean temperature, dew temperature, relative humidity, precipitation, ground air pressure, sea-level pressure, mean wind speed, total sun hours, insolation, and evapotranspiration) through cross-wavelet and Granger causality analysis for predictor selection. As a result, five factors (mean wind speed, sun hours, evaporation, minimum temperature, and daily precipitation) showed time sequential correlations with GWLs and were selected as predictors.
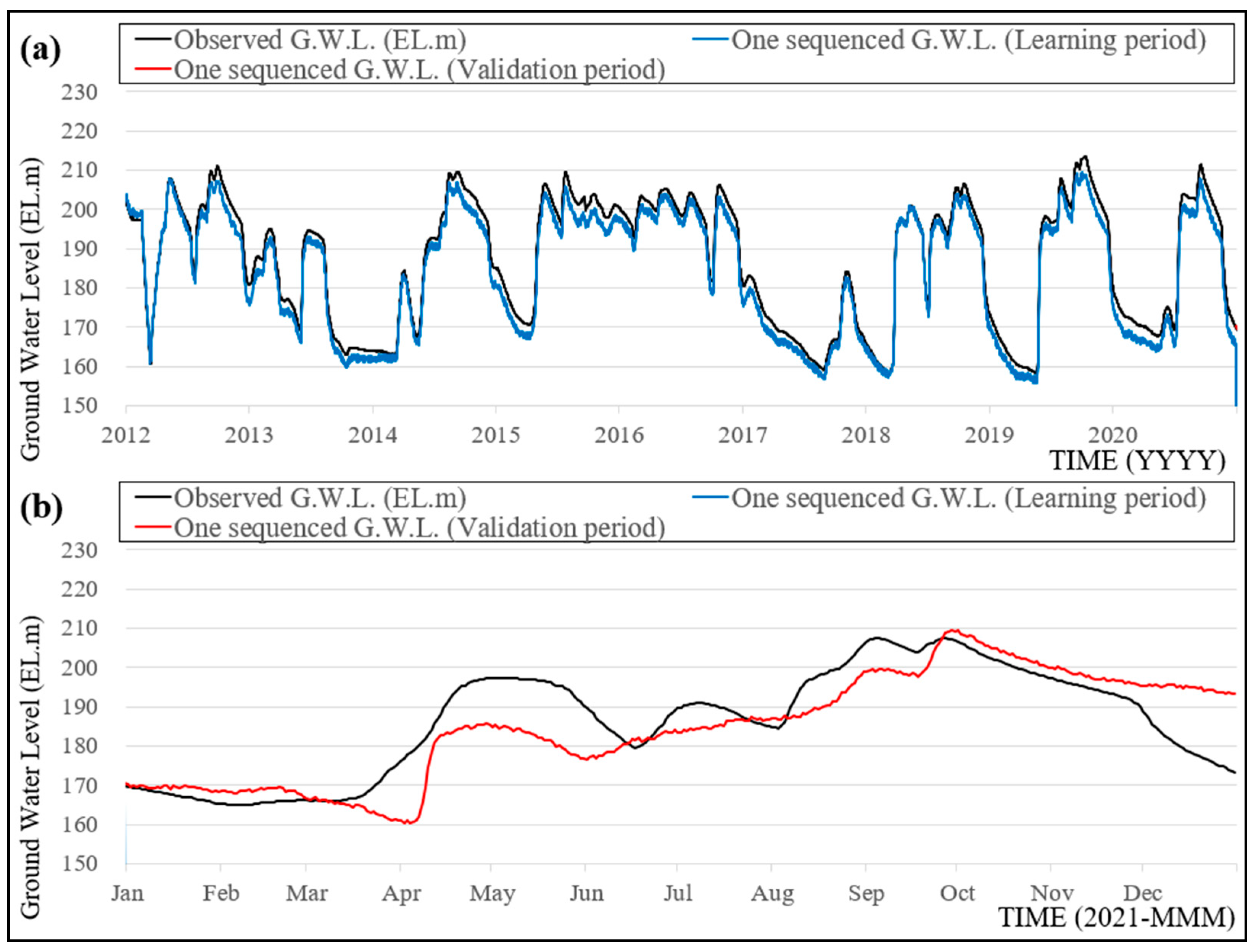
- An LSTM model, a representative deep learning method, was constructed using the observed GWLs of JH Gyorae-1 from 2012 to 2020, and the model was validated with the events of the year 2021. The simulation demonstrated a highly outstanding performance and applicability with R2, RMSE(m), and the Nash coefficient, which show the simulation efficiency of a model for its learning and validation periods of ≥0.97, ≤0.03 m, and ≥0.96, respectively.
- It proposed (i) derivatives-based learning and assessed the applicability to complement the lack of clarity of process for a particular result that deep-learning-based forecasts have. An LSTM model was constructed through learning based on the derivatives of GWLs and presented convincing results with R2, RMSE(m), and Nash coefficient of 0.93, 3.92 m, and 0.93, respectively, for the long-term (learning period) simulation, which used only the first observational GWL, and of 0.62, 8.32 m, and 0.60, respectively, for the 1-year validation period (2021). Therefore, it showed that the method can be utilized to aid decision-making when managers review deep learning models.
- It also proposed and assessed (ii) ensemble forecasting. As for ensemble forecasting, ±1-month GWL simulation and forecasting were repeated on a daily basis, and the GWLs for the following 2 weeks were forecasted using the medians of the forecasted time series. The result demonstrated that it is sufficiently applicable as R2, RMSE(m), and the Nash coefficient were, respectively, 0.97, 1.84 m, and 0.97 for the learning period and 0.91, 3.75 m, and 0.90 for the validation period.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jeju Special Self-Governing Province. Groundwater Information System. Available online: https://water.jeju.go.kr/JWR/pStatus.cs (accessed on 30 December 2022).
- Korea Water Resources Corporation. Comprehensive Water Resources Management Plan in Jeju Island; Jeju Special Self-Governing Province (JSSGP): Jeju, Republic of Korea, 2018; pp. 1–328. [Google Scholar]
- Kim, J.W.; Koh, G.W.; Won, J.H.; Han, C. A Study on the Determination of Management Groundwater Level on Jeju Island. J. KoSSGE 2005, 10, 12–19. (In Korean) [Google Scholar]
- Izady, A.; Davary, K.; Alizadeh, A.; Ziaei, A.N.; Alipoor, A.; Joodavi, A.; Brusseau, M.L. A framework toward developing a groundwater conceptual model. Arab. J. Geosci. 2013, 7, 3611–3631. [Google Scholar] [CrossRef]
- Xue, J.; Huo, Z.; Wang, F.; Kang, S.; Huang, G. Untangling the effects of shallow groundwater and deficit irrigation on irrigation water productivity in arid region: New conceptual model. Sci. Total Environ. 2018, 619, 1170–1182. [Google Scholar] [CrossRef]
- Dehghani, A. Numerical simulation of groundwater level using MODFLOW software (a case study: Narmab watershed, Golestan province). Int. J. Adv. Biol. Biomed. Res. 2013, 1, 858–873. [Google Scholar]
- Chakraborty, S.; Maity, P.K.; Das, S. Investigation, simulation, identification and prediction of groundwater levels in coastal areas of Purba Midnapur, India, using MODFLOW. Environ. Dev. Sustain. 2019, 22, 3805–3837. [Google Scholar] [CrossRef]
- Yang, C.-C.; Chang, L.-C.; Chen, C.-S.; Yeh, M.-S. Multi-objective Planning for Conjunctive Use of Surface and Subsurface Water Using Genetic Algorithm and Dynamics Programming. Water Resour. Manag. 2008, 23, 417–437. [Google Scholar] [CrossRef]
- Brunner, P.A.; Simmons, C.T. HydroGeoSphere: A Fully Integrated, Physically Based Hydrological Model. Ground Water 2011, 50, 170–176. [Google Scholar] [CrossRef] [Green Version]
- Van Walsum, P.; Veldhuizen, A. Integration Of Models Using Shared State Variables: Implementation In The Regional Hydrologic Modelling System SIMGRO. J. Hydrol. 2011, 409, 363–370. [Google Scholar] [CrossRef]
- Kurniawan, B.; Tapriziah, E.R.; Aryantie, M.H.; Rahmani, R.; Purnomo, A.D. Application of groundwater modeling to predict the effectiveness of various peat dome restoration methods in Pulang Pisau District, Central Kalimantan Province. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Proceedings of 2021 The 6th International Conference of Indonesia Forestry Researchers—Stream 1 Emerging Environmental Quality for Better Living, Tangerang, Indonesia, 8 September 2021; IOP Publishing: Bristol, UK, 2021; Volume 909, p. 012004. [Google Scholar]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’Adi, Z.; Mehr, A.D.; et al. Groundwater level prediction using machine learning models: A comprehensive review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Sahoo, S.; Russo, T.A.; Elliott, J.; Foster, I. Machine learning algorithms for modeling groundwater level changes in agricultural regions of the U.S. Water Resour. Res. 2017, 53, 3878–3895. [Google Scholar] [CrossRef] [Green Version]
- Rajaee, T.; Ebrahimi, H.; Nourani, V. A review of the artificial intelligence methods in groundwater level modeling. J. Hydrol. 2019, 572, 336–351. [Google Scholar] [CrossRef]
- Coppola, E.A., Jr.; Rana, A.J.; Poulton, M.M.; Szidarovszky, F.; Uhl, V.W. A neural network model for predicting aquifer water level elevations. Ground Water 2005, 43, 231–241. [Google Scholar] [CrossRef] [PubMed]
- Daliakopoulos, I.N.; Coulibaly, P.; Tsanis, I.K. Groundwater level forecasting using artificial neural networks. J. Hydrol. 2005, 309, 229–240. [Google Scholar] [CrossRef]
- Krishna, B.; Rao, Y.R.S.; Vijaya, T. Modelling groundwater levels in an urban coastal aquifer using artificial neural networks. Hydrol. Process 2007, 22, 1180–1188. [Google Scholar] [CrossRef]
- Rakhshandehroo, G.R.; Vaghefi, M.; Aghbolaghi, M.A. Forecasting Groundwater Level in Shiraz Plain Using Artificial Neural Networks. Arab. J. Sci. Eng. 2012, 37, 1871–1883. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.-W.; Sethi, R. Artificial neural network simulation of hourly groundwater levels in a coastal aquifer system of the Venice lagoon. Eng. Appl. Artif. Intell. 2012, 25, 1670–1676. [Google Scholar] [CrossRef] [Green Version]
- Jha, M.K.; Sahoo, S. Efficacy of neural network and genetic algorithm techniques in simulating spatio-temporal fluctuations of groundwater. Hydrol. Process 2014, 29, 671–691. [Google Scholar] [CrossRef]
- Chitsazan, M.; Rahmani, G.; Neyamadpour, A. Forecasting groundwater level by artificial neural networks as an alternative approach to groundwater modeling. J. Geol. Soc. India 2015, 85, 98–106. [Google Scholar] [CrossRef]
- Djurovic, N.; Domazet, M.; Stričević, R.; Pocuca, V.; Spalevic, V.; Pivic, R.; Gregoric, E.; Domazet, U. Comparison of Groundwater Level Models Based on Artificial Neural Networks and ANFIS. Sci. World J. 2015, 2015, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Mirzavand, M.; Khoshnevisan, B.; Shamshirband, S.; Kişi, O.; Ahmad, R.; Akib, S. RETRACTED ARTICLE: Evaluating groundwater level fluctuation by support vector regression and neuro-fuzzy methods: A comparative study. Nat. Hazards 2015, 102, 1611–1612. [Google Scholar] [CrossRef]
- Nourani, V.; Mousavi, S. Spatiotemporal groundwater level modeling using hybrid artificial intelligence-meshless method. J. Hydrol. 2016, 536, 10–25. [Google Scholar] [CrossRef]
- Salari, S.; Moghaddasi, M.; Ghaleni, M.M.; Akbari, M. Groundwater level prediction in Golpayegan aquifer using ANFIS and PSO combination. Iran. J. Soil Water Res. 2021, 5, 721–732. [Google Scholar]
- Chang, F.-J.; Chang, L.-C.; Huang, C.-W.; Kao, I.-F. Prediction of monthly regional groundwater levels through hybrid soft-computing techniques. J. Hydrol. 2016, 541, 965–976. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F. Groundwater level prediction in Apulia region (Southern Italy) using NARX neural network. Environ. Res. 2020, 190, 110062. [Google Scholar] [CrossRef] [PubMed]
- Wunsch, A.; Liesch, T.; Broda, S. Forecasting groundwater levels using nonlinear autoregressive networks with exogenous input (NARX). J. Hydrol. 2018, 567, 743–758. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Shin, M.-J.; Moon, S.-H.; Kang, K.; Moon, D.-C.; Koh, H.-J. Analysis of Groundwater Level Variations Caused by the Changes in Groundwater Withdrawals Using Long Short-Term Memory Network. Hydrology 2020, 7, 64. [Google Scholar] [CrossRef]
- Vu, M.; Jardani, A.; Massei, N.; Fournier, M. Reconstruction of missing groundwater level data by using Long Short-Term Memory (LSTM) deep neural network. J. Hydrol. 2020, 597, 125776. [Google Scholar] [CrossRef]
- Solgi, R.; Loáiciga, H.A.; Kram, M. Long short-term memory neural network (LSTM-NN) for aquifer level time series forecasting using in-situ piezometric observations. J. Hydrol. 2021, 601, 126800. [Google Scholar] [CrossRef]
- Lu, C.; Sun, L.; Lu, J. Spatiotemporal forecasting for groundwater level using a WT-LSTM model, In EGU General Assembly Conference Abstracts. In Proceedings of the EGU General Assembly 2020, Online, 4–8 May 2020; p. 6343. [Google Scholar]
- Moghaddam, H.K.; Moghaddam, H.K.; Kivi, Z.R.; Bahreinimotlagh, M.; Alizadeh, M.J. Developing comparative mathematic models, BN and ANN for forecasting of groundwater levels. Groundw. Sustain. Dev. 2019, 9, 100237. [Google Scholar] [CrossRef]
- Malekzadeh, M.; Kardar, S.; Shabanlou, S. Simulation of groundwater level using MODFLOW, extreme learning machine and Wavelet-Extreme Learning Machine models. Groundw. Sustain. Dev. 2019, 9, 100279. [Google Scholar] [CrossRef]
- Zeydalinejad, N. Artificial neural networks vis-à-vis MODFLOW in the simulation of groundwater: A review. Model. Earth Syst. Environ. 2022, 8, 2911–2932. [Google Scholar] [CrossRef]
- Orr, W.; Davis, J.L. Attributions of ethical responsibility by Artificial Intelligence practitioners. Inf. Commun. Soc. 2020, 23, 719–735. [Google Scholar] [CrossRef]
- Campolo, A.; Crawford, K. Enchanted Determinism: Power without Responsibility in Artificial Intelligence. Engag. Sci. Technol. Soc. 2020, 6, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Chung, I.M.; Lee, J.; Chang, S.W. Long-term prediction of groundwater level in Jeju Island using artificial neural network model. KSCE J. Civ. Environ. Eng. Res. 2017, 37, 981–987. [Google Scholar]
- Kang, K.G. Studies on the Hydrogeochemical Processes and Characteristics of Groundwater in the Pyoseon Watershed, Jeju Province. Ph.D. Thesis, Jeju National University, Jeju, Republic of Korea, 2010. [Google Scholar]
- Kim, S.-G.; Koo, M.-H.; Chung, I.-M. Development of a Transient Groundwater Flow Model in Pyoseon Watershed of Jeju Island: Use of a Convolution Method. J. Environ. Sci. Int. 2015, 24, 481–494. [Google Scholar] [CrossRef] [Green Version]
- National Climate Data Center (NDCD). Open MET Data Portal, Korea Meteorological Administration, Seoul, Korea. Available online: https://data.kma.go.kr/cmmn/main.do (accessed on 31 December 2022).
- National Institute of Environmental Research (NIER). Soil Groundwater Information System, Incheon, Korea. Available online: https://sgis.nier.go.kr/web (accessed on 31 December 2022).
- Jevrejeva, S.; Moore, J.C.; Grinsted, A. Influence of the Arctic Oscillation and El Niño-Southern Oscillation (ENSO) on ice conditions in the Baltic Sea: The wavelet approach. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Lin, J.; Qu, L. Feature extraction based on morlet wavelet and its application for mechanical fault diagnosis. J. Sound Vib. 2000, 234, 135–148. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Ding, M.; Chen, Y.; Bressler, S. Granger Causality: Basic Theory and Application to Neuroscience. In Handbook of Time Series Analysis; Schelter, B., Winterhalder, M., Timmer, J., Eds.; John and Wiley and Sons: Wienheim, Germany, 2006; ISBN 978-352-740-623-4. [Google Scholar]
- Granger, C.W.J. Essays in Econometrics: The Collected Papers of Clive W.J. Granger, 1st ed.; Cambridge University Press: Cambridge, UK, 2001; ISBN 978-354-071-334-0. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yu, Y.; Cao, J.; Zhu, J. An LSTM Short-Term Solar Irradiance Forecasting Under Complicated Weather Conditions. IEEE Access 2019, 7, 145651–145666. [Google Scholar] [CrossRef]
- Feng, R.; Fan, G.; Lin, J.; Yao, B.; Guo, Q. Enhanced Long Short-Term Memory Model for Runoff Prediction. J. Hydrol. Eng. 2021, 26, 04020063. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Gauch, M.; Kratzert, F.; Klotz, D.; Nearing, G.; Lin, J.; Hochreiter, S. Rainfall–runoff prediction at multiple timescales with a single Long Short-Term Memory network. Hydrol. Earth Syst. Sci. 2021, 25, 2045–2062. [Google Scholar] [CrossRef]
- Hrnjica, B.; Bonacci, O. Lake Level Prediction using Feed Forward and Recurrent Neural Networks. Water Resour. Manag. 2019, 33, 2471–2484. [Google Scholar] [CrossRef]
- Kardhana, H.; Valerian, J.R.; Rohmat, F.I.W.; Kusuma, M.S.B. Improving Jakarta’s Katulampa Barrage Extreme Water Level Prediction Using Satellite-Based Long Short-Term Memory (LSTM) Neural Networks. Water 2022, 14, 1469. [Google Scholar] [CrossRef]
- Tao, L.; He, X.; Li, J.; Yang, D. A multiscale long short-term memory model with attention mechanism for improving monthly precipitation prediction. J. Hydrol. 2021, 602, 126815. [Google Scholar] [CrossRef]
- Pathan, M.S.; Jain, M.; Lee, Y.H.; Al Skaif, T.; Dev, S. Efficient forecasting of precipitation using LSTM. In Proceedings of the IEEE Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021; pp. 2312–2316. [Google Scholar]
- Kuhn, M.; Johnson, K. Data pre-processing. In Applied Predictive Modeling; Springer: New York, NY, USA, 2013; pp. 27–59. [Google Scholar]
- Mayer, M.J.; Gróf, G. Extensive comparison of physical models for photovoltaic power forecasting. Appl. Energy 2020, 283, 116239. [Google Scholar] [CrossRef]
- Markovics, D.; Mayer, M.J. Comparison of machine learning methods for photovoltaic power forecasting based on numerical weather prediction. Renew. Sustain. Energy Rev. 2022, 161, 112364. [Google Scholar] [CrossRef]
- Jan, C.-D.; Chen, T.-H.; Lo, W.-C. Effect of rainfall intensity and distribution on groundwater level fluctuations. J. Hydrol. 2007, 332, 348–360. [Google Scholar] [CrossRef]
- Kim, I.; Lee, J.; Kim, J.; Lee, H.; Lee, J. Analysis of Groundwater Level Prediction Performance with Influencing Factors by Artificial Neural Network. J. Korean Geotech. Soc. 2021, 37, 19–31. [Google Scholar]
- Jung, Y.Y.; Koh, D.C.; Yu, Y.J.; Ko, K.S. Analysis of groundwater flow systems for springs in the southern slope of Jeju Island using hydrogeochemical parameters. J. Geol. Soc. Korea 2010, 46, 253–273. [Google Scholar]
- Kim, N.W.; Kim, Y.J.; Chung, I.M. Sensitivity analysis of hydrogeologic parameters by groundwater table fluctuation model in Jeju Island. KSCE J. Civ. Environ. Eng. Res. 2014, 34, 1409–1420. [Google Scholar]
- Obilor, E.I.; Amadi, E.C. Test for significance of Pearson’s correlation coefficient. Int. J. Innov. Math. Stat. Energy Policies 2018, 6, 11–23. [Google Scholar]
- Oh, S.-H.; Kim, Y.-C.; Koo, M.-H. Modeling Artificial Groundwater Recharge in the Hancheon Drainage Area, Jeju island, Korea. J. Soil Groundw. Environ. 2011, 16, 34–45. [Google Scholar] [CrossRef] [Green Version]
- Kim, N.-W.; Na, H.; Chung, I.-M. Delay Time Estimation of Recharge in the Hancheon Watershed, Jeju Island. J. Environ. Sci. Int. 2014, 23, 605–613. [Google Scholar] [CrossRef] [Green Version]
- Maraun, D.; Kurths, J. Cross wavelet analysis: Significance testing and pitfalls. Nonlinear Process Geophys. 2004, 11, 505–514. [Google Scholar] [CrossRef] [Green Version]
- Freeman, J.R. Granger Causality and the Times Series Analysis of Political Relationships. Am. J. Political Sci. 1983, 27, 327. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Saikia, P.; Paul, S.; Tsalavoutis, V.; Atiah, F.; Ravi, V.; Peters, A. A review of deep learning with special emphasis on architectures, applications and recent trends. Knowl. Based Syst. 2020, 194, 105596. [Google Scholar] [CrossRef] [Green Version]
- Kalnins, A. Multicollinearity: How common factors cause Type 1 errors in multivariate regression. Strat. Manag. J. 2018, 39, 2362–2385. [Google Scholar] [CrossRef]
- Wanas, N.; Auda, G.; Kamel, M.S.; Karray, F.A.K.F. On the optimal number of hidden nodes in a neural network. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering, Waterloo, ON, Canada, 25–28 May 1998; Volume 2, pp. 918–921. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 9 May 2015. [Google Scholar]
- Kwak, J.; Han, H.; Kim, S.; Kim, H.S. Is the deep-learning technique a completely alternative for the hydrological model?: A case study on Hyeongsan River Basin, Korea. Stoch. Environ. Res. Risk Assess. 2021, 36, 1615–1629. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Hitokoto, M.; Sakuraba, M. Applicability of the Deep Learning Flood Forecast Model against the Inexperienced Magnitude of Flood. EPiC Ser. Eng. 2018, 3, 901–907. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.S. Chapter 16-Data Mining and Deep Learning. In Nature-Inspired Optimization Algorithms, 2nd ed.; Yang, X.S., Ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 239–258. ISBN 978-0-12-821986-7. [Google Scholar]
- Zhang, B.; Li, N.; Shi, F.; Law, R. A deep learning approach for daily tourist flow forecasting with consumer search data. Asia Pac. J. Tour. Res. 2020, 25, 323–339. [Google Scholar] [CrossRef]
- Kellert, S.H. In the Wake of Chaos: Unpredictable Order in Dynamical Systems; University of Chicago Press: Chicago, IL, USA, 1993; p. 32. ISBN 978-0-226-42976-2. [Google Scholar]
- Strelioff, C.C.; Hübler, A.W. Medium-Term Prediction of Chaos. Phys. Rev. Lett. 2006, 96, 044101. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Wang, L.; Liu, J.; Li, W.; Zheng, Y. Options of sustainable groundwater development in Beijing Plain, China. Phys. Chem. Earth Parts A/B/C 2011, 47, 99–113. [Google Scholar] [CrossRef]
- Daryanavard, S.; Porr, B. Closed-Loop Deep Learning: Generating Forward Models With Backpropagation. Neural Comput. 2020, 32, 2122–2144. [Google Scholar] [CrossRef]
- Baek, Y.; Kim, H.Y. ModAugNet: A new forecasting framework for stock market index value with an overfitting prevention LSTM module and a prediction LSTM module. Expert Syst. Appl. 2018, 113, 457–480. [Google Scholar] [CrossRef]
- Hyun, Y.K.; Park, J.; Lee, J.; Lim, S.; Heo, S.I.; Ham, H.; Lee, S.M.; Ji, H.S.; Kim, Y. Reliability assessment of temperature and precipitation seasonal probability in current climate prediction systems. Atmosphere 2020, 30, 141–154. [Google Scholar]
- Blöschl, G.; Bierkens, M.F.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Renner, M. Twenty-three unsolved problems in hydrology (UPH)—A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef] [Green Version]







| Content | U.W.L. → Factor | Factor → U.W.L. | ||
|---|---|---|---|---|
| F-Value | Cri. Value | F-Value | Cri. Value | |
| ‘Average Temperature’ | 4.03 | 3.84 | 3.99 | 3.84 |
| ‘Minimum Temperature’ | 6.70 | 3.00 | 18.06 | 3.84 |
| ‘Maximum Temperature’ | 1.13 | 3.84 | 8.27 | 3.84 |
| ‘Precipitation’ | 13.91 | 1.65 | 10.16 | 3.84 |
| ‘Average Wind Speed’ | 17.83 | 3.00 | 6.22 | 3.00 |
| ‘Dew Temperature’ | 10.37 | 3.00 | 0.50 | 3.84 |
| ‘Relative Humidity’ | 11.54 | 3.00 | 0.64 | 3.84 |
| ‘Average Air Pressure’ | 6.84 | 3.00 | 0.29 | 3.84 |
| ‘Total Sun Hours’ | 28.61 | 3.84 | 11.87 | 3.84 |
| ‘Ground Temperature’ | 3.79 | 3.84 | 16.35 | 3.84 |
| ‘5 cm Underground Temperature’ | 2.37 | 3.84 | 18.86 | 3.84 |
| ‘Small Pan Evaporation’ | 15.77 | 3.84 | 15.16 | 3.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.; Jang, C.; Choi, J.; Kwak, J. A Case Study: Groundwater Level Forecasting of the Gyorae Area in Actual Practice on Jeju Island Using Deep-Learning Technique. Water 2023, 15, 972. https://doi.org/10.3390/w15050972
Kim D, Jang C, Choi J, Kwak J. A Case Study: Groundwater Level Forecasting of the Gyorae Area in Actual Practice on Jeju Island Using Deep-Learning Technique. Water. 2023; 15(5):972. https://doi.org/10.3390/w15050972
Chicago/Turabian StyleKim, Deokhwan, Cheolhee Jang, Jeonghyeon Choi, and Jaewon Kwak. 2023. "A Case Study: Groundwater Level Forecasting of the Gyorae Area in Actual Practice on Jeju Island Using Deep-Learning Technique" Water 15, no. 5: 972. https://doi.org/10.3390/w15050972





