Numerical Simulation and Characterization of the Hydromechanical Alterations at the Zafarraya Fault Due to the 1884 Andalusia Earthquake (Spain)
Abstract
1. Introduction

- To describe and analyze the hydrogeological phenomena induced by the Andalusian earthquake of 1884.
- To establish a hydromechanical conceptual model of the Zafarraya Fault that explains and allows understanding of these hydrological alterations.
- To implement a hydromechanical numerical model to simulate the conditions of the massif surrounding the main fault during the pre-seismic and co-seismic phases. The results obtained from this simulation allow us to understand and explain the features and effects of the 1884 major event.
- To perform both matching and calibration of both models.
2. Methodology
- Description of the hydrological alterations due to the 1884 Andalusia earthquake according to historical surveys.
- Based on bibliographic background, the next stage seeks the setup of the geological and hydrogeological framework and the seismotectonic characterization of the Zafarraya Fault surrounding area.
- Setup of a preliminary hydromechanical conceptual model.
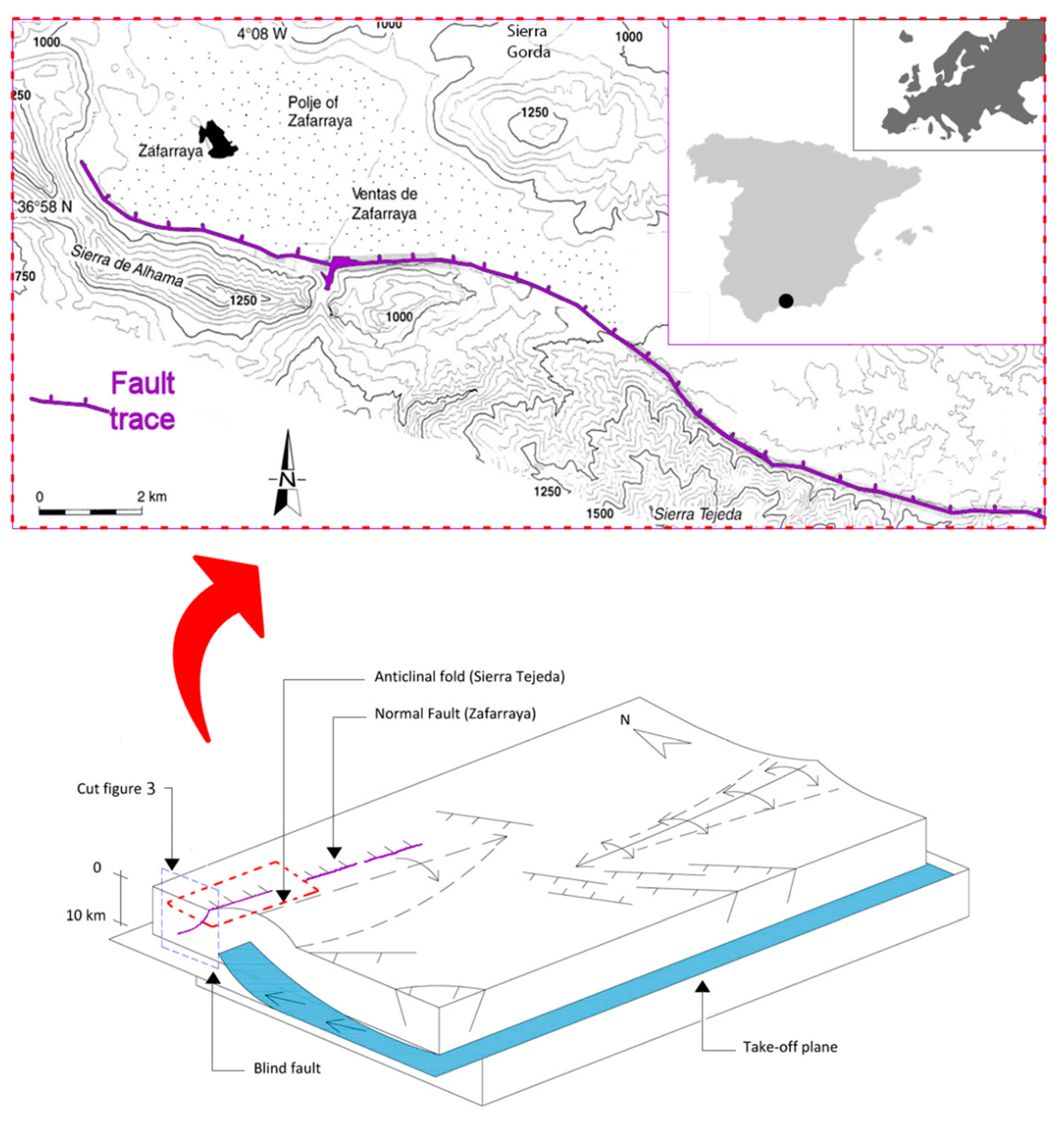
3. The Zafarraya Fault Geology and Hydrological Phenomena Induced by Andalusia Earthquake
3.1. The Zafarraya Fault: Tectonic Context, Displacement, and Recurrence Periods
- A.
- Sierra Gorda Karstic Aquifer: it holds a free aquifer with Jurassic limestone and dolomite and a Keuper impermeable bottom. The carbonate formations are more than 1000 m thick. The average rainfall in the area is 840 mm. Its hydrogeological parameters are: transmissivity T = 40 − 16.4 m2; storage coefficient S = 1.5%.
- B.
- Polje of Zafarraya detrital aquifer: made up of Miocene and Quaternary infill sediments from the basin, having a maximum thickness of 280 m. The upper Miocene and Quaternary sediments are about 60 m thick and include sandy and gravel alluvial deposits with clay intercalations. In general, this upper detrital aquifer feeds the limestone aquifer underneath, but sometimes the reverse happens due to heavy rains that flood the polje. The flow is directed mainly towards the NE, with a gradient of 0.085–1.7%. This aquifer is heavily exploited, with 400 wells, and the water table is shallow, less than 15 m deep.
3.2. Hydrogeological Alterations: Types and Geographical Distribution
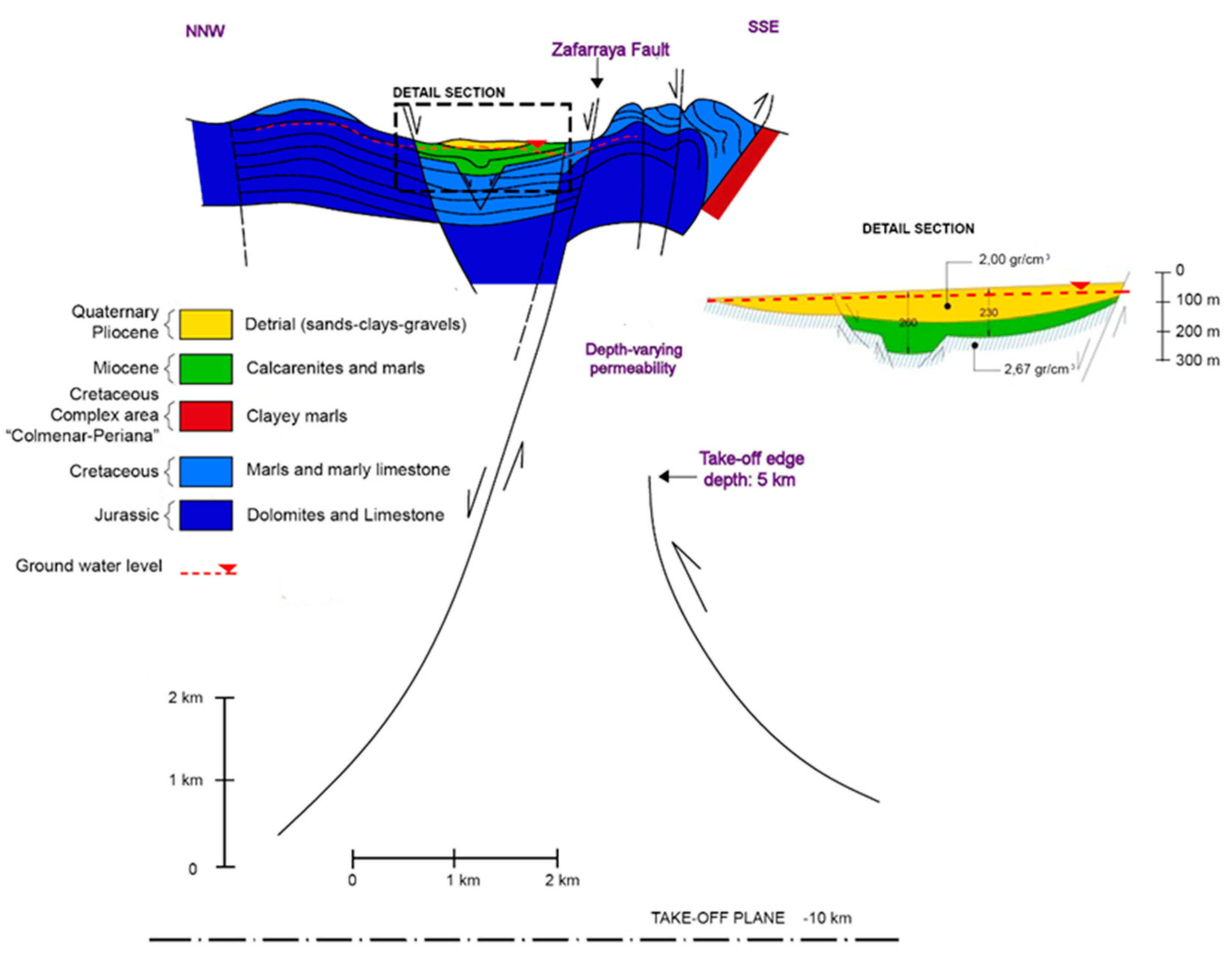
4. Geological Model of the Zafarraya Fault and Numerical Model Setup
4.1. 2D Geological Model of the Fault
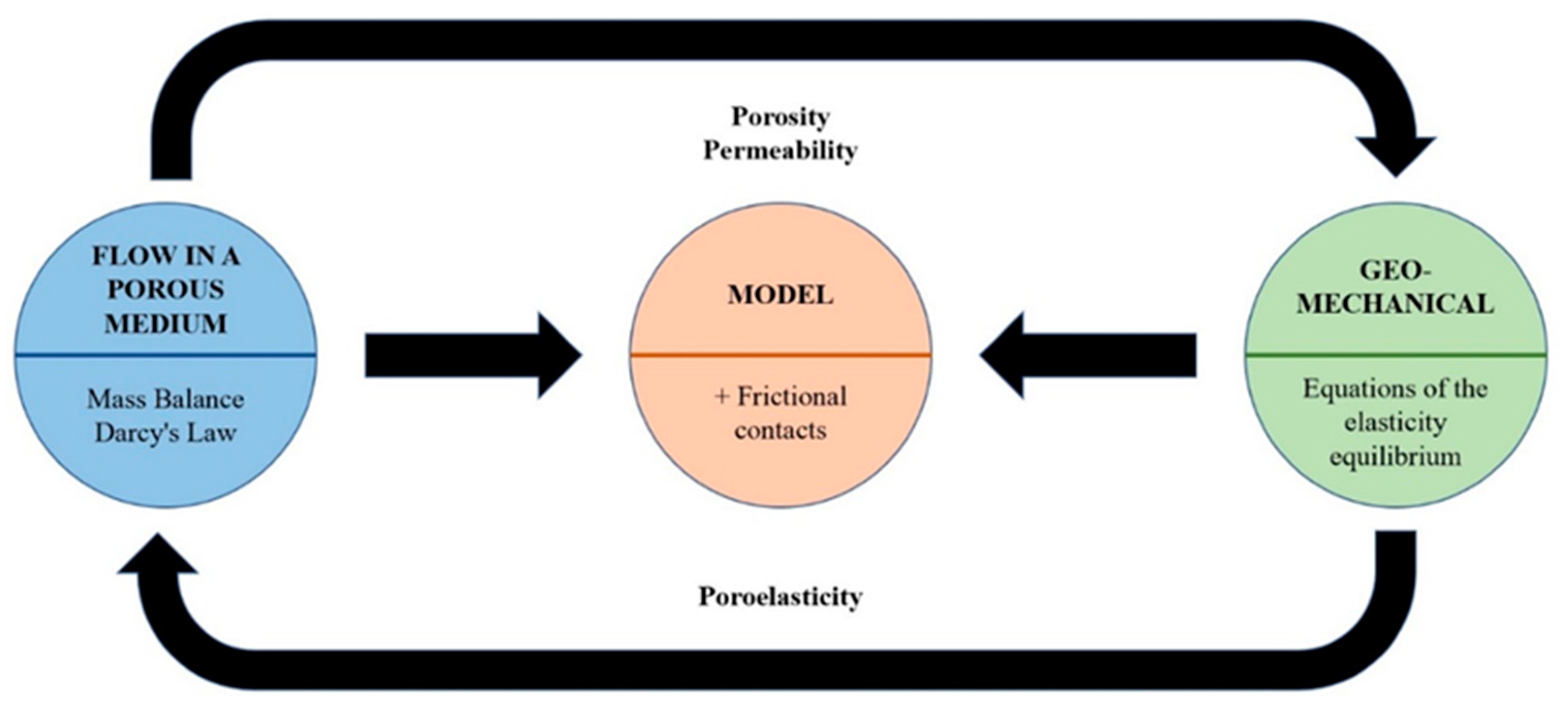
4.2. Coupled Physics Included in the Simulation Model
- is the fluid (water) density.
- is the constrained specific storage coefficient, which represents the volume of water either extracted from or added to storage in a confined aquifer per unit area of aquifer per unit decline or increase in the piezometric head. This unknown coefficient needs to be estimated through a model calibration. When the solid phase consists of a single constituent, the constrained specific storage becomes [40,41]:
- is the intrinsic permeability of the porous medium .
- is the dynamic viscosity of the fluid.
- is the Cauchy stress tensor.
- is the bulk rock density, and the dry rock density.
- is the gravity acceleration vector.
4.3. Numerical Model Setup
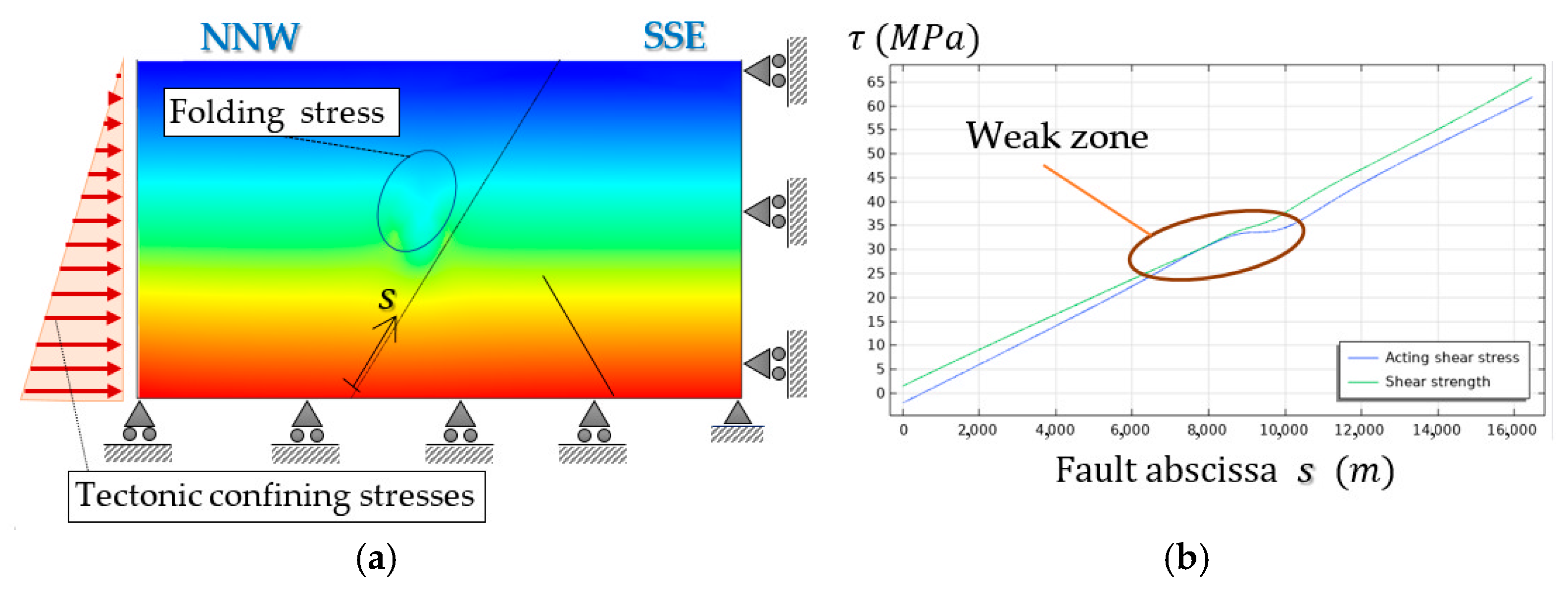
4.4. The Fault Frictional Model
- is the shear resistance at any fault point.
- is the cohesion term of the resistance, neglected in this study.
- We include a radiation damping term that acts as a velocity-dependent cohesion, , in the definition of fault strength to resolve the rupture dynamics. Then we consider a damping factor , with being the shear wave speed. The phenomenon of radiation damping accounts for the volumetric dissipation mechanism of seismic waves in the definition of the friction resistance of the fault [39,43,44].
- is the friction coefficient of the contact.
- is the effective contact (normal) pressure at any fault contact point. It is given by , with being the contact pressure between the fault edges (compressive pressures are positive). Its value is chosen as the maximum on both sides of the fault, [45]. The fault remains locked when the shear stress acting on the fault, , is lower than the frictional strength, ; otherwise, it slips.
4.5. The Ground Model and Properties
4.6. The Finite Element Domain
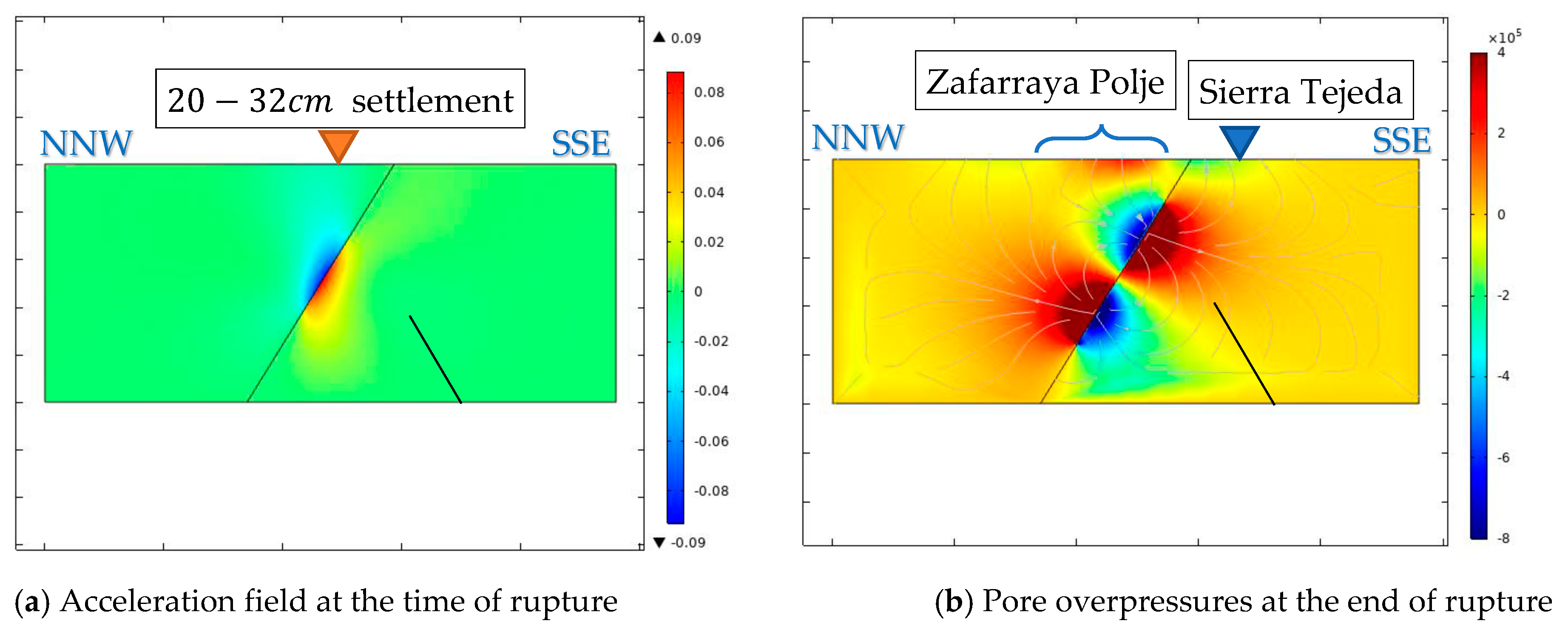
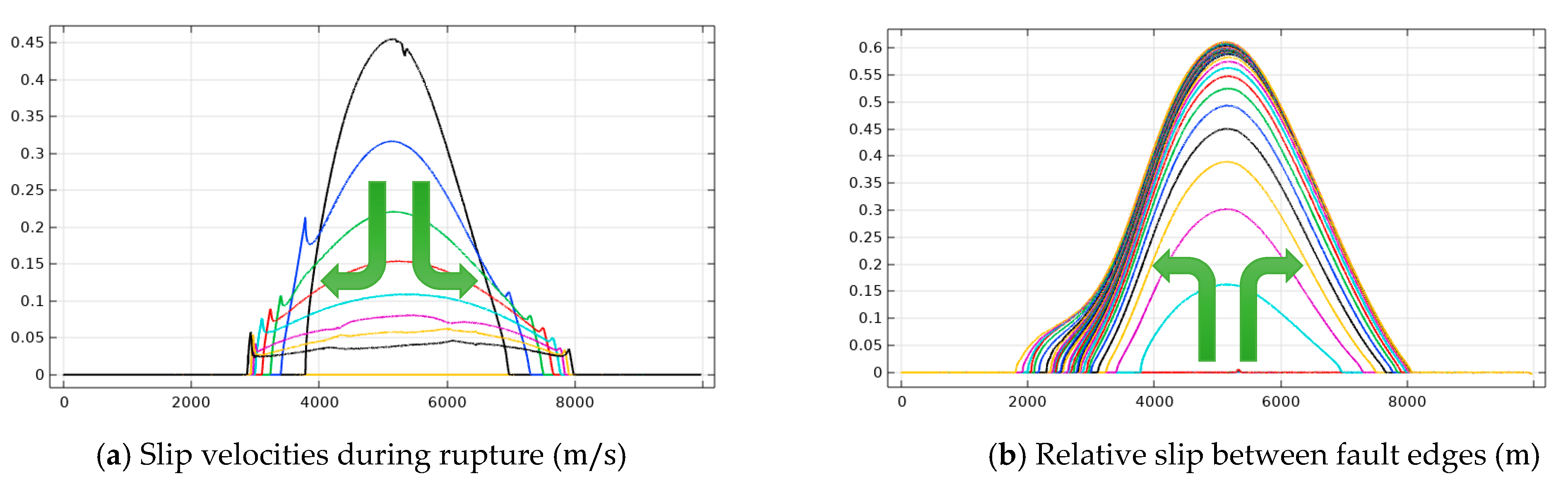
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Quidam, U. Cartas Desde Los Sitios Azotados Por Los Terremotos de Andalucía; Liberia Nacional y Extranjera: Madrid, Spain, 1885; p. 142. Available online: https://digibug.ugr.es/bitstream/handle/10481/7943/c-019-036%20%2837%29.pdf?sequence=1&isAllowed=y (accessed on 15 November 2022).
- Lasala y Collado, F. Memoria Del Comisario Regio Para la Reedificación de Los Pueblos Destruidos Por Los Terremotos En Las Provincias de Granada y Málaga; M. Minuesa de los Ríos, Impresor: Madrid, Spain, 1888; Available online: http://www.bibliotecavirtualdeandalucia.es/catalogo/es/catalogo_imagenes/grupo.do?path=150661 (accessed on 15 November 2022).
- Fouqué, F. Relations Entre les Phénomènes Presentés par le Tremblements de Terre de l’Andalousie et la Constitution Géologique de la Región qui en a été le Siege. Compt. Rend. Acad. Sci. Paris. 1885, 100, pp. 1113–1120. Available online: https://fr.wikisource.org/wiki/Les_Tremblements_de_terre/II/04 (accessed on 22 January 2023). (In French).
- Botella y Hornos, F.D. Los terremotos de Málaga y Granada. Bol. Soc. Geográfica Madr. 1885, t. XVII, 30. [Google Scholar]
- Rodríguez-Pascua, M.A.; Silva, P.G.; Perucha, M.A.; Giner Robles, J.L.; Élez, J.; Roquero, E. Efectos Ambientales del Terremoto de Arenas del Rey de 1884 (España). Aplicación de la Escala ESI07. In Resúmenes de la 3ª Reunión Ibérica Sobre Fallas Activas y Paleosismología IBERFAULT III; Universidad de Alicante: Alicante, Spain, 2018; pp. 147–150. [Google Scholar]
- Fernández de Castro, M.; Lasala, J.P.; Cortázar, D.; Tarín, J.G. Terremotos de Andalucía. Informe de la Comisión Nombrada Para su Estudio Dando Cuenta del Estado de Los Trabajos en 7 de Marzo de 1885. 1885. Available online: http://hdl.handle.net/10481/19269 (accessed on 15 November 2022).
- Taramelli, T.; Mercalli, G. I terremotti andalusi cominciati il 25 diciembre 1884. Atti R. Accad. Dei Lincei 1886, III, 116–222. [Google Scholar]
- Seco de Lucena, L. Crónicas sobre el terremoto de Andalucía de 1884. Memorias 1941, 1, 79–103. [Google Scholar]
- Udías, A.; Buforn, E.; Mattesini, M. Contemporary Publications in Europe on the Spanish Earthquake of 1884. Seismol. Res. Lett. 2022, 93, 3489–3497. [Google Scholar] [CrossRef]
- Mercalli, G.; Taramelli, T. Relazione Sulle Osservationi Fatte Durante un Viaggio Nelle Regioni della Spagna Colpìtte Dagli Ultimi Terremoto, Nota Preliminare Rendiccione R. Accademia dei Lincei June 1885. Available online: https://pubs.geoscienceworld.org/ssa/srl/article-abstract/93/6/3489/616413/Contemporary-Publications-in-Europe-on-the-Spanish?redirectedFrom=fulltext (accessed on 22 January 2023). (In Italian).
- MacPherson, J. Observaciones sobre los terremotos de Andalucía. An. Soc. Española Hist. Nat. 1885, XIV, 4–6. [Google Scholar]
- Wang, C.-Y.; Manga, M. Temperature and Composition Changes. In Earthquakes and Water; Springer: Berlin/Heidelberg, Germany, 2010; pp. 97–115. [Google Scholar]
- Santillán, D.; Sanz de Ojeda, A.; Cueto-Felgueroso, L.; Mosquera, J.C. Sismicidad inducida en embalses. In Una Aproximación Mediante un Modelo Conceptual. Hidrogeología: Retos y Experiencias; UIMP: Madrid, Spain, 2018. [Google Scholar]
- Wang, C.-Y.; Manga, M. Earthquakes and Water. In Lecture Notes in Earth Sciences; Springer: Berlin/Heidelberg, Germany, 2010; Volume 114, pp. 67–93. Available online: https://www.springer.com/series/772 (accessed on 22 January 2023).
- Sanz de Ojeda, A.; Alhama, I.; Sanz, E. Aquifer sensitivity to earthquakes: The 1755 Lisbon earthquake. J. Geophys. Res. Solid Earth 2019, 124, 8844–8866. [Google Scholar] [CrossRef]
- Muñoz, D.; Udías, A. Estudio de los parámetros y serie de réplicas del terremoto de Andalucia del 25 de diciembre de 1884 y de la sismicidad de la región Granada-Málaga. In El Terremoto de Andalucía del 25 de Diciembre de 1884; IGN: Madrid, Spain, 1981; pp. 95–125. Available online: http://www.ign.es/web/resources/sismologia/publicaciones/Andalucia1884.pdf (accessed on 15 November 2022).
- Galindo-Zaldívar, J.; Gil, A.J.; Borque, M.J.; González-Lodeiro, F.; Jabaloy, A.; Marín-Lechado, C.; Ruano, P.; Sanz de Galdeano, C. Desarrollo simultáneo reciente de pliegues y fallas en las Cordilleras Béticas: La Falla de Zafarraya y el Pliegue de Sierra Tejeda. Geo-Temas 2004, 6, 147–150. [Google Scholar]
- Yolsal-Çevikbilen, S.; Taymaz, T. Earthquake source parameters along the Hellenic subduction zone and numerical simulations of historical tsunamis in the Eastern Mediterranean. Tectonophysics 2012, 536, 61–100. [Google Scholar] [CrossRef]
- Cueto-Felgueroso, L.; Vila, C.; Santillán, D.; Mosquera, J.C. Numerical modeling of injection-induced earthquakes using laboratory-derived friction laws. Water Resour. Res. 2018, 54, 9833–9859. [Google Scholar] [CrossRef]
- Andrés, S.; Santillán, D.; Mosquera, J.; Cueto-Felgueroso, L. Thermo-Poroelastic Analysis of Induced Seismicity at the Basel Enhanced Geothermal System. Sustainability 2019, 11, 6904. [Google Scholar] [CrossRef]
- Andrés, S.; Santillán, D.; Mosquera, J.; Cueto-Felgueroso, L. Delayed weakening and reactivation of rate-and-state faults driven by pressure changes due to fluid injection. J. Geophys. Res. Solid Earth 2019, 124, 11917–11937. [Google Scholar] [CrossRef]
- Pampillón, P.; Santillán, D.; Mosquera, J.C.; Cueto-Felgueroso, L. Dynamic and quasi-dynamic modeling of injection-induced earthquakes in poroelastic Media. J. Geophys. Res. Solid Earth 2018, 123, 5730–5759. [Google Scholar] [CrossRef]
- Barbot, S.; Lapusta, N.; Avouac, J.-P. Under the Hood of the Earthquake Machine: Toward Predictive Modeling of the Seismic Cycle. Science 2012, 336, 707–710. [Google Scholar] [CrossRef]
- Comisión del Mapa Geológico de España. Estudios referentes al terremoto ocurrido en Andalucía el 25 de diciembre de 1884 y a la constitución geológica del suelo conmovido por las sacudidas, efectuados por la Comisión destinada al objeto por la Comisión de Ciencias de París. Bol. Com. Map. Geol. T. 1890, XXVI, 299–303. [Google Scholar]
- Instituto Geográfico Nacional, El terremoto de Andalucía de 25 de diciembre de 1884, Ed IGN, Madrid. 1981. Available online: http://www.ign.es/web/resources/sismologia/publicaciones/Andalucia1884.pdf (accessed on 15 November 2022).
- Orueta Duarte, D. Informes Sobre los Terremotos Ocurridos en el Sud de España en Diciembre de 1884 y Enero de 1885; Tip. y Lit. de Fausto Muñoz: Madrid, Spain, 1885; p. 51. [Google Scholar]
- Bizzarri, A. How to promote earthquake ruptures: Different nucleation strategies in a dynamic model with slip-weakening friction. Bull. Seismol. Soc. Am. 2010, 100, 923–940. [Google Scholar] [CrossRef]
- Srivastava, S.P.; Schouten, H.; Roest, W.R.; Klitgord, K.D.; Kovacs, L.C.; Verhoef, J.; Macnab, R. Iberian plate kinematics: A jumping plate boundary between Eurasia and Africa. Nature 1990, 344, 756–759. [Google Scholar] [CrossRef]
- Fernández-García, C.; Ruano, P. Caracterización de la geometría del Polje de Zafarraya a partir de prospección gravimétrica (Cordillera Bética). Geogaceta 2016, 59, 67–70. [Google Scholar]
- de Galdeano, C.S. The Zafarraya Polje (Betic Cordillera, Granada, Spain), a basin open by lateral displacement and bending. J. Geodyn. 2013, 64, 62–70. [Google Scholar] [CrossRef]
- López Chicano, M.; Pulido-Bosch, A. Síntesis hidrogeológica de los acuíferos de Sierra Gorda, Polje de Zafarraya y Hacho de Loja. In Libro Homenaje a Manuel del Valle Cardenete. Aportaciones al Conocimiento de los Acuíferos Andaluces; IGME, CHG, IAA (COPTJA), Diputación Provincial de Granada: Madrid, Spain, 2002; pp. 311–340. [Google Scholar]
- Reicherter, K.R.; Jabaloy, A.; Galindo-Zaldívar, J.; Ruano, P.; Becker-Heidmann, P.; Morales, J.; Reiss, S.; González-Lodeiro, F. Repeated palaeoseismic activity of the Ventas de Zafarraya fault (S Spain) and its relation with the 1884 Andalusian earthquake. Int. J. Earth Sci. 2003, 92, 912–922. [Google Scholar] [CrossRef]
- Reicherter, K.R.; Peters, G. Neotectonic evolution of the central Betic Cordilleras (southern Spain). Tectonophysics 2005, 405, 191–212. [Google Scholar] [CrossRef]
- López-Chicano, M. Contribución al Conocimiento del Sistema Hidrogeológico Kárstico de Sierra Gorda y su Entorno (Granada y Málaga). Ph.D. Thesis, Universidad de Granada, Granada, Spain, 1993. [Google Scholar]
- López Arroyo, A.; Martín Martín, A.J.; Mezcua Rodríguez, J. Terremoto de Andalucía. Influencia en sus efectos de las condiciones del terreno y del tipo de construcción. In El Terremoto de Andaluciía de 1884; Instituto Geográfico Nacional: Madrid, Spain, 1980; pp. 5–94. [Google Scholar]
- Udías, A.; Muñoz, D. The Andalusian earthquake of 25 December 1884. Tectonophysics 1979, 53, 291–299. [Google Scholar] [CrossRef]
- Rice, J.R.; Cleary, M.P. Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents. Rev. Geophys. 1976, 14, 227–241. [Google Scholar] [CrossRef]
- White, J.; Foxall, W. Assessing induced seismicity risk at CO2 storage projects: Recent progress and remaining challenges. Int. J. Greenh. Gas Control 2016, 49, 413–424. [Google Scholar] [CrossRef]
- Cueto-Felgueroso, L.; Santillán, D.; Mosquera, J.C. Stick-slip dynamics of flow-induced seismicity on rate and state faults. Geophys. Res. Lett. 2017, 44, 4098–4106. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics; John Wiley & Sons: London, UK, 2004. [Google Scholar]
- Verruijt, A. Theory and Problems of Poroelasticity; Delft University of Technology: Delft, The Netherlands, 2013; Volume 71. [Google Scholar]
- Moczo, P.; Kristek, J.; Galis, M.; Pazak, P.; Balazovjech, M. The finite-difference and finite-element modeling of seismic wave propagation and earthquake motion. Acta Phys. Slovaca 2007, 57, 177–406. [Google Scholar] [CrossRef]
- Rice, J.R. Spatio-temporal complexity of slip on a fault. J. Geophys. Res. 1993, 98, 9885–9907. [Google Scholar] [CrossRef]
- Lapusta, N.; Rice, J.R. Nucleation and early seismic propagation of small and large events in a crustal earthquake model. J. Geophys. Res. 2003, 108, B42205. [Google Scholar] [CrossRef]
- Jha, B.; Juanes, R. Coupled multiphase flow and poromechanics: A computational model of pore pressure effects on fault slip and earthquake triggering. Water Resour. Res. 2014, 50, 3776–3808. [Google Scholar] [CrossRef]
- Jonsson, S.; Segall, P.; Pedersen, R.; Björnsson, G. Postearthquake ground movements correlated to pore-pressure transients. Nature 2003, 424, 179–183. [Google Scholar] [CrossRef]
- Akita, F.; Matsumoto, N. Hydrological responses induced by the Tokachi-oki earthquake in 2003 at hot spring well in Hokkaido. Japan. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Rudnicki, J.W.; Rice, J.R. Effective normal stress alteration due to pore pressure changes induced by dynamic slip propagation on a plane between dissimilar materials. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Dunham, E.M.; Rice, J.R. Earthquake slip between dissimilar poroelastic materials. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Hanks, T.C.; Kanamori, H. A moment magnitude scale. J. Geophys. Res. Solid Earth 1979, 84, 2348–2350. [Google Scholar] [CrossRef]
- Biot, M.A. Mechanics of deformation and acoustic propagation in porous media. J. Appl. Phys. 1962, 33, 1482–1498. [Google Scholar] [CrossRef]
- Detournay, E.; Cheng, A.H.-D. Fundamentals of poroelasticity. In Comprehensive Rock Engineering: Principles, Practice and Projects; Hudson, J.A., Ed.; Pergamon: New York, NY, USA, 1993; pp. 113–171. [Google Scholar]
- Ismail-Zadeh, A.; Soloviev, A. Numerical Modelling of Lithospheric Block-and-Fault Dynamics: What Did We Learn About Large Earthquake Occurrences and Their Frequency? Surv. Geophys. 2022, 43, 503–528. [Google Scholar] [CrossRef]
- Rundle, J.B.; Rundle, P.B.; Donnellan, A.; Li, P.; Klein, W.; Morein, G.; Turcotte, D.; Grant, L. Stress transfer in earthquakes, hazard estimation and ensemble forecasting: Inferences from numerical simulations. Tectonophysics 2006, 413, 109–125. [Google Scholar] [CrossRef]
- Trifu, C.I. (Ed.) The Mechanism of Induced Seismicity; Birkhauser: Basel, Switzerland, 2002. [Google Scholar]
- Shapiro, S.A.; Rentsch, S.; Rothert, E. Fluid-induced seismicity: Theory, modeling, and applications. J. Eng. Mech. 2005, 131, 947–952. [Google Scholar] [CrossRef]
- Ellsworth, W.L. Injection-induced earthquakes. Science 2013, 341, 1225942. [Google Scholar] [CrossRef]
- Deng, K.; Liu, Y.; Harrington, R.M. Poroelastic stress triggering of the December 2013 Crooked Lake, Alberta, induced seismicity sequence. Geophys. Res. Lett. 2016, 43, 8482–8491. [Google Scholar] [CrossRef]
- Rutqvist, J.; Birkholzer, J.T.; Tsang, C.F. Coupled reservoir–geomechanical analysis of the potential for tensile and shear failure associated with CO2 injection in multilayered reservoir–caprock systems. Int. J. Rock Mech. Min. Sci. 2008, 45, 132–143. [Google Scholar] [CrossRef]
- McGarr, A.; Barbour, A.J. Wastewater disposal and the earthquake sequences during 2016 near Fairview, Pawnee, and Cushing, Oklahoma. Geophys. Res. Lett. 2017, 44, 9330–9336. [Google Scholar] [CrossRef]
- Catalli, F.; Rinaldi, A.; Gischig, V.; Nespoli, M.; Wiemer, S. The importance of earthquake interactions for injection-induced seismicity: Retrospective modeling of the Basel Enhanced Geothermal System. Geophys. Res. Lett. 2016, 43, 4992–4999. [Google Scholar] [CrossRef]
- Ellsworth, W.L.; Giardini, D.; Townend, J.; Ge, S.; Shimamoto, T. Triggering of the Pohang, Korea, earthquake (M w 5.5) by enhanced geothermal system stimulation. Seismol. Res. Lett. 2019, 90, 1844–1858. [Google Scholar] [CrossRef]
- Andrés, S.; Santillán, D.; Mosquera, J.C.; Cueto-Felgueroso, L. Hydraulic Stimulation of Geothermal Reservoirs: Numerical Simulation of Induced Seismicity and Thermal Decline. Water 2022, 14, 3697. [Google Scholar] [CrossRef]
- Segall, P.; Grasso, J.R.; Mossop, A. Poroelastic stressing and induced seismicity near the Lacq gas field, southwestern France. J. Geophys. Res. 1994, 99, 15423–15438. [Google Scholar] [CrossRef]
- Schultz, R.; Skoumal, R.J.; Brudzinski, M.R.; Eaton, D.; Baptie, B.; Ellsworth, W. Hydraulic fracturing-induced seismicity. Rev. Geophys. 2020, 58, e2019RG000695. [Google Scholar] [CrossRef]
- Moro, M.; Saroli, M.; Stramondo, S.; Bignami, C.; Albano, M.; Falcucci, E.; Gori, S.; Doglioni, C.; Polcari, M.; Wegmüller, U. New insights into earthquake precursors from InSAR. Sci. Rep. 2017, 7, 12035. [Google Scholar] [CrossRef]
- Chiaradonna, A.; Spadi, M.; Monaco, P.; Papasodaro, F.; Tallini, M. Seismic Soil Characterization to Estimate Site Effects Induced by Near-Fault Earthquakes: The Case Study of Pizzoli (Central Italy) during the Mw 6.7 2 February 1703, Earthquake. Geosciences 2022, 12, 2. [Google Scholar] [CrossRef]
- Kim, J.; Joun, W.-T.; Lee, S.; Kaown, D.; Lee, K.-K. Hydrogeochemical evidence of earthquake-induced anomalies in response to the 2017 MW 5.5 Pohang earthquake in Korea. Geochem. Geophys. Geosyst. 2020, 21, e2020GC009532. [Google Scholar] [CrossRef]
- Chang, K.W.; Yoon, H.; Kim, Y.; Lee, M.Y. Operational and geological controls of coupled poroelastic stressing and pore-pressure accumulation along faults: Induced earthquakes in Pohang, South Korea. Sci. Rep. 2020, 10, 2073. [Google Scholar] [CrossRef]
- Jung, Y.; Woo, J.U.; Rhie, J. Enhanced hypocenter determination of the 2017 Pohang earthquake sequence, South Korea, using a 3-D velocity model. Geosci. J. 2022, 26, 499–511. [Google Scholar] [CrossRef]
- Kim, K.H.; Ree, J.H.; Kim, Y.; Kim, S.; Kang, S.Y.; Seo, W. Assessing whether the 2017 Mw 5.4 Pohang earthquake in South Korea was an induced event. Science 2018, 360, 1007–1009. [Google Scholar] [CrossRef]
- McGarr, A.; Majer, E.L. The 2017 Pohang, South Korea, Mw 5.4 main shock was either natural or triggered, but not induced. Geothermics 2023, 107, 102612. [Google Scholar] [CrossRef]
- He, J.; Xia, W.; Lu, S.; Qian, H. Three-dimensional finite element modeling of stress evolution around the Xiaojiang fault system in the southeastern Tibetan plateau during the past~500 years. Tectonophysics 2011, 507, 70–85. [Google Scholar] [CrossRef]
- Baptista, M.A.; Miranda, P.M.A.; Miranda, J.M.; Victor, L.M. Rupture extent of the 1755 Lisbon earthquake inferred from numerical modeling of tsunami data. Phys. Chem. Earth 1996, 21, 65–70. [Google Scholar] [CrossRef]
- Mendes-Victor, L.; Oliveira, C.S.; Azevedo, J.; Ribeiro, A. The 1755 Lisbon Earthquake: Revisited; Mendes-Victor, L., Oliveira, C.S., Azevedo, J., Ribeiro, A., Eds.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 7. [Google Scholar] [CrossRef]
- Oliveira, C.S. Lisbon earthquake scenarios: A review on uncertainties, from earthquake source to vulnerability modelling. Soil Dyn. Earthq. Eng. 2008, 28, 890–913. [Google Scholar] [CrossRef]
- Silva, P.G.; Elez, J.; Pérez-López, R.; Giner-Robles, J.L.; Gómez-Diego, P.V.; Rodríguez-Pascua, M.; Bardají, T. The AD 1755 Lisbon Earthquake-Tsunami: Seismic source modelling from the analysis of ESI-07 environmental data. Quat. Int. 2021. [Google Scholar] [CrossRef]
- Lanza, F.; Diehl, T.; Deichmann, N.; Kraft, T.; Nussbaum, C.; Schefer, S.; Wiemer, S. The Saint-Ursanne earthquakes of 2000 revisited: Evidence for active shallow thrust-faulting in the Jura fold-and-thrust belt. Swiss J. Geosci. 2022, 115, 2. [Google Scholar] [CrossRef]

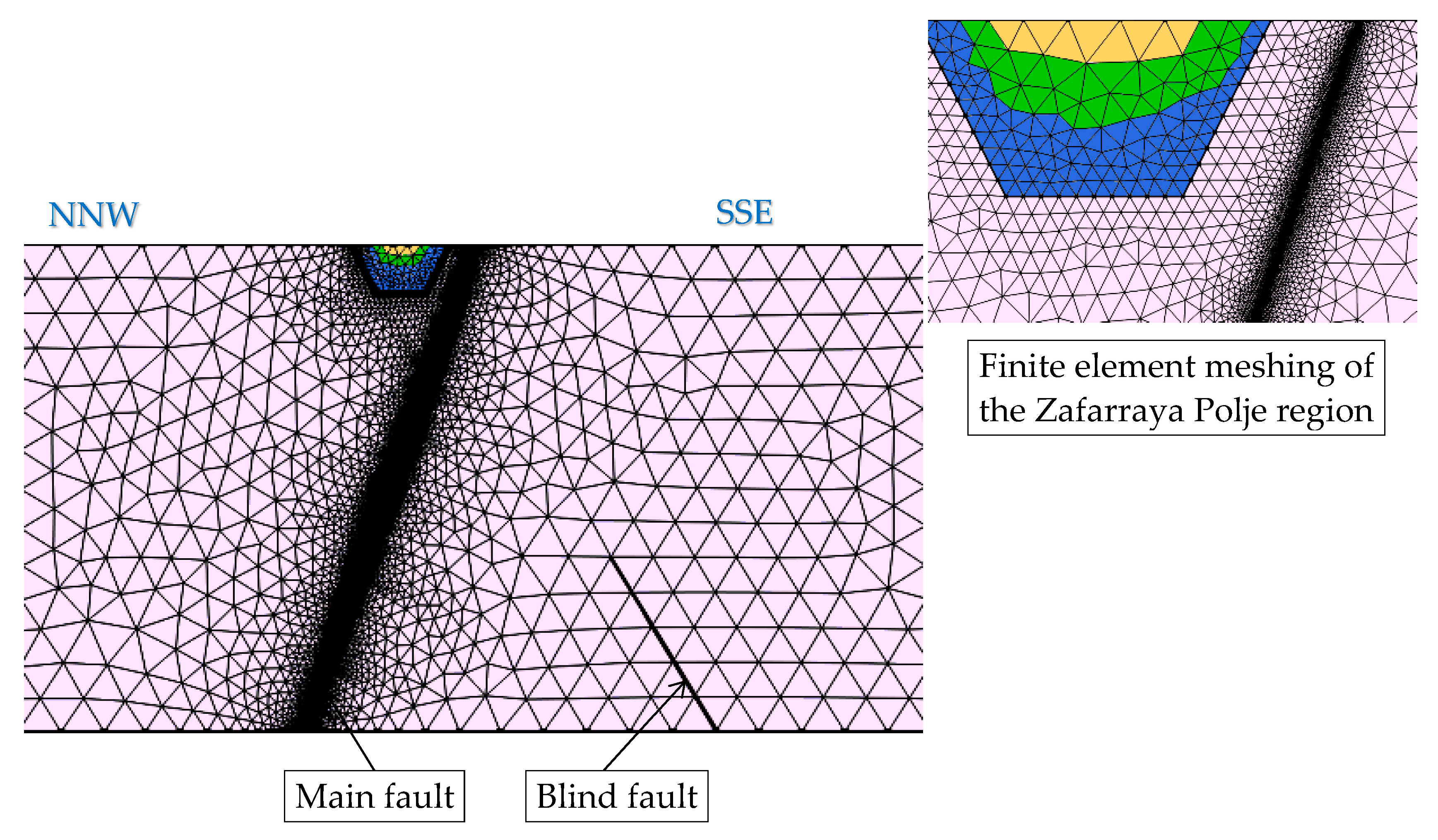
| Density (Ton/m3) | Effective Porosity (%) | Permeability (m/s) | Depth of Water Table (m) | |
|---|---|---|---|---|
| 1 | 2.00 | 13 | 1 m/day | <15 |
| 2 | 2.00 | 10 | 10−4–10−7 | - |
| 3 | 2.00 | 0.5 | 10−6 | - |
| 4 | - | 0.5 | - | - |
| 5 | 2.67 | 1.5 | 10−3–10−9 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mudarra-Hernández, M.; Mosquera-Feijoo, J.C.; Sanz-Pérez, E. Numerical Simulation and Characterization of the Hydromechanical Alterations at the Zafarraya Fault Due to the 1884 Andalusia Earthquake (Spain). Water 2023, 15, 850. https://doi.org/10.3390/w15050850
Mudarra-Hernández M, Mosquera-Feijoo JC, Sanz-Pérez E. Numerical Simulation and Characterization of the Hydromechanical Alterations at the Zafarraya Fault Due to the 1884 Andalusia Earthquake (Spain). Water. 2023; 15(5):850. https://doi.org/10.3390/w15050850
Chicago/Turabian StyleMudarra-Hernández, Manuel, Juan Carlos Mosquera-Feijoo, and Eugenio Sanz-Pérez. 2023. "Numerical Simulation and Characterization of the Hydromechanical Alterations at the Zafarraya Fault Due to the 1884 Andalusia Earthquake (Spain)" Water 15, no. 5: 850. https://doi.org/10.3390/w15050850
APA StyleMudarra-Hernández, M., Mosquera-Feijoo, J. C., & Sanz-Pérez, E. (2023). Numerical Simulation and Characterization of the Hydromechanical Alterations at the Zafarraya Fault Due to the 1884 Andalusia Earthquake (Spain). Water, 15(5), 850. https://doi.org/10.3390/w15050850







