1. Introduction
Due to the heterogeneous nature of geological media and our inability to completely know them [
1,
2,
3] our predictions of the hydrological processes in a slope inevitably involve uncertainties [
1,
4,
5,
6]. For example, the hydraulic properties generally exhibit significant spatial variabilities at multiple scales [
1,
7]. This leads to uncertainties in the slope seepage flow analysis, which contributes to the slope stability analysis.
Probabilistic methods become necessary for dealing with the uncertainty issues associated with our predictions of slope seepage [
1,
5,
8,
9]. Generally, given the statistical properties of hydraulic parameters, a Monte Carlo simulation method is used to derive the statistics such as the mean and variance of properties of the slope seepage field. Either a steady or transient analysis of the saturated or unsaturated flow in the slope can be carried out in a Monte Carlo simulation. For example, Gui et al. [
5] used Monte Carlo simulation to investigate the influence of variabilities in the hydraulic conductivity on the seepage and stability of an embankment dam. Using FLAC 5.0, Srivastava et al. [
10] conducted a Monte Carlo simulation to derive the statistical response of steady-state seepage flow due to spatially variable permeabilities. Cho [
2] obtained statistical responses of the seepage of an infinite slope under rainfall due to the spatial variability of hydraulic conductivity from the Monte Carlo simulation. Gomes et al. [
11] investigated the effect of uncertainties in the hydraulic properties on the pressure head via the Monte Carlo simulation of a three-dimensional flow model. Tang et al. [
12] considered the random rainfall pattern through the Monte Carlo simulation to produce its impacts on the pore-water pressure distribution and the assessment of rainfall-induced landslide. Li et al. [
13] applied the Monte Carlo simulation to the probability and sensitivity analysis of slope stability of a tailings dam under seepage. More recently, Monte Carlo simulation was used in the stochastic analysis of unsaturated slopes subjected to various rainfall intensities and patterns by [
14]. Few simplified assumptions are required by the Monte Carlo simulation except for the definition of the probability density function of the hydraulic properties [
15].
These appealing advantages of the Monte Carlo simulation method build on its high demand for computational time and storage space [
2,
15]. This demand becomes dreadful when addressing flow problems with fine meshes [
15]. In turn, this restricts the number of realizations that can be conducted in a Monte Carlo simulation [
5].
As an alternative, a first-order stochastic moment analysis approach [
16] has been used to conduct a two-dimensional probabilistic infiltration analysis in a hillslope. Although the derived statistics of slope seepage are at an accuracy of the first-order approximation, conducting a large number of simulations is avoided, thus easing the computational burden associated with the Monte Carlo simulation. In addition, similar to the Monte Carlo simulation, either the steady-state flow or the transient flow in the slope can be examined using the first-order analysis. With these advantages of the first-order approach, Cai et al. [
7] investigated the temporal and spatial propagation of the uncertainty of slope stability during rainfall, considering variabilities in the initial soil moisture, rainfall and soil hydraulic properties.
Although much work has been performed using the Monte Carlo simulation to date, much less attention has been paid to the influence of the grid density on the Monte Carlo simulation. In addition, the applying conditions of the first-order analysis remain unexplored. Moreover, at the present time, the effective flow profile and variability of seepage in two-dimensional, unsaturated heterogeneous slopes under conditions of steady rainfall infiltration, based on a spatially correlated hydraulic conductivity field, are not sufficiently understood.
The objectives of this study are to (1) conduct a probabilistic analysis of slope seepage under rainfall, considering the spatial variability of hydraulic conductivity and (2) test and compare the Monte Carlo simulation and the first-order analysis method applied in the probabilistic slope seepage analysis. The influence of the grid density on both methods and the applicability of the proposed first-order stochastic moment analysis approach are the focus. To this end, we first introduce how the first-order stochastic moment analysis works by analyzing the first-order moments of the pressure head. In
Section 2, we consider the spatial variability of the hydraulic conductivity and introduce the equations that govern the rainfall infiltration process. For the purpose of verifying the accuracy of the first-order analysis method, we also briefly introduce the Monte Carlo simulation of hydraulic responses, considering the spatial variability of the hydraulic conductivity in
Section 2. One focus of this study is the grid density, the influence of which on the probabilistic analysis by both Monte Carlo simulation and the first-order analysis method will be investigated. The model setups for the numerical simulation of the slope rainfall infiltration analysis are also provided in
Section 2. The results and discussions are provided in
Section 3, which includes the results of the effect of the spatial variability of hydraulic conductivity on the pressure heads by the proposed first-order stochastic moment analysis method and the Monte Carlo simulation verification, shedding light on the applying conditions of the first-order analysis in probabilistic slope seepage analysis. The article finally draws its conclusions in
Section 4.
2. Methodology
Based on the governing equations of the rainfall infiltration process, the first-order stochastic moment analysis of the pressure head, considering the spatial variability of the saturated hydraulic conductivity, is introduced. In addition, to verify the accuracy of the first-order analysis method, the Monte Carlo simulation of hydraulic responses, considering the spatial variability of the saturated hydraulic conductivity, is also briefly introduced. Finally, both the first-order analysis and the Monte Carlo simulation of rainfall infiltration are implemented via finite element simulations. Hence, the methodology section will be grouped into: (1) the governing equations for rainfall infiltration analysis, (2) first-order stochastic moment analysis, (3) Monte Carlo simulation verification and (4) the setup of the simulations.
2.1. Governing Equations for Rainfall Infiltration Analysis
The two-dimensional, steady-state flow in a slope under rainfall infiltration can be described by the following equation:
which is subject to the following boundary conditions:
where
and
denotes the coordinates along the horizontal
x-axis and vertical
z-axis, respectively;
denotes the pressure head, which is a function of the coordinates;
is the hydraulic conductivity–pressure constitutive function,
is the prescribed head at the Dirichlet boundary
,
is the specific flux at the Neumann boundary
and notations
and
are the components in the
x and
z directions, respectively, of a unit vector
that is normal to the boundary
.
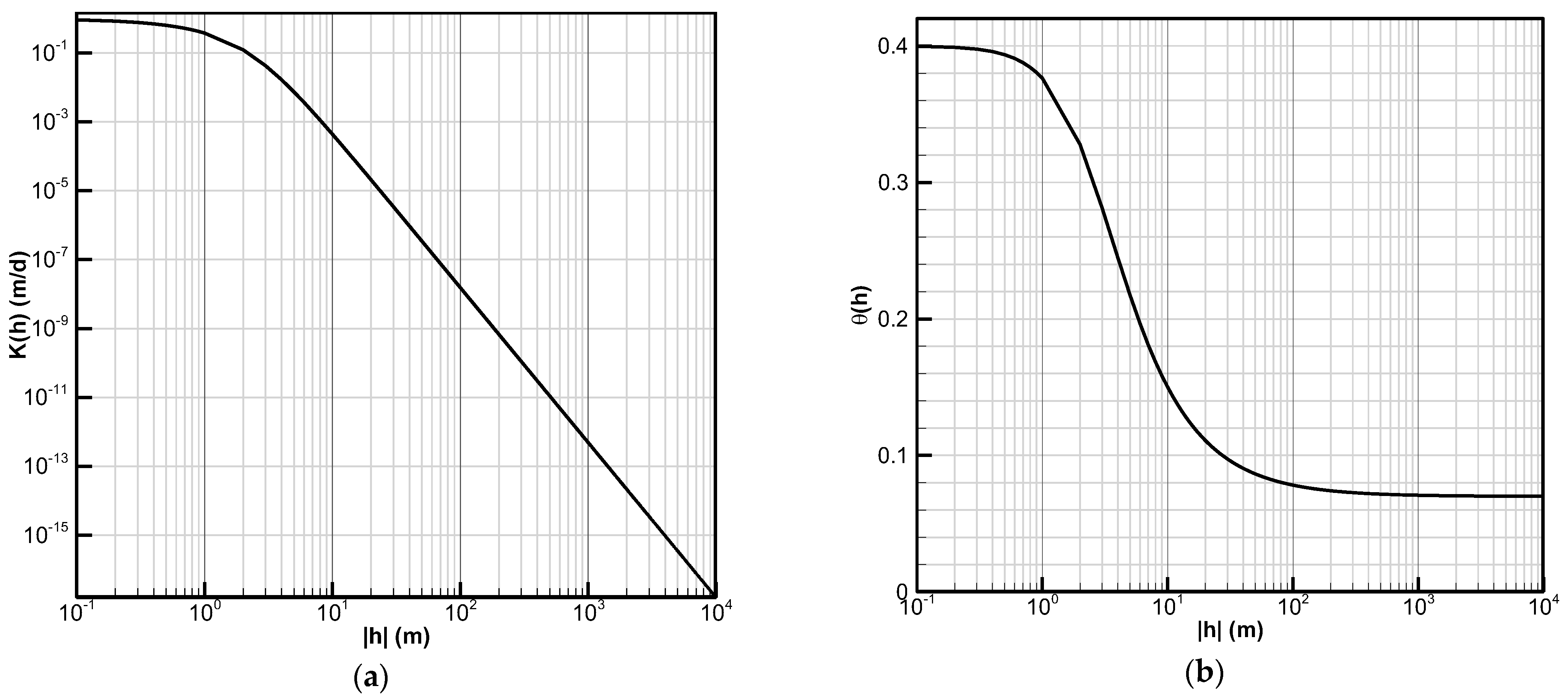
To describe the
and the volumetric water content,
, the hydraulic conductivity curve and the moisture retention curve (
Figure 1a,b) developed by [
17,
18] are adopted herein:
In which
is the saturated hydraulic conductivity;
,
and
are soil parameters, where
and
and
denote the saturated and residual moisture content, respectively;
represents the absolute value.
2.2. First-Order Stochastic Moment Analysis
Based on the governing equations of the rainfall infiltration, the first-order stochastic moment analysis of slope seepage can be discussed. In this section, the two-dimensional correlation structure of the saturated hydraulic conductivity, was constructed, and the first-order stochastic moment formulation of slope seepage was then derived.
2.2.1. Two-Dimensional Correlation Structure of Saturated Hydraulic Conductivity
Usually, a mean (
), a variance (
) and a correlation structure described by correlation length (
) are needed to define a correlated field. The correlation length,
represents the distance within which the hydraulic conductivities are correlated in space. Physically, the correlation lengths describe the average dimensions (e.g., length, thickness) of heterogeneity, such as layers or stratifications [
19].
If the saturated hydraulic conductivity is assumed to follow a lognormal random field, then
can be modeled as a normal distribution with a mean,
, and a variance,
, which are calculated from:
In this study, the saturated hydraulic conductivity was treated as a statistically stationary and isotropic field, which is reasonable when the soil of the slope is deposited with regionally similar soils and without a specific direction. In this type of field, the mean hydraulic properties are constant in the domain. The covariance (or correlation) between any two points in the simulation domain does not depend on their locations. It decreases with their distance within the correlation length, gradually becoming relatively small (or zero) beyond the correlation length. The correlation lengths in the horizontal and vertical directions were assumed to be the same. An exponential autocorrelation function was used as follows:
where
is the autocorrelation function of any two points,
and
.
2.2.2. First-Order Formulation
Natural logarithms of the saturated hydraulic conductivity are treated as a stochastic process in space, which is characterized by its mean,
, its variance,
and its spatial correlation function,
. Subsequently, the pressure head,
, is expanded in a Taylor series about
. After neglecting the second- and the higher-order terms, the first-order approximation of the pressure head can be written as:
where
is the perturbation of
;
is the mean pressure head, evaluated using the mean saturated hydraulic conductivity,
, and it represents the head in an equivalent homogeneous slope; and
denotes the head perturbation around the mean head
, resulting from spatial variability of
. The partial derivative is the sensitivity matrix, which is evaluated at the mean parameter
. According to Equation (7), the head perturbation can be written in a matrix form as:
Here, bold symbols denote either matrices or vectors.
is the sensitivity of
to change in
or a Jacobian matrix, which can be calculated by the adjoint method [
15,
20,
21,
22]. Multiplying Equation (8) with itself and taking the expectation leads to the covariance of the head:
where
are the covariance function matrices for
, which is calculated by
. The superscript
denotes the transpose. Each diagonal element of
is the head variance,
at location (
x,
z), representing the mean-square deviation of the head in a heterogeneous slope from the head, calculated using the mean parameter,
for the homogeneous slope.
2.3. Monte Carlo Simulation Verification
Despite the enormous computer effort required by a Monte Carlo simulation, this method is still the most widely acceptable method to obtain various statistical properties [
1]. In order to verify the accuracy of the first-order analysis method proposed in this study, Monte Carlo simulation was used. For one simulation, a series of realizations of a random field with the same mean (
),variance (
) and correlation length (
) were generated, and the hydraulic response was calculated for each realization. These hydraulic responses (e.g., pressure head) were then used to calculate statistical properties such as mean and variance, which can be compared with the results produced by the first-order analysis. In order to generate a statistically stationary and isotropic random field, the fast Fourier transform code, modified from [
23], was applied.
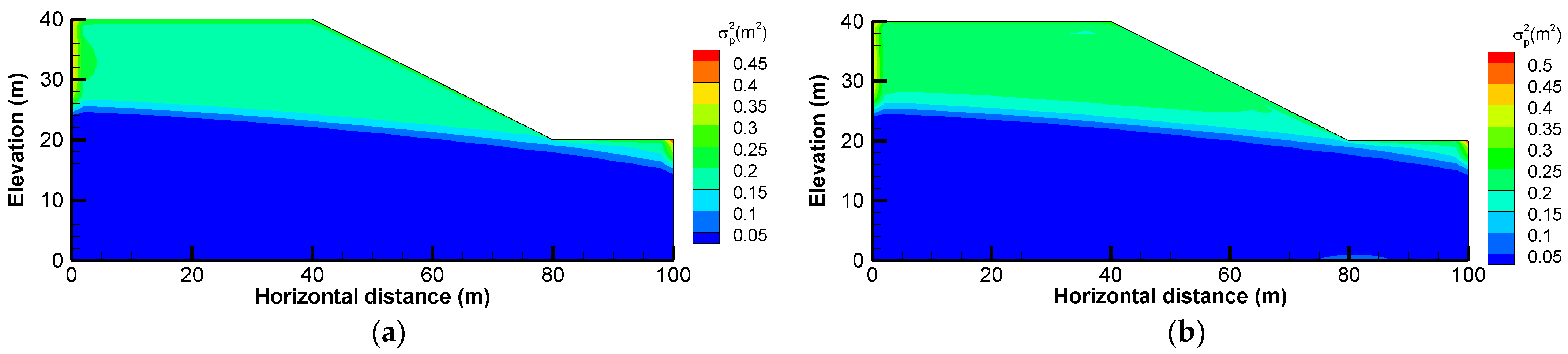
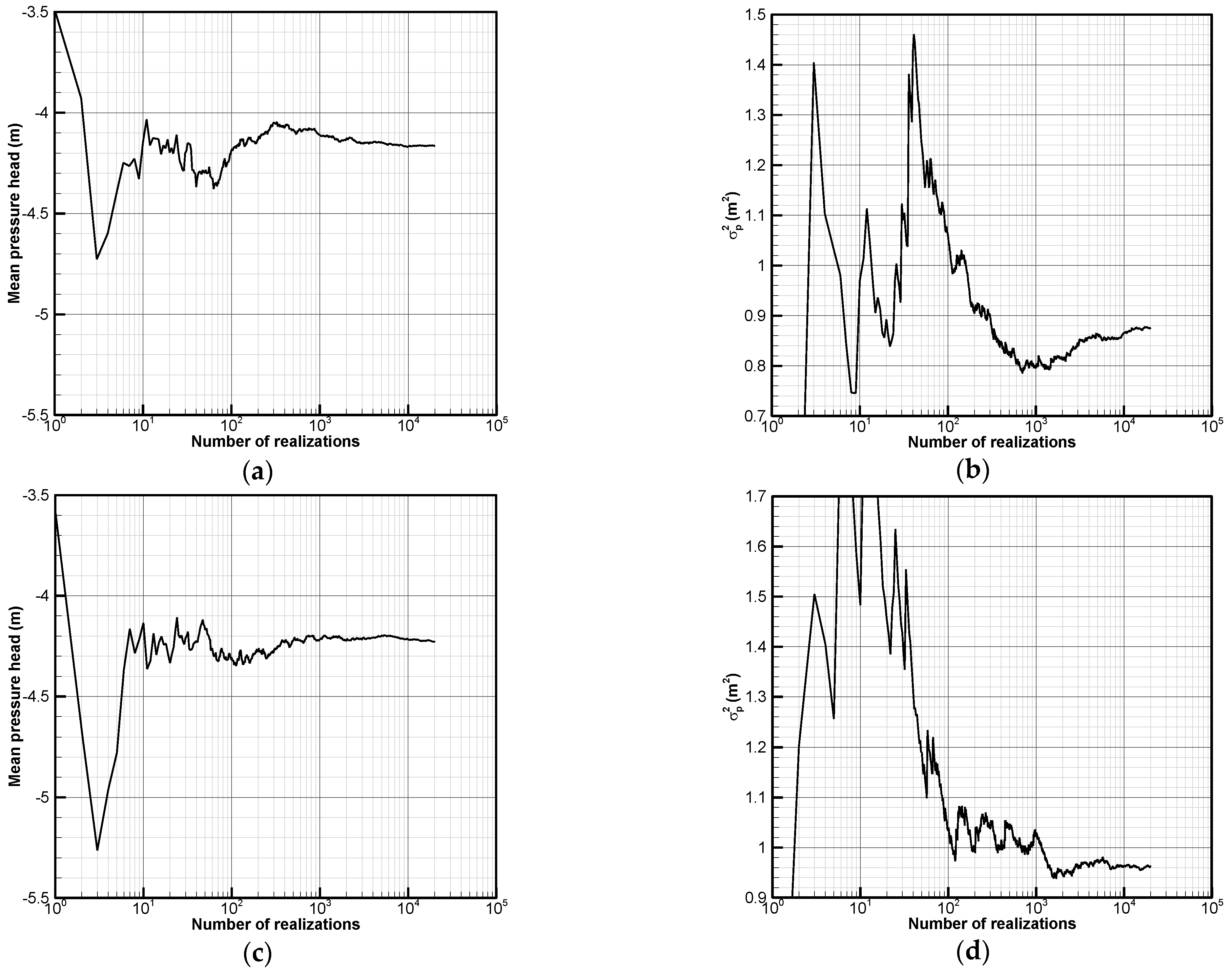
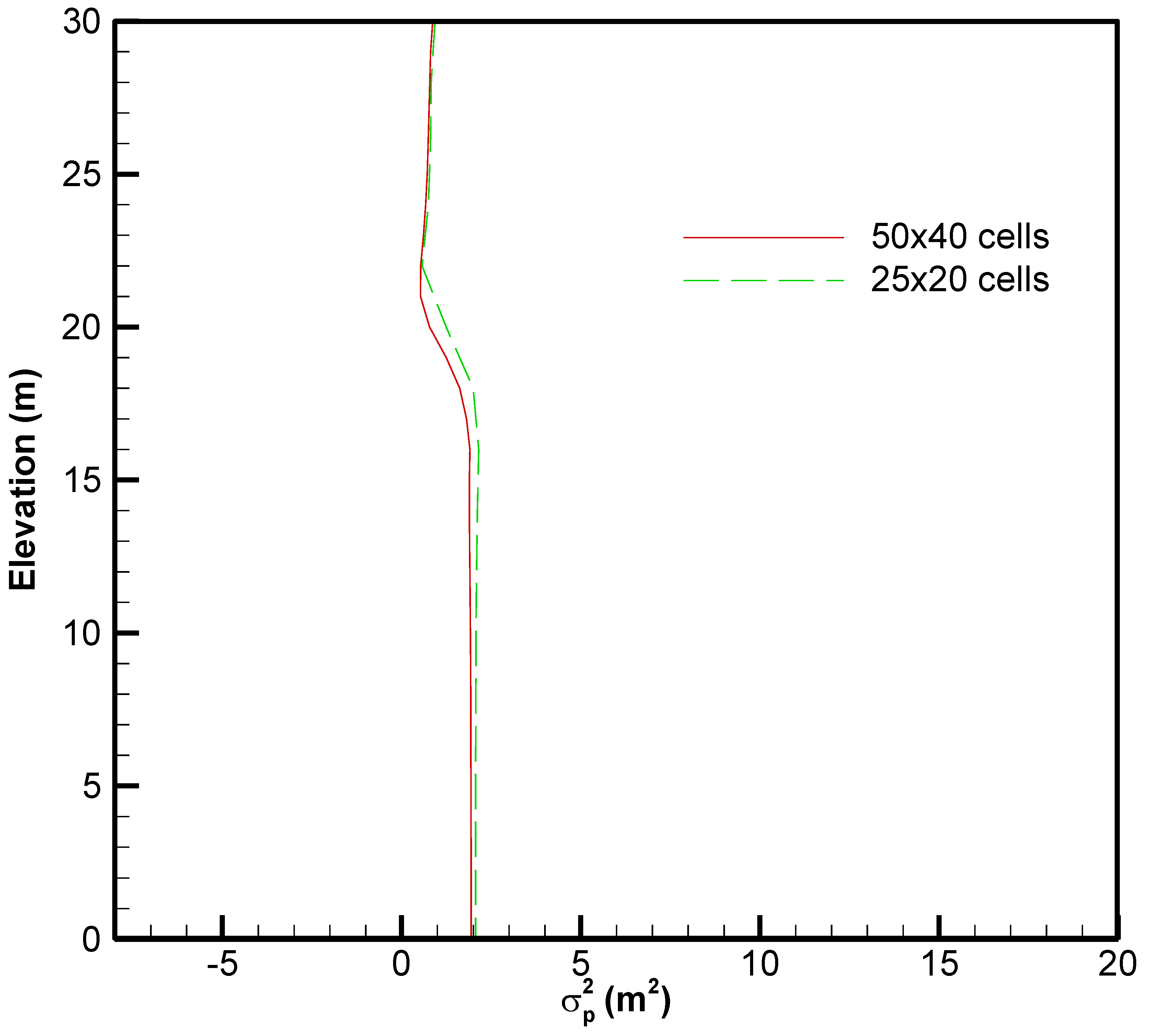
The grid density of the random field, which is crucial in a Monte Carlo simulation, decides the amount of random data appearing in one realization, and hence influences the number of realizations needed to reach convergence. A coarse grid with 25 × 20 cells and a fine grid with 50 × 40 cells of random fields are generated to investigate how the random field grid density affects the number of realizations required for a Monte Carlo simulation. These two sets of grid size have also been applied in the first-order analysis to test the algorithm stability of the first-order analysis approach.
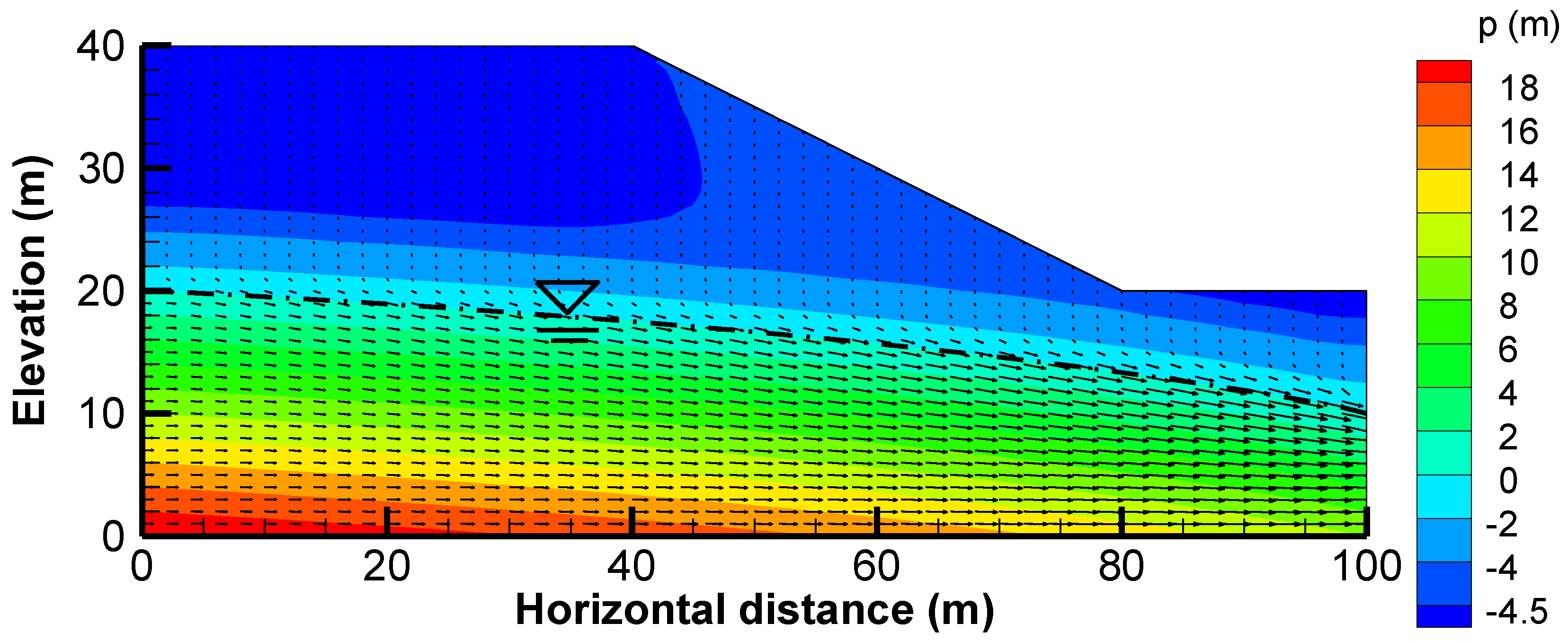
In addition, a single realization of a random field was generated using this fast Fourier transform method with the given mean, variance and correlation length of . This random field was then used to simulate the head response within a heterogeneous slope. The response within the heterogeneous slope was subsequently compared to the response derived from mean parameter, (homogeneous slope), to show the effect of heterogeneity on the pressure head profile.
2.4. Setup of Simulations
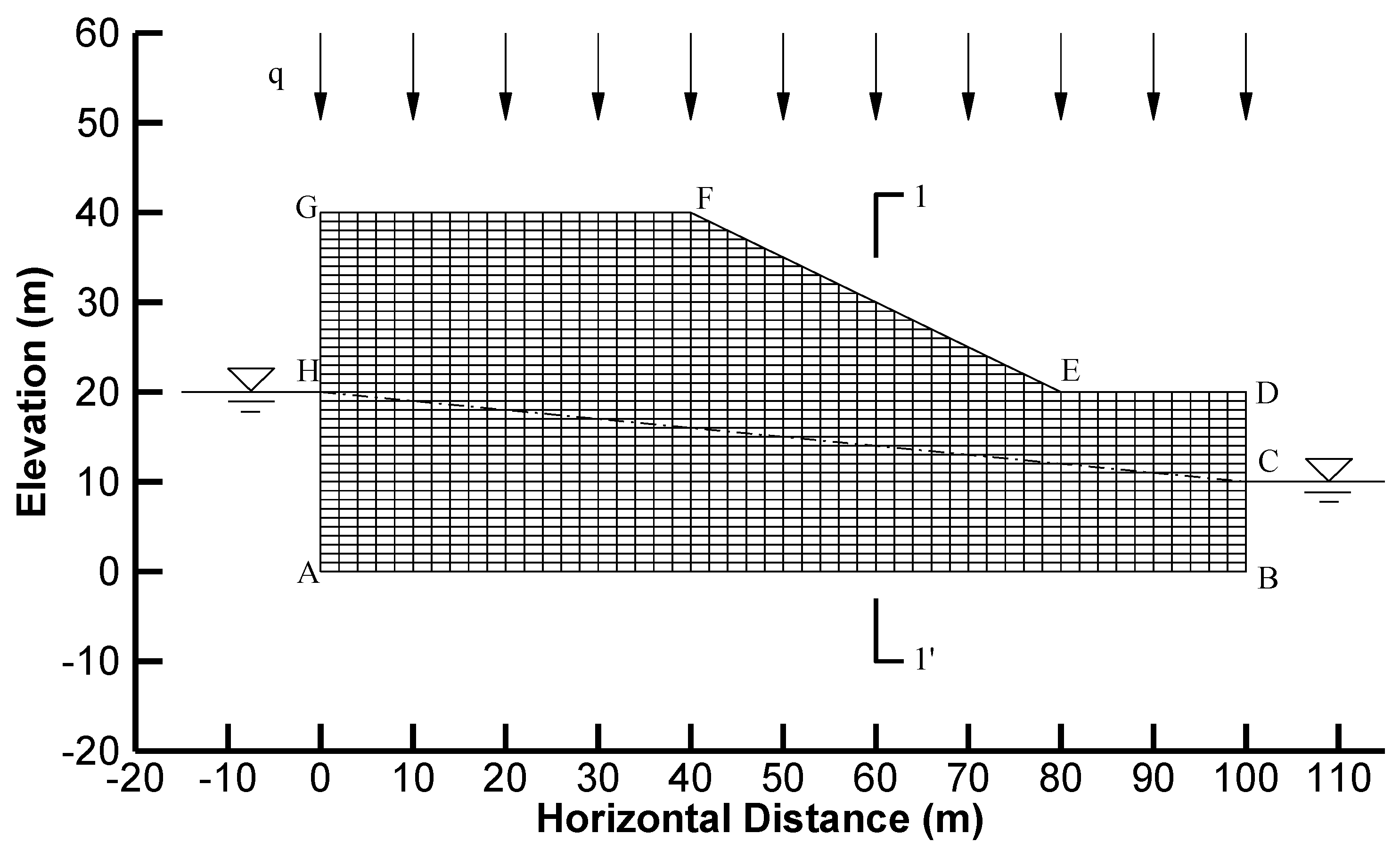
A finite element numerical modeling of the steady seepage flow due to rainfall infiltration was conducted within a 2D hypothetical slope (
Figure 2) and was based on a variably saturated flow and transport in 2D (VSAFT2) platform [
24]. Firstly, the simulation domain (100 m × 40 m) was evenly discretized into 50 × 40 elements and 2091 nodes. Then, the top right corner of the domain was truncated, and the shape of the remaining part, with 1610 elements and 1681 nodes, was the geometry of the slope (
Figure 2). The soil hydraulic parameters used in this study are listed in
Table 1. These parameter values are mainly from the study by [
25]. Based the published literature [
1,
5,
9,
10], the general range of
was suggested to be 0.1~0.7. The correlation length,
of
was suggested to be 0.025–100 times the slope height [
9]. Actually, the slope height, in addition to the grid size and the entire domain size, should be taken into consideration to determine a proper study range for correlation length [
26]. Hence, a range of 0.1–100 m of correlation length,
was proposed in this study (
Table 1). Finally, the ratio between the vertical infiltration flux and
was set as 0.01 [
9].
Figure 2 displays the boundary conditions for this analysis. The boundaries AH and BC remained a constant head, in which
and
. The boundary AB was impermeable, and the boundary GF had a constant vertical flux
. The boundaries FE, ED, GH and DC were defined as seepage faces [
16].
To comprehensively investigate the effect of variability in saturated hydraulic conductivity and to verify the first-order analysis approach proposed, a series of study cases were selected, shown in
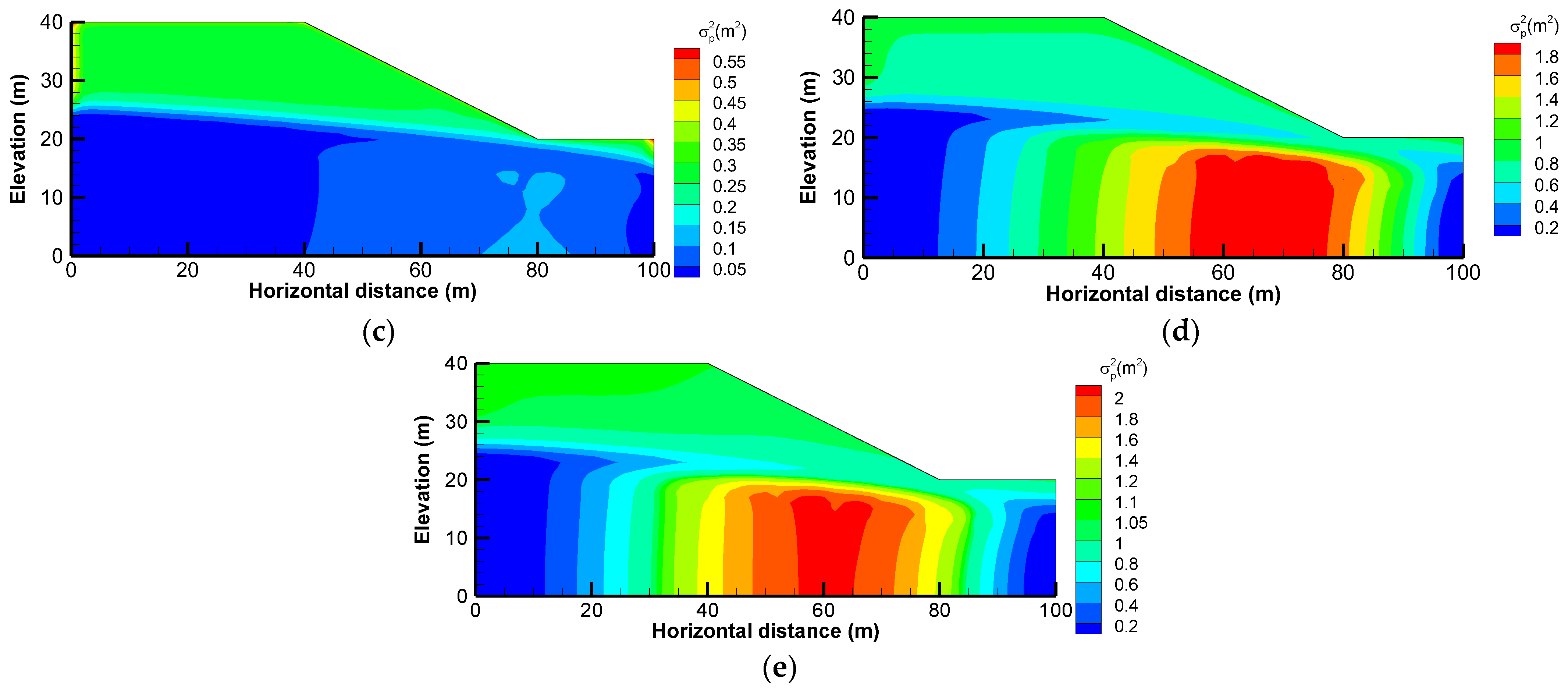
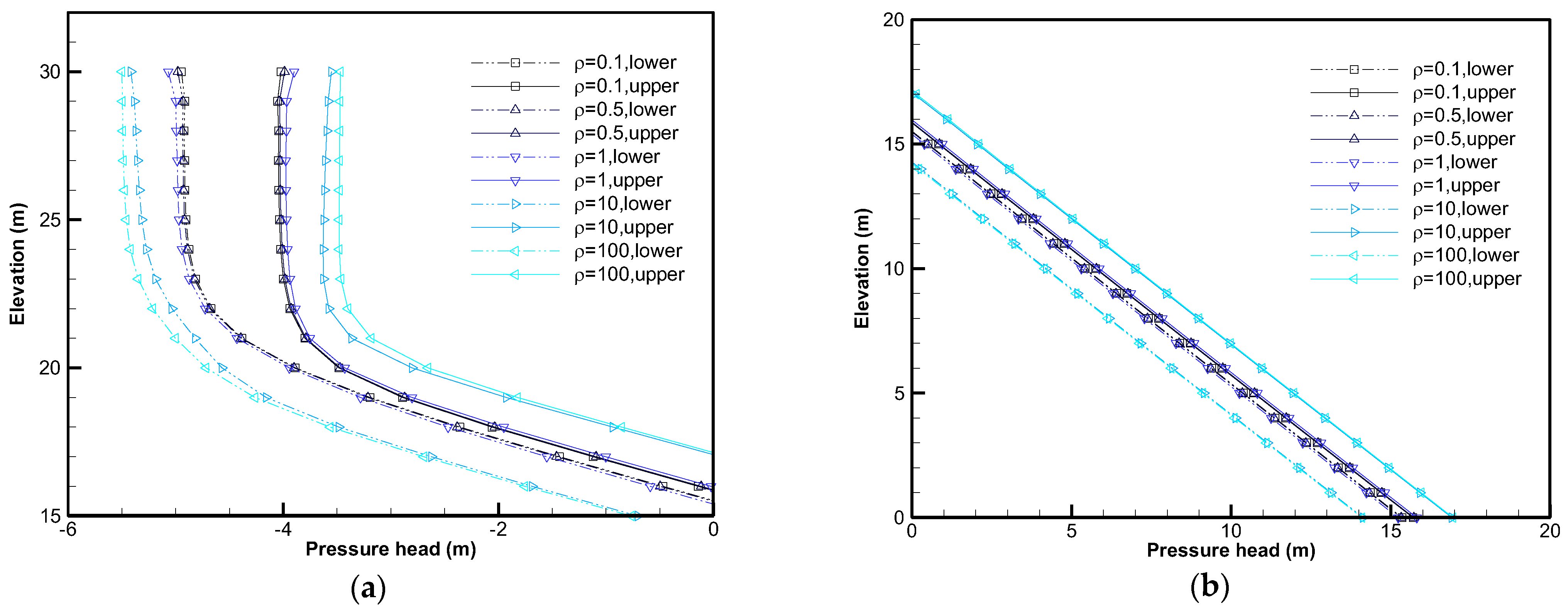
Table 2. From Case 1 to 5, the first-order analysis was carried out to study the variability of the pressure head with respect to the change in the correlation length,
, of
. A single realization of a
random field was generated for each
of
to calculate the head response within a heterogeneous slope. To use the result of the Monte Carlo simulation as a comparison to verify the accuracy of the first-order analysis method, a, Monte Carlo simulation with two different grid sizes (Case 8 and Case 9) were first conducted to find the number of realizations needed to reach convergence for different grid densities. These two cases with different grid sizes were also applied in the first-order analysis (Case 4 and Case 6). Second, both the Monte Carlo simulation (Case 8 and Case 10) and the first-order analysis (Case 4 and Case 7) were conducted at two
of 0.7 and 0.4.
4. Conclusions
This study conducts a probabilistic analysis of slope seepage under rainfall, considering the spatial variability of hydraulic conductivity. Both the commonly used Monte Carlo simulation method and the proposed first-order stochastic moment approach applied in the probabilistic slope seepage analysis are tested and compared with each other.
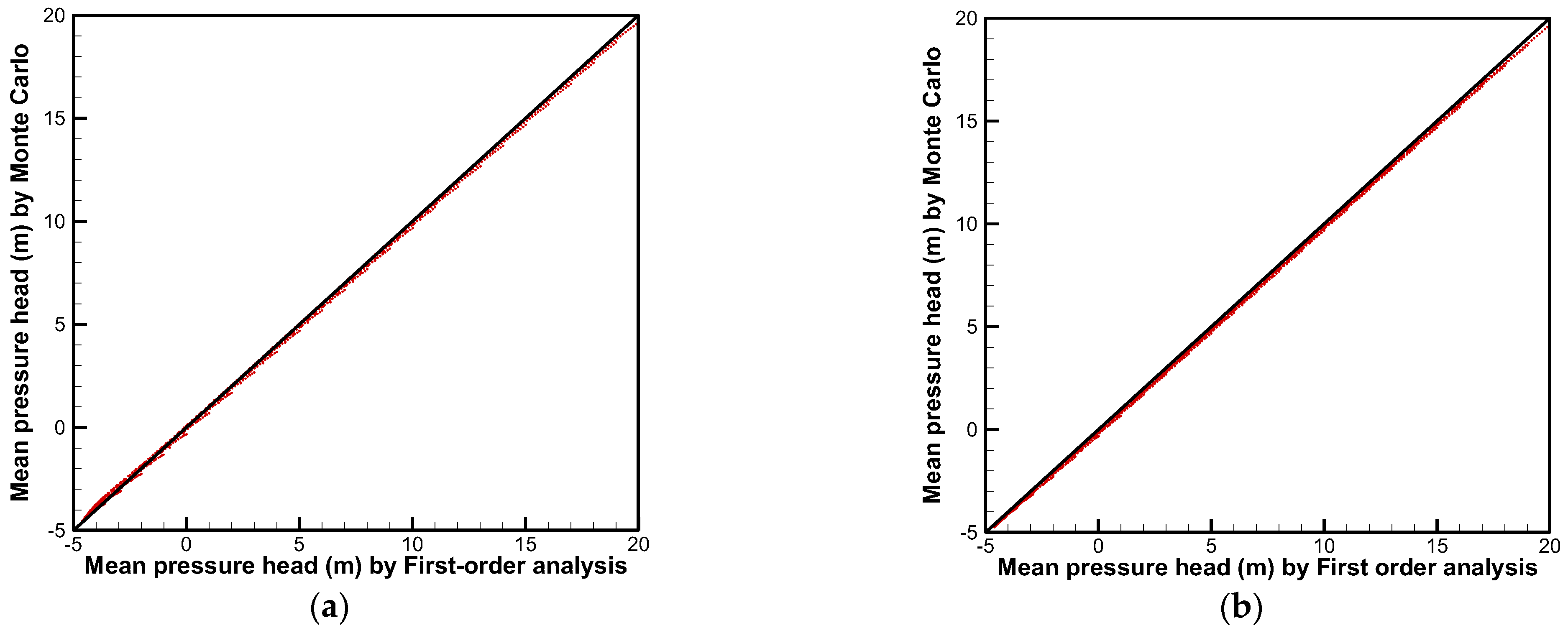
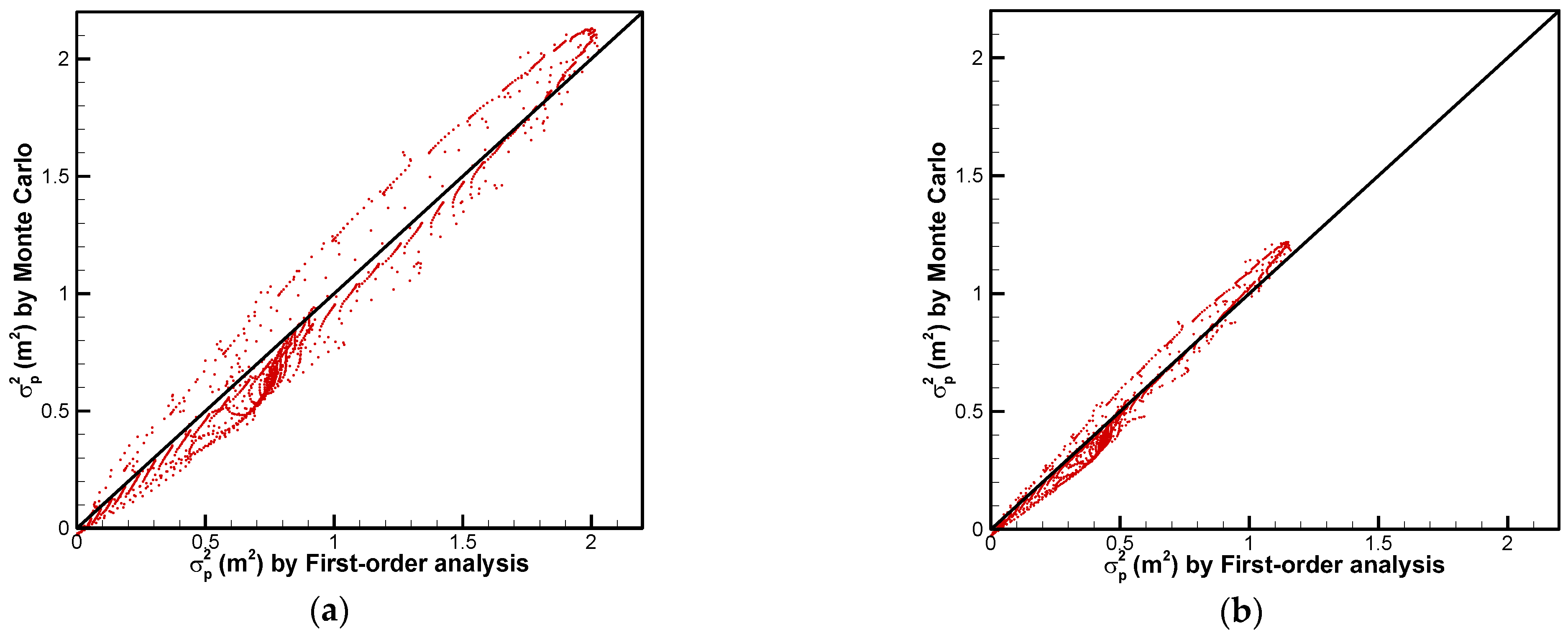
Results indicate that the first-order analysis approach is effective and applicable to the study of slope seepage flow. It is capable of obtaining statistics such as mean and variance at a high enough accuracy. With the aid of the first-order analysis approach, it is found that a larger value of the correlation length of leads to a higher value of the variability in the pressure head and a larger fluctuation of the phreatic surface in the slope. In a heterogeneous slope, the distribution of the pressure head is quite different from that of a homogeneous slope. Therefore, it is not possible to reproduce the hydraulic response of a real heterogeneous slope under steady rainfall infiltration from any equivalent homogeneous model. The upper and the lower bounds obtained from the first-order analysis approach provide an appropriate range to delineate the possible hydraulic response.
The Monte Carlo simulation is found to be time-consuming, requiring at least 10,000 realizations are to reach convergence. In addition, the number of realizations needed is sensitive to the grid density. A coarser grid case needs more realizations for convergence. If the number of realizations is not enough, the result is unreliable. In comparison, the first-order analysis approach reveals a good algorithm stability. The first-order analysis approach is strongly competitive for use in addressing probabilistic slope seepage analysis with fine meshes, especially for the calculation of the sensitivity or the cross-correlation of the pressure head with the hydraulic conductivity, which can be time-consuming and even hard to implement using the Monte Carlo simulation method.
Despite the many advantages of the first-order analysis, it should be emphasized that this approach is based on a first-order approximation. The accuracy of the approximation is generally satisfied when the variance and correlation length of are not too large. At a large variance and correlation length, a higher order approximation or an iterative approach is proposed (Li and Yeh, 1998), and its application in probabilistic slope seepage analysis may deserve further investigation. Regardless, this study highlights the applicability of the proposed first-order stochastic moment analysis method in the slope scenario.