Sand Transport with Cohesive Admixtures…—Laboratory Tests and Modeling
Abstract
:1. Introduction
2. Materials and Methods
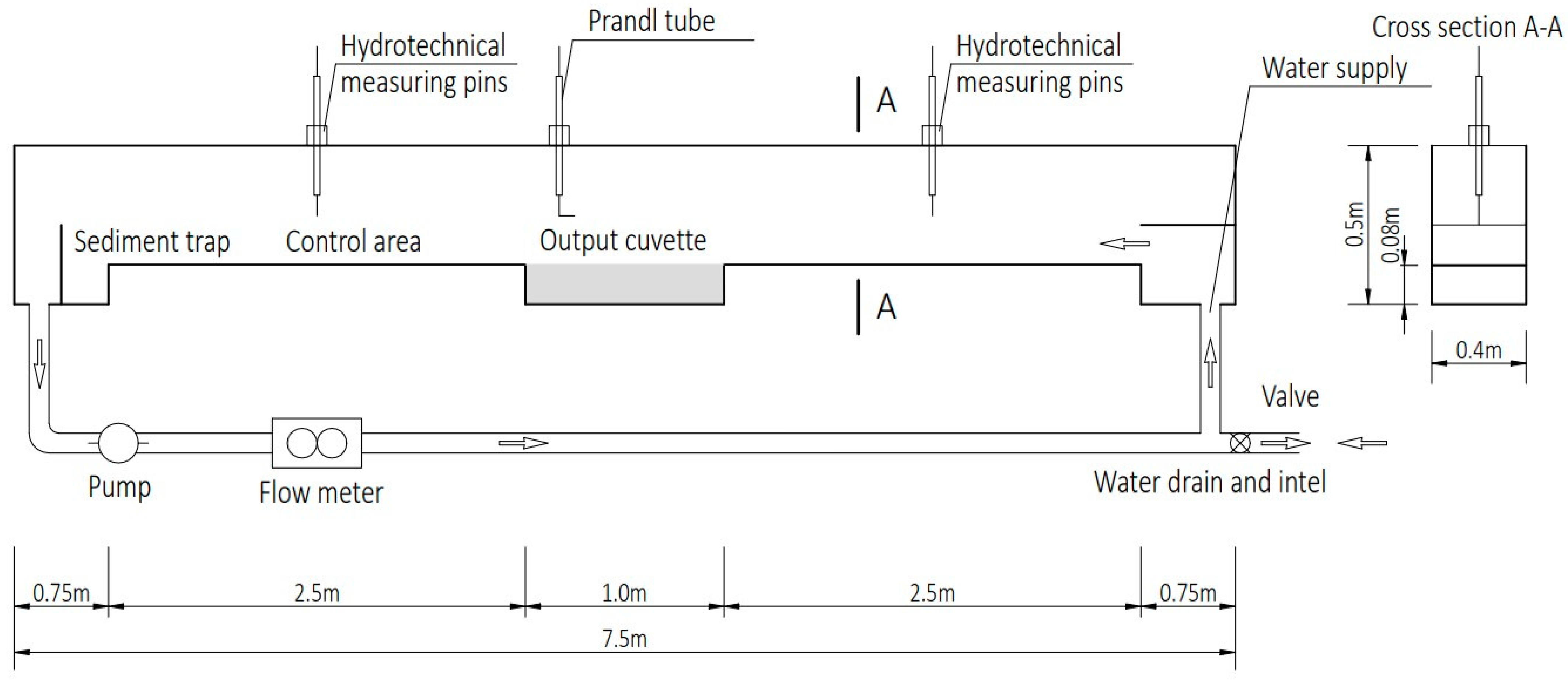
2.1. Experimental Setup Gdańsk 2021 Measurements
- Outflow section 0.73 m long with a bottom inlet—supplying the channel with water;
- The launch section is 2.50 m long;
- Tray—a cavity across the channel width with a length of 1.00 m and a height of 0.08 m;
- Test section with a length of 2.50 m;
- Sediment trap in the form of another tray—a cavity in the channel with a length of 0.73 m and a height of 0.08 m with a bottom drain—drainage of water from the channel.
2.2. The Scope of Measurements
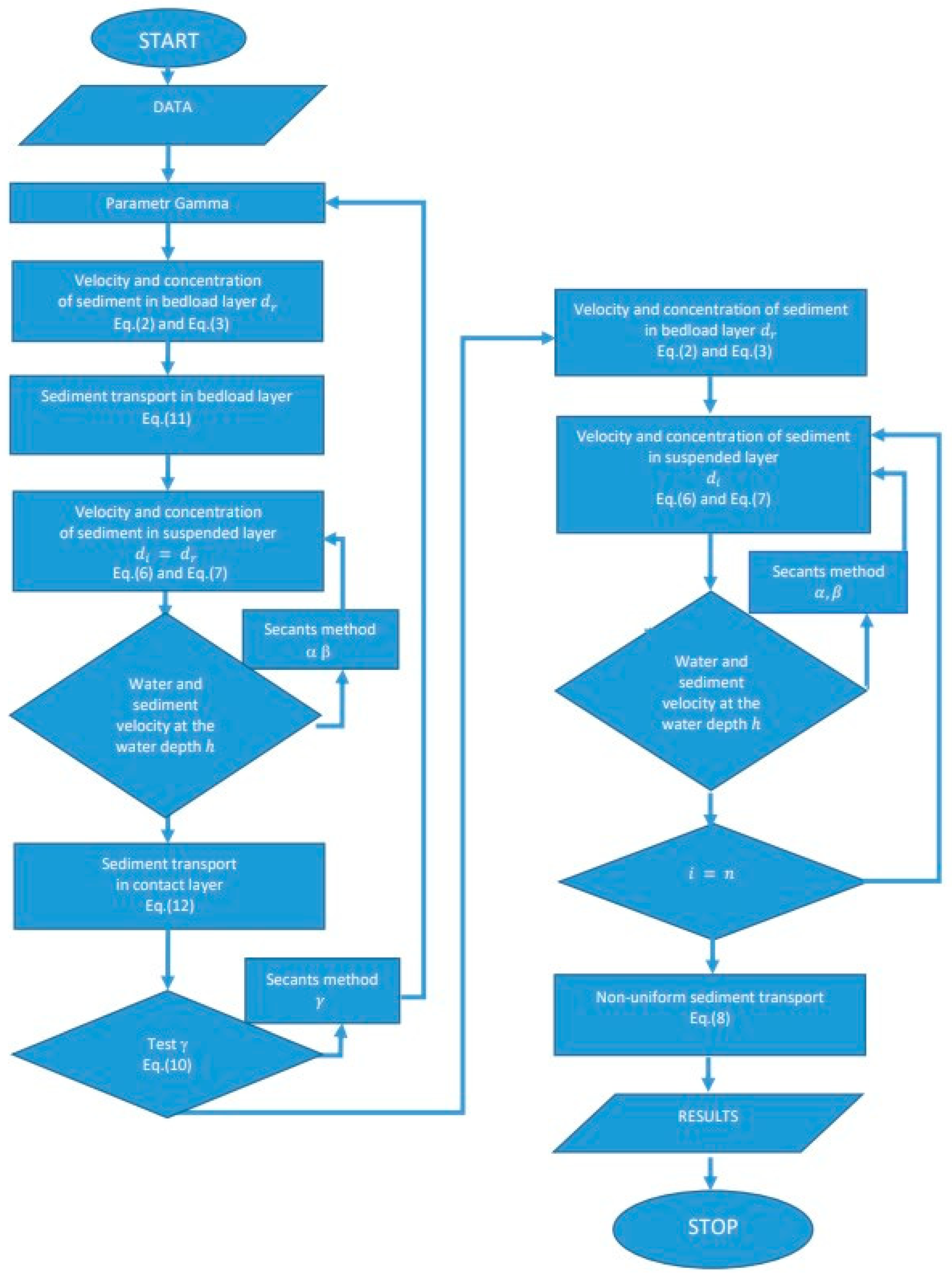
2.3. Theoretical Model
2.3.1. Basic Equations
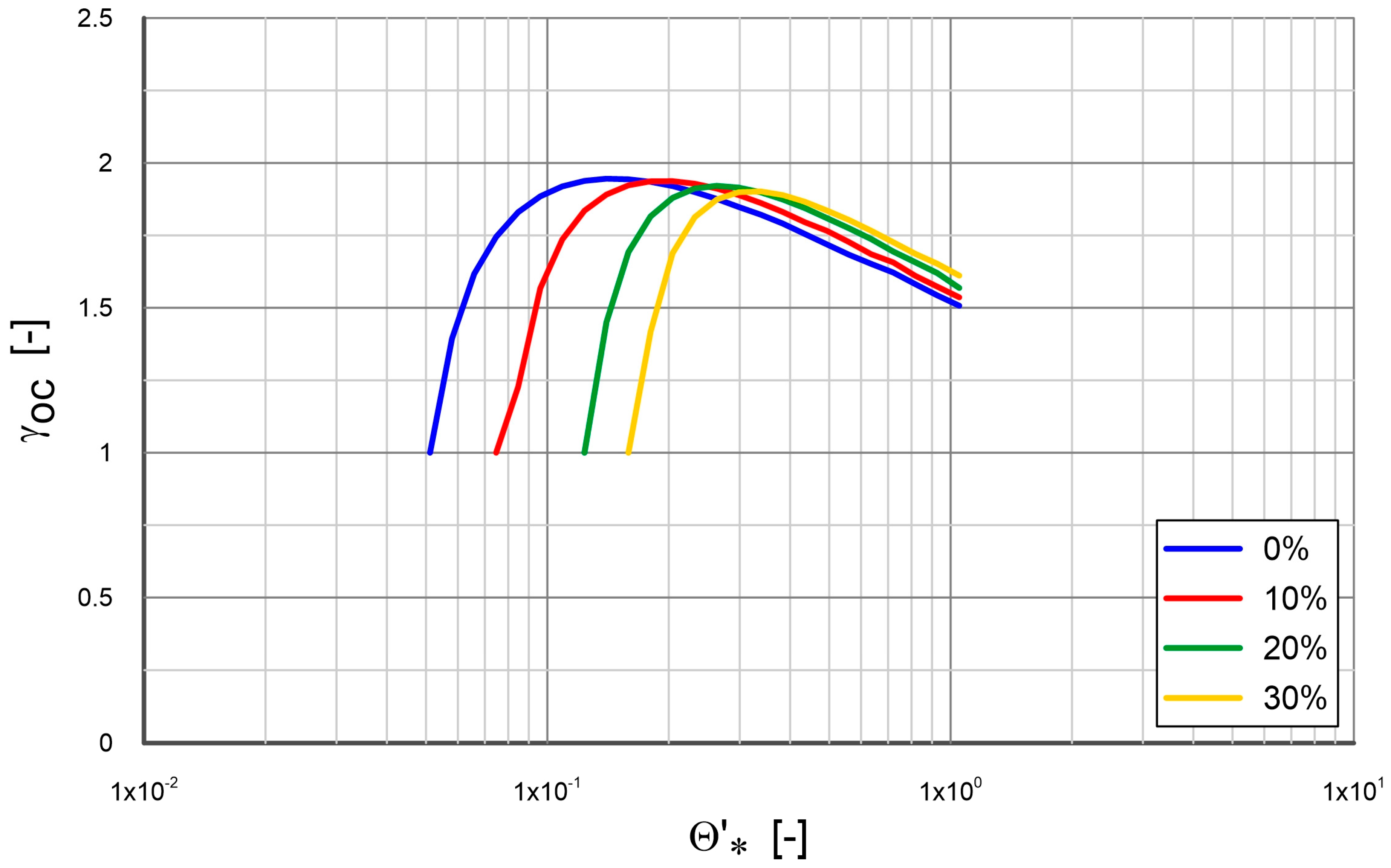
2.3.2. The Influence of Cohesion on Sand Transport
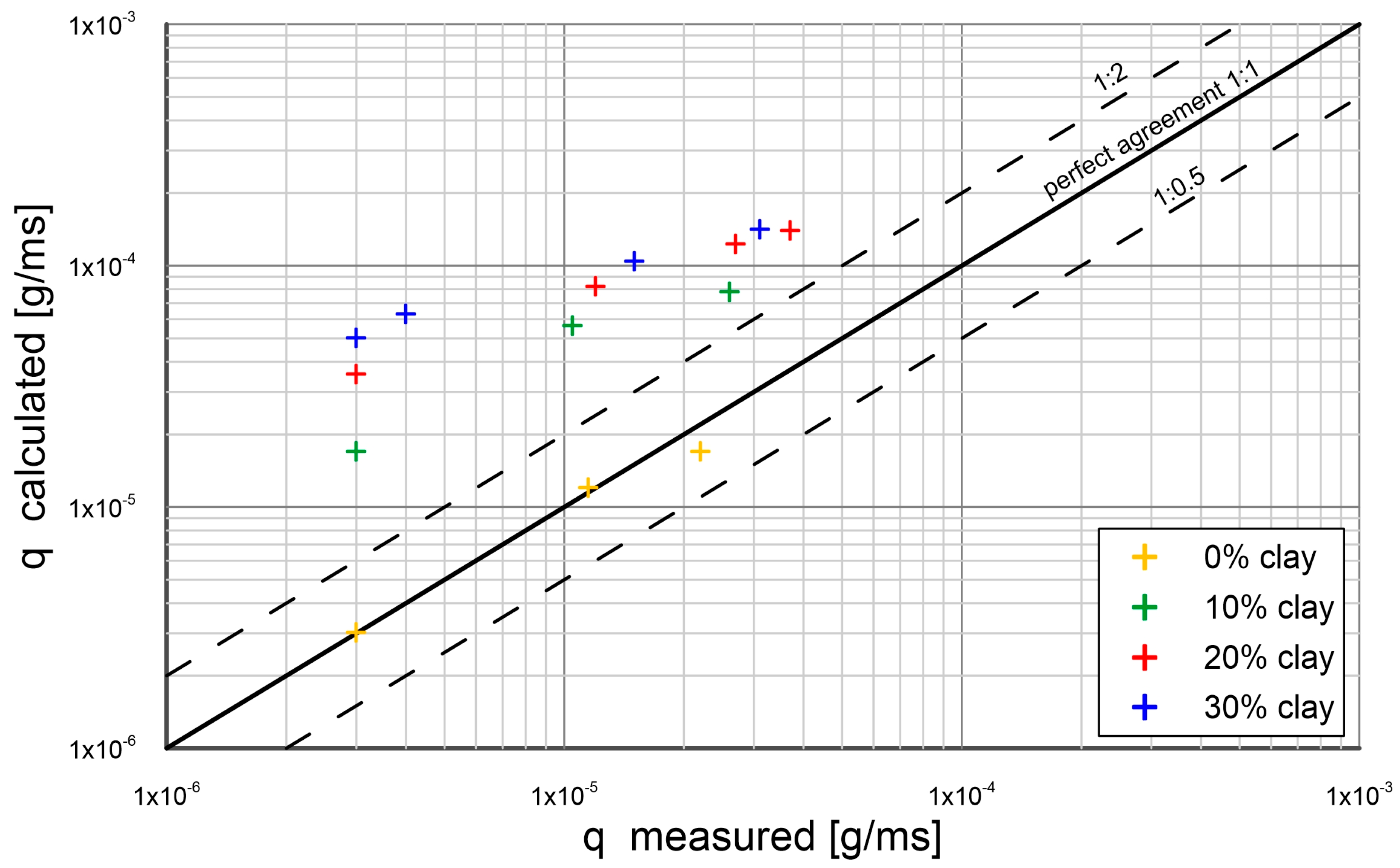
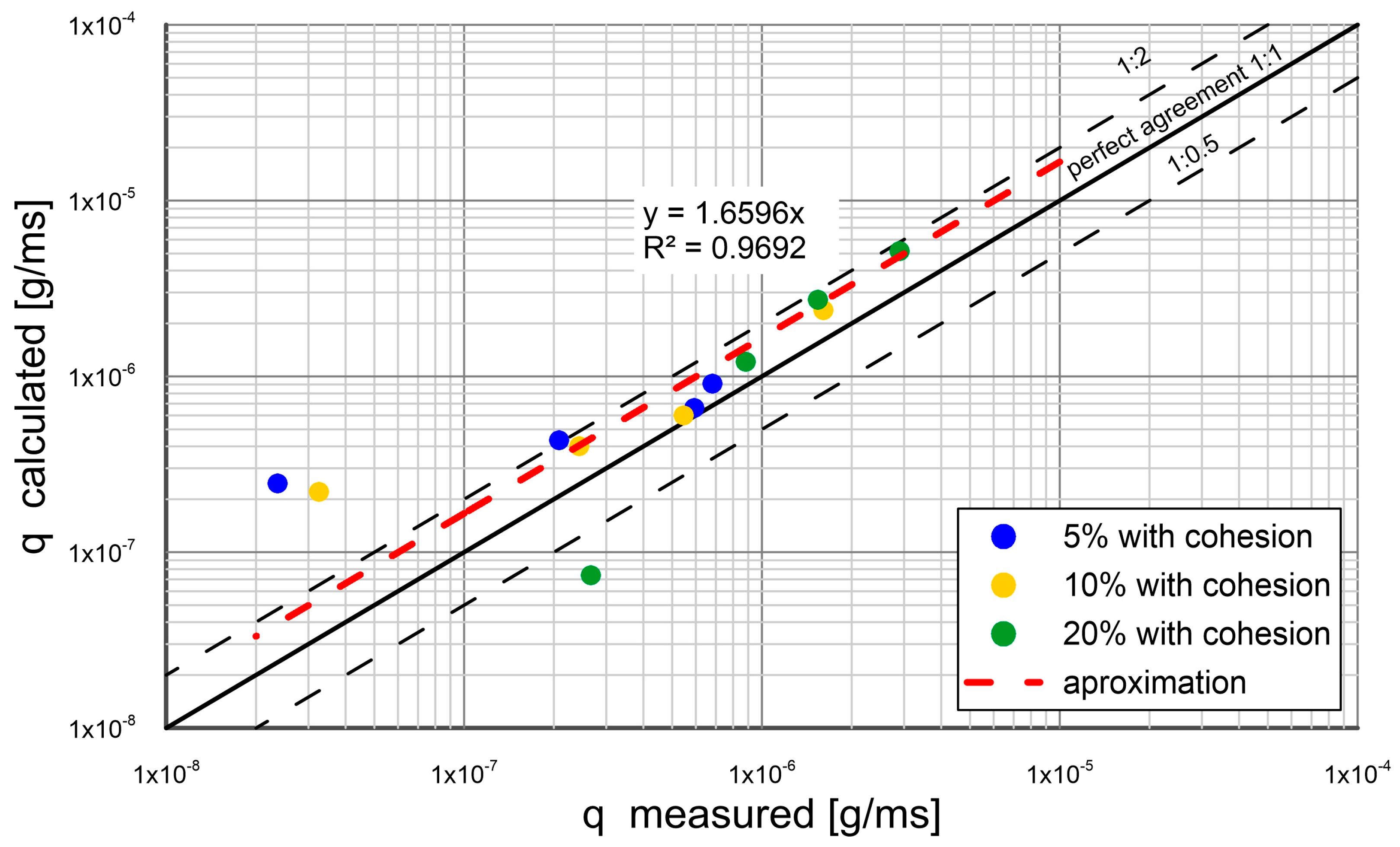
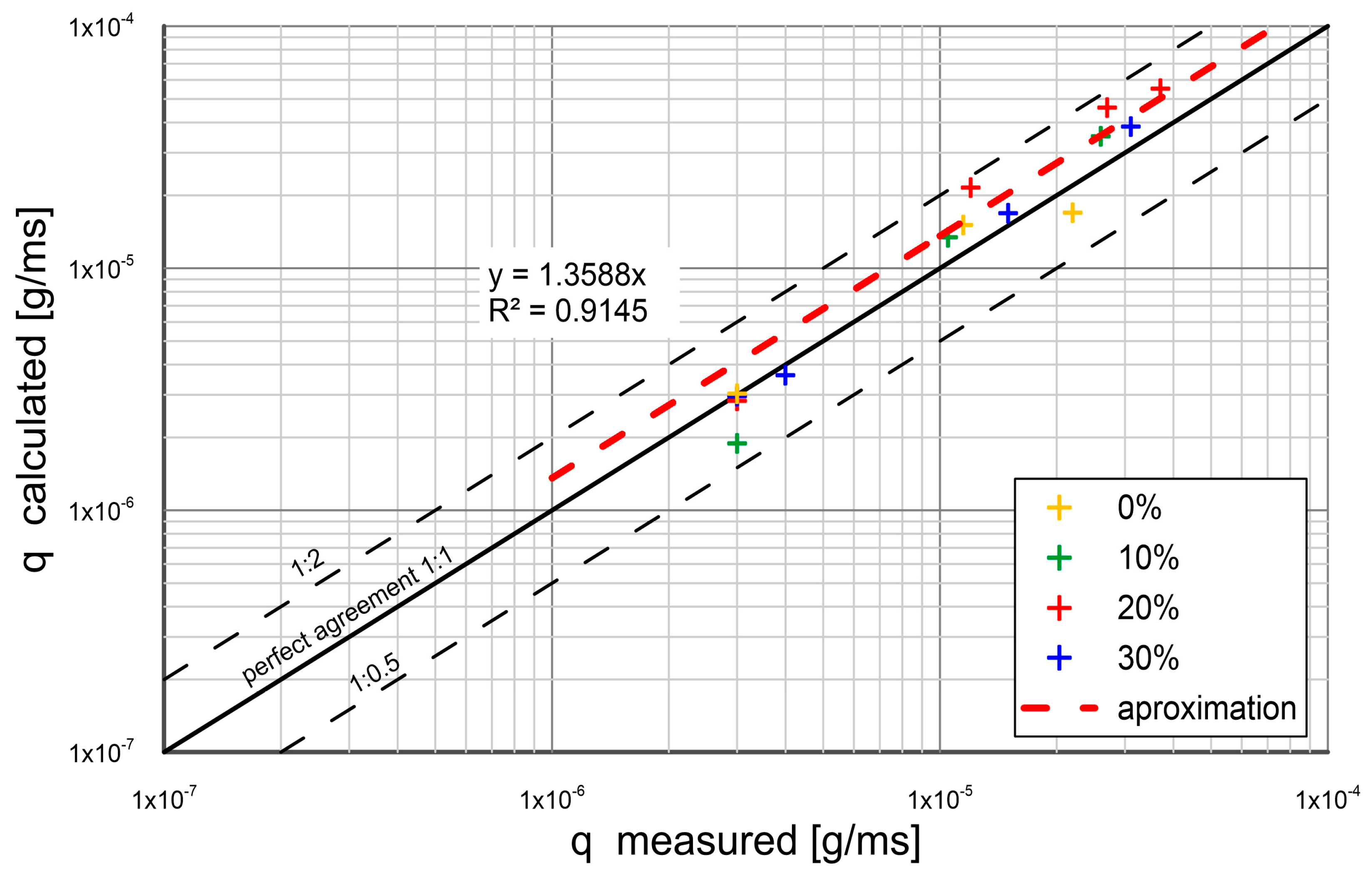
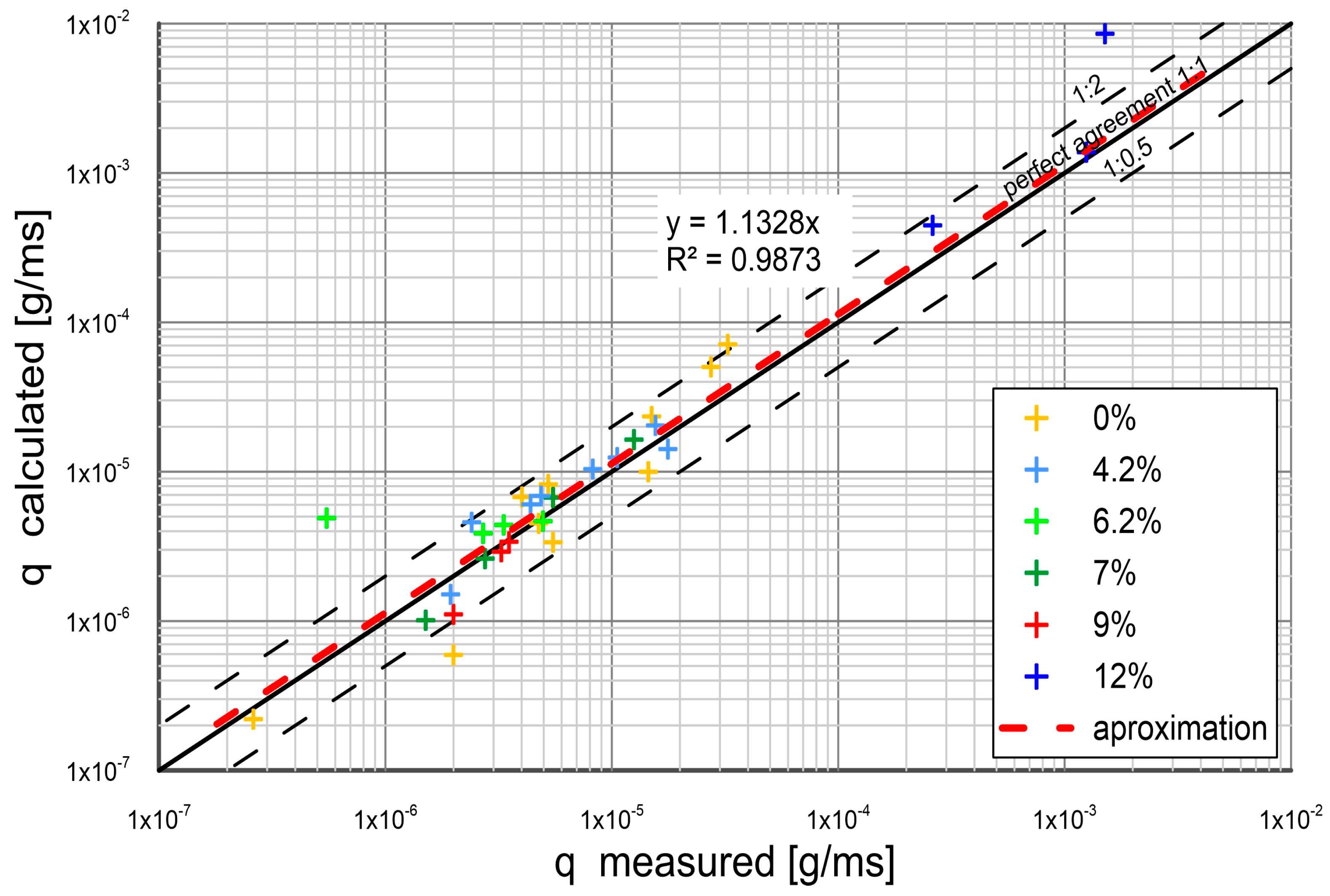
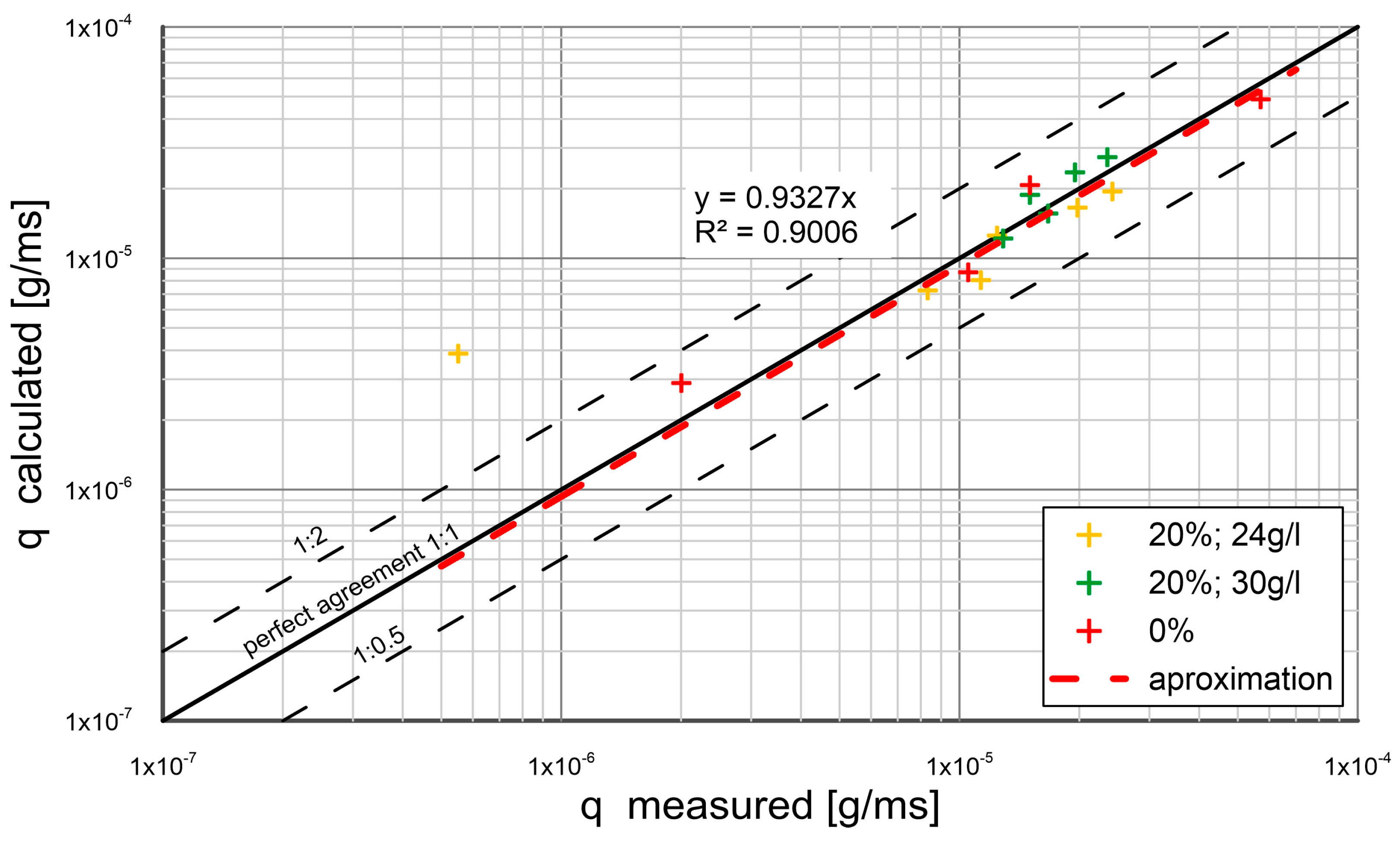
3. Comparison of Calculations with Measurements
4. Conclusions
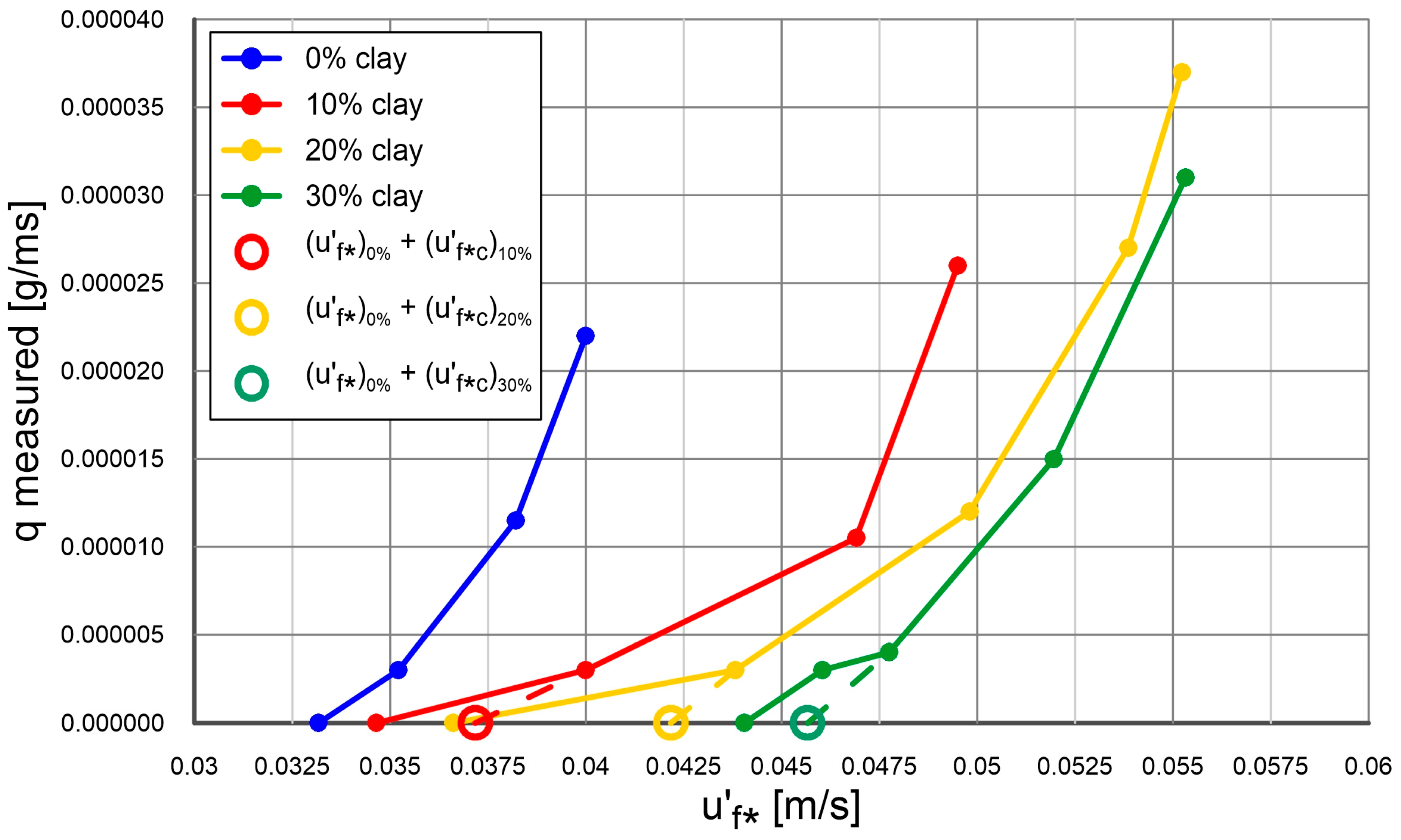
- The results of experimental data were compared with the results of theoretical analysis based on the three-layer model by Kaczmarek et al. [55] for uniform sediments in steady flow, by Kaczmarek et al. [56] for non-uniform sediments in the wave motion and by Zawisza et al. [59] for non-uniform sediments in the steady flow. An extension of these models is proposed here in order to determine the inhibitory effect of cohesion admixtures on the transport of sand fractions. The present model assumes, that the presence of small amount of cohesive fractions in sediment causes an increase in the critical shear stress for the incipient sand motion and consequently a reduction in the magnitude of sand transport. Then, the cohesive fractions are released from the bottom and dispersed in the water. From then on they do not affect the transport of sand fractions.
- In the present model the shear stress at the top of the contact layer is identified as an input data with the value obtained for experiments. This value increases depending on the content of cohesive fractions in sediment. The greater the content of these fractions, the greater the resistance to movement. The difference between the values of shear velocity for sediments with and without cohesive admixtures is also identified here as an input data with the value from experiments. This value is related with the stresses due to cohesion.
- It can be seen from the model results the cohesion reduces the shear stress at the top of the dense layer and, as a result, reduces vertical concentration and velocity profiles of sand fractions inside the dense on contact layers. Thus, transport rate of these fractions is reduced.
- In order to verify the proposed extension of a three layer model the experiments in the laboratory of the Institute of Hydro-Engineering of the Polish Academy of Sciences in Gdańsk were carried out. The experiments were carried out for sand alone and with cohesive admixtures in the form of clay in an amount of 5, 10, 15 and 20% by weight. The amount of sand fractions retained in the trap and along the control area was measured.
- The experimental results were composed with the calculations by the present model. The other results from literature were also used for comparison. An agreement between transport calculations of sand fractions in a substrate with different content of cohesive fractions and the results of measurements was obtained within plus/minus a coefficient of two of the measurements.
- The present model is applicable to non-uniform non-cohesive sediments with small amount of cohesive fractions, while assuming the maximum cohesive fraction content limited by the porosity of the soil. Moreover, at present, the modeling requires experimentally determined shear velocity. Further model development activities will comprise the measurements of stresses due to cohesion and their comparison with the present model estimations based on the shear velocity measurements.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du Boys, M.P. Le Rhone et les Rivieres a Lit affouillable. Ann. Ponts Chausses 1879, 18, 141–195. [Google Scholar]
- Smoluchowski, M. Versucheiner Mathematischen Theorie der Koagulations kinetic Kolloidlösun-gen. Z. Fur Phys. 1917, 92, 129–168. [Google Scholar]
- Camp, T.R.; Stein, P.C. Velocity Gradients and Internal Work in Fluid Motion. J. Boston Soc. Civ. Eng. 1943, 30, 219–237. [Google Scholar]
- Partheniades, E. Erosion and Deposition of Cohesive Soils. J. Hydraul. Div. 1965, 91, 105–139. [Google Scholar] [CrossRef]
- Migniot, C. Etude des propriétés physiques de different sediment strès fins et de leur comportement sous des actions hydrodynamiques. La Houille Blanche 1968, 7, 591–620. [Google Scholar] [CrossRef] [Green Version]
- Ives, K.J. (Ed.) Rate theories. In The Scientific Basic of Flocculation; Sijthoff and Noordoff International Publishers: Alphen aan den Rijn, The Netherlands, 1978; pp. 37–61. [Google Scholar]
- Winterwerp, J.C. A simple model for turbulence induced flocculation of cohesive sediment. J. Hydraul. Res. 1998, 36, 309–326. [Google Scholar] [CrossRef]
- Winterwerp, J.; Kranenburg, C. Fine Sediment Dynamics in the Marine Enviroment; Elsevier: Amsterdam, The Netherlands, 2002; ISBN 0-444-51136-9. [Google Scholar]
- McAnally, W.H.; Mehta, A.J. Aggregation Rate of Fine Sediment. J. Hydraul. Eng. 2000, 126, 883–892. [Google Scholar] [CrossRef]
- Tsai, C.-H.; Iacobellis, S.; Lick, W. Flocculation of Fine-Grained Lake Sediments Due to a Uniform Shear Stress. J. Great Lakes Res. 1987, 13, 135–146. [Google Scholar] [CrossRef]
- Lick, W.; Lick, J. Aggregation and Disaggregation of Fine-Grained Lake Sediments. J. Great Lakes Res. 1988, 14, 514–523. [Google Scholar] [CrossRef]
- Tsai, C.H.; Hwang, S.C. Flocculation of sediment from the Tanshui River estuary. Mar. Freshw. Res. 1995, 46, 383–392. [Google Scholar] [CrossRef]
- Winterwerp, J.C.; Manning, A.J.; Martens, C.; de Mulder, T.; Vanlede, J. A heuristic formula for turbulence-induced flocculation of cohesive sediment. Estuar. Coast. Shelf Sci. 2006, 68, 195–207. [Google Scholar] [CrossRef]
- Hawley, N. Settling velocity distribution of natural aggregates. J. Geophys. Res. Atmos. 1982, 87, 9489–9498. [Google Scholar] [CrossRef]
- Meakin, P. Fractal Aggregation. Adv. Colloid Interface 1988, 28, 249–331. [Google Scholar] [CrossRef] [PubMed]
- Dyer, K.; Manning, A. Observation of the size, settling velocity and effective density of flocs, and their fractal dimensions. J. Sea Res. 1999, 41, 87–95. [Google Scholar] [CrossRef]
- Kranenburg, C. The fractal structure of cohesive sediment aggregates. Estuar. Coast. Shelf Sci. 1994, 39, 451–460. [Google Scholar] [CrossRef]
- Merckelbach, L.M.; Kranenburg, C. Determining effective stress and permeability equations for soft mud from simple laboratory experiments. Géotechnique 2004, 54, 581–591. [Google Scholar] [CrossRef]
- Khelifa, A.; Hill, P.S. Models for effective density and settling velocity of flocs. J. Hydraul. Res. 2006, 44, 390–401. [Google Scholar] [CrossRef]
- Boyer, K.K.; Hult, G.T.M. Extending the supply chain: Integrating operations and marketing in the online grocery industry. J. Oper. Manag. 2005, 23, 642–661. [Google Scholar] [CrossRef]
- Winterwerp, J.C.; van Kesteren, W.G.M. Introduction to the Physics of Cohesive Sediment in the Marine Environment. In Developments in Sedimentology; Series no. 56; Elsevier: Amsterdam, The Netherlands, 2004; p. xiii + 466. ISBN 0-444-515534. [Google Scholar]
- Hjulstrom, F. Studies of Morphological Activity of Rivers as Illustrated by the River Fyris. Bull. Geol. Inst. Univ. Upps. 1935, 25, 221–527. [Google Scholar]
- Shields, A. Application of Similarity Principles and Turbulence Research to Bed-Load Movement; California Institute of Technology: Pasadena, CA, USA, 1936. [Google Scholar]
- Wiberg, P.L.; Smith, J.D. Calculations of the critical shear stress for motion of uniform and heterogeneous sediments. Water Resour. Res. 1987, 23, 1471–1480. [Google Scholar] [CrossRef]
- Dey, I. Grounding Grounded Theory: Guidelines for Qualitative Inquiry; Emerald Group Publishing Limited: Bradford, UK, 1999; p. 300. [Google Scholar]
- El Ganaoui, O.; Schaaff, E.; Boyer, P.; Amielh, M.; Anselmet, F.; Grenz, C. The deposition and erosion of cohesive sediments determined by a multi-class model. Estuar. Coast. Shelf Sci. 2004, 60, 457–475. [Google Scholar] [CrossRef]
- Mehta, A.J. Resuspension potential of cohesive sediment bed: Estuarine comparisons. In Proceedings of the Sixth Biennal International Estuarine Research Conference; Elsevier: New York, NY, USA, 1982; pp. 591–601. [Google Scholar]
- Mehta, A.J. Review notes on cohesive sediment erosion. In Proceedings of the a Specialty Conference on Quantitative Approaches to Coastal Sediment Processes; ASCE: New York, NY, USA, 1991; pp. 40–53. [Google Scholar]
- Parchure, T.M.; Mehta, A.J. Erosion of Soft Cohesive Sediment Deposits. J. Hydraul. Eng. 1985, 111, 1308–1326. [Google Scholar] [CrossRef]
- Sundborg, A. The River Klaralven. A Study of Flu- vial Processes. Geogr. Ann. 1956, 38, 238–316. [Google Scholar]
- Postma, H. Sediment Transport and Sedimentation in the Estuarine Environment; Estuaries, G.H., Ed.; American Association for Advancement of Science: Washington, DC, USA, 1967; pp. 158–179. [Google Scholar]
- Mitchener, H.; Torfs, H. Erosion of mud/sand mixtures. Coast. Eng. 1996, 29, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Raudkivi, A.J.; Witte, H.H. Development of Bed Features. J. Hydraul. Eng. 1990, 116, 1063–1079. [Google Scholar] [CrossRef]
- Dade, W.; Nowell, A.; Jumars, P. Predicting erosion resistance of muds. Mar. Geol. 1992, 105, 285–297. [Google Scholar] [CrossRef]
- Mehta, A.J. Nearshore and Estuarine Cohesive Sediment transport. In Coastal and Estuarine Studies; American Geophysical Union: Washington, DC, USA, 1993; Volume 42, 592p. [Google Scholar]
- Mehta, A.J.; Lee, S.-C. Problems in Linking the Threshold Condition for the Transport of Cohesionless and Cohesive Sediment Grain; Coastal and Oceanographic Engineering Department University of Florida Gainesville: Gainesville, FL, USA, 1994; pp. 170–177. [Google Scholar]
- Miller, M.C.; Mccave, I.N.; Komar, P.D. Threshold of sediment motion under unidirectional currents. Sedimentology 1977, 24, 507–527. [Google Scholar] [CrossRef]
- Sleath, J.F.A. Sea Bed Mechanics; Wiley Interscience: Chichester, UK, 1984; ISBN 047189091X/9780471890911. [Google Scholar]
- Dyer, K.R. Coastal and Estuarine Sediment Dynamics; Wiley Interscience: Chichester, UK, 1986; 342p. [Google Scholar]
- Voulgaris, G.; Wallbridge, S.; Tomlinson, B.N.; Collins, M.B. Laboratory investigations into wave period effects on sand bed erodibility under the combined action of waves and currents. Coastal Eng. 1995, 26, 117–134. [Google Scholar] [CrossRef]
- Le Hir, P.; Cann, P.; Waeles, B.; Jestin, H.; Bassoullet, P. Erodibility of natural sediments: Experiments on sand/mud mixtures from laboratory and field erosion tests. In Sediment and Ecohydraulics; Kusuda, T., Yamanishi, H., Spearman, J., Gailani, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 9, pp. 137–153. [Google Scholar] [CrossRef]
- Sanford, L.P. Modelling a dynamically varying mixed sediment bed with erosion, deposition, bioturbation, consolidation, and armoring. Comput. Geosci. 2008, 34, 1263–1283. [Google Scholar] [CrossRef]
- Waeles, B.; Le Hir, P.; Lesuer, P. A 3D morphodynamic process-based modeling of a mixed sand/mud coastal environment: The Seine estuary, France. In Sediment and Ecohydraulics. Proceedings in Marine Science; Kusuda, T., Yamanishi, H., Spearman, J., Gailani, J.Z., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 9, pp. 477–498. [Google Scholar]
- Mengual, B.; Le Hir, P.; Cayocca, F.; Garlan, T. Modelling Fine Sediment Dynamics: Towards a Common Erosion Law for Fine Sand, Mud and Mixtures. Water 2017, 9, 564. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Hernandez, E. The Influence of Cohesion on Sediment Movement in Channels of Circular Cross Section. Ph.D. Thesis, University of Newcastle upon Tyne, Newcastle upon Tyne, UK, 1990. [Google Scholar]
- Pluim-Van der Velden, E.T.; Bijker, E.W. Locals scour near submarine pipelines on a cohesive bottom. In Proceedings of the BOSS 92, 6th International Conference Behaviour of Offshore Structures, London, UK, 7–10 July 1992; BPP Tech Services Ltd.: London, UK. [Google Scholar]
- Panagiotopoulos, I.; Voulgaris, G.; Collins, M. The influence of clay on the threshold of movement of fine sandy beds. Coast. Eng. 1997, 32, 19–43. [Google Scholar] [CrossRef]
- De Sutter, R.; Huygens, M.; Verhoeven, R. Flume experiments of sediment transport in unsteady flow. In Transactions on Engineering Sciences; WIT: Cambridge, MA, USA, 1998; Volume 18, ISSN 1743-3533. [Google Scholar]
- Flemming, B.W.; Delafontaine, M.T. Mass physical properties of muddy intertidal sediments: Some applications, misapplications and non-applications. Cont. Shelf Res. 2000, 20, 1179–1197. [Google Scholar] [CrossRef]
- Riethmuller, R.; Heineke, M.; Kuhl, H.; Keuker-Rudiger, R. Chlorophyll a concentration as an index of sediment surface stabilization of microphyto—benthos. Cont. Shelf Res. 2000, 20, 1351–1372. [Google Scholar] [CrossRef]
- Van Ledden, M.; van Kesteren, W.; Winterwerp, J. A conceptual framework for the erosion behaviour of sand–mud mixtures. Cont. Shelf Res. 2004, 24, 1–11. [Google Scholar] [CrossRef]
- Banasiak, R.; Verhoeven, R. Transport of Sand and Partly Cohesive Sediments in a Circular Pipe Run Partially Full. J. Hydraul. Eng. 2008, 134, 216–224. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Sawczyński, S.; Biegowski, J. Hydrodynamic Equilibrium for Sediment Transport and Bed Response to Wave Motion. Acta Geophys. 2015, 63, 486–513. [Google Scholar] [CrossRef] [Green Version]
- Kaczmarek, L.M.; Sawczyński, S.; Biegowski, J. An Equilibrium Transport Formula for Modeling Sedimentation of Dredged Channels. Coast. Eng. J. 2017, 59, 1750015-1–1750015-35. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Biegowski, J.; Sobczak, Ł. Modeling of Sediment Transport in Steady Flow over Mobile Granular Bed. J. Hydraul. Eng. 2019, 145, 04019009. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Biegowski, J.; Sobczak, Ł. Modeling of Sediment Transport with a Mobile Mixed-Sand Bed in Wave Motion. J. Hydraul. Eng. 2022, 148, 04021054. [Google Scholar] [CrossRef]
- Radosz, I.; Zawisza, J.; Biegowski, J.; Paprota, M.; Majewski, D.; Kaczmarek, L.M. An Experimental Study on Progressive and Reverse Fluxes of Sediments with Fine Fractions in Wave Motion. Water 2022, 14, 2397. [Google Scholar] [CrossRef]
- Radosz, I.; Zawisza, J.; Biegowski, J.; Paprota, M.; Majewski, D.; Kaczmarek, L.M. An Experimental Study on Progressive and Reverse Fluxes of Sediments with Fine Fractions in the Wave Motion over Sloped Bed. Water 2023, 15, 125. [Google Scholar] [CrossRef]
- Zawisza, J.; Radosz, I.; Biegowski, J.; Kaczmarek, L.M. Transport of sediment mixtures in steady flow with an extra contribution of their finest fractions. Laboratory tests and modelling. Water, 2023; in press. [Google Scholar]
- Longo, S. Two-Phase Flow Modeling of Sediment Motion in Sheet-Flows above Plane Beds. J. Hydraul. Eng. 2005, 131, 366–379. [Google Scholar] [CrossRef] [Green Version]
- Deigaard, R. A note on the three-dimensional shear stress distribution in a surf zone. Coast. Eng. 1993, 20, 157–171. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research, Delft, The Netherlands, 7 June 1948; pp. 39–64. [Google Scholar]
- Torfs, H. Erosion of Mud/Sand Mixtures. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, October 1995. [Google Scholar]




| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Water depth | H | 0.05 | m |
| Test duration | T | 900–3600 | s |
| Representative diameter of bottom sediment grains | 0.23 | mm | |
| Diameter clay addition | 0.19 | mm | |
| Sediment density | 2.65 | g/cm3 | |
| Liquid density | 1.00 | g/cm3 | |
| Porosity of sediment | 0.4 | - |
| Type of Sediment | |
|---|---|
| Input sand | 0.23/0.22/0.14 |
| Trap deposits | - |
| TR_10_13 | 0.25/0.22/0.13 |
| TR_15_11 | 0.43/0.24/0.13 |
| TR_15_12 | 0.41/0.23/0.12 |
| TR_15_13 | 0.40/0.23/0.12 |
| TR_15_14 | 0.42/0.23/0.13 |
| TR_20_12 | 0.44/0.24/0.13 |
| TR_20_13 | 0.48/0.25/0.13 |
| TR_20_15 | 0.41/0.23/0.12 |
| Chemical Compound | Content |
|---|---|
| - SiO2 | 55.00–62.14% |
| - Al2O3 | 15.70–17.70% |
| - TiO2 | 0.70–0.90% |
| - Fe2O3 | 6.09–7.90% |
| - MnO | 0.04–0.17% |
| - MgO | 2.20–3.20% |
| - CaO | 0.33–1.81% |
| - Na2O | 0.06–0.26% |
| - K2O | 2.90–3.50% |
| - P2O5 | 0.05–0.18% |
| - roasting losses | 7.04–13.40% |
| Mineral | Content |
|---|---|
| - quartz | 17–25% |
| - kaolinite | 3–10% |
| - illit | 3–10% |
| - hematite | 3–5% |
| - plagioklaz | <3% |
| - potassium feldspar | <3% |
| - goethyt | <2% |
| - anatase | <5% |
| - mixed packet minerals (vermiculite/chlorite, smectite/illite) | 32–53% |
| - amorphous phase | 15% |
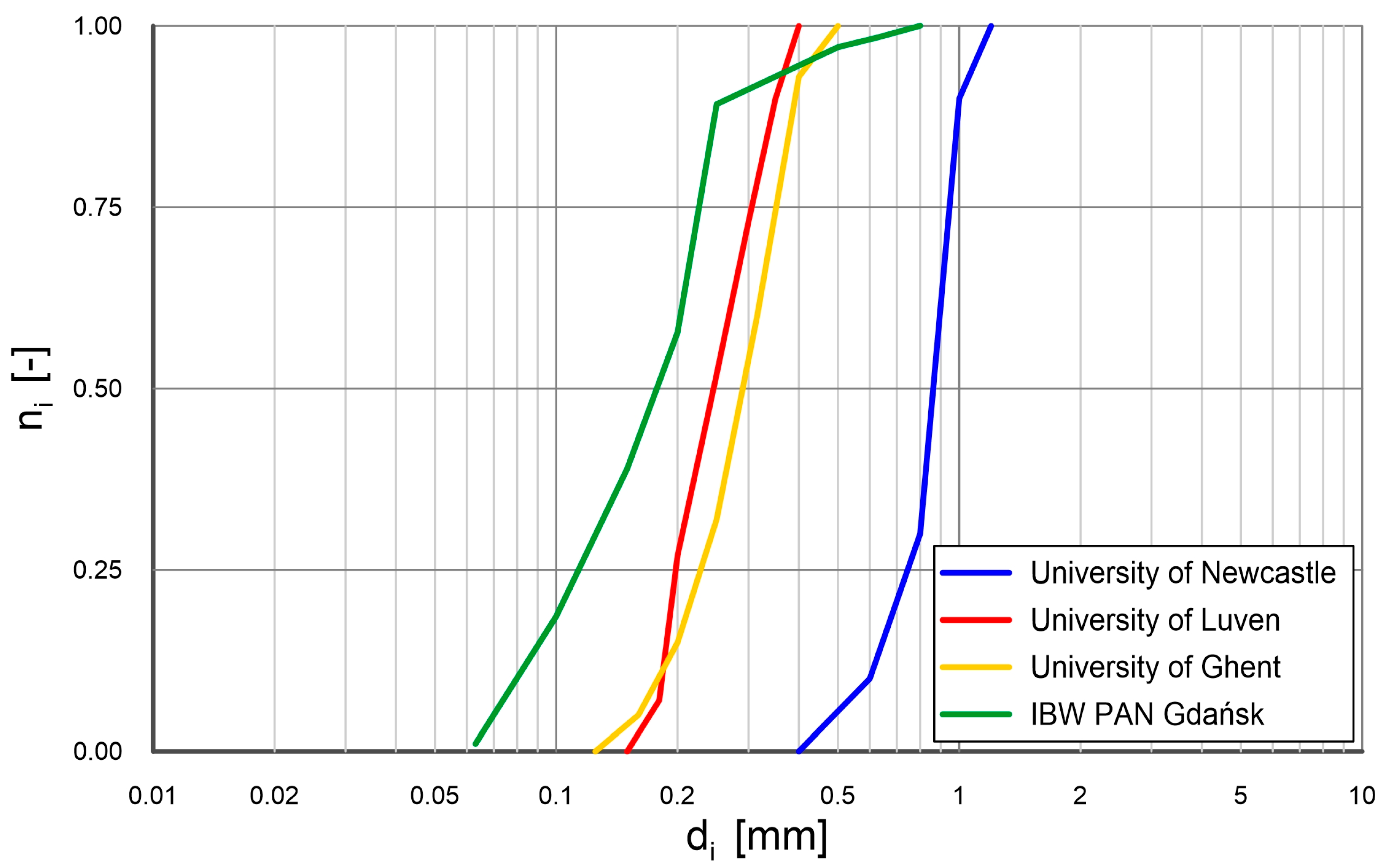
| Experiment | h [m] | Sand [mm] | [m/s] | Additional Substance | Percentage Share of Additional Substance [%] | [m/s] |
|---|---|---|---|---|---|---|
| UNewcastle 1990 Alvarez-Hernandez [45] | 0.081–0.310 | 0.90 | clay gel c = 24 g/L clay gel c = 30 g/L | 20 20 | 0.0025 0.0050 | |
| ULuven 1995 Torfs [63] | 0.053–0.195 | 0.21 | 0.028 ÷ 0.053 | montmorillonite | 7 9 | 0.0075 0.0900 |
| UGhent 1998 De Sutter et al. [48] | 0.081–0.095 | 0.32 | 0.033 ÷ 0.055 | clay | 10 20 30 | 0.0040 0.0090 0.0125 |
| IBW PAN Gdańsk 2021 | 0.05 | 0.22 | 0.031 ÷ 0.097 | clay | 5 10 20 | 0.0025 0.0035 0.0061 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zawisza, J.; Radosz, I.; Biegowski, J.; Kaczmarek, L.M. Sand Transport with Cohesive Admixtures…—Laboratory Tests and Modeling. Water 2023, 15, 804. https://doi.org/10.3390/w15040804
Zawisza J, Radosz I, Biegowski J, Kaczmarek LM. Sand Transport with Cohesive Admixtures…—Laboratory Tests and Modeling. Water. 2023; 15(4):804. https://doi.org/10.3390/w15040804
Chicago/Turabian StyleZawisza, Jerzy, Iwona Radosz, Jarosław Biegowski, and Leszek M. Kaczmarek. 2023. "Sand Transport with Cohesive Admixtures…—Laboratory Tests and Modeling" Water 15, no. 4: 804. https://doi.org/10.3390/w15040804






