CFD as a Decision Tool for Pumped Storage Hydropower Plant Flow Measurement Method
Abstract
:1. Introduction
2. Current State
2.1. Peak Load Hydropower Plant Orlík
2.2. Planned Transformation to PSP
2.3. CFD Model—Setup and Validation
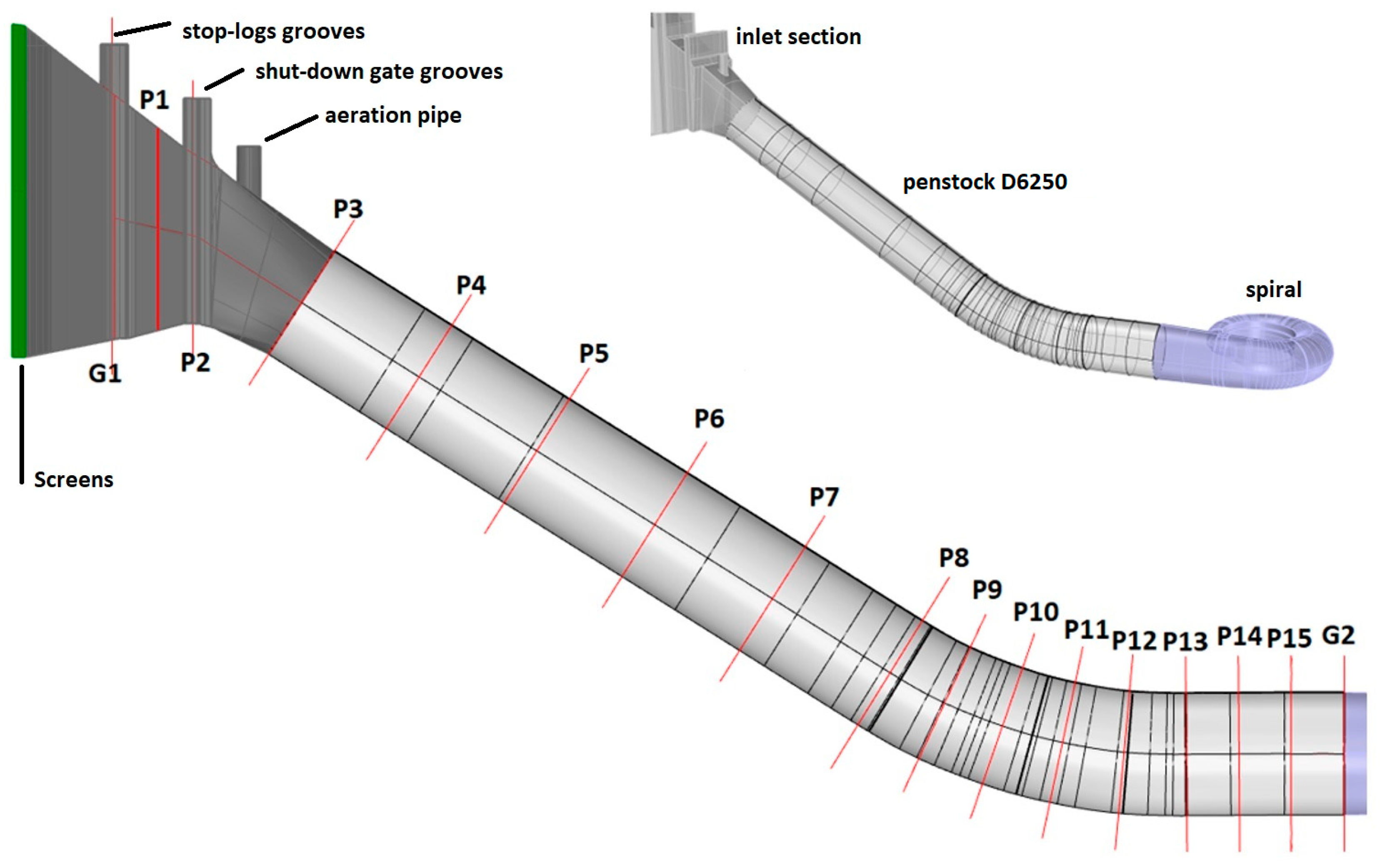
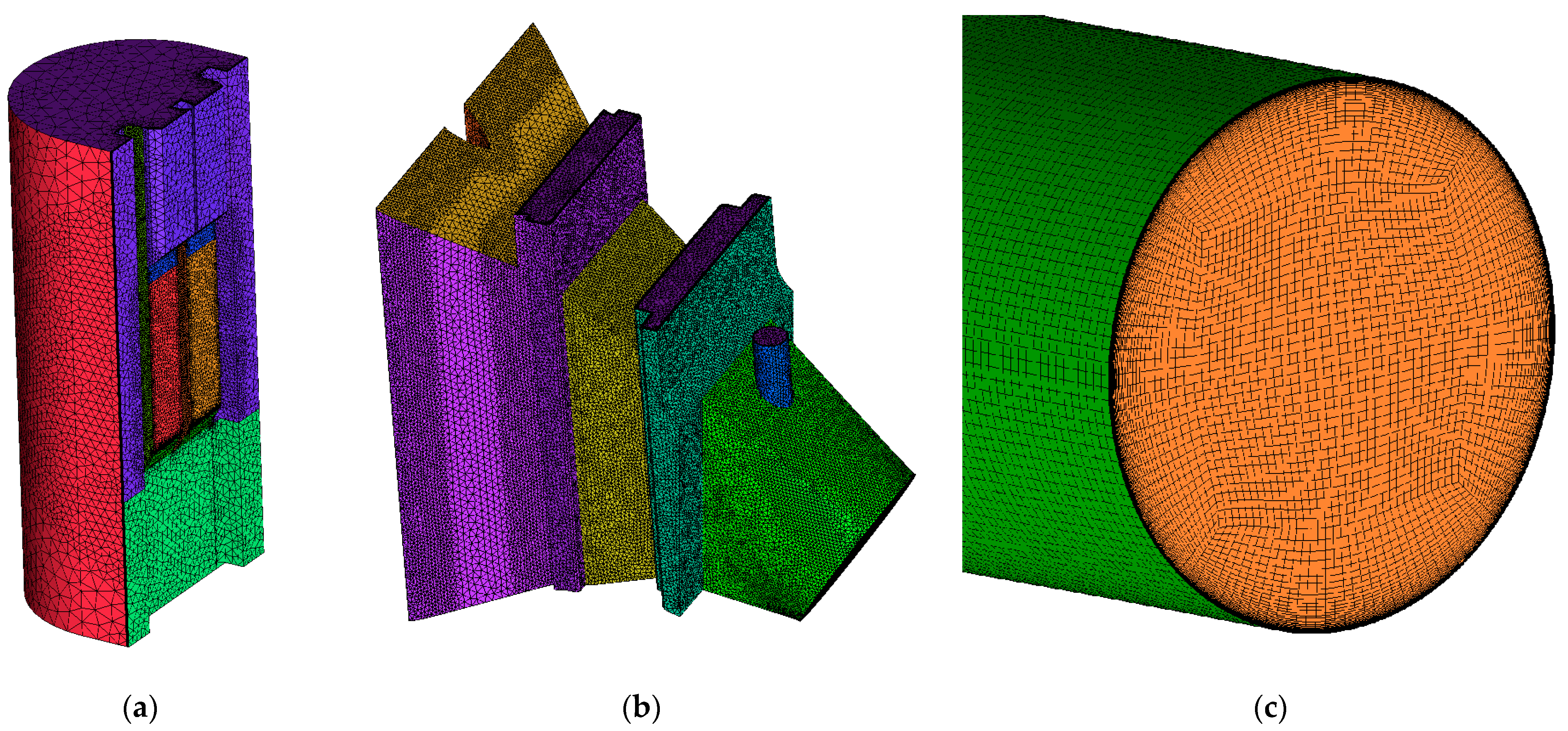
2.3.1. Three-Dimensional (3D) Model
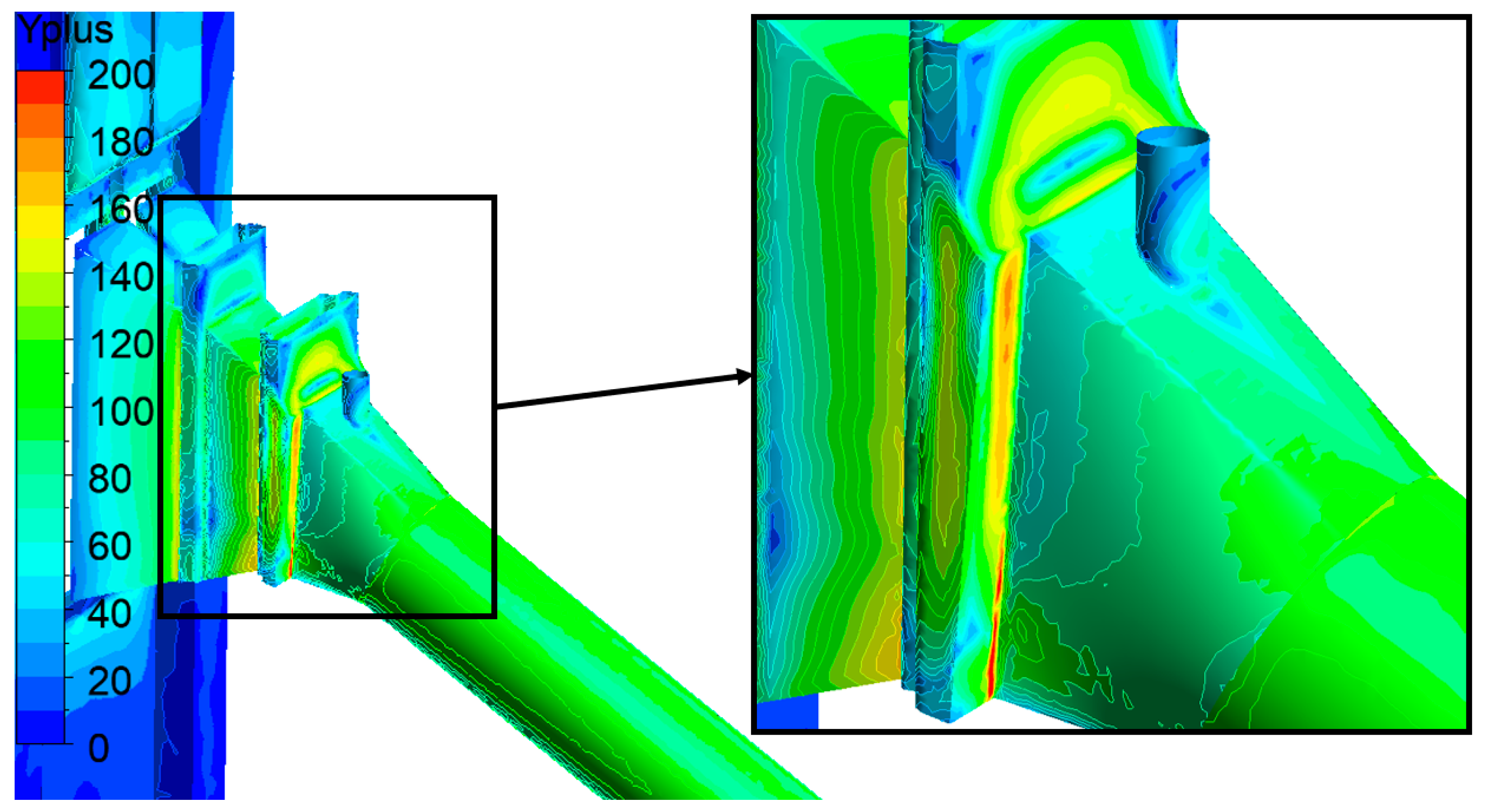
2.3.2. Computational Mesh
- Inlet with part of the reservoir;
- Screens (represented by porous domains);
- Intake object (with grooves and transition piece);
- Penstock DN6250;
- Spiral.
2.3.3. Numerical Setup
2.3.4. Comparison of Historical Measurements
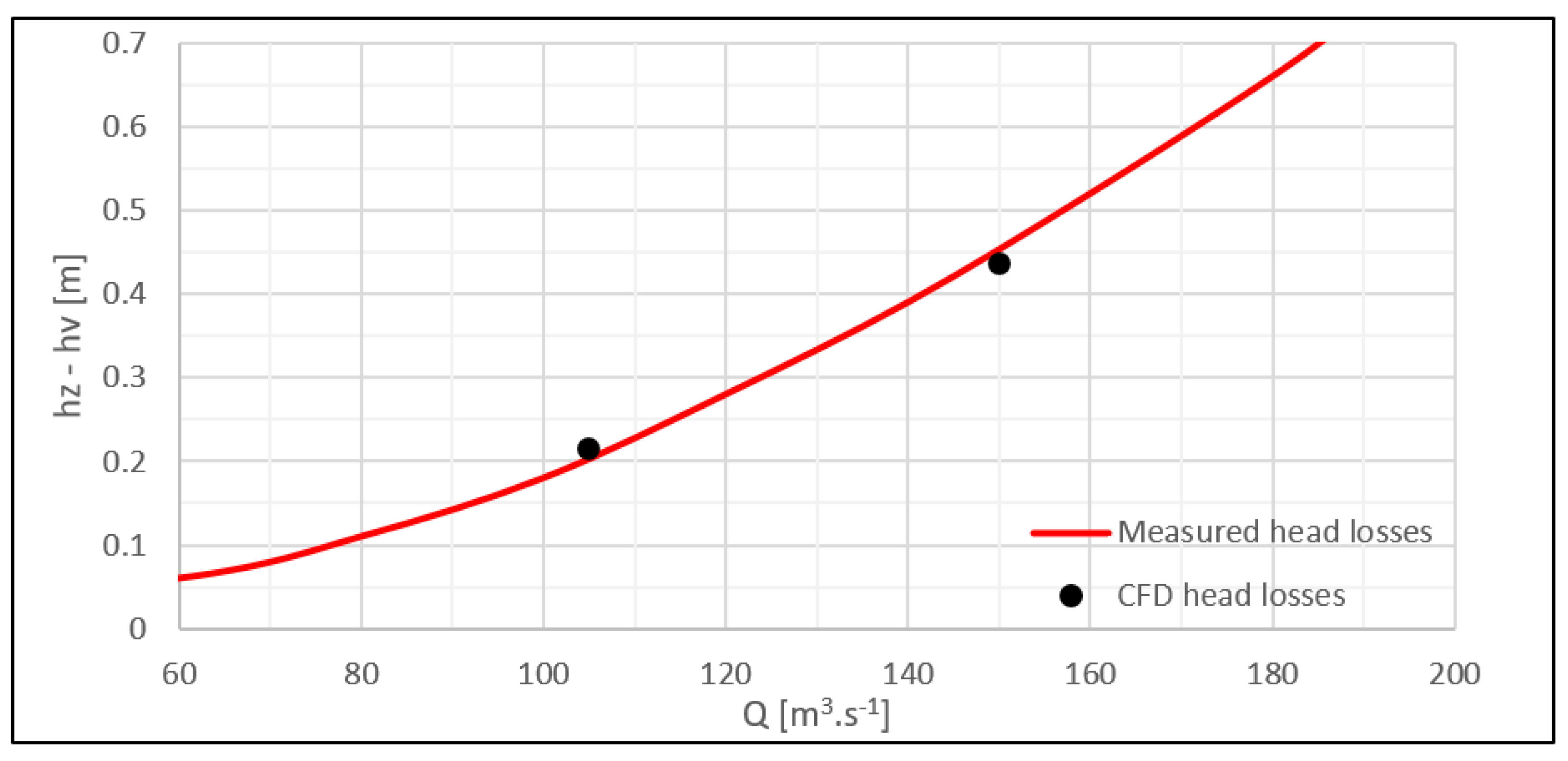
2.3.5. Hydraulic Losses
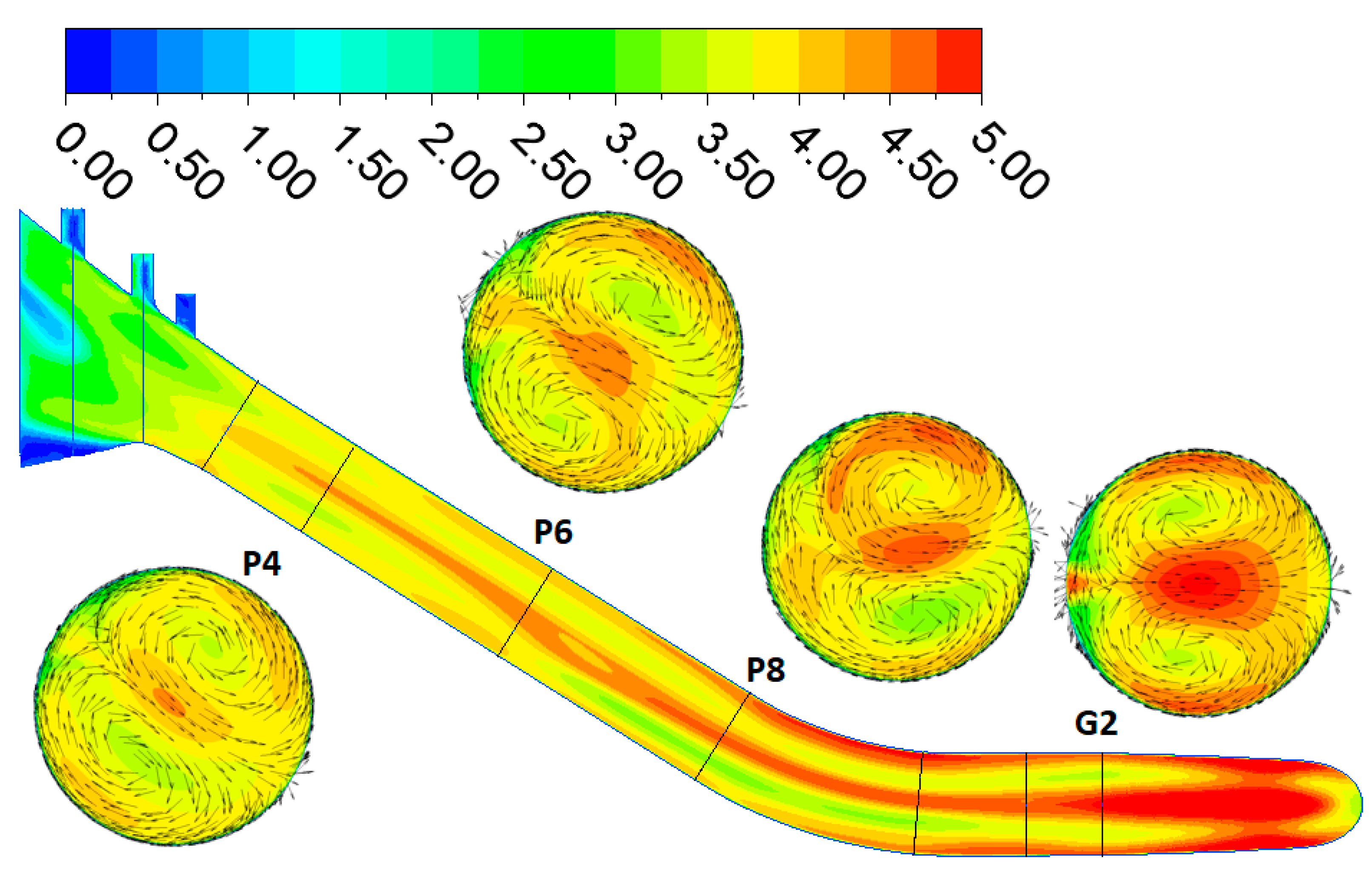
3. CFD Simulations for Planned PSP
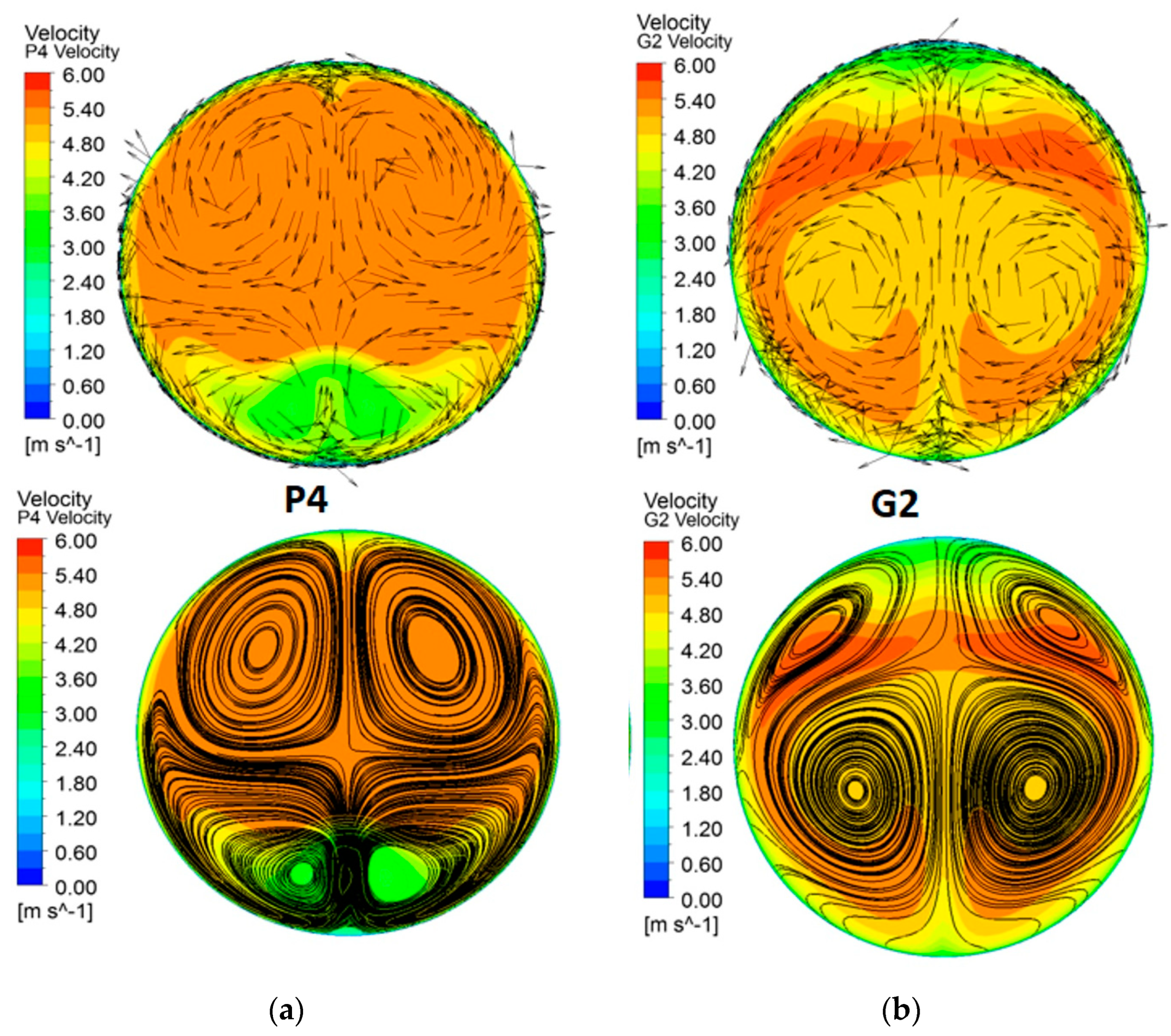
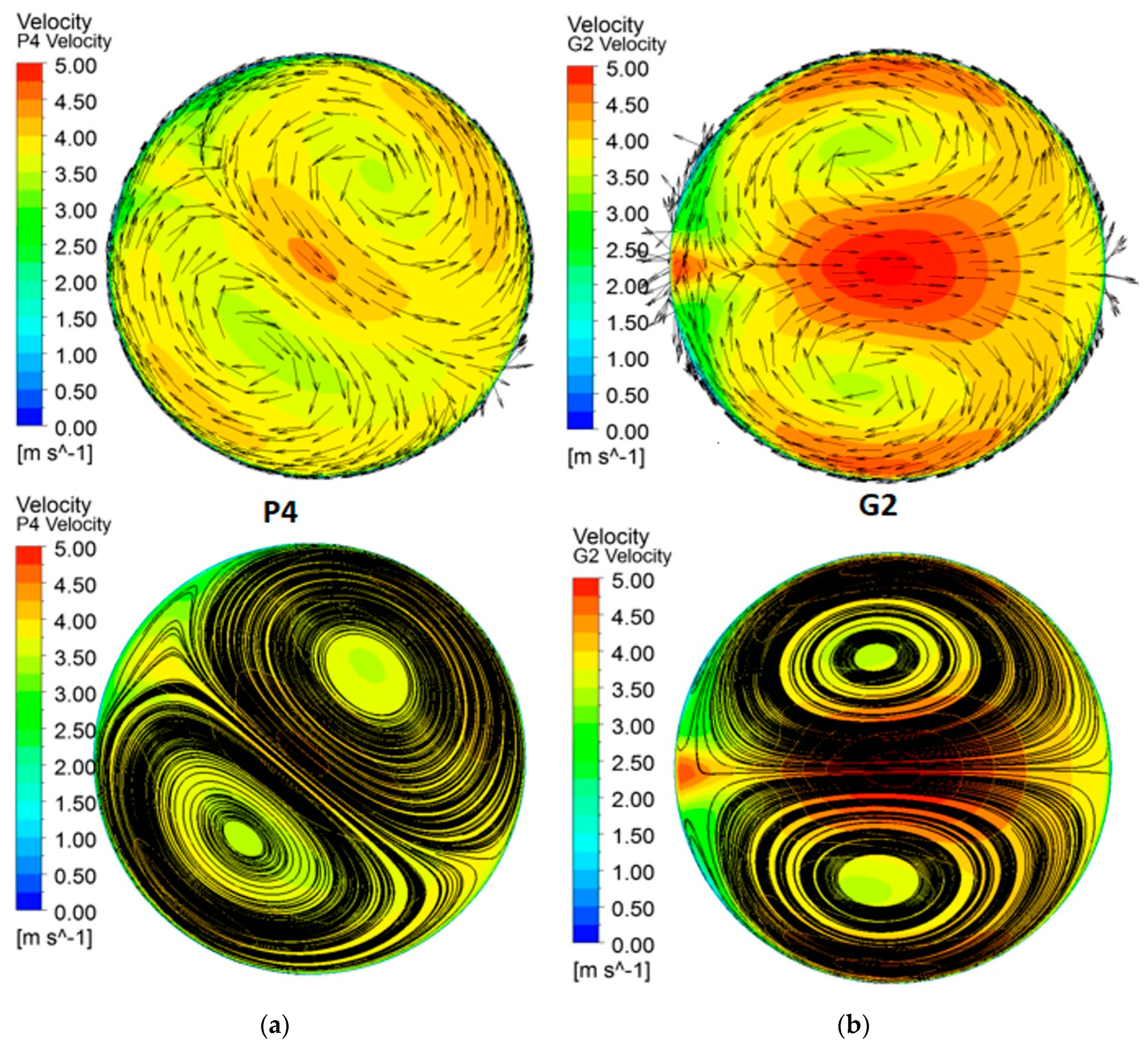
3.1. Turbine Regime
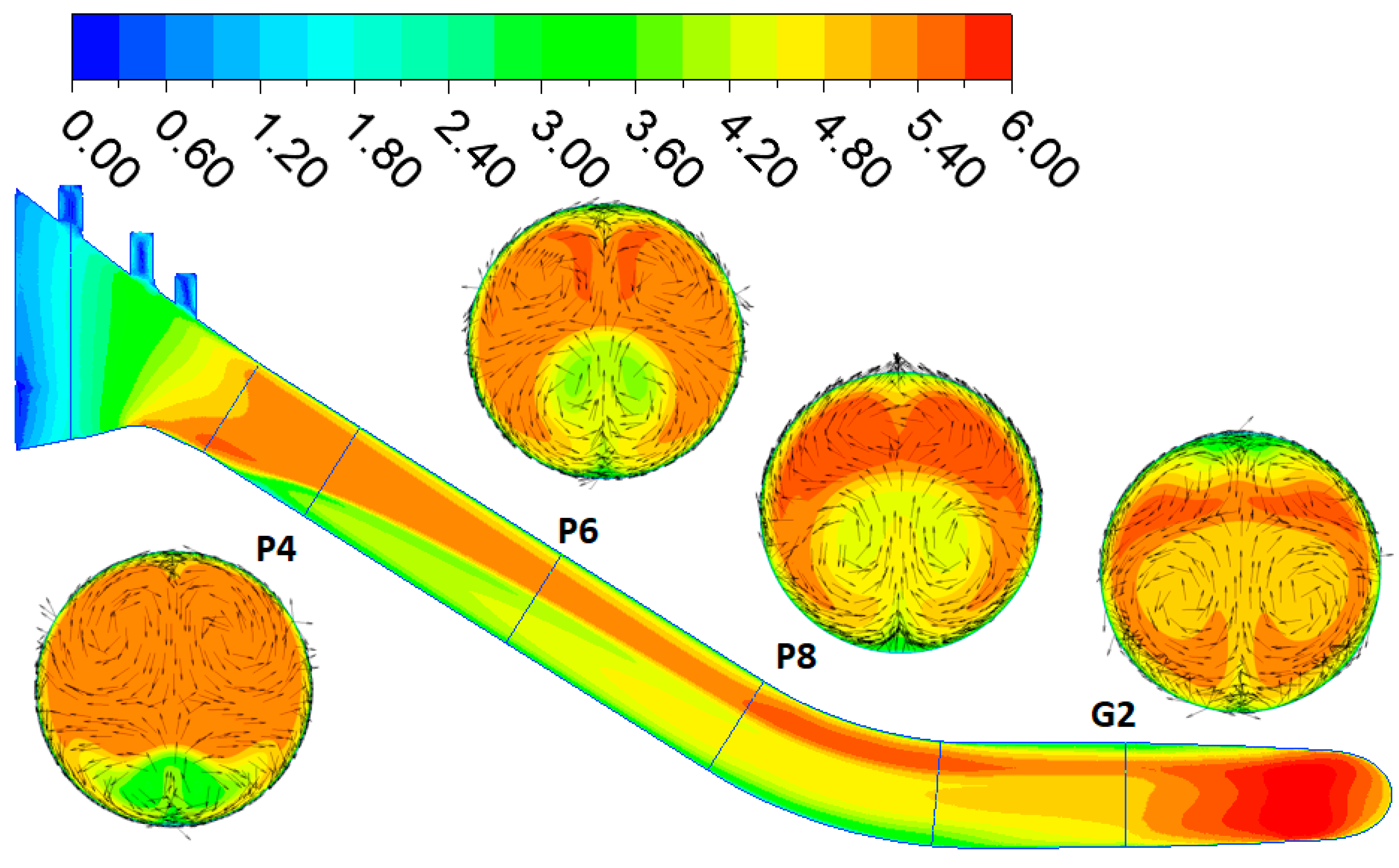
3.2. Pump Regime
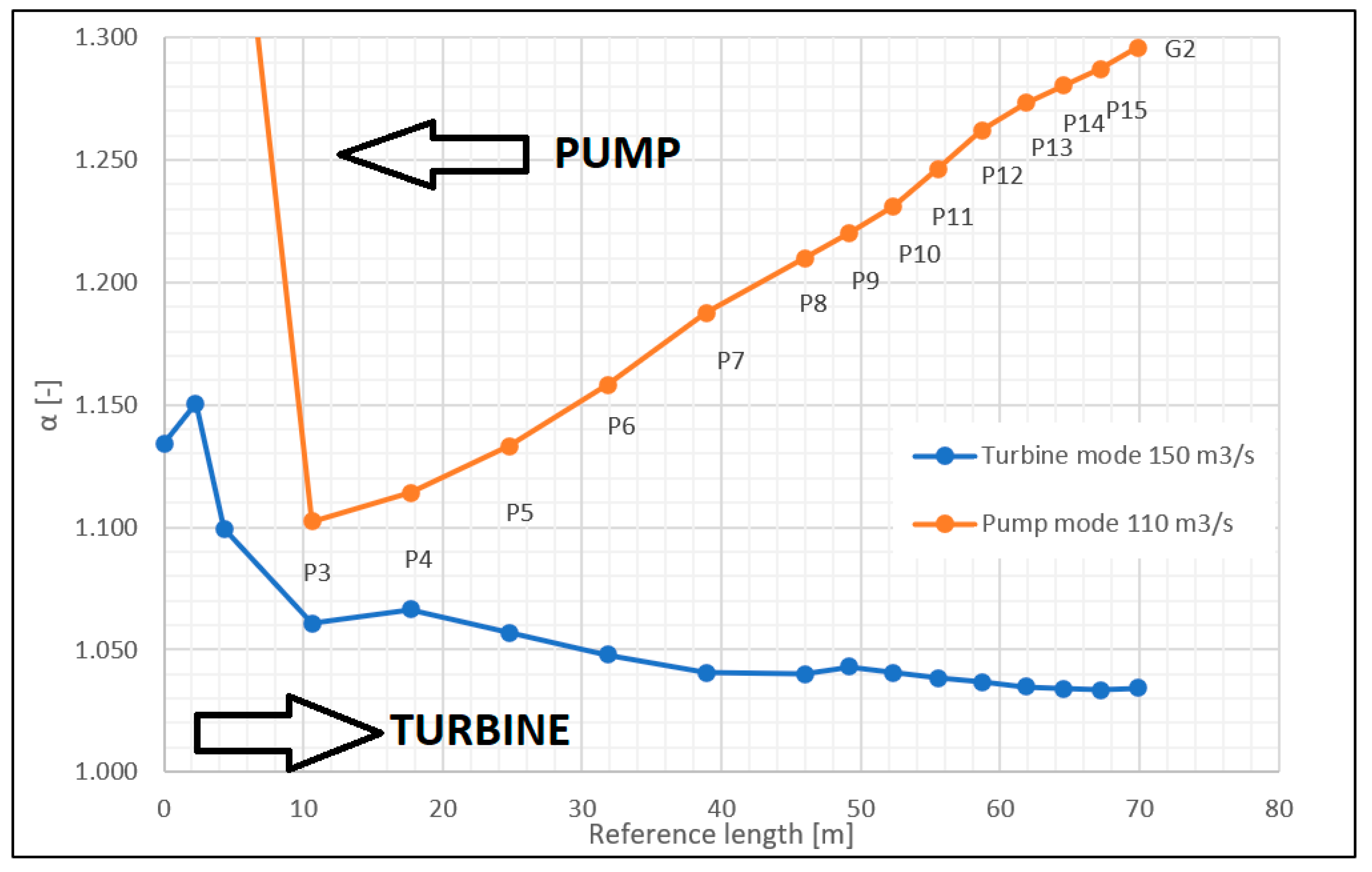
3.3. Comparison of Turbine and Pump Regime
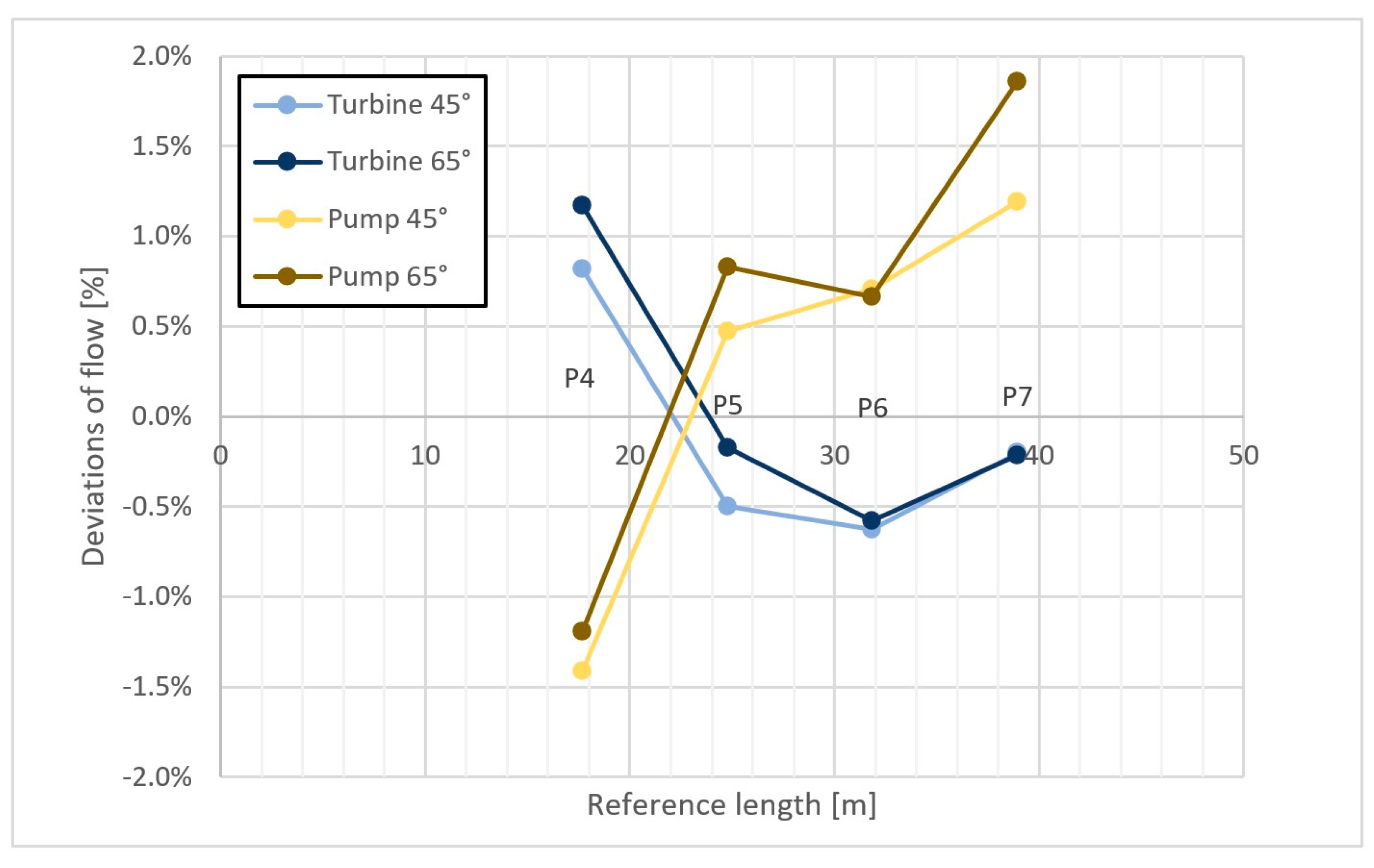
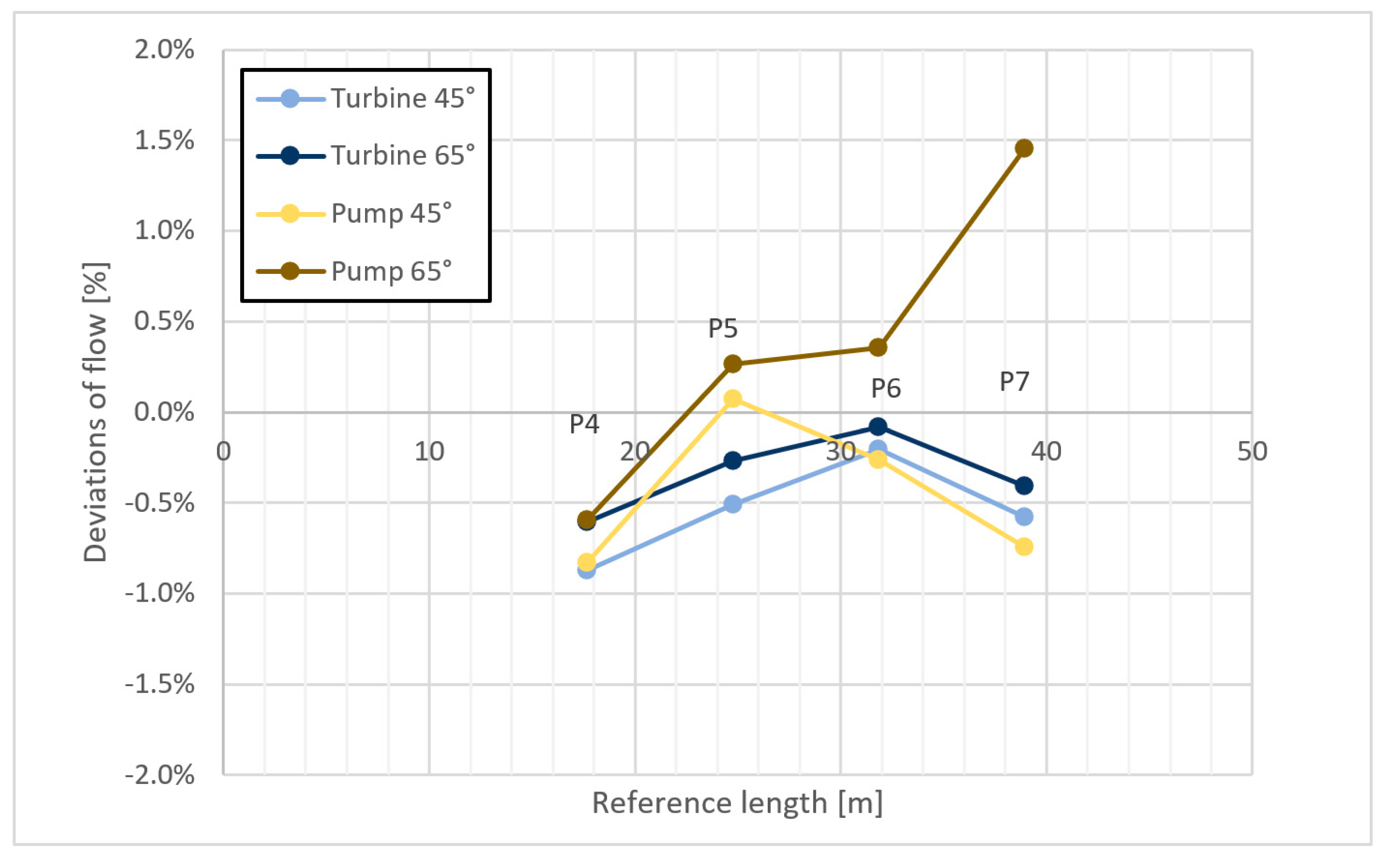
3.3.1. Coefficient for Non-Uniform Axial Velocity Profile [31]
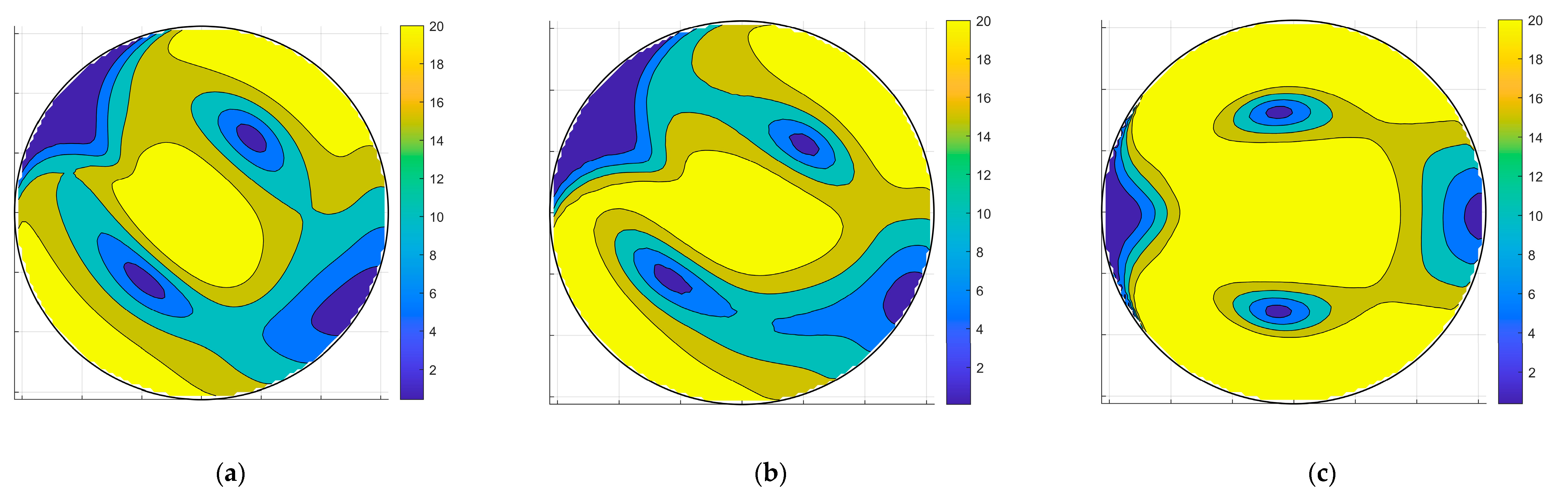
3.3.2. Index of Asymmetry
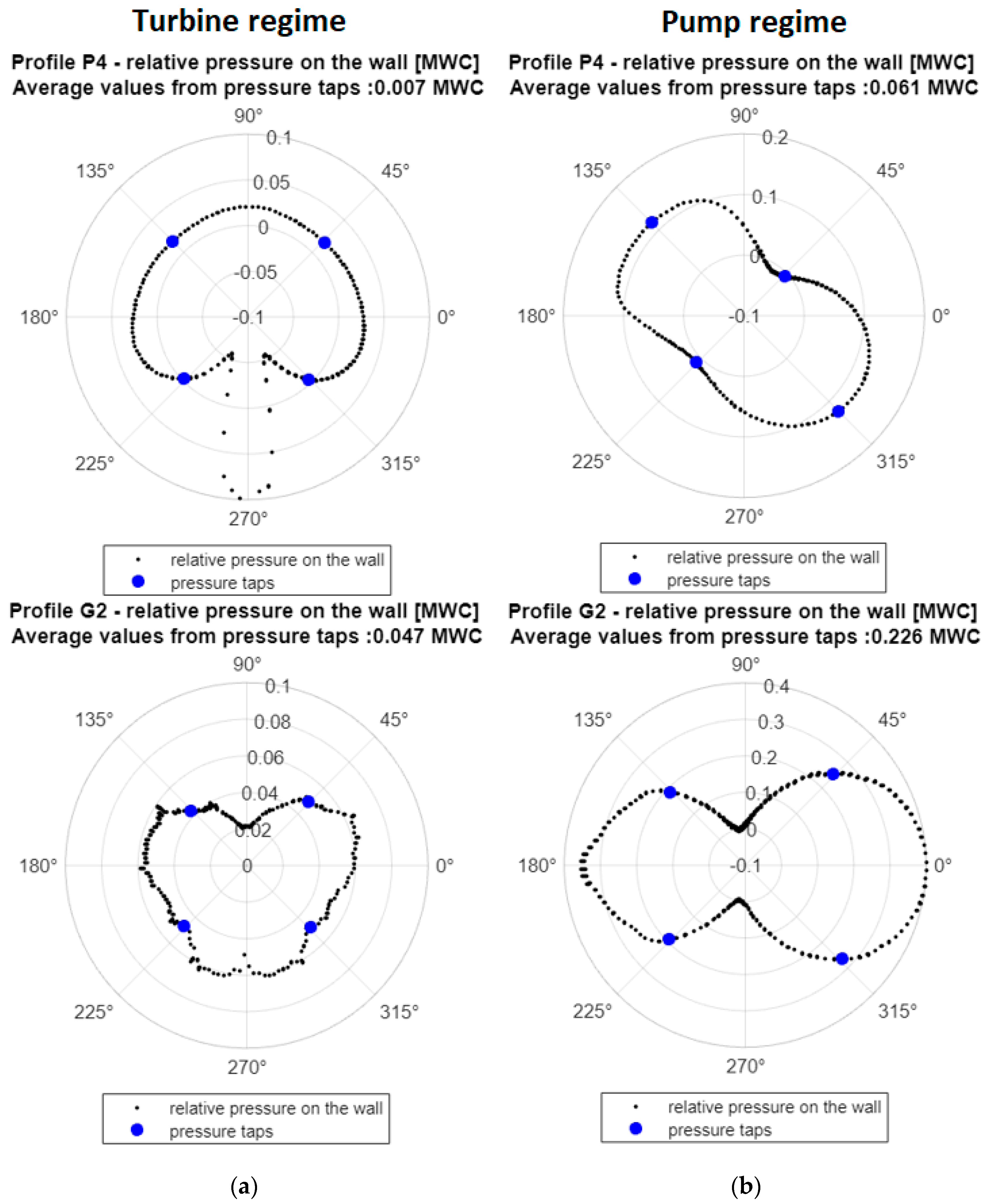
3.3.3. Pressure Field in the Penstock
4. Assessment of Flow Measurement Methods
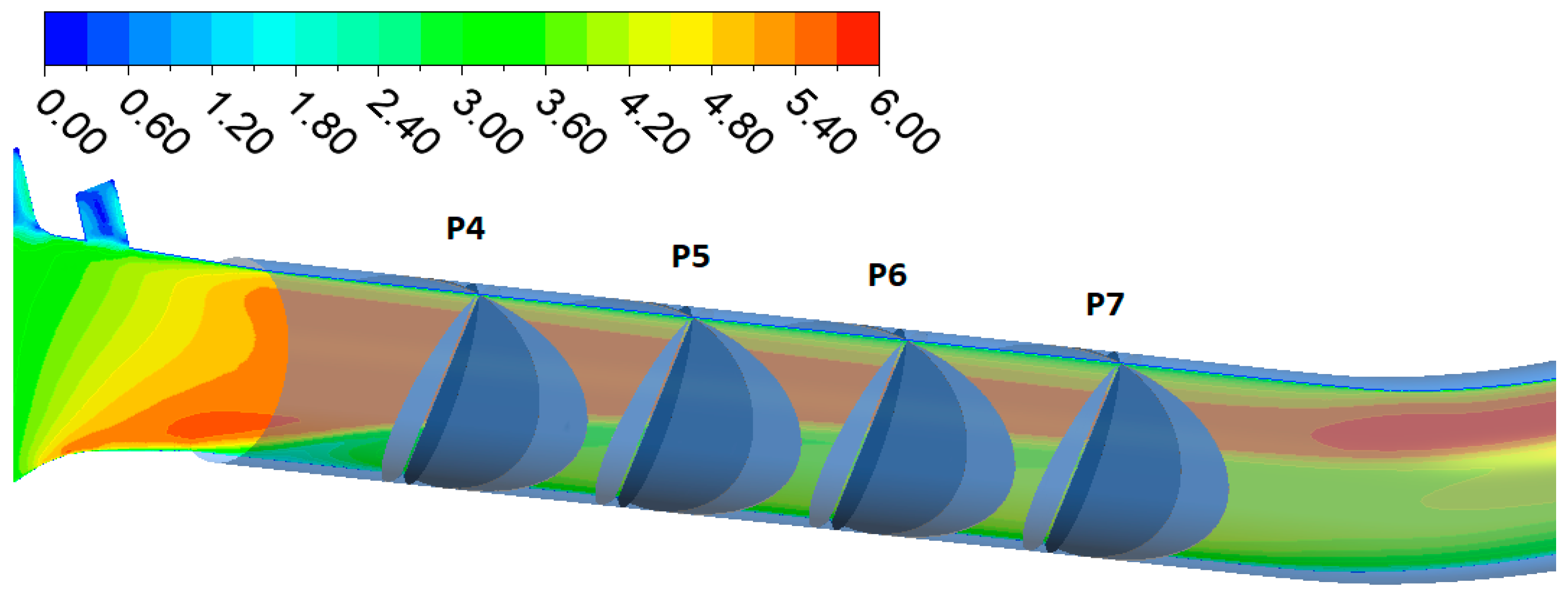
4.1. Current Meter Method
- If the swirl angle is <5°, Y < 0.05 and low turbulence when applying 6 probe radii, the total uncertainty of the flow measurement can be below 1.5%
- If the value of Y < 0.25 and when applying at least 6 measuring radii, the uncertainty of the flow measurement can be up to 2.2%.
- The positions of the measuring profiles from the 1994 measurement in the TG3 penstock have been adopted.
- For these positions, the values of normal velocities were subtracted from the CFD model simulation results.
- The mean cross-sectional velocity was calculated from these values according to ISO 3354.
4.2. Pressure–Time Method (Gibson Method)
- “Individual average pressure measurements around the measuring section should not differ from one another by more than 0.5% (0.5% E) of the specific hydraulic energy of the machine or 20% (20% pdyn) of the specific kinetic energy calculated from the average velocity in the measuring sections.” [34] (Chapter 11.4.2)
- “… the difference between the pressure measured at any one tap and the average of the pressures measured at all taps shall not exceed 20% of the dynamic pressure (20% pdyn). The average of the readings from any pair of opposite taps shall not differ from the average from any other pair of taps in the same cross-section by more than 10% of the dynamic pressure (10% pdyn).” [34] (Chapter 10.4.2.4)
Equivalent Geometrical Factor F
4.3. Ultrasonic Method
- Definition of chordal path positions in the base plane.
- Path rotation according to the position and inclination of the plane (A and B).
- Extraction of velocity components at the intersection of the created paths and plane sections (A and B) (Figure 18).
- Created averaged velocity components u, v, w.
- Transformation of velocities into two components—in the path direction and transverse component.
- The following flow calculation is exact according to ASME PTC 18-2020 for the given plane rotation and position in the conduit. The Gauss–Jacobi Method with OWICS weights was used in our case for four and nine paths.

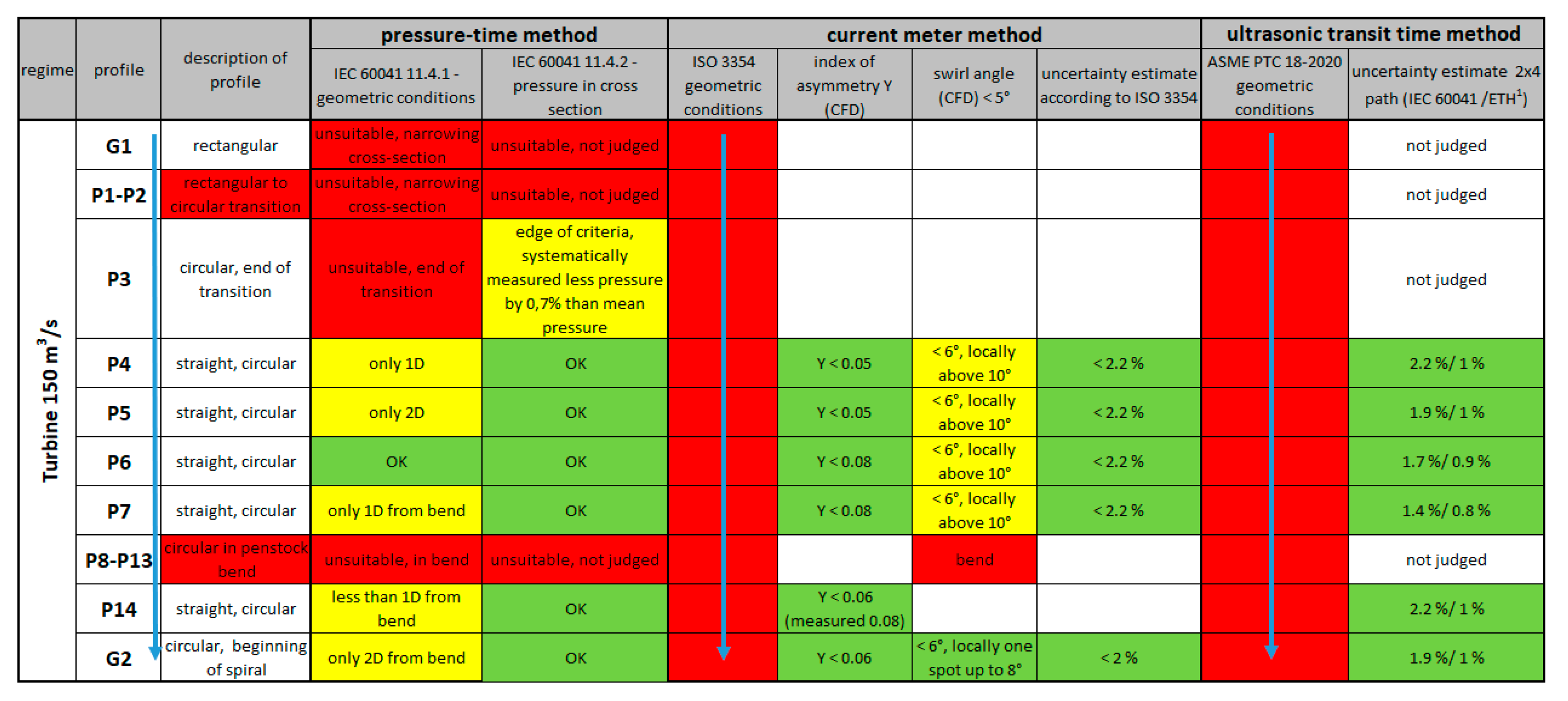
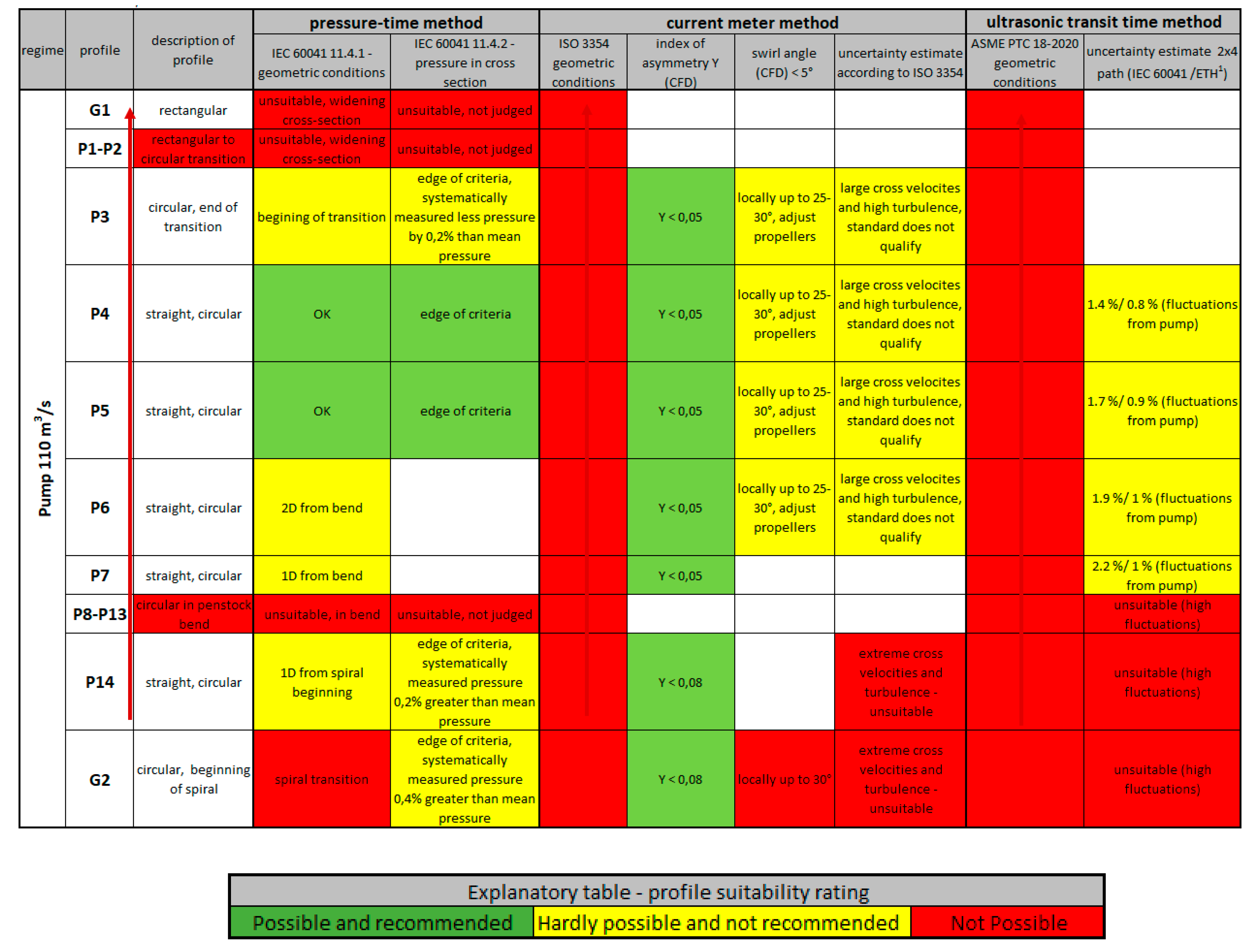
5. Tables of Suitability of Measurement Profiles and Uncertainty Quantification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zipf, M.; Most, D. Impacts of volatile and uncertain renewable energy sources on the German electricity system. In Proceedings of the 2013 10th International Conference on the European Energy Market (EEM) 2013, Stockholm, Sweden, 27–31 May 2013; pp. 1–8. [Google Scholar]
- Talaat, M.; Elkholy, M.; Farahat, M. Operating reserve investigation for the integration of wave, solar and wind energies. Energy 2020, 197, 117207. [Google Scholar] [CrossRef]
- Amiryar, M.; Pullen, K. A Review of Flywheel Energy Storage System Technologies and Their Applications. Appl. Sci. 2017, 7, 21. [Google Scholar] [CrossRef] [Green Version]
- Hedlund, M.; Lundin, J.; de Santiago, J.; Abrahamsson, J.; Bernhoff, H. Flywheel Energy Storage for Automotive Applications. Energies 2015, 8, 10636–10663. [Google Scholar] [CrossRef] [Green Version]
- Poland’s 820MWh pumped storage project to boost energy security. PEI 2022. Available online: https://www.powerengineeringint.com/energy-storage/polands-820mwh-pumped-storage-project-to-boost-energy-security/ (accessed on 8 December 2022).
- Luong, J.; Tran, C.; Ton-That, D. A Paradox over Electric Vehicles, Mining of Lithium for Car Batteries. Energies 2022, 15, 7997. [Google Scholar] [CrossRef]
- Gielen, D.; Gorini, R.; Leme, R.; Prakash, G.; Wagner, N.; Janeiro, L.; Collins, S.; Kadir, M.; Asmelash, E.; Saygin, D.; et al. World Energy Transitions Outlook: 1.5 °C Pathway, 1st ed.; IRENA: Abu Dhabi, the United Arab Emirates, 2021; ISBN 978-92-9260-334-2. [Google Scholar]
- Olabi, A.; Onumaegbu, C.; Wilberforce, T.; Ramadan, M.; Abdelkareem, M.; Al–Alami, A. Critical review of energy storage systems. Energy 2021, 214, 22. [Google Scholar] [CrossRef]
- Sandia National Laboratories DOE OE Global Energy Storage Database. Available online: www.sandia.gov/ess-ssl/global-energy-storage-database-home/ (accessed on 8 December 2022).
- Blakers, A.; Stocks, M.; Lu, B.; Cheng, C. A review of pumped hydro energy storage. Prog. Energy 2021, 3, 18. [Google Scholar] [CrossRef]
- Mongird, K.; Baxter, R.; Sprinkle, V. Energy Storage Grand Challenge Cost and Performance Assessment 2020: Technical Report; No. DOE/PA-0204 2020; First Edition, US Department of Energy: Washington, DC, USA, 2020.
- Pitorac, L.; Vereide, K.; Lia, L. Technical Review of Existing Norwegian Pumped Storage Plants. Energies 2020, 13, 4918. [Google Scholar] [CrossRef]
- Figgener, J.; Stenzel, P.; Kairies, K.; Linßen, J.; Haberschusz, D.; Wessels, O.; Angenendt, G.; Robinius, M.; Stolten, D.; Sauer, D. The development of stationary battery storage systems in Germany—A market review. J. Energy Storage 2020, 29, 20. [Google Scholar] [CrossRef]
- Ershad, A.; Ueckerdt, F.; Pietzcker, R.; Giannousakis, A.; Luderer, G. A further decline in battery storage costs can pave the way for a solar PV-dominated Indian power system. Renew. Sustain. Energy Transit. 2021, 1, 20. [Google Scholar] [CrossRef]
- van der Horst, D. NIMBY or not? Exploring the relevance of location and the politics of voiced opinions in renewable energy siting controversies. Energy Policy 2007, 35, 2705–2714. [Google Scholar] [CrossRef] [Green Version]
- Lugauer, F.; Kainz, J.; Gehlich, E.; Gaderer, M. Roadmap to Profitability for a Speed-Controlled Micro-Hydro Storage System Using Pumps as Turbines. Sustainability 2022, 14, 653. [Google Scholar] [CrossRef]
- Bayazıt, Y.; Bakış, R.; Koç, C. A study on transformation of multi-purpose dams into pumped storage hydroelectric power plants by using GIS model. Int. J. Green Energy 2021, 18, 308–318. [Google Scholar] [CrossRef]
- Teitel, M.; Dvorkin, D.; Haim, Y.; Tanny, J.; Seginer, I. Comparison of measured and simulated flow through screens: Effects of screen inclination and porosity. Biosyst. Eng. 2009, 104, 404–416. [Google Scholar] [CrossRef]
- Latif, M.; Sarwar, M.; Farooq, R.; Shaukat, N.; Ali, S.; Hashmi, A.; Tariq, M. Estimating Energy Efficient Design Parameters for Trash Racks at Low Head Hydropower Stations. Water 2022, 14, 2609. [Google Scholar] [CrossRef]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Prentice Hall: Harlow, UK, 2007; ISBN 978-013-1274-983. [Google Scholar]
- Carloni, A.; Conde, K.; Pantaleão, A.; Azevedo, J.; Rade, D. Validation and analysis of turbulence modeling in pipe elbow under secondary flow conditions. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 14. [Google Scholar] [CrossRef]
- Nicolle, J.; Cupillard, S. Prediction of dynamic blade loading of the Francis-99 turbine. J. Phys. Conf. Ser. 2015, 579, 17. [Google Scholar] [CrossRef] [Green Version]
- Celik, I. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 4. [Google Scholar]
- Menter, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Liu, S.; Wu, Y.; Jiao, L.; Wang, L.; Sun, Y. Numerical investigation of the hump characteristic of a pump-turbine based on an improved cavitation model. Comput. Fluids 2012, 68, 105–111. [Google Scholar] [CrossRef]
- Kantor, M.; Chalupa, M.; Souček, J.; Bílkova, E.; Nowak, P. Application of genetic algorithm methods for water turbine blade shape optimization. Manuf. Technol. 2020, 20, 453–458. [Google Scholar] [CrossRef]
- Kadivar, M.; Tormey, D.; McGranaghan, G. A review on turbulent flow over rough surfaces: Fundamentals and theories. Int. J. 2021, 10, 34. [Google Scholar] [CrossRef]
- Measurement of Clean Water Flow in Closed Conduit—Velocity-Area Method Using Current-Meters in Full Conduits and Under Regular Flow Condition, 3rd ed.; International Organization for Standartization: Geneva, Switzerland, 2008.
- Feng, J.; Benra, F.; Dohmen, H. Comparison of Periodic Flow Fields in a Radial Pump among CFD, PIV, and LDV Results. Int. J. Rotating Mach. 2009, 2009, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Yang, J.; Zeng, W.; Yang, J. Transient Pressure Analysis of a Prototype Pump Turbine: Field Tests and Simulation. J. Fluids Eng. 2018, 140, 10. [Google Scholar] [CrossRef]
- Dauhlhaug, O. A Study of Swirl Flow in Draft Tubes. Master’s Thesis, NTNU, Trondheim, Norway, 1997. [Google Scholar]
- Saemi, S.; Cervantes, M.; Raisee, M.; Nourbakhsh, A. Numerical investigation of the pressure-time method. Flow Meas. Instrum. 2017, 55, 44–58. [Google Scholar] [CrossRef]
- Saemi, S.; Raisee, M.; Cervantes, M.; Nourbakhsh, A. Numerical Investigation of the Pressure-Time Method Considering Pipe With Variable Cross Section. J. Fluids Eng. 2018, 140, 15. [Google Scholar] [CrossRef]
- Field Acceptance Tests to Determine the Hydraulic Performance of Hydraulic Turbines, Storage Pumps and Pump-Turbines, 3rd ed.; International Electrotechnical Commision: Geneva, Switzerland, 1996.
- American Society of Mechanical Engineers. Hydraulic Turbines and Pump-Turbines: Performance Test Codes, 1st ed.; The American Society of Mechanical Engineeers: New York, NY, USA, 2020. [Google Scholar]
- Measurement of Clean Water Flow in Closed Conduit—Velocity-Area Methods of Flow Measurement in Swirling or Asymmetric Flow Conditions in Circular Ducts by Means of Current-Meters or Pitot Static Tubes, 2nd ed.; International Organization for Standartization: Geneva, Switzerland, 2008.
- Romero-Gomez, P.; Harding, S.; Richmond, M. The effects of sampling location and turbulence on discharge estimates in short converging turbine intakes. Eng. Appl. Comput. Fluid Mech. 2017, 11, 513–525. [Google Scholar] [CrossRef] [Green Version]
- Gibson, N. Measurement of the Flow of Fluids in Closed Conduits 1921; Patent and Trademark Office: Washington, DC, USA.
- Adamkowski, A.; Janicki, W.; Lewandowski, M. Measurements of Discharge through a Pump-Turbine in Both Flow Directions Using Volumetric Gauging and Pressure-Time Methods. Energies 2020, 13, 4706. [Google Scholar] [CrossRef]
- Adamkowski, A. Discharge Measurement Techniques in Hydropower Systems with Emphasis on the Pressure-Time Method. Hydropower-Pract. Appl. 2012, 29, 83–111. [Google Scholar]
- Adamkowski, A.; Krzemianowski, Z.; Janicki, W. Flow rate measurement using the pressure-time method in a hydropower plant curved penstock. In Proceedings of the 7th International Conference On Hydraulic Efficiency Measurements IGHEM 2008, Milan, Italy, 3–6 September 2018; p. 13. [Google Scholar]
- Voser, A. Analyse und Fehleroptimierung der Mehrpfadigen Akustischen Durchflussmessung in Wasserkraftanlagen. Ph.D. Thesis, ETH Zürich, Zürich, Switzerland, 1999. [Google Scholar]
- Hug, S.; Staubli, T.; Gruber, P. Comparison of measured path velocities with numerical simulations for heavily disturbed velocity distributions. In Proceedings of the 9th International Conference On Hydraulic Measurement and Efficiency IGHEM 2012, Trondheim, Norway, 27–30 June 2012. [Google Scholar]




| Table of Basic Technical Information | Current State | Planned State | ||
|---|---|---|---|---|
| Turbine Type | Kaplan | Francis | Reversible Francis | |
| Turbine | Pump | |||
| Heads range (m) | 45–71.5 | 45–71.5 | 50–71.5 | 50–71.5 |
| Discharge range (m3.s−1) | 47.5–160 | 80–150 | 80–150 | 110 |
| Unit installed power (MW) | 91 | 93 | 91 | 76 |
| Variable | Value | Units | Description |
|---|---|---|---|
| ρ | 999.9 | kg.m−3 | specific mass |
| ν | 1.43 × 10−6 | m2.s−1 | kinematic viscosity |
| D | 6250 | mm | penstock diameter |
| L | 69.92 | m | centreline length G1 to G2 |
| Δ1 | 0.5 | mm | equivalent sand grain roughness of steel |
| Δ1/D | 8 × 10−5 | - | relative roughness of steel |
| Δ2 | 4 | mm | equivalent sand grain roughness of concrete |
| Δ2/D | 6.4 × 10−4 | - | relative roughness of concrete |
| Deviation | P4 | P8 | G2 |
|---|---|---|---|
| Turbine 150 m3.s−1 | −0.2% | −1.4% | −0.5% |
| Pump 110 m3.s−1 | −0.1% | −0.3% | +2.4% |
| Regime | Q | D | U | pdyn | 20%pdyn | 10%pdyn | 0.5%E |
|---|---|---|---|---|---|---|---|
| (m3.s−1) | (m) | (m.s−1) | (m w.c.) | (m w.c.) | (m w.c.) | (m w.c.) | |
| Turbine | 150 | 6.25 | 4.9 | 1.2 | 0.24 | 0.12 | 0.31 |
| Pump | 110 | 6.25 | 3.6 | 0.7 | 0.13 | 0.07 | 0.31 |
 |
 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souček, J.; Nowak, P.; Kantor, M.; Veselý, R. CFD as a Decision Tool for Pumped Storage Hydropower Plant Flow Measurement Method. Water 2023, 15, 779. https://doi.org/10.3390/w15040779
Souček J, Nowak P, Kantor M, Veselý R. CFD as a Decision Tool for Pumped Storage Hydropower Plant Flow Measurement Method. Water. 2023; 15(4):779. https://doi.org/10.3390/w15040779
Chicago/Turabian StyleSouček, Jiří, Petr Nowak, Martin Kantor, and Radek Veselý. 2023. "CFD as a Decision Tool for Pumped Storage Hydropower Plant Flow Measurement Method" Water 15, no. 4: 779. https://doi.org/10.3390/w15040779





