Abstract
Energy security is one of the main factors in the development and diffusion of microgrid applications. In networks operating without storage, the operation of their systems is greatly affected by sudden load demand and intermittent generation fluctuations. The main purposes of using energy storage systems in microgrids are stabilizing the intermittent generation of renewable energy sources locally, to ensure that energy production matches energy demands, participating in the frequency regulation process, maintaining the energy balance between generation and demand in renewable energy microgrids, and increasing energy reliability. This study investigates the frequency and power balance of an isolated microgrid system, by including storage systems (battery and pump-hydro). Realistic data for wind and solar sources are used for the optimal tuning of the proportional-integral controller, using the integral of the absolute error criterion multiplied by time, with a Quasi-Newton method. Simulation studies have been carried out, to investigate the performance of the microgrid system, by including the hydroelectric power plant system with pump storage for 24 h, under various operating conditions. The results reveal that by including the storage units in the system, it exhibits a more consistent and smooth dynamic performance, using renewable energy efficiently.
1. Introduction
Electricity is tantamount to modernity, as almost everything we associate with the 21st-century world is predicated on the availability of electricity. When people see light, they see the modern world; where they do not see light, there are one of two conditions: either nobody lives there or the place has not been electrified. If it has not been electrified there is no more precious gift to give those people than sustainable electricity.
The balance between production and consumption of electrical energy is of critical importance for societies where technological developments, industrialization, and population growth continue [1,2]. Studies have shown that fossil fuel energy products, including natural gas, coal, and oil, will not be able to respond to the increasing energy consumption trend at the same rate [3]. Today, many countries are developing a fundamentally new model for building and operating the energy industry, which is based on reducing the consumption of fossil resources and switching to renewable energy sources, such as wind, solar, water, and biomass [4]. This is due to the desire to protect the environment, limited reserves and rising prices for organic fuels, moral and physical aging of thermal and nuclear power facilities, etc. [5].
Sustainable electricity is not going to involve building gigantic coal plants. It’s going to involve photovoltaics wind that is locally sited. The storage is the key enabler here because wind and solar are intermittent [6]. Moreover, since they are intermittent they cannot be fully integrated into the baseload, which means, then, it is necessary to have some other source as a backup. Storage would make much more efficient use of the assets that we have. Since today, the designed grid can meet peak demand beak—it is 40% to 50% above average demand [7]. The other issue is that the grid is so different from everything else and every other commodity that we deal with. The way the grid operates, supply must be in balance with demand, everywhere at all times. However, with a battery, we would have the ability to do what refrigeration did to our food supply, or what storage tanks did to our water supply.
For this reason, with the effective and efficient use of energy and the inclusion of renewable energy sources in the energy sector, alternative ideas such as a microgrid have emerged against the classical energy grid [8]. It is with the aim of providing a reliable, safe, cost-effective, and environmentally friendly energy supply to consumers, that much attention is paid to the design and construction of power plants operating on renewable sources [9]. Microgrid systems have long been in use in landlocked islands, military areas, and service buildings, such as airports and hospitals. However, to give an example of a new type of microgrid, where renewable energy raises the feasibility, there is a current model in Brooklyn, New York, which started to be established in 2016, providing settlement with blockchain technology, where energy trading between individuals (homeowners) can take place [10]. Apart from this, as rooftop-solar-system installation and commissioning has become widespread, the microgrid application continues to become widespread in organized industrial zones, hospitals, and similar points, where energy continuity is high [11]. It should be noted that the advantage of these stations is that they can be built directly near the end user. This leads to a reduction in losses for the transformation and transmission of electrical energy, which contributes to the development of a smart microgrid with distributed generation. However, one of the disadvantages is that the operation of such stations is highly dependent on meteorological factors, affecting the operation of both individual power plants and the power system as a whole. Since the sun does not always shine, and the wind does not always blow, how to consolidate renewable energy sources? That is, to provide the energy in demand at all times, whatever the weather or the time of the day, is one of the biggest challenges today [12]. Therefore, with an increase in the installed capacities of solar and wind farms and an increase in the share of these stations in the total share of energy generation, the problem arises of ensuring the stable operation of the unified energy system and covering the required consumer-load schedule.
A good way is needed to store the energy for later. Nowadays, the main option is lithium-ion batteries. These can be seen in products such as Tesla’s home battery, Powerwall, and the utility-scale system, Powerpack [13]. However, though the price of lithium-ion is becoming cheaper, experts say it will remain too expensive in large-scale applications [14]. To get to the battery for the electrical grid, it is needed to look at a further cost reduction of 10 to 20× It is impossible for lithium-ion batteries to store more than four hours of energy at a sensible price point.
One thing is clear. For renewables to truly compete with fossil fuels, it is needed to figure out a better way to store energy [15]. From 2000 to 2018, installed wind power grew from 17,000 MW to over 563,000 MW [16]. Solar power grew from a mere 1250 MW to 485,000 MW, and it is not stopping there [16]. Renewables are expected to grow an additional 50% over the next five years. It is known today that solar PV and wind are the least expensive way to generate electricity. In particular, the price of solar photovoltaics has plummeted far faster than all forecasts predicted, after China flooded the market with cheap panels in the late 2000s [17].
Many analysts did not believe that solar was going to ever stand on its own without subsidies. Well, a few years later, even the most conservative analysts started realizing that solar was going to become economic in most parts of the world, rather quickly. In addition, as solar has gotten cheaper, so too have lithium-ion batteries, the technology that powers electric vehicles, our cell phones, and laptops [14]. Moreover, thanks to improved manufacturing techniques and economies of scale, costs have fallen 85%, since 2010 [18]. Nowadays, wind or solar with battery storage is oftentimes more economical than peaker plants, that is, power plants that only fire when demand is high [19]. For example, Tesla built the world’s largest lithium-ion battery in Australia, pairing it with a wind farm to deliver electricity during peak hours [20]. However, this does not mean lithium-ion is, necessarily, economical for other grid applications.
Lithium-ion has done remarkable things for technology, but, nowadays, the main alternative being explored is a flow battery [21]. Unlike lithium-ion, flow batteries store liquid electrolytes in external tanks, meaning the energy from the electrolyte and the actual source of power generation are decoupled. With lithium-ion tech, the electrolyte is stored within the battery itself. Electrolyte chemistries vary, but across the board, these aqueous systems do not pose a fire risk, and most do not face the same issues with capacity fade.
Besides batteries, another technology that will ensure the reliable operation of the microgrid is pump hydropower [22]. Currently, about 96% of the world’s energy storage comes from one technology: pumped hydro [23]. This system is pretty straightforward. When there’s excess energy on the grid, it is used to pump water uphill to a high-elevation reservoir. Then, when there is energy demand, the water is released, driving a turbine as it flows into a reservoir below.
Energy Vault, a gravity-based storage company founded in 2017, was inspired by the pump hydro concept and wanted to bring a new perspective. The company wanted to look at solving the storage problem with something much more environmental, much more low cost, much more scalable, and something that could be brought to market very quickly. Instead of moving water, Energy Vault uses cranes and wires to move 35-ton bricks up and down, depending on energy needs, in a process that’s automated with machine-vision software. The system consists of a tower crane that is utilizing excess solar or wind to drive motors and generators that lift and stack the bricks in a very specific sequence. Then, when the power is needed from the grid, that same system will lower the bricks and discharge the electricity. The system consists of a standard installation that could include 20 towers, providing a total of 350 MWh of storage capacity, enough to power around 40,000 homes for 24 h [24].
The other technology is thermal storage [25]. It is still an emerging technology in this space, but it has the potential to store energy for longer than flow batteries with a smaller footprint than gravity-based systems; currently, many companies are taking on this challenge. Basically, when there is excess electricity on the grid, it is used to heat up cheap carbon blocks, which are insulated inside a container. When needed, that heat is then converted back into electricity using a heat engine. The US-based company Antora is trying to solve a need that is currently, and will continue to be, unmet by lithium-ion batteries and that will, sort of, enable the next wave of integration of renewables on the grid.
There are other creative solutions, for example, Toronto-based Hydrostor is converting surplus electricity into compressed air [26], and the U.K.- and U.S.-based Highview Power is pursuing cryogenic storage [27]. That is, using excess energy to cool down air to the point where it liquefies. These ideas may seem far out, but the investment is pouring in and projects are being piloted around the world.
An accurate model of energy management for the hybrid power system assists to meet load demand, unit connection decisions, operating cost, and aligning emission levels, and the essential is the reliability of the microgrid. In this study, research is carried out on the operation and control of microgrids. Off-grid hybrid systems can, also, be combined with energy storage in pump hydro and batteries, to increase uptime in power generation. Various usage areas and potential benefits of battery-operated and pumped-water-based energy storage units have been examined from different perspectives in many studies in the literature.
Chinese scientists [28] propose to compensate for the intermittent nature of generation at solar and wind power plants, using the most traditional and proven energy storage technology—a pumped-storage power plant. The researchers developed a mathematical model of the proposed hybrid system and showed the principle of interaction of all stations with each other and with the end user. This hybrid system should provide energy to an isolated area group of consumers. The simulation results show that the intermittent nature of energy generation at SPPs and wind farms can be compensated for by pumped storage power plants. Thus, the use of pumped storage power plants, as part of hybrid energy systems operating on renewable energy sources, makes it possible to provide reliable power supply to individual settlements.
In Greece, on the island of Ikaria, a hybrid power plant is being built, which includes a wind farm and a pumped-storage power plant [29]. According to the results, this energy station should work for a dedicated load. The authors of the article proposed an algorithm for the operation of the control system of such a node and assessed the expected effect of the operation of a wind farm in conjunction with a pumped-storage power plant.
Another article [30] considers the option of using batteries as a storage device. The authors proposed a computer model that describes the operation of such a complex hybrid system. The paper considers various methods for predicting generation, depending on changes in meteorological factors, and proposes the determination of the optimal parameters of facilities, depending on the load parameters.
Another work assessed a similar project on the island of Crete (Greece) [31]. However, at the same time, various configurations of a pumped-storage plant are considered. In one version, this is a pumped-storage power plant with reversible hydroelectric units, and, in another version, pumps and turbines are used separately at the station.
William C. Davidon introduced the Quasi-Newton algorithm to the world scientific literature [32]. Gerbeau et al. used this technique in the optimization of difficult problems, such as fluid–structure interaction problems in blood flows [33]. Ono et al. used a Quasi-Newton optimization algorithm in the optimization of multi-objective problems in their study [34]. Sekine et al. proposed an algorithm for large-sized problems [35]. Zheng, and Wu, in their study, presented the modern control design of interconnected power systems [36]. They designed an optimal controller with a proportional controller and a different feedback scheme, using classical control methods for secondary control. Alaei et al. proposed a Quasi-Newton algorithm that is compared with a common PID controller in their study [37]. It should be noted that all studies consider the operation of hybrid power plants for a dedicated load, and not as an energy-generating unit in the structure of a unified energy system. Table 1 presents microgrid configurations, applied optimization techniques, generating sources, and used storage devices, by various authors in recently published studies.

Table 1.
Various optimization techniques, sources, and storage devices in microgrid systems.
As presented in Table 1, the main observations from the reviewed literature are listed below:
- The problem with solar and wind power plants is that the volume of electricity generation depends significantly on weather conditions. In cloudy weather or at night, energy generation at solar power plants is significantly reduced or completely absent. This can seriously affect the network’s overall operation.
- The inclusion of generating nodes with energy storage devices in the structure of microgrids improves the efficiency of the generated power, as well as improves the reliability of consumer supply.
- An isolated microgrid mainly relies on a diesel generator or battery energy storage system to store energy.
- Storage devices, such as batteries and flywheel generators, can play an important role in maintaining the stability of the overall operation of the microgrid system.
- Energy storage systems (pump-hydro) can play a key role. When the price of electricity is low, it pumps water from downstream to upstream.
- A pumped-hydro energy storage system makes a good alternative to batteries, by storing water (energy) to cope with the intermittent nature of renewable energy sources.
Electric demand rises as people become more reliant on energy in all aspects of their lives, putting an undue strain on the utility infrastructure. Microgrid systems rely on distributed energy resources and energy storage devices, to offer end users with a consistent and uninterrupted power supply. Although small-scale distributed energy resources may use both conventional and non-conventional resources, with growing environmental concerns, it is becoming increasingly important to employ non-conventional or renewable energy sources. Renewable energy sources, unlike conventional energy, are not something that can be produced and acquired in an instant by producers and users. With current technology, the majority of renewable energy sources are intermittent, necessitating the use of storage solutions to keep them operational. Electricity supply and demand must be balanced in electrical networks. The increase in the gap between these two states causes voltage and frequency deviations in the electrical power system. These deviations in frequency and voltage seriously threaten the stability of microgrid systems and this can, even, cause major power outages. One of the main problems for the microgrid is frequency control, so real-time matching between generation and demand is essential for the system to work stably and to keep the system frequency at a nominal value. In this study, the load frequency control problem, which considers batteries and pumped-hydro energy as an energy storage system for an island microsystem, will be examined.
Wind and solar power plants in the microgrid system can be installed on the roofs or gardens of the buildings, however, pump-hydropower plants can, also, be built on top of the building, while lower reservoirs can be placed in the basement. There are not many research studies on the practical application of pumped-hydro facilities in the residential area. A small hybrid system project with a micro-pump hydro-energy storage system, consisting of two 150 m3 water tanks with 100 m height difference, 100 Ah battery bank, and 18 kW solar PV in a 13-floor building on a Greek island, has been implemented. If micro-pump hydro-energy storage is built with a natural reservoir or built near a river, the installation costs are significantly lower [22].
Most of the studies reviewed in the literature and summarized in Table 1 have addressed the frequency control of isolated microgrid systems. Various storage devices, optimization techniques, and generators have been used to simulate the microgrid system. However, articles about the operation of a microgrid system, hourly load changes, and changing seasonal conditions have not been fully developed. The performance of the microgrid system on the pump-hydro energy-storage unit does not work much in the literature. In this study, the operational performance of a microgrid system is investigated, using realistic resource data under various operating boundaries, based on renewable energy. However, the general objective of the study states summarized below:
- To develop a detailed model of the microgrid system consisting of pump-hydro, photovoltaic, wind, and energy-storage systems as well as diesel generators.
- To design a MATLAB-based controller for the proposed system, using the Quasi-Newton optimization algorithm.
- To examine the technical performance of the proposed system, with and without an energy storage system, using realistic renewable resources data.
- To investigate whether it is suitable for storage applications of the renewable-based microgrid system, with the pump-type hydroelectric unit.
In the literature, there are many method solutions developed to be applied to different types of microgrids. In these studies, it was aimed to develop technical and cost-effective solutions in general, and different components of the system were considered. However, in none of these studies, frequency fluctuation and generation for the microgrid network were handled as stochastic. In addition to these, few studies have been found on the Quasi-Newton optimization method, for the reliable operation of the microgrid system. Due to the fact that the adequate level of living conditions that will be inherited by future generations depends on the steps to be taken today, the 7th sustainable development goal, which is one of the 17 goals for combating climate change and reducing inequalities all over the world, especially in developing countries such as Turkey, aims to “provide access to affordable, reliable, sustainable and modern energy for everyone” [53,54]. It can be observed in publications [55,56,57] that it represents a strong relationship between small hydroelectric power plants and batteries and is included in the renewable cluster as a promising, competitive energy source. With that in mind, this article examined trends in reducing frequency fluctuations, by using small hydropower and battery technology to achieve sustainable energy development. In this study, load-frequency optimization of the microgrid was carried out using the Quasi-Newton optimization technique, which is widely known in the literature, by costing, according to performance criteria for four different scenarios.
2. Modeling of the Isolated Microgrid System
The proposed microgrid system consists of storage systems (pump hydro and battery), a diesel generator, PV, and wind generator, as shown in Figure 1.
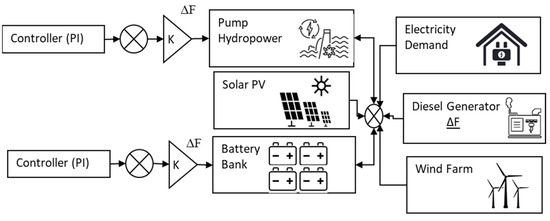
Figure 1.
Schematic diagram of the isolated microgrid.
The mathematical models, which enable the investor to find a feasible solution for the main component in the microgrid facility, are as follows:
2.1. Solar PV System
According to the data of the Electricity Works Survey Administration (EIE), the total annual average sunshine duration of the selected area is 2640 h, and the average total radiation intensity is 1311 kWh/year per square meter. The global formula for estimating the generated electricity at the output of a photovoltaic system is expressed as [22]:
where A denotes the total solar panel area (m2), Ԑ denotes irradiation of solar (kW/m2) (shadings not included), n represents panel efficiency (%), and T denotes ambient temperature (°C). The power output of a PVG system mainly depends on the ambient temperature (T) and irradiation (Ԑ), which is why A and n are taken as constants. The value of T is taken into account at 25 °C in this study. The realistic variation data of the solar radiation (kw/m2) for simulations are shown in Figure 2. The reference of maximum generating capacity is (0.8 p.u) by the PV generator, and the system worked on the basis of the maximum power-point-tracking technique. In this study, the transfer function for the solar power model is considered as:
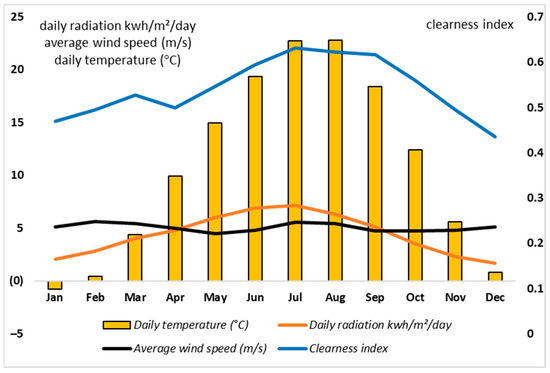
Figure 2.
Realistic renewable resources data of the selected area.
Although low profitability is seen as an insurmountable obstacle to the deployment of PV systems, the efficiency of photovoltaic panels designed for electricity generation from solar energy is increasing, and their costs are decreasing. According to the research [58], the economic viability of solar PV systems in mature markets is inversely proportional to the share of self-consumed energy. Using the discounted-cash-flow approach, [58] investigated the economic feasibility of PV plants installed in public buildings. The net present value and payback durations were calculated using the technique, by calculating the solar exposure level, facility size, self-consumption share, and power purchase price input variables. According to the research, numerous governmental acts have a major impact on the profitability of new PV facilities. At the same time, in mature markets, the profitability of PV facilities is, largely, determined by the percentage of self-consumption [58].
Furthermore, performance-enhancing strategies can lower the cost of energy. Increased grid purchase prices, as well as lower grid sales prices, have resulted in considerable self-supply. As a result, rather than moving extra energy to the grid, prosumers have concentrated on utilizing residual energy, which is excess energy for local demand, locally, to boost self-supply [59].
2.2. Diesel Generator
A diesel generator is used as a backup generating unit in the microgrid system that can provide continuous and reliable power supply during inadequate or less energy generation from PV- and wind-based generators. Using engine kinematics, the rate of mechanical work done by a diesel generator can be mathematically expressed by the following equation [22,60]:
where represents the incremental change in cylinder volume (m3/degree), R denotes the universal gas constant (R = 8.314 kJ/kmol K), S denotes the stroke length (m), L represents the length of connecting rod (m), Vdisp represents the displacement volume (m3), T denotes the instantaneous temperature (Kelvin) at any crank angle θ, and θ is the angular displacement with respect to bottom dead center. Referring to the synchronous generator of the conventional diesel engine generator model, the power output of the diesel generator is, directly, proportional to the inlet valve action, and the internal combustion engine action, consequently, a linearized transfer function is signified by the following, Equation (4):
where denotes power output (in p.u.) of diesel generator unit, denotes valve gain, denotes engine gain, denotes valve actuator delay, and denotes time constants.
2.3. Battery Energy Storage
Microgrid systems cannot provide the necessary and sufficient power to their users when wind and solar energy are insufficient. Elimination of the mentioned negativities is very important for the sustainability and reliability of the system. As a solution to this problem, battery groups are added to the system. The linearized transfer function model of the battery energy storage system can be expressed as follows [22]:
where represents power output of battery unit, denotes gain constants, and denotes time constants.
2.4. Wind Turbine
The estimate of the volume of generated energy at wind power plants was made analytically, using Equation (6). The wind speed values required for the calculations were obtained from NASA.
where = 1.22; air density in , V is the wind speed in m/s, and n is the total efficiency,
The efficiency of the generator and the converter is between the wind wheel and the generator. is the power coefficient of a wind turbine, depending on the profile of the blades and other regime parameters, with the value of 0.4 being taken in the calculations, while A is the area of the wind turbine in .
where r is blade length in meters. The blade tip speed ratio depends on the wind speed and the radius of the propeller. The value is calculated with the following formula and is a unitless quantity.
where is the angular velocity of the propeller (rad/s) and R is the radius of the propeller (m).
is a unitless quantity. When the shaft power of the propeller is divided by the power in the wind, the propeller power coefficient is found. The value of the propeller power coefficient is determined by the speed ratio and some constants, and its value is calculated by the formulas below [22].
The constants here are given as is 0.5176, is 116, is 0.4, is 5, is 21, and is 0.0068. The wind turbine produces electricity, as expressed in Equation (6). Regardless of the turbine used, under ideal conditions, a maximum of 59.3% of the available wind power can be converted into mechanical power. Real wind generators do not reach this theoretical optimum; however, good systems have power coefficients of about 0.4 to 0.5. Therefore, in order to have a realistic scenario, real wind and solar resources data available from NASA surface meteorology were used in the simulation. The wind and solar resource data, located at the latitude of 39°21.9′ N and longitude of 33°43.2′ E, near the Kaman district in Turkey, are used for the study. The annual average wind speed is 5.07 m/s, the annual average solar radiation is found to be 4.5 kWh/m2/day, the annual average temperature is 11 °C, and the clearness index is between 0.46 and 0.63 for the selected location, as displayed in Figure 2. The power output of the wind turbine generator, using the real source data of the wind speed has some limitations.
where Prated represents the rated power output at a rated wind speed of a single turbine, Vrat denotes the rated wind speed, V denotes the wind speed at the desired height, Vout represents cut-out speed, and Vin represents cut-in speeds. The relationship between wind speed and power for the wind turbine is shown in Figure 3. The horizontal axis is expressed in wind speed, measured in meters per second. The vertical axis is expressed in kilowatts.
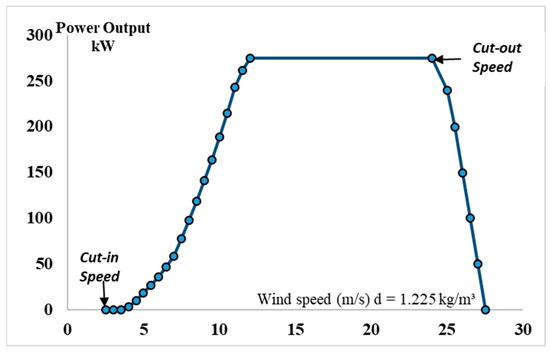
Figure 3.
Power curve using actual data for the wind turbine understudy.
In this study, the transfer function for the wind farm model is considered as:
2.5. System Dynamics Modeling with Pump Micro Hydro
The proposed system consists of micro-pump-storage hydropower and different renewable resource-based power generators with battery storage. The net change between total generation and consumption at any given time in the power of the system can be formulated as the difference between the system’s electricity generation and load demand.
where is net grid power deviations and is net demanded load power. The overall frequency dependent characteristic of a composite load may be expressed by the following equation:
where D is the system’s damping coefficient in (MW/Hz), M is the equivalent inertia constant of the proposed system, and is the frequency deviations of the microgrid.
2.6. Micro-Pumped-Hydro Storage System
In pumped-storage hydroelectric systems, there are two reservoirs, an upper and a lower one. Reservoirs can be a river, a natural lake, an existing dam reservoir, the sea, or an artificial built pool. When energy demand is high or electricity is expensive, electrical energy is produced, by reducing the water accumulated in the upper reservoir to the lower reservoir. When the energy demand is low or electricity is cheap, the pump is operated to raise the water from the lower reservoir level to the upper reservoir level. The reversible use of pump and turbine elements in pumped-storage hydroelectric systems can provide great advantages. While energy is produced by operating the system as a turbine at peak times with a reversible pump turbine, energy can be stored by sending water to the upper reservoir with the pump. Rather than generating electrical energy, pumped-storage power plants are the method of storing the energy required at peak times when the need is low, supplying it when the demand increases, and, also, maintaining the frequency stability of the microgrid system. In addition, since the electrical energy cannot be supplied to the grid when the need is low, the power plants have to be operated at low capacity. With pumped storage systems, solar and PV plants can be operated at full capacity, and excess energy can be stored.
The water flow in the pipeline in this study has a density of 6000 L per minute, and the proposed building is 25 m high. In this study, the efficiency of the proposed power plant is considered as 83%, and its nominal power is assumed to be 21 kW. The amount of energy that can be produced annually is 183.96 kWh, and the energy needs of 60 people per year can be met. The power that the plant can produce can be calculated with the following equation:
Let us assume that during the time t, s, the average water flow rate Q, m3/s, passes the volume of water W = Q t, m3. The total energy of the up and downstream reservoir flow in sections is calculated according to the Bernoulli equation. When using hydraulic reservoirs, energy production is carried out, as a result of the transition of the potential energy of water in the channel, into kinetic energy directly in the hydraulic converter. In this case, the power generated by the falling water will be:
when generating energy using the transit flow method, gross energy production, kWh, with variable water availability at a local hydroelectric complex, can be estimated by the formula:
with a variable flow power, in kW,
A number of operational constraints for various components of a hydroelectric power plant are listed below.
The reservoir storage volume limit:
The water discharge of the reservoir:
The characteristic curve of power plant generation:
The water balance equation:
The rate of the water flow through the turbine (Q) is a positive variable.
The initial and final reservoir storage levels:
The water use rights in Turkey:
The model of pumped-storage hydro systems consists of the actuator, the governor, the hydraulic turbine, and the transient droop compensator. The transfer function of the pump-hydro system is shown in Figure 4.
where is the actuator time constant, and denote the parameters of the ransient droop compensator system, represents the initial time of water of the turbine, and denotes the rated pumping power of a unit.
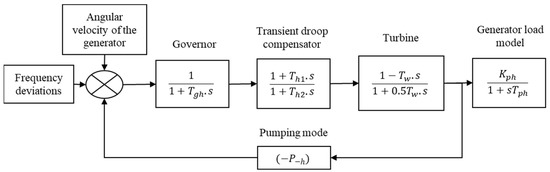
Figure 4.
The pump-hydro unit is obtained via the following transfer function representation [60].
3. Introduction to the Quasi-Newton Method
The common feature of most constrained and unconstrained nonlinear programming algorithms is the definition of a search direction and the derivation of a sequence of sequence points in this direction through one-dimensional search techniques. Thus, the one-dimensional search process, in both the search direction and humidity, determines these algorithms and distinguishes them from the others. The Quasi-Newton method, which is widely known and used in the derivation of research directions, has been developed in the last 30 years. As a result of the studies, minimization methods, called variable metrics, which find the approximation of the inverse of the Hessian matrix of the function to be optimized, by using the information obtained from the first-order derivatives, have emerged [61].
Let For k = 1,2,3…
Consider the problem
For a noise variable ξ.
The most straightforward adaptation of Quasi-Newton methods is to use BFGS with:
The equation finds the minimum of the problem; subject to
lb is Lower bounds, ub is Upper bounds, A and Aeq are matrices, f(x) is a function that returns a scalar, c(x) and ceq(x) are functions that return vectors, f(x), c(x), and ceq(x) can be nonlinear functions.
Objective Function Formulation to Design an Optimal Controller
In this study, a PI controller was used to stabilize the frequency depending on the load change in the single-zone interconnected power system, and the gains of the controller were found by the Quasi-Newton method. The frequency of the power system means the rotational speeds of the synchronous generators operating in the system, and if the electricity produced by the power system and the electrical energy drawn from the loads are equal, the frequency is 50 Hz. Load-frequency control is an automatic control method that re-establishes the active power balance, as a result of the deterioration of the load balance in electrical power systems, and adjusts the changed system frequency back to its nominal value.
Control planning for the off-grid microgrid is, in many cases, more important than the grid-connected mode. In this study, the off-grid microgrid system, in which the analysis processes are carried out, is shown in Figure 5.
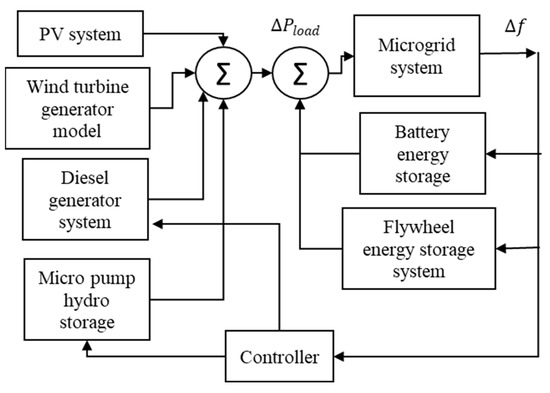
Figure 5.
Frequency response model for the microgrid.
While determining the PI controller parameter values, the integral of time multiplied absolute error criterion which is an error-based objective function is regarded. The equations of this function are given below.
where ΔF symbolizes the deviation of the frequency, and “ts” represents the total simulation time. The integral of the time multiplied absolute error-index criterion has been selected as an objective function, to optimize the gains of the PI controller in the present investigation. The minimization of the error-index using the Quasi-Newton method provides the optimized parameters of the microgrid system controllers, which can be subjected to the following limitations:
Minimize E;
where integral gains of the PI controller of a microgrid system, and symbolize controller for process parameters, with two corresponding variables, which are ub and lb in the optimization algorithm.
Load-frequency control applied to a power system has two main tasks. The first is to adjust the active power of the generator according to the demand, thus keeping the frequency value constant. The rotation speed of the turbine shaft, which is rotated by mechanical energy, also determines the frequency value of this electrical energy. In other words, by adjusting the energy produced in the turbine, the system frequency is, also, controlled. The second task of the load-frequency control is to provide a balanced production, by sharing the demanded load among the interconnected power systems, in order to reduce the operating costs.
4. Simulation Results and Analysis
The simulation model of an energy-generating unit, which includes a solar and wind power plant, and given consumer load schedules at different times, was built in the MATLAB software. The gain of PI controllers is optimized, using the Quasi-Newton method. Time-domain simulations are carried out, to investigate the system performances under the operating four different scenarios of the microgrid system. Details on the short-term scenarios considered to evaluate the role of batteries and small hydropower in improving the performance of the microgrid system are given in Table 2.

Table 2.
Various microgrid system scenarios under the study.
4.1. Non-Availability of Solar Power Full-Day
Determining the size of the hybrid energy system is a problem that needs to be solved by considering different criteria. By its nature, power generation from the sun does not show continuity and stability over time. Since solar energy is intermittent and unstable, an energy storage unit is needed to ensure the continuity of solar energy types. Therefore, the response of the microgrid will be tested as a result of a full-day solar outage in probable cloud, rain, storm, fog, and dust conditions.
4.2. Non-Availability of Wind Power Full-Day
In order to combat the energy production imbalances caused by the intermittent nature of wind energy and to show the effect of energy storage systems on the power-frequency responses of the microgrid system, it is assumed that wind-energy production is interrupted all day long. Although there are different spare reserve options, the ones that are suitable for the conditions of the country are seen as hydraulic energy and pumped-storage systems, which is, also, a hydraulic type. In addition, the fact that renewable energy sources generate power within the grid makes the power flow bidirectional. This makes control even more difficult.
4.3. Random Load Fluctuations and Variable Power Generation throughout the Day
The demand for electrical energy changes from season to season and, even, at different times of the day throughout the year. In order for electricity to be delivered to consumers continuously, safely, and in accordance with standards, generation plants must be operated properly. However, for stable operation, the load changes must be very small compared to the total power of the network. Voltage fluctuations, harmonic distortions, frequency fluctuations, voltage flickers, etc., can create disruptive effects. The power produced and consumed must be momentarily balanced (frequency stability). The changes in consumption demand at different times of the day are taken into account.
4.4. Sudden Variation of a Load Change with Day-to-Day Operations
This scenario is assumed to explore the operational behavior of the microgrid system during any surge load demand. It is essential that the system frequency remains constant no matter the load change. All production units that adjust the speed contribute to the overall change in production, regardless of the region where the load changes. In this case, 18% instantaneous load change in the microgrid at 07:00 am in the morning is taken into account to analyze the response of the microgrid system with and without energy storage. Moreover, it is considered that there may be a sudden 18% load reduction at 21:00 in the evening. The frequency result of the proposed microgrid system simulated with and without battery and pump-type hydroelectric energy storage systems, under the assumed scenarios shown in Table 2, is presented in Figure 6.
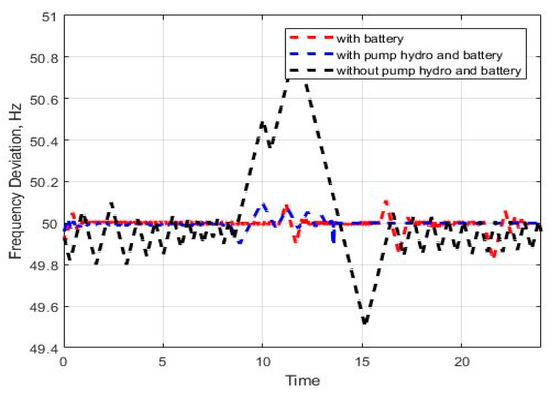
Figure 6.
Frequency response of the microgrid without solar power full-day.
The performances of the controllers used in this study were compared with simulation studies in terms of resistance to disturbances, such as output voltage settling time to reference value, sudden changes in load, overshoot, and input voltage. In this way, it is aimed to minimize the positional error. System delays and pre-settlement production oscillations cause short-term positive faults and, thus, instantaneous energy shortages. A sufficiently long power shortage is an undesirable situation, as it carries the risk of causing power outages in the system. In summary, virtual demand leads to overproduction, providing resistance to a positive fault condition. The reason for the long settling time of the system is due to the mismatch between load demand and production. The power generated during the day in the microgrid system is uneven, due to the intermittent nature of solar and wind generators. In this case, the frequency response will occur from unconventional sources. These mechanisms are listed as wind and solar resources, energy storage, and demand-side response.
When renewable generation is low or nonexistent, the undershoots frequency increases in a system without a storage component. However, the microgrid system, with battery and pump type hydropower facility, has a reliable frequency and much more stable structure compared to the system without hydroelectricity, even in the case of wind and solar generation outages all day (Figure 7). Pumped-storage hydropower is a type of hydroelectric energy storage, and its coordinated action with battery units ensures the balance of generation and demand. The coordinated action of pump-type hydropower and battery units sustain the generation and demand balance.
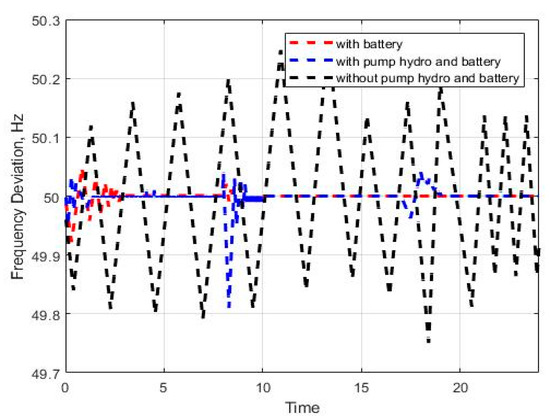
Figure 7.
Frequency response of the microgrid without wind power full-day.
Frequency stability is defined as the ability to maintain a stable frequency and produce the same value of frequency for any interval time throughout a specified period of time. The load-frequency control in the microgrid, in which the micro-pump-hydro energy-storage system is included, has ensured that the system remains stable.
The pumped-storage hydroelectric power plant operates in generation mode when the electricity price is high or the solar energy is high, using the water that is stored in a downstream reservoir. In times when the electrical energy is cheap, meaning, when the demand is low, the pumped-storage hydroelectric power plant operates in pump mode, pumping the water from the lower reservoir to the upper reservoir and storing the electrical energy as the potential energy of the water. Thereby pump-hydro effectively participates in maintaining microgrid stability, and better frequency dynamics are provided. Thus, it can be seen that the system with battery and pump-hydro energy storage achieves a better result leading to faster system frequency recovery. Thanks to energy-storage systems, frequency fluctuation can be limited by compensating for the mismatch between demand and generation. These results confirm that energy storage systems are essential components of a microgrid system with generation, due to the intermittent nature of renewable energy sources. As seen in Figure 8 and Figure 9, the frequency fluctuation is within the specified limits after the pump-hydro unit is included in the system.
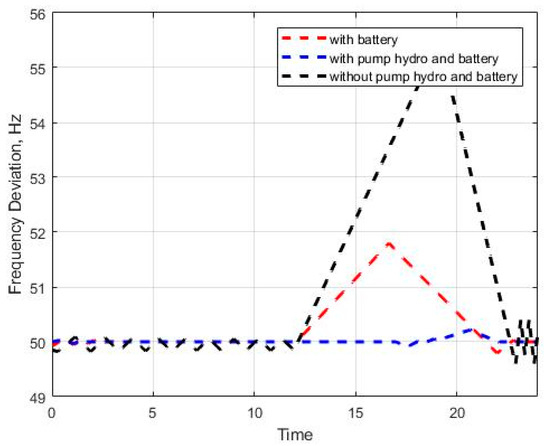
Figure 8.
Frequency response of the microgrid with random load fluctuations and variable power generation.
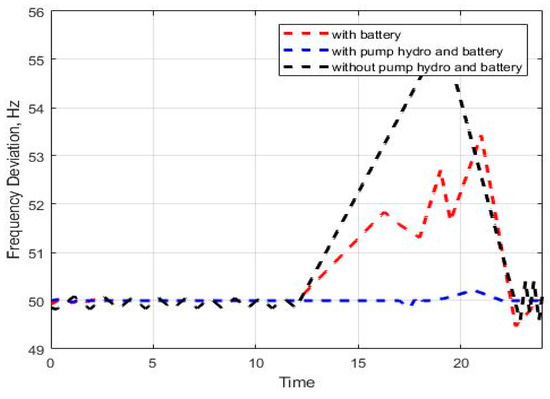
Figure 9.
Frequency response of the microgrid with a sudden variation of load change.
The power response of diesel generator, solar PV, and wind turbine micro-pump hydropower and battery, as well as load demand with respect to the assumed operating conditions of the microgrid system for a period of 24 h, is shown in Figure 10 and Figure 11. The power output of the microgrid system, when there is no solar energy during the day, is presented in Figure 11. Pump micro-hydro, wind, and battery systems work in coordination with each other and provide a continuous power supply for the stable operation of the grid. Given the intermittency of renewable sources, severe storm batteries and wind-based microgrids are not suitable for most off-grid applications without a diesel generator, which is, often, used as a boost.
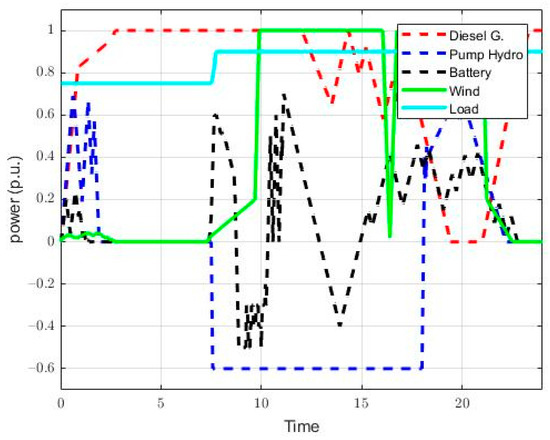
Figure 10.
Power response of the microgrid with storage system without full-day solar power.
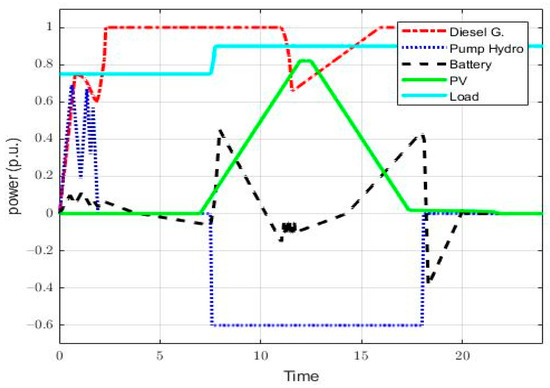
Figure 11.
Power response of the microgrid with storage system without full-day wind power.
Hydro energy can be used as an alternative, when the sun is out of power or inefficient for a full day. Thus, the continuity of energy production in the system is ensured. Under realistic conditions, such a probability depends on the geographic location of the network and is very low throughout the year. Consequently, in this study, the pumped storage hydropower plant can be operated in pumping mode between 15:00 and 16:00, by utilizing the power generated from the wind turbine. After filling the upper reservoir, the hydro pump operates in generation mode from 19:00 to 24:00, in the absence of renewable sources. By activating energy storage that charges using renewable generation, the flexibility of the system is increased and the power variations of electrical energy can be mitigated.
The fluctuation of the network in the absence of wind energy during the day is presented in Figure 11. The diesel generator responds to meet the load demand and pump hydropower operates in pump mode during daylight hours, when PV generation is available. Moreover, in case of sudden load change and for the reliable operation of the network, the energy demand is met by the battery units.
Figure 9 and Figure 10 represent the power response and load fluctuations of the grid during sudden load change conditions, respectively. In these cases, solar cells and wind turbines can generate power based on current renewable resource conditions. During the daytime, the diesel generator may shut down, and the generation from wind and sun is sufficient to meet the demand. Minimum and maximum wind speeds are designed for wind-turbine production. These limit speed values are given by the producer companies. Generation is not made below the minimum wind speed, and in extreme winds and strong storms, the turbine is turned off. In such a case, the battery groups activate the stored energy to meet the load demand, as shown in Figure 11. In case of sudden load change, the battery responds quickly and charges using renewable generation. On the other hand, the diesel generator helps to meet the energy demand, when there is no renewable generation.
Additionally, the pump hydro system works in peak demand hours and at night in production mode, reducing the load on the diesel generator. As seen in Figure 10, at 20:30 the power demand of the load was 0.85 pu, and this load demand was met by the batteries and pump-hydro until 23:00. If there is no hydroelectric power plant in the system, the power requirement is met by the diesel generator and battery groups. Therefore, after a pump-hydro unit is included in the proposed microgrid system, the fuel consumption in battery and diesel generator systems is less, compared to the system without a pump hydro unit. The achieved results show that the components of the microgrid system respond well to meet the load demand, and less frequency fluctuation of the system has occurred under various operating conditions.
Based on the results of the research, the following conclusions can be drawn:
- The electrical energy produced by the renewable energy source varies according to seasonal conditions. For this reason, in order to ensure the energy continuity of the system in the island-mode microgrid, diesel generators and batteries are used for the worst-case scenarios, where there is no access to electrical energy. This shows that renewable energy sources make a limited contribution to energy production.
- Energy storage technologies, such as batteries and pump hydro, are a solution to these problems, as they are integrated into the microgrid, to ensure reliability and quality in the efficiency of the power system with different renewable energy sources.
- Electricity is stored with storage systems, when energy prices are low and renewable resources are plentiful, and it is used when energy prices are high, thereby reducing energy costs. It provides support to users to increase the reliability of the power supply in case of failures in microgrids and sudden load changes. It, also, improves the power quality, by protecting the frequencies and voltages of the microgrids.
- A basic descent direction Quasi-Newton-mehtod-based optimization technique was applied, simultaneously, for smooth constrained optimization of all PI controllers during different operating conditions of the microgrid system. The frequency fluctuations were minimized by means of a descent-direction Quasi-Newton-method-based optimization method, namely, the Broyden–Fletcher–Goldfarb–Shanno technique.
- Battery groups and diesel generators are in the group of controllable sources, as they can adjust the energy production according to the load demand. For microgrid applications, a diesel generator is used as a secondary energy source and ensures energy continuity.
- It is aimed to coordinate the load flow between the components of the microgrid, meet the energy demand, maximize the benefit obtained from the wind and PV power system, and consume minimum fuel from the diesel generator in the network system, with the pump-hydro system in this direction.
5. Conclusions
In this study, for the island-mode situation, separate analyses of the situations, with and without the pump hydro in the microgrid system, are analyzed. The Quasi-Newton approach is used to optimize the controller of the microgrid system. The proposed microgrid system’s performance was examined for a 24 h period under several most likely operational scenarios. The frequency fluctuation function was reduced using the Broyden–Fletcher–Goldfarb–Shanno methodology, which is a descend-direction Quasi-Newton-based optimization method. This optimization method produced an ideal controller with a decentralized PI structure that was resistant to disturbances. Investigations revealed that pump hydro increases the flexibility of the system: during the maximum generation, the excess energy feeds the storage device, or it can be directed to the system, and during the period of maximum loads the storage device maintains the required power level with a lack of generation.
As a result, it has been seen that the pump hydro effectively reduces the dependency on the diesel generator and reduces the frequency fluctuation in weak production conditions, where renewable energy generation is insufficient, and in case of a sudden load increase. In future studies, the problem of determining renewable energy resource capacities that will minimize the dependency on diesel generators for the existing pump-hydro infrastructure can be studied. Thus, optimal energy investment, optimal frequency level, and self-sufficient microgrid design can be progressed.
In future studies, the effects of different optimization techniques, such as particle swarm optimization, gray wolf optimizer, and genetic algorithm, on the network frequency, can be investigated and compared. Moreover, controllers such as the proportional-integral-derivative (PID) controller, proportional-derivative controller, proportional-integral controller, and PID controller with filter controller can be compared, in terms of power systems control.
Author Contributions
Conceptualization, Supervision, Data curation, writing—original draft, software; H.H.C.; formal analysis, resources, writing—review and editing, investigation, A.R.; visualization, funding acquisition, writing—review and editing, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated during and/or analyzed in the current study are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cebulla, F.; Haas, J.; Eichman, J.; Nowak, W.; Mancarella, P. How much electrical energy storage do we need? A synthesis for the U.S., Europe, and Germany. J. Clean. Prod. 2018, 181, 449–459. [Google Scholar] [CrossRef]
- Cowie, P.; Townsend, L.; Salemink, K. Smart rural futures: Will rural areas be left behind in the 4th industrial revolution? J. Rural Stud. 2020, 79, 169–176. [Google Scholar] [CrossRef] [PubMed]
- Coban, H.H. A 100% renewable energy system: The case of Turkey in the year 2050. İleri Mühendislik Çalışmaları ve Teknol. Derg. 2020, 1, 130–141. Available online: https://dergipark.org.tr/en/pub/imctd/issue/59372/817991 (accessed on 10 March 2022).
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strateg. Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Olabi, A.G.; Abdelkareem, M.A. Renewable energy and climate change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Hien, R.K.T.; Shah, N. China’s roadmap to low-carbon electricity and water: Disentangling greenhouse gas (GHG) emissions from electricity-water nexus via renewable wind and solar power generation, and carbon capture and storage. Appl. Energy 2019, 235, 31–42. [Google Scholar] [CrossRef] [Green Version]
- Wada, Y.; van Beek, L.P.H.; Bierkens, M.F.P. Modelling global water stress of the recent past: On the relative importance of trends in water demand and climate variability. Hydrol. Earth Syst. Sci. 2011, 15, 3785–3808. [Google Scholar] [CrossRef] [Green Version]
- Perez-DeLaMora, D.A.; Quiroz-Ibarra, J.E.; Fernandez-Anaya, G.; Hernandez-Martinez, E.G. Roadmap on community-based microgrids deployment: An extensive review. Energy Rep. 2021, 7, 2883–2898. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Sawle, Y. Smart microgrid integration and optimization. In Active Electrical Distribution Network: A Smart Approach; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Orsini, L.; Kessler, S.; Wei, J.; Field, H. How the Brooklyn Microgrid and TransActive Grid are paving the way to next-gen energy markets. In The Energy Internet; Elsevier: Amsterda, The Netherlands, 2019; pp. 223–239. [Google Scholar]
- Raji, A.K.; Luta, D.N. Modeling and optimization of a community microgrid components. Energy Proc. 2019, 156, 406–411. [Google Scholar] [CrossRef]
- Zhongming, Z.; Linong, L.; Xiaona, Y.; Wangqiang, Z.; Wei, L. Climate Central Solutions Brief: Battery Energy Storage, 2019. Available online: https://www.climatecentral.org/pdfs/2019Batteries_Report.pdf (accessed on 10 March 2022).
- Sheha, M.N.; Powell, K.M. An economic and policy case for proactive home energy management systems with photovoltaics and batteries. Electr. J. 2019, 32, 6–12. [Google Scholar] [CrossRef]
- Ayeng’o, S.P.; Schirmer, T.; Kairies, K.P.; Axelsen, H.; Uwe Sauer, D. Comparison of off-grid power supply systems using lead-acid and lithium-ion batteries. Sol. Energy 2018, 162, 140–152. [Google Scholar] [CrossRef]
- Leonard, M.D.; Michaelides, E.E.; Michaelides, D.N. Energy storage needs for the substitution of fossil fuel power plants with renewables. Renew. Energy 2020, 145, 951–962. [Google Scholar] [CrossRef]
- Yanamandra, K.; Pinisetty, D.; Daoud, A.; Gupta, N. Recycling of li-ion and lead acid batteries: A review. J. Indian Inst. Sci. 2022, 2022, 1–15. [Google Scholar] [CrossRef]
- Stroup, M.A. Draining the flooded markets: Tariffs, suniva & solar energy investment. Indiana J. Glob. Leg. Stud. 2019, 26, 317–334. [Google Scholar] [CrossRef] [Green Version]
- Jäger-Waldau, A. Snapshot of Photovoltaics—February 2020. Energies 2020, 13, 930. [Google Scholar] [CrossRef] [Green Version]
- Mallapragada, D.S.; Sepulveda, N.A.; Jenkins, J.D. Long-run system value of battery energy storage in future grids with increasing wind and solar generation. Appl. Energy 2020, 275, 115390. [Google Scholar] [CrossRef]
- Zeng, H.; Sun, F.; Ge, W.; Su, A.; Gao, K.; Ge, Y.; Liu, A. Introduction of australian 100MW storage operation and its enlightenment to China. In Proceedings of the China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; pp. 2895–2900. [Google Scholar] [CrossRef]
- Pham-Truong, T.N.; Wang, Q.; Ghilane, J.; Randriamahazaka, H. Recent advances in the development of organic and organometallic redox shuttles for lithium-ion redox flow batteries. ChemSusChem 2020, 13, 2142–2159. [Google Scholar] [CrossRef]
- Dhundhara, S.; Verma, Y.P. Application of micro pump hydro energy storage for reliable operation of microgrid system. IET Renew. Power Gener. 2020, 14, 1368–1378. [Google Scholar] [CrossRef]
- Blakers, A.; Stocks, M.; Lu, B.; Cheng, C. A review of pumped hydro energy storage. Prog. Energy 2021, 3, 022003. [Google Scholar] [CrossRef]
- Shan, R.; Reagan, J.; Castellanos, S.; Kurtz, S.; Kittner, N. Evaluating emerging long-duration energy storage technologies. Renew. Sustain. Energy Rev. 2022, 159, 112240. [Google Scholar] [CrossRef]
- Yu, N.; Wang, R.Z.; Wang, L.W. Sorption thermal storage for solar energy. Prog. Energy Combust. Sci. 2013, 39, 489–514. [Google Scholar] [CrossRef]
- Beaugendre, E.; Lagrandeur, J.; Cheayb, M.; Poncet, S. Integration of vortex tubes in a trigenerative compressed air energy storage system. Energy Convers. Manag. 2021, 240, 1142225. [Google Scholar] [CrossRef]
- Hamdy, S.; Morosuk, T.; Tsatsaronis, G. Exergetic and economic assessment of integrated cryogenic energy storage systems. Cryogenics 2019, 99, 39–50. [Google Scholar] [CrossRef]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Technical feasibility study on a standalone hybrid solar-wind system with pumped hydro storage for a remote island in Hong Kong. Renew. Energy 2014, 69, 7–15. [Google Scholar] [CrossRef]
- Papaefthymiou, S.V.; Karamanou, E.G.; Papathanassiou, S.A.; Papadopoulos, M.P. A wind-hydro-pumped storage station leading to high RES penetration in the autonomous island system of Ikaria. IEEE Trans. Sustain. Energy 2010, 1, 163–172. [Google Scholar] [CrossRef]
- Ma, C.; Dong, S.; Lian, J.; Pang, X. Multi-objective sizing of hybrid energy storage system for large-scale photovoltaic power generation system. Sustainability 2019, 11, 5441. [Google Scholar] [CrossRef] [Green Version]
- Anagnostopoulos, J.S.; Papantonis, D.E. Simulation and size optimization of a pumped-storage power plant for the recovery of wind-farms rejected energy. Renew. Energy 2008, 33, 1685–1694. [Google Scholar] [CrossRef]
- Mishra, S.K.; Ram, B. Quasi-Newton Methods; Springer: Singapore, 2019. [Google Scholar]
- Gerbeau, J.-F.; Vidrascu, M. A Quasi-Newton Algorithm Based on a Reduced Model for Fluid-Structure Interaction Problems in Blood Flows. ESAIM Math. Model. Numer. Anal. 2003, 37, 631–647. [Google Scholar] [CrossRef] [Green Version]
- Ono, S.; Hirotani, Y.; Nakayama, S. A memetic algorithm for robust optimal solution search-Hybridization of multi-objective genetic algorithm and quasi-newton method. Int. J. Innov. Comput. Inf. Control. 2009, 5, 5011–5019. [Google Scholar]
- Sekine, T.; Namerikawa, T. Optimal Control Based on Quasi-Newton Method Considering Cooperation of Constrained Distributed Energy Resources. In Proceedings of the 2018 57th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Nara, Japan, 11–14 September 2018; pp. 958–963. [Google Scholar] [CrossRef]
- Zheng, W.; Wu, W. An adaptive distributed quasi-newton method for power system state estimation. IEEE Trans. Smart Grid 2018, 10, 5114–5124. [Google Scholar] [CrossRef]
- Alaei, H.K.; Yazdizadeh, A.; Aliabadi, A. Nonlinear predictive controller design for load frequency control in power system using quasi Newton optimization approach. In Proceedings of the IEEE International Conference on Control Applications (CCA), Hyderabad, India, 28–30 August 2013; pp. 679–684. [Google Scholar] [CrossRef]
- Liu, M.; Cheng, Z.; Zhang, Z.; Sun, M.; Deng, R.; Cheng, P.; Chow, M.Y. A Multi-Agent System Based Hierarchical Control Framework for Microgrids. In Proceedings of the EEE Power & Energy Society General Meeting (PESGM), Washington, DC, USA, 26–29 July 2021; pp. 13–17. [Google Scholar] [CrossRef]
- Eini, M.K.; Moghaddam, M.M.; Tavakoli, A.; Alizadeh, B. Improving the stability of hybrid microgrids by nonlinear centralized control in island performance. Int. J. Electr. Power Energy Syst. 2022, 136, 107688. [Google Scholar] [CrossRef]
- Veluchamy, K.; Veluchamy, M. A new energy management technique for microgrid system using muddy soil fish optimization algorithm. Int. J. Energy Res. 2021, 45, 14824–14844. [Google Scholar] [CrossRef]
- Seervi, A.; Saini, V.K. Centralize Energy Storage Scheduling for Prosumers in Residential Microgrid. In Proceedings of the 2nd International Conference on Power Electronics & IoT Applications in Renewable Energy and its Control (PARC), Mathura, India, 21–22 January 2022; pp. 1–6. [Google Scholar]
- Xie, P.; Jia, Y.; Chen, H.; Wu, J.; Cai, Z. Mixed-stage energy management for decentralized microgrid cluster based on enhanced tube model predictive control. IEEE Trans. Smart Grid 2021, 12, 3780–3792. [Google Scholar] [CrossRef]
- Swain, A.; Salkuti, S.R.; Swain, K. An optimized and decentralized energy provision system for smart cities. Energies 2021, 14, 1451. [Google Scholar] [CrossRef]
- Wang, Y.; Rousis, A.O.; Strbac, G. Resilience-driven optimal sizing and pre-positioning of mobile energy storage systems in decentralized networked microgrids. Appl. Energy 2022, 305, 117921. [Google Scholar] [CrossRef]
- Yakout, A.H.; Kotb, H.; Hasanien, H.M.; Aboras, K.M. Optimal Fuzzy PIDF load frequency controller for hybrid microgrid system using marine predator algorithm. IEEE Access 2021, 9, 54220–54232. [Google Scholar] [CrossRef]
- Li, H.; Rezvani, A.; Hu, J.; Ohshima, K. Optimal day-ahead scheduling of microgrid with hybrid electric vehicles using MSFLA algorithm considering control strategies. Sustain. Cities Soc. 2021, 66, 102681. [Google Scholar] [CrossRef]
- Fathi, M.; Khezri, R.; Yazdani, A.; Mahmoudi, A. Comparative study of metaheuristic algorithms for optimal sizing of standalone microgrids in a remote area community. Neural Comput. Appl. 2022, 34, 5181–5199. [Google Scholar] [CrossRef]
- Dey, B.; Bhattacharyya, B.; Devarapalli, R. A novel hybrid algorithm for solving emerging electricity market pricing problem of microgrid. Int. J. Intell. Syst. 2021, 36, 919–961. [Google Scholar] [CrossRef]
- Zaki Diab, A.A.; El-Rifaie, A.M.; Zaky, M.M.; Tolba, M.A. Optimal sizing of stand-alone microgrids based on recent metaheuristic algorithms. Mathematics 2022, 10, 140. [Google Scholar] [CrossRef]
- Ambia, M.N.; Meng, K.; Xiao, W.; Dong, Z.Y. Nested formation approach for networked microgrid self-healing in islanded mode. IEEE Trans. Power Deliv. 2021, 36, 452–464. [Google Scholar] [CrossRef]
- Ambia, M.N. Advanced Control of Multi-Microgrids for Grid Integration. Ph.D. Thesis, University of Sydney, Sydney, Australia, 2021. [Google Scholar]
- Dahiru, A.T.; Tan, C.W.; Salisu, S.; Lau, K.Y. Multi-configurational sizing and analysis in a nanogrid using nested integer linear programming. J. Clean. Prod. 2021, 323, 129159. [Google Scholar] [CrossRef]
- Villavicencio Calzadilla, P.; Mauger, R. The UN’s new sustainable development agenda and renewable energy: The challenge to reach SDG7 while achieving energy justice. J. Energy Nat. Resour. Law 2018, 36, 233–254. [Google Scholar] [CrossRef]
- Zakari, A.; Khan, I.; Tan, D.; Alvarado, R.; Dagar, V. Energy efficiency and sustainable development goals (SDGs). Energy 2022, 239, 122365. [Google Scholar] [CrossRef]
- Wang, X.; Chen, L.; Chen, Q.; Mei, Y.; Wang, H. Model and analysis of integrating wind and PV power in remote and core areas with small hydropower and pumped hydropower storage. Energies 2018, 11, 3459. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.; Blakers, A.; Stocks, M.; Lu, B. Pumped hydro energy storage and 100% renewable electricity for East Asia. Glob. Energy Interconnect. 2019, 2, 386–392. [Google Scholar] [CrossRef]
- Blakers, A.; Stocks, M.; Lu, B.; Cheng, C.; Stocks, R. Pathway to 100% Renewable Electricity. IEEE J. Photovoltaics 2019, 9, 1828–1833. [Google Scholar] [CrossRef]
- D’Adamo, I.; Falcone, P.M.; Gastaldi, M.; Morone, P. The economic viability of photovoltaic systems in public buildings: Evidence from Italy. Energy 2020, 207, 118316. [Google Scholar] [CrossRef]
- Wang, Y.; Das, R.; Putrus, G.; Kotter, R. Economic evaluation of photovoltaic and energy storage technologies for future domestic energy systems–A case study of the UK. Energy 2020, 203, 117826. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability; McGraw-Hill Book Company, Inc.: Columbus, OH, USA, 2007. [Google Scholar]
- Dennis, J.E., Jr.; Moré, J.J. Quasi-Newton Methods, Motivation and Theory. SIAM Rev. 1977, 19, 46–89. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).