1. Introduction
Lack of precipitation during a drought is a complex and cyclical phenomenon that has a negative impact on agricultural and water resources, as well as on society [
1,
2]. The damage caused by drought is relatively higher than other natural disasters, such as extreme drought in South China, which reduced the area of Honghu Lake and severely impacted tourism, aquaculture, and the public [
3]. Similar to this, the 2012 US drought cost over 12 billion USD in economic losses and subsequently raised food prices throughout the world [
4]. Future droughts are predicted to be more frequent and more intense due to climate change, urging water resource managers to implement comprehensive risk-mitigation measures [
5]. The creeping nature of drought can be beneficial for drought scientists to predict these events in advance [
6]. In recent decades, advancements in various drought modeling approaches have been observed, which will ultimately play a critical role in effective drought modeling and drought risk reduction.
Droughts can be characterized as agricultural, meteorological, hydrological, or socioeconomic based on the kind of water insufficiency, such as precipitation, runoff, soil moisture, and water availability, respectively [
7]. Among these categories, meteorological drought is the most important; it is barely dependent on precipitation and prolonged meteorological drought results in other drought categories [
8]. Several drought indices, including the standardized precipitation index (SPI), Palmer drought severity index, standardized precipitation evapotranspiration index (SPEI), standardized runoff index, etc., have been developed in the past few decades to model meteorological, hydrological, and agricultural drought [
5,
7]. Standardized drought indices have been utilized often for drought modeling because they are easy to use, flexible, and can estimate drought throughout many periods, with few data requirements [
3,
9].
It is crucial to anticipate a drought before it occurs, in addition to monitoring it [
10]. Despite the fact that predicting droughts is a challenging task owing to the inherent uncertainties and high degree of complexity [
11], drought forecasting analysis is essential for supplying pertinent data for drought risk reduction [
12]. In hydro-meteorological applications, physical and data-driven models are the most common drought forecasting models [
13]. Data-driven models create the strongest link between independent and dependent variables, whereas physical-based models are focused on understanding the real dynamics of a system [
14]. The parameter estimation of physical process-based models requires information regarding soil, land use, geography, topography, water abstraction, etc., which is not only difficult to obtain, but also poses difficulties in terms of deviating from a thorough scientific understanding of different physical processes [
15]. Because of the drawbacks of physical process-based models, data-driven models are used increasingly frequently in the field of hydrology and water management. Data-driven models such as machine learning models, regression models, and time-series models are commonly used in drought forecasting [
5,
16].
Data-driven models provide the capacity to anticipate droughts, according to Achite et al. [
16]. Maca and Pech [
17] utilized two types of artificial neural network (ANN) models to foresee droughts in two watersheds, namely Santa Ysabel Creek and Leaf River in South California. The results demonstrated that the hybrid ANN model outperformed the feed-forward ANN. Mokhtarzad et al. [
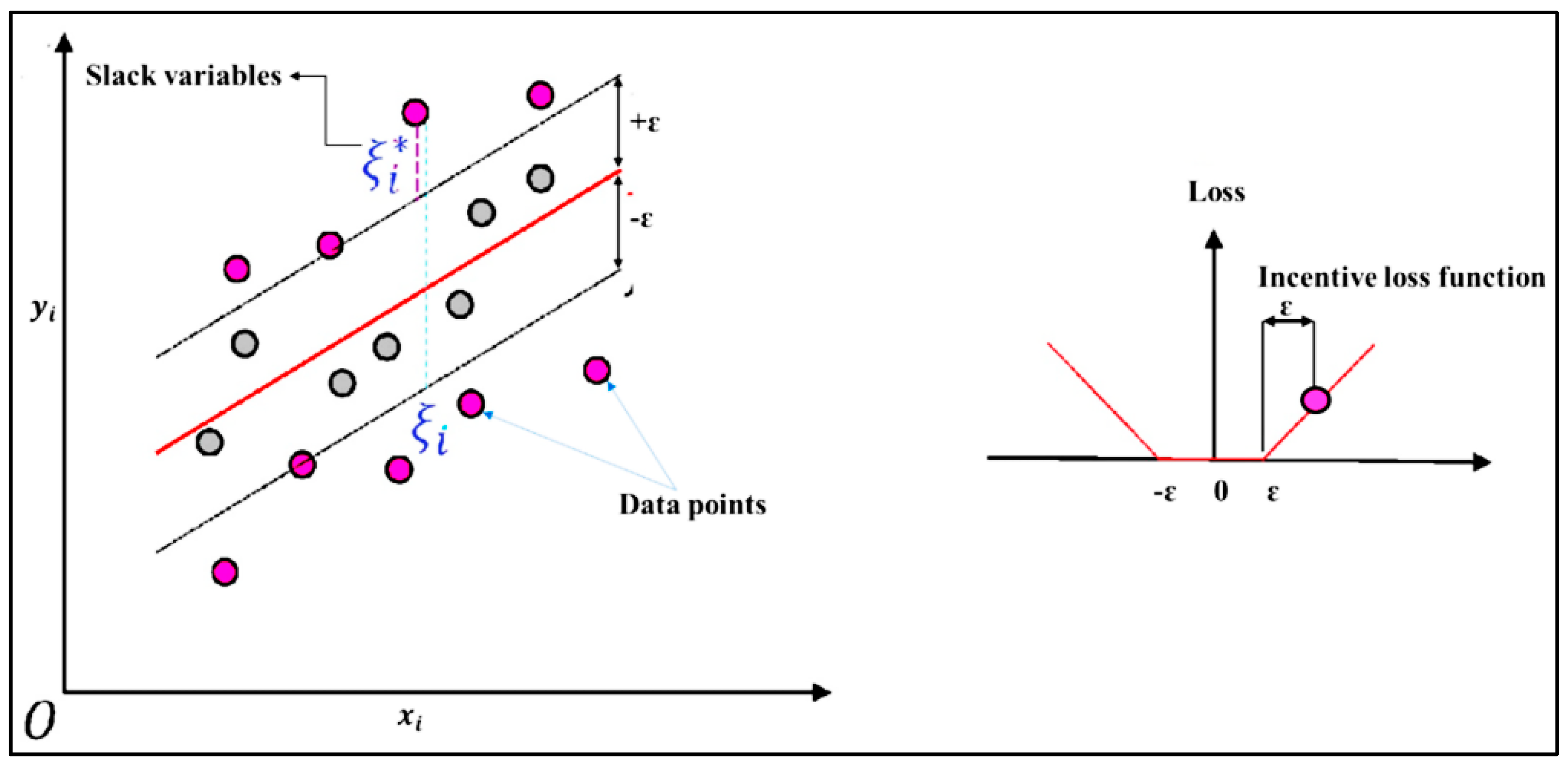
18] employed three machine learning approaches, ANN, adaptive neuro-fuzzy inference system (ANFIS), and support vector machine (SVM), to predict meteorological drought at seasonal timescales in Iran. Although the models’ ability to predict drought was demonstrated by the results, SVM outperformed ANN and ANFIS. Similarly, Sattar et al. [
19] used a Markov Bayesian classifier (MBC) to predict various classes of meteorological and hydrological drought. They reported that MBC had a range of 36% to 76% and 33% to 70% accuracy in forecasting both meteorological and hydrological drought, respectively. Jehanzaib et al. [
12] compared the performance of six ML models for hydrological drought forecasting and concluded that the performance of the decision tree model was found to be superior in terms of forecast accuracy and computation time. Adnan et al. [
20] integrated random vector functional link (RVFL) with the salp swarm algorithm, particle swarm optimization, hunger games search (HGS) algorithm, social spider optimization, genetic algorithm, and grey wolf optimization to forecast SPI at various timescales (3, 6, 9, and 12 months) and suggested that HGS-based RVFL can be used for drought forecasting with a high accuracy.
Most of the previous studies [
12,
13,
17,
18,
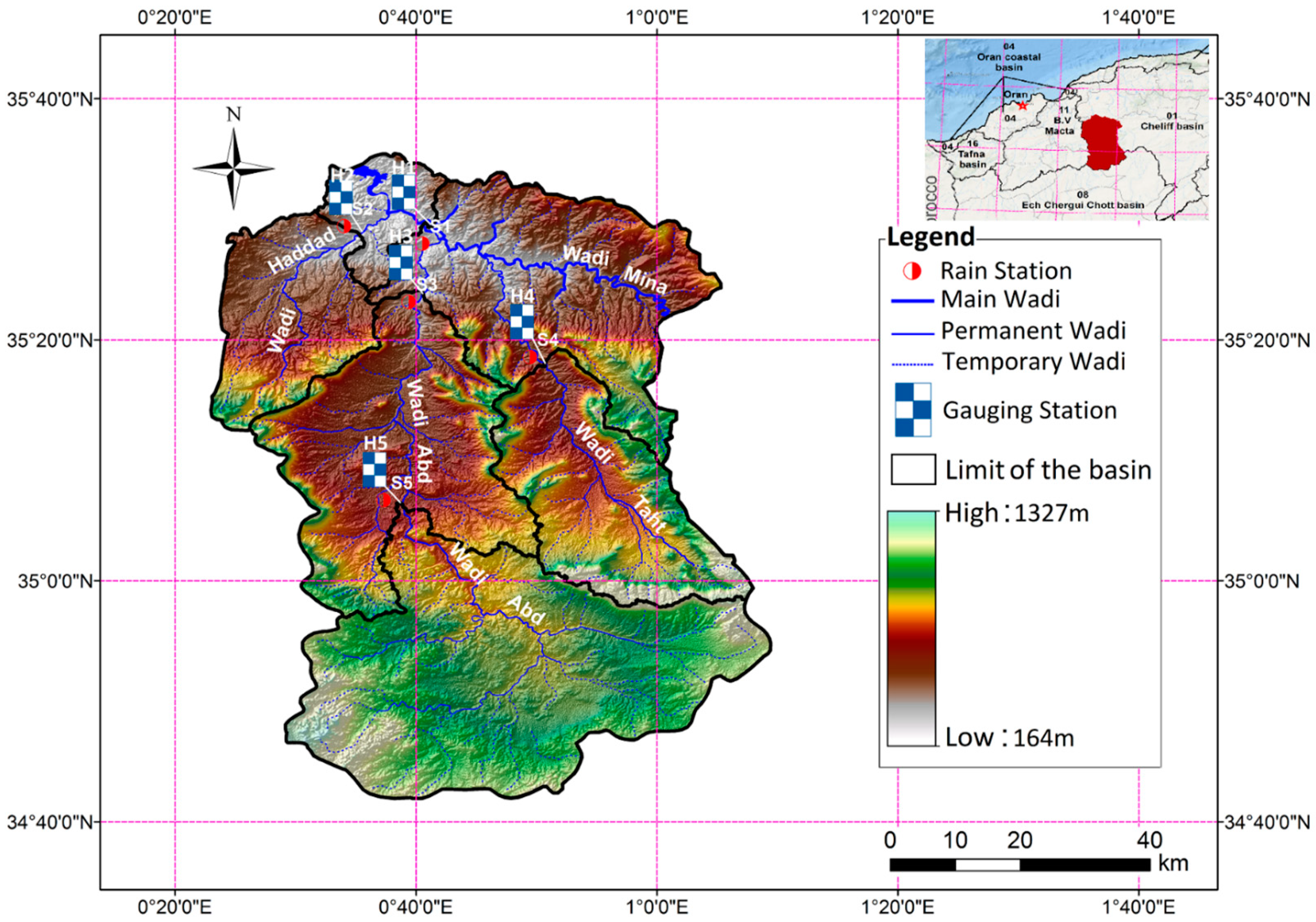
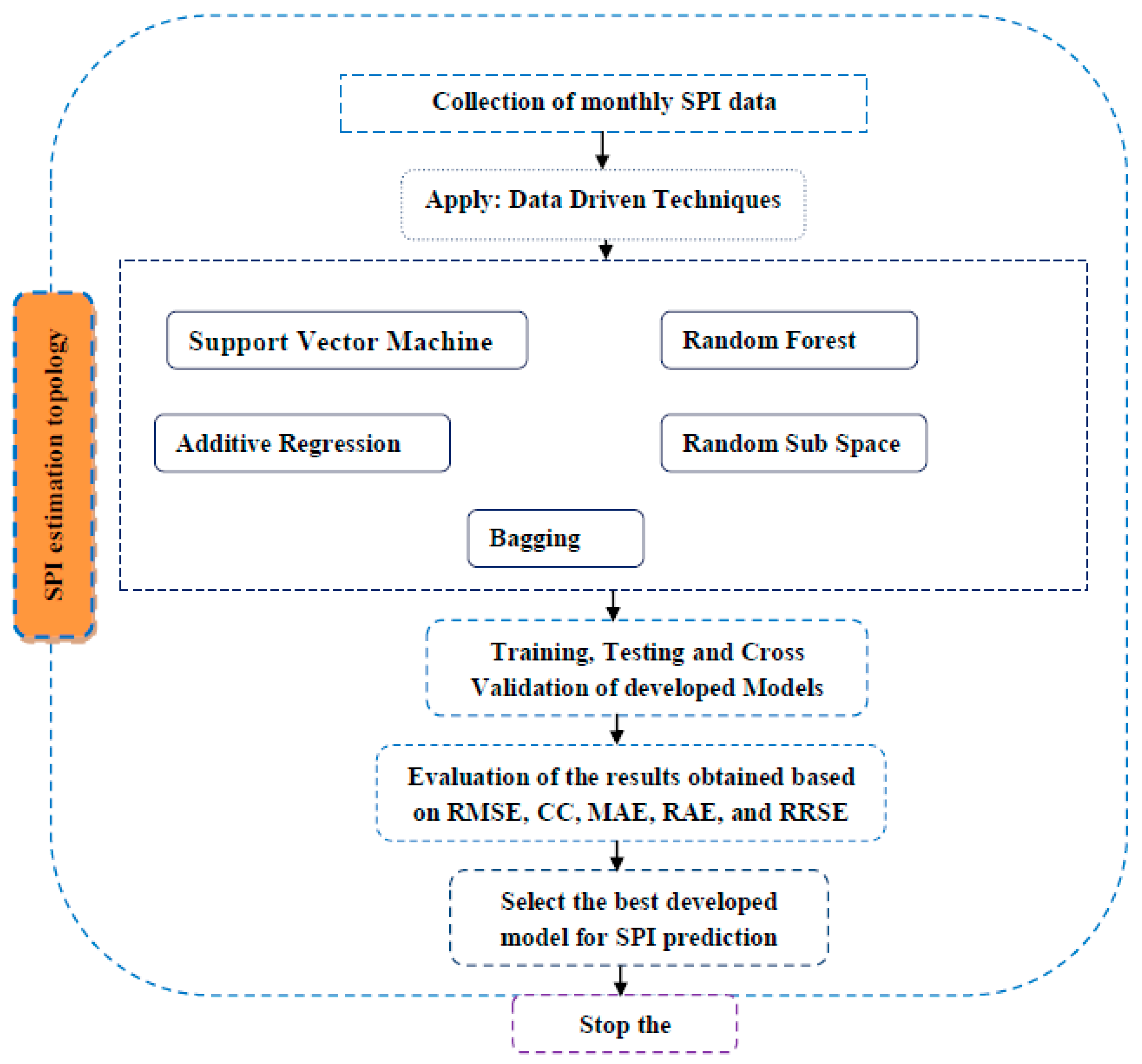
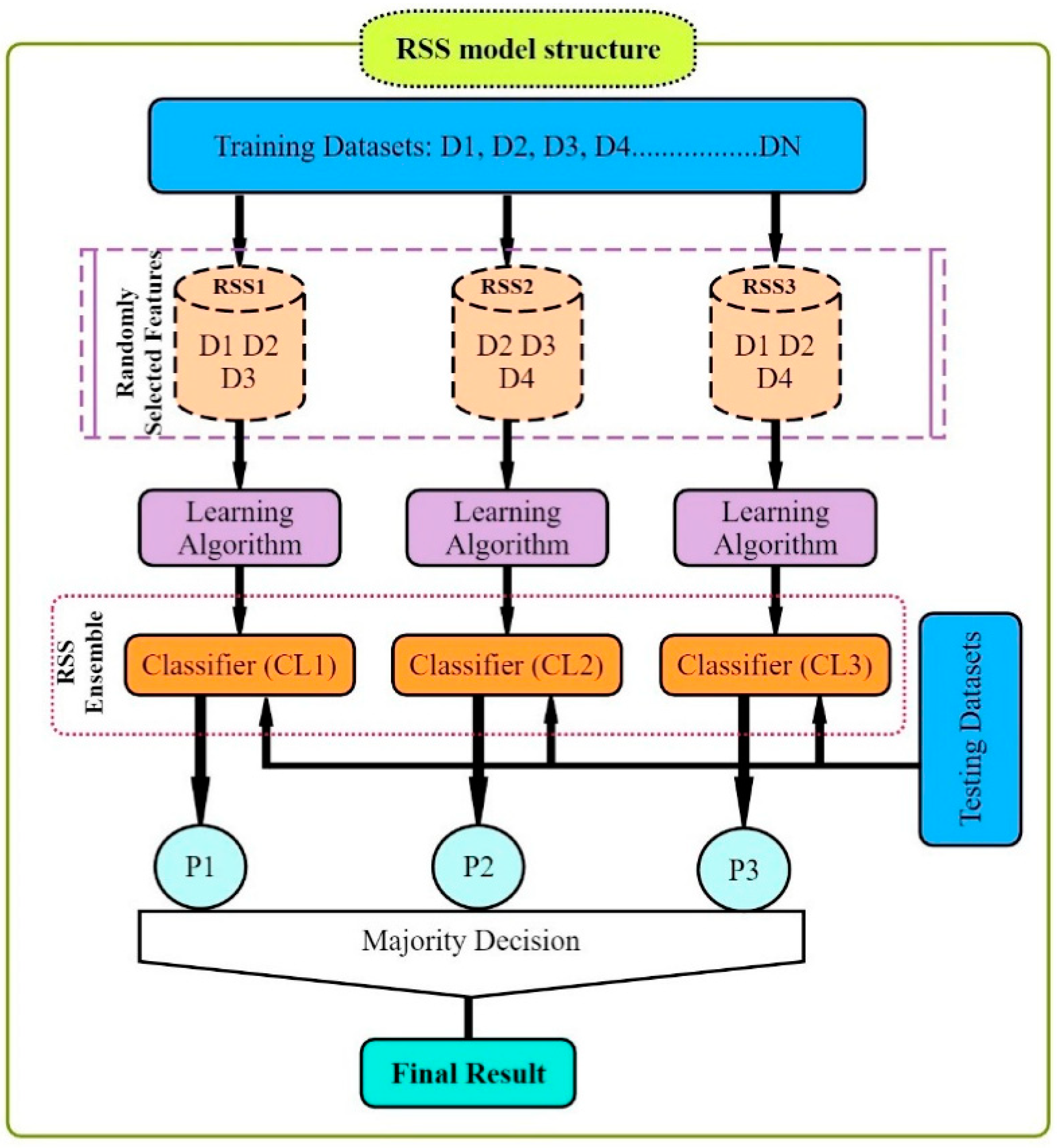
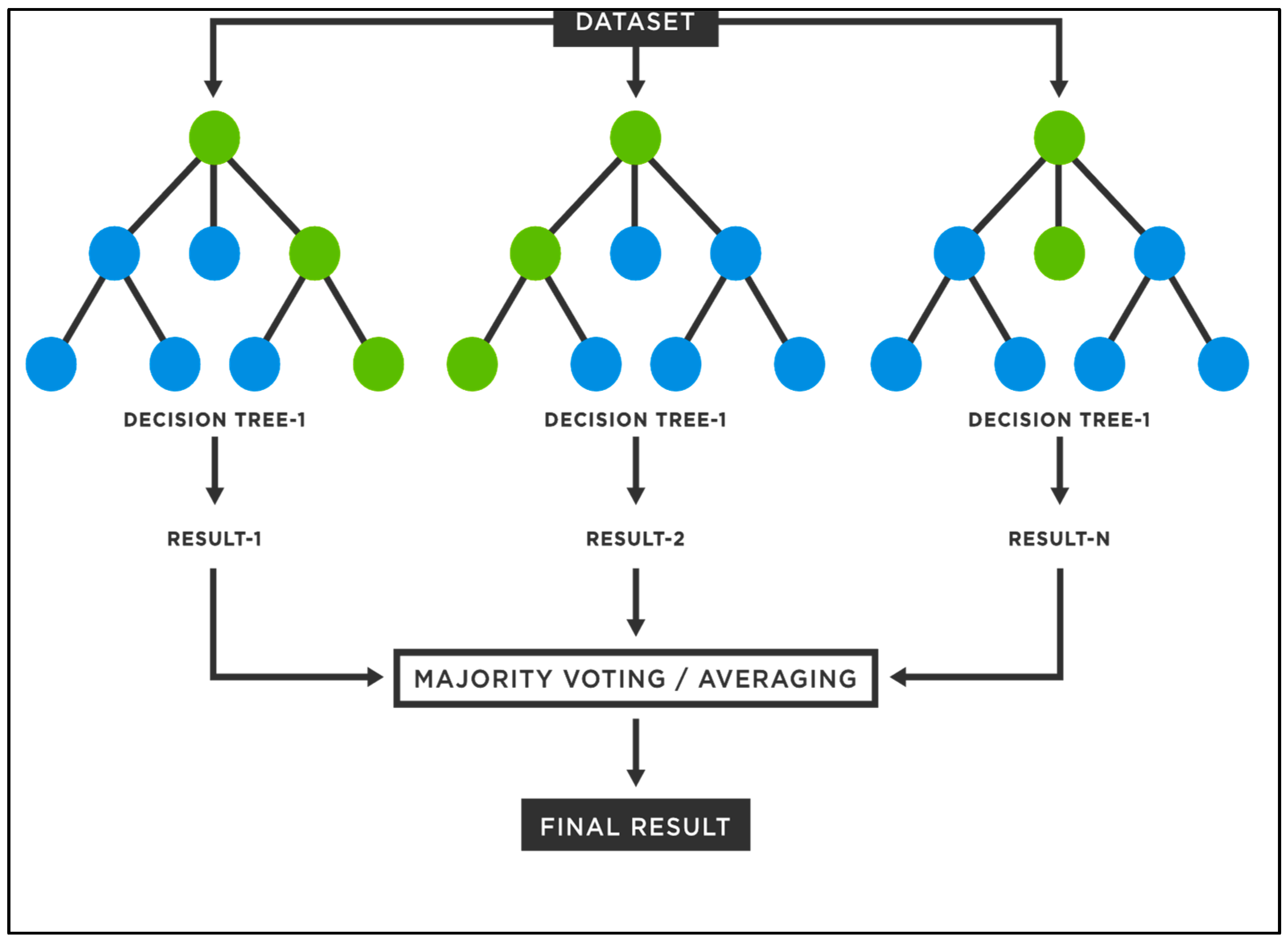
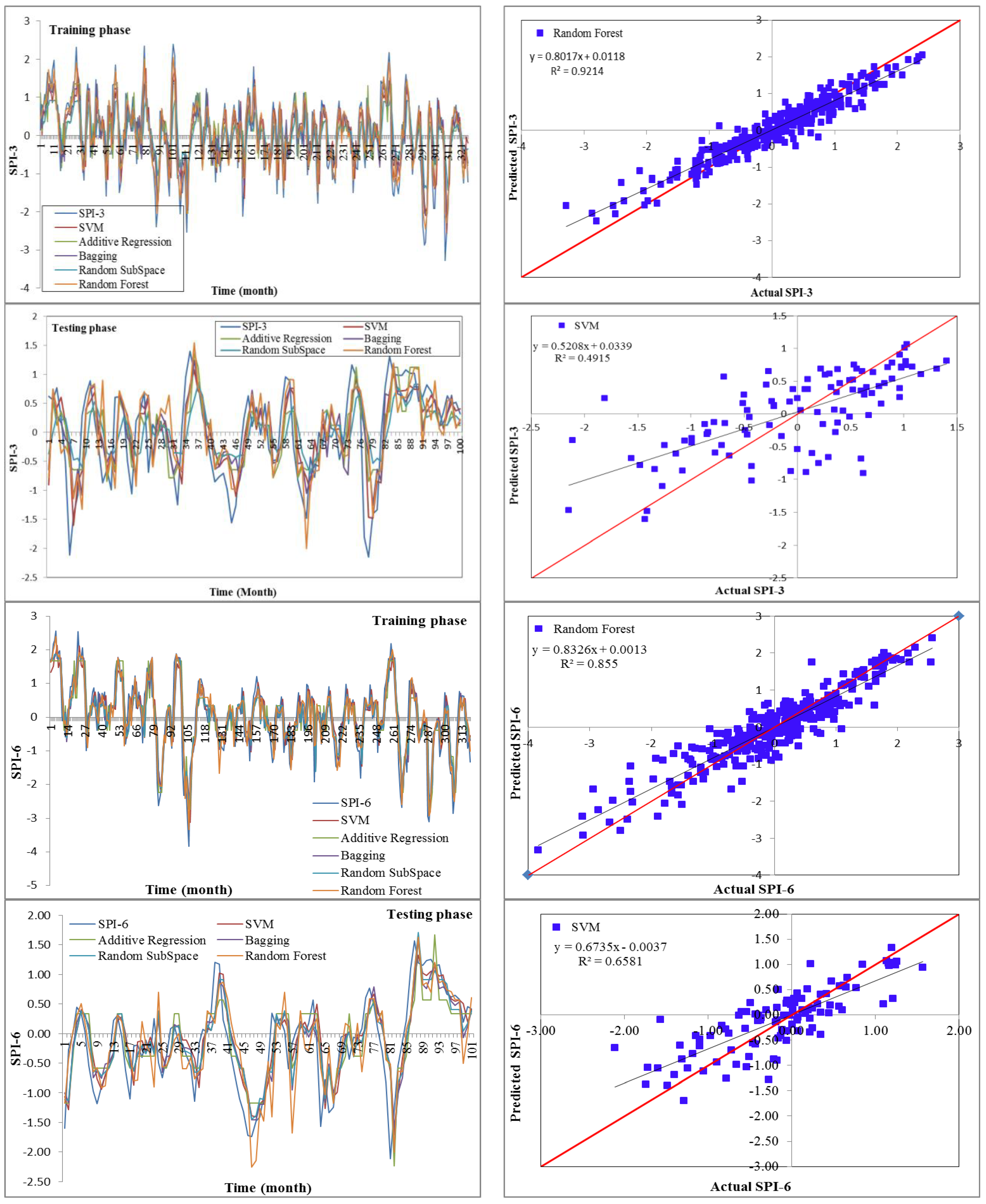
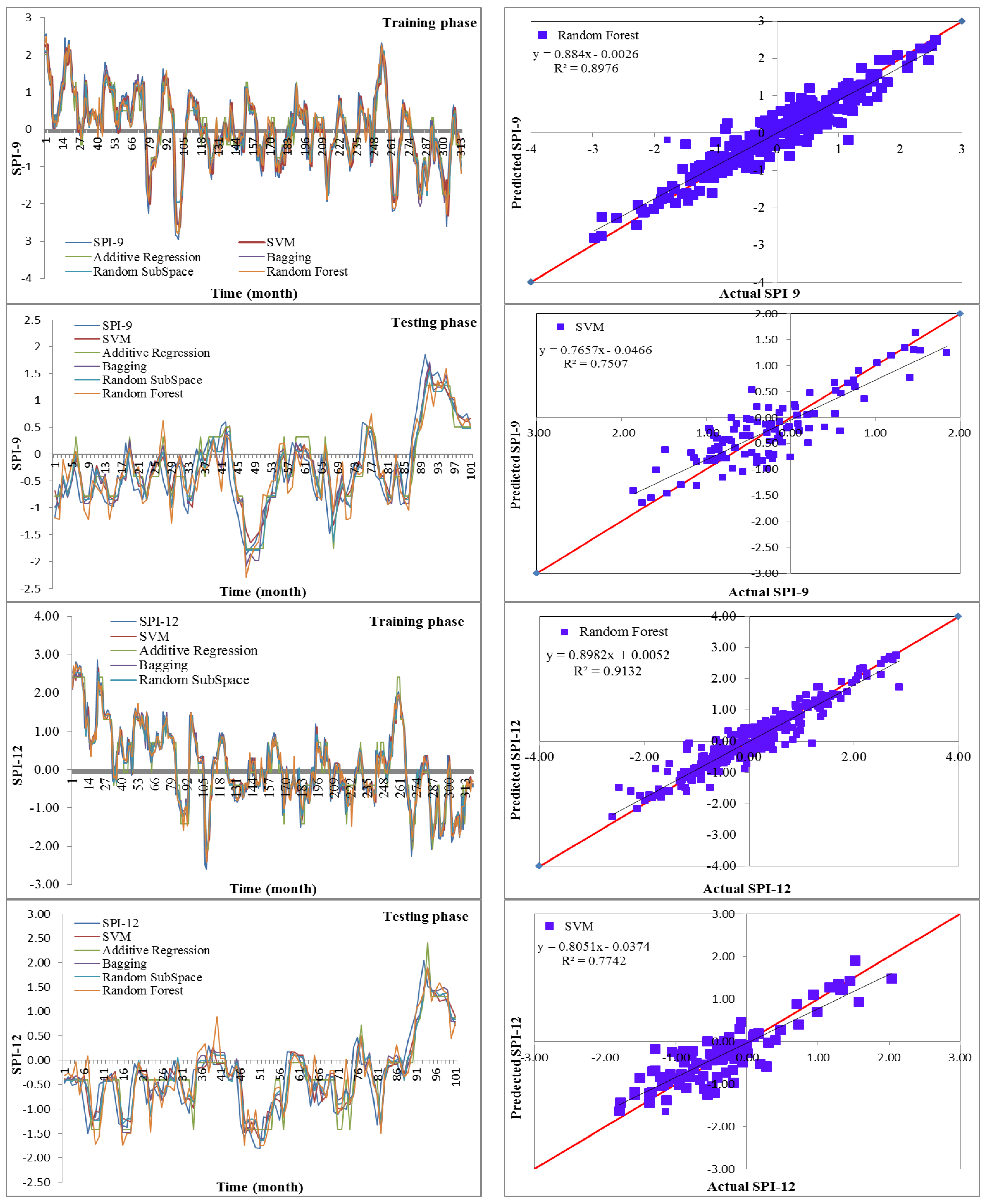
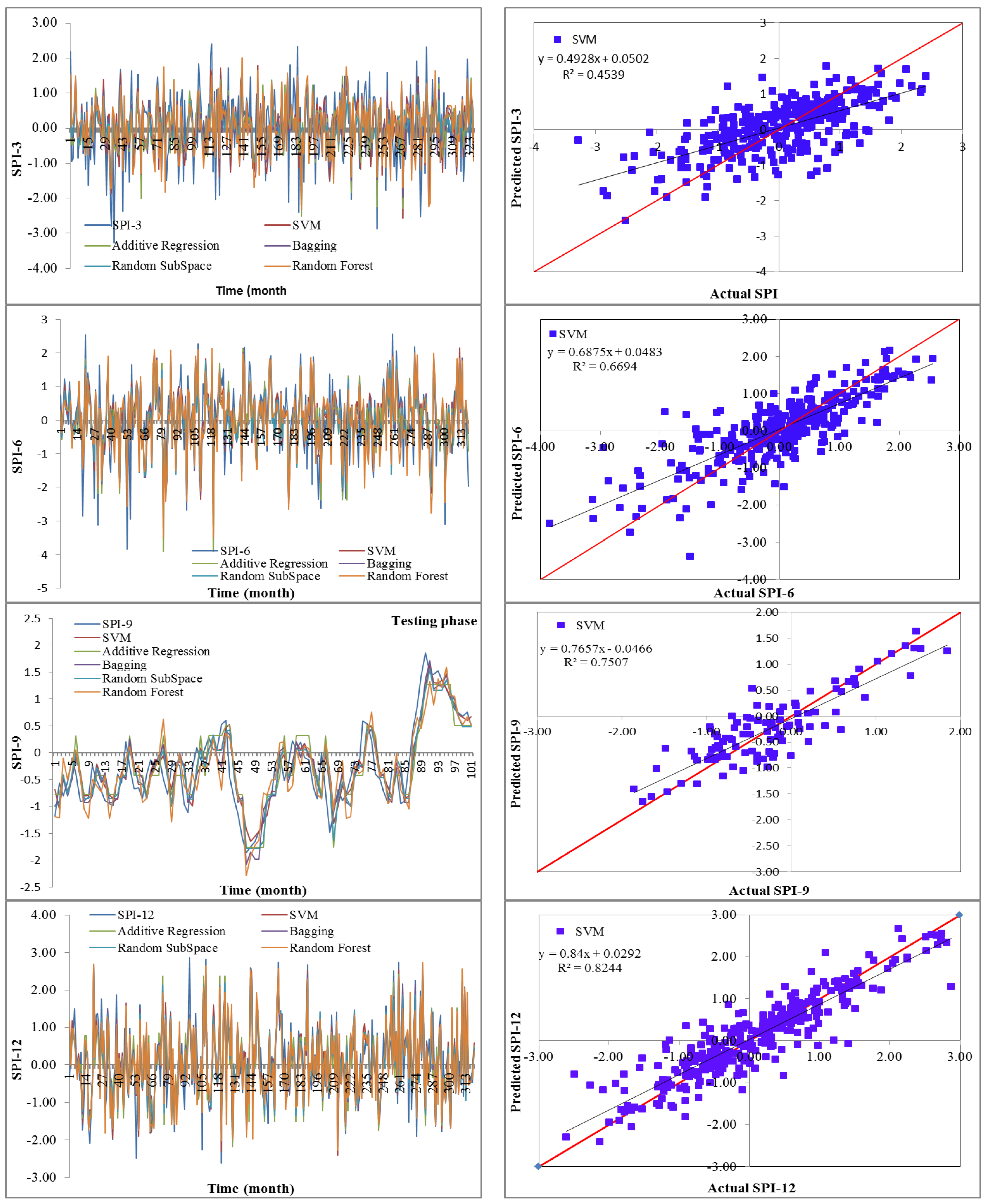
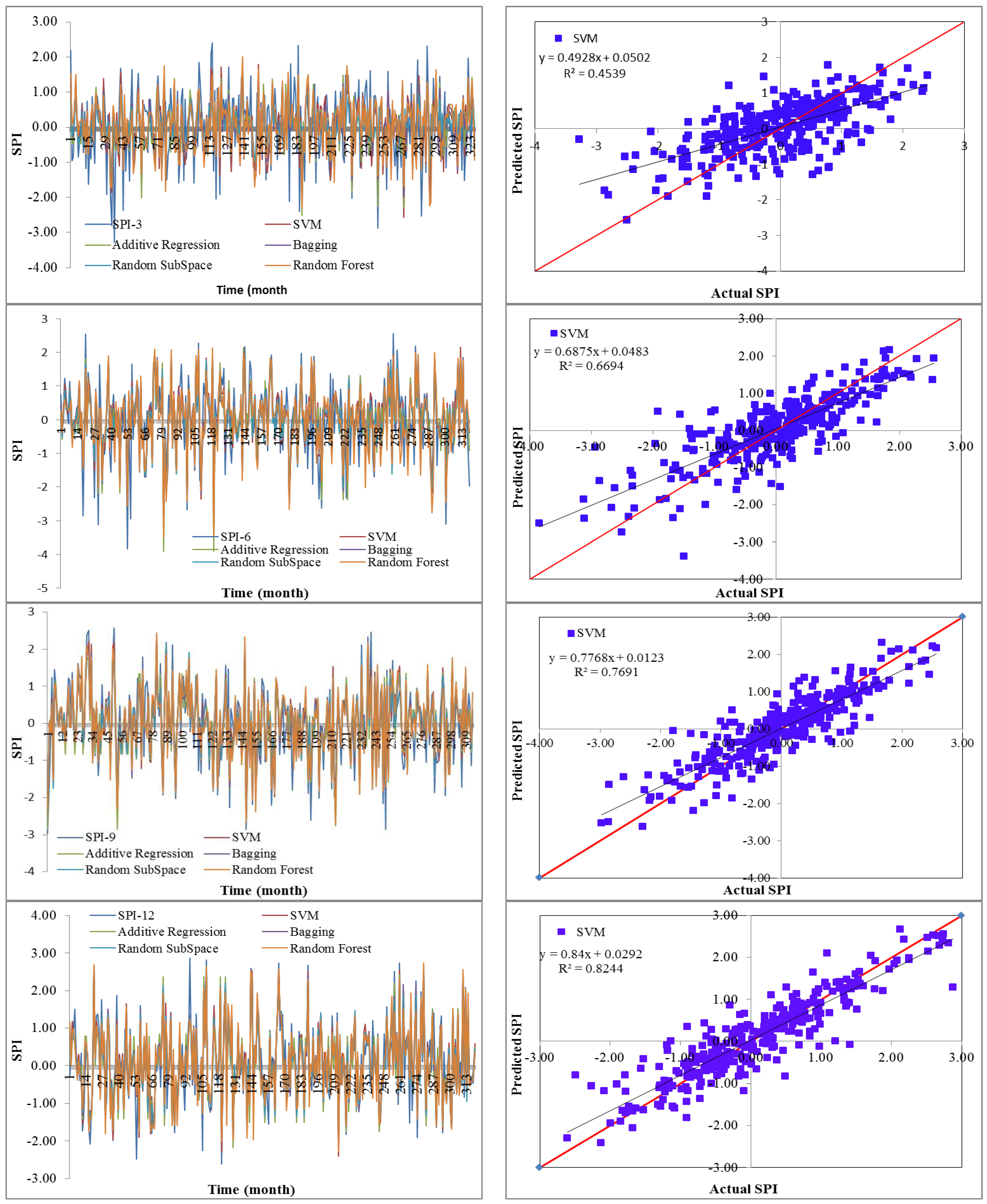
19] utilized data-driven models for drought forecasting at a single timescale. It is critical to assess the performance of various data-driven models for drought forecasting at multiple timescales to make sound recommendations. Therefore, this study employed five state-of-the-art machine learning models, namely SVM, additive regression, bagging, random subspace, and random forest, for drought forecasting at 3-, 6-, 9-, and 12-month timescales. This study used SPI for meteorological drought estimation at various timescales due to the overwhelming benefits of the standardized drought indices. The main goals of this work were to build models for forecasting meteorological droughts using various data-driven approaches and to assess their effectiveness at various timeframes using accuracy metrics.
5. Conclusions and Recommendations
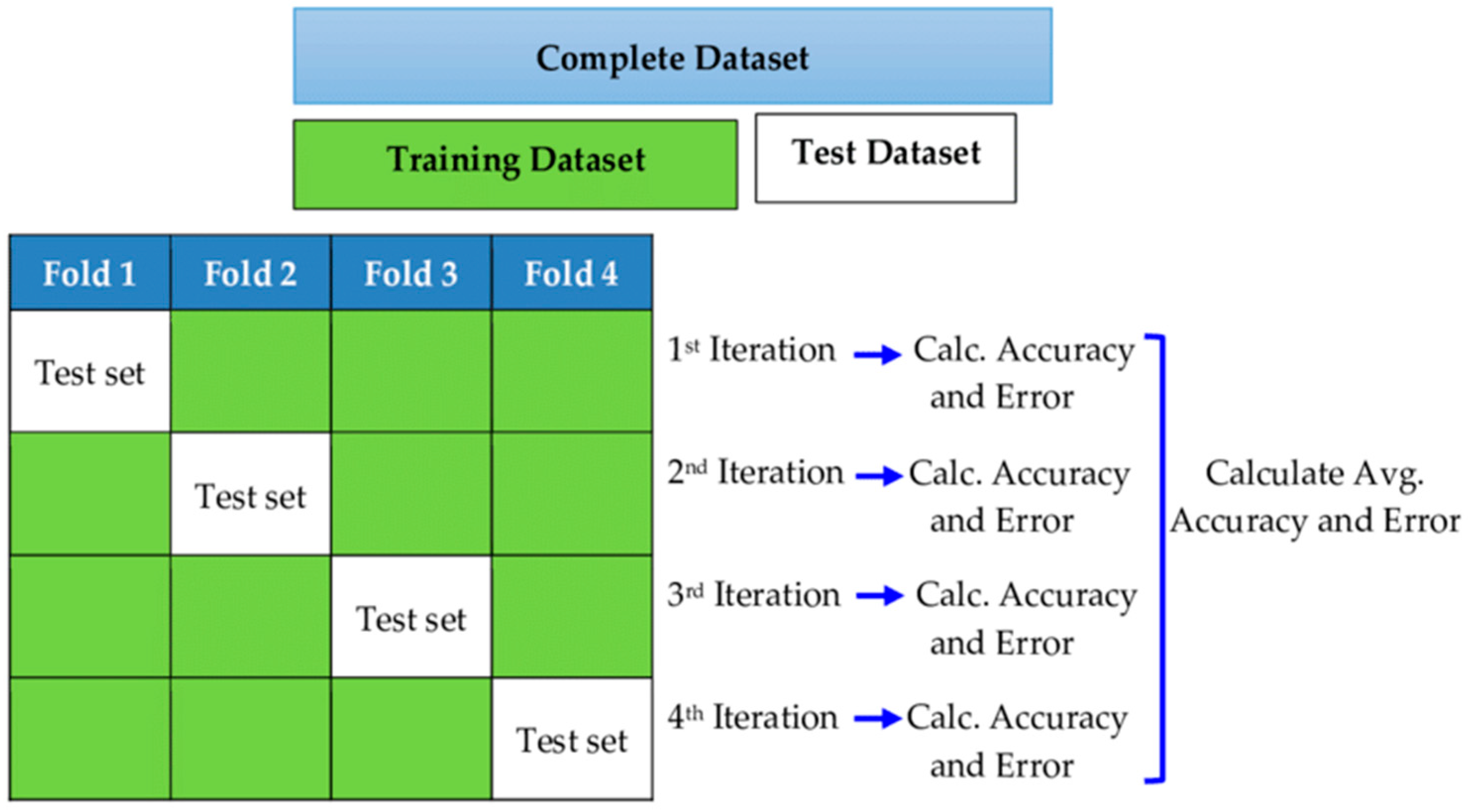
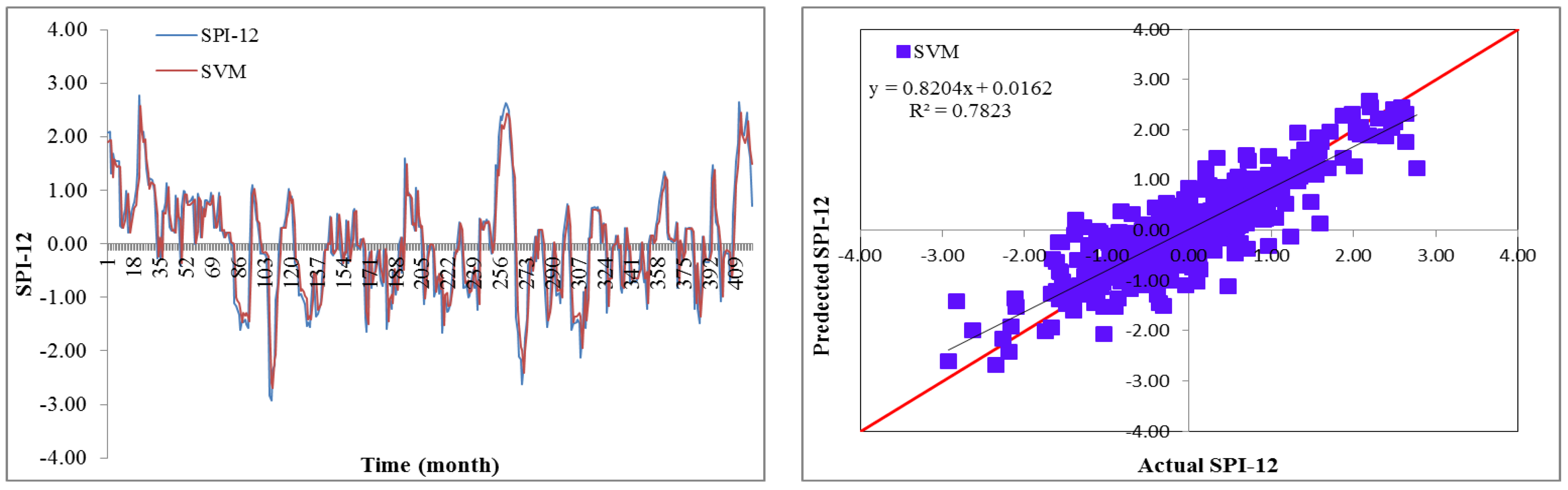
Drought has a detrimental influence on agricultural output, land and soil quality, desertification, food security, and water resources. Despite this, because of its complexity and several factors at various temporal and geographic dimensions, drought continues to be among the least understood natural phenomena. In the last ten years, the use of machine learning approaches to develop trustworthy models with high computational capabilities has drawn attention to the field of drought modelling. In this context, this research applied five machine learning models, namely support vector machine, additive regression, bagging, random subspace, and random forest, to anticipate a meteorological drought in the Wadi Mina basin, Algeria. Five performance assessment metrics were used to compare the performance of the developed models. The results indicated that SPI-12 performed the best when compared with the other timeframes. According to CC, MAE, RMSE, RAE, and RRSE with SPI-12 during the testing phase, SVM was able to achieve 0.880, 0.283, 0.371, 38.061, and 41.520, respectively. The results from cross-validation demonstrated that the SVM model outperformed the other models. The correlation coefficients ranged from 0.674 to 0.908 under all of the SPI periods. Its performance was validated at sub-basin 2 and satisfactory results were achieved. The suggested model provided a practical tool for managing intricate drought dynamics at various periods. Future studies should investigate the application of the proposed model in other basins of different countries. A trustworthy intelligent system might be developed using the suggested model to anticipate meteorological drought across a variety of timescales, aid in the management of sustainable water resources, and identify corrective actions in stations.