Next Article in Journal
Development of a Three-Dimensional CFD Model and OpenCV Code by Comparing with Experimental Data for Spillway Model Studies
Next Article in Special Issue
A Simplified Method of Iceberg Hydrodynamic Parameter Prediction
Previous Article in Journal
Model-Based Approach for Treated Wastewater Reuse Strategies Focusing on Water and Its Nitrogen Content “A Case Study for Olive Growing Farms in Peri-Urban Areas of Sousse, Tunisia”
Previous Article in Special Issue
Extreme Drought around Tomsk, Russia in Summer 2012 in Comparison with Other Regions in Western Siberia
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 15
Issue 4
10.3390/w15040752
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Comparing the Runoff Decompositions of Small Experimental Catchments: End-Member Mixing Analysis (EMMA) vs. Hydrological Modelling

by
Andrey Bugaets
1,*,
Boris Gartsman
1,2,
Tatiana Gubareva
1,2,
Sergei Lupakov
1,
Andrey Kalugin
2,
Vladimir Shamov
1 and
Leonid Gonchukov
1
1
Pacific Institute of Geography, FEB RAS, Vladivostok 690041, Russia
2
Water Problems Institute, RAS, Moscow 119333, Russia
*
Author to whom correspondence should be addressed.
Water 2023, 15(4), 752; https://doi.org/10.3390/w15040752
Submission received: 15 December 2022 / Revised: 1 February 2023 / Accepted: 8 February 2023 / Published: 14 February 2023
(This article belongs to the Special Issue Research on Hydrology and Hydrochemistry in Siberia and the Arctic)
Browse Figures
Review Reports Versions Notes

Abstract

:
This study is focused on the comparison of streamflow composition simulated with three well-known rainfall–runoff (RR) models (ECOMAG, HBV, SWAT) against hydrograph decomposition evaluated with End-Member Mixing Analysis (EMMA). In situ observations at two small mountain testbed catchments located in the south of Pacific Russia are used. All applied RR models and EMMA analysis demonstrate that two neighboring catchments disagree significantly on the mutual dynamics of the runoff sources. The RR models' benchmark test is based on proximity to EMMA hydrograph composition. Different aggregation intervals (season, month, and pentad) were applied to find a reasonable generalization period ensuring the clarity of results. ECOMAG is most conformable to EMMA outcome; HBV reflects flood events well enough; SWAT exhibits distinctive behavior compared to the other models. It is shown that, along with standard efficiency criteria of simulated and observed runoff proximity, EMMA analysis might provide useful auxiliary information for the validation of modelling results.

1. Introduction

Understanding runoff composition is a fundamental problem in hydrological science [1]. Most of the processes in hydrological systems take place underground and only a limited range of measurement techniques are available; the observation data need to be extrapolated in both space and time to predict the response of any catchment to a given rainfall event with an acceptable uncertainty [2]. Contribution of the different water masses to total runoff is time-dependent owing to the temporal variability of the flow response processes. In spite of the many publications on this subject, it is still a challenging task to determine how a catchment generates runoff as a whole system.
There is an undeniable consensus in the hydrological community that research on experimental catchments plays a key role in the understanding of the hydrological processes and provides essential outdoor laboratories for validation flow pathways and runoff generation mechanisms [3,4,5]. Small catchments are less inertial (more reactive to rainfall events) and offer potential noise reduction in the data compared with macro-scale data. Moreover, small catchments allow one to test hypotheses about runoff generation mechanisms due to relatively homogenous landscape properties. Alternatively, the greater catchment area complicates the interpretation of observational data and subsequent modelling results.
Sophisticated hydrological models are powerful tools to test hypotheses about catchment function and deal with uncertainties throughout the observation–conceptualization–modelling sequence [6]. Plausibly simulated streamflow can be obtained from models with distinct structures, providing the different runoff compositions, that is widely known as the equifinality effect. To narrow down the equifinality, it is necessary to evaluate the simulation results independently, that is, how realistically the model reflects the natural behavior of a hydrological system. However, the selection of hydrological models and the model structure uncertainties are still not fully understood [7,8,9,10,11]. Aggregation of outcome from different models or evolving model structure along axis of complexity using a “top-down“ strategy may lead to parsimonious model that provides useful insights into catchment behavior [10,12,13,14,15].
Catchment hydrology is still very much an empirical science [16,17], and it is common that some parts of a conceptual model may be more rigorously based on physical theory than others. Empirical approaches are still the basis or part of the numerous well-known rainfall–runoff (RR) models. The main reason to rely on this empirical knowledge is the scale-dependency of hydrological response unit (HRU)-based models, where they are more appropriate than any small-scale physical laws [18,19,20,21]. The model parameters are seldom directly measurable and are inferred from calibration. They are generally model-specific and represent average behavior in terms of both spatial and temporal variability [22]. Model structure uncertainty is as impactive on modelling outcome as parameter uncertainty, if mathematical formulation is not based on fundamental laws but adopts a set of lumped functions relating impact to the response [18].
All of the above creates a desire for alternative means of model evaluation in terms of how well a model captures the partitioning, storage, and release of water by a catchment [23]. End-member mixing analysis (EMMA) can provide estimates of the relative contributions of direct (surface) flow, deep groundwater flow, and soil percolation flow to total catchment runoff in the context of where these end-members can be easily separated and sampled [24,25,26,27]. Numerous researchers have indicated the importance of water chemistry for the transit time estimation and recognized the utility of tracers as an additional independent measure for model evaluation [27,28,29,30,31,32]. Despite gradual improvements in the reliability and economics of the field and laboratory methods, which provide necessary fine-time resolution data series at the present time [33,34], widespread application of EMMA is limited by the lack of suitable geochemical datasets.
This study is focused on a comparison of streamflow composition simulated with three well-known RR models (ECOMAG, HBV, SWAT) against the hydrograph decomposition obtained from EMMA. The main objective is to choose the RR model that best complies with EMMA in terms of the hydrograph separation that can be linked to a more accurate representation of real runoff generation processes. In general, it relates to the problem of harmonizing various approaches based on the solution of direct and inverse tasks of modelling. In the ideal case, the results of solving direct and inverse tasks should be the same or match closely.
The paper is laid out as follows: the next section describes the case study catchments, field observation details and all used models (EMMA, ECOMAG, SWAT, and HBV). Results of EMMA and hydrological simulations are presented in Section 3. For clarity, the results of hydrological model calibration are placed in the Appendix A, Appendix B and Appendix C. All results are generalized and discussed in Section 4; and finally, a summary and several concluding remarks are provided.

2. Description of Study Objects, Data, and Measurements Methods

The studied territory is the Pacific Russia boreal forests and is influenced by the East Asian Monsoon. Here, runoff modelling and hydrograph separation were performed for two small catchments (Elovy (3.5 km2) and Medvezhy (7.6 km2) creeks) that belong to the Upper-Ussuri Biocenological Experimental Station (45 km2, 44°02′ N, 134°11′ E). The considered area is characterized by mid-mountainous relief with moderately steep (Table 1), locally very steep, hillslopesof up to 30% [3,35]. The average altitudes are 500–700 m a.s.l, and maximal values reach 1100 m a.s.l. (Figure 1).
Air temperature dynamics is characterized by high variability from year to year; average, and absolute minimal and maximal values are +0.7 °C, −45 °C (in January) +38 °C (July–August), respectively. The annual average precipitation amount is 700–800 mm, up to 80% of which occurs during the warm period (from late April to October) as rain. Unstable intra-annual and long-term precipitation regimes of the territory define runoff formation conditions of the investigated catchments. Resources of shallow water are not significant in terms of local water balance due to fractured rocks. Small-river runoff can be vanishingly low during winter or summer drought periods and reach 30–50 mm d−1 during high-intensity rainfall caused by tropical cyclone–typhoon activity. The range of maximal daily heavy rain is 100–200 mm, and frequency of such events is assessed as one time per 5–6 years. The stable snowpack usually occurs in November, snow-cover depth reaches 0.5–1 m by the end of March, and the common range of the snow water equivalent is 100–200 mm.
Field observations were made from March to October in 2012–2018. Two weather stations (WS-GP1, Delta-T, Cambridge, UK) were mounted at 650 (Elovy catchment) and 750 m a.s.l. (Medvezhy catchment) to record air temperature and humidity, wind characteristics, and precipitation volume (see Table 1). Stream outlets were fitted with hydrostatic water-level loggers (Solinst 3001, Georgetown, ON, Canada). Observations temporal resolution was 15 min. Measurements of water discharges were run once in 2–4 days during low water periods, daily during average moisture conditions, and twice a day during flood periods. For discharge assessments, flow velocity was measured using magnetic inductive flow sensor (SEBA FlowSens, Kaufbeuren, Germany); cross-section geometry of riverbeds in permanent sites was measured simultaneously. To obtain daily discharge for the whole observation period, a water-level-discharge rating curve Q = f(H) was applied.
Hydrological properties of soil were obtained from 14 soil profiles (4 are located in the Medvezhy and 10 in the Elovy) [36]. The soil cover of the considered territory is dominated by the Cambisol group [37]. Brown forest soils here are characterized by a high rock fragment content (greater than 80% of profile volume) which leads to high infiltration rates (>30 mm/h).
Rainwater samples were collected to analyze chemical composition by using pyramidal funnels that were connected to polypropylene collectors. Soil water samples were taken with the vacuum lysimeters (DIK-8392, Daiki Rika Kogyo Co. Ltd., Kusatsu, Japan) installed at a depth of 0.35–0.80 m. Streamwater samples were collected simultaneously with discharge measurements. Streamflow temperature, pH, specific conductance, and total dissolved solids (TDS) were measured in situ using a handheld multiparameter meter (Yellow Springs Instrument, YSI Professional Plus, Yellow Springs, OH, USA).
The HCO3 concentration was taken to be equal to total alkalinity, and estimated in the field laboratory after 2–4 h of sampling by the potentiometric titration method in unfiltered water samples using the standard technique. Water samples for chemical analysis were filtered at the field laboratory through the Durapore filter (Millipore, Burlington, MA, USA) with a pore size of 0.45 μm. To determine the content of cations, about 10 mL of each filtered aliquot was acidified with purified nitric acid and stored in polypropylene bottles at room temperature prior to analysis. Then, filtration samples of water for DOC analysis were stored in 30 mL glass bottles at a temperature of 4–8 °C [38,39,40].
Laboratory analysis of samples was carried out at the Geochemistry Laboratory of the Pacific Institute of Geography of the Far Eastern Branch of the Russian Academy of Sciences. The content of cations Ca, Mg, K, Na was determined by Atomic Absorption Spectroscopic method using a Shimadzu AA 6800 spectrometer. Cl, NO3, SO4 were determined using a Shimadzu LC 10Avp liquid chromatograph. Dissolved Si was determined by spectrophotometry method using blue complex with ammonium molybdate, and DOC by a TOC analyzer—Shimadzu TOC-VCPN.
Data quality control was performed to discard obvious errors associated with the operation of loggers. According to that, the next simulation periods were suggested: from 2012 to 2014 for Elovy creek, and from 2015 to 2017 for Medvezhy creek. The nearest WMO weather station 31939 (Chuguevka) is located 35 km northwest of the observation sites, so its data were used to fill up observational gaps and the cold part of the years. WRF-ARW model output was applied to derive daily solar radiation interpolated from closest computational grid nodes.
In this study, three RR models (SWAT, HBV and ECOMAG) represent a wide range of conceptual diversity of approaches used to solve the direct task of runoff modelling. HBV is lumped storage-based, and the other two are considered as spatially distributed (HRU-based) models. They differ in the structure and methods of runoff generation mechanism parameterization, and physical and mathematical foundation (see Table 2).
The end-member mixing analysis (EMMA) framework is an example of solving the inverse task of modelling using methods of tracer hydrology. In contrast to imitation RR models, EMMA can be called an identification model, providing the interpretation and quantification of runoff generation sources. It is substantial: the discharges of different runoff sources are determined from direct observations of the water and tracer volumes using the mass balance equations system and some empirical relations. Overall, this could be interpreted as a sophisticated way to identify runoff sources.
All listed models are well known in the hydrological community and have previously been applied in the region [36,39,40,41,42,43]. For a description of the models’ structure, variables, and parameters, the original terms from the base publications are used. Detailed information can be obtained from references. A description of the models’ parameterization is provided in the Appendix A, Appendix B and Appendix C.

2.1. EMMA Model

End-Member Mixing Analysis (EMMA) is a commonly applied method to identify and quantify dominant runoff sources. This method is based on the assumption that waters, flowing through specific compartments of catchment, acquire its unique chemical signatures. Thus, some solutes can be used as natural tracers to determine the contributions of each water source (labelled as the “end-member”, EM) to total runoff. This hydrograph separation technique is based on the mass balances for the tracers and water, and assumes that: tracers are conservative; chemical signature of water contributions from various sources is constant and unique to make it distinguishable from others; mass conservation law applies to both the water quantity and solute quantity including mixing of water masses without their essential transformation [44,45].
Water runoff source identification and estimation of its contributions to streamflow (proportions) were performed using EMMA in combination with the diagnostic tools of mixing models. The algorithms for multidimensional statistical analysis used are implemented by the software library of extensions for Excel-Chemometrics [46]. According to the procedure described in Hooper [47], conservative tracers and the number of EMs that contribute to streamflow were identified from streamflow chemical data without using information about EMs. First, bivariate scatter plots of solutes against each other were analyzed for the linearity of mixing. Solutes that demonstrated collinear structure in the bivariate plots were considered as acceptable tracers. These solutes/tracers are variables of measured chemical data matrix G, n × p, where n is the number of samples, and p is the number of tracers. They are standardized using the mean and standard deviation of each solute. Standardized matrix G* was projected into a new Euclidean m-dimensional space U (m < p), obtaining matrix Ĝ* (n × m). This projection is made by principal component analysis (PCA) using eigenvectors S (p × p) extracted from the correlation matrix G*T G* according to the equation
Ĝ* = G* × ST × (S × ST)−1 × S
Conservative tracers and the number of EMs were determined by examining the relation of residuals E (the difference between Ĝ and G values, where Ĝ is destandardized Ĝ*) against the measured values for each solute. The dimension m of space U was increased until there was no structure (no correlation on the bivariate plots) to the residuals. Those solutes that exhibit a random pattern in the residuals, controlled by negligible correlation in the relations mentioned, are considered as conservative. Their number is denoted as k (k < p). The number of EMs is determined by m + 1.
Then EMMA was used with conservative tracers to identify EMs and to quantify the proportions of EMs in the streamflow following the procedure described in [45]. Streamflow samples chemical data were orthogonally projected using the truncated matrix of eigenvectors S1 (k × m) extracted from the matrix G1, which includes only k conservative tracers. Tracer concentrations in EMs were standardized using the mean and standard deviation of each tracer in streamflow samples and projected using the same eigenvectors S1. Mixing diagrams were plotted in the U-space to screen EMs which contribute to the streamflow. In our study, the first two or three principal components (PCs), or the PCA scores, were used to determine the proportions of the EMs in the runoff composition. Thus, the PCs are considered as the tracers for the mixing model—two tracers for a three-source mixing model or three tracers for a four-sources mixing model.
Determining the proportions of sources in the streamflow based on the mixing model is performed in the usual way, by solving a system of three or four mass balance equations for water and tracers, as described in [45]. Model validation was performed by multiplying the hydrograph separation results (proportions) on the measured solute concentrations in the EMs to reproduce the chemical data of streamflow for conservative solutes. The high correlation between the series of modelled and measured tracer concentrations in streamwater indicates the adequacy of the obtained mixing model.
Hooper [47] suggested that assumptions of linearity of mixing and conservative behavior of tracers can be evaluated using bivariate scatter plots and residuals derived from the selected model. Bivariate scatter plots should be developed for all potential combinations of available solutes. A collinear structure in the bivariate plots could be used to infer conservative behavior. These data were used to construct a correlation matrix followed by principal components analysis (PCA) to extract eigenvectors and eigenvalues. The eigenvectors form the basis for a new Euclidean space, U-space.

2.2. ECOMAG Model

ECOMAG (ECOlogical Model for Applied Geophysics) is the process-based, semi-distributed RR model [48]. The spatial structure of the ECOMAG model splits watershed into sub-basins based on topography, river network structure, soil and vegetation type, land use, and variability of climate characteristics. The main ECOMAG model equations were adopted from the full spatially distributed model [49] by neglecting secondary terms and spatial aggregation at subbasin scale. Daily resolution time series of precipitation, air temperature, and air relative humidity are used as inputs. Computation of river basin hydrological response is described by two main phases: calculating the effective precipitation for each sub-basin and then routing it through the river network. Runoff from sub-basin is calculated as the sum of three components: Horton overland (surface) flow (when rainfall has exceeded infiltration capacity and depression storage capacity), soil flow (sum of runoff from horizon A and B) and groundwater outflow (baseflow and infiltration from horizon B). In warm periods, precipitation is partially infiltrated and moves along the hillslopes (over impermeable surfaces) as interflow. Excess water produces surface flow and moves downslope towards the drainage network. The rest of the water that has not been drained into rivers as lateral or surface flow can be evaporated or percolated into deep aquifers. Within cold and mid-season periods, the model describes snowpack evolution and soil freezing–thawing cycle.

2.3. SWAT Model

The Soil and Water Assessment Tool (SWAT) is a semi-distributed hydro-ecological model [50,51]. This model uses the net of hydrological response units (HRUs) as the base elements to model main hydrological cycle processes—infiltration, evaporation, runoff generation, and soil hydrothermic and snow-cover dynamics. The daily volume of precipitation excess and surface runoff is calculated by the empirical SCS CN method. Kinematic wave approximation is used for channel routing. Daily rainfall, maximum and minimum air temperature, solar radiation, relative air humidity and wind speed are the inputs for the model. The SWAT uses air temperature to define input precipitation as rain or snow. Some of the precipitation, intercepted by canopy, can be evaporated. Then, the simulation is performed as two successive land and routing phases. The snow thawing is linearly related to snow cover depth and fraction of watershed area and air temperature. At the top of the soil profile, precipitated water can either flow overland or infiltrate into underlying strata if their temperature is positive, the field capacity of the upper layer is exceeded, and the underlying soil layer is not saturated. Water may be partially evaporated and turned into lateral or groundwater runoff components inside the soil profile. The dynamic of the lateral flow runoff component is calculated using the saturated conductivity of each soil layer. Percolated through a soil column, water is proportionally divided between unconfined and deep aquifers. Potential evaporation is used to calculate the water exchange between groundwater and the bottom of the soil profile.

2.4. HBV Model

The conceptual HBV model was developed by the Swedish Meteorological and Hydrological Institute (SMHI) [52]. The model consists of three main modules: snowmelt and snow accumulation, soil moisture and effective precipitation routine, and runoff transformation to catchment ’s outlet. The measured precipitation is supposed to be snow if the air temperature is lower than threshold temperature TT; otherwise, precipitation appears as rain. The simulated snowpack volume can be adjusted with correction factor SCF. The degree-day method is used for snowmelt calculation. Groundwater recharge and actual evaporation are simulated as functions of actual soil storage. The amount of water available for runoff generation is calculated as the ratio of actual soil moisture SM to field capacity FC and the power coefficient Beta-(SM/FC)Beta. The model first recharges the upper storage and then the lower storage using percolation parameter PERC. Surface flow appears when the upper storage capacity exceeds a certain threshold. Potential evapotranspiration (PET) is input to the model, which can be tuned by the Cet parameter. Actual evaporation is equal to PET when SM/FC is higher than the LP parameter; otherwise, a linear reduction is used. The runoff is calculated as the sum of three linear outflows: surface flow Q0, interflow Q1, and baseflow Q2 with three correspondent recession coefficients K0, K1, and K2. A transformation function with the triangular weighting parameter MAXBAS [53] is used for smoothing the total runoff to obtain the discharge at the outlet.

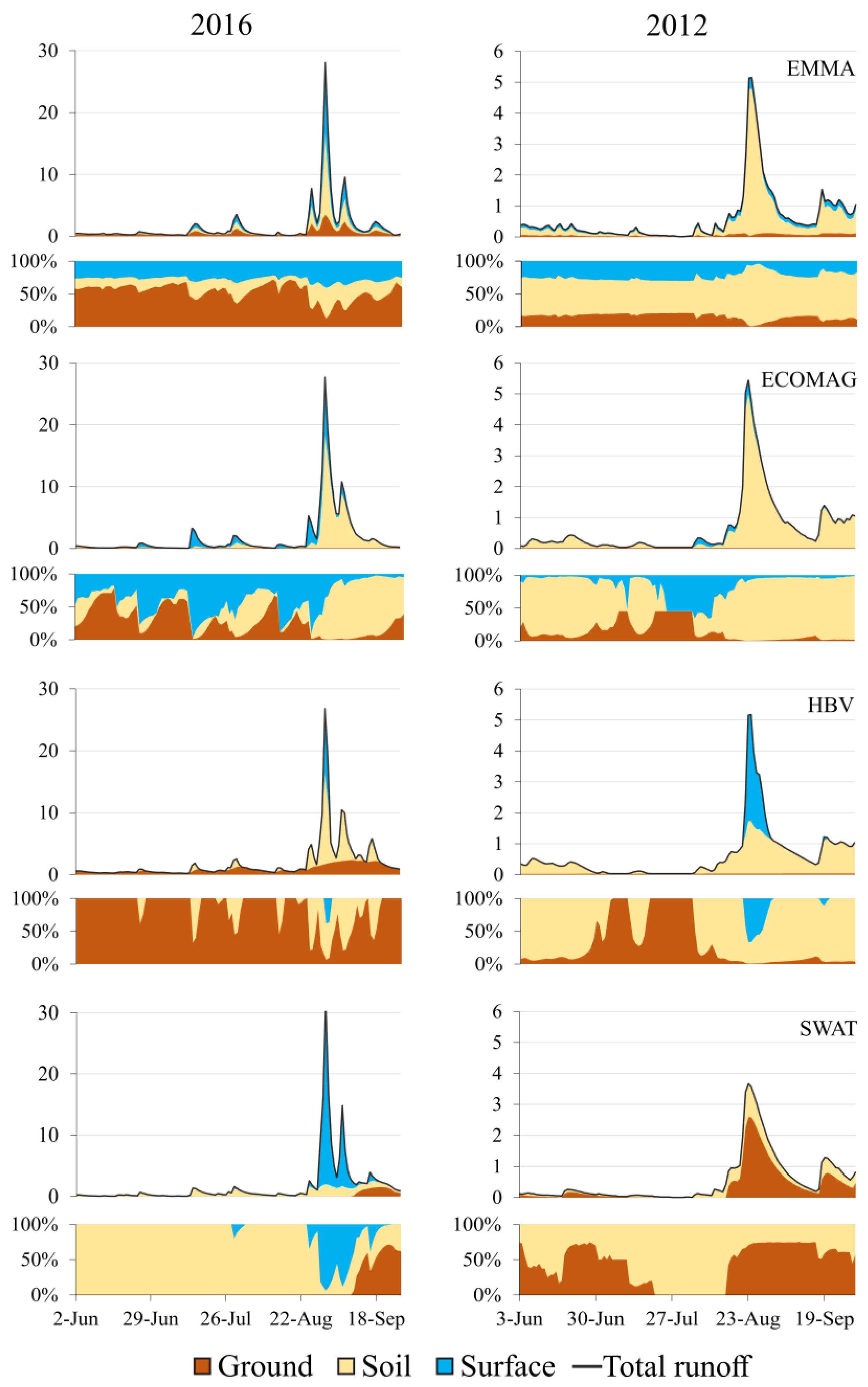
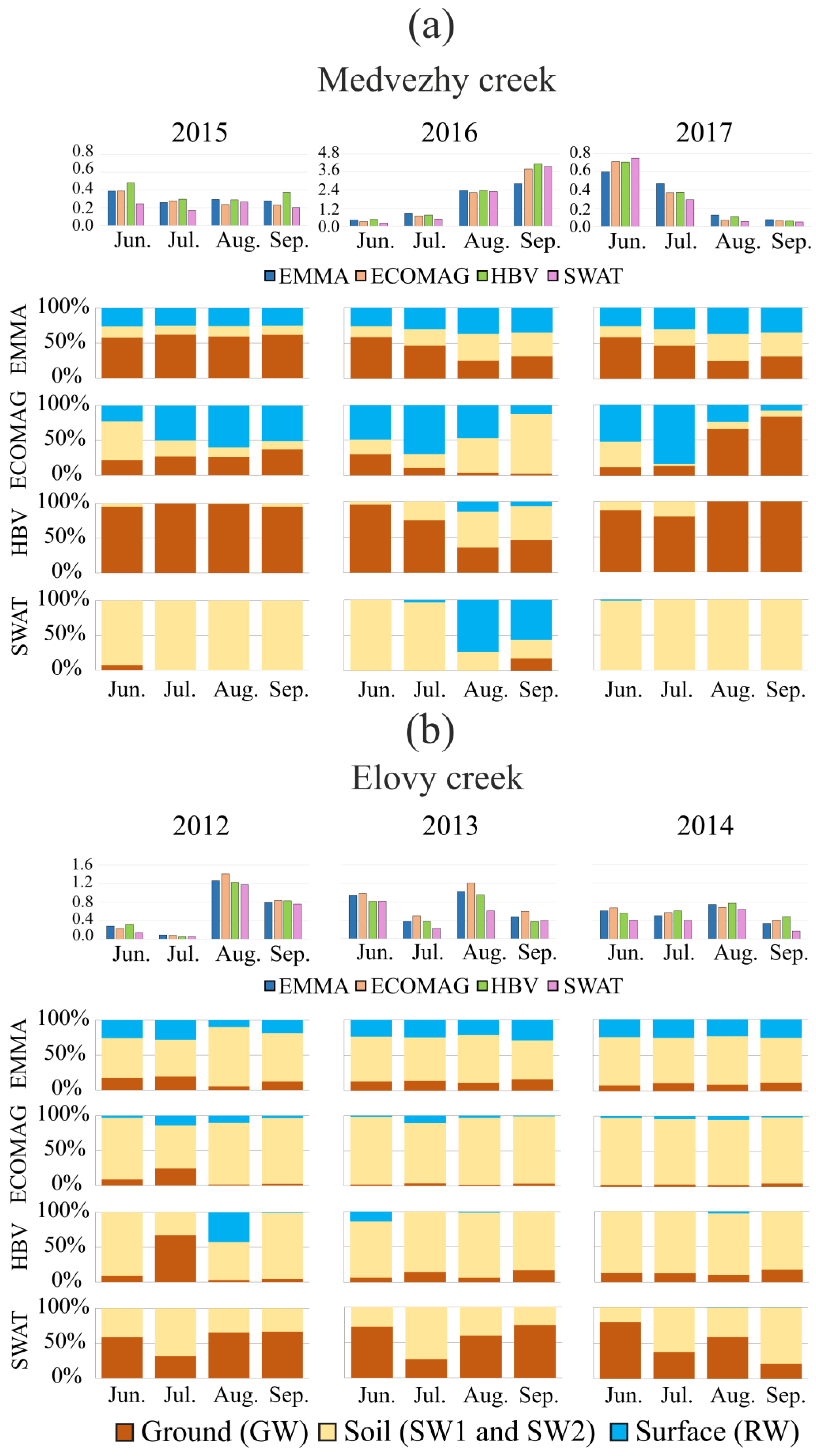
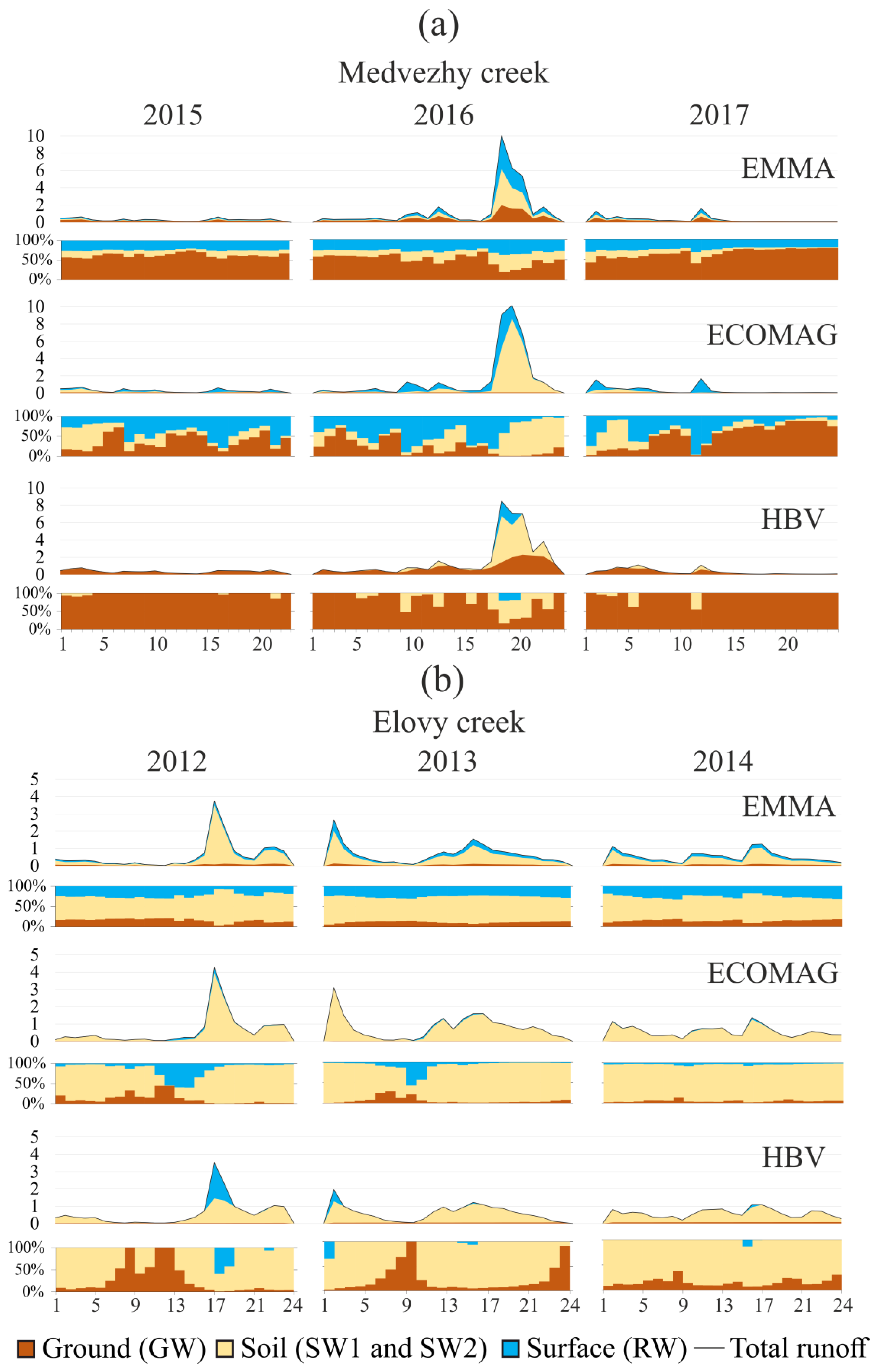
3. Results

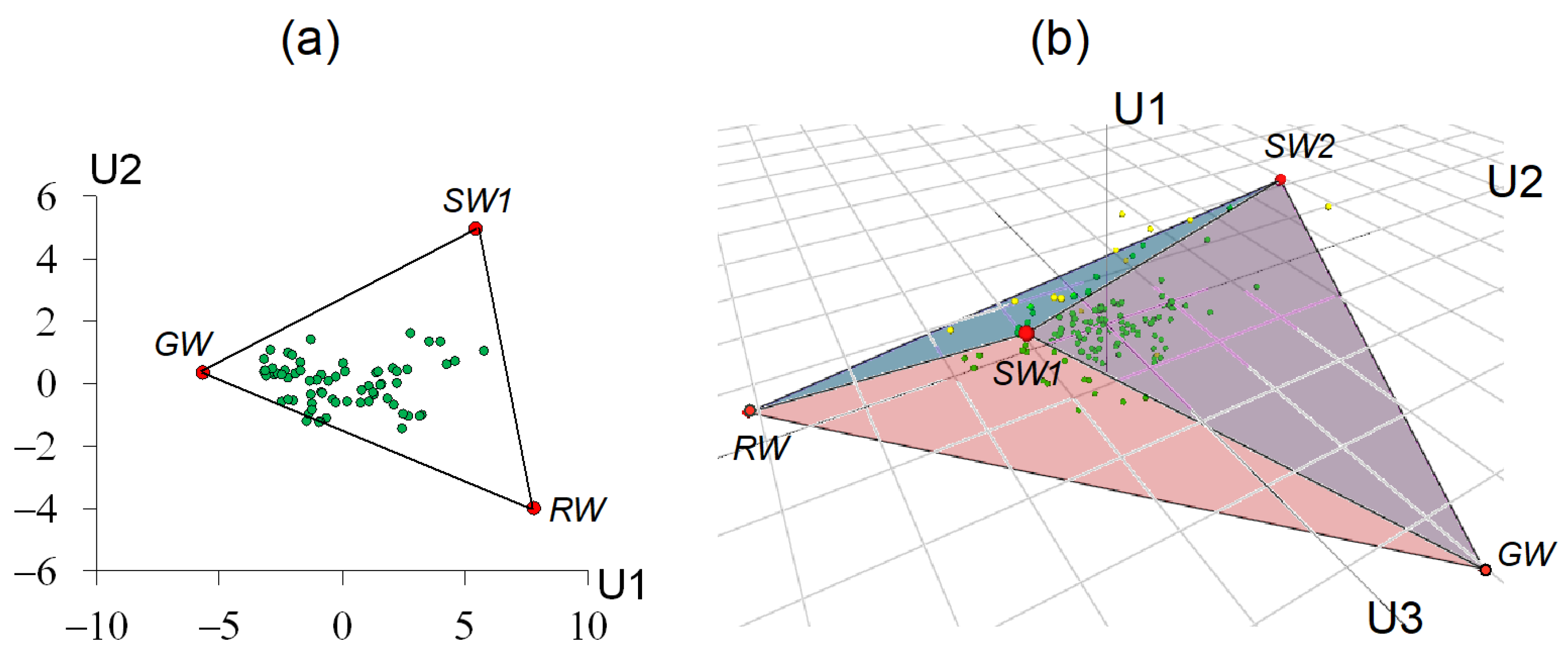
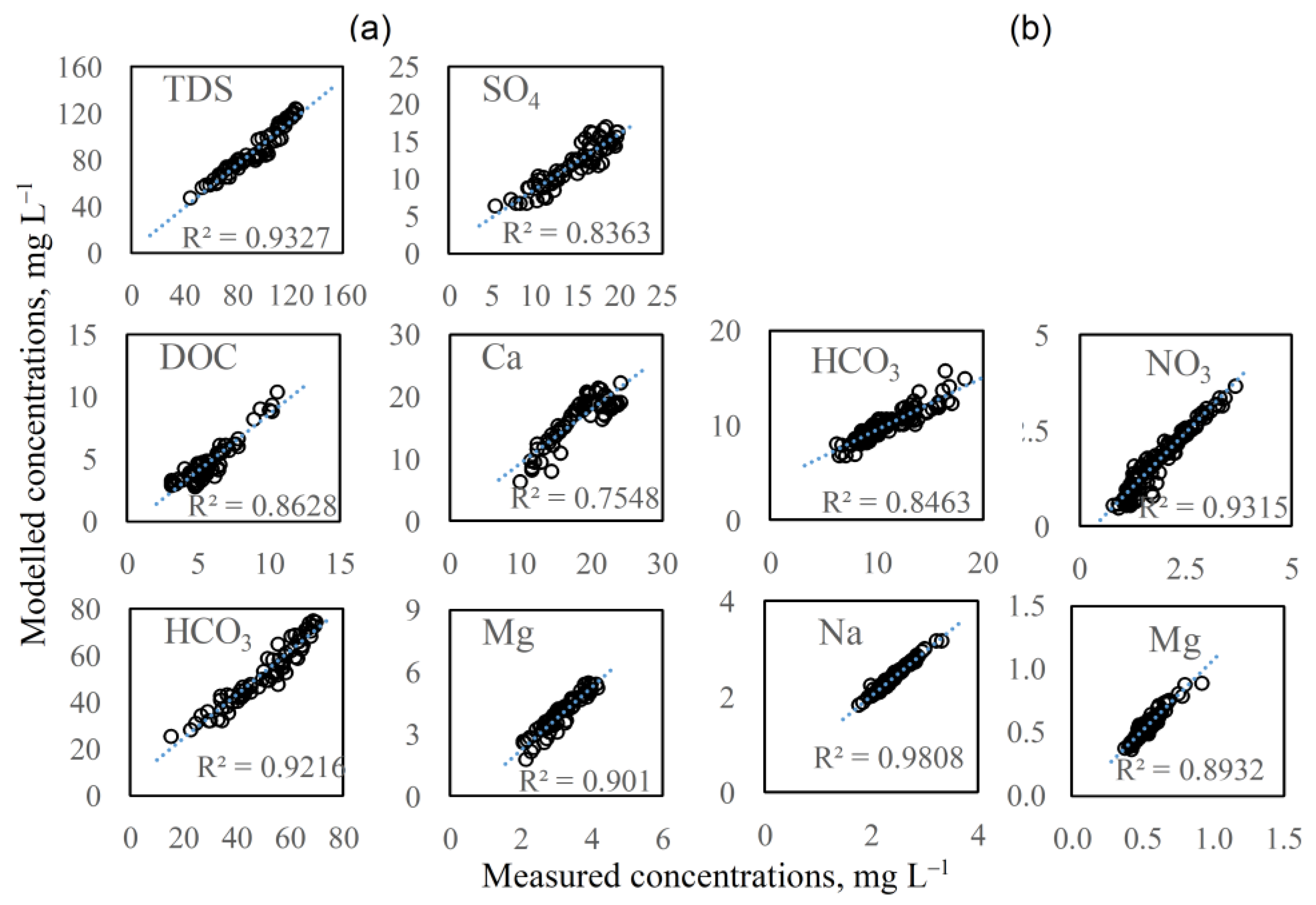
3.1. EMMA Results

The EMMA procedure was performed at the Medvezhy catchment for the period 2015–2017, and at the Elovy catchment for the period 2012–2014. Bivariate solute plots were constructed for all pairs of chemical indicators using streamwater samples for the whole period of observations. Diagrams depicting collinearity and linear trends were used to define tracers with conservative behavior. Stronger linear trends between pair solutes were observed at the Medvezhy catchment, and weaker linear trends were observed at the Elovy catchment, R2 < 0.5 (see Table 3).
For the Medvezhy catchment, PCA was performed for the matrix of chemical indicators including six solutes: TDS, DOC, HCO3, SO4, Ca, and Mg. The first two PCs explain more than 92% of the total variance of these data (see Table 4). Analysis of PCA-model residuals against measured values for individual solutes at two-dimensional mixing subspaces is shown in Figure 2a. The random pattern for each solute indicates that these six tracers could be considered as conservative and can be used for adopting the mixing model with three EMs.
For the Elovy catchment, a four-source mixing model is required to successfully represent the runoff generation in the Elovy Creek [39,54,55]. The fact that HCO3, Mg, NO3, Na tracers captured the 95% of the total variance is explained by the first three principal components. The hypothesis about conservatism of tracers (stable concentrations of tracers along their pathways) is confirmed by the randomness structures of residuals shown in Figure 2b.
Here, the strict randomness of the residuals is not always confirmed. Several known tests for randomness do not seem quite suitable because of inconvenient properties of data series—non-Gaussianity, uneven sampling, and discontinuous intra-series connectivity. This uncontrollably reduces the reliability of the test assessments. In this case, it is advisable to use only the simplest criteria and use their conclusions only as one of the arguments. We used as a test the critical values of the R2 assessments by sample (with its true value zero), calculated based on the well-known Fisher’s normalizing z-transform at a significance of 99% [56]. For samples of 69 and 126 members, the critical values of R2 are approximately 0.101 for the Medvezhy and 0.054 for the Elovy, respectively (compared with Figure 2).
In the case when the residuals are not completely random, but with an insignificant value of R2, the inclusion of the tracer can be justified by independent considerations and analysis of the simulation results as a whole. For example, R2 for Ca (see Figure 2a) is essentially non-random. However, there is a group of three outliers in this residual plot, related to samples taken during one week in May 2015. The exclusion of this group from the sample reduces the value of R2 by almost half, which serves as an argument for including this tracer in the model. The use of not completely conservative tracers decreases the accuracy and reliability of estimates in the mixing model. This fact was taken into account when discussing the conclusions below. The example above probably indicates that the existing dataset does not sufficiently account for the seasonal dynamics; hence the mixing models are considered reliable only for the summer-autumn rain-flood season (from June to September for the studied territory).
Mixing diagrams were constructed for each creek by orthogonally projecting the conservative tracer’s matrix of river samples into U-space. Tracers that averaged concentrations of EMs (Table 5) were also projected into the same U-space using eigenvectors. The two-dimensional mixing diagram for Medvezhy creek is presented in Figure 3a. River samples are located in the mixing subspace of tracers <U1, U2> and are bound by three sources. The mixing diagram for Elovy catchment represents the cloud of streamflow samples, which are located in the three-dimensional mixing subspace <U1, U2, U3> and determined by four sources (see Figure 3b). In both cases, the EM-based figures (triangle or tetrahedron) enclose most of the streamflow samples in the U-space. This geometrically confirms the possibility of representing each streamflow sample composition as a mixture of runoff sources, and generally verifies the mixing model.
The identification and interpretation of EMs for Medvezhy creek is unambiguous. Two EMs are related to ground and soil water (GW and SW1), and the third one to rainwater (RW). The GW is associated with streamflow samples taken during the low flow period and represents the baseflow component of the runoff. Samples of SW1 were taken from the upper organic horizon of soil and can be interpreted as lateral (or inter-soil) flow. RW reflects quick overland runoff that reached the drainage network almost without chemical transformation. The mixing subspace for Elovy catchment evolved to four EMs. The first three of them (RW, GW, and SW1) are the same as for Medvezhy, and the fourth, SW2, is associated with soil mineral source and sampled with a lysimeter at the bottom of the steep hillslope from fir-spruce forest soil with slow organic matter destruction.
The mixing models were finally verified by direct calculation of modelled tracer concentrations for every streamwater sample using EM tracer concentrations and estimated proportions of water runoff sources. The modelled and measured series of streamwater sample tracer concentration (Figure 4) are characterized by relatively high R2 values (0.75–0.98).
The EMMA runoff components and measured discharges were used to build the relationships: GW = f (Q) and SW1 = f (Q) at Medvezhy creek; GW = f (Q), SW1 = f (Q) and SW1 + SW2 = f (Q) at Elovy (see Figure 5). The proportions of RW (for both streams) and SW2 (for Elovy), which are weakly related to measured discharges, are determined as the remainder from the water balance equation. These relationships were used to calculate the daily streamflow composition series using the measured hydrographs.

3.2. Results of Hydrological Simulations

All used models were calibrated independently. Hydrological simulations were made continuously (winter season included) with daily time step and a one-year warm-up period. Calibration was performed manually using a trial-and-error approach. The details of the models’ parameters values appear in the Appendix A, Appendix B and Appendix C. Observed and simulated hydrographs for typhoon-induced flood events of 2012 and 2016 are shown in Figure 6. Model efficiency was assessed using common goodness-of-fit measures (determination factor R2, Nash and Sutcliffe efficiency (NSE) [57], and relative bias (BIAS, %) against the measured discharge at catchment outlets (see Table 6). NSE is categorized as “very good” when its value > 0.75 and “unsatisfactory” when its value < 0.5, interim ranges (0.75 > NSE > 0.65 and 0.65 > NSE > 0.5) are defined as “good” and “satisfactory”, respectively. According to BIAS values, simulation results are assumed to be unacceptable if |BIAS| > 25%, “satisfactory” if |BIAS| > 15% and < 25%, “good” for if |BIAS| < 15% < and > 10%, and “very good” if |BIAS| < 10% [58]. According to these criteria, more complex and sophisticated models provide better results for both catchments, and ECOMAG outperforms SWAT in most cases. HBV provides good results for the period of high flow but demonstrates poor performance for low flow (0.01–1.0 mm d−1) periods.

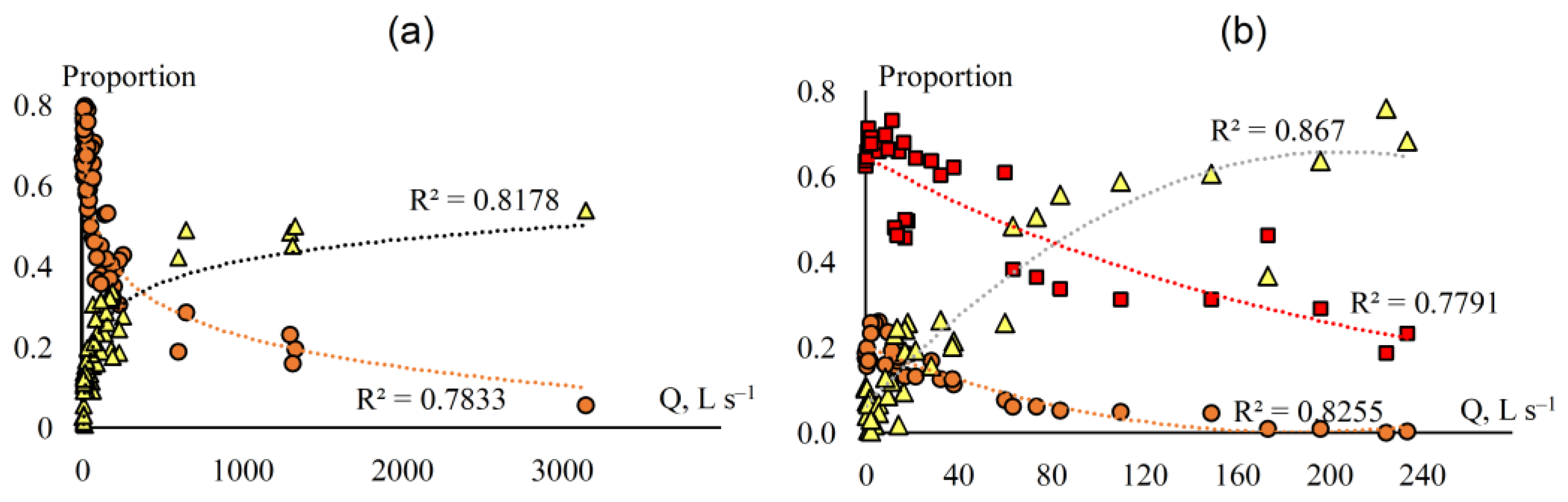
4. Discussion of Hydrograph Separations

The dynamics of runoff composition for the years with significant flood events is presented in Figure 7. All RR models demonstrated that two neighboring small catchments significantly differ in the mutual dynamics of the runoff sources. Geochemical analysis confirmed the differences in runoff generation processes at the both studied catchments. For the Medvezhy catchment, the mixing model provided a typical three-source stable structure and reliable estimates of the source proportions. The proportion of soil runoff for this catchment is relatively small. Conversely, the soil runoff proportion for the Elovy catchment is more significant against surface and groundwater. The younger geology and higher elevation range within this smaller and narrower catchment, with at least two apparent soil–vegetation belts, led to applying a four-source (with two different soil water sources) EMMA model.
From the resulting simulated series, data on runoff constituents were extracted, which directly depend on the model applied. These data were compared with runoff sources obtained from EMMA. Here, we would like to highlight the two main aspects concerning the correctness of further comparison of runoff composition provided by different models.
First, it is difficult to reconcile the interpretations of modelled runoff constituents. The hydrological models derive runoff sources from hydro-physical and hydraulic characteristics of each proposed flow path. Their results are conditioned by the different basic concepts used, always more or less speculative. On the other hand, the tracer separation model is based on the interpretation of measured hydrochemical data related to water residence time, geochemical features of rocks, and interaction intensity with soil matrix. The runoff sources in different models, denoted by the same terms, may not have the same sense. The problem of compatibility and reconciling of different interpretations of the river flow structure is one of the most complex problems of runoff theory and is beyond the scope of this study.
Second, the comparison may be complicated by relatively low accuracy and instability in daily runoff proportions, “measured” by EMMA. This is due to both the well-known limitations of EMMA (incomplete conservatism of tracers and spatial variability of sources) and the limited number of samples leading to significant dispersion in statistical relationships used to calculate daily series of the runoff constituents. Concerning this latter problem, data aggregation in longer time intervals should allow one to mutually compensate for the random errors and to smooth the instability in daily runoff fractions. Therefore, the range of data aggregation intervals (season, month, and pentad) are applied to find a reasonable data generalization period, ensuring the clarity of the results.
The further benchmark analysis is based on the ranking of proximity of runoff constituents simulated by RR models to hydrograph decomposition by EMMA, regarded as an identification model. Each RR model used (ECOMAG, HBV, SWAT) provides three runoff fractions related to surface, soil, and groundwater. The EMMA mixing model separated the Medvezhy catchment runoff to three sources that correspond to the runoff structure of hydrological models. For the Elovy catchment, two EMMA soil flow sources are summarized to match the structure of the three runoff components’ structure in other models.
As the first step, the most generalized seasonal (June–September) data aggregation (see Table 7) was examined. The total seasonal runoff volume for the Medvezhy catchment is reproduced more accurately: by ECOMAG in 2015 and by HBV in 2017; in 2016, SWAT and ECOMAG demonstrate almost identical proximity. The seasonal runoff composition, provided by EMMA, was captured best using ECOMAG for the dry seasons of 2015 and 2017. However, during the high-water season of 2016, it was impossible to choose the best hydrograph separation (as the closest to reference EMMA) among the three simulated variants discussed.
In most cases of the Elovy catchment runoff separation (see Table 7), HBV seems slightly better than ECOMAG, and it was the most successful in the estimation of the groundwater constituent. SWAT for both catchments provided an essentially different runoff composition from EMMA and greatly underestimated the Elovy catchment total seasonal runoff volume. Thus, seasonal data aggregation is not optimal for an unambiguous selection of the best simulation model, at least for the available data.
Next, monthly data aggregations were used to rank the RR models according to a better approximation to the reference EMMA. The monthly aggregation of the three runoff simulation results was compared with 12 observed monthly runoff volumes (four months in each of the three years) and their 36 source proportions estimated by EMMA (see Figure 8). For each case, the simulation providing the closest approximation was fixed, and then the total number of the best results was calculated.
For the Medvezhy catchment, the closest proximity of the ECOMAG and EMMA runoff composition is more obvious (see Figure 8). Comparison of monthly runoff volumes showed the approximate parity between HBV and ECOMAG-7 versus five cases (SWAT loses all the cases). ECOMAG runoff composition is close to EMMA results in 22 out of 36 cases; it is followed by HBV with 11 cases, while SWAT is successful only in 3 cases.
Conversely, for the Elovy catchment, the runoff compositions of the HBV and ECOMAG models are close to the EMMA hydrograph separation (see Figure 8). For runoff volumes of the Elovy catchment, both ECOMAG and HBV score five cases, and SWATthe remaining two cases. The Elovy monthly runoff source proportions provided by HBV and ECOMAG are close to EMMA estimates in 16 cases, and SWAT—in 4 cases. An advantage of the HBV model clearly appears in the estimation of the groundwater fraction in streamflow. This is also an advantage of the ECOMAG model—in the estimation of the surface water fraction. The SWAT model hydrograph decomposition based on monthly analysis appear to be uncompetitive.
Based on results of a five-day data aggregation comparison (see Figure 9), the advantage of the ECOMAG model becomes more pronounced for the Medvezhy catchment. The ECOMAG runoff source dynamics is very similar to the EMMA decomposition. However, for the outstanding 2016 flood event, HBV results are closer to EMMA, while the ECOMAG provided significantly different runoff composition. For the Elovy catchment, it is hard to choose with confidence the best approximation to EMMA decomposition from the results of the ECOMAG and HBV models. It should be noted along the three years (2012–2014) forming the observation series on the Elovy catchment are similar in terms of volume and regime of runoff, in contrast to 2015–2017, included in the observation series on the Medvezhy catchment. An extreme event similar to the flood of 2016 was not observed at the Elovy catchment.
In accordance with comparison results, the ECOMAG model yielded the best agreement with EMMA, HBV was second, and the SWAT model (despite outperforming HBV by NSE efficiency somewhat) was last. The competitive advantage of the ECOMAG model is provided by the proportion comparability of all three runoff sources and the mutual dynamics of their proportions as well. However, while surface runoff estimated by ECOMAG is in good agreement with EMMA, groundwater source estimations differ markedly. In some cases, the HBV model is able to reproduce the EMMA ground runoff quite accurately, but rather the overall pattern over relatively long (seasonal) intervals, not its detailed behavior. At all times, SWAT showed more difference from EMMA than other models.
EMMA clearly explained the differences in hydrological behavior between the catchments due to the need to use four end-members for the Elovy catchment instead of the usual three for the Medvezhy catchment. The need to use a four-component mixing model suggests that the soil interflow of Elovy catchment is more complex in its organization compared to that ofthe Medvezhy catchment.
The simplified lumped models (e.g., HBV) provide the classical storage-based composition of the resulting hydrograph. More sophisticated models, by means of the hydrological characteristics of the soil horizons, allow one to separate the interflow by means of soil horizon hydrological constants (WP, AWC, FC), and vertical and horizontal filtration within one or more layers.
All the above-noted inferences about the representative features of runoff generation in various models were formulated only preliminarily based on the limited data used. The difference in performance can also be partly attributed to the subjective choice of the final model parameterization. It should be concluded that the monthly and synoptic (five/ten days) data aggregation are the scales at which the seasonal runoff dynamics is well suited to clearly compare the RR models with representation of flood events in aggregated view.

5. Conclusions

This article demonstrates the results of comparing the simulated runoff hydrographs and runoff constituents obtained by calibration of three different RR models (SWAT, HBV, ECOMAG), with observed runoff hydrographs and the runoff sources’ dynamics provided by EMMA. For the study, we used in situ observations in two typical small experimental catchments of the mountain-taiga region in the south of Pacific Russia. Both the RR and tracer models provide unequivocal evidence that two neighboring small catchments significantly differ in the structure of runoff generation processes related to differences in the geological and landscape structure. It is shown that compliance with EMMA results may provide useful auxiliary information for validation of hydrological modelling results besides the use of standard efficiency criteria that reflect the proximity of simulated and observed runoff values.
Summarizing the above, we can give a preliminary answer to the question that motivated this study. Comparison of runoff composition obtained with direct and inverse modelling can rank the RR models in terms of physical description completeness of the runoff generation processes. At the same time, the problem of reaching a detailed model-to-model correspondence of runoff composition dynamics remains an urgent challenge. This requires development of unified classifications of water mass types within a river basin and knowledge of runoff generation mechanisms taking into account regional specifics. All conclusions are preliminarily based on limited observation data from two analyzed objects. The main perspectives of the research require progress towards development in methodology, terminological, and conceptual compatibility of interpretations of streamflow composition behind various approaches.

Author Contributions

Conceptualization, A.B. and B.G.; methodology, S.L., T.G., and A.K.; validation, S.L., L.G. and A.K.; formal analysis, A.B., B.G., S.L., L.G. and V.S.; investigation, V.S., B.G. and T.G.; writing—original draft preparation, A.B. and S.L.; writing—review and editing, B.G., V.S., T.G. and L.G.; visualization, B.G., T.G. and S.L.; supervision, A.B.; project administration, B.G.; funding acquisition, B.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Governmental Order to Water Problems Institute, Russian Academy of Sciences subject no. FMWZ-2022-0001; Governmental Order to Pacific Institute of Geography, Far-Eastern Branch Russian Academy of Sciences subjects no. 122020900184-5 and 122011400135-0.

Data Availability Statement

Available upon request.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

ECOMAG hydrological simulation results
The ECOMAG model was used by the authors for large watersheds of lowland rivers in European Russia [59,60], Arctic rivers [61], and the Amur River [62] and for medium-sized semi-mountain rivers [63]. In this study, the model was applied to the scale of an experimental catchment in Russia for the first time. The average area of model units for the studied catchments varies within 0.3–0.5 km2. In the model, soil and groundwater flow was described by the Darcy equation, and surface flow was described by the kinematic wave equation. In conditions of high soil moisture, the actual evaporation was equal to the potential, and then, it decreased linearly to zero as the soil moisture decreased to the wilting point. Potential evaporation was estimated according to the Dalton method. The snowmelt rate is calculated using the degree-day method. Initial parameter values were assigned from available measurements and databases. During calibration, the ratio between the initial and optimized parameter values is fixed [64]. The values of the main calibrated parameters are presented in Table A1.
In the previous experience of applying ECOMAG for the whole Upper-Ussuri River basin [65], it was found that the most sensitive parameters were EK and GFB. To simulate the hydrological response to intensive rainfall of the small studied mountain catchments with steep hillslopes and high horizontal soil saturated hydraulic conductivity, two additional parameters, GFA and GROUND, were incorporated into the calibration procedure. Calibrated values for vertical and horizontal saturated hydraulic conductivity (GFB and GFA) demonstrated an unexpected large difference for two closely located catchments. The GFA value for Elovy creek was an order of magnitude greater in comparison with Medvezhy creek, and the GFB parameter, on the contrary, was lower. Soil evaporation coefficient (EK) was slightly higher for Elovy creek. The baseflow constant parameter (GROUND) was an order of magnitude smaller than the values obtained in the previous study for its major watershed [65] and differed by almost two orders of magnitude for the two studied catchments. All these facts indicate the difference in the runoff generation and distinctive geological and geomorphological conditions of the studied objects. Given the study of the runoff over the summer period, the model was insensitive to the parameters of the intensity of snowmelt (ALF) as well as the temperature threshold for the precipitation phase (TCR) and snowmelt (TSN). For both studied catchments, the air temperature gradient (TGR) was a normal value, and the precipitation gradient (PGR) was not used because the precipitation in the model was determined from the data of two automatic weather stations, which are representative of the catchments.
Table
Table A1. Values of ECOMAG calibrated parameters.
Table A1. Values of ECOMAG calibrated parameters.
ParameterShort NameMedvezhyElovy
Coef. of vertical saturated hydraulic conductivityGFB8.36.5
Coef. of horizontal saturated hydraulic conductivityGFA110
Soil evaporation coefficientEK0.750.8
Baseflow constant, mm day−1GROUND0.0090.0001
Coef. of snowmelt intensity, mm day−1 °CALF0.280.45
Critical air temperature snow/rain, °CTCR0.50.5
Snowmelt air temperature, °CTSN0.10.1
Air temperature gradient, °C 100 m−1TGR−0.6−0.6
Precipitation gradient, mm 100 m−1PGR00
Coef. of vertical saturated hydraulic conductivityGFB8.36.5
Coef. of horizontal saturated hydraulic conductivityGFA110

Appendix B

SWAT hydrological simulation results
The ArcSWAT 2012 GIS interface was used for preparing simulation and model calibration. Model HRUs are subbasins with an area of 1–3 km2. Potential evaporation was computed by the Penman–Monteith method. Channel routing was simulated by variable travel time method. A set of calibrated parameters and their values are presented in Table A2. Values of CN2 (runoff curve number) of both basins correspond to group “A” of high infiltration capacity soils [66]. Calibrated values of the evaporation compensation factor (ESCO) from soil profile allow the roots of trees to extract water from all soil layers for evapotranspiration. Parameters for groundwater simulation (DEP_IMP, ALPHA_BF, GW_DELAY and GWQMIN) were specified during model calibration.
High values of OV_N for Medvezhy creek mean that, during flood events, most of the rainwater quickly infiltrates the soil and reaches the catchment drainage network as interflow through the system of subsoil drains [43,67,68]. The roughness should be considered as total hillslope flow resistance [36,69]. In the case of Elovy creek, the model is insensitive to the OV_N parameter, which means that a fraction of surface flow is negligible. The principal difference is between ESCO and RCHRG_DP parameters. It means that Elovy basin evaporates more water and Medvezhy loses significant amounts of water from the soil profile to recharge deep aquifers (losses). The model systematically underestimates the maximum runoff for both catchments. This can be explained by two facts: the first is an underestimation of CN value for the soil saturation condition, and the second is an overestimation of rainfall losses for the vegetation to intercept during periods of heavy rains (>100 mm day−1).
Table
Table A2. Values of SWAT calibrated parameters.
Table A2. Values of SWAT calibrated parameters.
ParameterShort NameMedvezhyElovy
SCS runoff curve number for moisture condition II CN235.035.0
Roughness coefficient for overland flowOV_N30.00.01
Evaporation compensation from soilESCO0.10.46
Travel time of lateral flow, daysLAT_TTIME3.57.7
Depth of the impervious layer, mDEP_IMP4.255.1
Baseflow recession constantALPHA_BF0.250.13
Time to reach the groundwater, daysGW_DELAY1.51.55
Recharge of deep aquifer coefficientRCHRG_DP0.550.24
Threshold for return flow to occur, mmGWQMN500.0
Capillary rise coefficientGW_REVAP0.20.2
Threshold for GW_REVAP to occur, mmREVAPMN250
Slope length for lateral subsurface flow, mSLSOIL4859

Appendix C

HBV hydrological simulation results
HBV-light standard version was used; calibration was performed manually using the user-interface developed by [53]. PET was calculated by the Penman – Monteith method on a daily basis. Obtained model parameters (see Table A3) clearly demonstrate the difference in FC, Beta, PERC, recession, and Cet factors for investigated catchments. The instream-routed MAXBAS is in the same range. The obtained soil profile-related parameters lead to deeper and more permeable soil for Medvezhy. The difference in Cet parameter is low and can be explained by the watershed hillslope aspect. Higher values of recession coefficients for Medvezhy correspond to fast lateral flow. Special attention is drawn to the recession coefficient K2 for Elovy creek. The value of K2 actually means that this part is not presented for this small catchment. The used model version does not allow deep aquifer losses, so in case of long-term calculation, the near-zero value of K2 will lead to accumulation of water in low storage and significant bias in modelling results.
Table
Table A3. Values of HBV calibrated parameters.
Table A3. Values of HBV calibrated parameters.
ParameterShort NameMedvezhyElovy
Max. soil storage content, mmFC350150
PET limitLP0.20.58
Recharge parameterBeta1.72.7
Max. percolation rate, mm day−1PERC2.61.6
Upper zone limit, mmHL2845
Recession coef.K00.990.16
Recession coef.K10.400.03
Recession coef.K20.130.0001
Length of triangular weighting function, daysMAXBAS1.82.9
PET correction factor, 1 °C−1Cet00.03

References

  1. Heidbüchel, I.; Troch, P.A.; Lyon, S.W.; Weiler, M. The master transit time distribution of variable flow systems. Water Resour. Res. 2012, 48, W06520. [Google Scholar] [CrossRef]
  2. Perrin, C.; Michel, C.; Andreassian, V. Improvement of a Parsimonious Model for Streamflow Simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
  3. Gartsman, B.I.; Shamov, V.V. Field studies of runoff formation in the Far East region based on modern observational instruments. Water Resour. 2015, 42, 766–775. [Google Scholar] [CrossRef]
  4. Cerda, A.; Novara, A.; Dlapa, P.; Lopez-Vicente, M.; Ubeda, X.; Popovic, Z.; Mekonnen, M.; Terol, E.; Janizadeh, S.; Mbarki, S.; et al. Rainfall and water yield in Macizo del Caroig, Eastern Iberian Peninsula. Event runoff at plot scale during a rare flash flood at the Barranco de Benacancil. Cuad. Investig. Geografica 2021, 47, 95–119. [Google Scholar] [CrossRef]
  5. Széles, B.; Parajka, J.; Hogan, P.; Silasari, R.; Pavlin, L.; Strauss, P.; Blöschl, G. The added value of different data types for calibrating and testing a hydrologic model in a small catchment. Water Resour. Res. 2020, 56, e2019WR026153. [Google Scholar] [CrossRef] [PubMed]
  6. Dunn, S.M.; Freer, J.E.; Weiler, M.; Kirkby, M.J.; Seibert, J.; Quinn, P.F.; Lischeid, G.; Tetzlaff, D.; Soulsby, C. Conceptualization in catchment modeling: Simply learning? Hydrol. Process. 2008, 22, 2389–2393. [Google Scholar] [CrossRef]
  7. Johnson, M.S.; Coon, W.F.; Mehta, V.K.; Steenhuis, T.S.; Brooks, E.S.; Boll, J. Application of two hydrologic models with different runoff mechanisms to a hillslope dominated watershed in the northeastern US: A comparison of HSPF and SMR. J. Hydrol. 2003, 284, 57–76. [Google Scholar] [CrossRef]
  8. Butts, M.B.; Payne, J.T.; Kristensen, M.; Madsen, H. An evaluation of the impact of model structure on hydrological modeling uncertainty for streamflow simulation. J. Hydrol. 2004, 298, 242–266. [Google Scholar] [CrossRef]
  9. Clark, M.P.; Slater, A.G.; Rupp, D.E.; Woods, R.A.; Vrugt, J.A.; Gupta, H.V.; Wagener, T.; Hay, L.E. Framework for Understanding Structural Errors (FUSE): A modular framework to diagnose differences between hydrological models. Water Resour. Res. 2008, 44, W00B02. [Google Scholar] [CrossRef]
  10. Clark, M.P.; Kavetski, D.; Fenicia, F. Pursuing the method of multiple working hypotheses for hydrological modelling. Water Resour. Res. 2011, 47, W09301. [Google Scholar] [CrossRef] [Green Version]
  11. Li, H.; Xu, C.-Y.; Beldring, S. How much can we gain with increasing model complexity with the same model concepts? J. Hydrol. 2015, 527, 858–871. [Google Scholar] [CrossRef]
  12. Atkinson, S.E.; Woods, R.A.; Sivapalan, M. Climate and landscape controls on water balance model complexity over changing landscapes. Water Resour. Res. 2002, 38, 1314. [Google Scholar] [CrossRef]
  13. Sivapalan, M.; Blöschl, G.; Zhang, L.; Vertessy, R. Downward approach to hydrological prediction. Hydrol. Process. 2003, 17, 2101–2111. [Google Scholar] [CrossRef]
  14. Marshall, L.; Sharma, A.; Nott, D. Modeling the catchment via mixtures: Issues of model specification and validation. Water Resour. Res. 2006, 42, W11409. [Google Scholar] [CrossRef]
  15. Bai, Y.; Wagener, T.; Reed, P. A top-down framework for watershed model evaluation and selection under uncertainty. Environ. Modell. Softw. 2009, 24, 901–916. [Google Scholar] [CrossRef]
  16. Hornberger, G.H.; Beven, K.; Cosby, B.J.; Sappington, D.E. Shenandoah WaterShed Study: Calibration of A Topography-Based, Variable Contributing Area Hydrological Model to a Small Forested Catchment. Water Resour. Res. 1985, 21, 1841–1850. [Google Scholar] [CrossRef]
  17. Tauro, F.; Selker, J.; Van De Giesen, N.; Abrate, T.; Uijlenhoet, R.; Porfiri, M.; Manfreda, S.; Caylor, K.; Moramarco, T.; Benveniste, J.; et al. Measurements and Observations in the XXI century (MOXXI): Innovation and multidisciplinarity to sense the hydrological cycle. Hydrol. Sci. J. 2018, 63, 169–196. [Google Scholar] [CrossRef]
  18. Beven, K. Rainfall-Runoff Modeling: The Primer; Wiley-Blackwell: Chichester, UK, 2012. [Google Scholar]
  19. Beven, K.; Germann, P. Macropores and water flow in soils revisited. Water Resour. Res. 2013, 49, 3071–3092. [Google Scholar] [CrossRef]
  20. Gao, Y.; Sarker, S.; Sarker, T.; Leta, O.T. Analyzing the critical locations in response of constructed and planned dams on the Mekong River Basin for environmental integrity. Environ. Res. Commun. 2022, 4, 101001. [Google Scholar] [CrossRef]
  21. Sarker, S.; Veremyev, A.; Boginski, V.; Singh, A. Critical Nodes in River Networks. Sci. Rep. 2019, 9, 11178. [Google Scholar] [CrossRef] [Green Version]
  22. Vrugt, J.A.; Diks, C.G.H.; Gupta, H.V.; Bouten, W.; Verstraten, J.M. Improved treatment of uncertainty in hydrologic modeling: Combining the strengths of global optimization and data assimilation. Water Resour. Res. 2005, 41, W01017. [Google Scholar] [CrossRef]
  23. Lischeid, G. Combining hydrometric and hydrochemical data sets for investigating runoff generation processes: Tautologies, inconsistencies and possible explanations. Geogr. Compass. 2008, 2, 255–280. [Google Scholar] [CrossRef]
  24. Clark, I.; Fritz, P. Environmental Isotopes in Hydrogeology; CRC Press: New York, NY, USA, 1997. [Google Scholar]
  25. Evans, C.; Davies, T.D. Causes of concentration/discharge hysteresis and its potential as a tool for analysis of episode hydrochemistry. Water Resour. Res. 1998, 34, 129–137. [Google Scholar] [CrossRef]
  26. Burns, D.A.; McDonnell, J.J.; Hooper, R.P.; Peters, N.E.; Freer, J.E.; Kendall, C.; Beven, K. Quantifying contributions to storm runoff through end-member mixing analysis and hydrologic measurements at the Panola Mountain Research watershed (Georgia, USA). Hydrol. Process. 2001, 15, 1903–1924. [Google Scholar] [CrossRef]
  27. Soulsby, C.; Piegat, K.; Seibert, J.; Tetzlaff, D. Catchment-scale estimates of flow path partitioning and water storage based on transit time and runoff modelling. Hydrol. Process. 2011, 25, 3960–3976. [Google Scholar] [CrossRef]
  28. McGuire, K.J.; Weiler, M.; McDonnell, J.J. Integrating tracer experiments with modeling to assess runoff processes and water transit times. Adv. Water Resour. 2007, 30, 824–837. [Google Scholar] [CrossRef]
  29. Fenicia, F.; McDonnell, J.J.; Savenije, H.H.G. Learning form model improvement: On the contribution of complementary data to process understanding. Water Resour. Res. 2008, 44, W0619. [Google Scholar] [CrossRef]
  30. Fenicia, F.; Wrede, S.; Kavetski, D.; Pfister, L.; Hoffmann, L.; Savenije, H.H.G.; McDonnell, J.J. Assessing the impact of mixing assumptions on the estimation of streamwater mean residence time. Hydrol. Process. 2010, 24, 1730–1741. [Google Scholar] [CrossRef]
  31. McDonnell, J.J.; McGuire, K.; Aggarwal, P.; Beven, K.; Biondi, D.; Destouni, G.; Dunn, S.; James, A.; Kirchner, J.; Kraft, P.; et al. How old is streamwater? Open questions in catchment transit time conceptualization, modeling and analysis. Hydrol. Process. 2010, 24, 1745–1754. [Google Scholar] [CrossRef]
  32. McMillan, H.; Tetzlaff, D.; Clark, M.; Soulsby, C. Do time-variable tracers aid the evaluation of hydrological model structure? A multimodel approach. Water Resour. Res. 2012, 48, W05501. [Google Scholar] [CrossRef] [Green Version]
  33. Birkel, C.; Soulsby, C. Advancing tracer-aided rainfall-runoff modeling: A review of progress, problems and unrealised potential. Hydrol. Process. 2015, 29, 5227–5240. [Google Scholar] [CrossRef]
  34. Beven, K. Towards a methodology for testing models as hypotheses in the inexact sciences. Proc. R. Soc. A 2019, 475, 20180862. [Google Scholar] [CrossRef]
  35. Kozhevnikova, N.K. Dynamics of weather and climatic characteristics and ecological functions of a small forest basin. Contemp. Probl. Ecol. 2009, 2, 436–443. [Google Scholar] [CrossRef]
  36. Bugaets, A.N.; Pshenichnikova, N.F.; Tereshkina, A.A.; Lupakov, S.Y.; Gartsman, B.I.; Shamov, V.V.; Gonchukov, L.V.; Golodnaya, O.M.; Krasnopeyev, S.M.; Kozhevnikova, N.K. Digital Soil Mapping for Hydrological Modeling by the Example of Experimental Catchments in the South of Primorsky Krai. Eurasian Soil Sc. 2021, 54, 1375–1384. [Google Scholar] [CrossRef]
  37. IUSS Working Group WRB. World Reference Base for Soil Resources, World Soil Resources Reports, No. 106. In International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; FAO: Rome, Italy, 2015. [Google Scholar]
  38. Boldeskul, A.G.; Shamov, V.V.; Gartsman, B.I.; Kozhevnikova, N.K. Main ions in water of different genetic types in a small river basin: Case experimental studies in central Sikhote-Alin. Russ. J. Pac. Geol. 2014, 33, 90–101. (In Russian) [Google Scholar]
  39. Gubareva, T.S.; Gartsman, B.I.; Shamov, V.V.; Boldeskul, A.G.; Kozhevnikova, N.K. Genetic disintegration of the runoff hydrograph. Russ. Meteorol. Hydrol. 2015, 40, 215–222. [Google Scholar] [CrossRef]
  40. Gubareva, T.S.; Boldeskul, A.G.; Gartsman, B.I.; Shamov, V.V. Analysis of natural tracers and genetic runoff components in mixing models: Case study of small basins in Primor’e. Water Resour. 2016, 43, 629–639. [Google Scholar] [CrossRef]
  41. Lupakov, S.Y.; Bugaets, A.N.; Shamov, V.V. Application of Different Structures of HBV Model to Studying Runoff Formation Processes: Case Study of Experimental Catchments. Water Resour. 2021, 48, 512–520. [Google Scholar] [CrossRef]
  42. Bugaets, A.N.; Gartsman, B.I.; Tereshkina, A.A.; Gonchukov, L.V.; Bugaets, N.D.; Sidorenko, N.Y.; Pshenichnikova, N.F.; Krasnopeyev, S.M. Using the SWAT Model for Studying the Hydrological Regime of a Small River Basin (the Komarovka River, Primorsky Krai). Russ. Meteorol. Hydrol. 2018, 43, 323–331. [Google Scholar] [CrossRef]
  43. Bugaets, A.N.; Gartsman, B.I.; Lupakov, S.Y.; Shamov, V.V.; Gonchukov, L.V.; Pshenichnikova, N.F.; Tereshkina, A.A. Modeling the Hydrological Regime of Small Testbed Catchments Based on Field Observations: A Case Study of the Pravaya Sokolovka River, the Upper Ussuri River Basin. Water Resour. 2019, 46, S8–S16. [Google Scholar] [CrossRef]
  44. Christophersen, N.; Neal, C.; Hooper, R.P.; Vogt, R.D.; Andersen, S. Modeling stream water chemistry of soilwater end-members—A step towards second-generation acidification models. J. Hydrol. 1990, 116, 307–320. [Google Scholar] [CrossRef]
  45. Christophersen, N.; Hopper, R.P. Multivariate analysis of stream water chemical data: The use of principal component analysis for the end-member mixing problem. Water Resour. Res. 1992, 28, 99–107. [Google Scholar] [CrossRef]
  46. Pomerantsev, A. Chemometrics in Excel; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
  47. Hooper, R.P. Diagnostic tools for mixing models of stream water chemistry. Wat. Resour. Res. 2003, 39, 1055. [Google Scholar] [CrossRef]
  48. Motovilov, Y.G.; Gottschalk, L.; Engeland, L.; Rodhe, A. Validation of a distributed hydrological model against spatial observation. Agric. Forest Meteorol. 1999, 98–99, 257–277. [Google Scholar] [CrossRef]
  49. Kuchment, L.S.; Demidov, V.N.; Motovilov, Y.G. Formirovanie Rechnogo Stoka [Runoff Formation]; Nauka: Moscow, Russia, 1983. (In Russian) [Google Scholar]
  50. Arnold, J.G.; Allen, P.M.; Bernhardt, G. A comprehensive surface—Groundwater flow model. J. Hydrol. 1993, 142, 47–69. [Google Scholar] [CrossRef]
  51. Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R. Soil and Water Assessment Tool Theoretical Documentation, Version 2009; Texas A&M University: College Station, TX, USA, 2011. [Google Scholar]
  52. Bergstrom, S. Development and Application of a Conceptual Runoff Model for Scandinavian Catchments; Univ. Lund. Bull.: Norrkoping, Sweden, 1976. [Google Scholar]
  53. Seibert, J.; Vis, M.J.P. Teaching hydrological modeling with a user-friendly catchment-runoff-model software package. Hydrol. Earth Syst. Sci. 2012, 16, 3315–3325. [Google Scholar] [CrossRef]
  54. Gubareva, T.S.; Gartsman, B.I.; Solopov, N.V. A model of mixing of four river runoff recharge sources using hydrochemical tracers in the problem of hydrograph separation. Water Resour. 2018, 45, 827–838. [Google Scholar] [CrossRef]
  55. Gubareva, T.S.; Gartsman, B.I.; Shamov, V.V.; Lutsenko, T.N.; Boldeskul, A.G.; Kozhevnikova, N.K.; Lupakov, S.Y. Runoff components of small catchments in Sikhote-Alin: Summarizing the results of field measurements and tracer modelling. Izvestiya Rossiiskoi Akademii Nauk. Seriya Geograficheskaya 2019, 6, 126–140. [Google Scholar] [CrossRef]
  56. Zar, J. Biostatistical Analyses; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
  57. Nash, J.E.; Sutclifee, J.V. River flow forecasting through conceptual models. Part 1—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
  58. Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
  59. Motovilov, Y.G. Hydrological simulation of river basins at different spatial scales: 2. Test results. Water Resour. 2016, 43, 743–753. [Google Scholar] [CrossRef]
  60. Kalugin, A.S. The impact of climate change on surface, subsurface and groundwater flow: A case study of the Oka River (European Russia). Water Resour. 2019, 46, S31–S39. [Google Scholar] [CrossRef]
  61. Gelfan, A.; Kalugin, A.; Krylenko, I.; Nasonova, O.; Gusev, Y.; Kovalev, E. Does a successful comprehensive evaluation increase confidence in a hydrological model intended for climate impact assessment? Clim. Chang. 2020, 163, 1165–1185. [Google Scholar] [CrossRef]
  62. Kalugin, A.S.; Motovilov, Y.G. Runoff formation model for the Amur River basin. Water Resour. 2018, 45, 149–159. [Google Scholar] [CrossRef]
  63. Kalugin, A. Process-based modeling of the high flow of a semi-mountain river under current and future climatic conditions: A case study of the Iya River (Eastern Siberia). Water 2021, 13, 1042. [Google Scholar] [CrossRef]
  64. Gelfan, A.N.; Motovilov, Y.G.; Krylenko, I.; Moreido, V.M.; Zakharova, E. Testing the robustness of the physically based ECOMAG model with respect to changing conditions. Hydrol. Sci. J. 2015, 60, 1266–1285. [Google Scholar] [CrossRef]
  65. Motovilov, Y.G.; Bugaets, A.N.; Gartsman, B.I.; Gonchukov, L.V.; Kalugin, A.S.; Moreido, V.M.; Suchilina, Z.A.; Fingert, E.A. Assessing the Sensitivity of a Model of Runoff Formation in the Ussuri River Basin. Water Resour. 2018, 45, S128–S134. [Google Scholar] [CrossRef]
  66. USDA SCS National Engineering Handbook; Government Printing: Washington, DC, USA, 1956.
  67. Gerrard, A.J. Soils and Landforms: An Integration of Geomorphology and Pedology; George Allen and Unwin: London, UK, 2018. [Google Scholar]
  68. Gartsman, B.I.; Gubareva, T.S.; Lupakov, S.Y.; Shamov, V.V.; Shekman, E.A.; Orlyakovskii, A.V.; Tarbeeva, A.M. The forms of linear structure of overland flow in medium-height mountain regions: Case study of the Sikhote Alin. Water Resour. 2020, 47, 179–188. [Google Scholar] [CrossRef]
  69. Bugaets, A.N.; Gartsman, B.I.; Gelfan, A.N.; Motovilov, Y.G.; Sokolov, O.V.; Gonchukov, L.V.; Kalugin, A.S.; Moreido, V.M.; Suchilina, Z.; Fingert, E. The Integrated System of Hydrological Forecasting in the Ussuri River Basin Based on the ECOMAG Model. Geosciences 2018, 8, 5. [Google Scholar] [CrossRef] [Green Version]
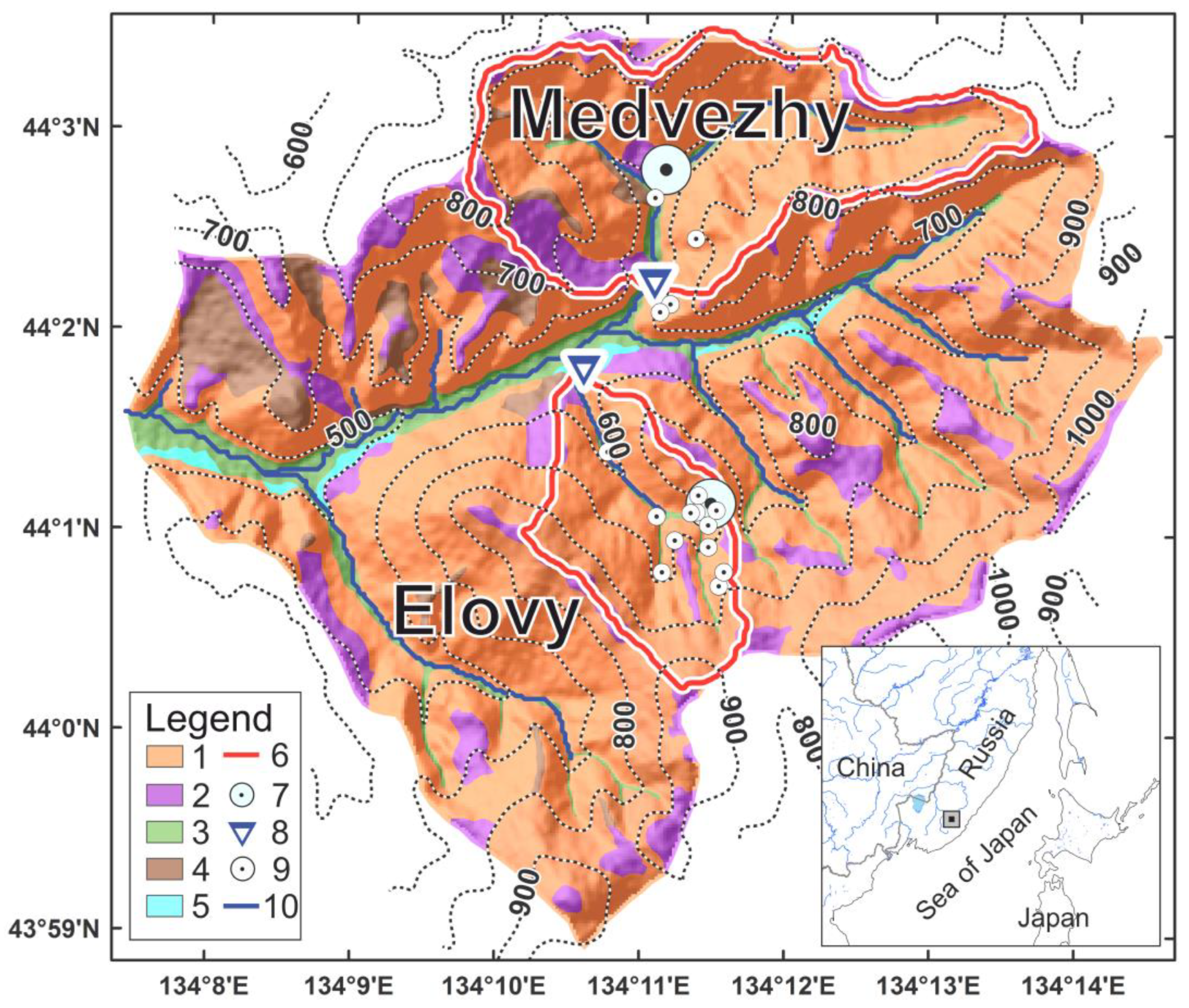
Water 15 00752 g001 550
Figure 1. The experimental catchments’ topography (vertical distance between iso-level lines is 100 m), localization of observational sites, and soil cover: 1—Dystric Cambisols Humic and Nechic, 2—Dystric Skeletic Leptosols (Humic), 3—Dystric Fluvisols and Sapric Histosols, 4—Dystric Cambisols Gleyic and Stagnic, 5—Dystric Fluvic Cambisols, 6—catchments’ boundary, 7—weather stations, 8—stream gauges, 9—soil lysimeters, 10—river network.
Figure 1. The experimental catchments’ topography (vertical distance between iso-level lines is 100 m), localization of observational sites, and soil cover: 1—Dystric Cambisols Humic and Nechic, 2—Dystric Skeletic Leptosols (Humic), 3—Dystric Fluvisols and Sapric Histosols, 4—Dystric Cambisols Gleyic and Stagnic, 5—Dystric Fluvic Cambisols, 6—catchments’ boundary, 7—weather stations, 8—stream gauges, 9—soil lysimeters, 10—river network.
Water 15 00752 g001
Water 15 00752 g002 550
Figure 2. The residual plots for two-dimensional mixing subspace: (a) Medvezhy catchment; (b) Elovy catchment.
Figure 2. The residual plots for two-dimensional mixing subspace: (a) Medvezhy catchment; (b) Elovy catchment.
Water 15 00752 g002
Water 15 00752 g003 550
Figure 3. Mixing diagrams in the U-space for: (a) Medvezhy catchment; (b) Elovy catchment. RW—rainwater, GW—groundwater, SW1, SW2—soil water.
Figure 3. Mixing diagrams in the U-space for: (a) Medvezhy catchment; (b) Elovy catchment. RW—rainwater, GW—groundwater, SW1, SW2—soil water.
Water 15 00752 g003
Water 15 00752 g004 550
Figure 4. Comparison of modelled and measured series of streamwater sample tracer concentrations: (a) Medvezhy catchment; (b) Elovy catchment.
Figure 4. Comparison of modelled and measured series of streamwater sample tracer concentrations: (a) Medvezhy catchment; (b) Elovy catchment.
Water 15 00752 g004
Water 15 00752 g005 550
Figure 5. Streamflow constituents’ rating curves: (a) Medvezhy catchment; (b) Elovy catchment; GW—orange dots, SW1—yellow triangles, and SW1 + SW2—red squares.
Figure 5. Streamflow constituents’ rating curves: (a) Medvezhy catchment; (b) Elovy catchment; GW—orange dots, SW1—yellow triangles, and SW1 + SW2—red squares.
Water 15 00752 g005
Water 15 00752 g006 550
Figure 6. Dynamics of precipitation (1), calculated (2—ECOMAG, 3—SWAT, 4—HBV) and observed (5) runoff for the whole period of hydrological simulation ((a)—Medvezhy creek, (b)—Elovy creek) and examples of flood events ((c)—Medvezhy creek, (d)—Elovy creek).
Figure 6. Dynamics of precipitation (1), calculated (2—ECOMAG, 3—SWAT, 4—HBV) and observed (5) runoff for the whole period of hydrological simulation ((a)—Medvezhy creek, (b)—Elovy creek) and examples of flood events ((c)—Medvezhy creek, (d)—Elovy creek).
Water 15 00752 g006
Water 15 00752 g007 550
Figure 7. Examples of calculated absolute (mm) and relative (%) fraction of daily runoff constituents for Medvezhy catchment (left panel) and Elovy catchment (right panel).
Figure 7. Examples of calculated absolute (mm) and relative (%) fraction of daily runoff constituents for Medvezhy catchment (left panel) and Elovy catchment (right panel).
Water 15 00752 g007
Water 15 00752 g008 550
Figure 8. Comparison of calculated monthly absolute (mm) and relative (%) proportions of runoff constituents: (a)—Medvezhy catchment, (b)—Elovy catchment.
Figure 8. Comparison of calculated monthly absolute (mm) and relative (%) proportions of runoff constituents: (a)—Medvezhy catchment, (b)—Elovy catchment.
Water 15 00752 g008
Water 15 00752 g009 550
Figure 9. Comparison of calculated pentad absolute (mm) and relative (%) proportions of runoff constituents: (a)—Medvezhy catchment, (b)—Elovy catchment.
Figure 9. Comparison of calculated pentad absolute (mm) and relative (%) proportions of runoff constituents: (a)—Medvezhy catchment, (b)—Elovy catchment.
Water 15 00752 g009
Table
Table 1. Catchments main characteristics.
Table 1. Catchments main characteristics.
CharacteristicsElovyMedvezhy
Area, km23.57.6
Avg. height, m722704
Max. height, m962869
Avg. slope, %13.513.8
Max. slope, %28.731.5
Mean annual precipitation, mm 1780830
Mean annual temperature, °C 13.03.2
Avg. discharge, mm day−1 10.650.75
Note(s): 1 based on observations for the period: 01.01.11–31.12.14 for Elovy creek and the period 01.01.14–31.12.17 for Medvezhy creek.
Table
Table 2. Hydrological models main characteristics.
Table 2. Hydrological models main characteristics.
CharacteristicsECOMAGSWATHBV
Spatial discretizationHRUHRULumped
Temporal discretizationDailyDailyDaily
Number of calibrated parameters111210
Snow component basisDegree-dayDegree-dayDegree-day
Potential evapotranspirationDalton methodPenman–MonteithPenman–Monteith
Actual evapotranspirationLinear reduction in PET by soil storage contentReduction in PET by soil water contentLinear reduction in PET by soil storage content
Surface flowKinematic waveSCS curve numberLinear storage
Soil flowDarcy’s lawKinematic storage modelLinear storage
Groundwater flowDarcy’s lawLinear storage Linear storage
Routing methodKinematic waveVariable travel timeTriangular weighted
Table
Table 3. Pairwise correlations of the concentrations of solutes, ranked by R2 (n is the number of samples).
Table 3. Pairwise correlations of the concentrations of solutes, ranked by R2 (n is the number of samples).
R2Medvezhy Catchment, n = 69Elovy Catchment, n = 126
>0.71TDS—HCO3, SO4—Mg, HCO3—Mg, TDS—Mg–
0.7–0.61DOC—SO4, HCO3—SO4, SO4—Ca, HCO3—Ca, TDS—Ca, Ca—Mg–
0.6–0.51TDS—SO4, DOC—Mg–
0.5–0.41–HCO3—Mg, HCO3—TDS, SO4—NO3
0.4–0.3–NO3—HCO3, NO3—Na, HCO3—Na, Na—TDS
Table
Table 4. The percent of variance explained by PC (U) for individual catchments.
Table 4. The percent of variance explained by PC (U) for individual catchments.
CatchmentTracersU1 *U2U3U4U5U6
MedvezhyTDS, DOC, HCO3, SO4, Ca, Mg83.68.6
(92.2)		4.4
(96.7)		2.1
(98.7)		0.9
(99.6)		0.4
(100)
ElovyHCO3, Mg, NO3, Na64.820.2
(85.0)		9.7
(94.7)		5.3
(100)		--
Note(s): * Values in parentheses—the cumulative percent of total variance explained by set of PCs from the first to the current.
Table
Table 5. Chemical composition of end-members. n—number of samples, range of concentrations is in the numerator, average values are in the denominator.
Table 5. Chemical composition of end-members. n—number of samples, range of concentrations is in the numerator, average values are in the denominator.
Tracer, mg/LMedvezhy CatchmentElovy Catchment
End-Members
Rainwater (n = 36)Groundwater (n = 15)Soilwater (n = 12)Rainwater (n = 36)Groundwater (n = 5)Soil Water 1 (n = 13)Soil Water 2 (n = 7)
HCO3<0.1–2.3075.6–90.314.6–24.3<0.1–2.3014.2–19.210.4–18.06.71–9.76
0.3784.319.40.3716.413.78.11
Mg<0.02–0.131.66–5.183.25–5.36<0.02–0.10.85–1.040.34–0.610.39–0.55
0.053.474.560.050.980.40.48
TDS0.05–14.9121–16330.5–100----
5.3214663.8
DOC0.18–5.602.50–4.764.10–42.9----
1.773.5618.1
SO4<0.32–5.7516.2–29.04.07–9.09----
1.4223.96.71
Ca<0.1–6.7817.8–38.96.96–22.7----
0.6527.815.4
NO3---<0.2–5.1<0.2–0.72<0.2–0.152.13–7.45
1.170.390.054.66
Na---0.04–1.02.82–2.994.72–7.802.00–2.66
0.142.915.792.41
Table
Table 6. Goodness-of-fit characteristics for runoff simulations with different models.
Table 6. Goodness-of-fit characteristics for runoff simulations with different models.
ModelMedvezhyElovy
YearR2NSEBIAS, %YearR2NSEBIAS, %
ECOMAG20150.920.91−520120.930.91−0.3
20160.920.90820130.870.8013
20170.910.87−620140.840.834
2015–20170.920.9042012–20140.900.8910
SWAT20150.940.88−2020120.900.90−4
20160.890.85620130.820.81−1
20170.690.67−1220140.930.88−13
2015–20170.900.86−12012–20140.860.86−6
HBV20150.350.35−820120.960.961
20160.920.911820130.830.83−6
20170.560.53−320140.640.624
2015–20170.910.91122012–20140.880.88−0.3
Table
Table 7. Seasonal runoff constituents obtained from rainfall–runoff models and hydrograph separation by EMMA.
Table 7. Seasonal runoff constituents obtained from rainfall–runoff models and hydrograph separation by EMMA.
SourceMedvezhyElovy 1
SWATHBVECOMAGEMMASWATHBVECOMAGEMMA
20152012
Surface, %0.00.043.525.60.022.17.715.1
Soil, %97.82.829.914.635.372.389.375.5
Ground, %2.297.226.659.864.75.63.09.4
Total, mm26.943.934.637.264.674.17874.1
20162013
Surface, %577.832.134.40.05.03.524.4
Soil, %33.343.763.03336.285.994.266.3
Ground, %9.748.54.932.663.89.12.39.3
Total, mm211.3233.4213.3195.262.276.6100.385.6
20172014
Surface, %0.70.058.327.30.11.03.823.8
Soil, %99.313.322.918.345.486.292.863.2
Ground, %086.718.854.454.512.83.312.9
Total, mm3538.13738.749.473.771.066.6
2015–20172012–2013
Surface, %44.15.735.832.10.09.34.921.2
Soil, %47.834.454.828.438.481.592.368.4
Ground, %8.159.99.439.561.69.22.810.4
Total, mm273.1315.5284.9271.2176.2224.3249.3226.3
Note(s): 1 Soil flow proportion for Elovy catchment obtained by EMMA is the sum of the SW1 (soil organic) and SW2 (soil mineral) parts; see Section 3 for details.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Bugaets, A.; Gartsman, B.; Gubareva, T.; Lupakov, S.; Kalugin, A.; Shamov, V.; Gonchukov, L. Comparing the Runoff Decompositions of Small Experimental Catchments: End-Member Mixing Analysis (EMMA) vs. Hydrological Modelling. Water 2023, 15, 752. https://doi.org/10.3390/w15040752

AMA Style

Bugaets A, Gartsman B, Gubareva T, Lupakov S, Kalugin A, Shamov V, Gonchukov L. Comparing the Runoff Decompositions of Small Experimental Catchments: End-Member Mixing Analysis (EMMA) vs. Hydrological Modelling. Water. 2023; 15(4):752. https://doi.org/10.3390/w15040752

Chicago/Turabian Style

Bugaets, Andrey, Boris Gartsman, Tatiana Gubareva, Sergei Lupakov, Andrey Kalugin, Vladimir Shamov, and Leonid Gonchukov. 2023. "Comparing the Runoff Decompositions of Small Experimental Catchments: End-Member Mixing Analysis (EMMA) vs. Hydrological Modelling" Water 15, no. 4: 752. https://doi.org/10.3390/w15040752

APA Style

Bugaets, A., Gartsman, B., Gubareva, T., Lupakov, S., Kalugin, A., Shamov, V., & Gonchukov, L. (2023). Comparing the Runoff Decompositions of Small Experimental Catchments: End-Member Mixing Analysis (EMMA) vs. Hydrological Modelling. Water, 15(4), 752. https://doi.org/10.3390/w15040752

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop