Assessing the Influence of a Bias Correction Method on Future Climate Scenarios Using SWAT as an Impact Model Indicator
Abstract
1. Introduction
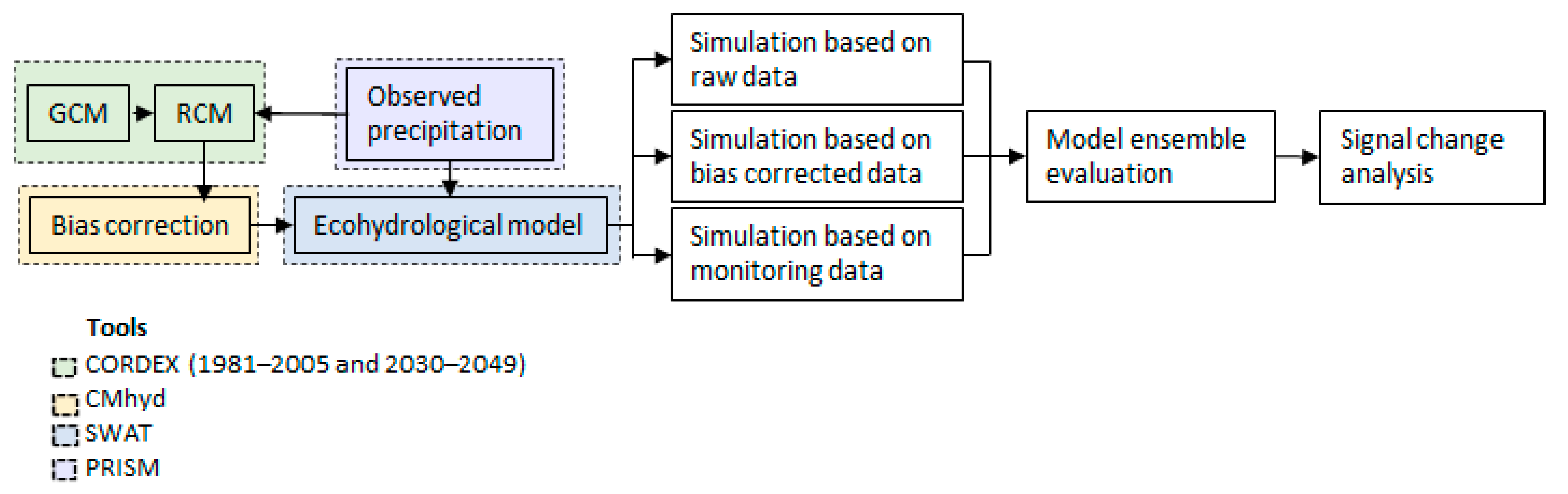
2. Materials and Methods
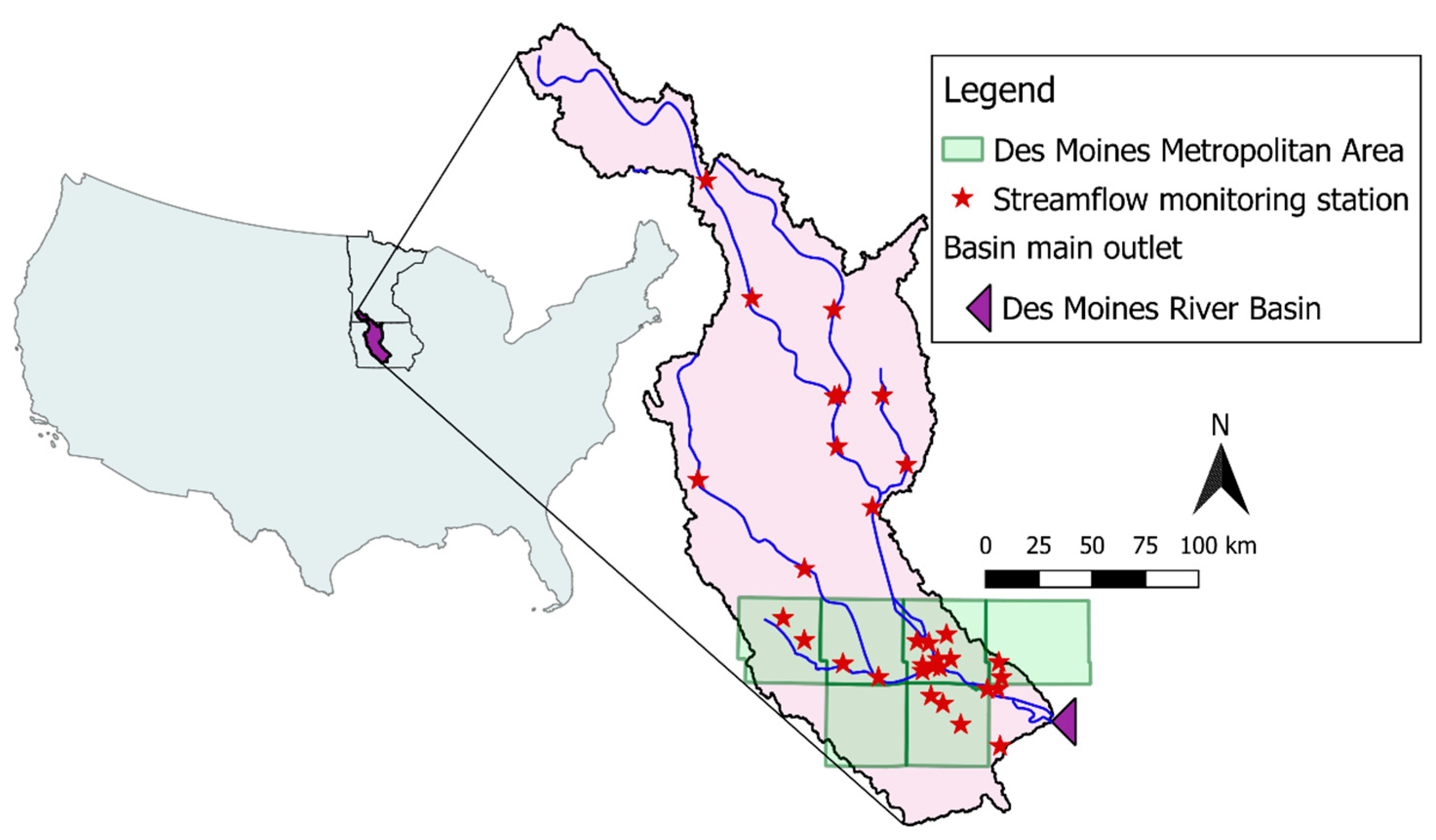
2.1. Study Area
2.2. Climate Models and SWAT Ecohydrological Model
2.2.1. Climate Models and the CORDEX Platform
2.2.2. SWAT Ecohydrological Model
2.2.3. Bias Correction
2.3. Statistical Evaluation
3. Results and Discussion
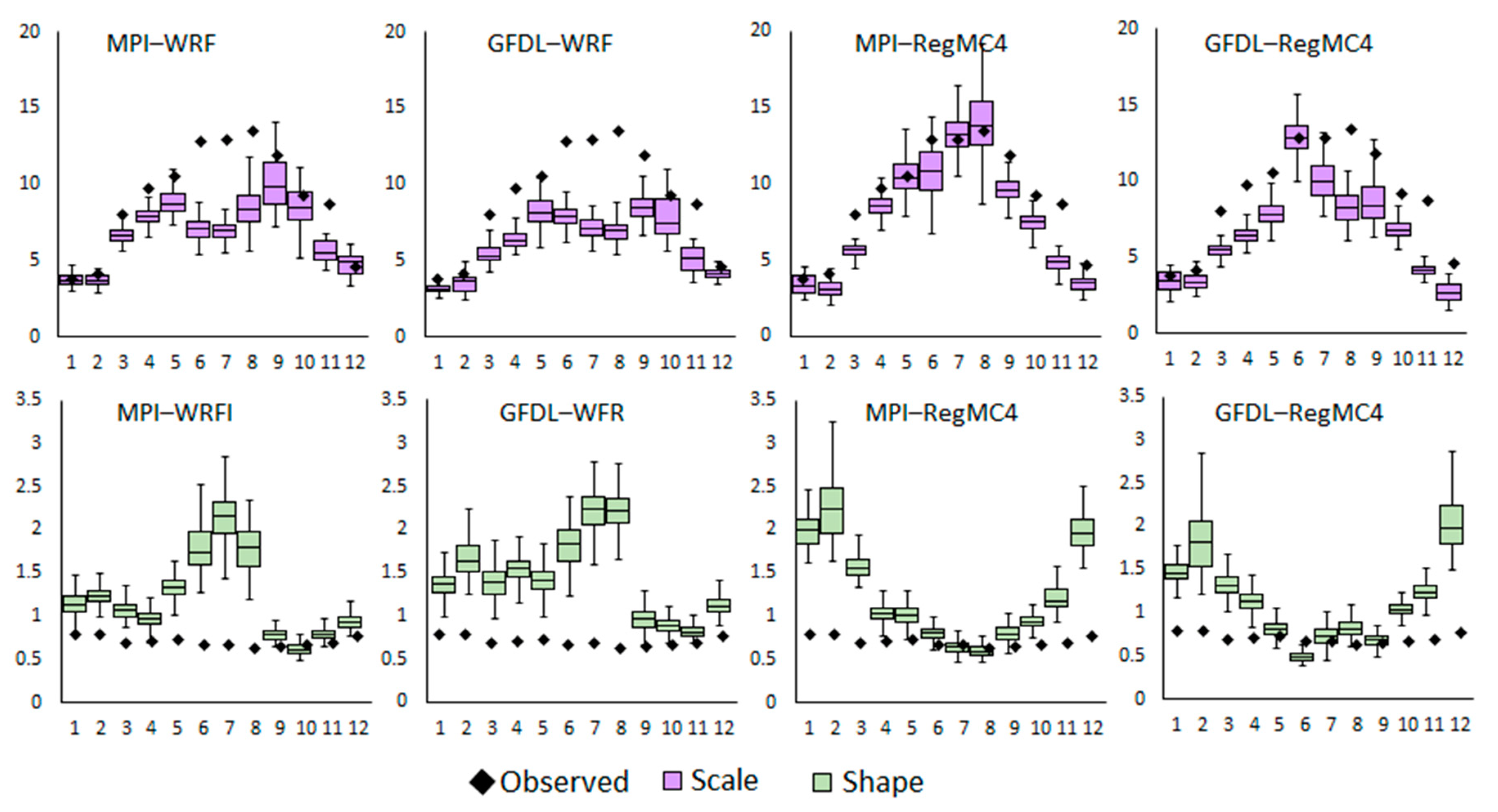
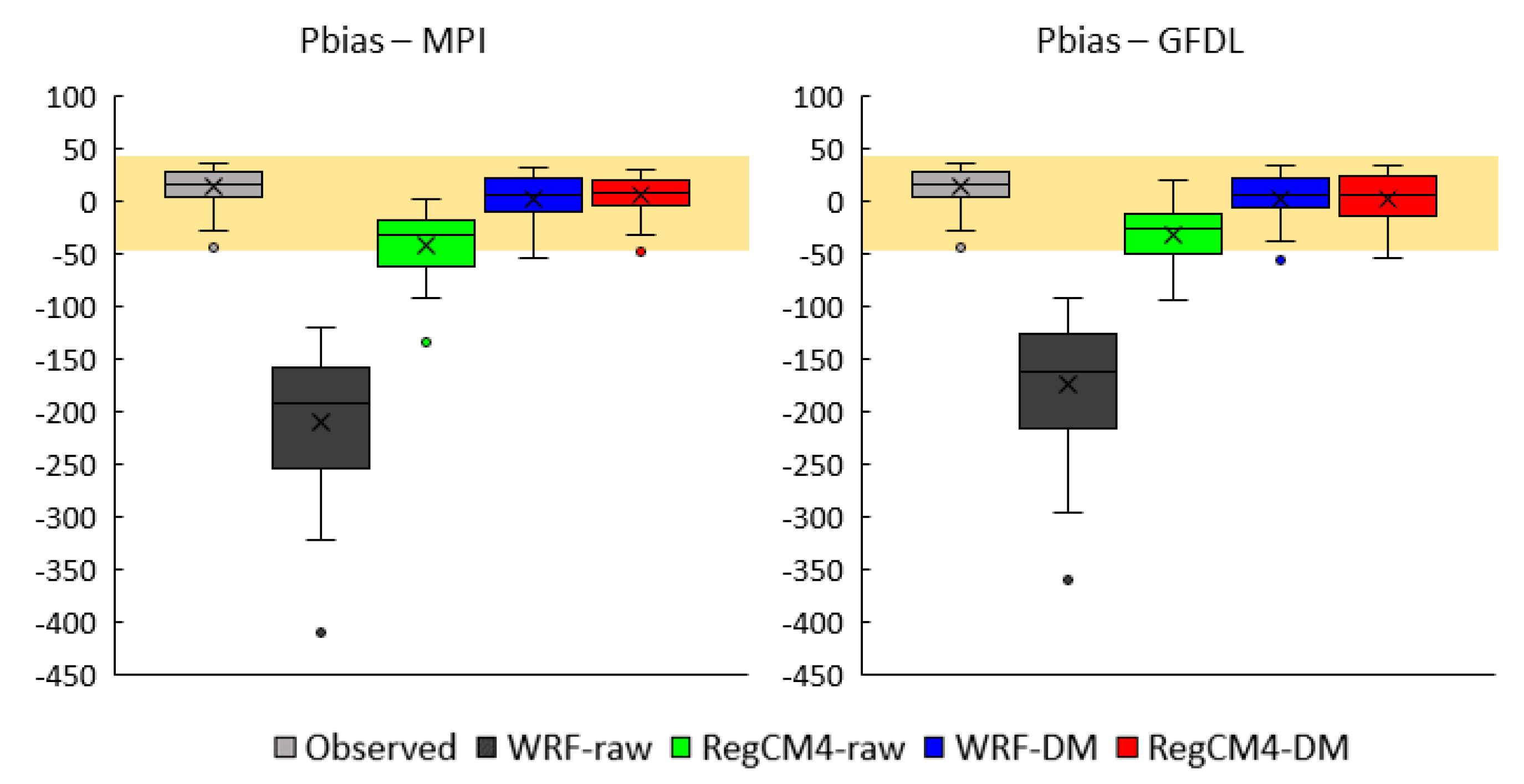
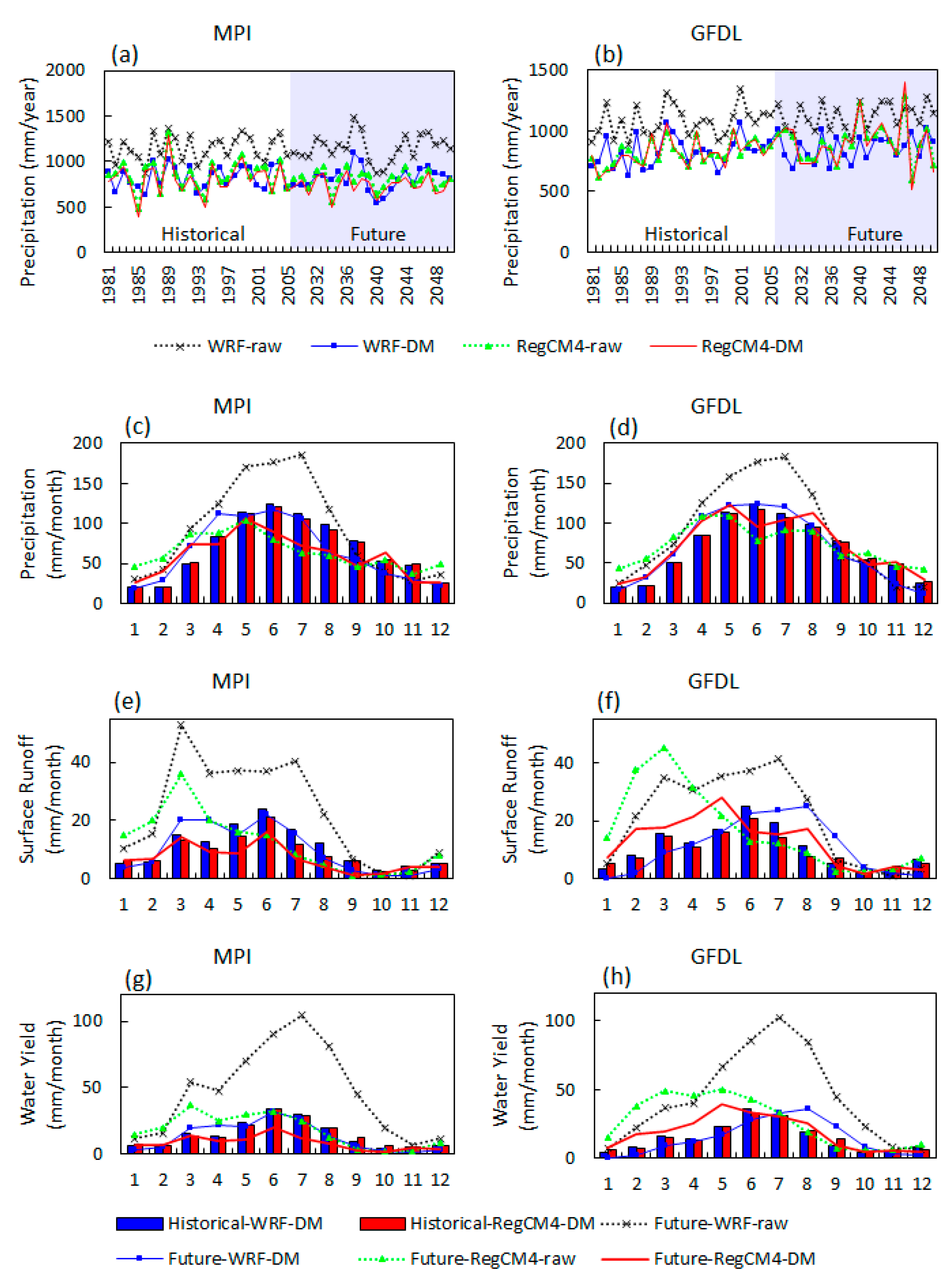
3.1. Historical Precipitation, Surface Runoff, Water Yield, and Streamflow
3.2. Future Precipitation, Surface Runoff, and Water Yield
Bias-Correction Models Showed Changes in Prediction Signals
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maraun, D.; Widmann, M.; Gutiérrez, J.M.; Kotlarski, S.; Chandler, R.E.; Hertig, E.; Wibig, J.; Huth, R.; Wilcke, R.A. VALUE: A framework to validate downscaling approaches for climate change studies. Earth’s Futur. 2015, 3, 1–14. [Google Scholar] [CrossRef]
- Pierce, D.W.; Barnett, T.P.; Santer, B.D.; Gleckler, P.J. Selecting global climate models for regional climate change studies. Proc. Natl. Acad. Sci. USA 2009, 106, 8441–8446. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report: Longer Report; IPCC: Geneva, Switzerland, 2015. [Google Scholar]
- Schwalm, C.R.; Glendon, S.; Duffy, P.B. RCP8.5 tracks cumulative CO2 emissions. Proc. Natl. Acad. Sci. USA 2020, 117, 19656–19657. [Google Scholar] [CrossRef] [PubMed]
- Pinto, I.; Jack, C.; Hewitson, B. Process-based model evaluation and projections over southern Africa from Coordinated Regional Climate Downscaling Experiment and Coupled Model Intercomparison Project Phase 5 models. Int. J. Clim. 2018, 38, 4251–4261. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. LARGE AREA HYDROLOGIC MODELING AND ASSESSMENT PART I: MODEL DEVELOPMENT. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Williams, J.R.; Arnold, J.G.; Kiniry, J.R.; Gassman, P.W.; Green, C.H. History of model development at Temple, Texas. Hydrol. Sci. J. 2008, 53, 948–960. [Google Scholar] [CrossRef]
- Bieger, K.; Arnold, J.G.; Rathjens, H.; White, M.J.; Bosch, D.D.; Allen, P.M.; Volk, M.; Srinivasan, R. Introduction to SWAT+, A Completely Restructured Version of the Soil and Water Assessment Tool. JAWRA J. Am. Water Resour. Assoc. 2016, 53, 115–130. [Google Scholar] [CrossRef]
- Ehret, U.; Zehe, E.; Wulfmeyer, V.; Warrach-Sagi, K.; Liebert, J. HESS Opinions "Should we apply bias correction to global and regional climate model data?". Hydrol. Earth Syst. Sci. 2012, 16, 3391–3404. [Google Scholar] [CrossRef]
- Sørland, S.L.; Schär, C.; Luethi, D.; Kjellström, E. Bias patterns and climate change signals in GCM-RCM model chains. Environ. Res. Lett. 2018, 13, 074017. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Is bias correction of regional climate model (RCM) simulations possible for non-stationary conditions? Hydrol. Earth Syst. Sci. 2013, 17, 5061–5077. [Google Scholar] [CrossRef]
- Singh, V.; Jain, S.K.; Singh, P. Inter-comparisons and applicability of CMIP5 GCMs, RCMs and statistically downscaled NEX-GDDP based precipitation in India. Sci. Total. Environ. 2019, 697, 134163. [Google Scholar] [CrossRef] [PubMed]
- Stéfanon, M.; Martin-StPaul, N.K.; Leadley, P.; Bastin, S.; Dell’Aquila, A.; Drobinski, P.; Gallardo, C. Testing climate models using an impact model: What are the advantages? Clim. Chang. 2015, 131, 649–661. [Google Scholar] [CrossRef]
- Wörner, V.; Kreye, P.; Meon, G. Effects of Bias-Correcting Climate Model Data on the Projection of Future Changes in High Flows. Hydrology 2019, 6, 46. [Google Scholar] [CrossRef]
- Bathurst, J.; Ewen, J.; Parkin, G.; O’Connell, P.; Cooper, J. Validation of catchment models for predicting land-use and climate change impacts. Blind validation for internal and outlet responses. J. Hydrol. 2004, 287, 74–94. [Google Scholar] [CrossRef]
- Kundu, S.; Khare, D.; Mondal, A. Individual and combined impacts of future climate and land use changes on the water balance. Ecol. Eng. 2017, 105, 42–57. [Google Scholar] [CrossRef]
- Pandey, B.K.; Khare, D.; Kawasaki, A.; Meshesha, T.W. Integrated approach to simulate hydrological responses to land use dynamics and climate change scenarios employing scoring method in upper Narmada basin, India. J. Hydrol. 2021, 598, 126429. [Google Scholar] [CrossRef]
- Chagas, V.B.P.; Chaffe, P.L.B.; Blöschl, G. Climate and land management accelerate the Brazilian water cycle. Nat. Commun. 2022, 13, 5136. [Google Scholar] [CrossRef] [PubMed]
- Iowa Climate Statement 2013: A Rising Challenge to Iowa Agriculture. Available online: https://cgrer.uiowa.edu/sites/cgrer.uiowa.edu/files/pdf_files/Iowa%20Climate%20Statement%202013%20A%20Rising%20Challenge%20to%20Iowa%20Agriculture_October_18_2013_FINAL.pdf (accessed on 5 January 2023).
- Iowa Climate Statement 2019: Dangerous Heat Events Will Be More Frequent and Severe. Available online: http://www.craiganderson.org/wp-content/uploads/caa/ClimateChangeDocs/2019IowaClimateStatement.pdf (accessed on 5 January 2023).
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Beven, K.; Lamb, R. The uncertainty cascade in model fusion. Geol. Soc. London Spéc. Publ. 2014, 408, 255–266. [Google Scholar] [CrossRef]
- Clark, M.P.; Wilby, R.L.; Gutmann, E.D.; Vano, J.A.; Gangopadhyay, S.; Wood, A.W.; Fowler, H.J.; Prudhomme, C.; Arnold, J.R.; Brekke, L.D. Characterizing Uncertainty of the Hydrologic Impacts of Climate Change. Curr. Clim. Chang. Rep. 2016, 2, 55–64. [Google Scholar] [CrossRef]
- Brighenti, T.M.; Gassman, P.W.; Schilling, K.E.; Srinivasan, R.; Liebman, M.; Thompson, J.R. Determination of accurate baseline representation for three Central Iowa watersheds within a HAWQS-based SWAT analyses. Sci. Total. Environ. 2022, 839, 156302. [Google Scholar] [CrossRef]
- Gassman, P.; Reyes, M.; Green, C.; Arnold, J.; Gassman, P. The Soil And Water Assessment Tool: Historical Development, Applications, and Future Research Directions Invited Review Series. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Yang, X.; Haywood, J. A review of SWAT applications, performance and future needs for simulation of hydro-climatic extremes. Adv. Water Resour. 2020, 143, 103662. [Google Scholar] [CrossRef]
- Akoko, G.; Le, T.; Gomi, T.; Kato, T. A Review of SWAT Model Application in Africa. Water 2021, 13, 1313. [Google Scholar] [CrossRef]
- USDA-NRCS (U.S. Department of Agriculture, Natural Resources Conservation Service). Soil Data Access: Query Services for Custom Access to Soil Data; USDA-NRCS: Washington, DC, USA. Available online: https://sdmdataaccess.nrcs.usda.gov/ (accessed on 5 January 2023).
- Peel, M.; Finlayson, B.; Mcmahon, T. Hydrology and Earth System Sciences Updated World Map of the Köppen-Geiger Climate Classification. 2007. Available online: www.hydrol-earth-syst-sci.net/11/1633/2007/ (accessed on 5 January 2023).
- McGinnis, S.; Mearns, L. Building a climate service for North America based on the NA-CORDEX data archive. Clim. Serv. 2021, 22, 100233. [Google Scholar] [CrossRef]
- PRISM (Parameter-Elevation Relationships on Independent Slopes Model). Climate Group, PRISM Climate Data, Northwest Alliance for Computational Science and Engineering; Oregon State University: Corvallis, OR, USA; Available online: https://www.prism.oregonstate.edu/ (accessed on 5 January 2023).
- USGS National Water Information System, Streamflow Data Access. 2021. Available online: https://waterdata.usgs.gov/nwis (accessed on 5 January 2023).
- WRCP (World Climate Research Programme). CMIP Phase 5 (CMIP5); World Meteorological Organization: Geneva, Switzerland; Available online: https://www.wcrp-climate.org/wgcm-cmip/wgcm-cmip5 (accessed on 5 January 2023).
- Giorgi, F.; Jones, C.; Asrar, G. Addressing Climate Information Needs at the Regional Level: The CORDEX Framework. 2009. Available online: http://wcrp.ipsl (accessed on 5 January 2023).
- CORDEX Simulations Summary. Summary of Regional Climate Change Simulations Available for the CORDEX Domains. Available online: https://cordex.org/wp-content/uploads/2020/12/Summary_CORDEX_simulations_Nov_2020.pdf (accessed on 5 January 2023).
- NCAR (National Center for Atmospheric Research). NA-CORDEX Simulation Matrix. The North American CORDEX Program; NCAR Climate Data Gateway: Boulder, CO, USA; Available online: https://na-cordex.org/simulation-matrix.html (accessed on 5 January 2023).
- Giorgi, F.; Coppola, E.; Solmon, F.; Mariotti, L.; Sylla, M.B.; Bi, X.; Elguindi, N.; Diro, G.T.; Nair, V.; Giuliani, G.; et al. RegCM4: Model description and preliminary tests over multiple CORDEX domains. Clim. Res. 2012, 52, 7–29. [Google Scholar] [CrossRef]
- Brighenti, T.M.; Bonumá, N.B.; Srinivasan, R.; Chaffe, P.L.B. Simulating sub-daily hydrological process with SWAT: A review. Hydrol. Sci. J. 2019, 64, 1415–1423. [Google Scholar] [CrossRef]
- Neitsch, S.; Arnold, J.; Kiniry, J.; Williams, J. College Of Agriculture And Life Sciences Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Arnold, J.; Moriasi, D.; Gassman, P.; Abbaspour, K.; White, M.; Srinivasan, R.; Santhi, C.; Harmel, R.; van Griensven, A.; van Liew, M.; et al. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. Available online: http://swatmodel.tamu.edu (accessed on 5 January 2023). [CrossRef]
- Rathjens, H.; Bieger, K.; Srinivasan, R.; Arnold, J. CMhyd User Manual. Documentation for Preparing Simulated Climate Change Data for Hydrologic Impact Studies. 2016. Available online: https://swat.tamu.edu/media/115265/bias_cor_man.pdf (accessed on 5 January 2023).
- Sangelantoni, L.; Tomassetti, B.; Colaiuda, V.; Lombardi, A.; Verdecchia, M.; Ferretti, R.; Redaelli, G. On the Use of Original and Bias-Corrected Climate Simulations in Regional-Scale Hydrological Scenarios in the Mediterranean Basin. Atmosphere 2019, 10, 799. [Google Scholar] [CrossRef]
- de Amorim, P.B.; Chaffe, P.B. Towards a comprehensive characterization of evidence in synthesis assessments: The climate change impacts on the Brazilian water resources. Clim. Chang. 2019, 155, 37–57. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correction, Quantile Mapping, and Downscaling: Revisiting the Inflation Issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Sangelantoni, L.; Russo, A.; Gennaretti, F. Impact of bias correction and downscaling through quantile mapping on simulated climate change signal: A case study over Central Italy. Theor. Appl. Clim. 2018, 135, 725–740. [Google Scholar] [CrossRef]
- USGS Hydrologic Unit Codes (HUCs) Explained. Available online: https://nas.er.usgs.gov/hucs.aspx (accessed on 5 January 2023).
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Jackson, E.K.; Roberts, W.; Nelsen, B.; Williams, G.P.; Nelson, E.J.; Ames, D.P. Introductory overview: Error metrics for hydrologic modelling—A review of common practices and an open source library to facilitate use and adoption. Environ. Model. Softw. 2019, 119, 32–48. [Google Scholar] [CrossRef]
- Meng, J.; Li, L.; Hao, Z.; Wang, J.; Shao, Q. Suitability of TRMM satellite rainfall in driving a distributed hydrological model in the source region of Yellow River. J. Hydrol. 2014, 509, 320–332. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; van Liew, M.; Bingner, R.; Harmel, R.; Veith, T. Model Evaluation Guidelines For Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 1983, 50, 885–900. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correcting Climate Change Simulations—A Critical Review. Curr. Clim. Chang. Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef]
- Muerth, M.J.; Gauvin St-Denis, B.; Ricard, S.; Velázquez, J.A.; Schmid, J.; Minville, M.; Caya, D.; Chaumont, D.; Ludwig, R.; Turcotte, R. On the need for bias correction in regional climate scenarios to assess climate change impacts on river runoff. Hydrol. Earth Syst. Sci. 2013, 17, 1189–1204. [Google Scholar] [CrossRef]
- Maraun, D.; Shepherd, T.G.; Widmann, M.; Zappa, G.; Walton, D.; Gutiérrez, J.M.; Hagemann, S.; Richter, I.; Soares, P.M.; Hall, A.; et al. Towards process-informed bias correction of climate change simulations. Nat. Clim. Change 2017, 7, 764–773. [Google Scholar] [CrossRef]
- Padrón, R.S.; Gudmundsson, L.; Seneviratne, S.I. Observational Constraints Reduce Likelihood of Extreme Changes in Multidecadal Land Water Availability. Geophys. Res. Lett. 2019, 46, 736–744. [Google Scholar] [CrossRef] [PubMed]
- Herger, N.; Abramowitz, G.; Sherwood, S.; Knutti, R.; Angélil, O.; Sisson, S.A. Ensemble optimisation, multiple constraints and overconfidence: A case study with future Australian precipitation change. Clim. Dyn. 2019, 53, 1581–1596. [Google Scholar] [CrossRef]
- Sanderson, B.M.; Knutti, R. On the interpretation of constrained climate model ensembles. Geophys. Res. Lett. 2012, 39, 2012gl052665. [Google Scholar] [CrossRef]




| Model | Type | Modeling Centers | Resolution a |
|---|---|---|---|
| MPI-ESM-LR | GCM | Max Planck Institute for Meteorology Earth System Model | 1.90° |
| GFDL-ESM2M | GCM | National Oceanic and Atmospheric Administration/Geophysical Fluid Dynamics Laboratory | 2.45° |
| WRF | RCM | National Center for Atmospheric Research | 0.44°/0.22° |
| RegCM4 b | RCM | International Center for Theoretical Physics | 0.44°/0.22° |
| ME (mm) | BIAS (%) | STDE (mm) | RMSE (mm) | |||||
|---|---|---|---|---|---|---|---|---|
| raw | DM | raw | DM | raw | DM | raw | DM | |
| MPI-RegCM4 | 3.93 | −0.14 | 5.84 | −0.21 | 50.39 | 55.99 | 60.33 | 59.46 |
| MPI-WRF | 28.46 | 1.37 | 41.97 | 2.03 | 84.69 | 55.35 | 75.71 | 58.08 |
| GFDL-RegCM4 | 0.96 | 0.26 | 1.61 | 0.38 | 45.77 | 57.55 | 59.87 | 61.06 |
| GFDL-WRF | 22.42 | 1.46 | 33.11 | 2.15 | 75.96 | 55.48 | 67.55 | 57.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brighenti, T.M.; Gassman, P.W.; Gutowski, W.J., Jr.; Thompson, J.R. Assessing the Influence of a Bias Correction Method on Future Climate Scenarios Using SWAT as an Impact Model Indicator. Water 2023, 15, 750. https://doi.org/10.3390/w15040750
Brighenti TM, Gassman PW, Gutowski WJ Jr., Thompson JR. Assessing the Influence of a Bias Correction Method on Future Climate Scenarios Using SWAT as an Impact Model Indicator. Water. 2023; 15(4):750. https://doi.org/10.3390/w15040750
Chicago/Turabian StyleBrighenti, Tássia Mattos, Philip W. Gassman, William J. Gutowski, Jr., and Janette R. Thompson. 2023. "Assessing the Influence of a Bias Correction Method on Future Climate Scenarios Using SWAT as an Impact Model Indicator" Water 15, no. 4: 750. https://doi.org/10.3390/w15040750
APA StyleBrighenti, T. M., Gassman, P. W., Gutowski, W. J., Jr., & Thompson, J. R. (2023). Assessing the Influence of a Bias Correction Method on Future Climate Scenarios Using SWAT as an Impact Model Indicator. Water, 15(4), 750. https://doi.org/10.3390/w15040750







