Freeze–Thaw Cycle Effects on the Energy Dissipation and Strength Characteristics of Alkali Metakaolin-Modified Cement Soil under Impact Loading
Abstract
:1. Introduction
2. Test
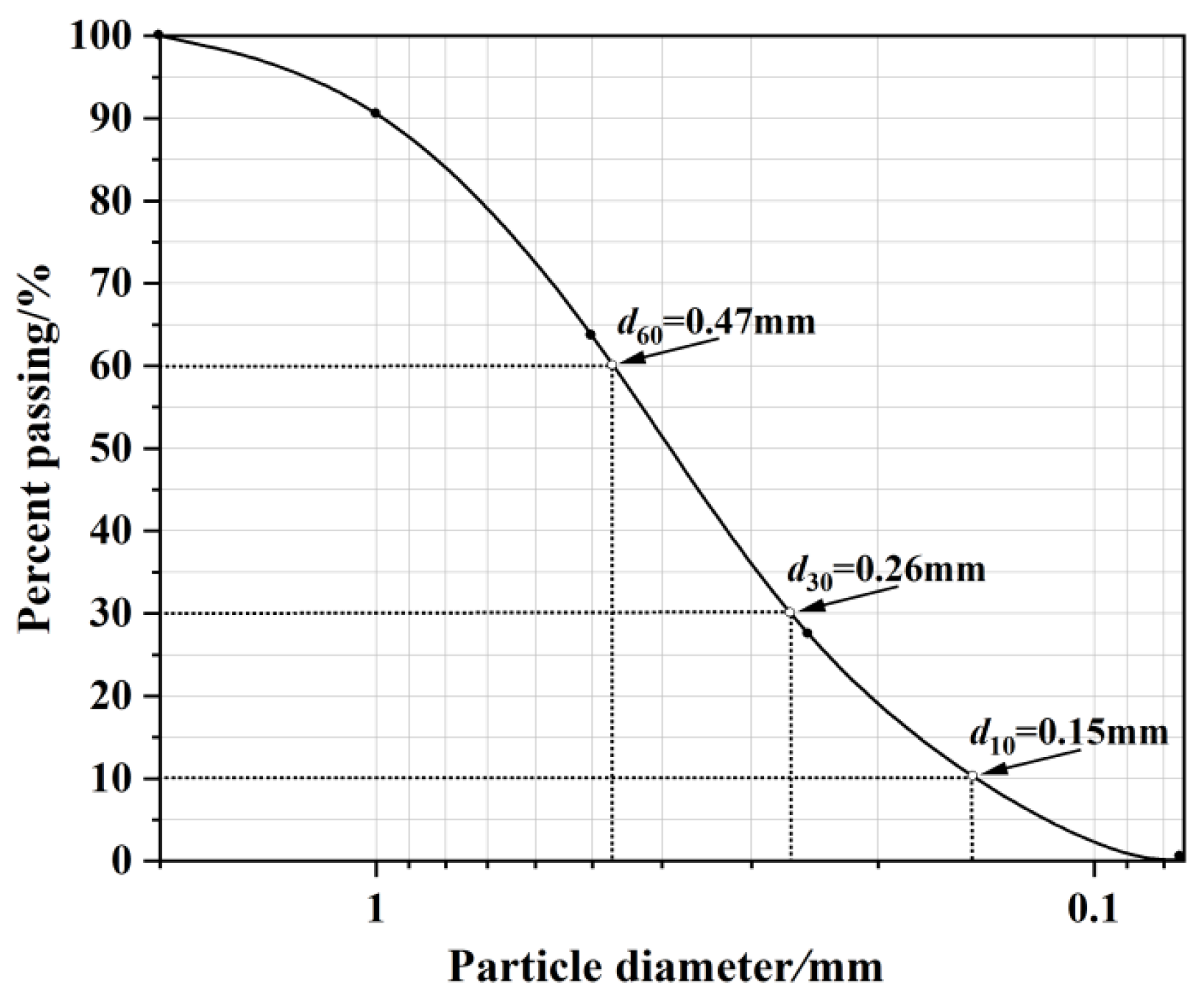
2.1. Testing Material
2.2. Specimen Preparation
2.3. Test Scheme
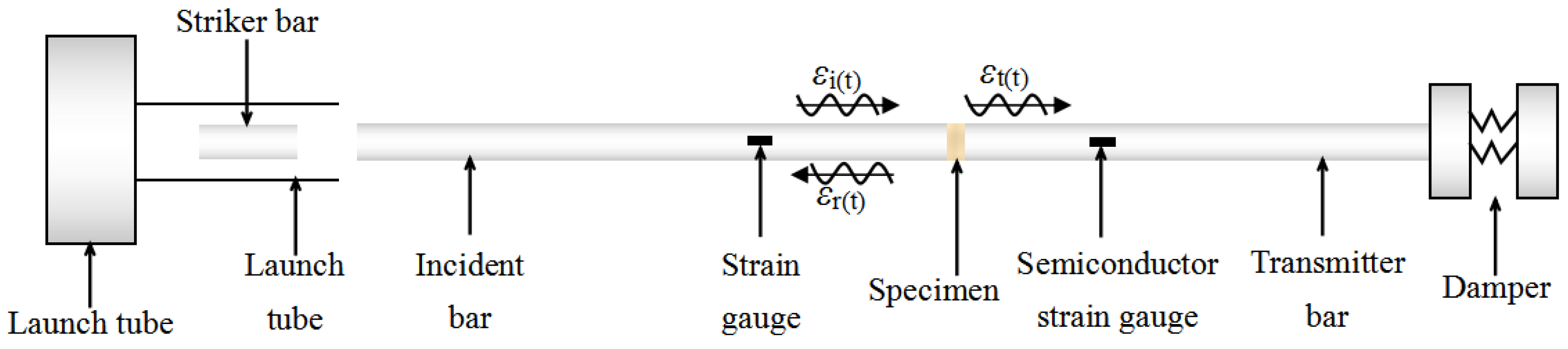
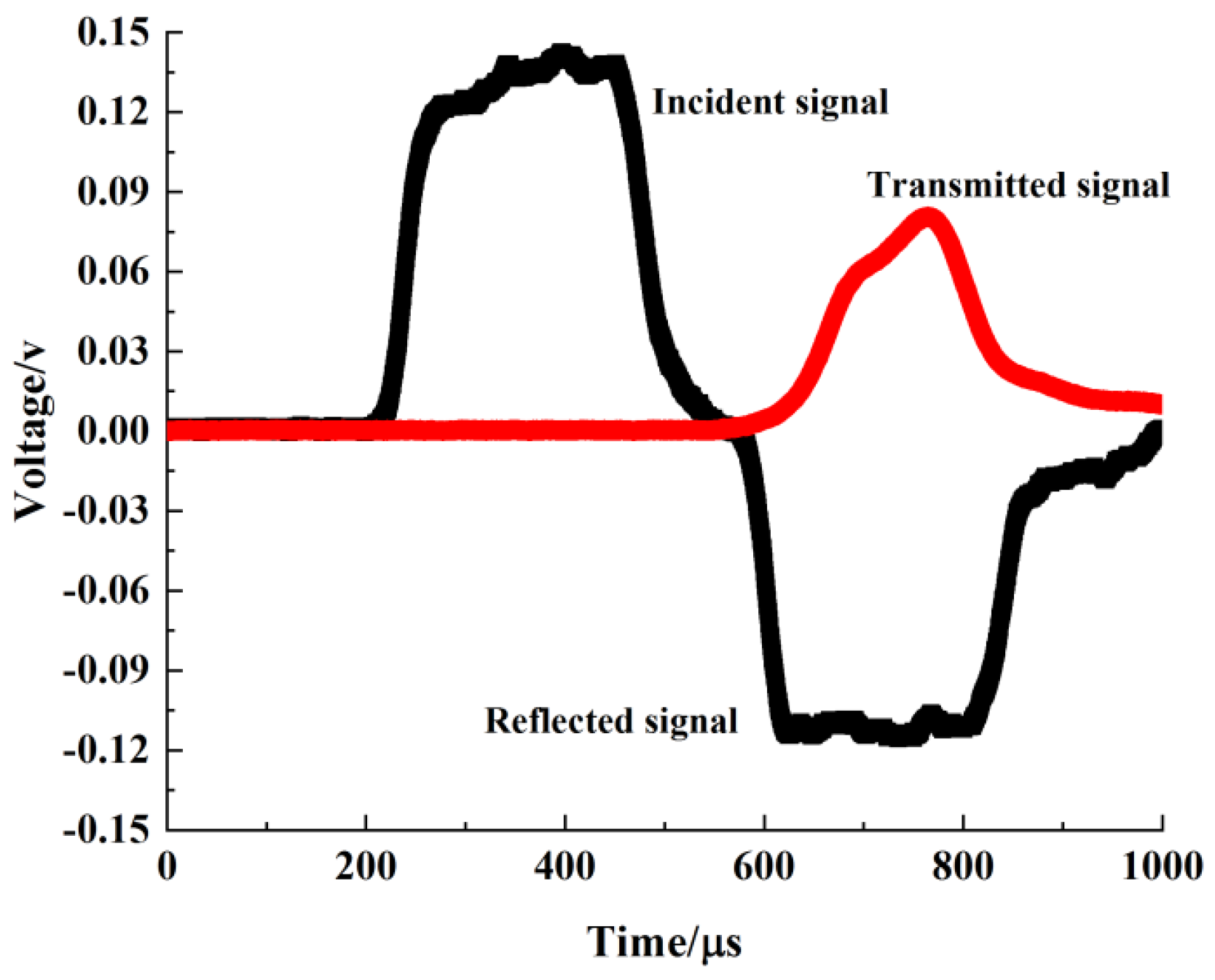
2.4. Testing Equipment
3. Test Results and Analysis
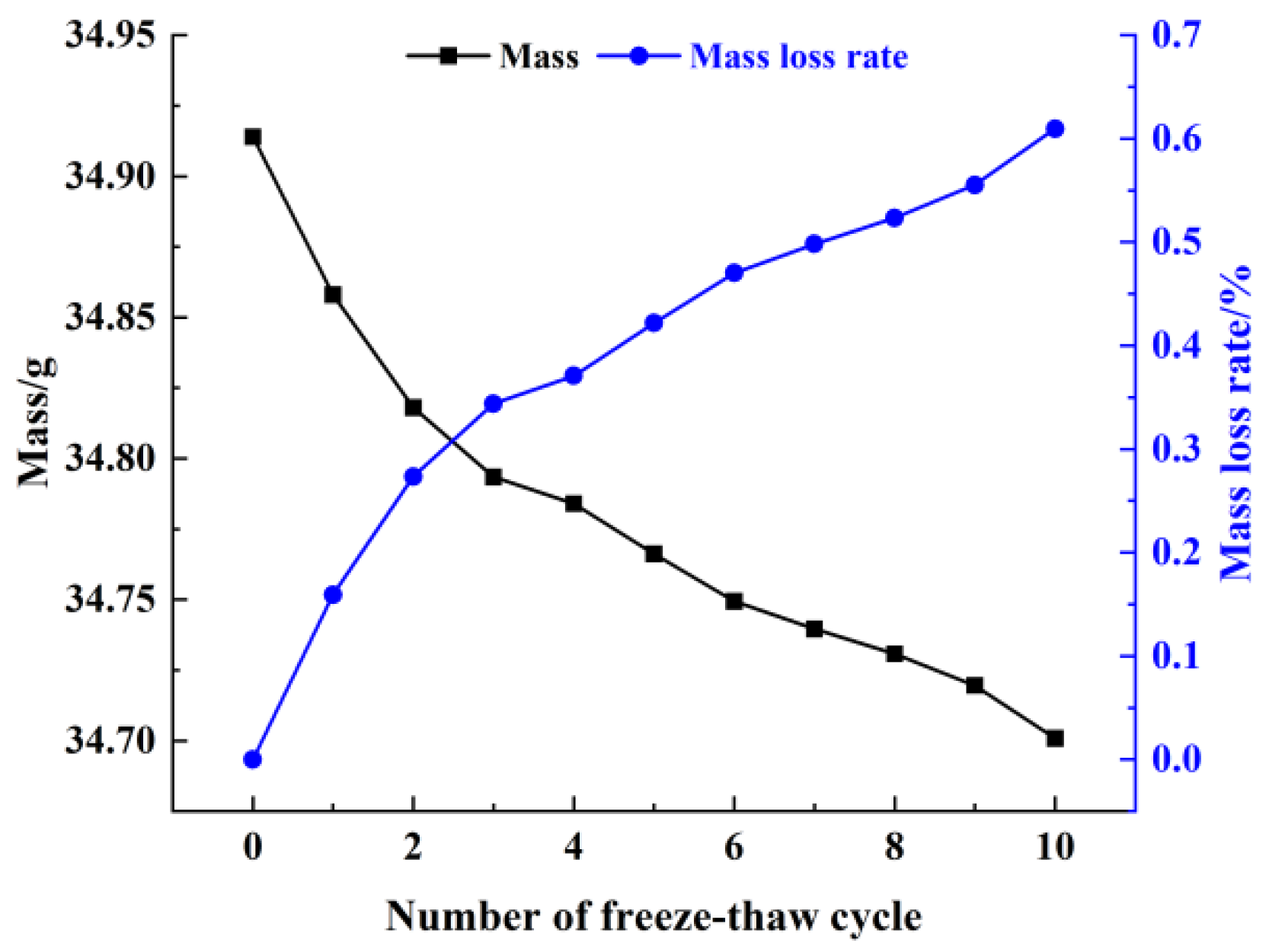
3.1. Mass Loss Rate
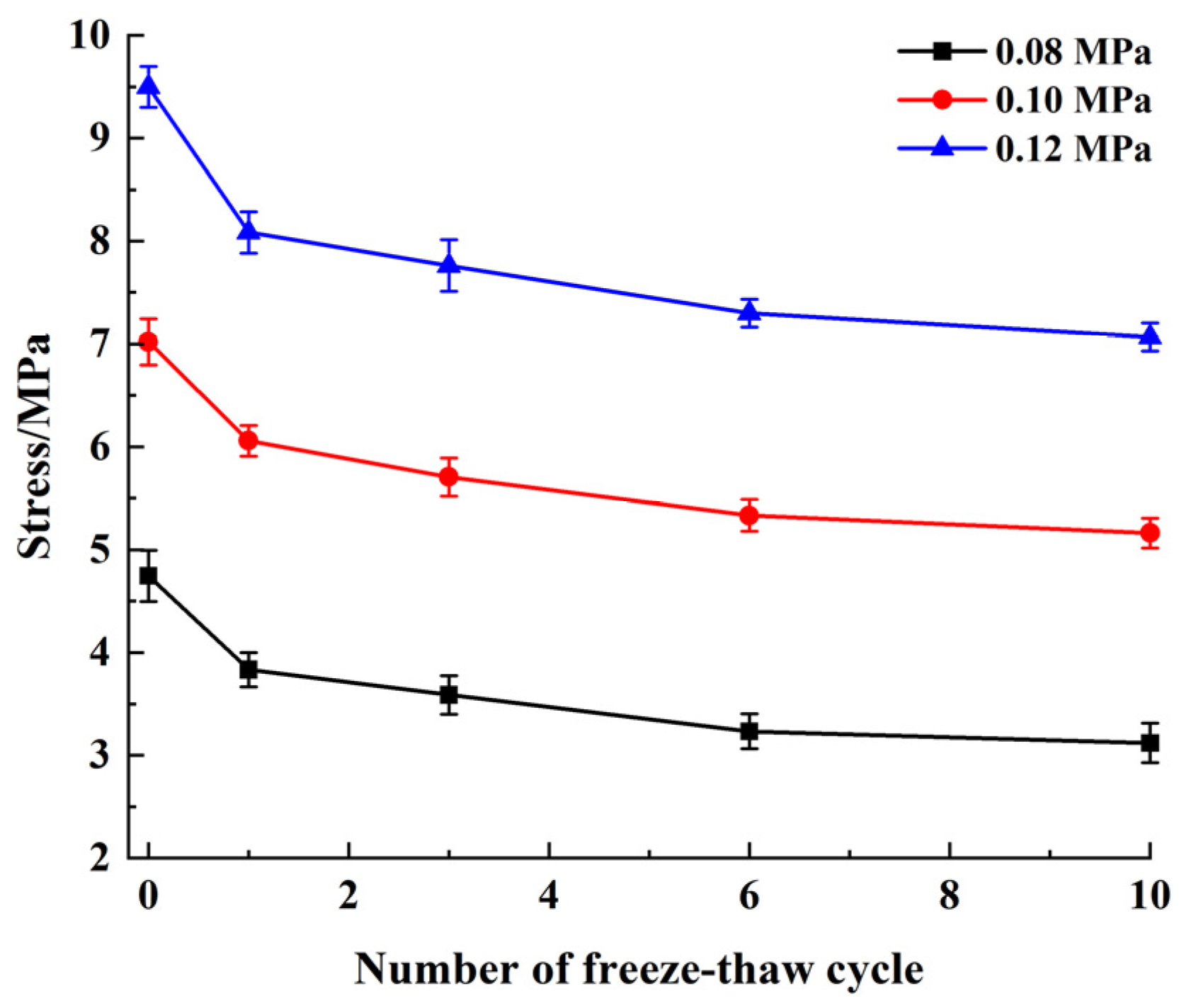
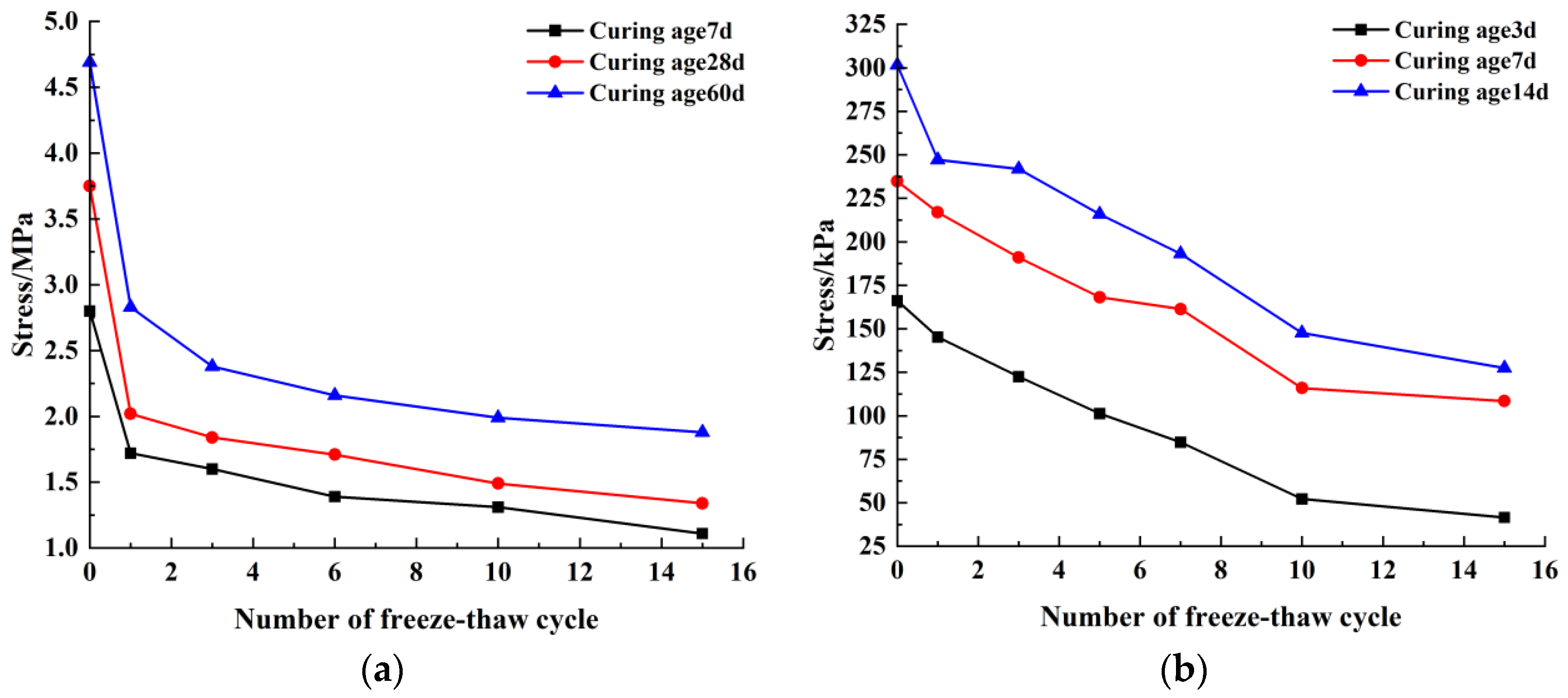
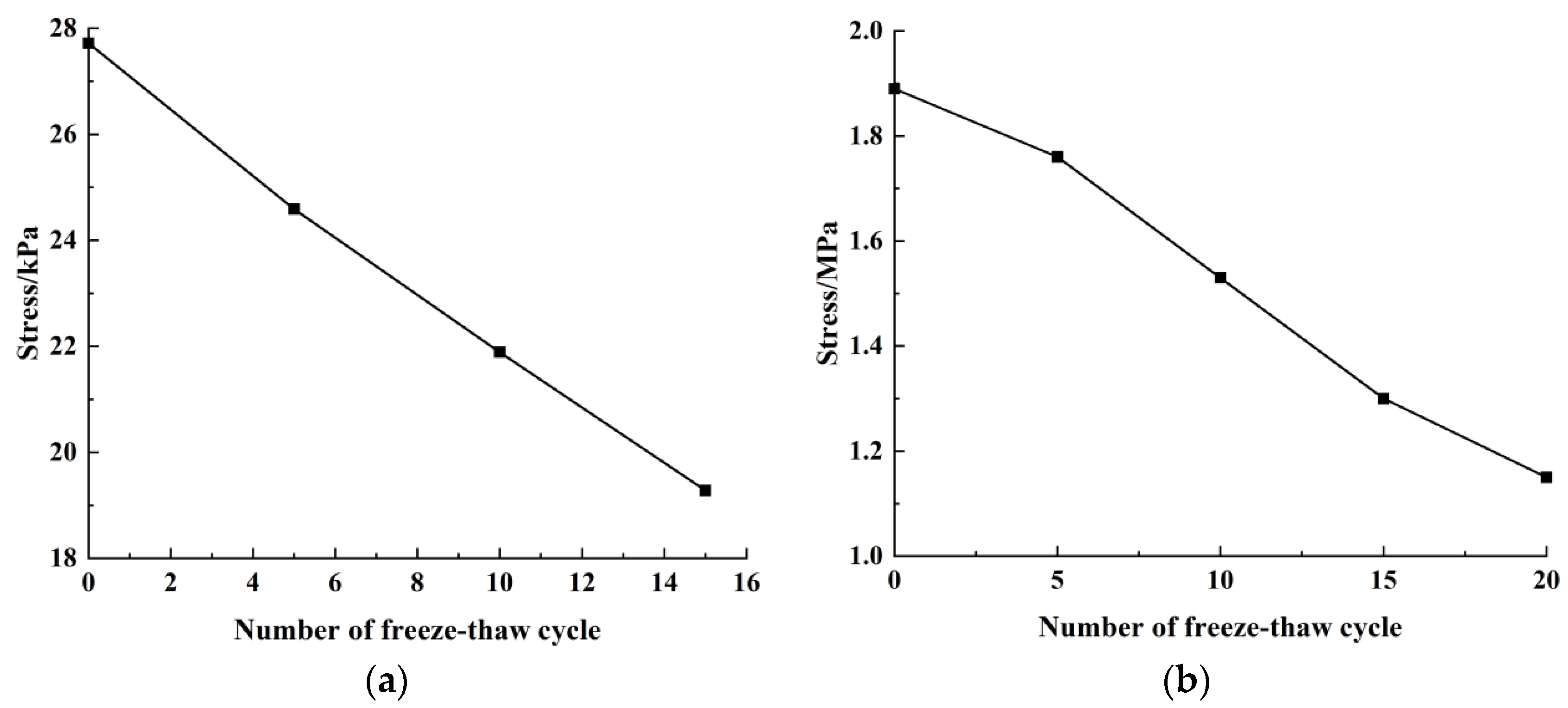
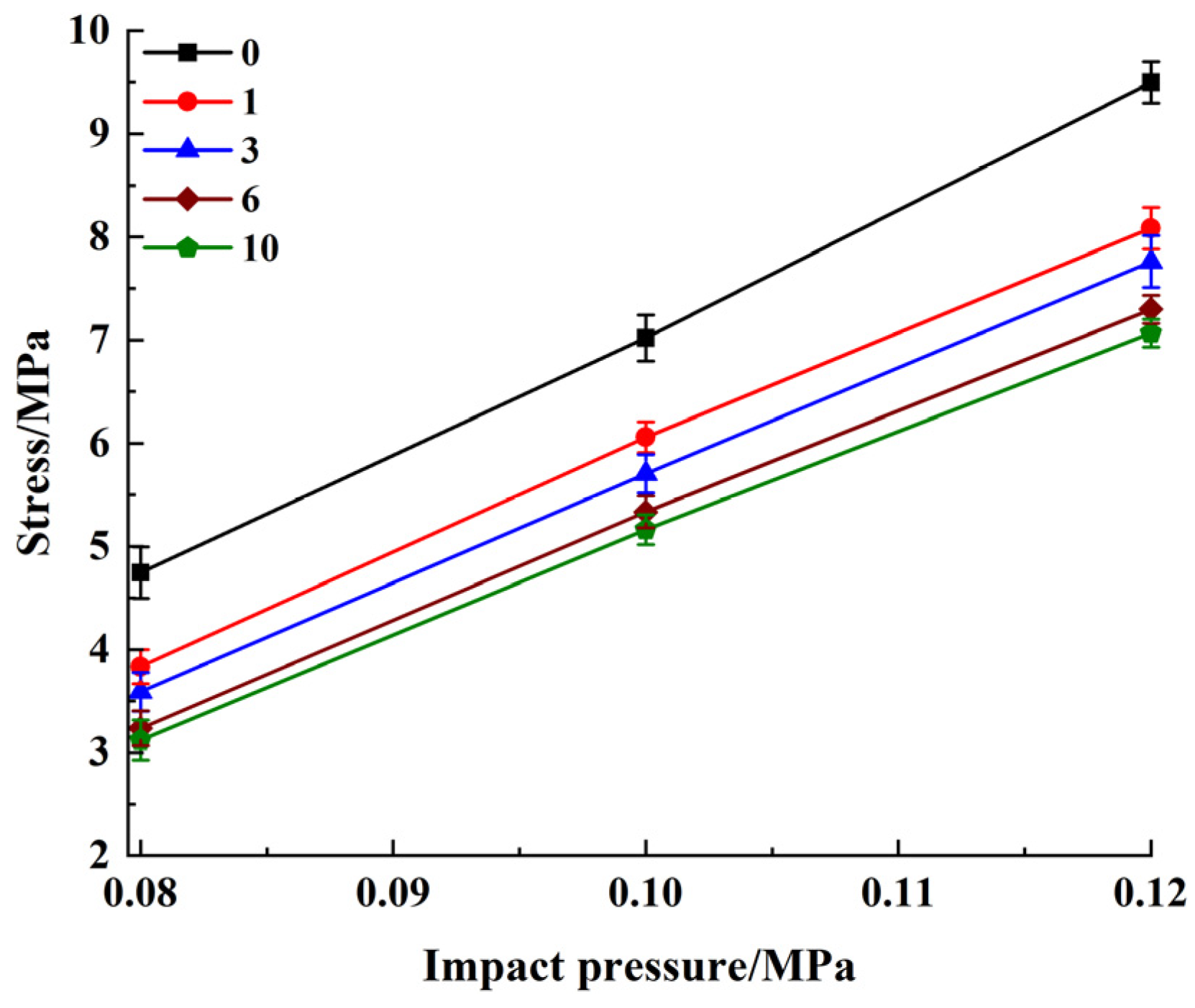
3.2. Strength
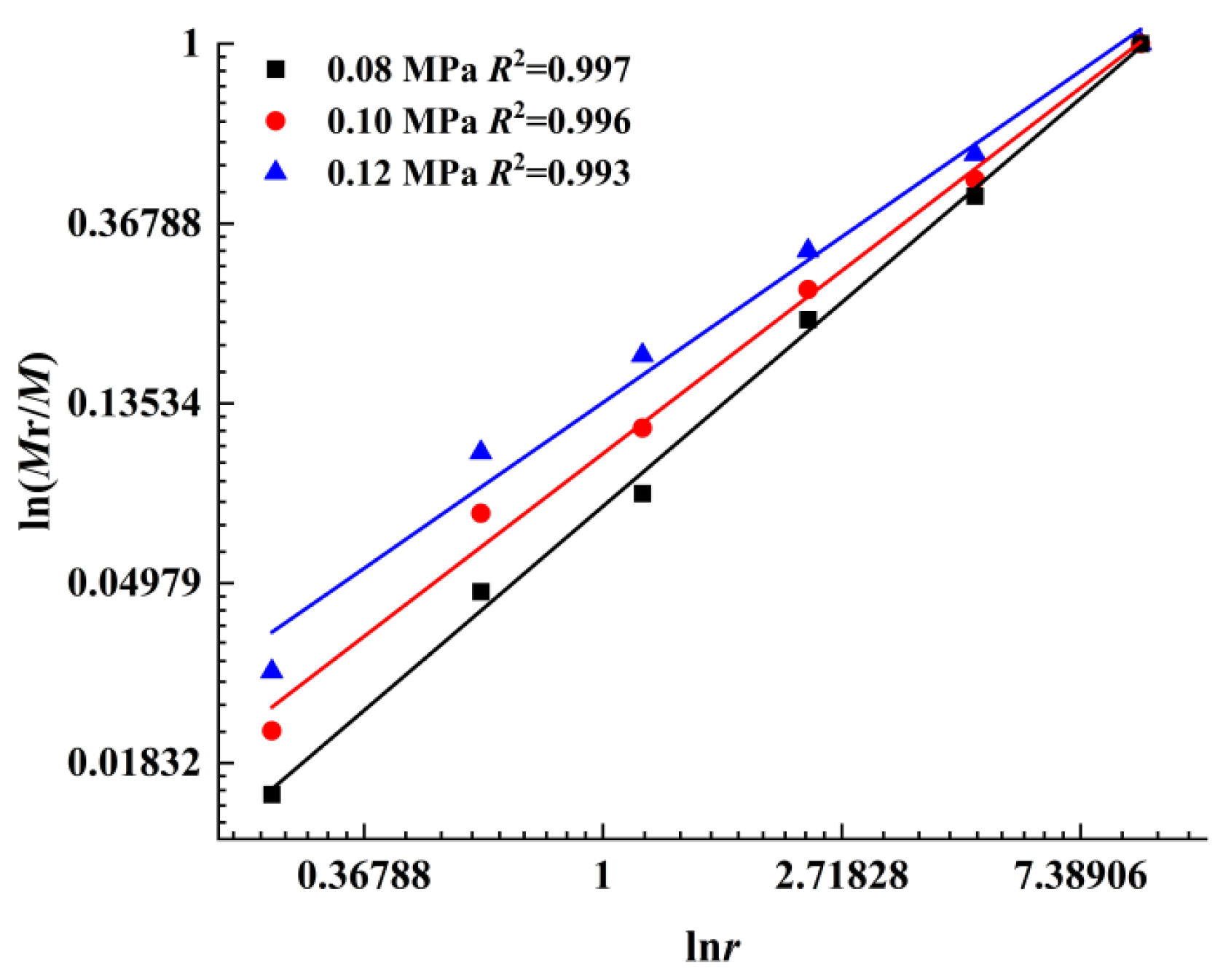
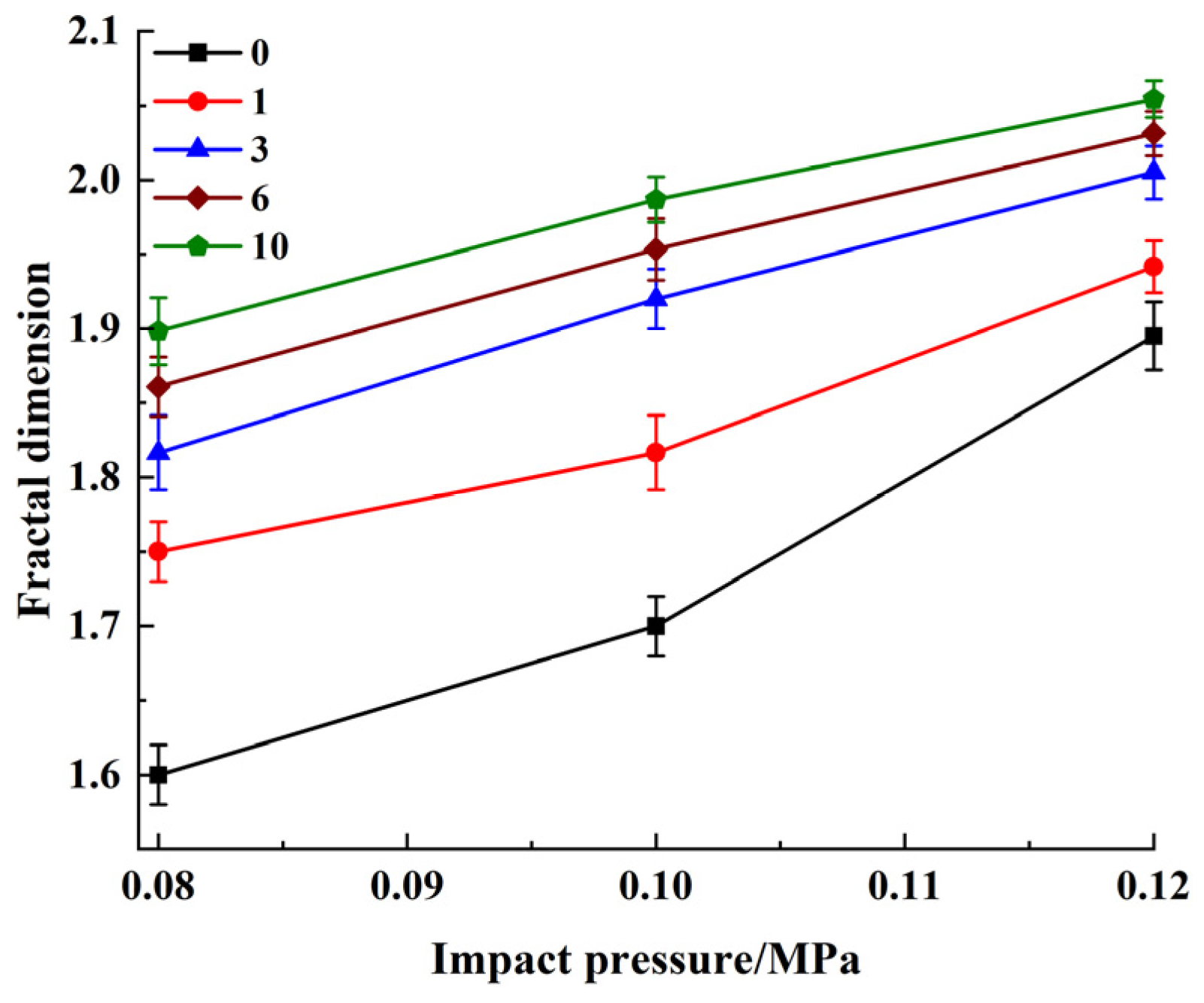
3.3. Shape Features
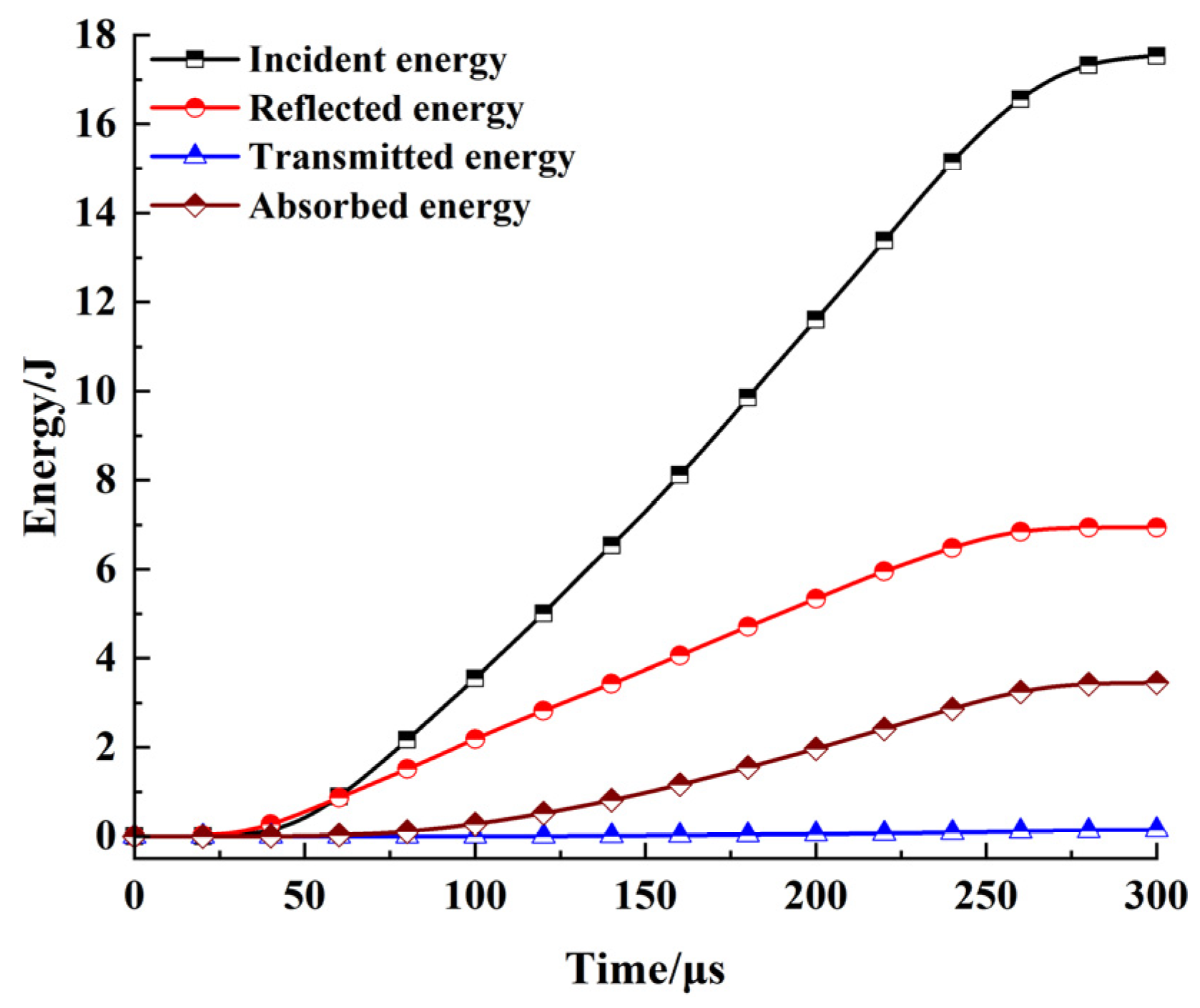
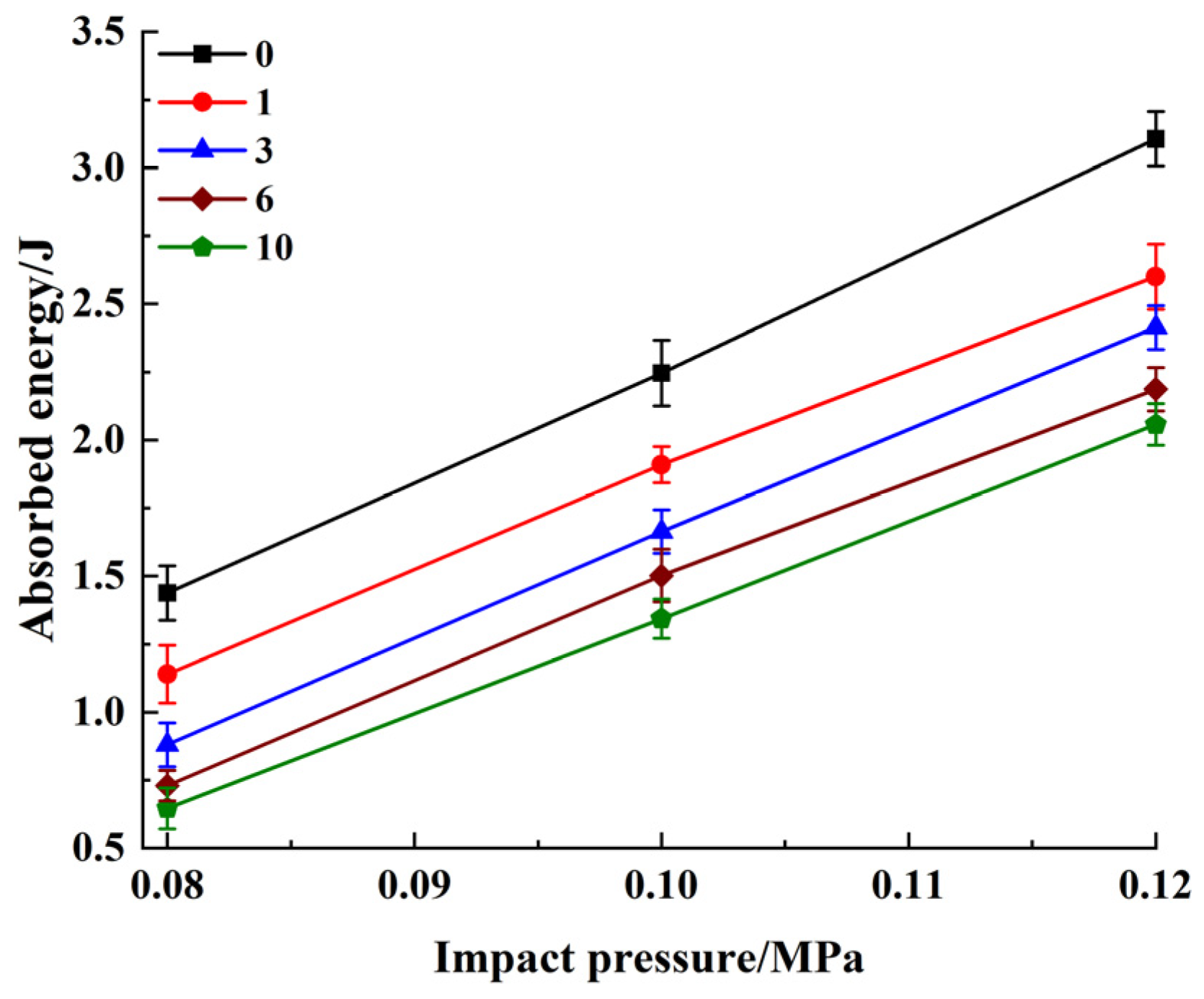
3.4. Energy Dissipation Characteristics
4. The Modified Dynamic Constitutive Model
4.1. Derivation Process
4.2. Damage Variable
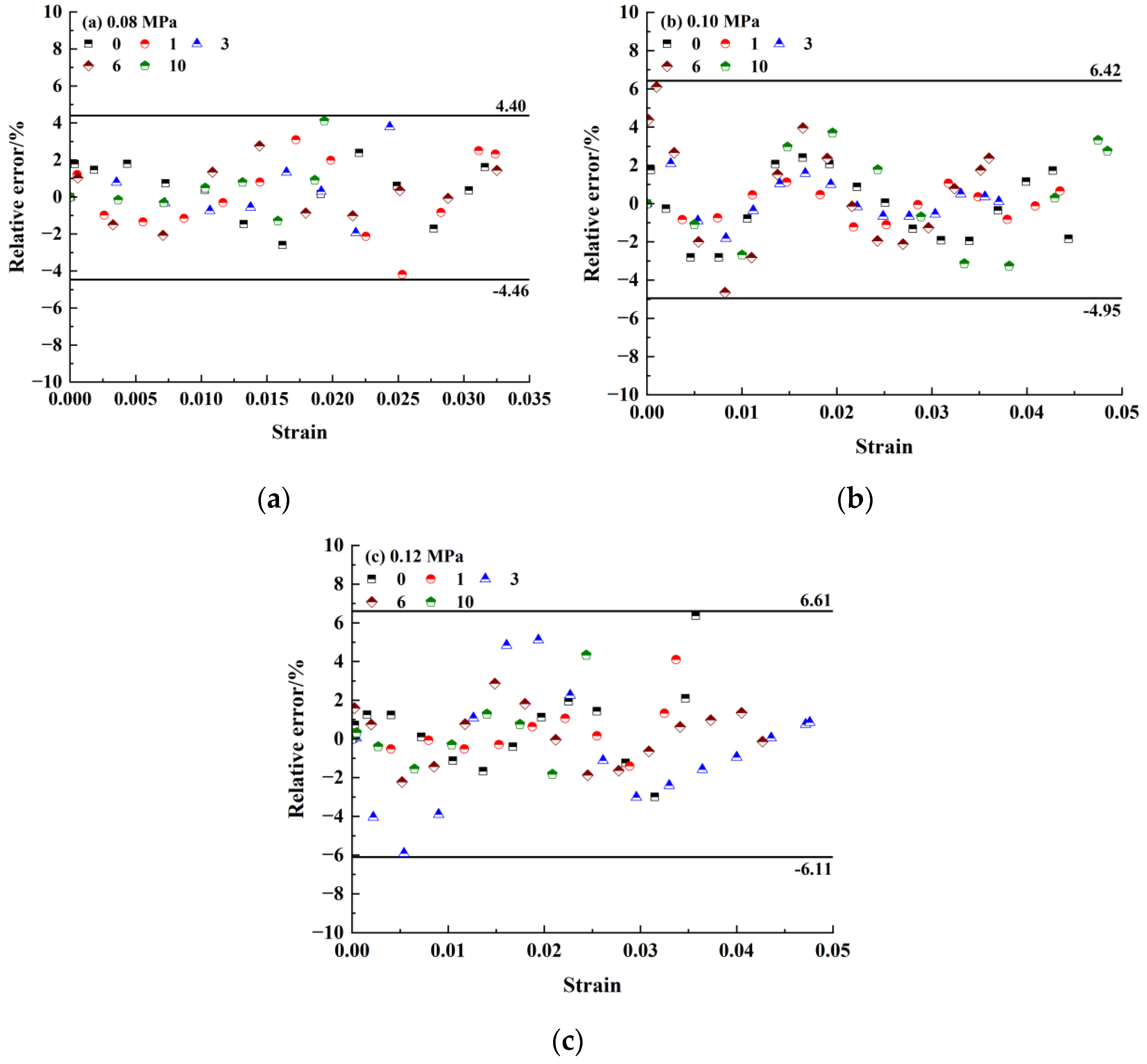
4.3. Model Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eskisar, T.; Altun, S.; Kalipcilar, I. Assessment of Strength Development and Freeze-Thaw Performance of Cement Treated Clays at Different Water Contents. Cold Reg. Sci. Technol. 2015, 111, 50–59. [Google Scholar] [CrossRef]
- Shang, H.S.; Yi, T.H.; Song, Y.P. Behavior of Plain Concrete of a High Water-Cement Ratio after Freeze-Thaw Cycles. Materials 2012, 5, 1698–1707. [Google Scholar] [CrossRef]
- Liu, H.; Sun, S.; Wei, H.; Li, W. Effect of Freeze-Thaw Cycles on Static Properties of Cement Stabilised Subgrade Silty Soil. Int. J. Pavement Eng. 2022, 23, 3770–3782. [Google Scholar] [CrossRef]
- Yang, B.; Ji, R.J.; Lan, Q.; Yang, J.-M.; Xu, J. Sulfate Freeze-Thaw Resistance of Magnesium Potassium Phosphate Cement Mortar. Materials 2022, 15, 3342. [Google Scholar] [CrossRef]
- Shibi, T.; Kamei, T. Effect of Freeze-Thaw Cycles on the Strength and Physical Properties of Cement-Stabilised Soil Containing Recycled Bassanite and Coal Ash. Cold Reg. Sci. Technol. 2014, 106, 36–45. [Google Scholar] [CrossRef]
- Wang, T.L.; Liu, J.K.; Tian, Y.H. Static Properties of Cement and Lime Modified Soil Subjected to Freeze-Thaw Cycles. Rock Soil Mech. 2011, 32, 193–198. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Shen, X.D.; Song, X.Y. Experimental Study on Frost-resistance of Red Clay Cemented Soil. Bull. Chin. Ceram. Soc. 2012, 31, 702–705+710. (In Chinese) [Google Scholar] [CrossRef]
- Chen, S.L.; Shi, J.J.; Yu, T. Effect of Freezing-thawing Cycle on the Mechanical Behaviors of Cemented Soil. J. Basic Sci. Eng. 2014, 22, 343–349. (In Chinese) [Google Scholar] [CrossRef]
- Cui, H.H.; Pei, G.L.; Yao, S.J.; Wang, G.Y.; Zhang, Z.G. Experimental Study of Mechanical Properties of Cement Soil of Different Curing Time Subjected to Freezing-Thawing Cycles. J. Glaciol. Geocryol. 2018, 40, 110–115. (In Chinese) [Google Scholar]
- Ding, M.T.; Zhang, F.; Ling, X.Z. Effects of Freeze-Thaw Cycles on Mechanical Properties of Polypropylene Fiber and Cement Stabilized Clay. Cold Reg. Sci. Technol. 2018, 154, 155–165. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, S.P. Fiber-reinforced Fly Ash Subbases in Rural Roads. J. Transp. Eng. 2008, 134, 171–180. [Google Scholar] [CrossRef]
- Guo, Q.; Wei, M.L.; Du, G.Y.; Xue, H.C.; Liu, S.Y. Research on Strength Behavior and Micro-mechanism of AMC Stabilized High Liquid Limit Clay. J. China Univ. Min. Technol. 2018, 47, 838–845. (In Chinese) [Google Scholar] [CrossRef]
- Lake, C.B.; Yousif, M.A.M.; Jamshidi, R.J. Examining Freeze-thaw Effects on Performance and Morphology of a Lightly Cemented Soil. Cold Reg. Sci. Technol. 2017, 134, 33–44. [Google Scholar] [CrossRef]
- Gao, C.H.; Ma, Q.Y. Analysis of Silty Clay Stabilized by Cement Mortar Based on Split Hopkinson Pressure Bar Experimental. Acta Mater. Compos. Sin. 2018, 35, 1629–1635. (In Chinese) [Google Scholar] [CrossRef]
- Ma, Q.Y.; Gao, C.H. Effect of Basalt Fiber on the Dynamic Mechanical Properties of Cement-Soil in SHPB Test. J. Mater. Civ. Eng. 2018, 30, 04018185. [Google Scholar] [CrossRef]
- Ma, D.D.; Ma, Q.Y.; Huang, K.; Zhang, R.R. Pore Structure and Dynamic Mechanical Properties of Geopolymer Cement Soil Based on Nuclear Magnetic Resonance Technique. Chin. J. Geotech. Eng. 2021, 43, 572–578. (In Chinese) [Google Scholar]
- Tong, X.F.; Gong, X.N.; Jiang, Y.S. Elastic-plastic Damage Model of Cement-Stabilized Soil. Eng. Mech. 2002, 19, 33–38. (In Chinese) [Google Scholar]
- Sun, K.; Chen, Z.L.; Lu, D.C. An Elastoplastic Constitutive Model Incorporating Cementation Effect of Stabilizer-Treated Soils. Rock Soil Mech. 2018, 39, 1589–1597. (In Chinese) [Google Scholar]
- Hu, Y.Y.; Yu, Q.Z.; Zhang, C.J. Duncan-chang model for fiber reinforced solidified sludge. J. Zhejiang Univ. Eng. Sci. 2017, 51, 1500–1508. (In Chinese) [Google Scholar]
- Wang, J.; Ding, G.Y.; Pan, L.Y. Study of Mechanics Behavior and Constitutive Model of Cemented Soil Under Static Triaxial Tests. Rock Soil Mech. 2010, 31, 1407–1412. (In Chinese) [Google Scholar] [CrossRef]
- Sagidullina, N.; Abdialim, S.; Kim, J.; Satyanaga, A.; Moon, S.-W. Influence of Freeze–Thaw Cycles on Physical and Mechanical Properties of Cement-Treated Silty Sand. Sustainability 2022, 14, 7000. [Google Scholar] [CrossRef]
- Zhang, J.S.; Duan, X.L. Effects of Freeze-thaw Cycles on Damage Characteristics and Energy Dissipation of Soil-cement at Different Ages. Bull. Chin. Ceram. Soc. 2019, 38, 2144–2151. (In Chinese) [Google Scholar]
- Wang, H.B.; Chen, C. Experimental Study on the Strength of Cement Soil Impacted by the Nano-CaCO3 Under the Cycling of Freeze-thaw. Sci. Technol. Eng. 2017, 17, 348–353. [Google Scholar]
- Ma, D.D.; Xiang, H.S.; Ma, Q.Y.; Kaunda, E.E.; Huang, K.; Su, Q.Q.; Yao, Z.M. Dynamic Damage Constitutive Model of Frozen Silty Soil with Prefabricated Crack under Uniaxial Load. J. Eng. Mech. 2021, 147, 04021033. [Google Scholar] [CrossRef]
- Li, R.; Liu, L.; An, H.; Wang, Y. Study on Dynamic Constitutive Model of Polypropylene Concrete under Real-Time High-Temperature Conditions. Appl. Sci. 2022, 12, 1482. [Google Scholar] [CrossRef]
- Mishra, S.; Chakraborty, T.; Matsagar, V.; Loukus, J.; Bekkala, B. High Strain-Rate Characterization of Deccan Trap Rocks Using SHPB Device. J. Mater. Civ. Eng. 2018, 30, 04018059. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Y.; An, H. Fractal Characteristics and Energy Dissipation of Granite After High-Temperature Treatment Based on SHPB Experiment. Front. Earth Sci. 2022, 10, 861847. [Google Scholar] [CrossRef]
- Ma, Q.Y.; Huang, K.; Ma, D.D. Energy Absorption Characteristics and Theoretical Analysis of Frozen Clay with Pre-Existing Cracks under Uniaxial Compressive Impact Load. Cold Reg. Sci. Technol. 2021, 182, 103206. [Google Scholar] [CrossRef]
- Zhai, Y.; Meng, F.; Li, Y.; Li, Y.; Zhao, R.; Zhang, Y. Research on Dynamic Compression Failure Characteristics and Damage Constitutive Model of Sandstone after Freeze-Thaw Cycles. Eng. Fail. Anal. 2022, 140, 106577. [Google Scholar] [CrossRef]






| Composition | SiO2 | Al2O3 | CaO | Fe2O3 | TiO2 | MgO | K2O | Na2O | Others |
|---|---|---|---|---|---|---|---|---|---|
| Percentage/% | 72.3 | 14.3 | 0.8 | 5.4 | 1.3 | 2.1 | 3.1 | 0.5 | 0.2 |
| Composition | SiO2 | Al2O3 | CaO | Fe2O3 | SO3 | MgO | Na2O | K2O |
|---|---|---|---|---|---|---|---|---|
| Percentage/% | 19.6 | 6.5 | 66.3 | 3.5 | 2.5 | 0.7 | 0.6 | 0.3 |
| Composition | SiO2 | Al2O3 | Fe2O3 | Na2O | K2O | Others |
|---|---|---|---|---|---|---|
| Percentage/% | 54 | 43 | 1 | 0.3 | 0.2 | 1.5 |
| Impact Pressure/MPa | Strain Rate | Freeze–Thaw Times | Strength/MPa | Fractal Dimension |
|---|---|---|---|---|
| 0.08 | 182 | 0 | 4.79 | 1.60 |
| 1 | 3.83 | 1.75 | ||
| 3 | 3.52 | 1.82 | ||
| 6 | 3.32 | 1.86 | ||
| 10 | 3.26 | 1.88 | ||
| 0.10 | 219 | 0 | 6.90 | 1.71 |
| 1 | 6.08 | 1.82 | ||
| 3 | 5.69 | 1.92 | ||
| 6 | 5.51 | 1.96 | ||
| 10 | 5.29 | 1.93 | ||
| 0.12 | 252 | 0 | 9.55 | 1.92 |
| 1 | 8.06 | 1.94 | ||
| 3 | 7.79 | 2.01 | ||
| 6 | 7.44 | 2.03 | ||
| 10 | 7.23 | 2.04 |
| Freeze–Thaw Cycle | Wi/J | Wr/J | Wt/J | Ws/J | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.08 MPa | 0.10 MPa | 0.12 MPa | 0.08 MPa | 0.10 MPa | 0.12 MPa | 0.08 MPa | 0.10 MPa | 0.12 MPa | 0.08 MPa | 0.10 MPa | 0.12 MPa | |
| 0 | 11.06 | 17.11 | 23.92 | 8.94 | 14.10 | 19.99 | 0.68 | 0.76 | 0.82 | 1.44 | 2.25 | 3.11 |
| 1 | 11.21 | 17.02 | 23.86 | 9.47 | 14.38 | 20.49 | 0.60 | 0.73 | 0.77 | 1.14 | 1.91 | 2.60 |
| 3 | 10.96 | 16.98 | 24.02 | 9.56 | 14.63 | 20.87 | 0.52 | 0.69 | 0.74 | 0.88 | 1.66 | 2.41 |
| 6 | 11.11 | 17.14 | 23.79 | 9.90 | 14.97 | 20.88 | 0.48 | 0.67 | 0.72 | 0.73 | 1.50 | 2.19 |
| 10 | 11.12 | 17.05 | 23.88 | 10.01 | 15.80 | 21.13 | 0.46 | 0.63 | 0.69 | 0.65 | 1.34 | 2.06 |
| Impact Pressure/MPa | Freeze–Thaw Cycles | A | α | β | Ea | E2 | θ2 | |
|---|---|---|---|---|---|---|---|---|
| 0.08 | 0 | 182 | 2.97 | −1.54 | −6.40 | −4.60 × 106 | 4.60 × 106 | 3 |
| 1 | 182 | 0.15 | 0.59 | 2.09 | 4.63 × 106 | −4.63 × 106 | 3 | |
| 3 | 182 | 1.38 | 0.95 | 4.16 | 3.57 × 106 | −3.57 × 106 | 3 | |
| 6 | 182 | 0.49 | 0.47 | 1.99 | 4.35 × 106 | −4.35 × 106 | 3 | |
| 10 | 182 | 0.84 | 0.46 | 1.80 | 1.38 × 106 | −1.38 × 106 | 3 | |
| 0.10 | 0 | 219 | 0.04 | −0.26 | −0.21 | −1.23 × 104 | 1.23 × 104 | 3 |
| 1 | 219 | 322.92 | 1.25 | 8.39 | 4.23 × 105 | −4.23 × 105 | 3 | |
| 3 | 219 | 0.16 | −0.54 | −1.41 | 1.61 × 106 | −1.61 × 106 | 3 | |
| 6 | 219 | −9.24 | −0.36 | −1.22 | 9.81 × 106 | 9.81 × 106 | 3 | |
| 10 | 219 | 44.75 | −1.19 | −2.16 | −1.75 × 106 | 1.75 × 106 | 3 | |
| 0.12 | 0 | 252 | 12.24 | −0.99 | −0.85 | −3.62 × 103 | 3.62 × 103 | 3 |
| 1 | 252 | 0.03 | 1.06 | 3.88 | 2.94 × 106 | −2.94 × 106 | 3 | |
| 3 | 252 | 0.20 | 0.41 | 1.75 | 3.54 × 106 | −3.54 × 106 | 3 | |
| 6 | 252 | 135.49 | 1.87 | 11.29 | −1.30 × 106 | 1.30 × 106 | 3 | |
| 10 | 252 | 0.13 | 1.12 | 4.26 | 9.71 × 106 | −9.71 × 106 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.; Wang, H.; Huang, K. Freeze–Thaw Cycle Effects on the Energy Dissipation and Strength Characteristics of Alkali Metakaolin-Modified Cement Soil under Impact Loading. Water 2023, 15, 730. https://doi.org/10.3390/w15040730
Huang K, Wang H, Huang K. Freeze–Thaw Cycle Effects on the Energy Dissipation and Strength Characteristics of Alkali Metakaolin-Modified Cement Soil under Impact Loading. Water. 2023; 15(4):730. https://doi.org/10.3390/w15040730
Chicago/Turabian StyleHuang, Kun, Heng Wang, and Kai Huang. 2023. "Freeze–Thaw Cycle Effects on the Energy Dissipation and Strength Characteristics of Alkali Metakaolin-Modified Cement Soil under Impact Loading" Water 15, no. 4: 730. https://doi.org/10.3390/w15040730





