1. Introduction
According to the global climate risk index 2021, approximately 11,000 extreme meteorological disasters have occurred in the past 20 years, resulting in approximately 475,000 deaths and economic losses of nearly USD 2.56 trillion. Global warming caused by greenhouse gas emissions has significantly affected the regional hydroatmospheric cycle process, resulting in frequent occurrence of disaster problems such as extreme drought, rainstorm, flood, high temperatures, and heat waves, which have seriously restricted the balanced development of regional economy, society, and ecological environment [
1,
2,
3,
4]. Floods are the most common and harmful among all kinds of natural disasters. They have a high frequency of occurrence, a wide range of coverage, and a strong ability to damage the environment, causing heavy losses to countries and citizens [
5].
Reservoirs are the most common water conservancy projects used for runoff regulation and flood control, so they are an important research object for flood control. Reservoir operation refers to the operation of upstream water according to different inflow conditions, using reservoir storage function, combined with the existing storage capacity, which is an important nonengineering measure. In reservoir operation, different constraints are set up to optimize the problem, such as water balance, discharge constraints, water level constraints, etc. This is a high-dimensional, nonlinear, multistage, multiconstraint process [
6,
7]. Therefore, determining how to use modern methods to realize flood control of a reservoir is an important and practical problem.
At present, mathematical programming methods and emerging intelligent heuristic optimization algorithms are most often used to solve the reservoir (group) optimal operation problem. The advantages of mathematical programming, dynamic programming [
8], linear programming [
9], nonlinear programming [
10], and other methods are well established; however, they also have some problems. During reservoir operation, due to the diversity of research contents and complex data, it is difficult to give consideration to efficiency and accuracy, and it is easy to produce the “dimensionality problem” [
11,
12,
13]. In order to better solve this problem, researchers continue to explore optimization algorithms and make great breakthroughs. The emergence of modern intelligent heuristic optimization algorithms is the result of continuous exploration, such as particle swarm optimization (PSO) [
14], genetic algorithm (GA) [
15], water cycle algorithm (GCA) [
16], and improved firefly algorithm (YYFA) [
17]. These modern heuristic algorithms have strong robustness, and overcome the shortcomings of low efficiency of traditional algorithms to a certain extent. However, due to the diversity and complexity of reservoir flood control operation by itself, as well as the actual flood control operation process, there will be a variety of uncertainties. In the process of solving the optimal solution, a simple optimization algorithm has difficulty meeting various constraints at the same time, so it also needs to adopt relevant constraint processing techniques.
In recent years, due to the simple and efficient execution process of the penalty function, researchers have widely used constrained evolutionary algorithms to solve the reservoir constraint problem [
18,
19,
20,
21,
22,
23]. However, due to the difficulty in selecting the penalty factor, the performance of the algorithm strongly depends on the selection of the parameter, which makes it difficult to obtain high-quality solutions. The processing technique based on ε constraint was proposed by Takahama and Sakai [
24]. The core idea is that individuals whose degree of default is less than ε are regarded as feasible solutions through the setting value of ε, and it makes full use of the information of the infeasible solution with better objective function value in the infeasible region. Compared with the penalty function method, it has better convergence [
17,
25,
26,
27].
The bald eagle search algorithm (BES) is a new swarm intelligence algorithm proposed in recent years [
28]. The algorithm has simple initial conditions and strong global search ability, and can effectively solve various complex numerical optimization problems. In the past, this algorithm has been applied to a variety of practical problems for optimization [
29,
30,
31,
32,
33]. Nevertheless, BES may fall into local optimal solution and fail in the computation of reservoir flood control operation. Therefore, this paper proposes an improved bald eagle search algorithm (CABES) to solve the reservoir flood control operation problem. By introducing Cauchy mutation, integrating adaptive weight factor and Levy flight strategy, the optimal solution position is perturbed and mutated to improve the anti-local extreme value ability, improve the search accuracy of the algorithm, mine the global optimal solution, and combine the constraint processing technology to obtain the optimal flood control operation scheme.
The rest of this paper is as follows:
Section 2 introduces the CABES algorithm and constraint processing technology.
Section 3 presents the flood control operation model. The specific reservoir information and operation scheme analysis are discussed in
Section 4.
Section 5 provides the final conclusion.
4. Case Studies
In order to verify the rationality and superiority of the CABES algorithm, as well as the difference between the two constraint processing technologies, this paper selects two single reservoirs and a multi-reservoir system for flood control operation. Among them, Shafan Reservoir and Dahuofang Reservoir in China are selected for the single reservoirs, and three reservoirs in the Luan River Basin are selected for the multi-reservoir system.
In the process of flood control and dispatch, the flood process of Shafan Reservoir has the characteristics of relatively few flood sequences and short duration. However, the flood process of Dahuofang Reservoir has many sequences and a long period of time. Therefore, in theory, a flood control operation model with a stronger performance and higher computing power is required to complete the operation. Compared with the single-reservoir operation, the multi-reservoir system has different regulation performance, different hydrological characteristics, and different profit goals. It is not only possible but also necessary to carry out the joint dispatch of the multi-reservoir system. By implementing the joint dispatch of the multi-reservoir system, the advantages of each reservoir project will be better exhibited, and the goals of flood control and profit will be achieved.
In order to enhance the depth of the analysis of the results, this section also uses the original BES algorithm and the classic PSO algorithm to perform flood control operation for the abovementioned reservoirs (groups) by combining two constraint processing techniques, and compares the results with those of the ε-CABES algorithm. Parameters of each algorithm are selected from those of the optimal solution obtained in each original document [
17,
50,
51].
Because the Shafan Reservoir, Dahuofang Reservoir, and Luanhe Reservoir group have different constraints and difficulties in solving, in order to ensure that the operation scheme meets the constraints and reaches the optimal solution, some parameters are different according to different reservoir characteristics. The parameter settings are shown in
Table 4.
4.1. Basic Information of Reservoirs
Shafan Reservoir is located in Jinhua City, Zhejiang Province. The reservoir controls a watershed area of 131 km
2. The design flood control standard is once in 50 years, and the check flood standard is once in 1000 years. The basin map of Shafan Reservoir is shown in
Figure 2a. When the starting water level is the normal storage level of 270 m, the maximum allowable water level for flood control is the design flood level of 272.91 m, and the safe discharge of the downstream channel of the reservoir is 400 m
3/s. There are only five time periods, and the flood control dispatch work is carried out based on the criterion of maximum peak shaving.
Another reservoir is Dahuofang Reservoir, located in Liaoning Province, which is a comprehensive water conservancy project in the Hun River Basin [
52]. The reservoir controls a drainage area of 5437 km
2, and its main function is flood control and urban water supply.
Figure 2b shows the reservoir basin map. The design flood standard of the reservoir is once in a thousand years, and the design check flood standard is once in a thousand years. According to the latest approved flood control standard of Dahuofang Reservoir, the design flood level of the reservoir is 136.63 m, and the check flood level is 139.32 m. The normal high-water level and flood-limit water level of the reservoir are 131.5 m and 126.4–127.8 m, respectively. Taking the flood of Dahuofang Reservoir on 28 July 1991 as an example, there are 46 flood periods. The reservoir operation is based on the principle of maximum peak shaving. In the computation, it is necessary to ensure the safe operation demand of the reservoir, reduce the discharge volume as much as possible, and homogenize the flood discharge process of the reservoir.
The multi-reservoir system is located in the Luan River Diversion Project located in Qianxi County, Hebei Province, China. It is mainly composed of Panjiakou Reservoir, Daheiting Reservoir, and Taolinkou Reservoir. The Panjiakou Reservoir is located in the middle reaches of the Luan River, the Daheiting Reservoir is located on the main stream of the Luan River 30 km downstream of the main dam of the Panjiakou Water Control Project, and the Taolinkou Reservoir is located on the Qinglong River, a tributary of the Luan River. The map of the Luanhe River Basin is shown in
Figure 2c. The three reservoirs form a mixed-type multi-reservoir system, and the basic characteristics of each reservoir are shown in
Table 5. During the flood control of the multi-reservoir system, there is a flood process between the three reservoirs and the control point in Luan County, and it is necessary to carry out flood computation to obtain the outflow process of the total watershed. The locations between different reservoirs and flood control points are shown in
Figure 2d. The specific flood evolution steps and relevant information of the watershed can be found in Chen et al. (2021).
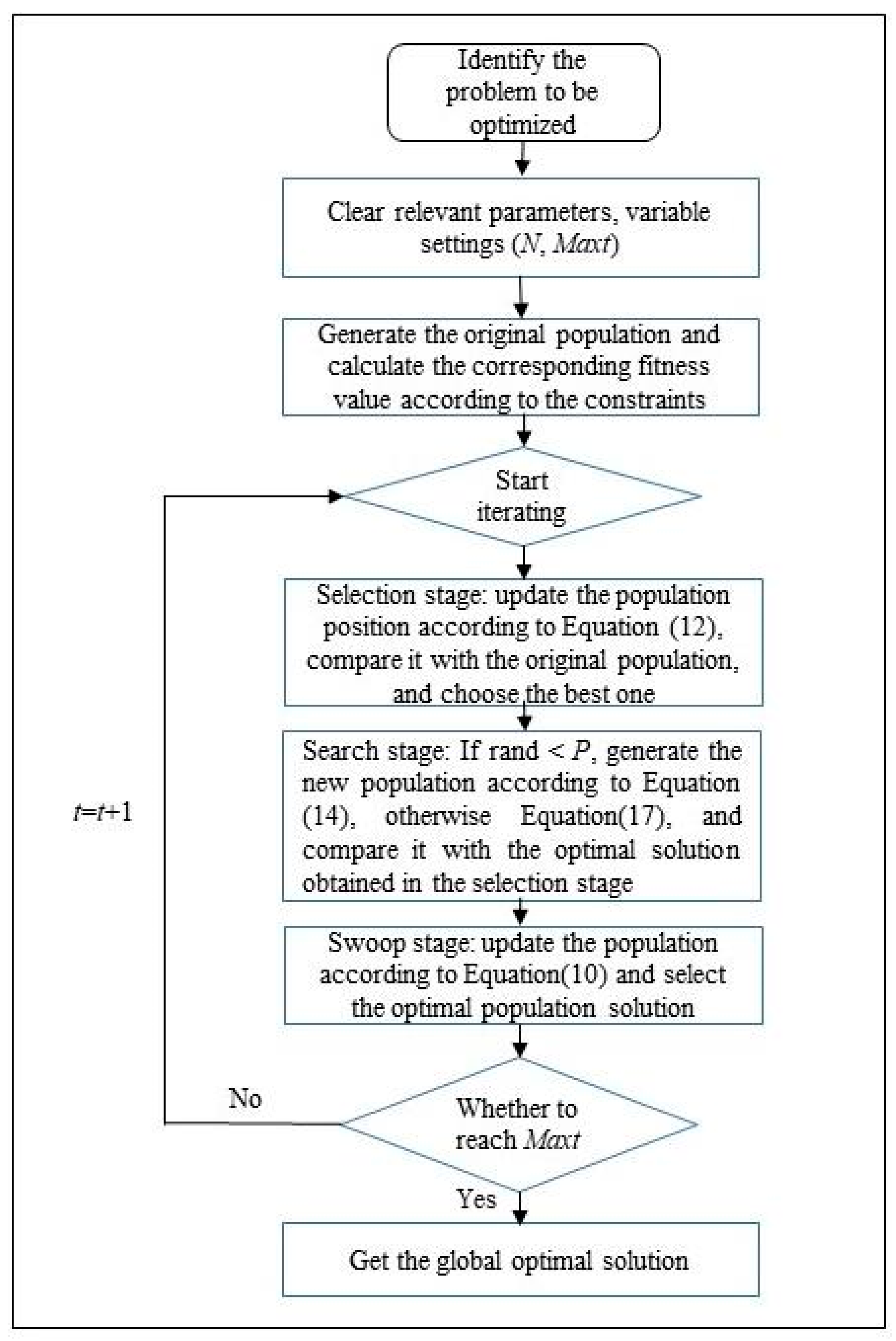
4.2. Flood Control Operation Process Based on CABES Algorithm
The steps of using the ε-CABES algorithm to solve reservoir flood control operation are summarized as follows:
- Step 1.
(Initialization): Population size N, total iterations Maxt, constraint violation ε, or penalty factor c are determined. According to the water level at the end of different periods of the reservoir, the number of N groups of particles at the end of the period is randomly generated as the initial population of each generation. According to the constraint conditions, the corresponding fitness value is computed.
- Step 2.
(Selection stage): The selection operation is performed according to Equation (12). Through the new position solution generated by the Cauchy mutation, the relevant constraints are used to solve the objective function value, and then combined with Equation (17) to select the pros and cons of the solution.
- Step 3.
(Search stage): A new position solution is generated according to Equation (14) or Equation (17). The objective function value is also computed according to the constraints, and the optimal solution is selected in combination with Equation (21).
- Step 4.
(Swoop stage): The position solution generated by Equation (10) is compared with the previous solution through the search and selection stages by Equation (21).
- Step 5.
If the current number of iterations reaches the maximum number of iterations, the iteration ends and the optimal result is obtained. Otherwise, continue to Steps 2–4 and continue to iterate.
Similarly, the steps of CABES flood control operation using penalty function method are roughly the same as those of ε-CABES flood control operation. The difference is that Equation (23) is used when using constraints to solve the objective function value. Moreover, in the three stages of steps 2–4, the comparison of Equation (21) is no longer used; instead, the comparison of the size of the fitness value is simply used to evaluate the pros and cons of the solution.
4.3. Results and Discussion
In this section, the flood control operation of two single reservoirs and a three-reservoir mixed multi-reservoir system is computed. CABES, BES, and PSO are used, and two constraint processing techniques are combined. In order to avoid random differences, the three algorithms run independently 10 times. The parameters used in the algorithm are shown in
Table 4. The flood control operation results of each method, the objective function values generated in the operation process, and the comparison of iteration duration are recorded. In order to verify the stability of the algorithm, five eigenvalues such as ‘minimum value ‘and’ standard deviation’ are used for analysis.
Table 6,
Table 7 and
Table 8 are the operation results of the Shafan Reservoir, Dahuofang Reservoir, and Luanhe multi-reservoir system. Only the data of successful dispatching are recorded in each table.
Figure 3 and
Figure 4, respectively, show the operation process and convergence curve of Shafan Reservoir and Dahuofang Reservoir. The left side is the operation process, and the right side shows the convergence curve of each algorithm in the iteration process.
Figure 5 shows the operation process and convergence curve of ε-CABES in the Luanhe multi-reservoir system.
Figure 6,
Figure 7,
Figure 8,
Figure 9 and
Figure 10 show the flow charts of CF-CABES, ε-BES, CF-BES, ε-PSO, and CF-PSO operation failures. Here, the Panjiakou Reservoir is used as an example that does not meet the constraints.
It can be seen from
Table 6 that the final peak shaving rate obtained by using the six methods of ε-CABES, ε-BES, ε-PSO, CF-CABES, CF-BES, and CF-PSO to solve the flood control operation strategy in Shafan Reservoir is the same. Stable results can be obtained for each computation. In
Figure 3, the operation results of the three algorithms are the same. This is because Shafan Reservoir has fewer variables and simple constraints, and the flood period is short, which belongs to a relatively simple reservoir scheduling problem. Therefore, the requirement for the solution level of the algorithm is not high. It can be seen from
Figure 3 that even if different constraint processing techniques are combined, the convergence process curves of each algorithm are very close, and the later stage reaches the same level of stability and obtains the same optimal solution.
It can be seen from
Table 7 that under the same constraint processing technology, when solving the flood control scheme of Dahuofang Reservoir, the peak clipping rate of CABES is 0.23% higher than that of BES. As shown in
Figure 4, for CABES, BES, and PSO combined with different constraint processing techniques, the final results are not the same. CABES and BES find a suitable scheduling scheme, while PSO does not meet the constraints, so it does not schedule successfully. This is because, compared with Shafan Reservoir, Dahuofang Reservoir has more complex variables and constraints, and higher requirements for the algorithm. Moreover, the standard deviation of the CABES algorithm is far less than that of the BES algorithm when it is used to find a dispatching scheme for many times, which shows that the CABES algorithm has a better stability when it is used to solve slightly complex reservoirs. In the case of the same algorithm, the ε constraint processing method and penalty function method have the same effect. Similarly, in terms of standard deviation, the reservoir operation scheme obtained by using the ε constraint processing method is more stable than the penalty function method. However, neither ε-PSO nor CF-PSO found a suitable operation scheme.
From
Table 8, it can be found that only the ε-CABES method finds a suitable operation scheme when solving the flood control operation scheme for the mixed multi-reservoir system.
Figure 5 shows the flood control operation process of the three reservoirs and the flood routing process of the Luanxian control point. The Luanxian control point includes the confluence process after the optimal joint operation, the original confluence process, the flood regulation flow of each reservoir, and the water from the two subareas of the Luanxian control point. The bottom of the figure records the iterative process curve of the algorithm. The curve of the algorithm is stable in the later operation, indicating that the result is stable and convergent, and it is considered that the optimal value is reached. Therefore, ε-CABES achieves the goal of joint flood control operation.
From
Figure 6,
Figure 7,
Figure 8,
Figure 9 and
Figure 10, it can be found that the flood level does not return to the initial level at the last moment of operation, when CF-CABES solves Panjiakou Reservoir under the same optimization algorithm, and there is a danger for the next flood control. Under the same constrained processing technique, when ε-BES is compared to ε-CABES, the discharge flow exceeds the lower discharge flow constraint and therefore does not meet the constraint. CF-BES, CF-PSO, and ε-PSO do not find a suitable operation solution because they all exceed the lower discharge flow constraint.
This shows that for the reservoir operation problem with few constraints and simple variables (Shafan Reservoir), the traditional optimization algorithms such as PSO and BES can be solved perfectly. However, when facing the Dahuofang Reservoir with increasing constraints and more complex dimensions, the PSO algorithm has difficulty in finding a suitable operation solution, and the BES algorithm is quite effective. Yet, when facing the Luanhe multi-reservoir system with multiple reservoirs, only ε-CABES finds a suitable operation solution.
4.4. Conclusions of the Case Study Results
Through the three examples of two single reservoirs and a reservoir cluster of three reservoirs, the following findings are made.
- (1)
The length of flood period of a reservoir (group) has different requirements for the performance of algorithm and constraint processing technology. For reservoirs with few time periods, this is a simple operation problem, which requires low computational power of algorithms. Therefore, different algorithms combined with different constraint processing techniques can achieve appropriate flood control operation effects. With the increase of the number of time periods, better algorithms are needed to find the optimal strategy. The combination of conventional algorithms and constraint processing technology is difficult to sustain.
- (2)
Through the flood control operation results of the Dahuofang Reservoir and Luan River Basin multi-reservoir system with more time periods, it can be observed that, under the same constraint processing technology, the CABES optimization algorithm proposed in this paper can achieve better results than those of the BES optimization algorithm before improvement, while the classical PSO algorithm does not find a suitable operation scheme in both instances. This demonstrates that as the complexity of the solution problem increases, the CABES algorithm obtained by improving the Cauchy mutation strategy and fusing the adaptive weighting factor with the Levy flight strategy is somewhat advanced and practical, improving the ability of the original algorithm to solve complex problems.
- (3)
When the same algorithm uses two constraint processing techniques, the results of the operation scheme obtained by the two constraint processing methods are consistent when solving the operation scheme of Shafan Reservoir and Dahuofang Reservoir. However, in the dispatching of a mixed multi-reservoir system, the dispatching results are quite different. Therefore, it can be considered that the ε constraint treatment technology and the penalty function method have the same effect on the optimization treatment technology of a single reservoir, but the optimization effect of the ε constraint treatment technology is better than that of the penalty function method on more complex constraint problems.
5. Conclusions
Reservoir (group) flood control operation is a complex high-dimensional problem with many constraints. To solve this problem, this paper proposes a new constrained optimization algorithm, namely, ε-CABES algorithm. The algorithm combines the advantages of the BES algorithm and the ε constraint processing technology. In order to verify the rationality and effectiveness of the method, an example computation is carried out through the flood control operation of two single reservoirs and the joint flood control operation of a multi-reservoir system, and another processing technology is used. The penalty function method and the optimization algorithms BES and PSO are compared and analyzed. The main conclusions are as follows:
- (1)
The CABES algorithm is used to solve the three instances, and the comparative analysis with the operation results of the BES and PSO algorithms shows that the CABES algorithm has better global search ability and better solution accuracy. Cauchy mutation and fusion of adaptive weight factor and Levy flight strategy can improve the performance of the algorithm in solving reservoir optimal operation.
- (2)
The effect of the ε constraint processing technique is equivalent to that of the penalty function method in the relatively simple single-reservoir operation problem, and in the more complex multi-reservoir operation problem, the solution effect is ahead of the penalty function method. In general, the ε constraint processing technology has better convergence and achieves better optimization results.
- (3)
For the dispatching problem of Shafan Reservoir with short time period, the dispatching schemes required by different algorithms are basically the same; for Dahuofang Reservoir with long time period, the dispatching schemes of each algorithm are different. It shows that the length of the number of periods in the reservoir operation will affect the stability and difference of the operation results of each algorithm.
- (4)
The ε-CABES algorithm can better solve the strong constraints, multistage, and nonlinear combination problems in the optimal operation of reservoir flood control, and provides an effective method for the optimal operation of reservoir flood control.
To sum up, this paper discusses the proposed algorithm and constraint processing technology by taking reservoir (group) flood control operation as an example. In solving the reservoir problem with short flood period and simple process, the coupling of conventional classical algorithms PSO, BES, and penalty function method can be solved. However, as the scale of the reservoir increases and the time period becomes longer, it becomes a more complex constraint problem. The methods mentioned above are not enough to find a suitable flood control operation strategy, and algorithms and constraints with better performance and higher solution accuracy are required, that is, the ε-CABES method proposed in this paper. However, it should be noted that as the complexity of the problem increases, the time consumed by the ε-CABES method is more than that of the penalty function constrained evolution method. Therefore, the next stage of work is to find more suitable optimization algorithms and processing technologies, and improve the complexity of the model as much as possible while improving the model’s optimization capabilities.