Dynamic Control of Yearly Drawdown Level of Overyear Regulation Reservoir in Cascade System
Abstract
:1. Introduction
2. Methodology
2.1. Joint Optimal Scheduling Model
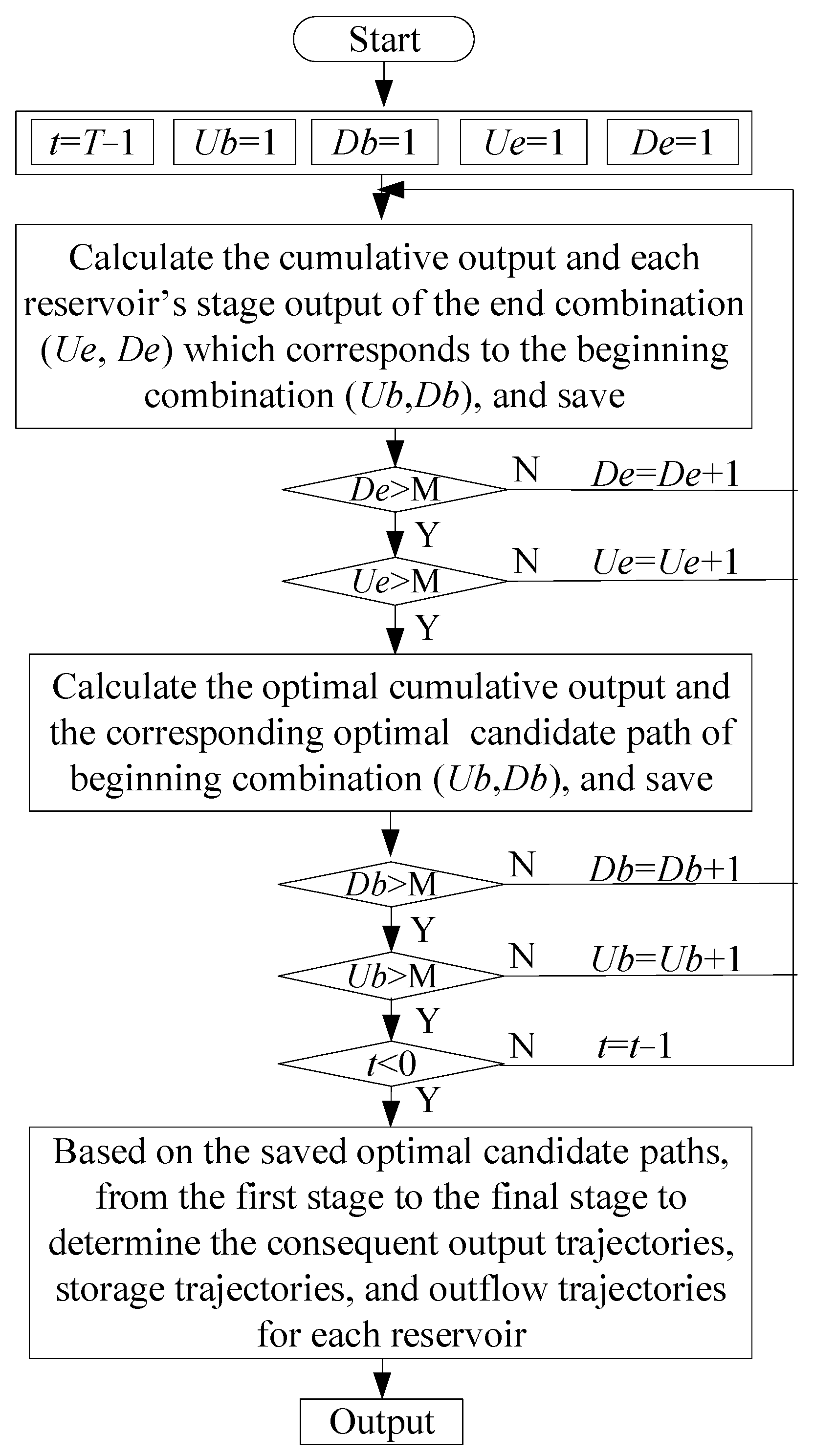
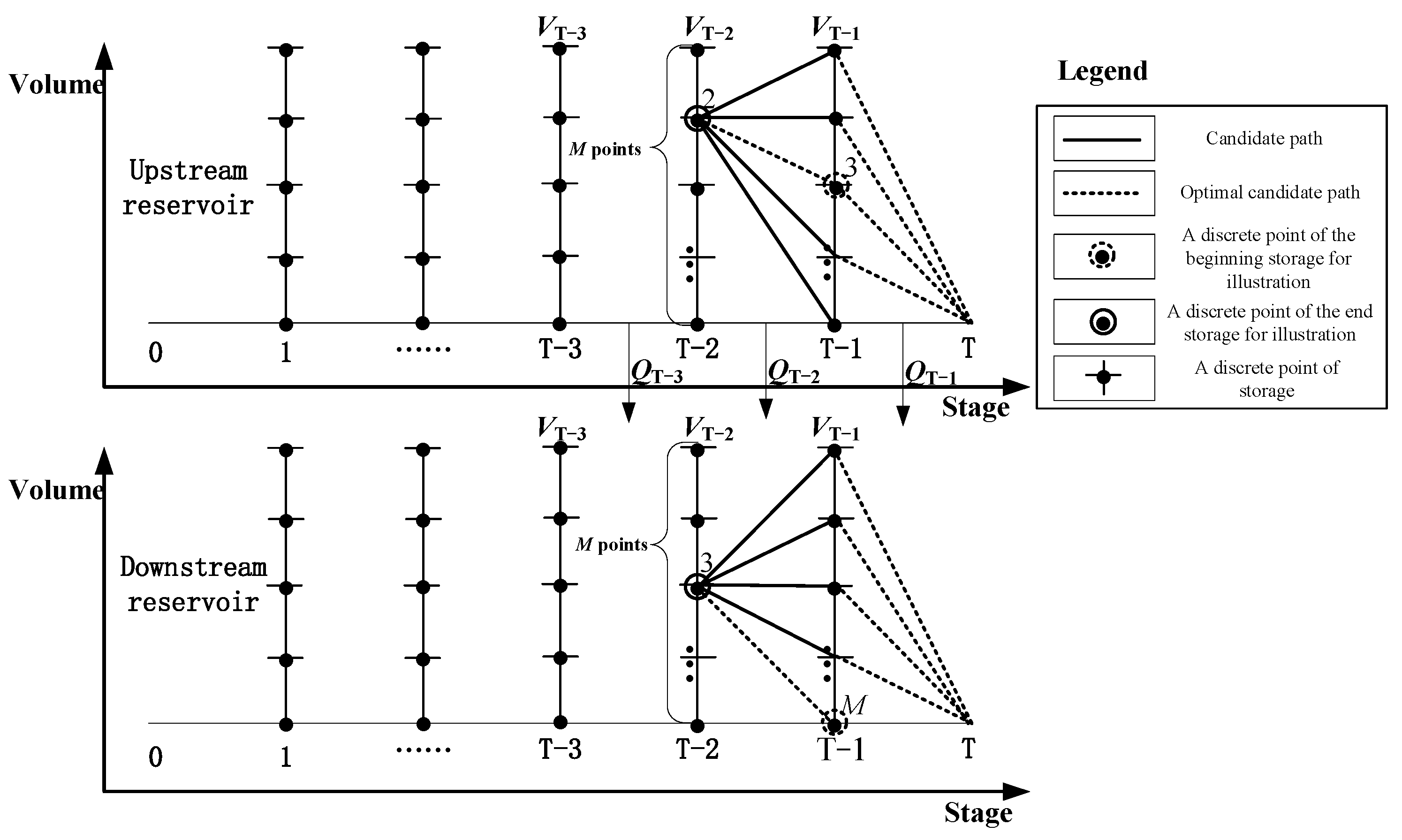
2.2. Multidimensional DP for Solving the Model
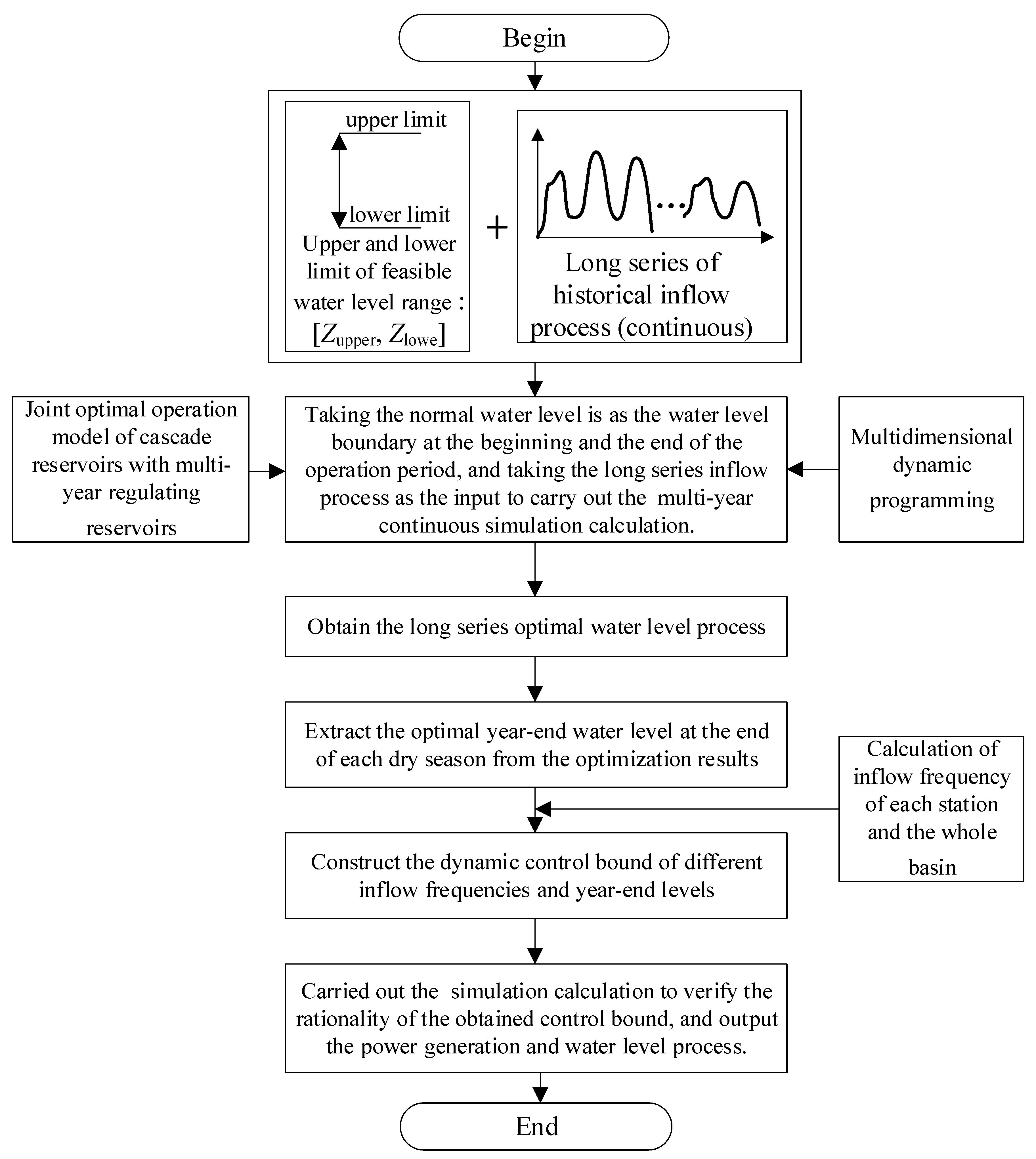
2.3. Dynamic Control Bound Construction of Yearly Drawdown Level
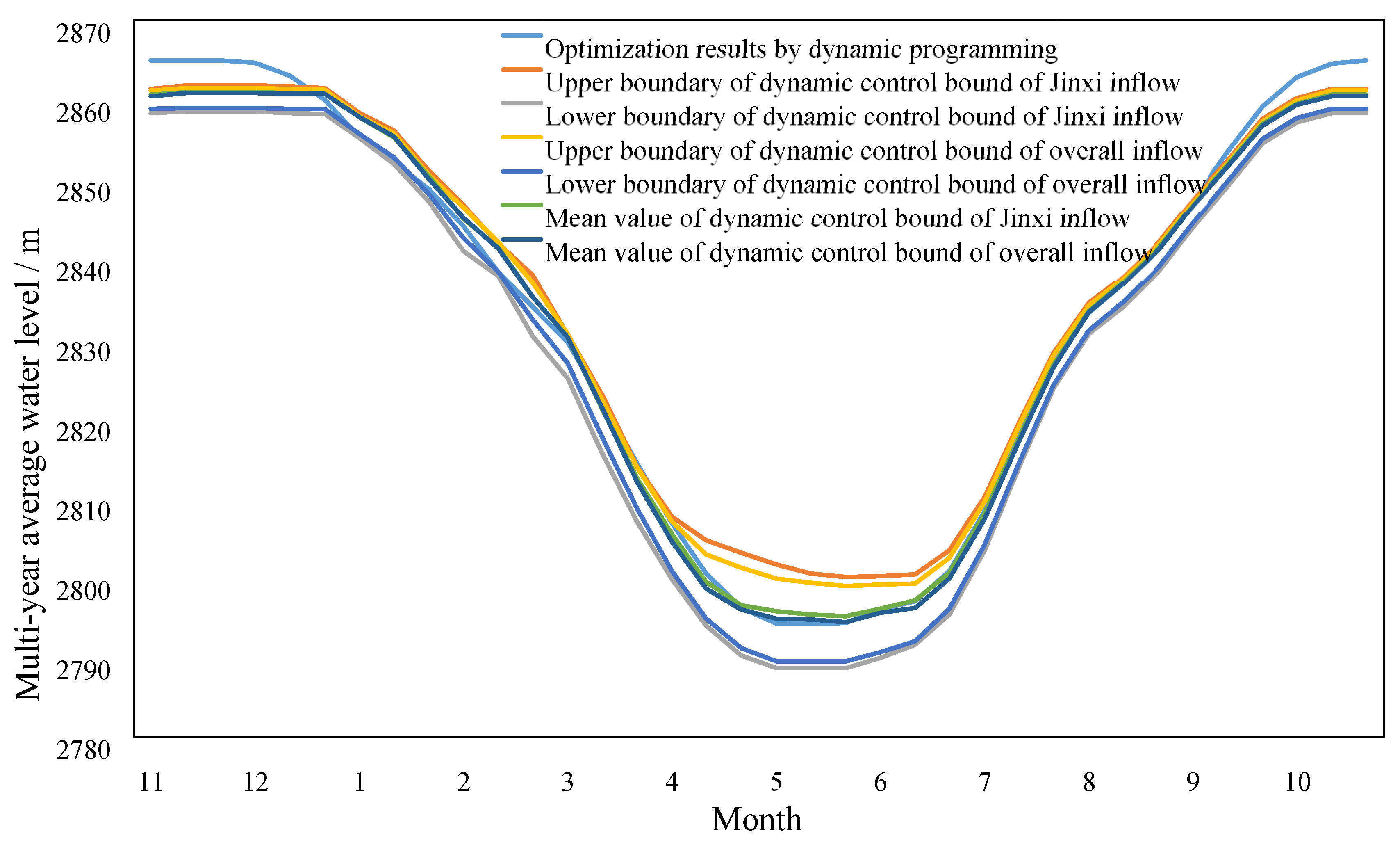
3. Case Study
3.1. Study Area
3.2. Results and Analysis
4. Conclusions
- (1)
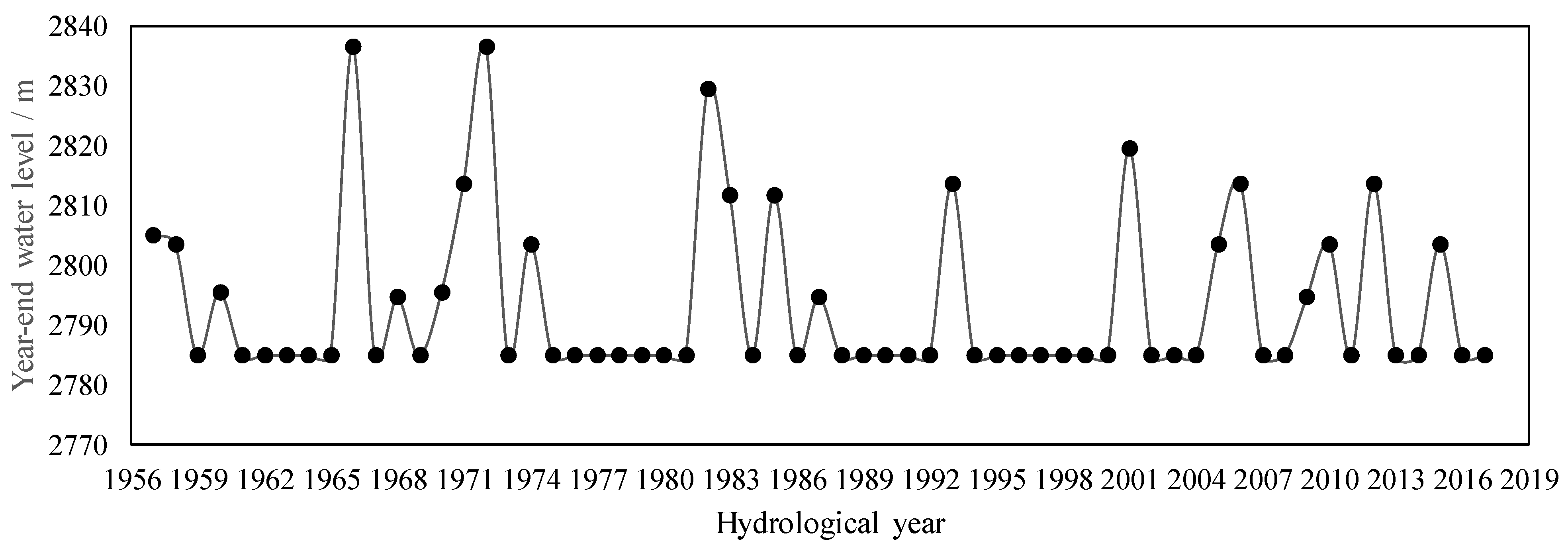
- The inflow series of the station in the middle of the basin and the calculated overall inflow series can both well represent the inflow situation of the whole basin. In these two cases, the relationship between the inflow frequency and the scatter points of the yearly drawdown level is relatively centralized and stable. The results of the inflow series of stations that are located in the upper and lower parts of the basin are relatively poor.
- (2)
- Under the control mode of the fixed yearly drawdown level, the maximum annual average power generation of the cascade system is 100.580 billion kWh, and the corresponding optimal yearly drawdown level is 2785 m, which is the dead water level. That is to say, if the yearly drawdown level is to be fixed, the dead water level is the best for the Lianghekou reservoir.
- (3)
- For the dynamic control bounds constructed by the two selected inflow series, the results calculated from their upper boundaries, lower boundaries and mean values are not significant, and their maximum differences are 0.110 billion kWh and 0.107 billion kWh, respectively. This shows that the results of the dynamic control bounds constructed by the two selected inflow series both have little fluctuation, which can well cope with the impact of inflow uncertainty on scheduling results.
- (4)
- The dynamic control bound constructed based on the overall inflow of the river basin is slightly better than that based on the inflow of the Jinxi station. In all the three cases where the upper boundary, lower boundary and mean value are used as the control rules, the power generation of the former is 0.01% higher than that of the latter.
- (5)
- By constructing a dynamic control mode of the yearly drawdown level, 63.4%~76.3% of the benefits of the lifting space of yearly drawdown level optimization can be realized by the dynamic control bound proposed in this paper, which has a very remarkable effect.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Db: | the index of beginning-state variables of downstream reservoirs. |
| De: | the index of end-state variables of downstream reservoirs. |
| E: | power generation over the whole scheduling period (kWh). |
| Epti: | the evaporation capacity of the ith reservoir in the tth stage (m3/s). |
| f t*(V): | the sum of optimal outputs from the present stage t to the last stage T. |
| Hti: | the average water head of the ith hydropower station in the tth stage (m). |
| Iti: | the average interval inflow of the ith reservoir in the tth stage (m3/s). |
| Ki: | the output coefficient of the ith hydropower station. |
| Nti: | the output of the ith hydropower station in the tth stage (kW). |
| Nit,min: | the lower limit of Nit. |
| Nit,max: | the upper limit of Nit. |
| Nt(Vt−1,Qt): | the total output of the tth stage. |
| qti: | the outflow through the turbines of the ith reservoir in the tth stage (m3/s). |
| Qit: | the average discharge of the ith reservoir in the tth stage (m3/s). |
| Qt: | the discharge flow determined by Vt−1 and Vt. |
| Qt = (Qt1, Qt2, …, Qt n)’: | the decision variable vector. |
| Qit,min: | the lower limit of Qit. |
| Qit,max: | the upper limit of Qit. |
| T: | the total number of stages over the whole scheduling period. |
| Dt: | a set of feasible decisions that satisfy the constraints of the reservoir. |
| Δt: | the duration of a stage (h). |
| Ub: | the index of beginning-state variables of upstream reservoirs. |
| Ue: | the index of end-state variables of upstream reservoirs. |
| Vit: | the storage volume of the ith reservoir in the tth stage (m3). |
| Vt: | the storage state at the beginning of the stage t. |
| Vit,min: | the lower limit of Vit. |
| Vit,max: | the upper limit of Vit. |
| V0i: | the storage volume of the ith reservoir at the beginning of the first stage. |
| Vbi: | the storage volume of the ith reservoir at the beginning of the whole scheduling period. |
| VTi: | the storage volume of the ith reservoir at the end of the Tth stage. |
| Vei: | the storage volume of the ith reservoir at the end of the whole scheduling period. |
| Vt−1 = (Vt−11, Vt−12, …, Vt−1n)’: | the state variable vector. Vt1, Vt2, and Vt3 are discretized, i.e., (Vt1,1, Vt1,2, …, Vt1,M), (Vt2,1, Vt2,2, …, Vt2,M) and (Vt3,1, Vt3,2, …, Vt3,M). |
| : | |
| : | the optimal cumulative output of a storage volume combination VT at the end of the Tth stage (kW). |
| Wti: | the average discharge of abandoned water of the ith reservoir in the tth stage (m3/s). |
References
- Siddiqui, O.; Dincer, I. Comparative assessment of the environmental impacts of nuclear, wind and hydro-electric power plants in Ontario: A life cycle assessment. J. Clean. Prod. 2017, 164, 848–860. [Google Scholar] [CrossRef]
- Jurasz, J.; Mikulik, J.; Krzywda, M.; Ciapała, B.; Janowski, M. Integrating a wind- and solar-powered hybrid to the power system by coupling it with a hydroelectric power station with pumping installation. Energy 2018, 144, 549–563. [Google Scholar]
- Lu, S.; Shang, Y.; Li, W.; Peng, Y.; Wu, X. Economic benefit analysis of joint operation of cascaded reservoirs. J. Clean. Prod. 2018, 179, 731–737. [Google Scholar] [CrossRef]
- Bertone, E.; O’ Halloran, K.; Stewart, R.A.; de Oliveira, G.F. Medium-term storage volume prediction for optimum reservoir management: A hybrid data-driven approach. J. Clean. Prod. 2017, 154, 353–365. [Google Scholar]
- Allawi, M.F.; Jaafar, O.; Mohamad Hamzah, F.; El-Shafie, A. Novel reservoir system simulation procedure for gap minimization between water supply and demand. J. Clean. Prod. 2019, 206, 928–943. [Google Scholar] [CrossRef]
- Arena, C.; Cannarozzo, M.; Mazzola, M.R. Exploring the Potential and the Boundaries of the Rolling Horizon Technique for the Management of Reservoir Systems with over-Year Behaviour. Water Resour. Manag. 2017, 31, 867–884. [Google Scholar] [CrossRef]
- Guo, X.; Chen, J.; Ma, G. Research on yearly drawdown level of overyear regulating storage reservoir for timed power tariff. J. Hydroelectr. Eng. 2004, 23, 27. [Google Scholar]
- Yuan, W.; Wang, F. Study on year-end water level of overyear regulating storage reservoir in power market. J. Hydroelectr. Eng. 2012, 31, 94–98. [Google Scholar]
- Zhang, Y.; Jiang, Z.; Ji, C.; Sun, P. Contrastive analysis of three parallel modes in multi-dimensional dynamic programming and its application in cascade reservoirs operation. J. Hydrol. 2015, 529, 22–34. [Google Scholar]
- Wang, J.; Huang, W.; Ma, G.; Wang, Y. Determining the optimal year-end water level of a overyear regulating storage reservoir: A case study. Water Sci. Technol. Water Supply 2016, 16, 284–294. [Google Scholar] [CrossRef]
- Liu, J.; Huang, C.; Zeng, G. Comparative analysis of year-end water level determining methods for cascade carryover storage reservoirs. IOP Conf. Ser. Earth Environ. Sci. 2017, 82, 1–8. [Google Scholar]
- Ehteram, M.; Karami, H.; Mousavi, S.F.; Farzin, S.; Kisi, O. Optimization of energy management and conversion in the multi-reservoir systems based on evolutionary algorithms. J. Clean. Prod. 2017, 168, 1132–1142. [Google Scholar]
- Jiang, Z.; Liu, P.; Ji, C.; Zhang, H.; Chen, Y. Ecological flow considered multi-Objective storage energy operation chart optimization of large-scale mixed reservoirs. J. Hydrol. 2019, 577, 123949. [Google Scholar] [CrossRef]
- Li, R.; Jiang, Z.; Li, A.; Yu, S.; Ji, C. An improved shuffled frog leaping algorithm and its application in the optimization of cascade reservoir operation. Hydrol. Sci. J. 2018, 63, 15–16. [Google Scholar] [CrossRef]
- Liu, S.; Xie, Y.; Fang, H.; Huang, Q.; Huang, S.; Wang, J.; Li, Z. Impacts of inflow variations on the long term operation of a multi-hydropower-reservoir system and a strategy for determining the adaptable operation rule. Water Resour. Manag. 2020, 34, 1649–1671. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.Z.; Ren, K.; Huang, Q.; Huang, G.H.; Cheng, G.H.; Li, K.L. Examining the applicability of different sampling techniques in the development of decomposition-based streamflow forecasting models. J. Hydrol. 2019, 568, 534–550. [Google Scholar]
- Goulter, I.C.; Tai, F.-K. Practical implications in the use of stochastic dynamic programming for reservoir operation. JAWRA J. Am. Water Resour. Assoc. 2007, 21, 65–74. [Google Scholar] [CrossRef]
- Adib, A.; Samandizadeh, M.A. Comparison ability of GA and DP methods for optimization of released water from reservoir dam based on produced different scenarios by Markov chain method. Int. J. Optim. Civ. Eng. 2016, 6, 43–62. [Google Scholar]
- Jiang, Z.; Ji, C.; Qin, H.; Feng, Z. Multi-stage progressive optimality algorithm and its application in energy storage operation chart optimization of cascade reservoirs. Energy 2018, 148, 309–323. [Google Scholar]
- Zhang, Z.; Zhang, S.; Geng, S.; Jiang, Y.; Li, H.; Zhang, D. Application of decision trees to the determination of the yearly drawdown level of a carryover storage reservoir based on the iterative dichotomizer 3. Int. J. Electr. Power Energy Syst. 2015, 64, 375–383. [Google Scholar]
- Jiang, Z.; Tang, Z.; Liu, Y.; Chen, Y.; Feng, Z.; Xu, Y.; Zhang, H. Area moment and error basedforecasting difficulty and its application ininflow forecasting level evaluation. Water Resour. Manag. 2019, 33, 4553–4568. [Google Scholar] [CrossRef]





| Item | Unit | Lianghekou | Yangfanggou | Jinxi | Jindong | Guandi | Ertan | Tongzilin |
|---|---|---|---|---|---|---|---|---|
| Normal level | m | 2865 | 2088 | 1880 | 1646 | 1330 | 1200 | 1015 |
| Dead level | m | 2785 | 2094 | 1800 | 1640 | 1321 | 1155 | 1010 |
| Annual average runoff | m3/s | 664 | 896 | 1200 | 1220 | 1430 | 1670 | 1928 |
| Mean annual precipitation | mm | 897 | None | None | 932 | 1077 | 1038 | 1040 |
| Temperature | °C | 10.9 | 13.7 | 13.7 | 13.7 | 18.6 | 19.8 | 19.7 |
| Flood control level | m | 2845.9 | None | 1859 | None | None | 1190 | None |
| Regulation performance | --- | Overyear | Daily | Yearly | Daily | Daily | Seasonal | Daily |
| Range of operating water level in dry season | m | [2845.9, 2865] | 2092 | [1859, 1880] | 1644 | 1328 | [1190, 1200] | 1013.5 |
| Range of operating water level in flood season | m | [2785, 2865] | 2092 | [1800, 1880] | 1644 | 1328 | [1155, 1200] | 1013.5 |
| Yearly Drawdown Level/m | Total Power Generation/Billion kWh |
|---|---|
| 2785 | 100.58 |
| 2790 | 100.55 |
| 2795 | 100.49 |
| 2800 | 100.43 |
| 2805 | 100.30 |
| 2810 | 100.16 |
| 2815 | 99.95 |
| 2820 | 99.72 |
| 2825 | 99.43 |
| 2830 | 99.08 |
| 2835 | 98.64 |
| 2840 | 98.10 |
| 2845 | 97.37 |
| Computation Method | Total Power Generation/Billion kWh | Increment Compared to Fixed Water Level Mode |
|---|---|---|
| Upper boundary of the dynamic control bound constructed based on Jinxi inflow series | 101.255 | 0.67% |
| Lower boundary of the dynamic control bound constructed based on Jinxi inflow series | 101.173 | 0.59% |
| Mean value of the dynamic control bound constructed based on Jinxi inflow series | 101.283 | 0.70% |
| Upper boundary of the dynamic control bound constructed based on the overall inflow series | 101.267 | 0.68% |
| Lower boundary of the dynamic control bound constructed based on the overall inflow series | 101.183 | 0.60% |
| Mean value of the dynamic control bound constructed based on the overall inflow series | 101.290 | 0.71% |
| Fixed yearly drawdown level (determined by discretized water levels) | 100.580 | 0.00% |
| Optimal calculation results based on multidimensional DP | 101.520 | 0.93% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Z.; Jiang, Z.; Yuan, X. Dynamic Control of Yearly Drawdown Level of Overyear Regulation Reservoir in Cascade System. Water 2023, 15, 665. https://doi.org/10.3390/w15040665
Chang Z, Jiang Z, Yuan X. Dynamic Control of Yearly Drawdown Level of Overyear Regulation Reservoir in Cascade System. Water. 2023; 15(4):665. https://doi.org/10.3390/w15040665
Chicago/Turabian StyleChang, Zongye, Zhiqiang Jiang, and Xiaohui Yuan. 2023. "Dynamic Control of Yearly Drawdown Level of Overyear Regulation Reservoir in Cascade System" Water 15, no. 4: 665. https://doi.org/10.3390/w15040665




