Landslide Displacement Prediction of Shuping Landslide Combining PSO and LSSVM Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Time Series Theory
2.2. PSO Algorithm
2.3. LSSVM Algorithm
2.4. PSO-LSSVM Algorithm
- (a)
- Initialize parameters containing population size m, number of iterations , learning factor c, initial position , and initial velocity of the particles, etc.;
- (b)
- Predict learning samples by the particle vectors in the LSSVM. A prediction error of the current position of each particle is regarded as a fitness value of each particle. By comparing the current fitness value of each particle with its optimal fitness value, the current position is taken as the optimal position if the former is better than the latter;
- (c)
- Compare the adaptation value of each particle’s optimal position with the adaptation value of the population’s optimal position. If the former is better than the latter, this particle’s optimal position is replaced with the population’s optimal position;
- (d)
- Calculate an inertial weight and update the and of each particle by Equations (5) and (6);
- (e)
- Judge whether the maximum iteration is achieved or the accuracy requirement is satisfied. If any condition is reached, the procedure is ended and the optimal solution is found. Contrarily, step (b) will continue to be executed, and a new round of searches will be conducted.
2.5. Prediction Performance Measure
3. Case Study
3.1. Geological Condition
3.2. Deformation Characteristics
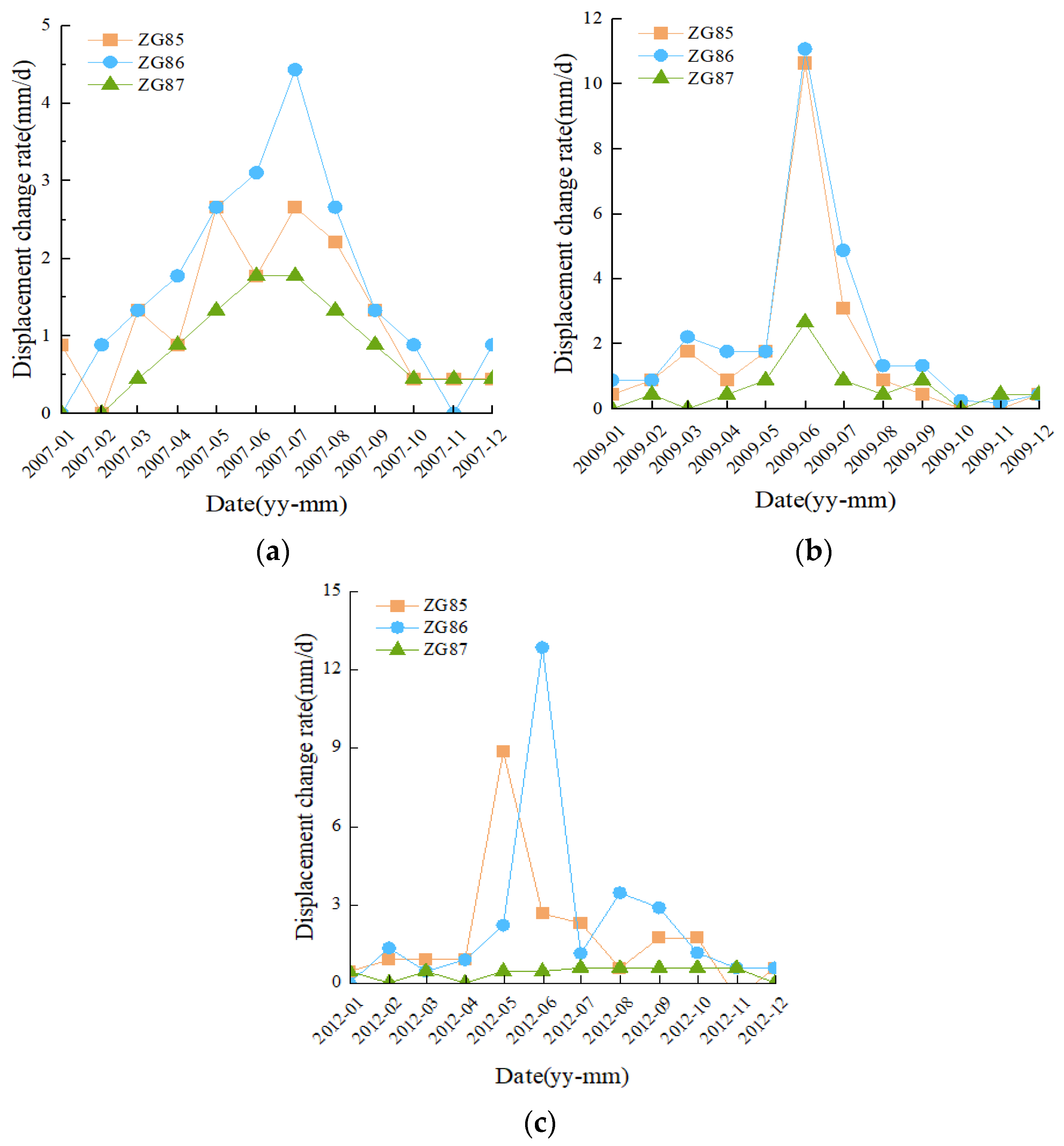
3.2.1. Ground Deformation Characteristics
3.2.2. Analysis of Test Data
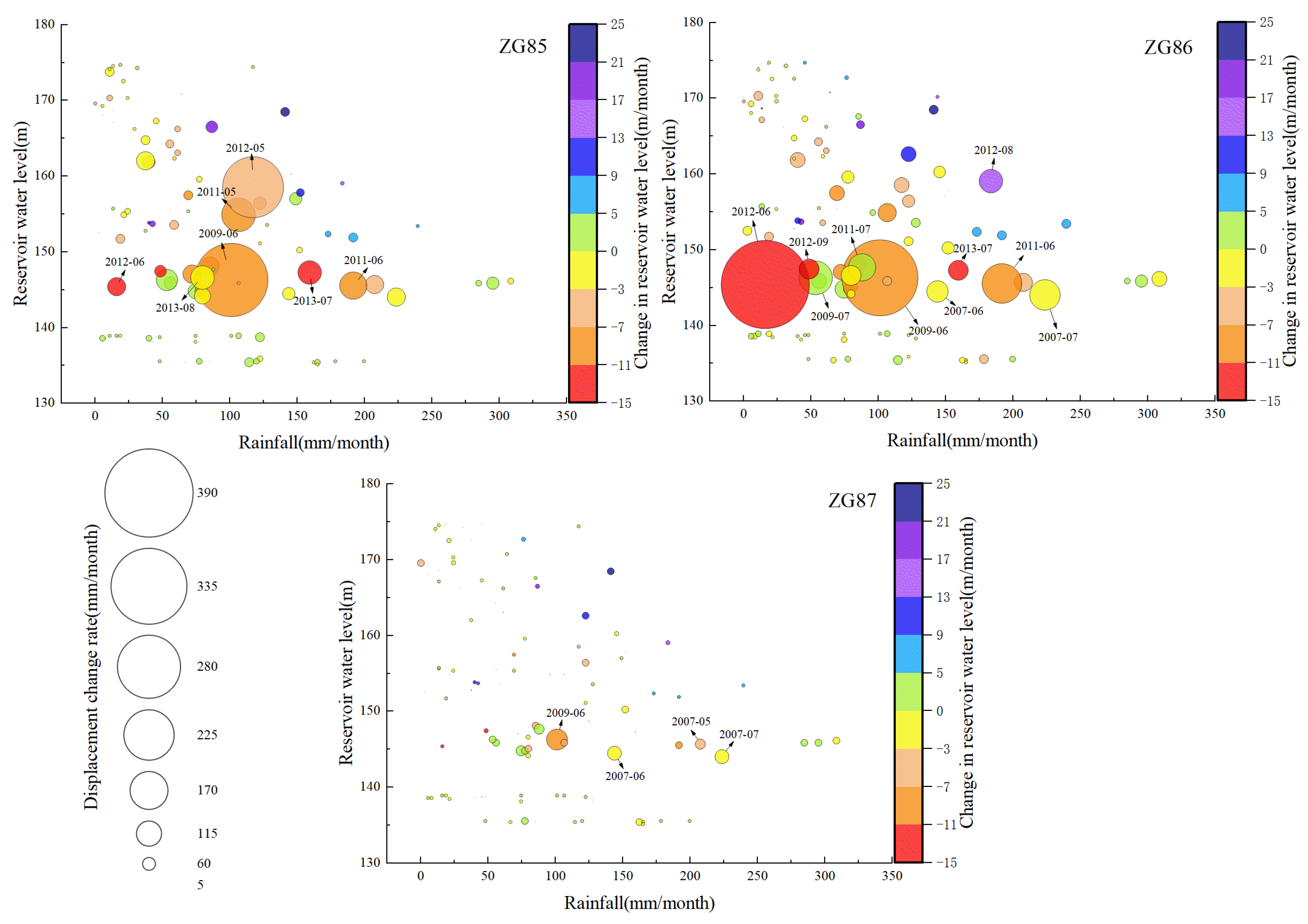
3.3. Triggering Factors Analysis
3.3.1. Foundation of Geological Factors
3.3.2. Effects of Reservoir Water Level and Rainfall
4. Results
4.1. Training Process
- (a)
- Divide the data set. The PTD from June 2004 to October 2011 is considered as the training data, and the two years of data from November 2011 to September 2013 are considered as the prediction data;
- (b)
- Set the parameters in the PSO. Supposing that the penalty factor C is [0.1, 1000], the kernel parameter is [0.01, 1000], the number of the particle swarm is 20, the maximum number of iterations is 200, the learning factor = = 1.5, and the inertial weight ω = 0.5;
- (c)
- Determine the value of optimization parameters;
- (d)
- Train the LSSVM model. The optimal penalty factor C is installed as 229.12, and the kernel parameter is installed as 0.01 in the LSSVM, obtained by the optimization of the PSO. Afterward, the fitness value of the model is calculated by the optimal parameters.
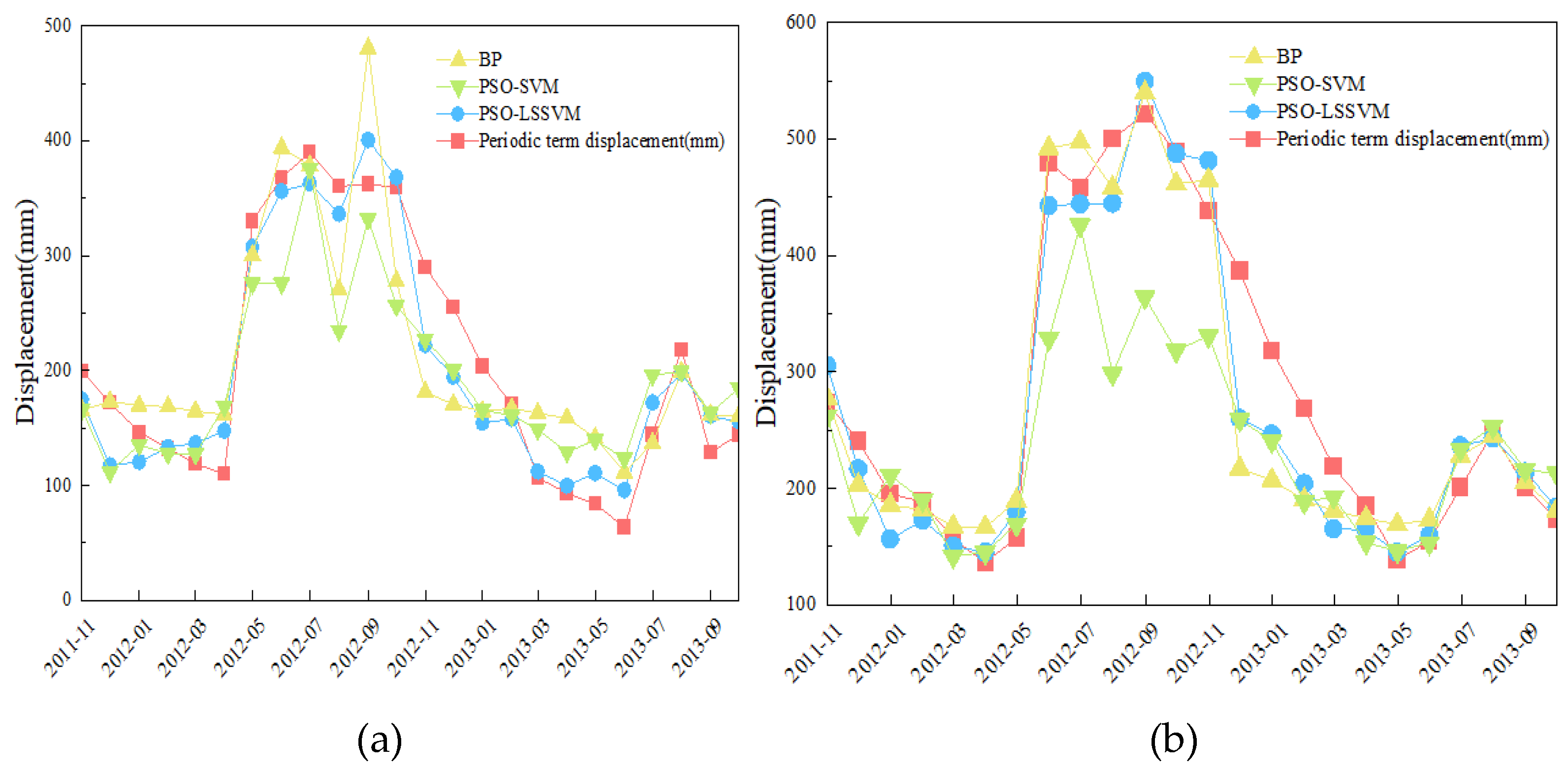
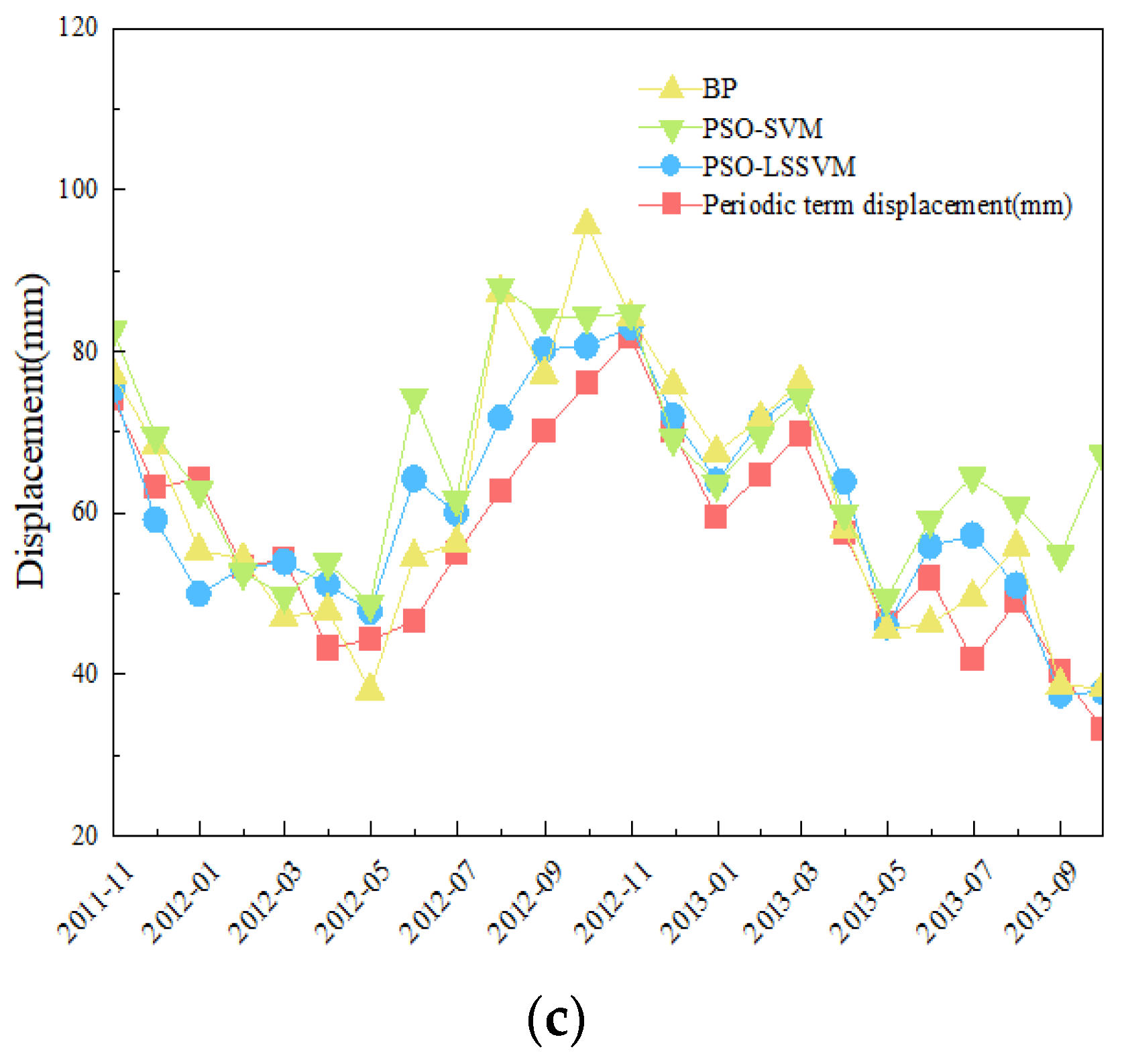
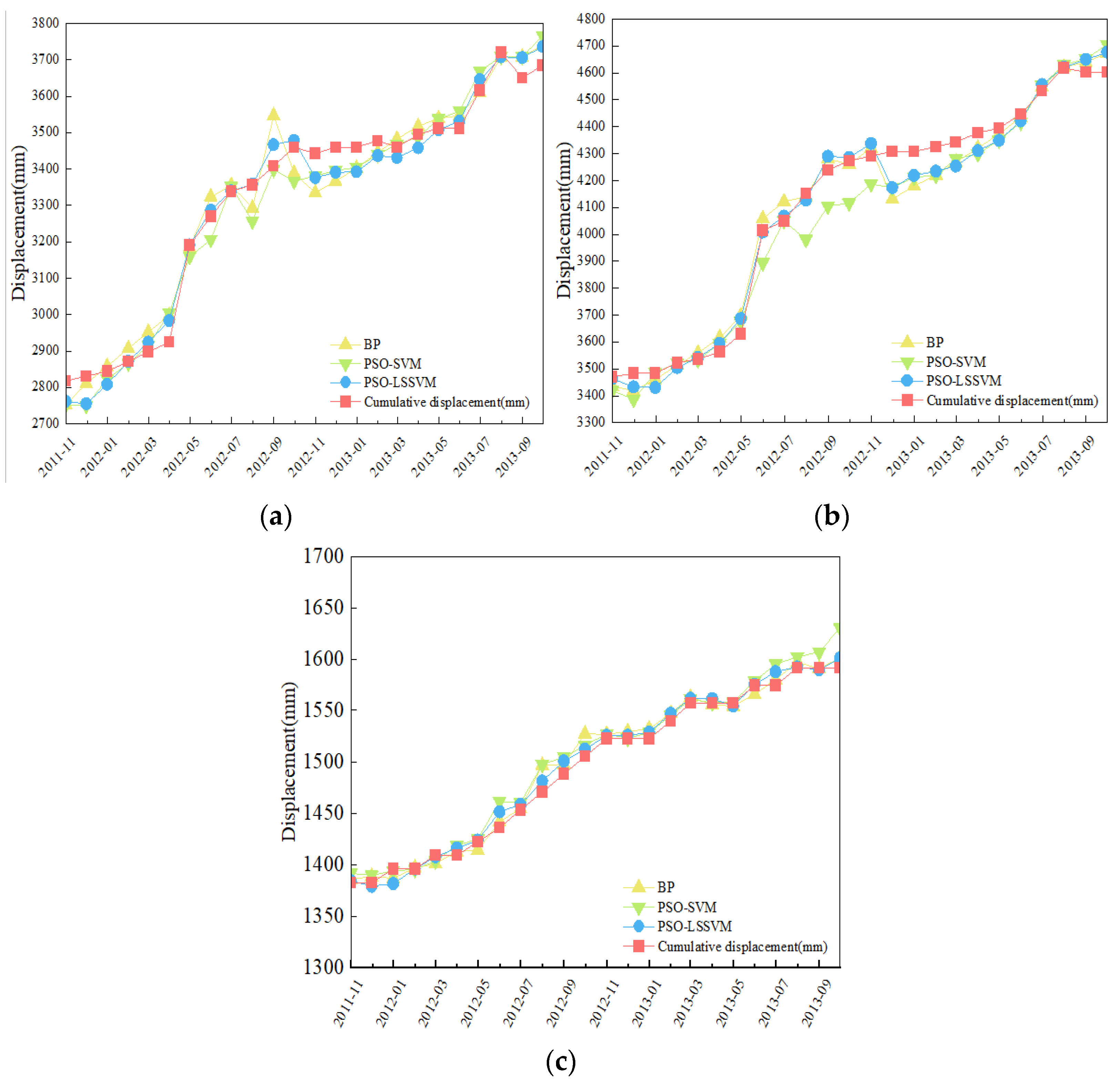
4.2. Results and Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Su, Z.; Wang, Y.; Zhang, H. Study on the Failure Mechanism, Safety Grading and Rainfall Threshold of Landslide Caused by Typhoon Rainstorm. Geotech. Geol. Eng. 2022, 40, 2201–2211. [Google Scholar] [CrossRef]
- Tang, H.; Wasowski, J.; Juang, C.H. Geohazards in the three Gorges Reservoir Area, China–Lessons learned from decades of research. Eng. Geol. 2019, 261, 105267. [Google Scholar] [CrossRef]
- Li, C.; Fu, Z.; Wang, Y.; Tang, H.; Yan, J.; Gong, W.; Yao, W.; Criss, R.E. Susceptibility of reservoir-induced landslides and strategies for increasing the slope stability in the Three Gorges Reservoir Area: Zigui Basin as an example. Eng. Geol. 2019, 261, 105279. [Google Scholar] [CrossRef]
- Ren, F.; Wu, X.; Zhang, K.; Niu, R. Application of wavelet analysis and a particle swarm-optimized support vector machine to predict the displacement of the Shuping landslide in the Three Gorges, China. Environ. Earth Sci. 2015, 73, 4791–4804. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; Zhang, G.; Gui, L.; Yang, B.; Liu, L. Landslide displacement prediction using discrete wavelet transform and extreme learning machine based on chaos theory. Environ. Earth Sci. 2016, 75, 1376. [Google Scholar] [CrossRef]
- Huang, F.; Huang, J.; Jiang, S.; Zhou, C. Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng. Geol. 2017, 218, 173–186. [Google Scholar] [CrossRef]
- Lian, C.; Zeng, Z.; Yao, W.; Tang, H. Ensemble of extreme learning machine for landslide displacement prediction based on time series analysis. Neural Comput. Appl. 2014, 24, 99–107. [Google Scholar] [CrossRef]
- Goh, A.T.C. Back-propagation neural networks for modeling complex systems. Artif. Intell. Eng. 1995, 9, 143–151. [Google Scholar] [CrossRef]
- Zhu, X.; Ma, S.; Xu, Q.; Liu, W. A WD-GA-LSSVM model for rainfall-triggered landslide displacement prediction. J. Mt. Sci. 2018, 15, 156–166. [Google Scholar] [CrossRef]
- Fang, K.; Tang, H.; Li, C.; Su, X.; An, P.; Sun, S. Centrifuge modelling of landslides and landslide hazard mitigation: A review. Geosci. Front. 2023, 14, 101493. [Google Scholar] [CrossRef]
- Meyer, D.; Leisch, F.; Hornik, K. The support vector machine under test. Neurocomputing 2003, 55, 169–186. [Google Scholar] [CrossRef]
- Han, H.; Shi, B.; Zhang, L. Prediction of landslide sharp increase displacement by SVM with considering hysteresis of groundwater change. Eng. Geol. 2021, 280, 105876. [Google Scholar] [CrossRef]
- Ma, J.; Wang, Y.; Niu, X.; Jiang, S.; Liu, Z. A comparative study of mutual information-based input variable selection strategies for the displacement prediction of seepage-driven landslides using optimized support vector regression. Stoch. Environ. Res. Risk Assess. 2022, 36, 3109–3129. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, H.; Huang, J.; Wen, T.; Ma, J.; Zhang, J. A comparative study of different machine learning methods for reservoir landslide displacement prediction. Eng. Geol. 2022, 298, 106544. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X.; Liao, R.; Wan, J.; He, Z.; Zhao, Z.; Zhang, Y.; Su, Z. Research on displacement prediction of step-type landslide under the influence of various environmental factors based on intelligent WCA-ELM in the Three Gorges Reservoir area. Nat. Hazards 2021, 107, 1709–1729. [Google Scholar] [CrossRef]
- Wen, T.; Tang, H.M.; Wang, Y.K.; Lin, C.Y.; Xiong, C.R. Landslide displacement prediction using the GA-LSSVM model and time series analysis: A case study of Three Gorges Reservoir, China. Nat. Hazards Earth Syst. Sci. 2017, 17, 2181–2198. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, J.; He, Z.; Tan, J.; Li, C. A novel displacement prediction method using gated recurrent unit model with time series analysis in the Erdaohe landslide. Nat. Hazards 2021, 105, 783–813. [Google Scholar] [CrossRef]
- Gao, W.; Dai, S.; Chen, X. Landslide prediction based on a combination intelligent method using the GM and ENN: Two cases of landslides in the Three Gorges Reservoir, China. Landslides 2020, 17, 111–126. [Google Scholar] [CrossRef]
- Li, S.; Wu, N. A new grey prediction model and its application in landslide displacement prediction. Chaos Solitons Fractals 2021, 147, 110969. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, J.; Liao, R.; Zhang, M.; Zhang, Y.; Wang, X.; Su, Z. Application of an enhanced BP neural network model with water cycle algorithm on landslide prediction. Stoch. Environ. Res. Risk Assess. 2021, 35, 1273–1291. [Google Scholar] [CrossRef]
- Hecht-Nielsen; Robert. Theory of the backpropagation neural network. Neural Netw. 1988, 1, 445. [Google Scholar] [CrossRef]
- Zeng, J.; Tan, Z.H.; Matsunaga, T.; Shirai, T. Generalization of Parameter Selection of SVM and LS-SVM for Regression. Mach. Learn. Knowl. Extr. 2019, 1, 745–755. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Intrieri, E.; Ahmed, B.; Catani, F. Displacement prediction of step-like landslide by applying a novel kernel extreme learning machine method. Landslides 2018, 15, 2211–2225. [Google Scholar] [CrossRef]
- Deng, W.; Yao, R.; Zhao, H.; Yang, X.; Li, G. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 2019, 23, 2445–2462. [Google Scholar] [CrossRef]
- Miao, F.; Wu, Y.; Xie, Y.; Li, Y. Prediction of landslide displacement with step-like behavior based on multialgorithm optimization and a support vector regression model. Landslides 2018, 15, 475–488. [Google Scholar] [CrossRef]
- Cai, Z.; Xu, W.; Meng, Y.; Shi, C.; Wang, R. Prediction of landslide displacement based on GA-LSSVM with multiple factors. Bull. Eng. Geol. Environ. 2016, 75, 637–646. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Y.; Huo, Z.; Peng, X.; Araiba, K.; Wang, G. Movement of the Shuping landslide in the first four years after the initial impoundment of the Three Gorges Dam Reservoir, China. Landslides 2008, 5, 321–329. [Google Scholar] [CrossRef]
- Wu, Q.; Tang, H.; Ma, X.; Wu, Y.; Hu, X.; Wang, L.; Criss, R.; Yuan, Y.; Xu, Y. Identification of movement characteristics and causal factors of the Shuping landslide based on monitored displacements. Bull. Eng. Geol. Environ. 2019, 78, 2093–2106. [Google Scholar] [CrossRef]
- Wen, T.; Tang, H.; Huang, L.; Wang, Y.; Ma, J. Energy evolution: A new perspective on the failure mechanism of purplish-red mudstones from the Three Gorges Reservoir area, China. Eng. Geol. 2020, 264, 105350. [Google Scholar] [CrossRef]
- Huang, D.; Gu, D.M.; Song, Y.X.; Cen, D.F.; Zeng, B. Towards a complete understanding of the triggering mechanism of a large reactivated landslide in the Three Gorges Reservoir. Eng. Geol. 2018, 238, 36–51. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, Y.; Tang, H.; Fang, K.; Jiang, Y.; Liu, C.; Wang, L.; Wang, X.; Kang, J. Investigation on the shear properties of discontinuities at the interface between different rock types in the Badong formation, China. Eng. Geol. 2018, 245, 280–291. [Google Scholar] [CrossRef]




| Correlation ( ) | ZG85 | ZG86 | ZG87 |
|---|---|---|---|
| Period displacement over previous month | 0.855 | 0.842 | 0.822 |
| Period displacement over two previous months | 0.871 | 0.863 | 0.836 |
| Period displacement over three previous months | 0.844 | 0.882 | 0.849 |
| Period displacement over previous half year | 0.921 | 0.931 | 0.890 |
| Period displacement over previous year | 0.788 | 0.804 | 0.899 |
| Correlation ( ) | ZG85 | ZG86 | ZG87 |
|---|---|---|---|
| Rainfall over previous month | 0.849 | 0.843 | 0.862 |
| Rainfall over previous two months | 0.845 | 0.861 | 0.866 |
| RWL | 0.851 | 0.818 | 0.808 |
| Change in RWL over previous month | 0.837 | 0.852 | 0.844 |
| Model | BP | PSO-SVM | PSO-LSSVM | |
|---|---|---|---|---|
| R2 | ZG85 | 0.7157 | 0.7955 | 0.9095 |
| ZG86 | 0.8631 | 0.8079 | 0.9091 | |
| ZG87 | 0.8047 | 0.4813 | 0.7727 | |
| MAE | ZG85 | 45.3365 | 45.8643 | 26.9320 |
| ZG86 | 33.1825 | 58.2599 | 30.7913 | |
| ZG87 | 6.4461 | 9.6564 | 5.5371 | |
| RMSE | ZG85 | 55.3498 | 54.5718 | 31.9132 |
| ZG86 | 49.8766 | 83.9435 | 41.6055 | |
| ZG87 | 8.4063 | 13.1436 | 7.2638 | |
| Model | BP | PSO-SVM | PSO-LSSVM | |
|---|---|---|---|---|
| R2 | ZG85 | 0.9607 | 0.9718 | 0.9810 |
| ZG86 | 0.9753 | 0.9680 | 0.9823 | |
| ZG87 | 0.9875 | 0.9834 | 0.9932 | |
| MAE | ZG85 | 47.5004 | 45.4348 | 34.6488 |
| ZG86 | 49.5306 | 69.0451 | 44.5890 | |
| ZG87 | 7.2304 | 9.7076 | 5.7296 | |
| RMSE | ZG85 | 57.8430 | 54.1392 | 42.4378 |
| ZG86 | 64.1690 | 86.0639 | 55.4179 | |
| ZG87 | 9.2874 | 13.6112 | 7.3380 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, W.; Wen, T.; Li, D.; Guo, W.; Quan, Z.; Wang, Y.; Huang, D.; Hu, M. Landslide Displacement Prediction of Shuping Landslide Combining PSO and LSSVM Model. Water 2023, 15, 612. https://doi.org/10.3390/w15040612
Jia W, Wen T, Li D, Guo W, Quan Z, Wang Y, Huang D, Hu M. Landslide Displacement Prediction of Shuping Landslide Combining PSO and LSSVM Model. Water. 2023; 15(4):612. https://doi.org/10.3390/w15040612
Chicago/Turabian StyleJia, Wenjun, Tao Wen, Decheng Li, Wei Guo, Zhi Quan, Yihui Wang, Dexin Huang, and Mingyi Hu. 2023. "Landslide Displacement Prediction of Shuping Landslide Combining PSO and LSSVM Model" Water 15, no. 4: 612. https://doi.org/10.3390/w15040612






