Analysis of the Effects of Reservoir Operating Scenarios on Downstream Flood Damage Risk Using an Integrated Monte Carlo Modelling Approach
Abstract
1. Introduction
2. Materials and Methods
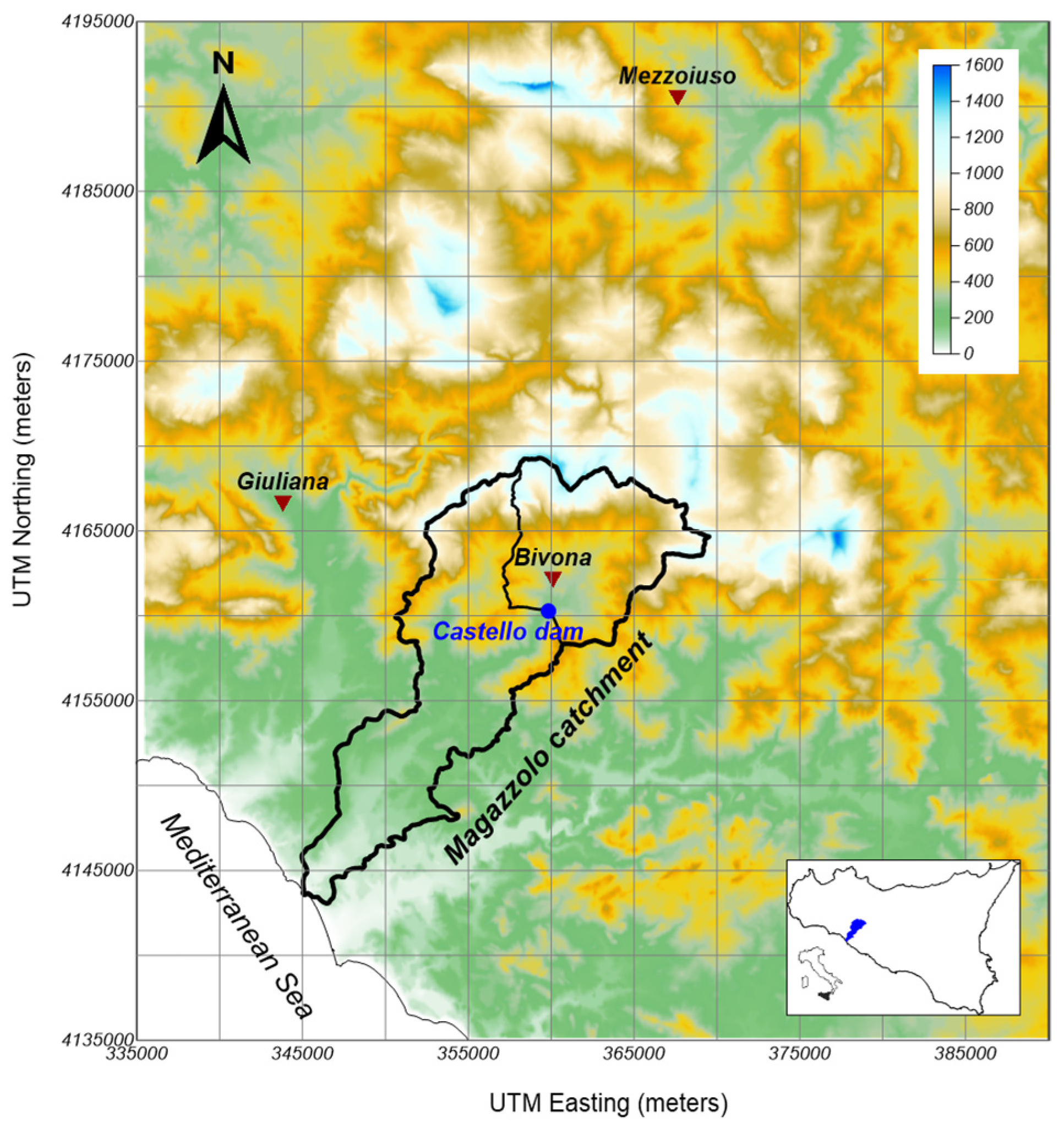
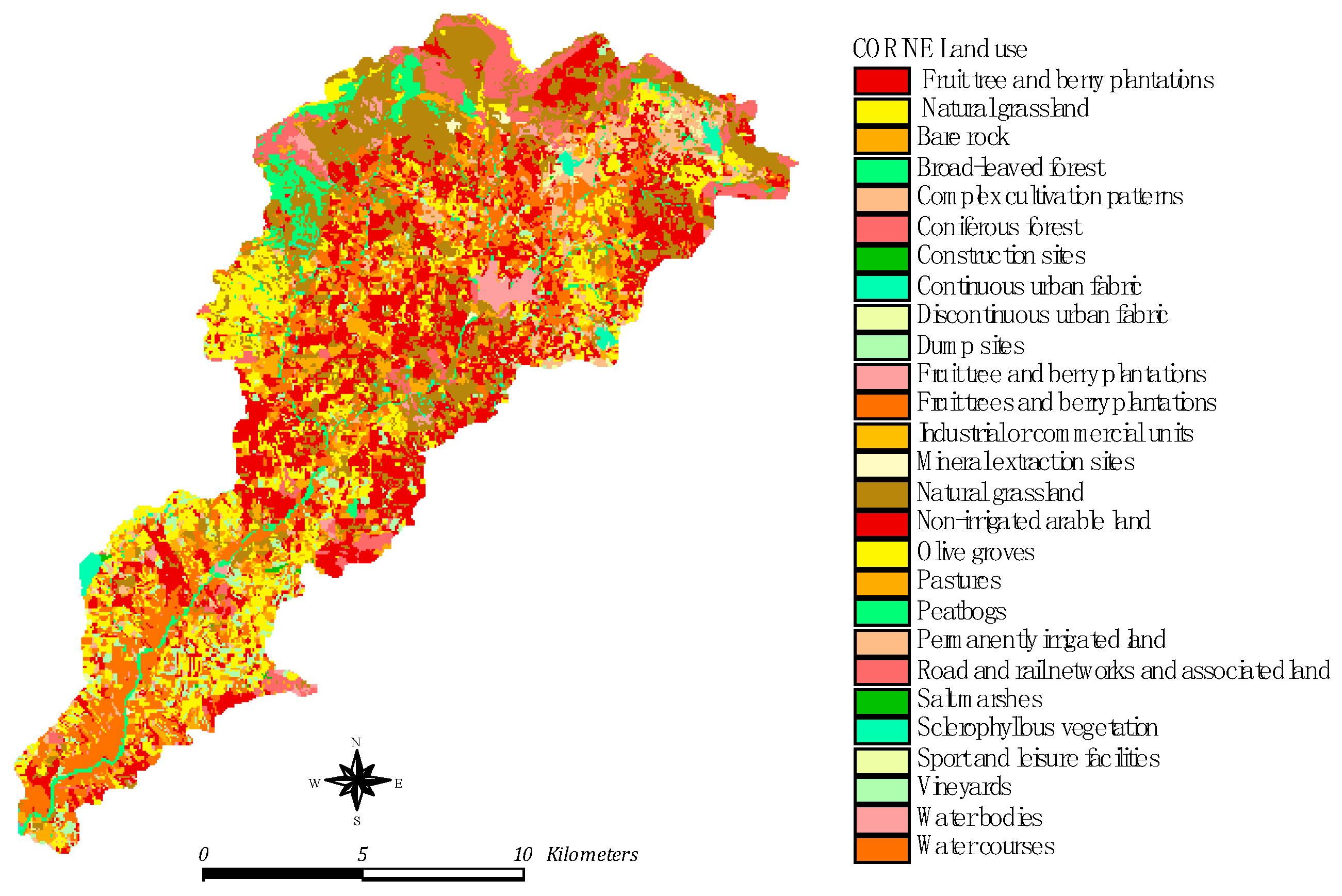
2.1. Case Study and Data
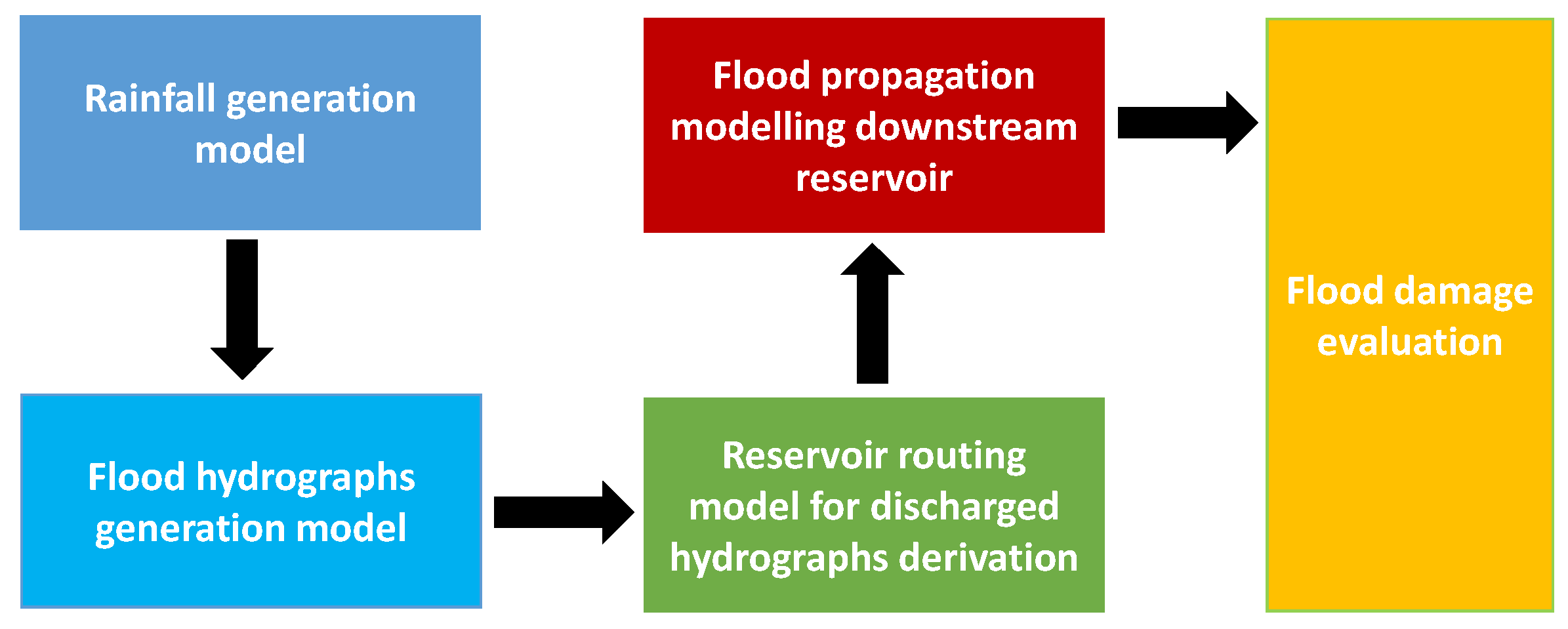
2.2. The methodology
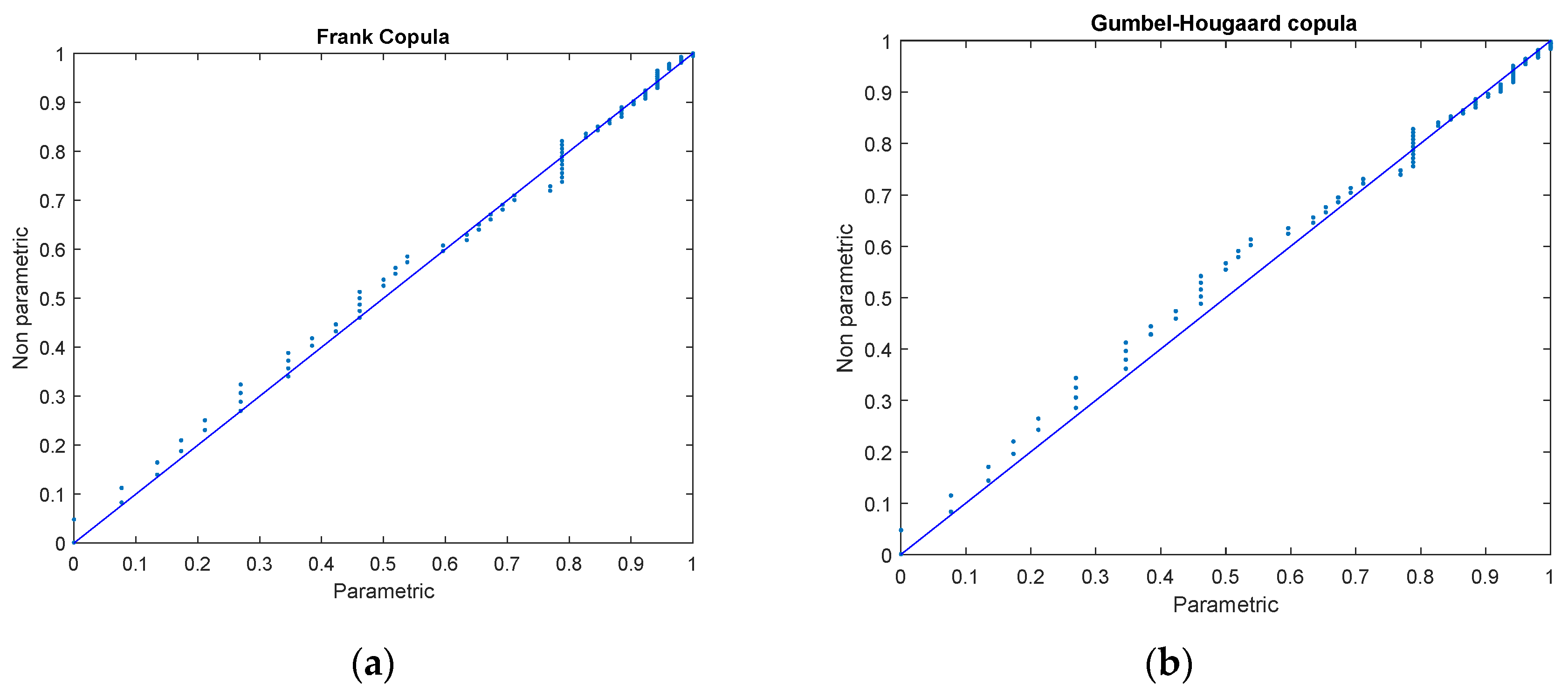
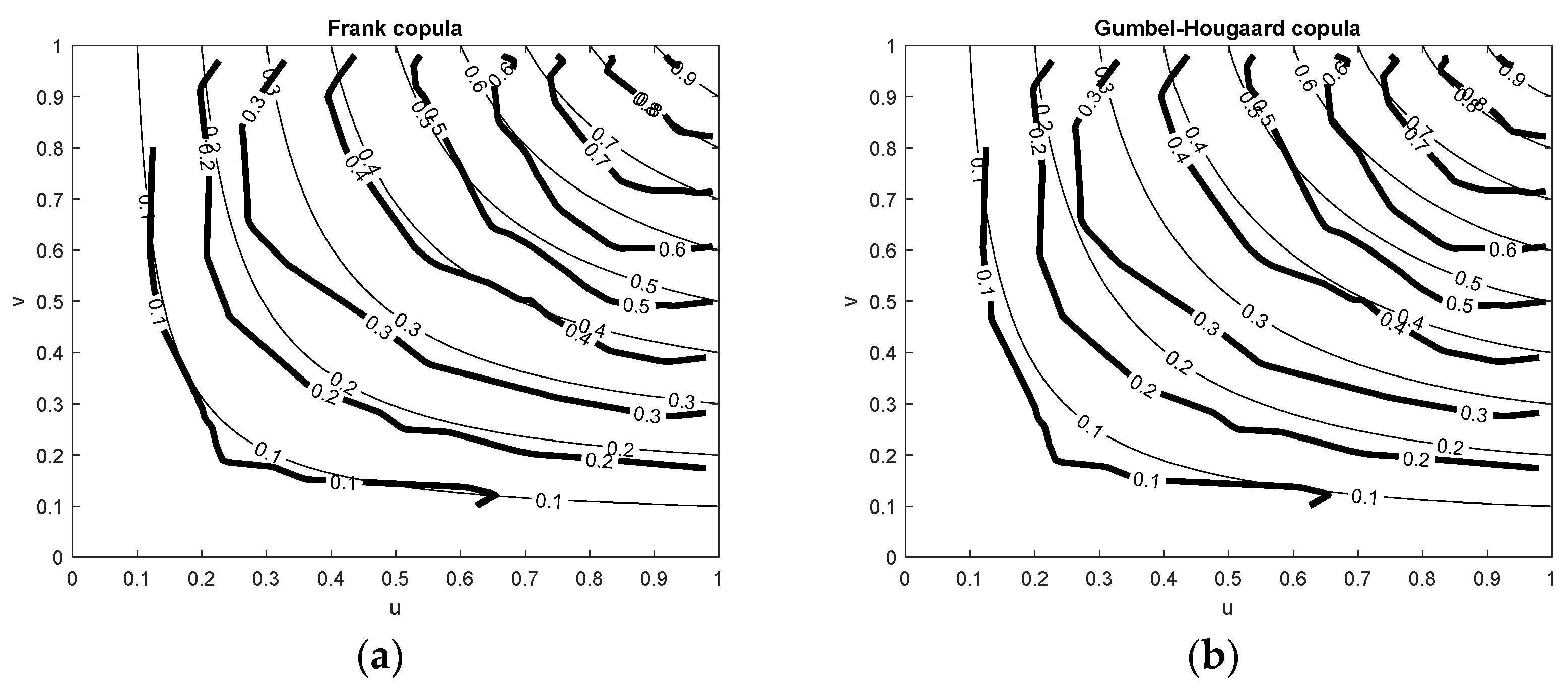
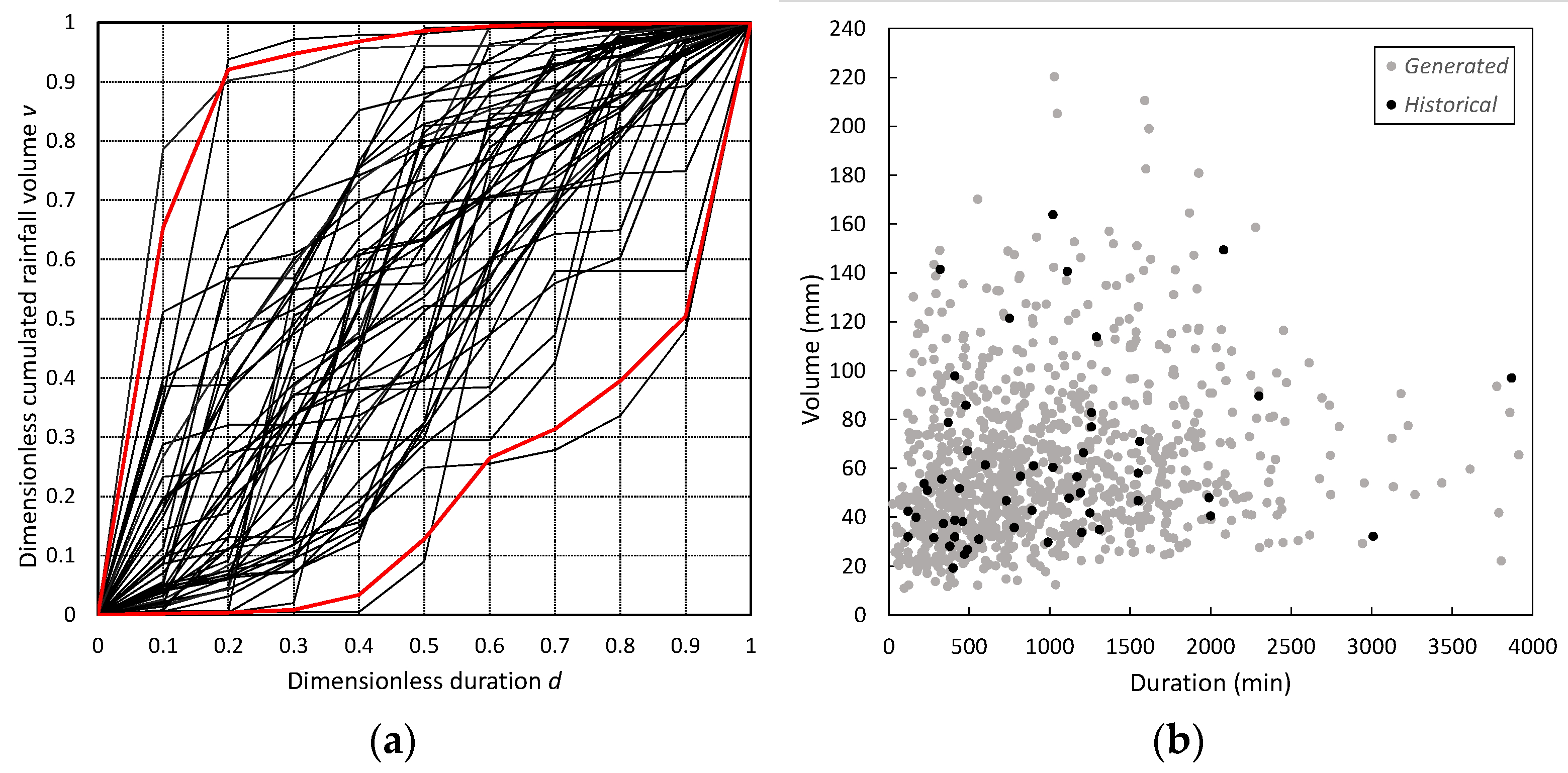
2.2.1. Rainfall Generation Model
2.2.2. Flood Hydrographs Generation Model
2.2.3. Reservoir Routing Model for Discharged Hydrographs Derivation
2.2.4. Flood Propagation Modelling Downstream Reservoir
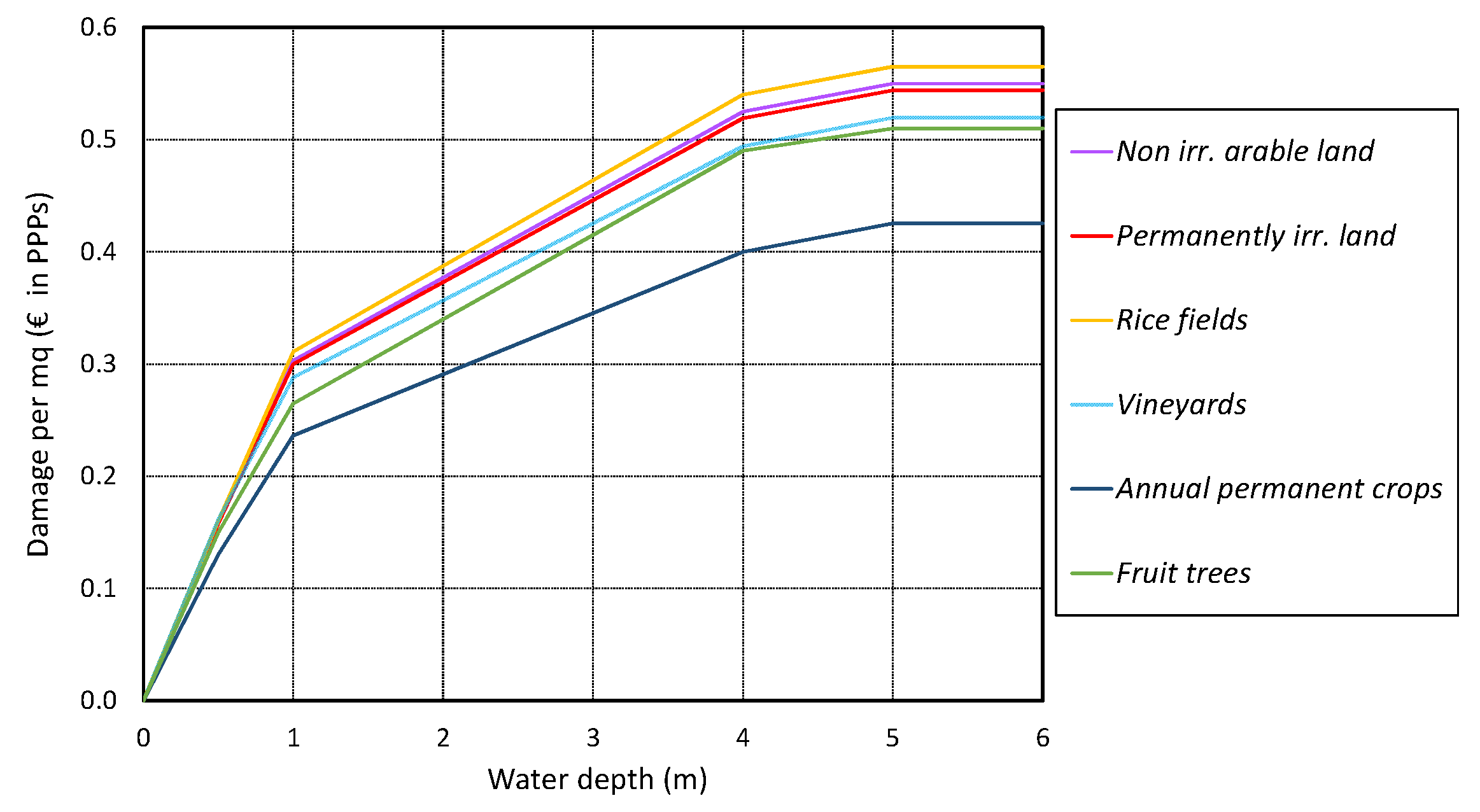
2.2.5. Flood Damage Evaluation
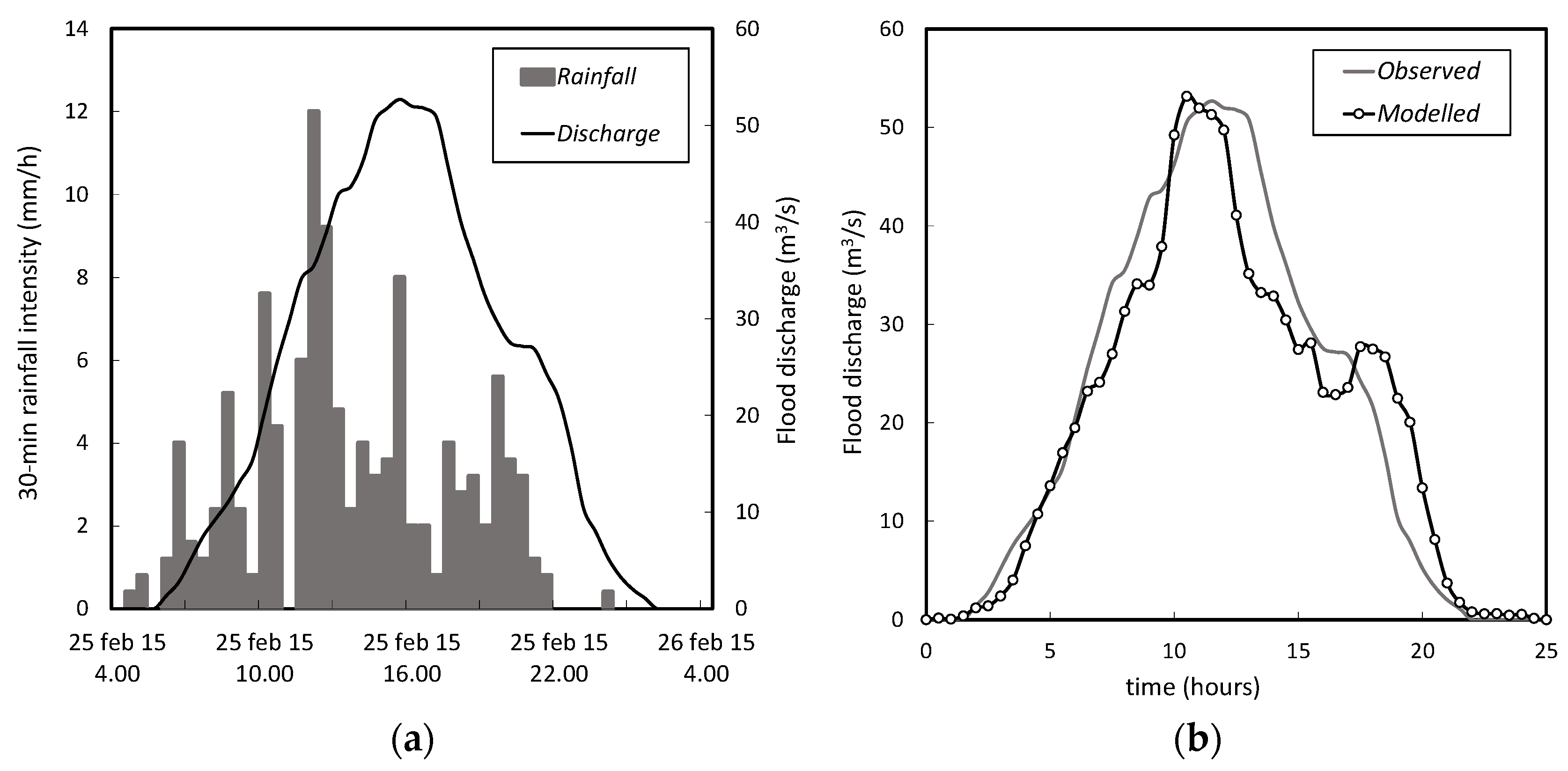
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, S.; Zhang, H.; Chen, H.; Peng, D.; Liu, P.; Pang, B. A reservoir flood forecasting and control system for China / Un système chinois de prévision et de contrôle de crue en barrage. Hydrol. Sci. J. 2004, 49, 959–972. [Google Scholar] [CrossRef]
- Bruwier, M.; Erpicum, S.; Pirotton, M.; Archambeau, P.; Dewals, B.J. Assessing the operation rules of a reservoir system based on a detailed modelling chain. Nat. Hazards Earth Syst. Sci. 2015, 15, 365–379. [Google Scholar] [CrossRef]
- Iveti´c, D.; Milašinovi´c, M.; Stojkovi´c, M.; Šoti´c, A.; Charbonnier, N.; Milivojevi´c, N. Framework for Dynamic Modelling of the Dam and Reservoir System Reduced Functionality in Adverse Operating Conditions. Water 2022, 14, 1549. [Google Scholar] [CrossRef]
- Tedla, M.G.; Cho, Y.; Jun, K. Flood Mapping from Dam Break Due to Peak Inflow: A Coupled Rainfall–Runoff and Hydraulic Models Approach. Hydrology 2021, 8, 89. [Google Scholar] [CrossRef]
- Dobson, B.; Wagener, T.; Pianosi, F. An argument-driven classification and comparison of reservoir operation optimization methods. Adv. Water Resour. 2019, 128, 74–86. [Google Scholar] [CrossRef]
- Gabriel-Martin, I.; Sordo-Ward, A.; Garrote, L.; Granados, I. Hydrological Risk Analysis of Dams: The Influence of Initial Reservoir Level Conditions. Water 2019, 11, 461. [Google Scholar] [CrossRef]
- Luino, F.; Tosatti, G.; Bonaria, V. Dam Failures in the 20th Century: Nearly 1000 Avoidable Victims in Italy Alone. J. Environ. Sci. Eng. 2014, 3, 19–31. Available online: http://www.cnr.it/prodotto/i/285435 (accessed on 15 November 2022).
- Bocchiola, B.; Rosso, R. Safety of Italian dams in the face of flood hazard. Adv. Water Resour. 2014, 71, 23–31. [Google Scholar] [CrossRef]
- Direttiva del Presidente del Consiglio dei Ministri 8 luglio 2014. Indirizzi Operativi Inerenti All’attività di Protezione Civile Nell’ambito dei Bacini in cui Siano Presenti Grandi Dighe. Available online: https://www.dighe.eu/normativa/allegati/2014_Direttiva_PCM_8-07.pdf (accessed on 8 July 2014). (In Italian).
- Koutsoyiannis, D.; Economou, A. Evaluation of the parameterization-simulation-optimization approach for the control of reservoir systems. Water Resour. Res. 2003, 39, 1170–1434. [Google Scholar] [CrossRef]
- Huang, L.; Xiang, L.; Fang, H.; Yin, D.; Si, Y.; Wei, J.; Liu, J.; Hu, X.; Zhang, L. Balancing social, economic and ecological benefits of reservoir operation during the flood season: A case study of the Three Gorges Project, China. J. Hydrol. 2019, 572, 422–434. [Google Scholar] [CrossRef]
- Giuliani, M.; Lamontagne, J.R.; Reed, P.M.; Castelletti, A. A State-of-the-Art Review of Optimal Reservoir Control for Managing Conflicting Demands in a Changing World. Water Resour. Res. 2021, 57, e2021WR029927. [Google Scholar] [CrossRef]
- Papathanasiou, C.; Serbis, D.; Mamassis, N. Flood mitigation at the downstream areas of a transboundary river. Water Utility J. 2013, 3, 33–42. [Google Scholar]
- Hardesty, S.; Shen, X.; Nikolopoulos, E.; Anagnostou, E. A Numerical Framework for Evaluating Flood Inundation Hazard under Different Dam Operation Scenarios—A Case Study in Naugatuck River. Water 2018, 10, 1798. [Google Scholar] [CrossRef]
- Zhou, T.; Jin, J. Comparative analysis of routed flood frequency for reservoirs in parallel incorporating bivariate flood frequency and reservoir operation. J. Flood Risk. Manag. 2021, 14, e12705. [Google Scholar] [CrossRef]
- Shen, G.; Lu, Y.; Zhang, S.; Xiang, Y.; Sheng, J.; Fu, J.; Fu, S.; Liu, M. Risk dynamics modeling of reservoir dam break for safety control in the emergency response process. Water Supply 2021, 21, 1356–1371. [Google Scholar] [CrossRef]
- Acreman, M.C. A simple stochastic model of hourly rainfall for Farnborough, England. Hydrol. Sci. J. 1990, 35, 119–148. [Google Scholar] [CrossRef]
- Cameron, D.; Beven, K.; Tawn, J. An evaluation of three stochastic rainfall models. J. Hydrol. 2000, 228, 130–149. [Google Scholar] [CrossRef]
- Vandenberghe, S.; Verhoest, N.E.C.; Buyse, E.; De Baets, B. A stochastic design rainfall generator based on copulas and mass curves. Hydrol. Earth Syst. Sci. 2010, 14, 2429–2442. [Google Scholar] [CrossRef]
- Volpi, E.; Fiori, A. Design event selection in bivariate hydrological frequency analysis. Hydrol. Sci. J. 2012, 57, 1506–1515. [Google Scholar] [CrossRef]
- Brigandì, G.; Aronica, G.T. Generation of Sub-Hourly Rainfall Events through a Point Stochastic Rainfall Model. Geosciences 2019, 9, 226. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C.; Kottegoda, N.T.; Rosso, R. Extremes in Nature. An Approach Using Copulas; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Genest, C.; Favre, A.C. Everything you always wanted to know about copula modeling but were afraid to ask. J. Hydrol. Eng. ASCE 2007, 12, 347–368. [Google Scholar] [CrossRef]
- Requena, A.I.; Mediero, L.; Garrote, L. A bivariate return period based on copulas for hydrologic dam design: Accounting for reservoir routing in risk estimation. Hydrol. Earth Syst. Sci. 2013, 17, 3023–3038. [Google Scholar] [CrossRef]
- Balistrocchi, M.; Orlandini, S.; Ranzi, R.; Bacchi, B. Copula-based modeling of flood control reservoirs. Water Resour. Res. 2017, 53, 9883–9900. [Google Scholar] [CrossRef]
- Rizwan, M.; Guo, S.; Yin, J.; Xiong, F. Deriving Design Flood Hydrographs Based on Copula Function: A Case Study in Pakistan. Water 2019, 11, 1531. [Google Scholar] [CrossRef]
- Tan, Q.; Mao, Y.; Wen, X.; Jin, T.; Ding, Z.; Wang, Z. Copula-based modeling of hydraulic structures using a nonlinear reservoir model. Hydrol. Res. 2021, 52, 1577. [Google Scholar] [CrossRef]
- Klein, B.; Schumann, A.H.; Pahlow, M. Copulas—New Risk Assessment Methodology for Dam Safety. In Flood Risk Assessment and Management; Schumann, A.H., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 149–185. [Google Scholar] [CrossRef]
- Huizinga, J.; De Moel, H.; Szewczyk, W. Global Flood Depth-damage Functions. JRC Technical Report. Available online: https://publications.jrc.ec.europa.eu›JRC105688 (accessed on 30 May 2022).
- Candela, A.; Brigandì, G.; Aronica, G.T. Estimation of synthetic flood design hydrographs using a distributed rainfall-runoff model coupled with a copula-based single storm rainfall generator. Nat. Hazards Earth Syst. Sci. 2014, 14, 1819–1833. [Google Scholar] [CrossRef]
- Kao, S.-C.; Govindaraju, R.S. Probabilistic structure of storm surface runoff considering the dependence between average intensity and storm duration of rainfall events. Water Resour. Res. 2007, 43, W06410. [Google Scholar] [CrossRef]
- Genest, C.; Rivest, L. Statistical inference procedures for bivariate Archimedean copulas. J. Amer. Statist. Assoc. 1993, 88, 1034–1043. [Google Scholar] [CrossRef]
- Maidment, D.R. Handbook of Hydrology; McGraw-Hill International: New York, NY, USA, 1992. [Google Scholar]
- Kottegoda, N.T.; Rosso, R. Applied Statistics for Civil and Environmental Engineers; Blackwell Publishing Ltd.: Oxford, UK, 2008. [Google Scholar]
- Huff, F. Time Distribution Rainfall in Heavy Storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Wooding, R.A. A hydraulic model for the catchment stream problem: 1.-Kinetic wave theory. J. Hydrol. 1965, 3, 254–267. [Google Scholar] [CrossRef]
- US Department of Agriculture. Soil Conservation Service, National Engineering Handbook, Hydrology: Sec.4; US Department of Agriculture: Washington, DC, USA, 1986. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Yevjevich, V.M. Analytical integration of the differential equation for water storages. J. Res. Nat. Bureau Stand.-B. Math. Math. Phys. 1959, 63, 43–52. Available online: https://nvlpubs.nist.gov/nistpubs/jres/63B/jresv63Bn1p43_A1b.pdf (accessed on 30 May 2022). [CrossRef]
- Aronica, G.T.; Tucciarelli, T.; Nasello, C. 2D Multilevel Model for Flood Wave Propagation in Flood-Affected Areas. J. Water Resour. Plan. Manag.-ASCE 1998, 124, 210. [Google Scholar] [CrossRef]
- Aronica, G.T.; Candela, A. Derivation of flood frequency curves in poorly gauged catchments using a simple stochastic hydrological rainfall-runoff model. J. Hydrol. 2007, 347, 132–142. [Google Scholar] [CrossRef]
- Candela, A.; Aronica, G.T. Probabilistic Flood Hazard Mapping Using Bivariate Analysis Based on Copulas. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, A4016002-A1. [Google Scholar] [CrossRef]
- Rusmini, M. Pan-European Flood Hazard and Damage Assessment; Evaluation of a New If-SAR Digital Terrain Model for Flood Depth and Flood Extent Calculation. Available online: https://webapps.itc.utwente.nl/librarywww/papers_2009/msc/aes/rusmini.pdf (accessed on 30 May 2022).
- INEA. Il Valore della Terra. Available online: https://rica.crea.gov.it/download.php?id=938 (accessed on 30 May 2022).
- Bonaccorso, B.; Aronica, G.T. Estimating Temporal Changes in Extreme Rainfall in Sicily Region (Italy). Water Resour. Manag. 2016, 30, 5651–5670. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Brigandì, G.; Aronica, G.T. Regional sub-hourly extreme rainfall estimates in Sicily under a scale invariance framework. Water Resour. Manag. 2020, 34, 4363–4380. [Google Scholar] [CrossRef]
- Doherty, J. PEST: Model Independent Parameter Estimation; Watermark Numerical Computing: Brisbane, Australia, 2010. Available online: https://www.epa.gov/sites/default/files/documents/PESTMAN.PDF (accessed on 30 May 2022).
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An algorithm for least-squares estimation of non-linear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Ponce, V.; Hawkins, R. Runoff Curve Number: Has It Reached Maturity? J. Hydrol. Eng. 1996, 1, 11–19. [Google Scholar] [CrossRef]


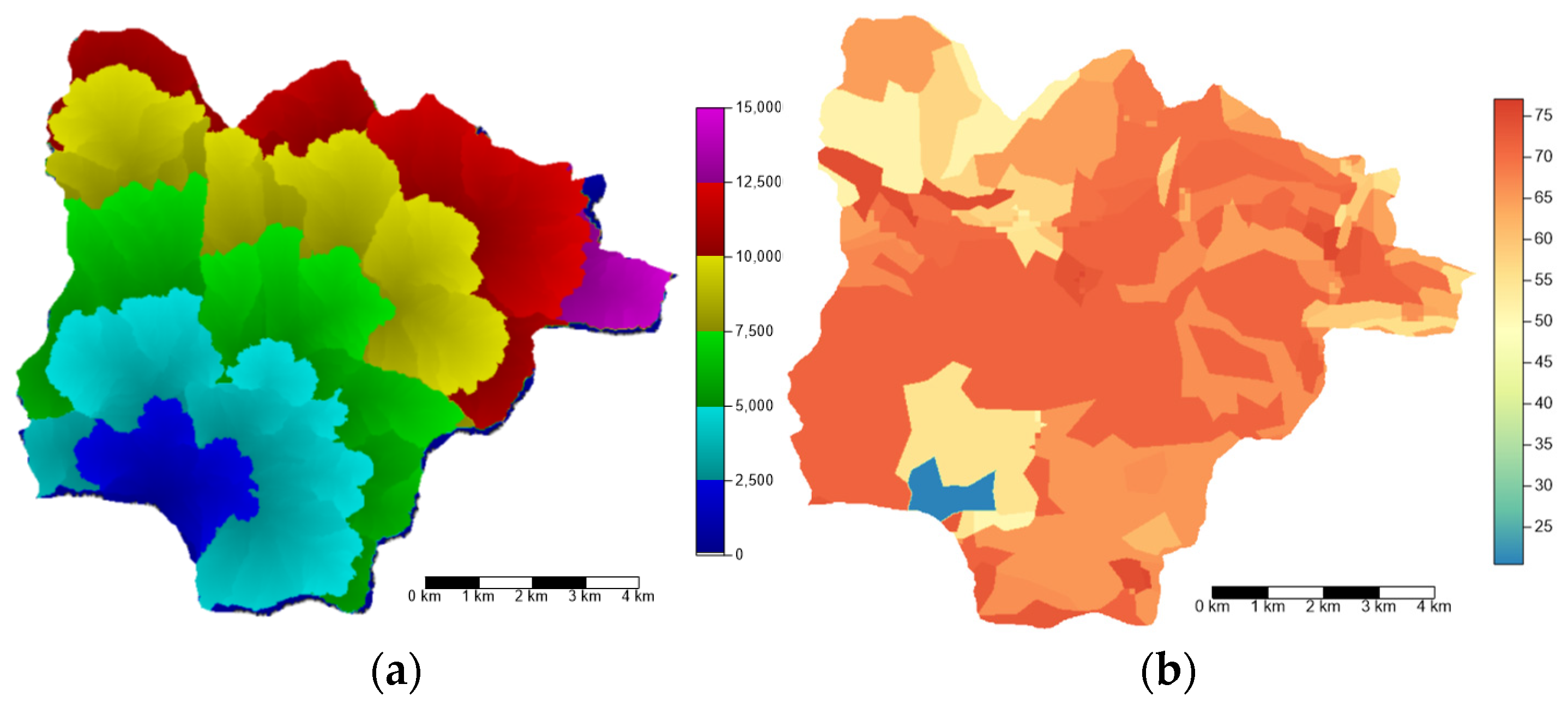
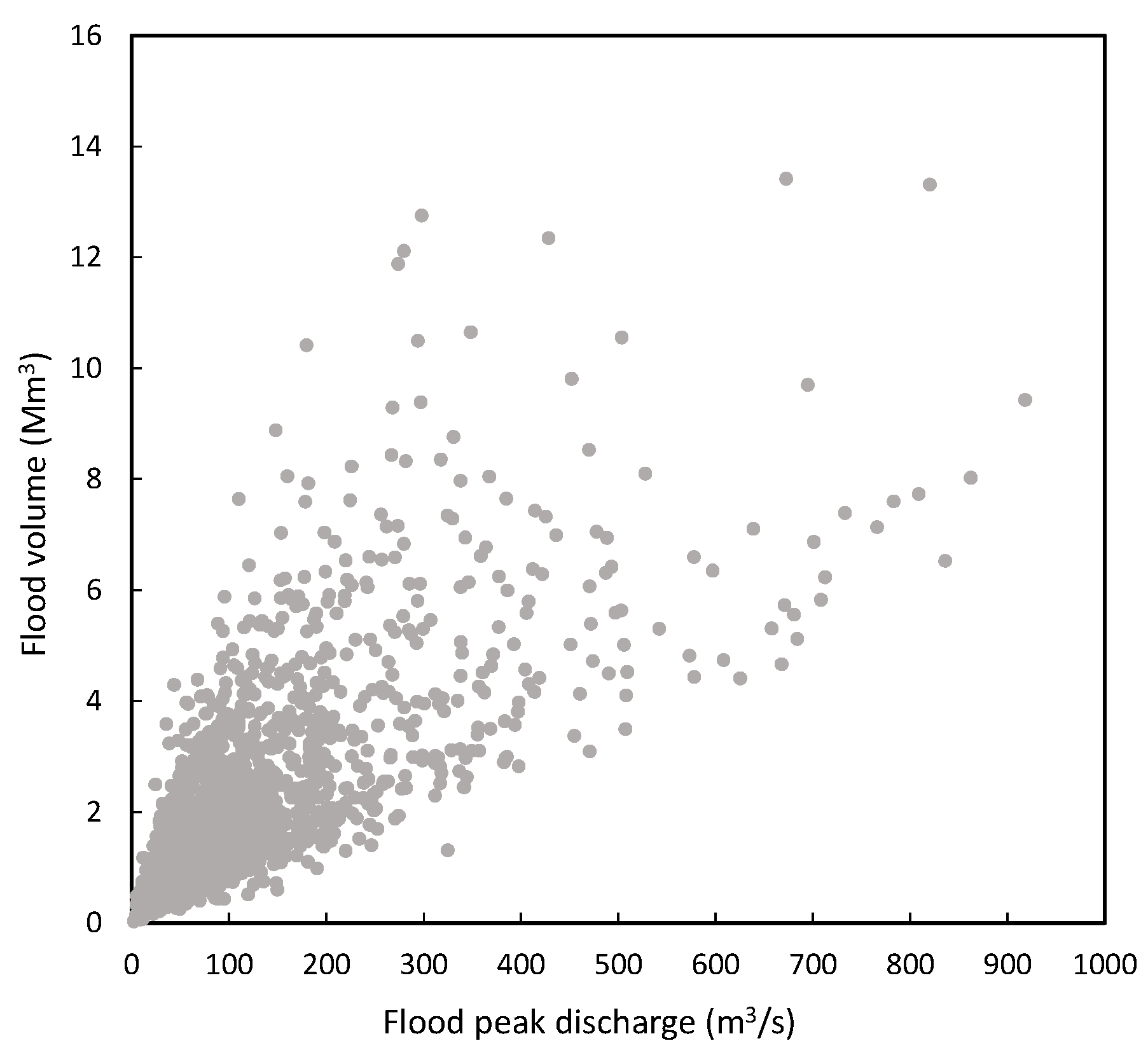
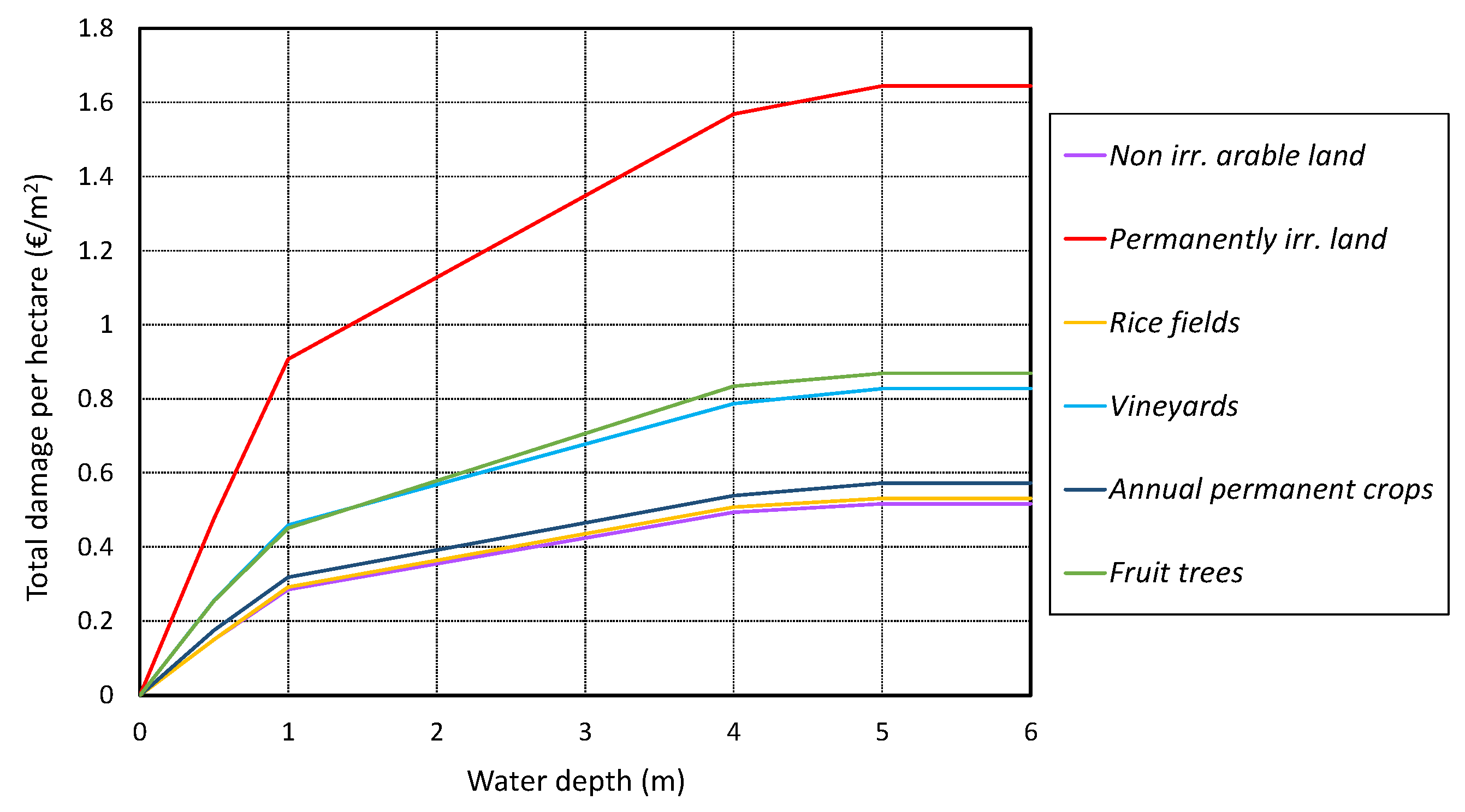


| Main Agricultural Surface | Average Values per M2 (Euros) |
|---|---|
| Non irrigable arable land | 0.9403 |
| Fruit trees | 1.9614 |
| Permanently irrigated land | 3.0224 |
| Vineyards | 1.5923 |
| Annual and permanent crops | 1.3474 |
| Duration (min) | Volume (mm) | Iavg (mm/h) | Imax,30′ (mm/h) | |
|---|---|---|---|---|
| Length of record (years) | 17 (2003–2020) | |||
| Number of events | 52 | |||
| Max | 3870 | 163.8 | 26.51 | 84.80 |
| Min | 120 | 19.2 | 0.64 | 9.20 |
| Mean | 955.58 | 60.84 | 6.12 | 37.76 |
| Standard deviation | 743.96 | 34.35 | 5.38 | 20.01 |
| Copula | θ |
|---|---|
| Gumbel–Hougard | 1.2427 |
| Frank | 2.1407 |
| Return Time | Qmax/Vtot | IWL1 (293.65 m) | IWL2 (290.00 m) |
|---|---|---|---|
| 50 years | 653.0 m3/s | € 735,738 | € 354,563 |
| 7.92 Mm3 | |||
| 100 years | 824.0 m3/s | € 811,862 | € 560,765 |
| 8.99 Mm3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brigandì, G.; Candela, A.; Aronica, G.T. Analysis of the Effects of Reservoir Operating Scenarios on Downstream Flood Damage Risk Using an Integrated Monte Carlo Modelling Approach. Water 2023, 15, 550. https://doi.org/10.3390/w15030550
Brigandì G, Candela A, Aronica GT. Analysis of the Effects of Reservoir Operating Scenarios on Downstream Flood Damage Risk Using an Integrated Monte Carlo Modelling Approach. Water. 2023; 15(3):550. https://doi.org/10.3390/w15030550
Chicago/Turabian StyleBrigandì, Giuseppina, Angela Candela, and Giuseppe Tito Aronica. 2023. "Analysis of the Effects of Reservoir Operating Scenarios on Downstream Flood Damage Risk Using an Integrated Monte Carlo Modelling Approach" Water 15, no. 3: 550. https://doi.org/10.3390/w15030550
APA StyleBrigandì, G., Candela, A., & Aronica, G. T. (2023). Analysis of the Effects of Reservoir Operating Scenarios on Downstream Flood Damage Risk Using an Integrated Monte Carlo Modelling Approach. Water, 15(3), 550. https://doi.org/10.3390/w15030550







