Research on the Influence of Siltation Height of Check Dams the on Discharge Coefficient of Broad-Crested Weirs
Abstract
1. Introduction
2. Experimental Design
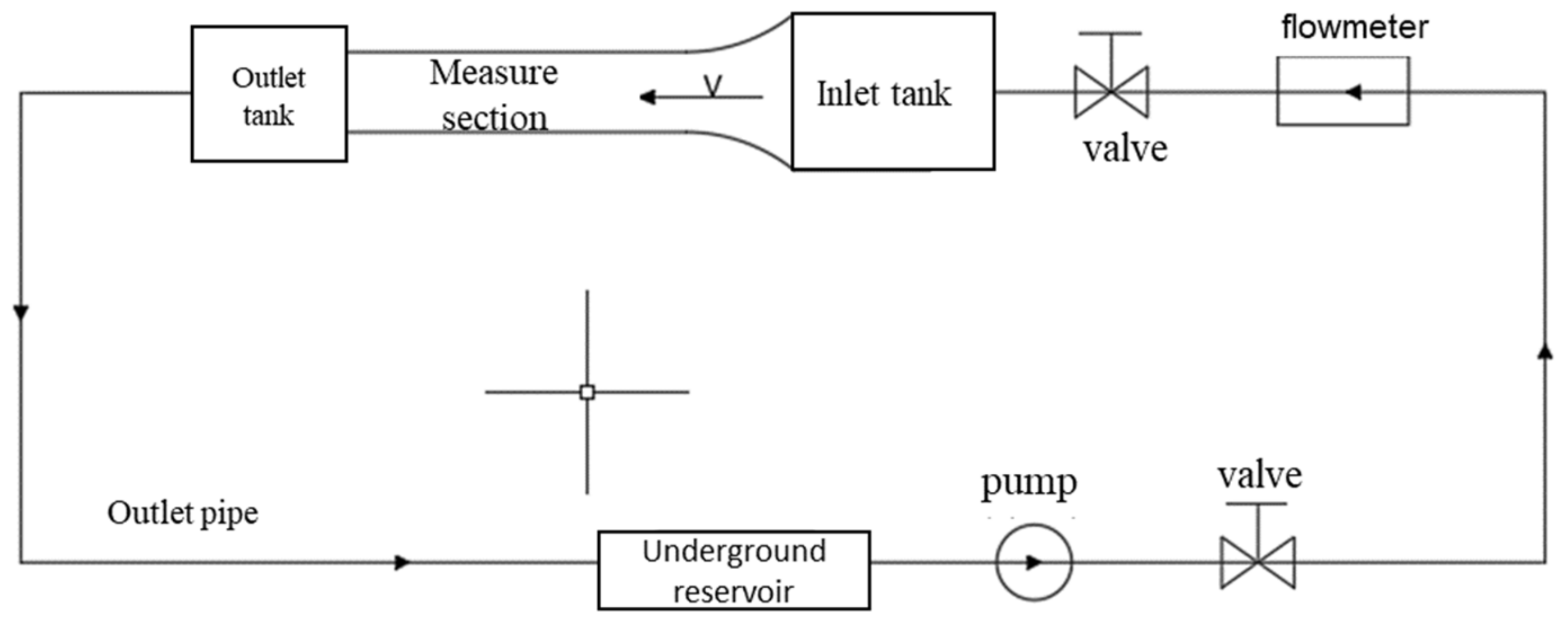
2.1. Experimental System
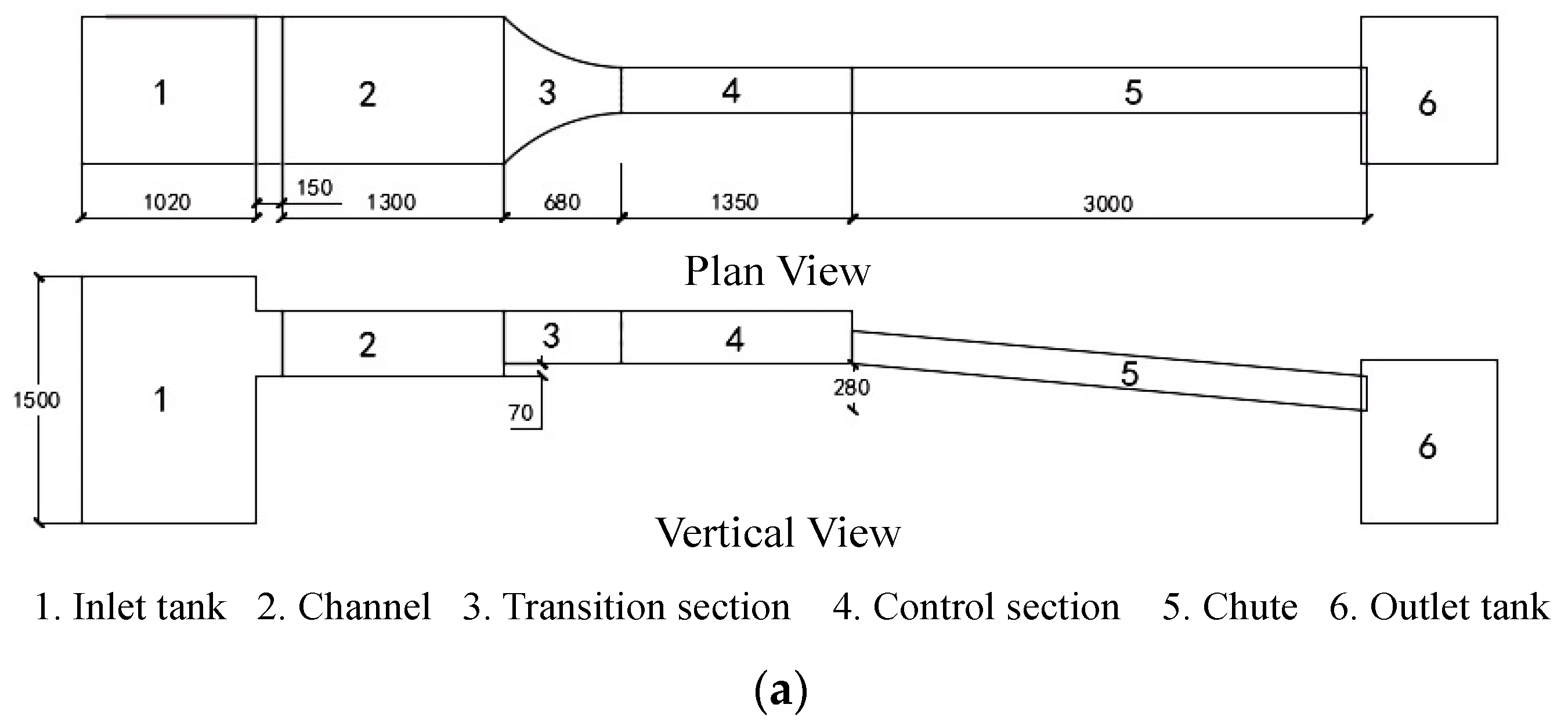
2.2. Physical Model
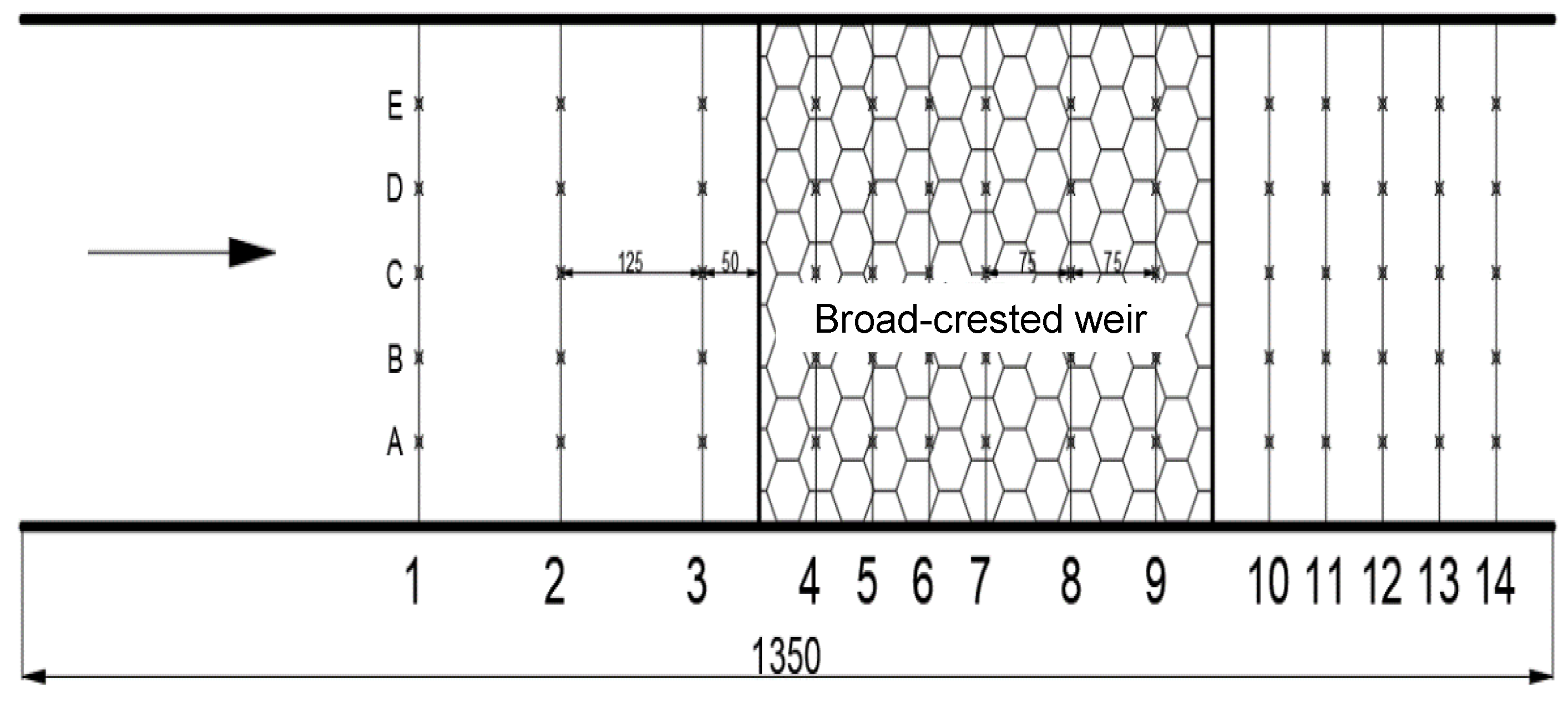
2.3. Measurement Scheme
2.4. Experimental Case
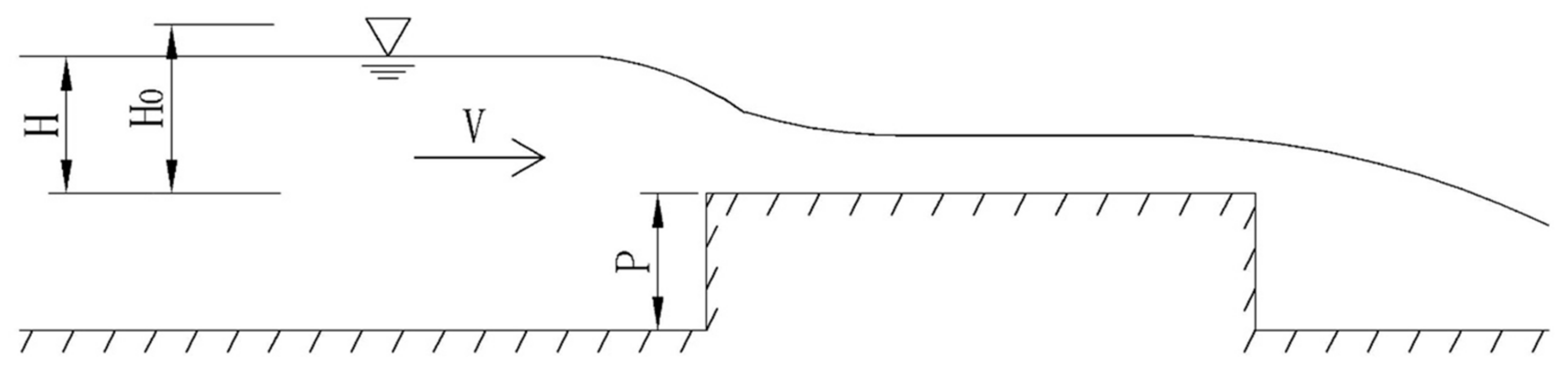
2.5. Test Principle
- (1)
- Average velocity of sectionwhere Q is the discharge, v is the average velocity of the discharge section, and A is the discharge section area.
- (2)
- Total hydraulic head over the weirwhere H0 is the total head over the weir; H is the hydraulic head, that is, the height of the upstream water surface above the weir crest; V0 is the average velocity of the discharge section.
- (3)
- Discharge calculation formula of the weirwhere Q is the discharge; is the submergence coefficient; is the coefficient of lateral shrinkage; m is discharge coefficient; b is width of the weir; H0 is the total head over the weir.
3. Results
3.1. Flow Pattern
3.2. Variation in Water Surface Profile along the Weir
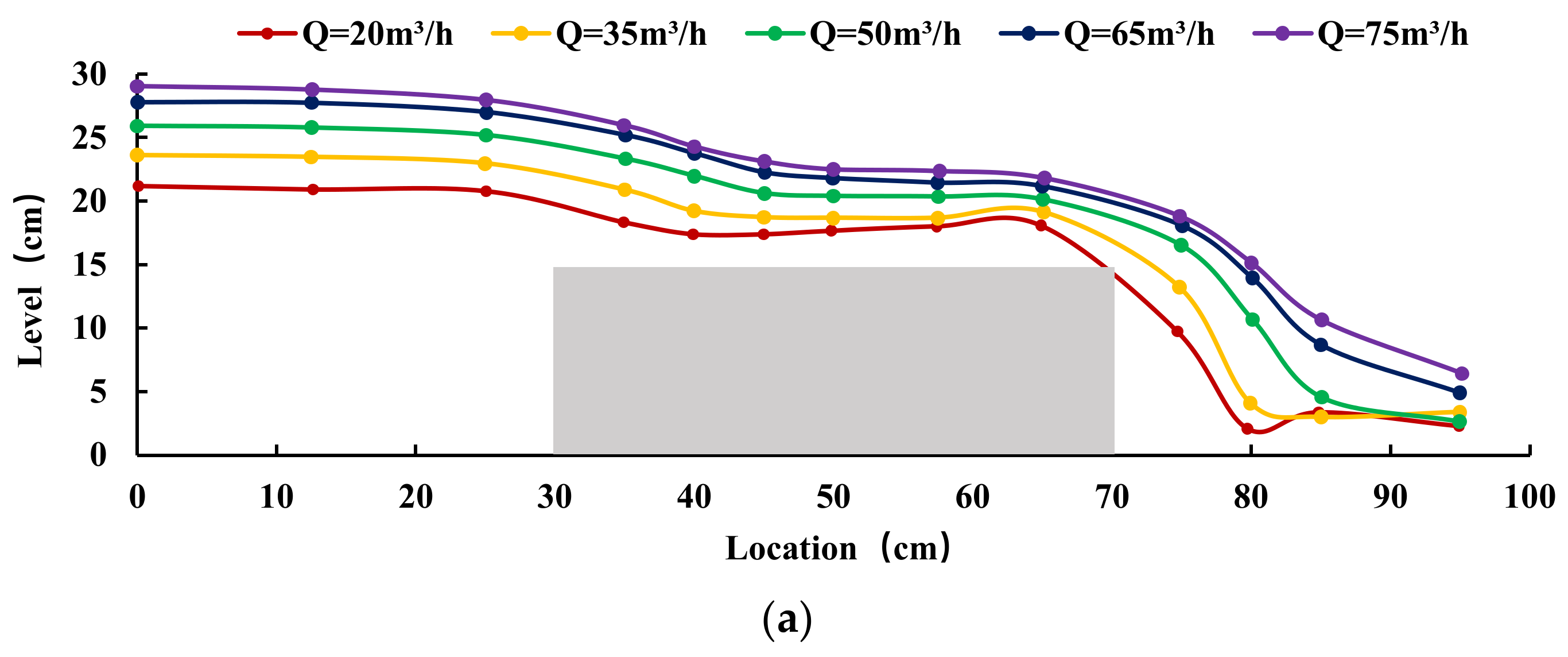
3.2.1. Influence of Discharge on the Level of Flow at the Same Siltation Height
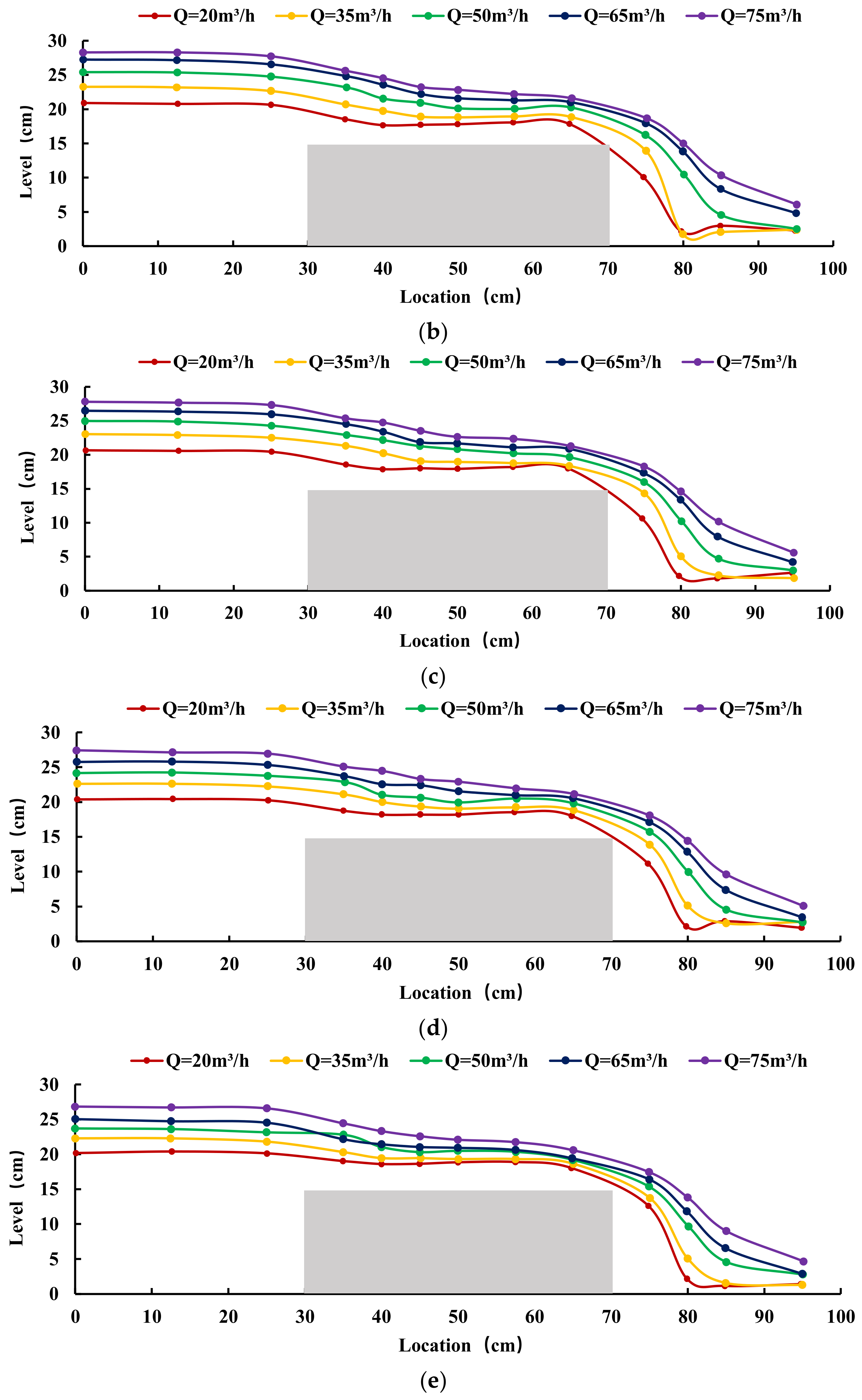
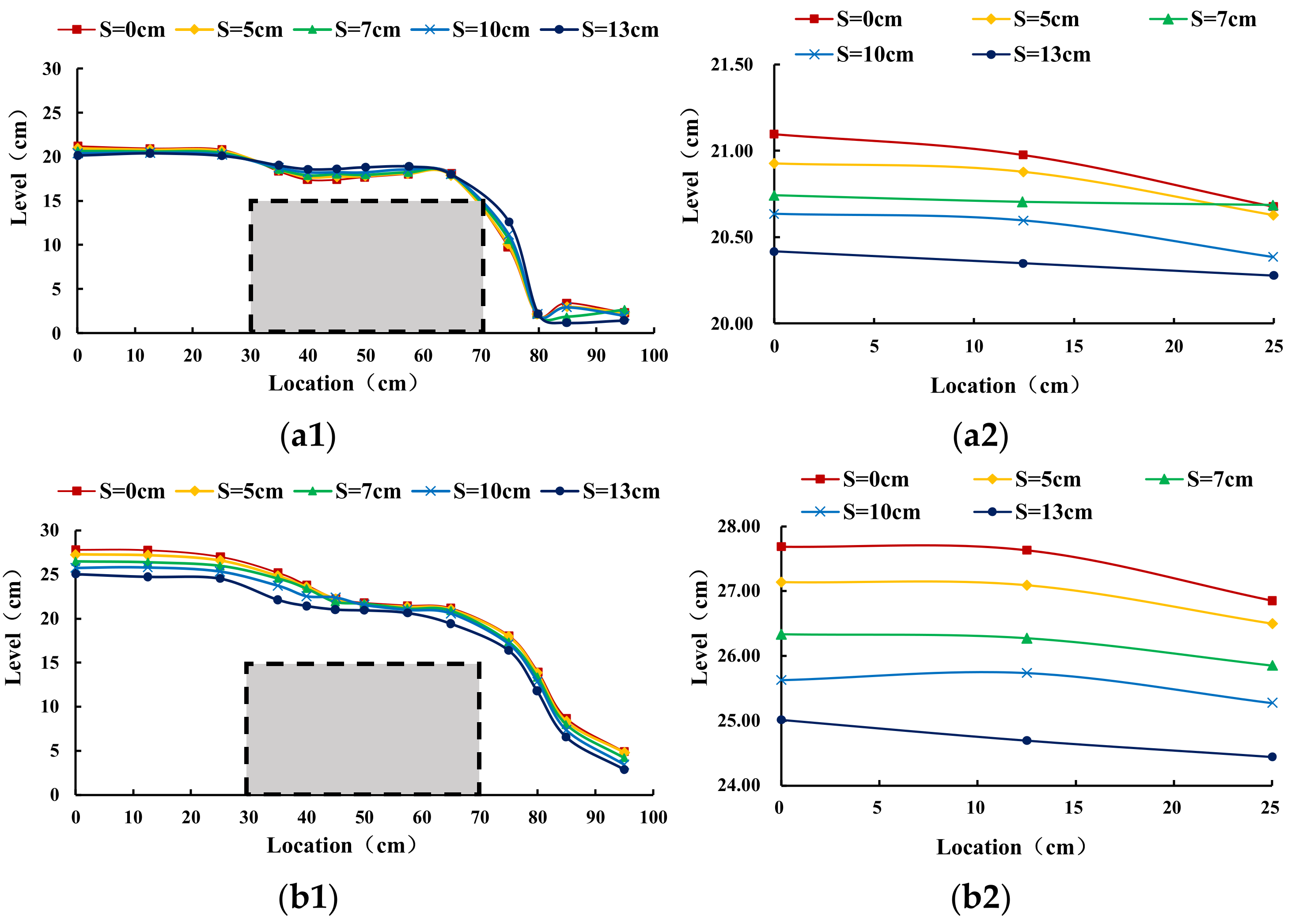
3.2.2. Influence of Siltation Height on the Level of Flow at the Same Discharge
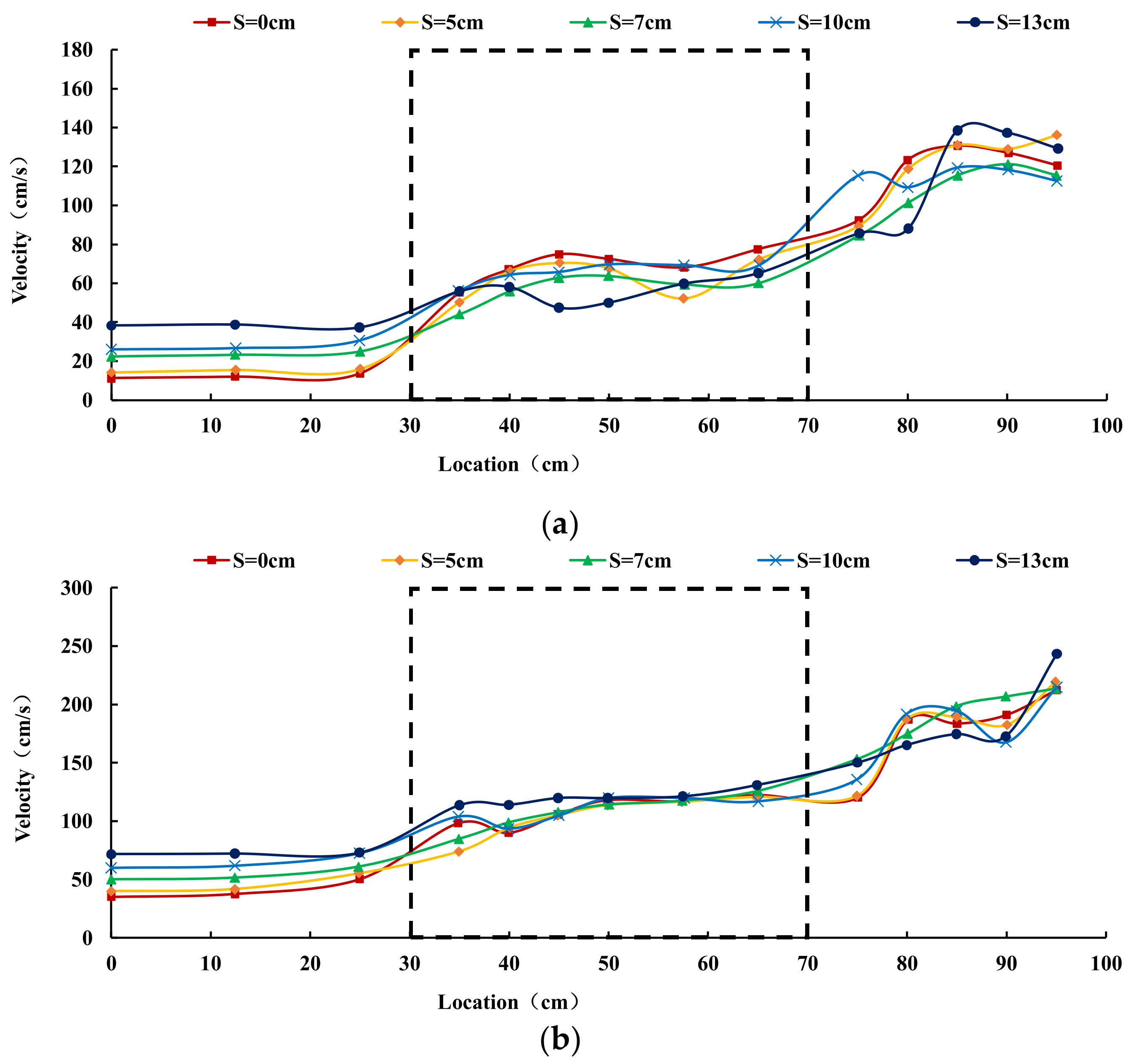
3.3. Distribution of the Velocity along the Weir
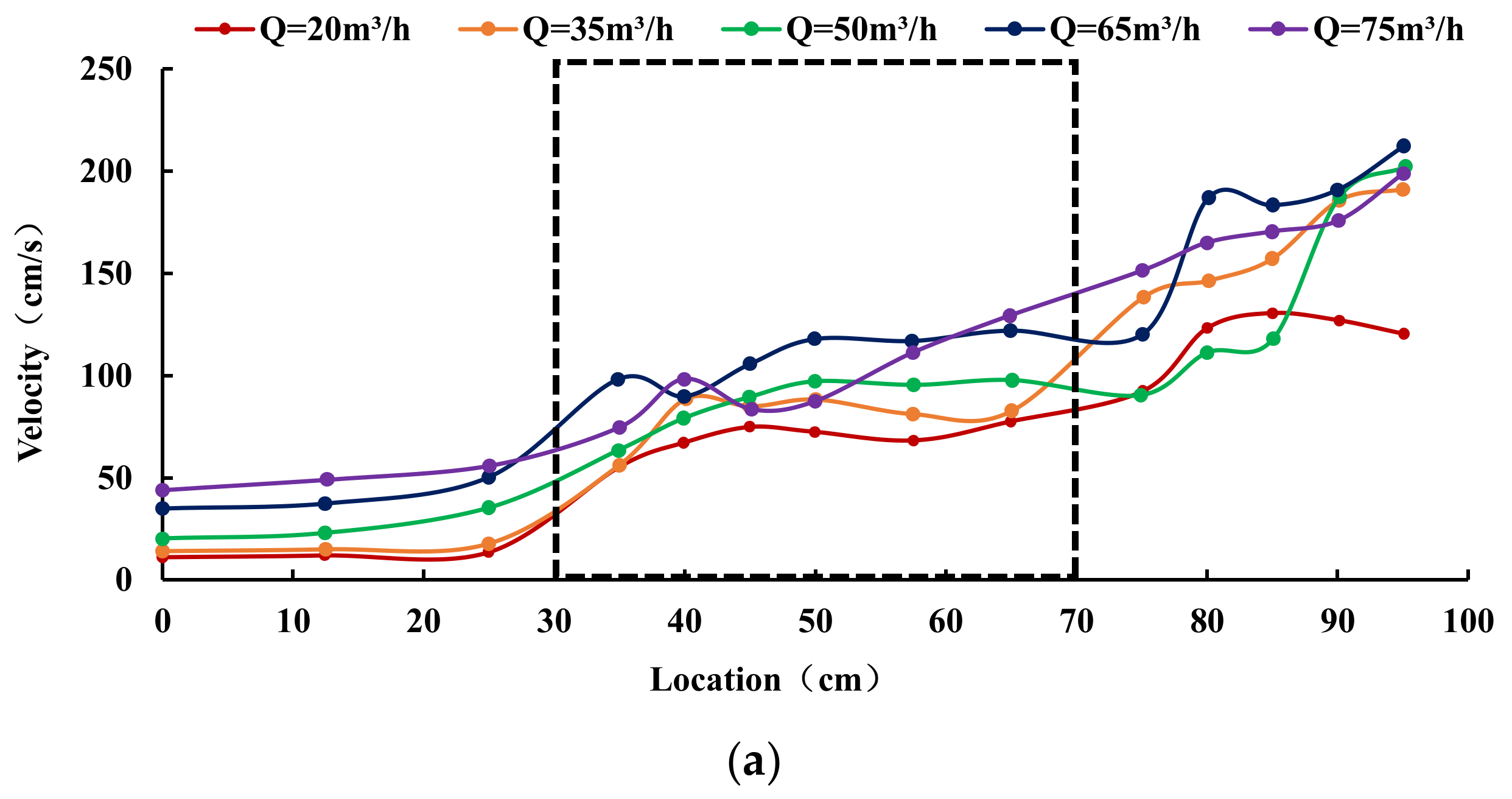
3.3.1. Influence of Discharge on the Velocity of Flow at the Same Siltation Height
3.3.2. Influence of Siltation Height on the Velocity of Flow at the Same Discharge
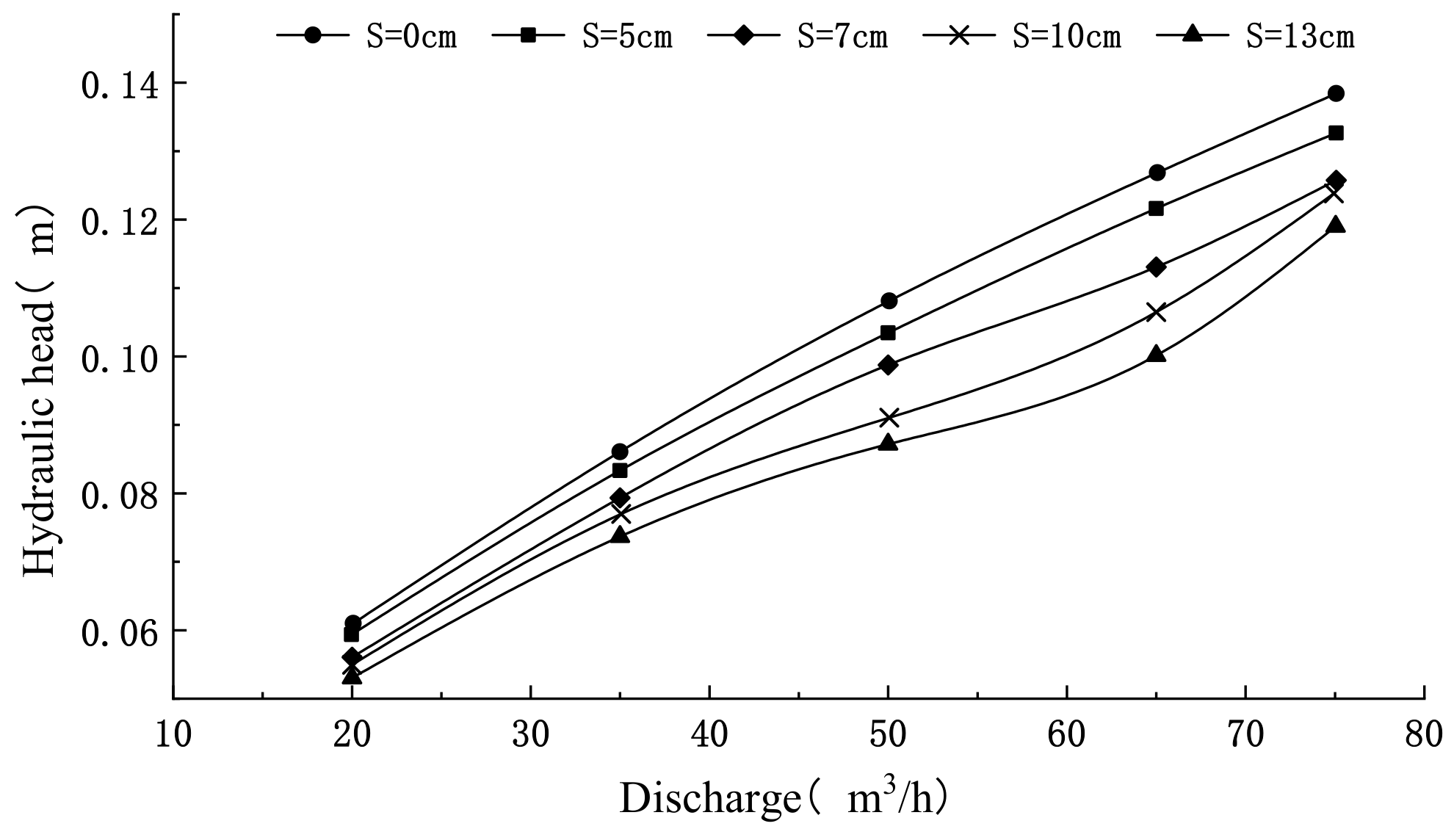
3.4. Relationship between Hydraulic Head and Discharge or Siltation Height
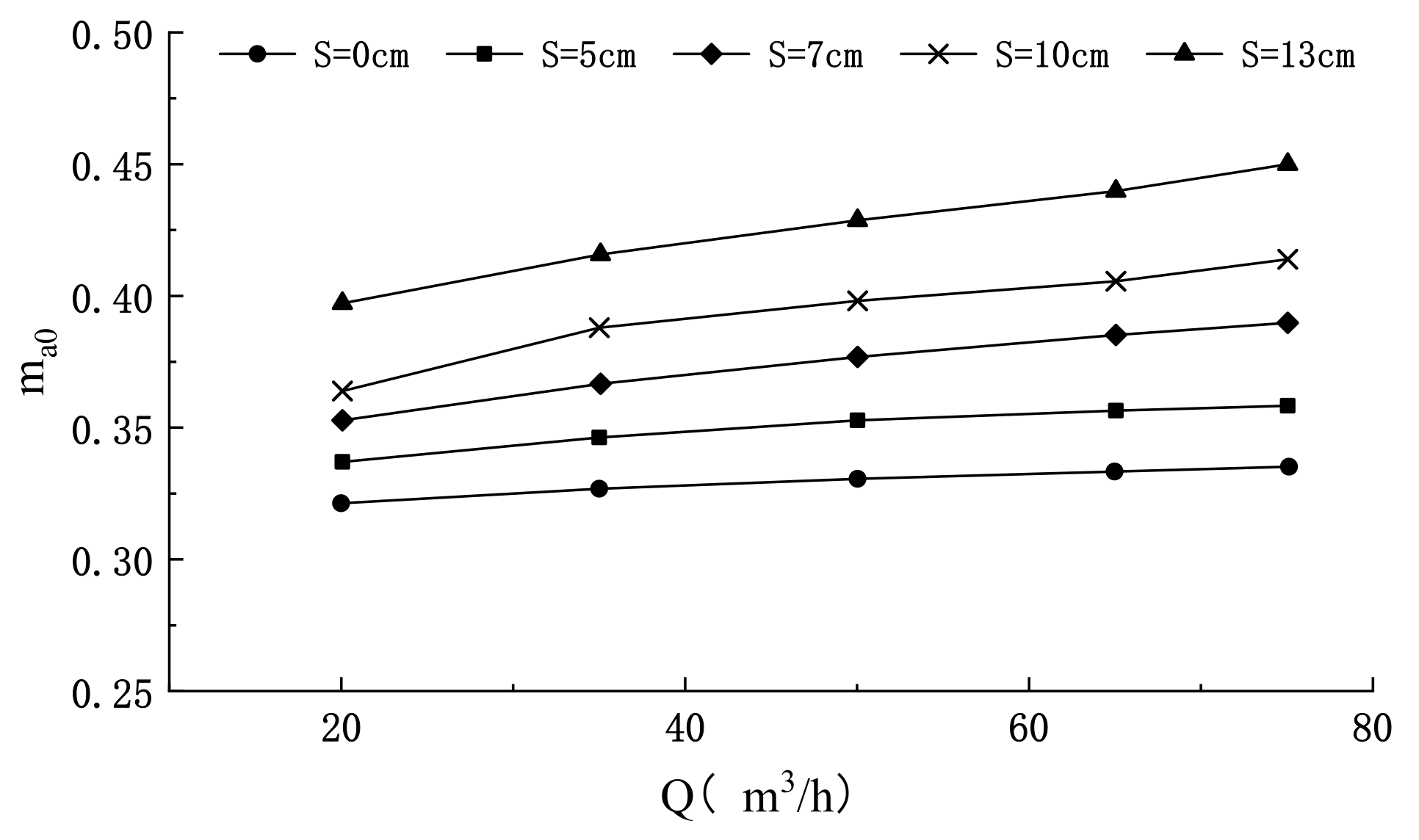
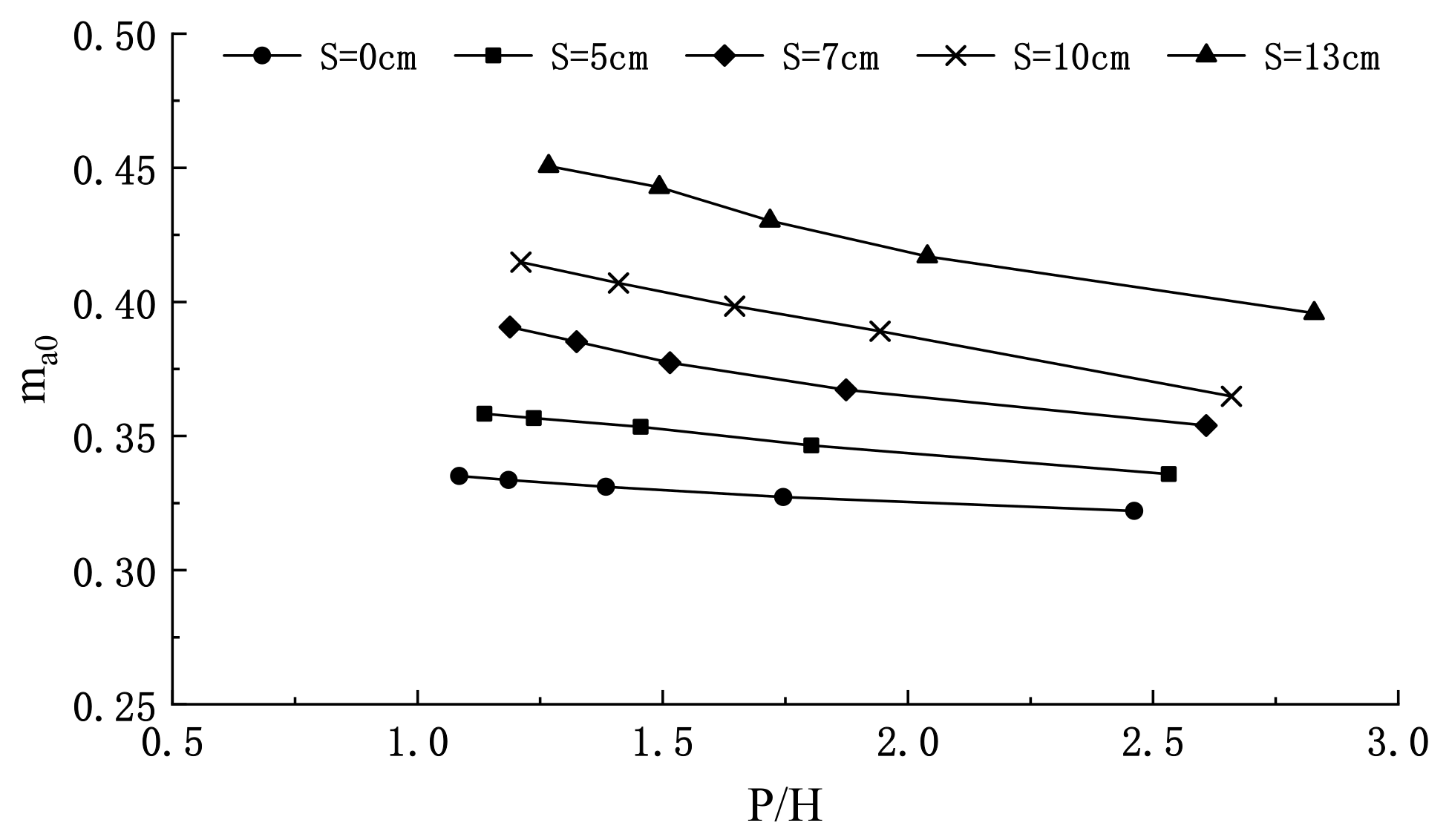
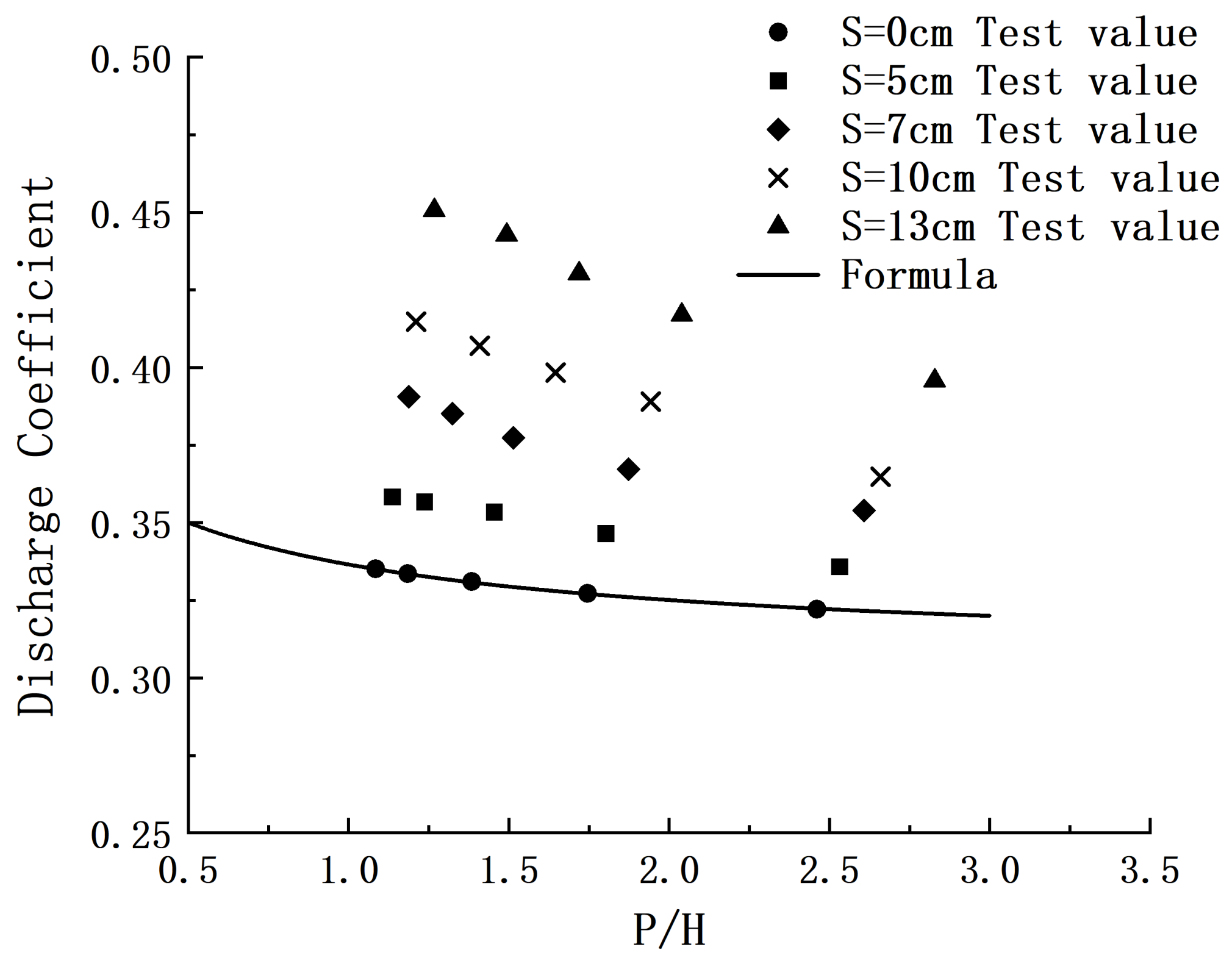
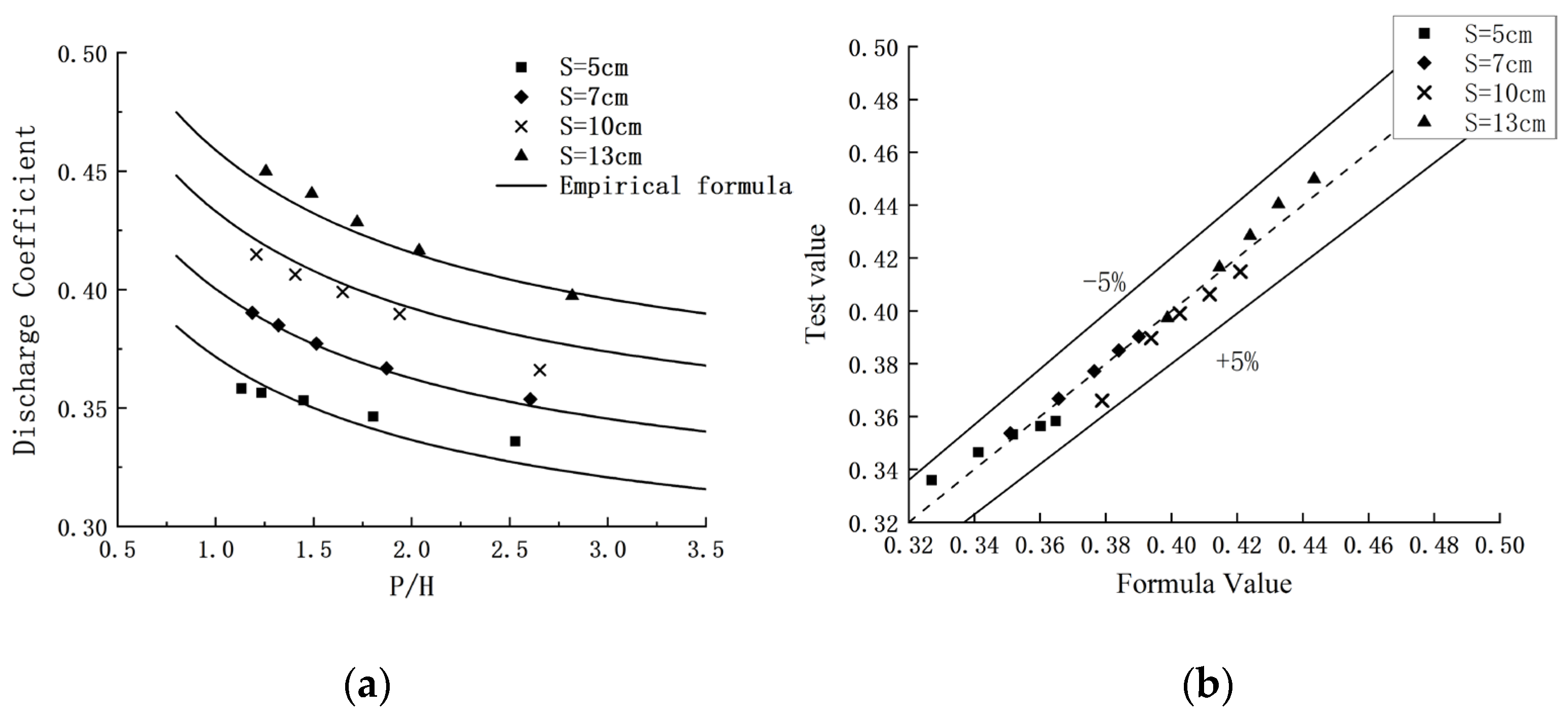
3.5. Formula for Discharge Coefficient of the Broad-Crested Weir
4. Conclusions
- (1)
- With an increase in the siltation height, the backwater phenomenon of the flow in the upstream part of the broad-crested weir gradually decreases. The water level over the weir decreases, and the overall flow pattern gradually develops towards the open channel. This means that floods will pass more easily through spillways.
- (2)
- In the same siltation height condition, the water surface profile along the flow increases with an increase in discharge. However, in the same discharge condition, the water surface profile along the flow decreases with an increase in the siltation height, which reflects that the increase in siltation height improves the overflow capacity of the broad-crested weir.
- (3)
- The effects of discharge and siltation height change on the surface velocity of a broad-crested weir are concentrated in the front part of the weir, and the effects on the back part of the weir are smaller. In the same siltation condition, the surface velocity of the flow in front of the weir increases with an increase in the discharge. In the same discharge condition, the surface velocity of the water in front of the broad-crested weir gradually increases with an increase in the siltation height.
- (4)
- From the above analysis of hydraulic characteristics, we know that the influence of siltation on overflow should be considered in engineering design work. Therefore, we propose a new formula to calculate the discharge coefficient that meets the accuracy requirements. It can be applied to the estimation of discharge in practical reinforcement work on check dams.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, X. Discuss check dam and Yellow River treatment. ZHIHUANGKEJIXINXI 1994, 6, 7–8. [Google Scholar]
- Gu, Y. Li Yizhi, pioneer of modern water conservancy in China. ZHIHUAI 2014, 10, 37–38. [Google Scholar]
- Wei, X.; Li, Z.; Li, P. Study on depositing process of check dam on the loess plateau. Bull. Soil Water Conserv. 2006, 26, 10–13, 31. [Google Scholar]
- Wei, X.; Li, Z.; Li, X. Analysis of the grey correlation between sediment effect for dam-land of typical checking dam and corresponding erosive rainfall. J. Saf. Environ. 2007, 7, 101–104. [Google Scholar]
- Ye, H.; Shi, J.; Hou, H. Exploration on the sedimentary rate assessment in silt retention dam based on GIS and GPS. Acta Geol. Sin. 2006, 80, 1633–1636. [Google Scholar]
- Wang, Y.; Fu, B.; Hou, F. Estimation of sediment volume trapped by check-dam based on differential GPS technique. Trans. Chin. Soc. Agric. Eng. 2009, 25, 79–83. [Google Scholar]
- Ramos, I.; Navarro, J.; Martin, F. Analysis of methods to determine the sediment retained by check dams and to estimate erosion rates in badlands. Environ. Monit. Assess. 2016, 188, 405. [Google Scholar] [CrossRef]
- Tang, H.; Pan, H.; Ran, Q. Impacts of filled check dams with different deployment strategies on the flood and sediment transport processes in a loess plateau catchment. Water 2020, 12, 1319. [Google Scholar] [CrossRef]
- Niu, Y. Existing problems and solutions of reservoir spillway. Yellow River 1995, 10, 37–40. [Google Scholar]
- Hua, Z. A calculating formula for spillway capacity of drowned wide crest weirs. J. Hohai Univ. 1998, 3, 99–103. [Google Scholar]
- Wang, X.; Zhang, Y. Discharge coefficient and submerged coefficient of streamlined broad crest weir. Power Syst. Clean Energy 2012, 11, 82–84, 89. [Google Scholar]
- Yu, H. Critical submerged method applied to the computation of flow over broad crested weirs. J. Chongqing Jiaotong Univ. 1998, 17, 28–30. [Google Scholar]
- Tian, J.; Li, G.; Ji, A. Discussion on weir flow coefficient for broad-crest ridge-free weirs. Adv. Sci. Technol. Water Resour. 2003, 3, 34–35, 70. [Google Scholar]
- Shan, C.; Qi, Q. The calculation and discussion of the discharge coefficient for stepless, broad-crest weirs. Traffic Eng. Technol. Natl. Def. 2008, 5, 31–32, 58. [Google Scholar]
- Li, R.; Tian, Z.; Deng, J. Experimental and theoretical study on gated free flow discharge coefficient for broad-crested ridge-free weir. Water Resour. Power 2015, 11, 88–90, 154. [Google Scholar]
- Yang, L.; Liang, Y.; Fan, R.; Wu, Q. Research on outflow of gate hole of broad-crested weir with sill. Yellow River 2010, 2, 107–108. [Google Scholar]
- Kim, N.; Nakagawa, H.; Kawaike, K.; Zhang, H. Estimation of debris flow discharge coefficient considering sediment concentration. Int. J. Sediment Res. 2019, 34, 1–7. [Google Scholar] [CrossRef]
- Banihabib, M.; Bibak, A.; Tanhapour, M. Empirical equation for the assessment of the effect of sediment concentration on the discharge coefficient of slit dams. Arab. J. Geosci. 2022, 15, 574. [Google Scholar] [CrossRef]
- Říha, J.; Duchan, D.; Zachoval, Z.; Erpicum, S.; Archambeau, P.; Pirotton, M.; Dewals, B. Performance of a shallow-water model for simulating flow over trapezoidal broad-crested weirs. J. Hydrol. Hydromech. 2019, 67, 322–328. [Google Scholar] [CrossRef]
- Dehghani, H.; Varaki, M. Experimental investigation of upstream sedimentation and downstream bed levels’ effects on discharge coefficients of trapezoidal labyrinth weirs. Arab. J. Geosci. 2021, 14, 1999. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharma, N.; Lama, G.F.C.; Hasan, M.; Garg, R.; Busico, G.; Alharbi, R.S. Three-dimensional hole size (3DHS) Approach for water flow turbulence analysis over emerging sand bars: Flume-scale experiments. Water 2022, 14, 1889. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Gui, L.; Zhang, J.; Li, Y. Research on the Influence of Siltation Height of Check Dams the on Discharge Coefficient of Broad-Crested Weirs. Water 2023, 15, 510. https://doi.org/10.3390/w15030510
Wang Z, Gui L, Zhang J, Li Y. Research on the Influence of Siltation Height of Check Dams the on Discharge Coefficient of Broad-Crested Weirs. Water. 2023; 15(3):510. https://doi.org/10.3390/w15030510
Chicago/Turabian StyleWang, Zhijian, Lili Gui, Jiaxuan Zhang, and Yongye Li. 2023. "Research on the Influence of Siltation Height of Check Dams the on Discharge Coefficient of Broad-Crested Weirs" Water 15, no. 3: 510. https://doi.org/10.3390/w15030510
APA StyleWang, Z., Gui, L., Zhang, J., & Li, Y. (2023). Research on the Influence of Siltation Height of Check Dams the on Discharge Coefficient of Broad-Crested Weirs. Water, 15(3), 510. https://doi.org/10.3390/w15030510




