Study on Forecasting Break-Up Date of River Ice in Heilongjiang Province Based on LSTM and CEEMDAN
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. CEEMDAN
2.3. LSTM Network
2.4. Fundamental Frameworks of CEEMDAN-LSTM
- (1)
- Obtain the break-up date series and decompose it into subsequences (multiple IMFs and a residual series) by CEEMDAN.
- (2)
- Divide the IMFs and residual series into training data and forecast data, and normalize them.
- (3)
- Calculate the maximum autocorrelation order of each IMF and residual series (shown in Table 3), and build the LSTM to forecast the value of IMFs and residual series.
- (4)
- Denormalize and evaluate the forecast result.
2.5. Performance Evaluation
3. Result
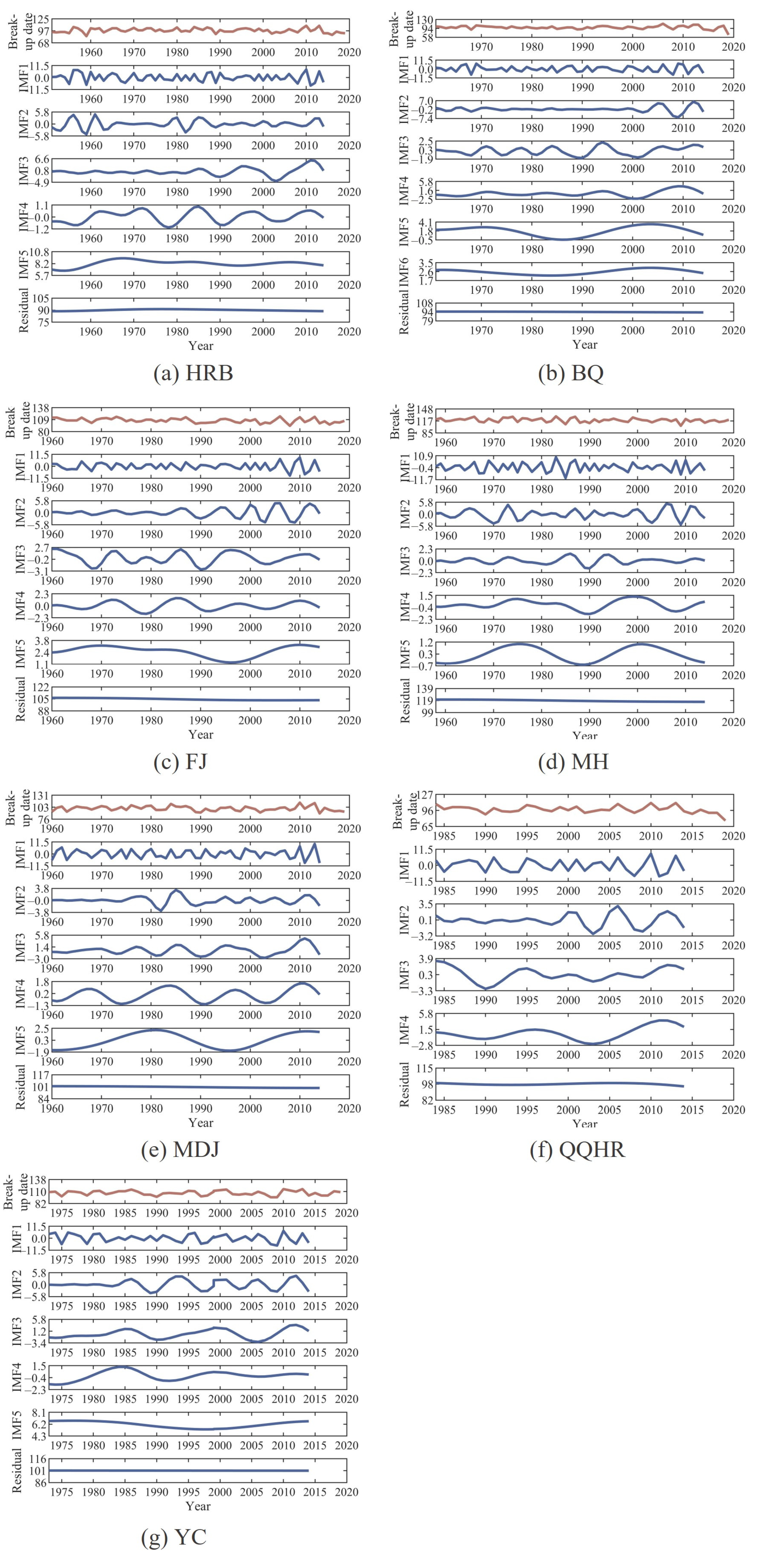
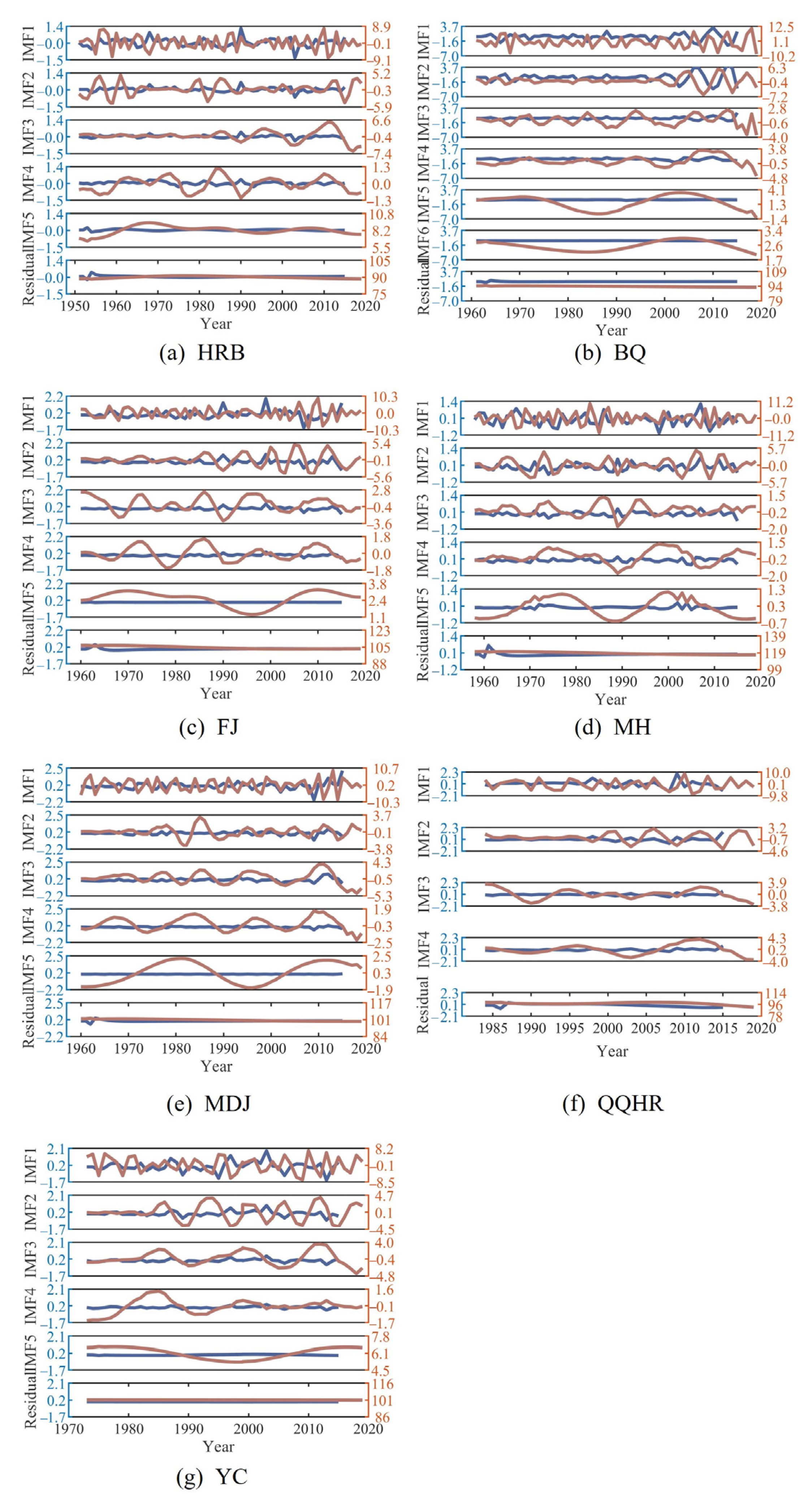
3.1. Results of Decomposing the Observed Break-Up Date Series Using CEEMDAN
3.2. Result of LSTM Applied to Forecast the Break-Up Date
3.3. Result of CEEMDAN-LSTM Applied to Forecast the Break-Up Date
4. Discussion
4.1. Reasons for the Improvement of the Forecasting Accuracy of Break-Up Date by CEEMDAN-LSTM
4.2. Reasons for the Lower Forecasting Accuracy of BQ and QQHR by LSTM
4.3. The Performance of LSTM in Forecasting the Black Swan Events
5. Conclusions
- (1)
- CEEMDAN decomposed the observed break-up date series into subsequences according to different fluctuations and frequencies. The observed break-up date series with a larger standard deviation, compared with a similar break-up date series in length, had relatively more decomposed subsequences. With the decomposition processing, the frequency and fluctuation degree of subsequence decreased, and the sample values of subsequence increased. The residual series had the lowest fluctuation degree and frequency, which was close to linear and varied slightly around the long-term average.
- (2)
- The subsequence decomposed by CEEMDAN with a lower fluctuation degree or smaller sample values compared with the observed series for LSTM obtained a higher forecasting accuracy. The IMF1 and IMF2 had smaller values, the MAE values for forecasting results of IMF1 and IMF2 were small with the order of magnitude of 10−1. The IMF5, IMF6, and residual series had lower fluctuation degrees, and the MAE values of forecasting results of IMF5, IMF6, and residual series were small with the order of magnitude of 10−2 and 10−3.
- (3)
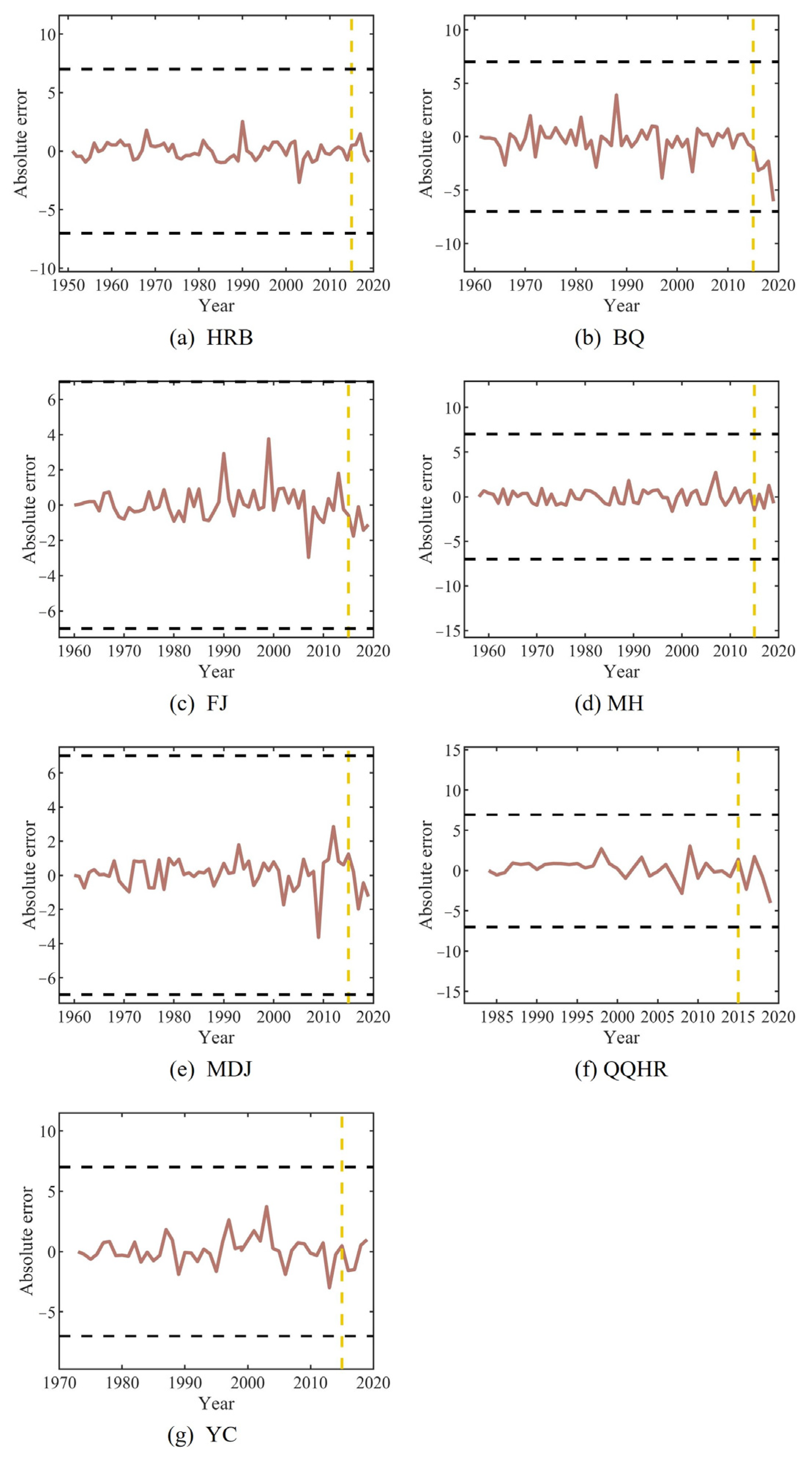
- Among the performance evaluation of the LSTM for all seven stations, the absolute error ranged from −13 to 12, the MAE values ranged from 0.80 to 6.40, the QR values were above 60%, the RMSD values ranged from 1.37 to 5.97, the R values ranged from 0.51 to 0.97, and the S values ranged from 0.87 to 0.99.
- (4)
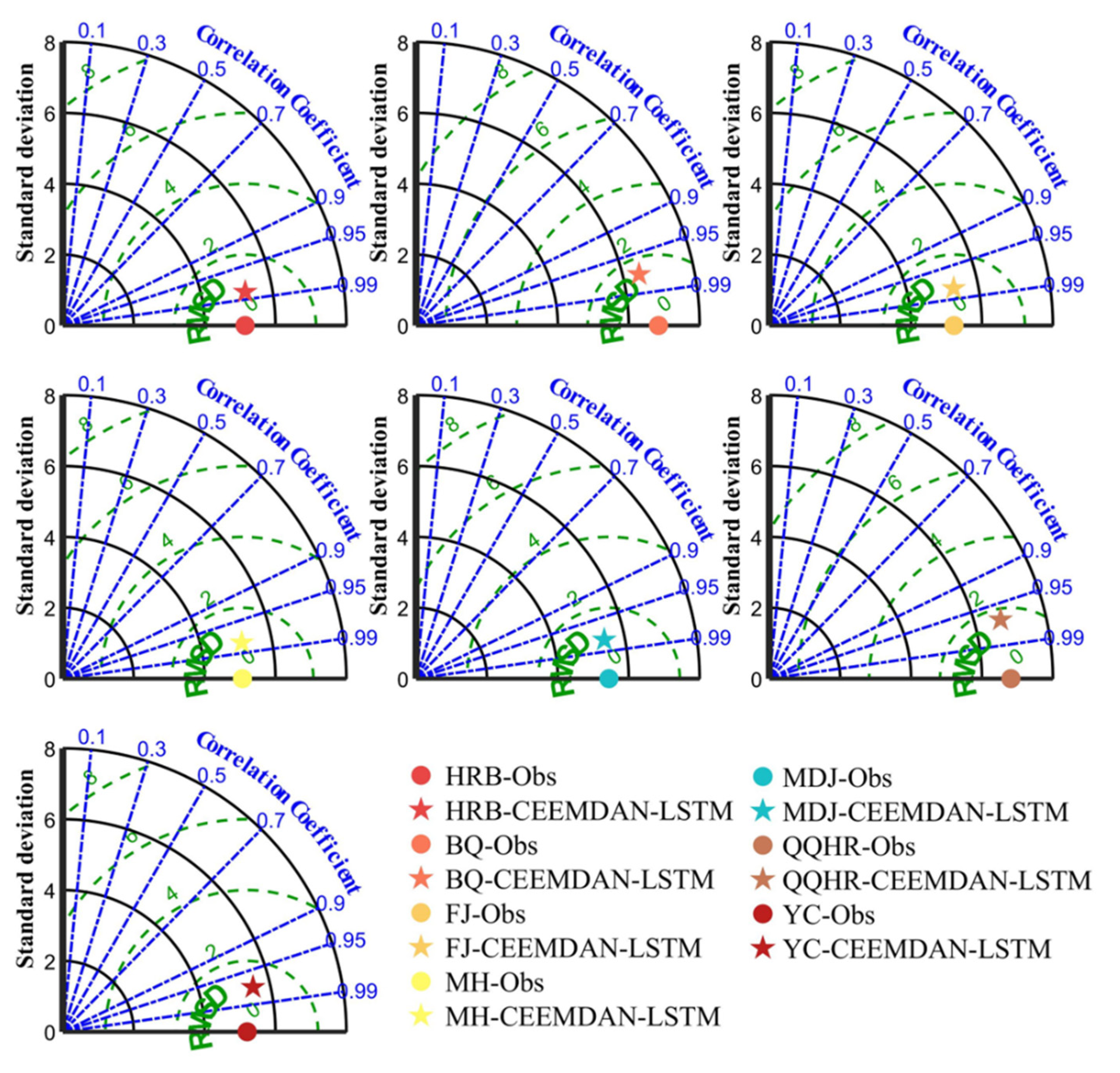
- The forecasting accuracy was obviously improved by LSTM coupled with CEEMDAN. CEEMDAN-LSTM performed better than LSTM. In the performance evaluation of the CEEMDAN-LSTM for all seven stations, the absolute error ranged from −6 to 4, the MAE values ranged from 0.75 to 3.40, the QR values improved to 100%, the RMSD values ranged from 0.95 to 1.69, the R values ranged from 0.97 to 0.98, and the S values improved to 0.99.
- (5)
- CEEMDAN can reduce the influence of the few samples on the forecasting accuracy of LSTM. The forecasting accuracy by LSTM was obviously improved after decomposing the observed break-up date series of QQHR with a short length by CEEMDAN. The MAE value of forecasting results for QQHR decreased from 6.33 to 1.83, the QR value was improved from 80% to 100%, and the S value was improved from 0.87 to 0.99.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Beltaos, S.; Prowse, T. River-ice hydrology in a shrinking cryosphere. Hydrol. Process. 2009, 23, 122–144. [Google Scholar] [CrossRef]
- Terry, J.A.; Sadeghian, A.; Lindenschmidt, K.-E. Modelling dissolved oxygen/sediment oxygen demand under ice in a shallow eutrophic prairie reservoir. Water 2017, 9, 131. [Google Scholar] [CrossRef] [Green Version]
- Morales-Marín, L.A.; Sanyal, P.R.; Kadowaki, H.; Li, Z.; Rokaya, P.; Lindenschmidt, K.E. A hydrological and water temperature modelling framework to simulate the timing of river freeze-up and ice-cover breakup in large-scale catchments. Environ. Model. Softw. 2019, 114, 49–63. [Google Scholar] [CrossRef]
- de Rham, L.P.; Prowse, T.D.; Bonsal, B.R. Temporal variations in river-ice break-up over the Mackenzie River Basin, Canada. J. Hydrol. 2008, 349, 441–454. [Google Scholar] [CrossRef]
- Cunjak, R.A.; Prowse, T.D.; Parrish, D.L. Atlantic salmon in winter; “the season of parr discontent”. Can. J. Fish. Ocean. Sci. 1998, 55 (Suppl. S1), 161–180. [Google Scholar] [CrossRef]
- Gray, D.M.; Prowse, T.D. Snow and floating ice. In Handbook of Hydrology; McGraw-Hill: New York, NY, USA, 1993; pp. 7.1–7.58. [Google Scholar]
- Beltaos, S.; Burrell, B.C. Effects of River-Ice Breakup on Sediment Transport and Implications to Stream Environments: A Review. Water 2021, 13, 2541. [Google Scholar] [CrossRef]
- Marsh, P. Modelling water-levels for a lake in the Mackenzie Delta. In Proceedings of the Symposium: Cold Regions Hydrology; American Water Resources Association Technical Publication Series No. TPS-86-1; Kane, D.L., Ed.; American Water Resources Association: Woodbridge, VA, USA, 1986; pp. 22–25. [Google Scholar]
- Lesack, L.F.W.; Hecky, R.E.; March, P. The influence of frequency and duration of flooding on the nutrient chemistry of Mackenzie Delta lakes. In Environmental Interaction and Implication of Development; NHRI Symposium 4; National Hydrology Research Institute, Environment Canada: Saskatoon, SK, Canada, 1991; pp. 19–36. [Google Scholar]
- Peters, D.L.; Prowse, T.D.; Pietroniro, A.; Leconte, R. Flood Hydrology of the Peace-Athabasca Delta, Northern Canada. Hydrol. Process. 2006, 20, 4073–4096. [Google Scholar] [CrossRef]
- Fatemehalsadat, M.; Rachid, L.; Karem, C.; Sebastien, R.; Yves, G. Ice jam formation, breakup and prediction methods based on hydroclimatic data using artificial intelligence: A review. Cold Reg. Sci. Technol. 2020, 174, 103032. [Google Scholar]
- Shevnina, E.V.; Solov’eva, Z.S. Long-term Variability and Methods of Forecasting Dates of Ice Break-Up in the Mouth Area of the Ob and Yenisei Rivers. Russ. Meteorol. Hydrol. 2007, 33, 458–465. [Google Scholar] [CrossRef]
- Flato, G. Calculation of ice jam thickness profile. J. Hydraul. Res. 1986, 28, 737–743. [Google Scholar]
- Beltaos, S. Numerical computation of river ice jams. Can. J. Civ. Eng. 1993, 20, 88–99. [Google Scholar] [CrossRef]
- Flato, G.M.; Gerard, R. Calculation of ice jam profiles. In Proceedings, 4th Workshop on River Ice, Montreal, Paper C-3; CGU-HS Committee on River Ice Processes and the Environment: Edmonton, AB, Canada, 1986. [Google Scholar]
- Hicks, F.E.; Steffler, P.M. Characteristic dissipative Galerkin scheme for openchannel flow. J. Hydraul. Eng. 1992, 118, 337–352. [Google Scholar] [CrossRef]
- Carson, R.W.; Andres, D.; Beltaos, S.; Groeneveld, J.; Healy, D.; Hicks, F.; Liu, L.; Shen, H. Tests of river ice jam models. In Proceedings of the 11th Workshop on River Ice, Canmore, AB, Canada, 14–16 May 2001; pp. 14–16. [Google Scholar]
- DHI. MIKE11 Reference Manual; Danish Hydraulic Institute: Hørsholm, Denmark, 2005. [Google Scholar]
- Lindenschmidt, K.E. RIVICE—A non-proprietary, open-source, one-dimensional river-ice model. Water 2017, 9, 314. [Google Scholar] [CrossRef] [Green Version]
- Hungtao, S.; Su, J.; Liu, L. SPH simulation of river ice dynamics. J. Comput. Phys. 2000, 165, 752–770. [Google Scholar]
- Fu, H.; Guo, X.L.; Yang, K.L.; Wang, T. Ice accumulation and thickness distribution before inverted siphon. J. Hydrodyn. 2017, 29, 840–846. [Google Scholar] [CrossRef]
- Wang, T.; Guo, X.L.; Fu, H.; Guo, Y.X.; Li, J.Z. Breakup ice jam forecasting based on neural network theory and formation factor. In Proceedings of the E-Proceedings of the 38th IAHR World Congress, Panama City, Panama, 1–6 September 2019. [Google Scholar] [CrossRef]
- Chen, S.; Ji, H. Fuzzy Optimization Neural Network Approach for Ice Forecast in the Inner Mongolia Reach of the Yellow River. Hydrol. Sci. J. 2005, 50, 330. [Google Scholar] [CrossRef]
- Massie, D.D.; White, K.D.; Daly, S. Application of neural networks to predict ice jam occurrence. Cold Reg. Sci. Technol. 2002, 35, 115–122. [Google Scholar] [CrossRef]
- Wang, Y.N.; Yuan, Z.; Liu, H.Q.; Xing, Z.X.; Ji, Y.; Li, H.; Fu, Q.; Mo, C.X. A new scheme for probabilistic forecasting with an ensemble model based on CEEMDAN and AM-MCMC and its application in precipitation forecasting. Expert Syst. Appl. 2022, 187, 115872. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall—Runoff modelling using Long-Short-Term-Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the application of EMD and EEMD on time-frequency analysis of seismic signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Kisi, O.; Singh, V.P. Daily water level forecasting using wavelet decomposition and artificial intelligence techniques. J. Hydrol. 2015, 520, 224–243. [Google Scholar] [CrossRef]
- Dai, S.; Niu, D.; Li, Y.; Shuyu, D.; Dongxiao, N.; Yan, L. Daily peak load forecasting based on complete ensemble empirical mode decomposition with adaptive noise and support vector machine optimized by modified grey wolf optimization algorithm. Energies 2018, 11, 163. [Google Scholar] [CrossRef] [Green Version]
- Tan, Q.F.; Lei, X.H.; Wang, X.; Wang, H.; Wen, X.; Ji, Y.; Kang, A.Q. An adaptive middle and long-term runoff forecast model using EEMD-ANN hybrid approach. J. Hydrol. 2018, 567, 767–780. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Liu, Y.; Wang, L.; Yang, L.; Liu, X.; Wang, L. Runoff prediction and analysis based on improved ceemdan-os-qr-elm. IEEE Access 2021, 9, 57311–57324. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, Z.; Wang, K. Prediction of runoff in the upper YangtzeY river based on ceemdan-nar model. Water Sci. Technol. Water Supply 2021, 21, 3307–3318. [Google Scholar]
- Sibtain, M.; Li, X.; Nabi, G.; Azam, M.I.; Bashir, H. Development of a three-stage hybrid model by utilizing a two-stage signal decomposition methodology and machine learning approach to predict monthly runoff at swat river basin, Pakistan. Discret. Dyn. Nat. Soc. 2020, 2020, 7345676. [Google Scholar]
- Zhang, J.; Xiao, H.; Fang, H. Component-based reconstruction prediction of runoff at multi-time scales in the source area of the yellow river based on the arma model. Water Resour. Manag. 2022, 36, 1–16. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: A noise assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control. 2014, 14, 19–29. [Google Scholar] [CrossRef]
- Liang, H.; Bressler, S.L.; Desimone, R.; Fries, P. Empirical mode decomposition: A method for analyzing neural data. Neurocomputing 2005, 65–66, 801–807. [Google Scholar] [CrossRef]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E.; Flandrin, P. Noise-assisted emd methods in action. Adv. Adapt. Data Anal. 2013, 4, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning Long-Term Dependencies with Gradient Descent is Difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F.A. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Li, W.; Kiaghadi, A.; Dawson, C. Exploring the best sequence LSTM modeling architecture for flood prediction. Neural Comput. Applic. 2021, 33, 5571–5580. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Wang, J.; Luo, Y.; Tang, L.; Ge, P. A new weighted CEEMDAN-based prediction model: An experimental investigation of decomposition and non-decomposition approaches. Knowl. Based Syst. 2018, 160, 188–199. [Google Scholar] [CrossRef]
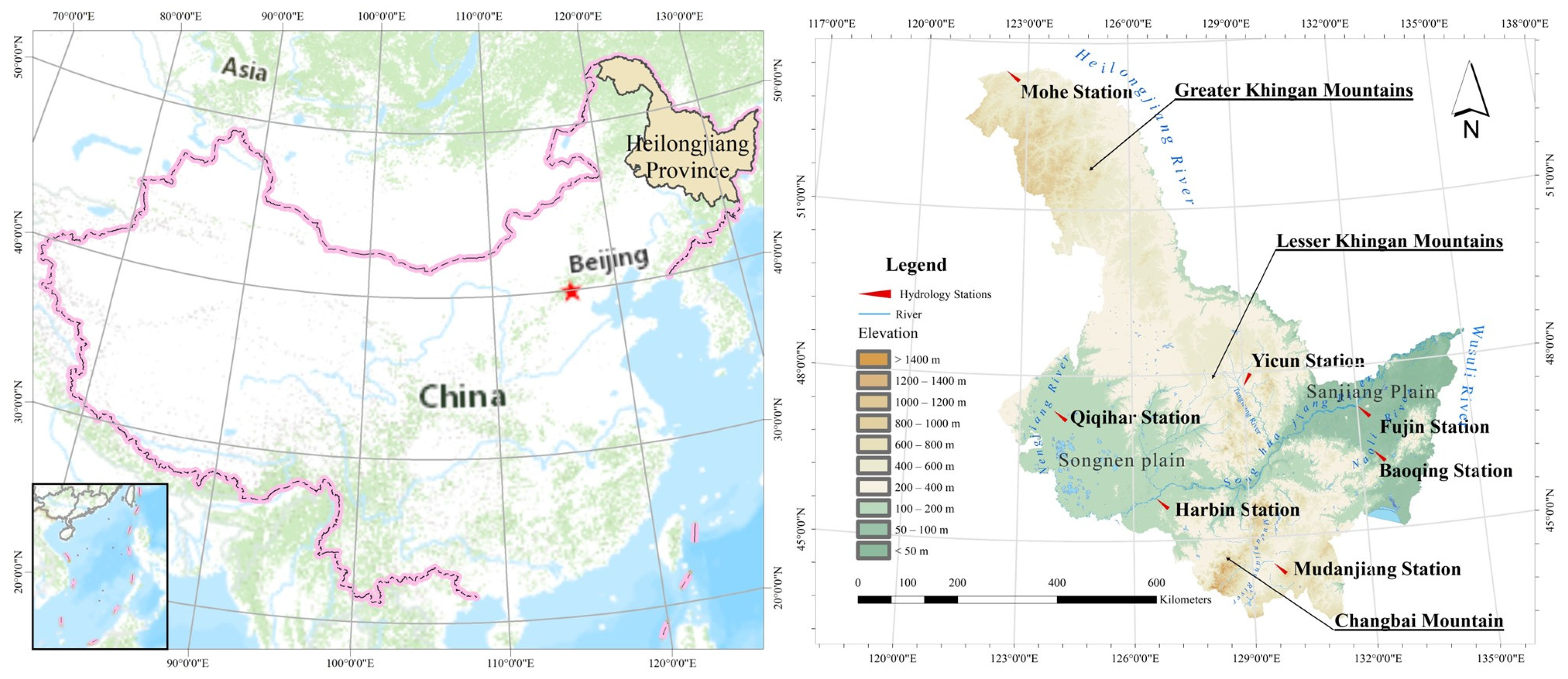


| Station | HRB | BQ | FJ | MH | MDJ | QQHR | YC |
|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| Time span | 1951–2019 | 1961–2019 | 1960–2019 | 1958–2019 | 1960–2019 | 1984–2019 | 1973–2019 |
| Series length (year) | 69 | 59 | 69 | 62 | 60 | 36 | 47 |
| Mean | Day 98 | Day 97 | Day 107 | Day 119 | Day 101 | Day 98 | Day 107 |
| Standard deviation (day) | 5.14 | 6.84 | 5.21 | 5.07 | 5.44 | 6.82 | 5.20 |
| Range (day) | 25 | 45 | 23 | 25 | 25 | 34 | 19 |
| Model | Station | HRB | BQ | FJ | MH | MDJ | QQHR | YC |
|---|---|---|---|---|---|---|---|---|
| LSTM | Maximum autocorrelation order | 14 | 3 | 1 | 16 | 3 | 6 | 2 |
| Model | Station | HRB | BQ | FJ | MH | MDJ | QQHR | YC |
|---|---|---|---|---|---|---|---|---|
| CEEMDAN-LSTM | IMF1 | 1 | 2 | 2 | 1 | 2 | 1 | 2 |
| IMF2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |
| IMF3 | 1 | 1 | 1 | 4 | 1 | 1 | 1 | |
| IMF4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| IMF5 | 1 | 1 | 1 | 1 | 1 | - | 1 | |
| IMF6 | - | 1 | - | - | - | - | - | |
| Residual | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Period | Performance Evaluation Index | HRB | BQ | FJ | MH | MDJ | QQHR | YC |
|---|---|---|---|---|---|---|---|---|
| Training | Range of AE | [−8, 9] | [−9, 9] | [−6, 5] | [−13, 9] | [−5, 4] | [−11, 12] | [−8, 9] |
| MAE | 2.53 | 2.61 | 1.69 | 2.48 | 0.80 | 3.97 | 2.71 | |
| QR(%) | 95.31 | 96.30 | 100.00 | 91.23 | 100.00 | 75.19 | 95.24 | |
| Forecast | Range of AE | [−6, 0] | [−10, 8] | [0, 4] | [−2, 4] | [1, 2] | [−13, −1] | [0, 3] |
| MAE | 1.80 | 6.40 | 2.00 | 2.67 | 2.17 | 6.33 | 1.67 | |
| QR(%) | 100.00 | 60.00 | 100.00 | 100.00 | 100.00 | 80.00 | 100.00 |
| Station | HRB | BQ | FJ | MH | MDJ | QQHR | YC |
|---|---|---|---|---|---|---|---|
| S | 0.93 | 0.95 | 0.99 | 0.95 | 0.99 | 0.87 | 0.99 |
| RMSD | 3.58 | 3.96 | 2.27 | 3.87 | 1.37 | 5.97 | 3.10 |
| R | 0.72 | 0.82 | 0.91 | 0.66 | 0.97 | 0.51 | 0.83 |
| SDo | 5.14 | 6.84 | 5.21 | 5.07 | 5.44 | 6.82 | 5.20 |
| SDf | 3.95 | 5.50 | 5.23 | 4.05 | 5.65 | 4.64 | 5.27 |
| Period | Performance Evaluation Index | HRB | BQ | FJ | MH | MDJ | QQHR | YC |
|---|---|---|---|---|---|---|---|---|
| Training | Range of AE | [−3, 3] | [−4, 4] | [−3, 4] | [−2, 3] | [−4, 3] | [−3, 3] | [−3, 4] |
| MAE | 0.75 | 1.97 | 0.79 | 0.77 | 0.87 | 1.35 | 1.01 | |
| QR(%) | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |
| Forecast | Range of AE | [−1, 1] | [−6, −1] | [−2, 1] | [−2, 2] | [−1, 1] | [−4, 2] | [−2, 2] |
| MAE | 0.80 | 3.40 | 0.83 | 1.17 | 0.83 | 1.83 | 1.00 | |
| QR(%) | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Station | HRB | BQ | FJ | MH | MDJ | QQHR | YC |
|---|---|---|---|---|---|---|---|
| S | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| RMSD | 0.95 | 1.55 | 1.05 | 1.02 | 1.10 | 1.69 | 1.27 |
| R | 0.98 | 0.97 * | 0.98 | 0.98 | 0.98 | 0.97 ** | 0.97 *** |
| SDo | 5.14 | 6.84 | 5.21 | 5.07 | 5.44 | 6.82 | 5.20 |
| SDf | 5.23 | 6.45 | 5.31 | 5.15 | 5.42 | 6.73 | 5.51 |
| Station | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | Residual |
|---|---|---|---|---|---|---|---|
| HRB | 0.293 | 0.155 | 0.126 | 0.095 | 0.042 | - | 0.037 |
| BQ | 0.741 | 0.511 | 0.288 | 0.265 | 0.073 | 0.035 | 0.053 |
| FJ | 0.342 | 0.213 | 0.105 | 0.089 | 0.004 | - | 0.043 |
| MH | 0.362 | 0.233 | 0.134 | 0.100 | 0.071 | - | 0.054 |
| MDJ | 0.368 | 0.157 | 0.185 | 0.082 | 0.029 | - | 0.043 |
| QQHR | 0.569 | 0.298 | 0.158 | 0.170 | - | 0.163 | |
| YC | 0.455 | 0.222 | 0.163 | 0.083 | 0.086 | - | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Wang, Y.; Xing, Z.; Wang, X.; Fu, Q. Study on Forecasting Break-Up Date of River Ice in Heilongjiang Province Based on LSTM and CEEMDAN. Water 2023, 15, 496. https://doi.org/10.3390/w15030496
Liu M, Wang Y, Xing Z, Wang X, Fu Q. Study on Forecasting Break-Up Date of River Ice in Heilongjiang Province Based on LSTM and CEEMDAN. Water. 2023; 15(3):496. https://doi.org/10.3390/w15030496
Chicago/Turabian StyleLiu, Mingyang, Yinan Wang, Zhenxiang Xing, Xinlei Wang, and Qiang Fu. 2023. "Study on Forecasting Break-Up Date of River Ice in Heilongjiang Province Based on LSTM and CEEMDAN" Water 15, no. 3: 496. https://doi.org/10.3390/w15030496
APA StyleLiu, M., Wang, Y., Xing, Z., Wang, X., & Fu, Q. (2023). Study on Forecasting Break-Up Date of River Ice in Heilongjiang Province Based on LSTM and CEEMDAN. Water, 15(3), 496. https://doi.org/10.3390/w15030496








