Trend Analysis and Identification of the Meteorological Factors Influencing Reference Evapotranspiration
Abstract
:1. Introduction
2. Data and Methods
2.1. The FAO-Penman-Monteith Method
2.2. Mann-Kendall Test
2.3. Sen’s Slope Estimator
2.4. Sensitivity Analysis
2.5. Contribution Rate
2.6. Study Area and Data
3. Results
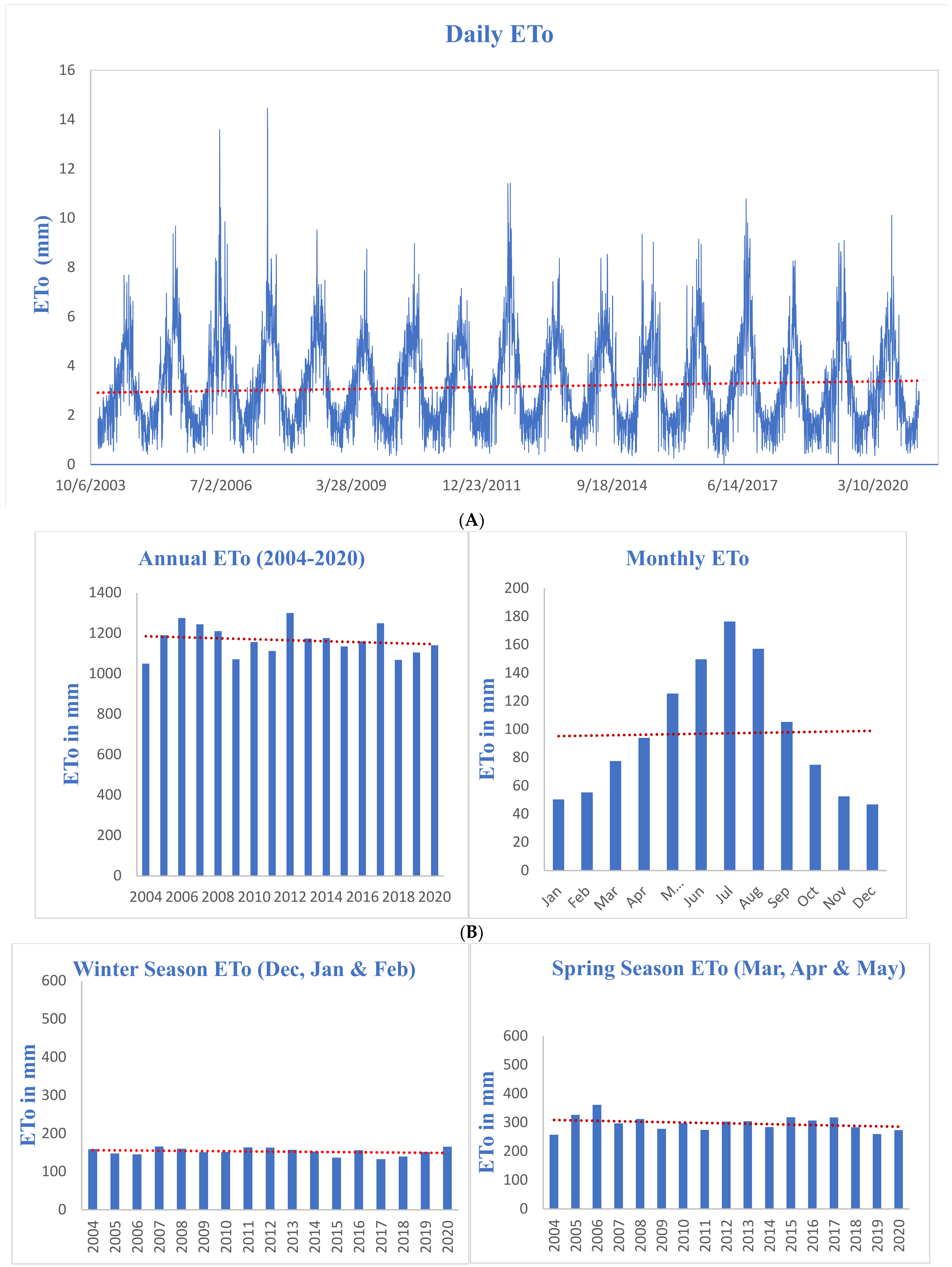
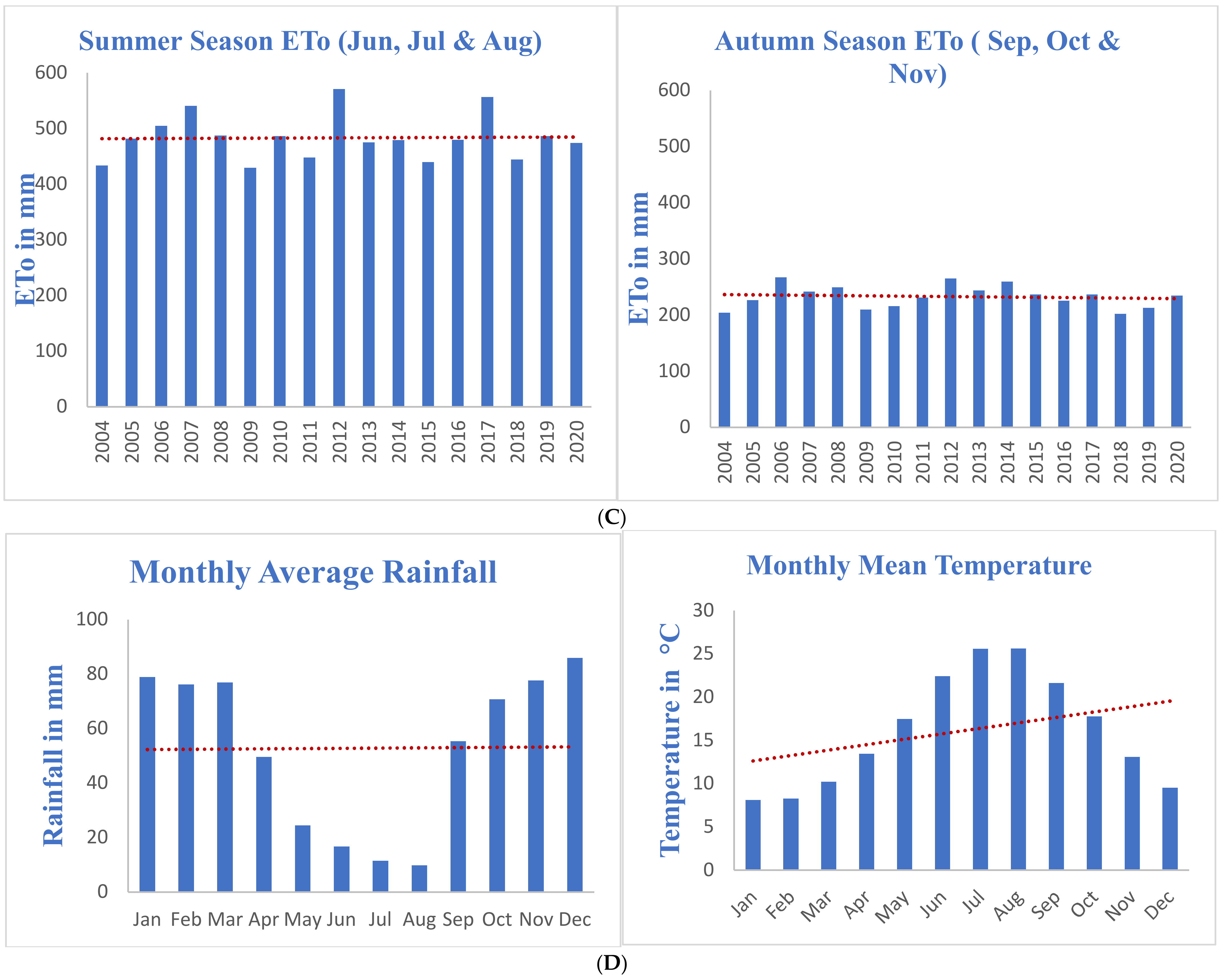
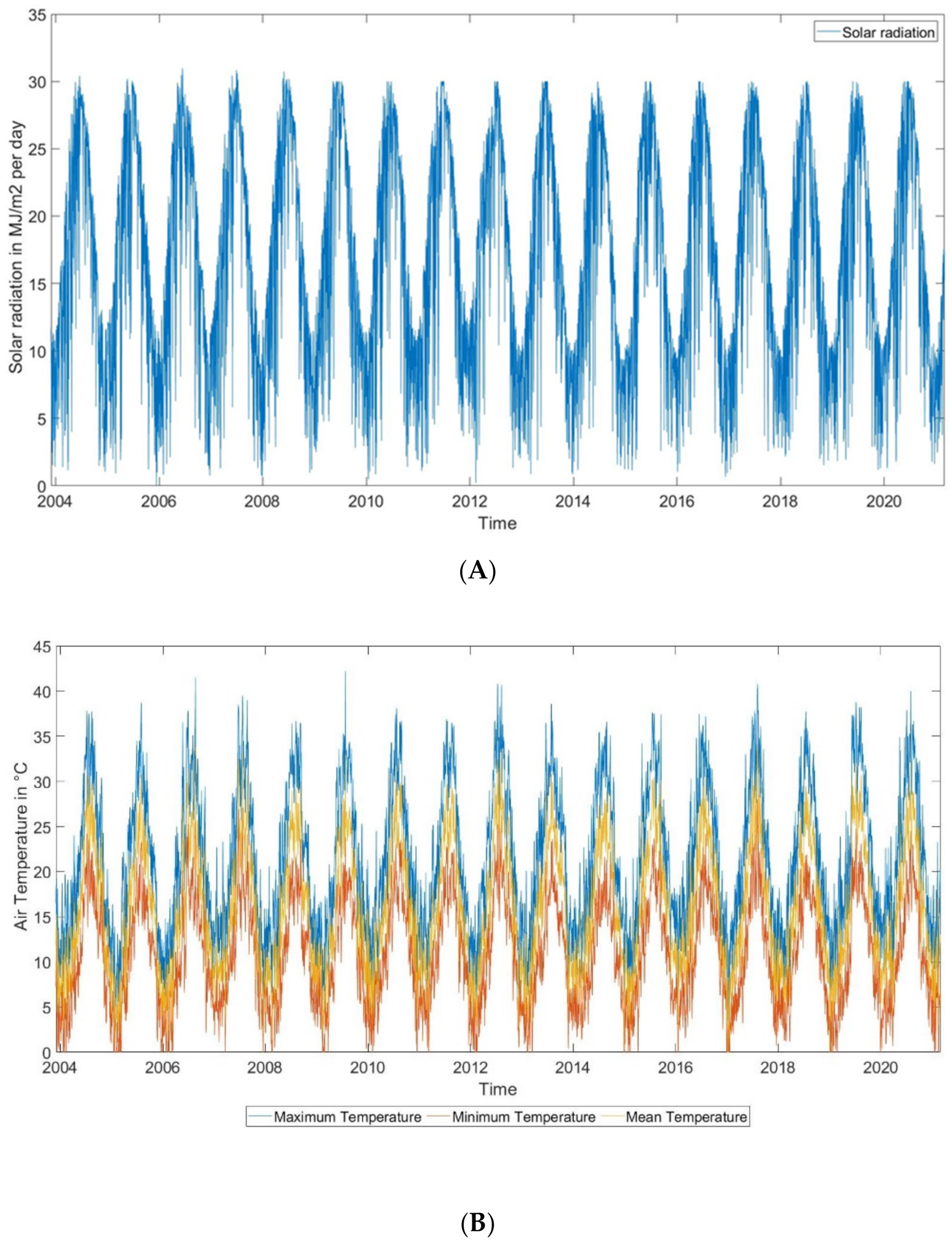
3.1. MK-Test Trends of Meteorological Factors and ETo
3.2. Sen’s Slope (Magnitude of the Trend)
3.3. Sensitivity of ETo to Climatic Factors
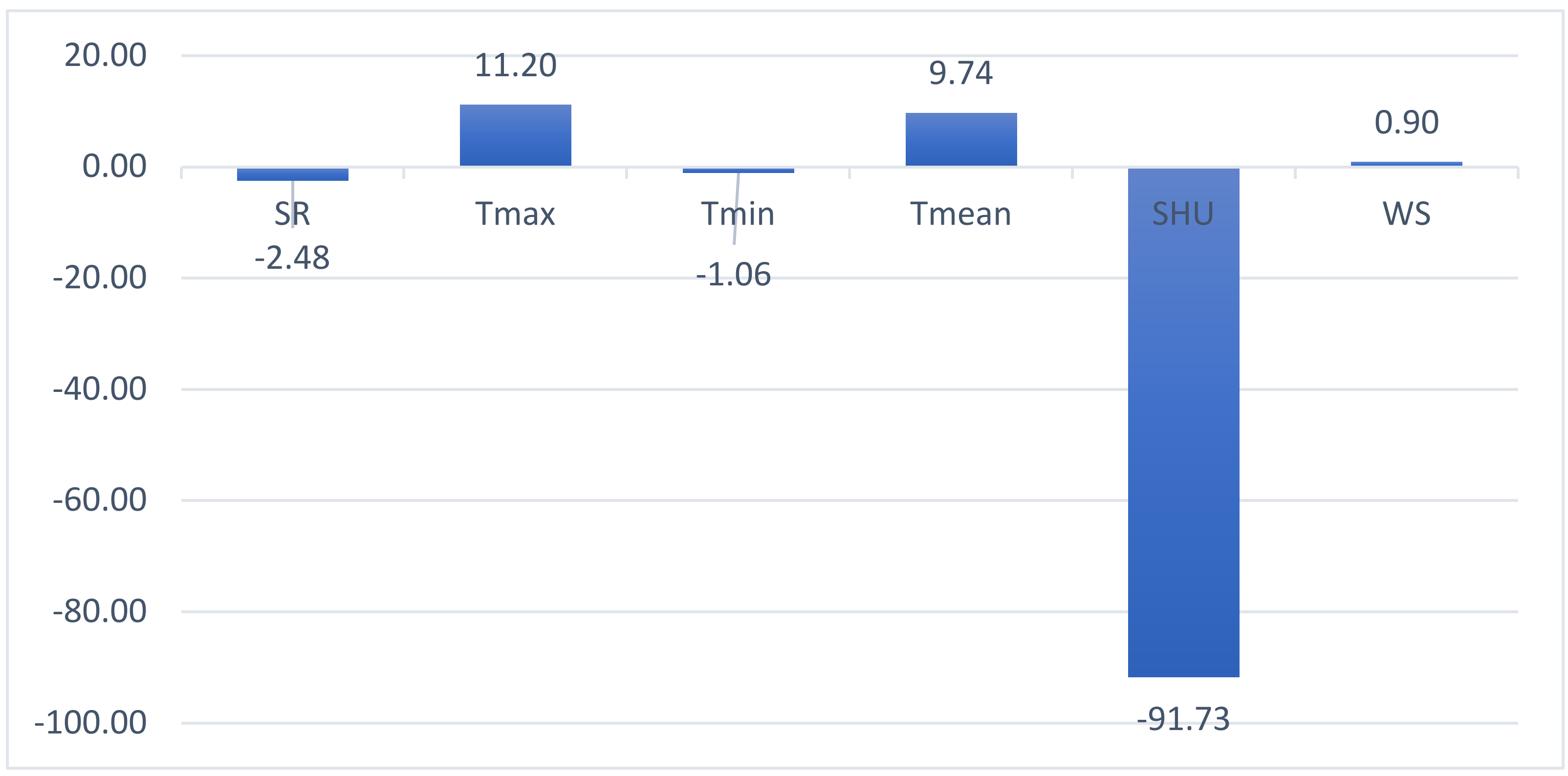
3.4. Contribution Rate of Climatic Factors for the Variation of ETo
4. Discussion
4.1. Trend of Climatic Factors and ETo
4.2. Sensitivity of ETo and Contribution Rate of Climatological Elements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ochoa-Sánchez, A.; Crespo, P.; Carrillo-Rojas, G.; Sucozhañay, A.; Célleri, R. Actual Evapotranspiration in the High Andean Grasslands: A Comparison of Measurement and Estimation Methods. Front. Earth Sci. 2019, 7, 139. [Google Scholar] [CrossRef] [Green Version]
- Glenn, E.P.; Nagler, P.L.; Huete, A.R. Vegetation Index Methods for Estimating Evapotranspiration by Remote Sensing. Surv. Geophys. 2010, 31, 531–555. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, Z.; Zhangzhong, L.; Yu, J.; Shi, K.; Yao, L. Spatiotemporal Distribution Characteristics of Reference Evapotranspiration in Shandong Province from 1980 to 2019. Water 2020, 12, 3495. [Google Scholar] [CrossRef]
- Parajuli, K.; Jones, S.B.; Tarboton, D.G.; Flerchinger, G.N.; Hipps, L.E.; Allen, L.N.; Seyfried, M.S. Estimating actual evapotranspiration from stony-soils in montane ecosystems. Agric. For. Meteorol. 2018, 265, 183–194. [Google Scholar] [CrossRef] [Green Version]
- Ellsäßer, F.; Röll, A.; Stiegler, C.; Hendrayanto; Hölscher, D. Introducing QWaterModel, a QGIS plugin for predicting evapotranspiration from land surface temperatures. Environ. Model. Softw. 2020, 130, 104739. [Google Scholar] [CrossRef]
- He, D.; Liu, Y.; Pan, Z.; An, P.; Wang, L.; Dong, Z.; Zhang, J.; Pan, X.; Zhao, P. Climate change and its effect on reference crop evapotranspiration in central and western Inner Mongolia during 1961–2009. Front. Earth Sci. 2013, 7, 417–428. [Google Scholar] [CrossRef]
- Mueller, B.; Seneviratne, S.I.; Jimenez, C.; Corti, T.; Hirschi, M.; Balsamo, G.; Ciais, P.; Dirmeyer, P.; Fisher, J.B.; Guo, Z.; et al. Evaluation of global observations-based evapotranspiration datasets and IPCC AR4 simulations. Geophys. Res. Lett. 2011, 38, 6. [Google Scholar] [CrossRef] [Green Version]
- Long, D.; Singh, V.P. A Two-source Trapezoid Model for Evapotranspiration (TTME) from satellite imagery. Remote Sens. Environ. 2012, 121, 370–388. [Google Scholar] [CrossRef]
- Dickinson, R.E. Modeling Evapotranspiration for Three-Dimensional Global Climate Models. In Climate Processes and Vlimate Sensitivity; Geophysical Monograph Series; AGU Publishing: Washington, DC, USA, 1984; Volume 29, ISBN 9781118666036. [Google Scholar] [CrossRef]
- Dezsi, Ş.; Mîndrescu, M.; Petrea, D.; Rai, P.K.; Hamann, A.; Nistor, M.-M. High-resolution projections of evapotranspiration and water availability for Europe under climate change. Int. J. Clim. 2018, 38, 3832–3841. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, W.; Shao, Q.; Xing, W.; Ding, Y.; Fu, J. The response of reference evapotranspiration to climate change in Xinjiang, China: Historical changes, driving forces, and future projections. Int. J. Clim. 2019, 40, 235–254. [Google Scholar] [CrossRef]
- Han, D.; Wang, G.; Liu, T.; Xue, B.-L.; Kuczera, G.; Xu, X. Hydroclimatic response of evapotranspiration partitioning to prolonged droughts in semiarid grassland. J. Hydrol. 2018, 563, 766–777. [Google Scholar] [CrossRef]
- Hui-Mean, F.; Yusop, Z.; Yusof, F. Drought analysis and water resource availability using standardised precipitation evapotranspiration index. Atmos. Res. 2018, 201, 102–115. [Google Scholar] [CrossRef]
- Kingston, D.G.; Todd, M.C.; Taylor, R.G.; Thompson, J.R.; Arnell, N.W. Uncertainty in the estimation of potential evapotranspiration under climate change. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Zhang, F.; Jing, Y.; Liu, Y.; Sun, G. Response of evapotranspiration to changes in land use and land cover and climate in China during 2001–2013. Sci. Total. Environ. 2017, 596–597, 256–265. [Google Scholar] [CrossRef] [PubMed]
- Nam, W.-H.; Hong, E.-M.; Choi, J.-Y. Has climate change already affected the spatial distribution and temporal trends of reference evapotranspiration in South Korea? Agric. Water Manag. 2015, 150, 129–138. [Google Scholar] [CrossRef]
- Alemu, H.; Kaptué, A.T.; Senay, G.B.; Wimberly, M.C.; Henebry, G. Evapotranspiration in the Nile Basin: Identifying Dynamics and Drivers, 2002–2011. Water 2015, 7, 4914–4931. [Google Scholar] [CrossRef]
- Choudhary, D. Methods of Evapotranspiration; CCS Haryana Agricultural University: Hisar, India, 2018. [Google Scholar] [CrossRef]
- Gharsallah, O.; Facchi, A.; Gandolfi, C. Comparison of six evapotranspiration models for a surface irrigated maize agro-ecosystem in Northern Italy. Agric. Water Manag. 2013, 130, 119–130. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Prueger, J.H.; Kustas, W.P.; Anderson, M.C.; Alfieri, J.G. Evapotranspiration: Evolution of Methods to Increase Spatial and Temporal Resolution. Am. Soc. Agron. 2016, 7, 159–193. [Google Scholar] [CrossRef]
- Tanner, C.B. Measurement of evapotranspiration. Irrig. Agric. Lands 1967, 11, 534–574. [Google Scholar]
- Moeletsi, M.E.; Walker, S.; Hamandawana, H. Comparison of the Hargreaves and Samani equation and the Thornthwaite equation for estimating dekadal evapotranspiration in the Free State Province, South Africa. Phys. Chem. Earth Parts A/B/C 2013, 66, 4–15. [Google Scholar] [CrossRef]
- Gul, S.; Ren, J.; Xiong, N.; Khan, M.A. Design and analysis of statistical probability distribution and non-parametric trend analysis for reference evapotranspiration. Peerj 2021, 9, e11597. [Google Scholar] [CrossRef]
- Tegos, A.; Malamos, N.; Koutsoyiannis, D. A parsimonious regional parametric evapotranspiration model based on a simplification of the Penman–Monteith formula. J. Hydrol. 2015, 524, 708–717. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Q.; Cui, B. Spatial distribution and temporal variation of reference evapotranspiration during 1961–2006 in the Yellow River Basin, China. Hydrol. Sci. J. 2011, 56, 1015–1026. [Google Scholar] [CrossRef] [Green Version]
- Gocic, M.; Trajkovic, S. Analysis of trends in reference evapotranspiration data in a humid climate. Hydrol. Sci. J. 2013, 59, 165–180. [Google Scholar] [CrossRef]
- Shadmani, M.; Marofi, S.; Roknian, M. Trend Analysis in Reference Evapotranspiration Using Mann-Kendall and Spearman’s Rho Tests in Arid Regions of Iran. Water Resour. Manag. 2011, 26, 211–224. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, I.; Tang, D.; Wang, T.; Wang, M.; Wagan, B. Precipitation Trends over Time Using Mann-Kendall and Spearman’s rho Tests in Swat River Basin, Pakistan. Adv. Meteorol. 2015, 2015, 431860. [Google Scholar] [CrossRef] [Green Version]
- Kamal, N.; Pachauri, S. Mann-Kendall, and Sen’s Slope Estimators for Precipitation Trend Analysis in North-Eastern States of India. Int. J. Comput. Appl. 2019, 177, 7–16. [Google Scholar] [CrossRef]
- Blain, G.C. Removing the influence of the serial correlation on the Mann-Kendall test. Rev. Bras. Meteorol. 2014, 29, 161–170. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Geng, M.; Wu, Q.; Liang, Y. Study on the spatial-temporal variation in evapotranspiration in China from 1948 to 2018. Sci. Rep. 2020, 10, 17139. [Google Scholar] [CrossRef]
- Bouklikha, A.; Habi, M.; Elouissi, A.; Benzater, B.; Hamoudi, S. The Innovative Trend Analysis Applied to Annual and Seasonal Rainfall in the Tafna Watershed (Algeria). Rev. Bras. Meteorol. 2020, 35, 631–647. [Google Scholar] [CrossRef]
- Al Buhairi, M.H. Analysis of Monthly, Seasonal and Annual Air Temperature Variability and Trends in Taiz City-Republic of Yemen. J. Environ. Prot. 2010, 1, 401–409. [Google Scholar] [CrossRef] [Green Version]
- Caloiero, T.; Coscarelli, R.; Ferrari, E. Assessment of seasonal and annual rainfall trend in Calabria (southern Italy) with the ITA method. J. Hydroinformatics 2019, 22, 738–748. [Google Scholar] [CrossRef]
- Merabtene, T.; Siddique, M.; Shanableh, A. Assessment of Seasonal and Annual Rainfall Trends and Variability in Sharjah City, UAE. Adv. Meteorol. 2016, 2016, 6206238. [Google Scholar] [CrossRef] [Green Version]
- Ndiaye, P.; Bodian, A.; Diop, L.; Deme, A.; Dezetter, A.; Djaman, K.; Ogilvie, A. Trend and Sensitivity Analysis of Reference Evapotranspiration in the Senegal River Basin Using NASA Meteorological Data. Water 2020, 12, 1957. [Google Scholar] [CrossRef]
- Ghafouri-Azar, M.; Bae, D.-H.; Kang, S.-U. Trend Analysis of Long-Term Reference Evapotranspiration and Its Components over the Korean Peninsula. Water 2018, 10, 1373. [Google Scholar] [CrossRef] [Green Version]
- Sonali, P.; Kumar, D.N. Spatio-temporal variability of temperature and potential evapotranspiration over India. J. Water Clim. Chang. 2016, 7, 810–822. [Google Scholar] [CrossRef]
- Liuzzo, L.; Noto, L.V.; Arnone, E.; Caracciolo, D.; La Loggia, G. Modifications in Water Resources Availability Under Climate Changes: A Case Study in a Sicilian Basin. Water Resour. Manag. 2014, 29, 1117–1135. [Google Scholar] [CrossRef]
- Negm, A.; Jabro, J.; Provenzano, G. Assessing the suitability of American National Aeronautics and Space Administration (NASA) agro-climatology archive to predict daily meteorological variables and reference evapotranspiration in Sicily, Italy. Agric. For. Meteorol. 2017, 244–245, 111–121. [Google Scholar] [CrossRef]
- Negm, A.; Minacapilli, M.; Provenzano, G. Spatial disaggregation of POWER-NASA air temperatures and effects on grass reference evapotranspiration in Sicily, Italy. In EGU General Assembly Conference Abstracts; European Geosciences Union: Vienna, Austria, 2017; p. 13591. [Google Scholar]
- Borzì, I.; Bonaccorso, B.; Aronica, G.T. The Role of DEM Resolution and Evapotranspiration Assessment in Modeling Groundwater Resources Estimation: A Case Study in Sicily. Water 2020, 12, 2980. [Google Scholar] [CrossRef]
- Minacapilli, M.; Ciraolo, G.; Cammalleri, C.; D’urso, G. Evaluating actual evapotranspiration by means of mul-ti-platform remote sensing data: A case study in Sicily. IAHS-AISH Publ. 2007, 316, 207–219. [Google Scholar]
- Provenzano, G.; Ippolito, M. Using the ERA5 dataset of atmospheric variables to estimate daily reference evapotranspiration in Sicily, Italy. 4–5. In EGU General Assembly 2021; EGU: Vienna, Austria, 2021. [Google Scholar] [CrossRef]
- Aschale, T.M.; Sciuto, G.; Peres, D.J.; Gullotta, A.; Cancelliere, A. Evaluation of Reference Evapotranspiration Estimation Methods for the Assessment of Hydrological Impacts of Photovoltaic Power Plants in Mediterranean Climates. Water 2022, 14, 2268. [Google Scholar] [CrossRef]
- Consoli, S.; Russo, A.; Snyder, R. Estimating Evapotranspiration Of Orange Orchards Using Surface Renewal And Remote Sensing Techniques. AIP Conf. Proc. 2006, 852, 185–192. [Google Scholar] [CrossRef]
- Minacapilli, M.; Agnese, C.; Blanda, F.; Cammalleri, C.; Ciraolo, G.; D’Urso, G.; Iovino, M.; Pumo, D.; Provenzano, G.; Rallo, G. Estimation of actual evapotranspiration of Mediterranean perennial crops by means of remote-sensing based surface energy balance models. Hydrol. Earth Syst. Sci. 2009, 13, 1061–1074. [Google Scholar] [CrossRef] [Green Version]
- Willett, K.M.; Gillett, N.P.; Jones, P.D.; Thorne, P.W. Attribution of observed surface humidity changes to human influence. Nature 2007, 449, 710–712. [Google Scholar] [CrossRef]
- Hobbins, M.T. The Variability of ASCE Standardized Reference Evapotranspiration: A Rigorous, CONUS-Wide Decomposition and Attribution. Trans. ASABE 2016, 59, 561–576. [Google Scholar] [CrossRef] [Green Version]
- Nikam, B.R.; Kumar, P.; Garg, V.; Thakur, P.K.; Aggarwal, S.P. Comparative evaluation of different potential evapotranspi-ration estimation approaches. Int. J. Res. Eng. Technol. 2014, 3, 544–552. [Google Scholar]
- Alexandris, S.; Stricevic, R.; Petkovic, S. Comparative analysis of reference evapotranspiration from the surface of rainfed grass in central Serbia, calculated by six empirical methods against the Penman-Monteith formula. Eur. Water 2008, 21, 17–28. [Google Scholar]
- Almorox, J.; Senatore, A.; Quej, V.H.; Mendicino, G. Worldwide assessment of the Penman–Monteith temperature approach for the estimation of monthly reference evapotranspiration. Arch. Meteorol. Geophys. Bioclimatol. Ser. B 2016, 131, 693–703. [Google Scholar] [CrossRef]
- Chen, D.; Gao, G.; Xu, C.-Y.; Guo, J.; Ren, G. Comparison of the Thornthwaite method and pan data with the standard Pen-man-Monteith estimates of reference evapotranspiration in China. Clim. Res. 2005, 28, 123–132. [Google Scholar] [CrossRef]
- van der Schrier, G.; Jones, P.D.; Briffa, K.R. The sensitivity of the PDSI to the Thornthwaite and Penman-Monteith parame-teriza- tions for potential evapotranspiration. J. Geophys. Res. Earth Surf. 2011, 116, 1–16. [Google Scholar] [CrossRef]
- Seginer, I. The Penman—Monteith Evapotranspiration Equation as an Element in Greenhouse Ventilation Design. Biosyst. Eng. 2002, 82, 423–439. [Google Scholar] [CrossRef]
- Al-Sudani, H.I.Z. Derivation Mathematical Equations for Future Calculation of Potential Evapotranspiration in Iraq, A Review of Application of Thornthwaite Evapotranspiration. Iraqi J. Sci. 2019, 60, 1037–1048. [Google Scholar] [CrossRef]
- Anapalli, S.S.; Fisher, D.K.; Reddy, K.N.; Wagle, P.; Gowda, P.H.; Sui, R. Quantifying soybean evapotranspiration using an eddy covariance approach. Agric. Water Manag. 2018, 209, 228–239. [Google Scholar] [CrossRef]
- Kjelgaard, J.; Bellocchi, G. Evaluation of estimated weather data for calculating Penman-Monteith reference crop evapotranspiration. Irrig. Sci. 2004, 23, 39–46. [Google Scholar] [CrossRef]
- Hashemi, F.; Habibian, M. Limitations of temperature-based methods in estimating crop evapotranspiration in arid-zone agricultural development projects. Agric. Meteorol. 1979, 20, 237–247. [Google Scholar] [CrossRef]
- Quej, V.H.; Almorox, J.; Arnaldo, J.A.; Moratiel, R. Evaluation of Temperature-Based Methods for the Estimation of Refer-ence Evapotranspiration in the Yucatán Peninsula, Mexico. J. Hydrol. Eng. 2019, 24, 1040–1049. [Google Scholar] [CrossRef]
- Sharifi, A.; Dinpashoh, Y. Sensitivity Analysis of the Penman-Monteith reference Crop Evapotranspiration to Climatic Variables in Iran. Water Resour. Manag. 2014, 28, 5465–5476. [Google Scholar] [CrossRef]
- Subedi, A.; Chávez, J.L. Crop Evapotranspiration (ET) Estimation Models: A Review and Discussion of the Applicability and Limitations of ET Methods. J. Agric. Sci. 2015, 7, p50. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-Fao Irrigation and Drainage Paper 56; Fao: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Peng, L.; Li, Y.; Feng, H. The best alternative for estimating reference crop evapotranspiration in different sub-regions of mainland China. Sci. Rep. 2017, 7, 5458. [Google Scholar] [CrossRef] [Green Version]
- Diop, L.; Bodian, A.; Diallo, D. Spatiotemporal Trend Analysis of the Mean Annual Rainfall in Senegal. Eur. Sci. J. ESJ 2016, 12, 231–245. [Google Scholar] [CrossRef]
- Wu, H.; Xu, M.; Peng, Z.; Chen, X. Temporal variations in reference evapotranspiration in the Tarim River basin, Central Asia. PLoS ONE 2021, 16, e0252840. [Google Scholar] [CrossRef]
- Hu, M.; Sayama, T.; Try, S.; Takara, K.; Tanaka, K. Trend Analysis of Hydroclimatic Variables in the Kamo River Basin, Japan. Water 2019, 11, 1782. [Google Scholar] [CrossRef] [Green Version]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Darshana; Pandey, A.; Pandey, R.P. Analysing trends in reference evapotranspiration and weather variables in the Tons River Basin in Central India. Stoch. Environ. Res. Risk Assess. 2012, 27, 1407–1421. [Google Scholar] [CrossRef]
- Irmak, S.; Payero, J.O.; Martin, D.L.; Irmak, A.; Howell, T.A. Sensitivity Analyses and Sensitivity Coefficients of Standardized Daily ASCE-Penman-Monteith Equation. J. Irrig. Drain. Eng. 2006, 132, 564–578. [Google Scholar] [CrossRef]
- Liang, L.; Li, L.; Zhang, L.; Li, J.; Li, B. Sensitivity of penman-monteith reference crop evapotranspiration in Tao’er River Basin of northeastern China. Chin. Geogr. Sci. 2008, 18, 340–347. [Google Scholar] [CrossRef]
- Patle, G.T.; Sengdo, D.; Tapak, M. Trends in major climatic parameters and sensitivity of evapotranspiration to climatic parameters in the eastern Himalayan region of Sikkim, India. J. Water Clim. Chang. 2019, 11, 491–502. [Google Scholar] [CrossRef]
- Lenhart, T.; Eckhardt, K.; Fohrer, N.; Frede, H.-G. Comparison of two different approaches of sensitivity analysis. Phys. Chem. Earth Parts A/B/C 2002, 27, 645–654. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Cancelliere, A.; Rossi, G. Probabilistic forecasting of drought class transitions in Sicily (Italy) using Stand-ardized Precipitation Index and North Atlantic Oscillation Index. J. Hydrol. 2015, 526, 136–150. [Google Scholar] [CrossRef]
- Torina, A.; Khoury, C.; Caracappa, S.; Maroli, M. Ticks Infesting Livestock on Farms in Western Sicily, Italy. Exp. Appl. Acarol. 2006, 38, 75–86. [Google Scholar] [CrossRef] [PubMed]
- Jain, S.K.; Kumar, V. Trend analysis of rainfall and temperature data for India. Curr. Sci. 2012, 102, 37–49. [Google Scholar]
- Mohammad, P.; Goswami, A. Temperature and precipitation trend over 139 major Indian cities: An assessment over a century. Model. Earth Syst. Environ. 2019, 5, 1481–1493. [Google Scholar] [CrossRef]
- Mondal, A.; Khare, D.; Kundu, S. Spatial and temporal analysis of rainfall and temperature trend of India. Theor. Appl. Clim. 2014, 122, 143–158. [Google Scholar] [CrossRef]
- Saboohi, R.; Soltani, S.; Khodagholi, M. Trend analysis of temperature parameters in Iran. Theor. Appl. Clim. 2012, 109, 529–547. [Google Scholar] [CrossRef]
- Subash, N.; Sikka, A.K. Trend analysis of rainfall and temperature and its relationship over India. Theor. Appl. Clim. 2013, 117, 449–462. [Google Scholar] [CrossRef]
- Huss, M.; Farinotti, D.; Bauder, A.; Funk, M. Decadal trend of climate in the Tibetan Plateau—Regional temperature and precipitation. Hydrol. Process. Int. J. 2008, 22, 3056–3065. [Google Scholar]
- Liuzzo, L.; Bono, E.; Sammartano, V.; Freni, G. Long-term temperature changes in Sicily, Southern Italy. Atmos. Res. 2017, 198, 44–55. [Google Scholar] [CrossRef]
- Liuzzo, L.; Bono, E.; Sammartano, V.; Freni, G. Analysis of spatial and temporal rainfall trends in Sicily during the 1921–2012 period. Theor. Appl. Clim. 2015, 126, 113–129. [Google Scholar] [CrossRef]
- Jones, P. Maximum and minimum temperature trends in Ireland, Italy, Thailand, Turkey and Bangladesh. Atmos. Res. 1995, 37, 67–78. [Google Scholar] [CrossRef]
- Brunetti, M.; Buffoni, L.; Maugeri, M.; Nanni, T. Trends of Minimum and Maximum Daily Temperatures in Italy from 1865 to 1996. Theor. Appl. Clim. 2000, 66, 49–60. [Google Scholar] [CrossRef]
- Ventura, F.; Pisa, P.R.; Ardizzoni, E. Temperature and precipitation trends in Bologna (Italy) from 1952 to 1999. Atmos. Res. 2002, 61, 203–214. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. Trend analysis of monthly mean values and extreme indices of daily temperature in a region of southern Italy. Int. J. Clim. 2017, 37, 284–297. [Google Scholar] [CrossRef]
- Caloiero, T.; Guagliardi, I. Climate change assessment: Seasonal and annual temperature analysis trends in the Sardinia region (Italy). Arab. J. Geosci. 2021, 14, 2149. [Google Scholar] [CrossRef]
- Mollema, P.; Antonellini, M.; Gabbianelli, G.; Laghi, M.; Marconi, V.; Minchio, A. Climate and water budget change of a Mediterranean coastal watershed, Ravenna, Italy. Environ. Earth Sci. 2011, 65, 257–276. [Google Scholar] [CrossRef]
- Segnalini, M.; Bernabucci, U.; Vitali, A.; Nardone, A.; Lacetera, N. Temperature humidity index scenarios in the Mediterranean basin. Int. J. Biometeorol. 2012, 57, 451–458. [Google Scholar] [CrossRef]
- Abu-Taleb, A.A.; Alawneh, A.J.; Smadi, M. Statistical Analysis of Recent Changes in Relative Humidity in Jordan. Am. J. Environ. Sci. 2007, 3, 75–77. [Google Scholar] [CrossRef] [Green Version]
- Kousari, M.R.; Ekhtesasi, M.R.; Tazeh, M.; Naeini, M.A.S.; Zarch, M.A.A. An investigation of the Iranian climatic changes by considering the precipitation, temperature, and relative humidity parameters. Theor. Appl. Clim. 2010, 103, 321–335. [Google Scholar] [CrossRef]
- Huss, M.; Farinotti, D.; Bauder, A.; Funk, M. Changes in rainfall and relative humidity in river basins in northwest and central India. Hydrol. Process. Int. J. 2008, 22, 2982–2992. [Google Scholar]
- Manara, V.; Beltrano, M.C.; Brunetti, M.; Maugeri, M.; Sanchez-Lorenzo, A.; Simolo, C.; Sorrenti, S. Sunshine duration variability and trends in Italy from homogenized instrumental time series (1936-2013). J. Geophys. Res. Atmos. 2015, 120, 3622–3641. [Google Scholar] [CrossRef] [Green Version]
- Che, H.Z.; Shi, G.Y.; Zhang, X.-Y.; Arimoto, R.; Zhao, J.Q.; Xu, L.; Wang, B.; Chen, Z.H. Analysis of 40 years of solar radiation data from China, 1961–2000. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, L.; Lin, A.; Zhang, M.; Niu, Z. Innovative trend analysis of solar radiation in China during 1962–2015. Renew. Energy 2018, 119, 675–689. [Google Scholar] [CrossRef]
- Ohmura, A. Observed decadal variations in surface solar radiation and their causes. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Eymen, A.; Köylü, U. Seasonal trend analysis and ARIMA modeling of relative humidity and wind speed time series around Yamula Dam. Meteorol. Atmos. Phys. 2018, 131, 601–612. [Google Scholar] [CrossRef]
- Jiang, Y.; Luo, Y.; Zhao, Z.; Tao, S. Changes in wind speed over China during 1956–2004. Theor. Appl. Clim. 2009, 99, 421–430. [Google Scholar] [CrossRef]
- Laib, M.; Golay, J.; Telesca, L.; Kanevski, M. Multifractal analysis of the time series of daily means of wind speed in complex regions. Chaos Solitons Fractals 2018, 109, 118–127. [Google Scholar] [CrossRef] [Green Version]
- Klink, K. Trends and Interannual Variability of Wind Speed Distributions in Minnesota. J. Clim. 2002, 15, 3311–3317. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Aeini, A.; Talaee, P.H.; Mohammadi, K. Trend analysis of reference evapotranspiration in the western half of Iran. Agric. For. Meteorol. 2011, 151, 128–136. [Google Scholar] [CrossRef]
- Peres, D.J.; Modica, R.; Cancelliere, A. Assessing Future Impacts of Climate Change on Water Supply System Performance: Application to the Pozzillo Reservoir in Sicily, Italy. Water 2019, 11, 2531. [Google Scholar] [CrossRef] [Green Version]
- Peres, D.J.; Senatore, A.; Nanni, P.; Cancelliere, A.; Mendicino, G.; Bonaccorso, B. Evaluation of EURO-CORDEX (Coordinated Regional Climate Downscaling Experiment for the Euro-Mediterranean area) historical simulations by high-quality observational datasets in southern Italy: Insights on drought assessment. Nat. Hazards Earth Syst. Sci. 2020, 20, 3057–3082. [Google Scholar] [CrossRef]
- Peres, D.J.; Bonaccorso, B.; Palazzolo, N.; Cancelliere, A.; Mendicino, G.; Senatore, A. Projected changes of hy-drologic variables and drought indices in southern Italy through an optimized Euro-CORDEX climate model ensemble weighted average. Hydrol. Sci. J. 2022; under review. [Google Scholar]
- Stefanidis, S.; Alexandridis, V. Precipitation and Potential Evapotranspiration Temporal Variability and Their Relationship in Two Forest Ecosystems in Greece. Hydrology 2021, 8, 160. [Google Scholar] [CrossRef]


| Sensitivity Coefficient | Sensitivity Level |
|---|---|
| 0.00 ≤ || < 0.05 | Negligible |
| 0.05 ≤ || < 0.2 | Moderate |
| 0.2 ≤ || < 1 | High |
| 1.00 ≤ || | Very high |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | Win | Spr | Sum | Aut | Annual | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tmax | 1.1 | 1.19 | 2.27 | 1.44 | 0.91 | 1.77 | 1.61 | 1.69 | 2.43 | 0.78 | 1.69 | 1.86 | 1.77 | 2.14 | 1.98 | 1.49 | 1.31 |
| Tmin | 0.08 | 0.95 | 0.99 | 0.62 | −0.49 | −0.21 | 1.19 | 2.18 | 2.14 | 0.01 | 1.36 | −0.37 | 0.12 | 0.33 | 1.03 | 1.4 | 1.19 |
| Tmean | 0.12 | 1.03 | 1.94 | 1.36 | 0.29 | 0.45 | 1.69 | 1.77 | 2.35 | 0.29 | 1.77 | 0.62 | 0.95 | 2.51 | 2.18 | 1.49 | 1.58 |
| SR | −0.95 | −0.54 | −0.7 | 0.62 | −1.65 | −0.33 | −0.78 | −1.2 | −1.07 | −1.44 | −2.02 | 0.95 | −0.12 | −0.87 | −0.91 | −2.6 | −1.44 |
| WS | 2.68 | 0.99 | 1.03 | 1.28 | 2.76 | 2.18 | 2.97 | 1.73 | 0.77 | 0.95 | 2.39 | 2.23 | 2.76 | 2.02 | 0.95 | 0.86 | 0.95 |
| HU | 0.41 | 0.5 | 2.27 | 2.27 | 2.12 | 2.84 | 3.17 | 2.39 | 2.12 | 2.02 | 1.22 | 2.02 | 0.86 | 2.21 | 2.03 | 1.31 | 1.31 |
| ETo | −1.85 | −0.95 | −1.11 | 0.45 | −1.28 | −0.62 | 0.54 | 0.21 | 0.45 | 0.04 | −2.51 | −0.95 | −0.54 | −0.78 | −0.21 | −0.54 | −0.78 |
| RF | −0.04 | 0.45 | −0.62 | −1.19 | 0.29 | −0.49 | 0.46 | 0.64 | −0.21 | 0.33 | 0.95 | 0.5 | −1.28 | −0.29 | −0.04 | −2.6 | −1.61 |
| Climatological Element | Sensitivity Coefficient |x| | Sensitivity Level |
|---|---|---|
| Net solar radiation | |0.53| | High |
| Maximum temperature | |1.35| | Very high |
| Minimum temperature | |−0.28| | High |
| Mean temperature | |1.46| | Very high |
| Specific humidity | |−2.68| | Very high |
| Wind speed | |0.02| | Negligible |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aschale, T.M.; Peres, D.J.; Gullotta, A.; Sciuto, G.; Cancelliere, A. Trend Analysis and Identification of the Meteorological Factors Influencing Reference Evapotranspiration. Water 2023, 15, 470. https://doi.org/10.3390/w15030470
Aschale TM, Peres DJ, Gullotta A, Sciuto G, Cancelliere A. Trend Analysis and Identification of the Meteorological Factors Influencing Reference Evapotranspiration. Water. 2023; 15(3):470. https://doi.org/10.3390/w15030470
Chicago/Turabian StyleAschale, Tagele Mossie, David J. Peres, Aurora Gullotta, Guido Sciuto, and Antonino Cancelliere. 2023. "Trend Analysis and Identification of the Meteorological Factors Influencing Reference Evapotranspiration" Water 15, no. 3: 470. https://doi.org/10.3390/w15030470





