Deriving Operating Rules of Hydropower Reservoirs Using Multi-Strategy Ensemble Henry Gas Solubility Optimization-Driven Support Vector Machine
Abstract
:1. Introduction
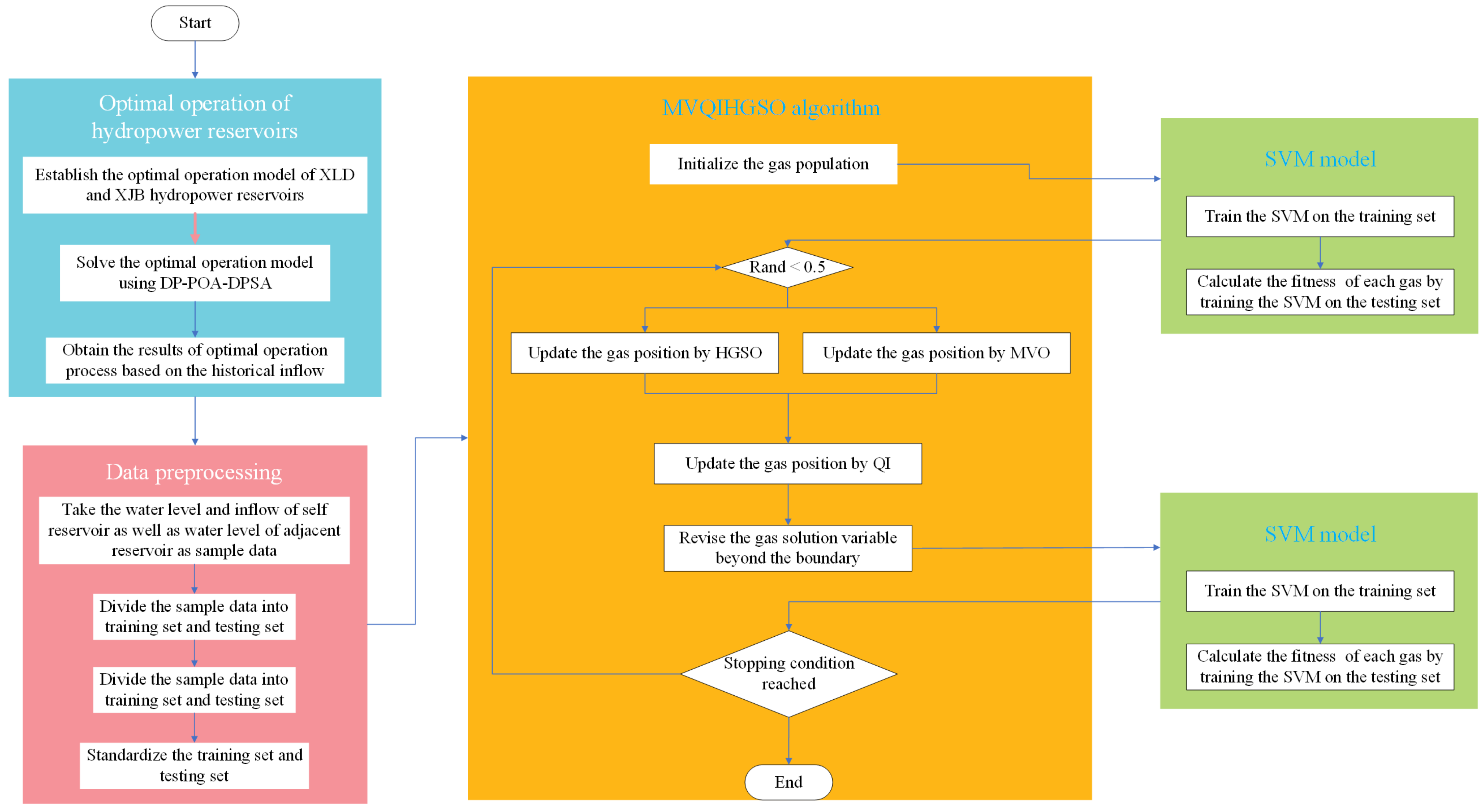
2. Materials and Methods
2.1. Optimal Operation Model of Hydropower Reservoirs
2.1.1. Objectives
2.1.2. Constraints
2.2. Summary of Henry Gas Solubility Optimization (HGSO)
2.3. The Proposed MVQIHGSO
2.3.1. Multi-verse Optimizer (MVO)
2.3.2. Quadratic Interpolation Strategy (QI)
2.3.3. The Proposed Enhanced HGSO Algorithm
| Algorithm 1. Detailed information of MVQIHGSO algorithm. |
| Pseudocode of the MVQIHGSO 01: Inputs: the population size N; the maximum number of iteration MaxIt; the constant values including c1, c2, c3 in Equations (2) and (3), c4 and c5 in Equation (6), α, β, and ε in Equatios (4) and (5); the number of groups l 02: Initialize the gas population within the lower and upper boundary 03: Divide the gas population into specific groups with the same Henry’s constant value 04: Evaluate the gas of each group in the population 05: Obtain the best gas of the whole population and the l best gases corresponding to l groups 06: for it from 1 to MaxIt do 07: Generate random number r within [0, 1] 08: if r smaller than 0.5 do 09: Update the gas position by basic HGSO 10: else do 11: Update the gas position by MVO 12: end if 13: Sort the updated gas population by HGSO and MVO 14: Updating the gas population from 1 to N-2 by QI strategy based on greedy law 15: Evaluate the fitness of the final updated gas population 16: Update the best gas position obtained so far and the l best gases corresponding to l groups 17: end for 18: Outputs: the best global gas position and the corresponding optimal fitness value |
2.4. Support Vector Machine
3. Experimental Evaluation and Discussion
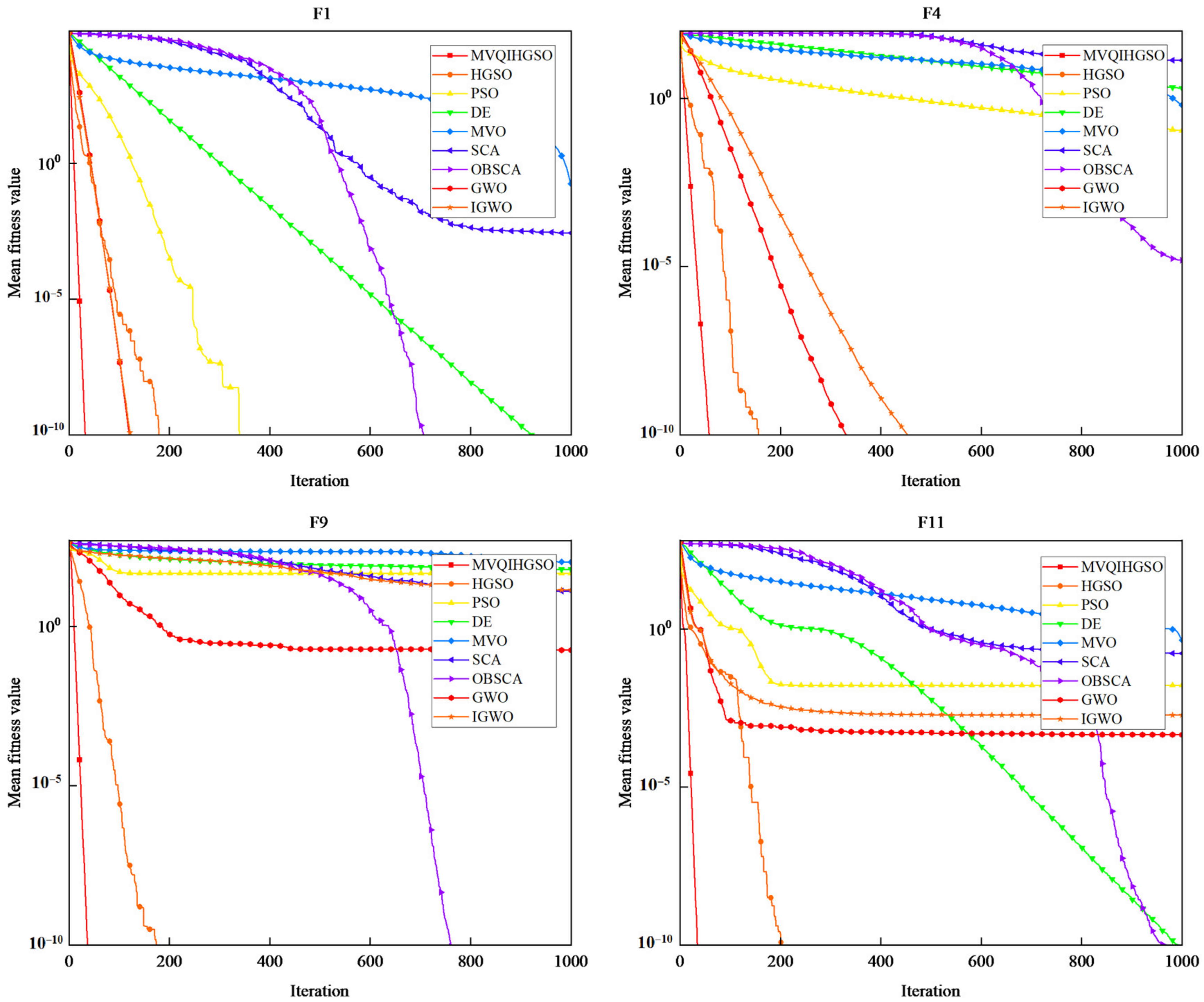
3.1. Statistical Results and Analysis
3.2. Non-Parameter Test Results and Analysis
4. Case Study
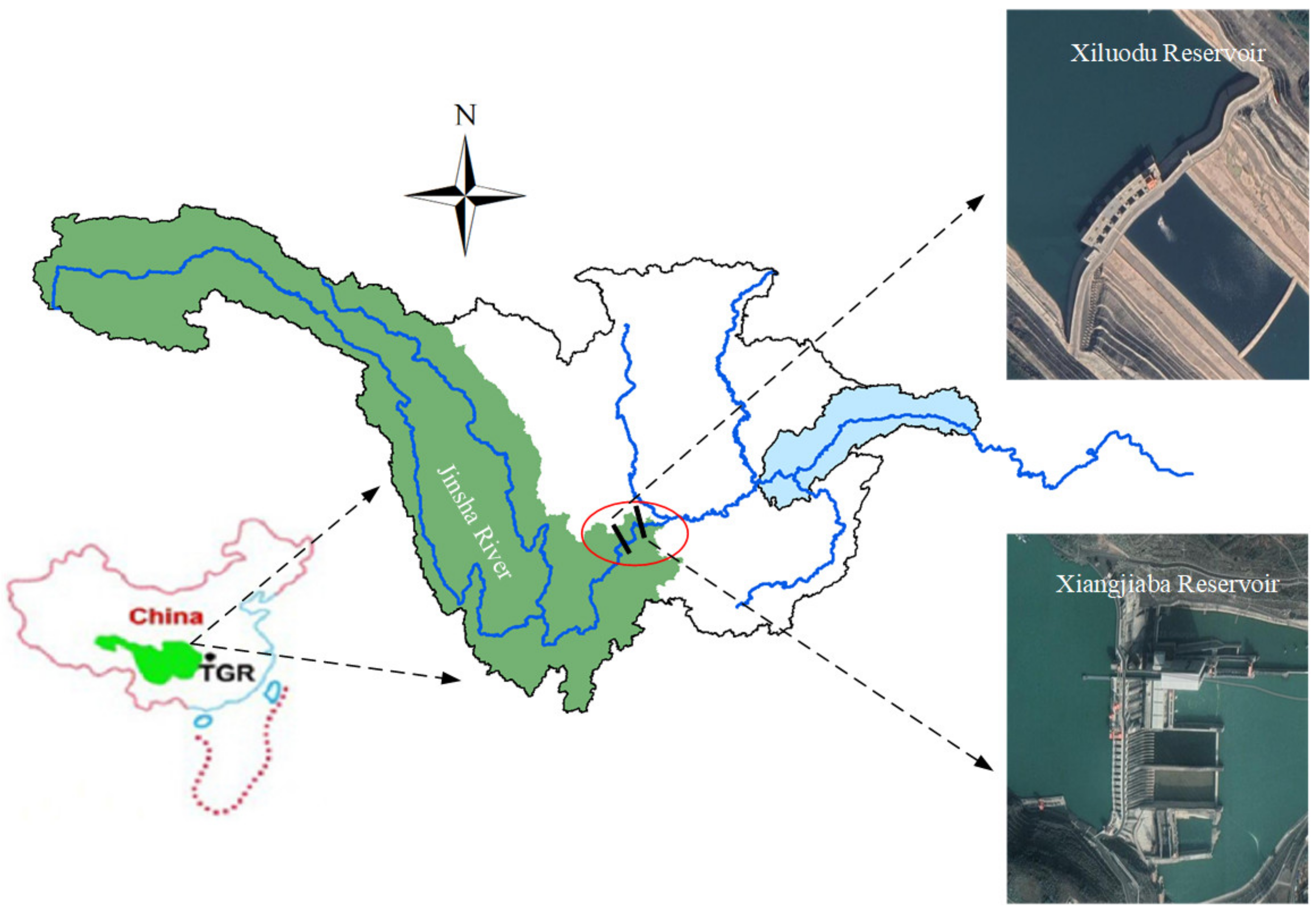
4.1. Study Region
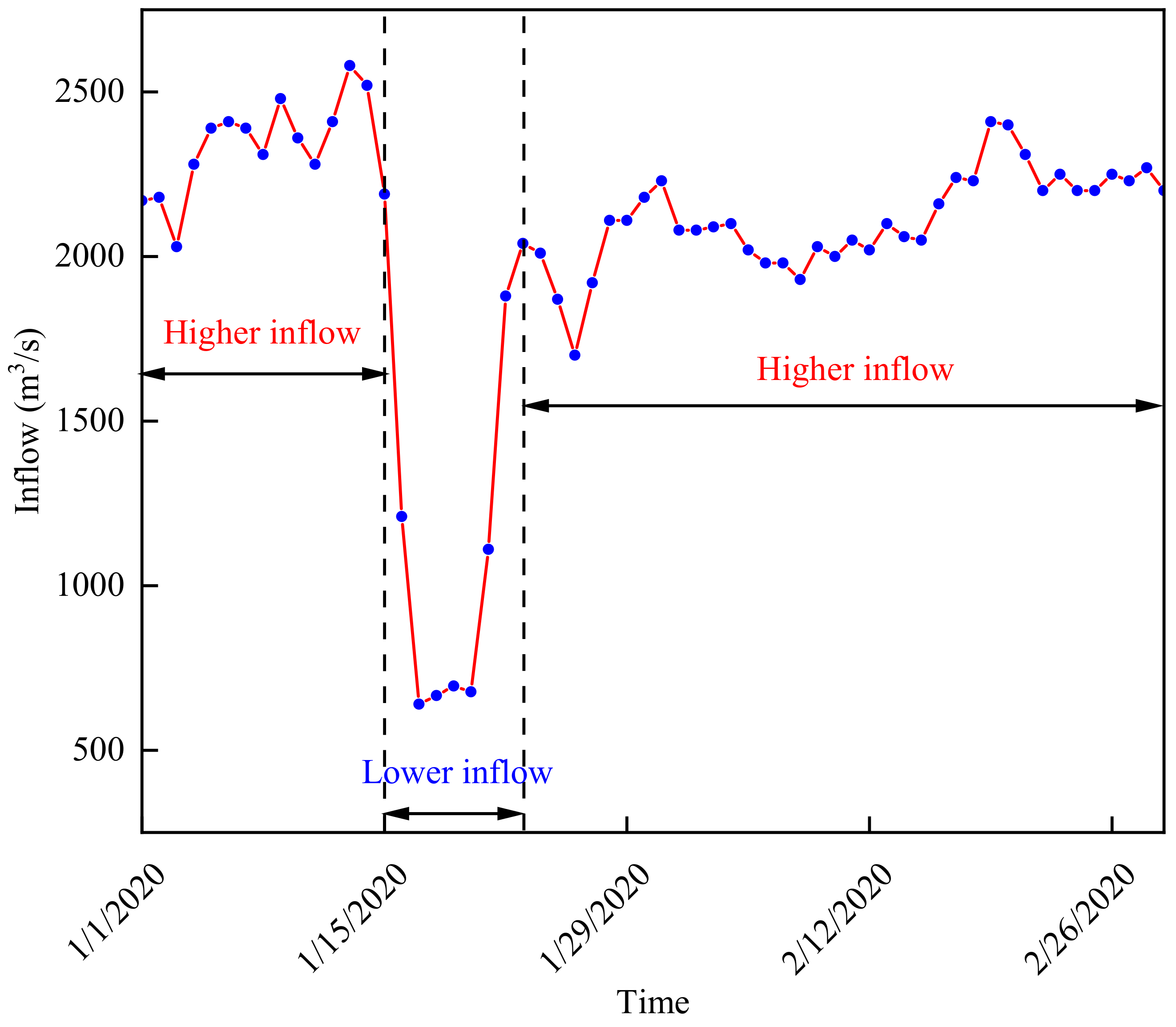
4.2. Data Description
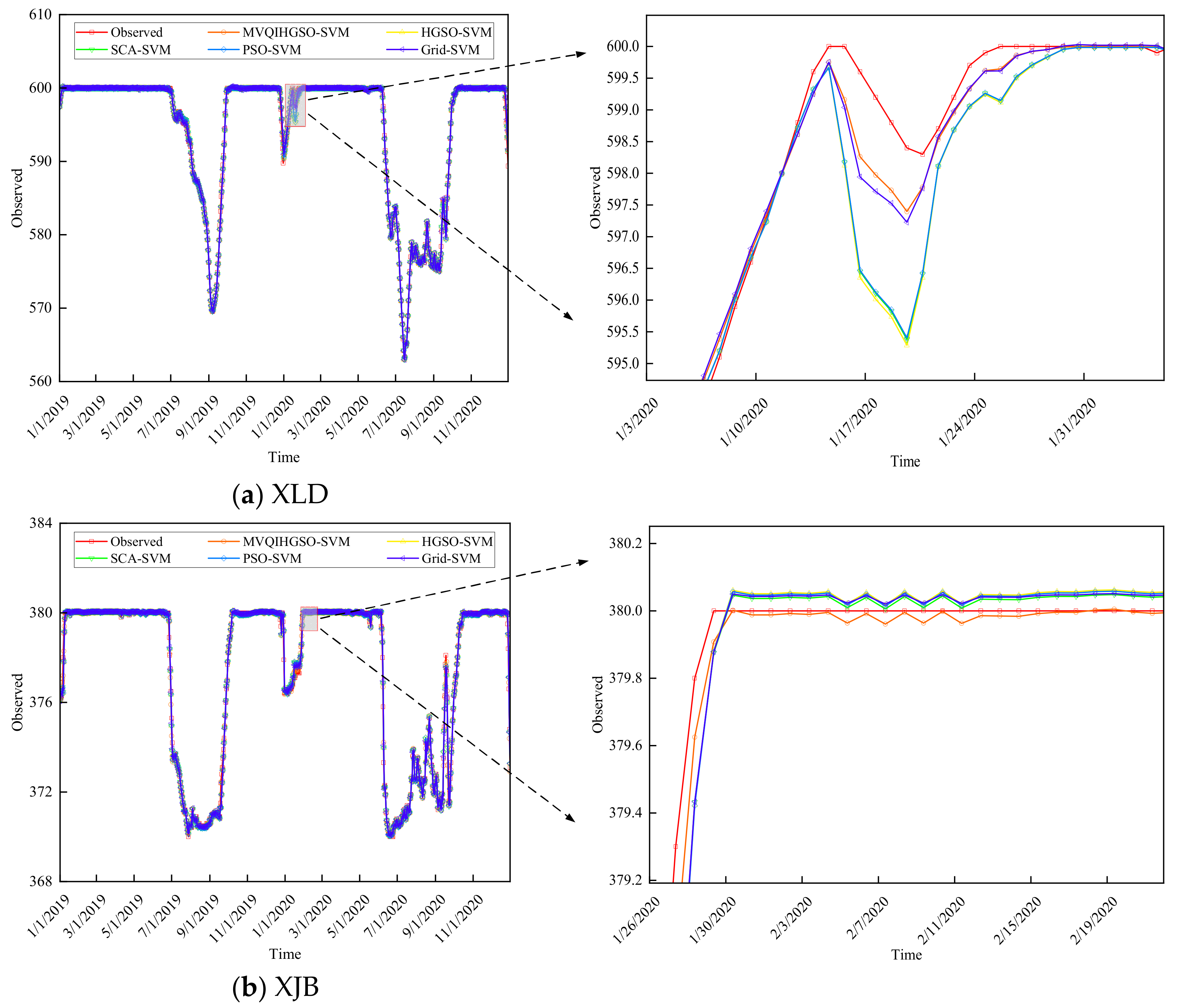
4.3. Results and Discussion
5. Conclusions
- (1)
- Multiple strategies are equipped into HGSO to improve its performance in exploration and exploitation. The multi-verse optimizer (MVO) is used to enhance the exploration capability of basic HGSO and help the inferior agent to escape from local optimal. Quadratic interpolation (QI) is used to improve the exploitation ability of HGSO. Finally, the exploration and exploitation are balanced by integrating the multiple strategies.
- (2)
- MVQIHGSO with multiple strategies is benchmarked by 23 classical benchmark functions. The results demonstrates that MVQIHGSO outperforms most of the well-known metaheuristic algorithms and has a superior efficacy compared to the competitors based on the convergence accuracy and speed.
- (3)
- MVQIHGSO-SVM model is used to derive operating rules of hydropower reservoirs. The XLD and XJB in the upper Yangtze River are selected as a case study. The results indicate that the proposed MVQIHGSO-SVM model can accurately obtain the joint operation rules of hydropower reservoirs. The total hydropower generation calculated by the proposed hybrid model is closer to the optimal operation result, and the hydropower generation increased the most compared to conventional scheduling, reaching 22.25 × 108 kWh, increasing by 1.15%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhai, R.; Tao, F. Contributions of climate change and human activities to runoff change in seven typical catchments across China. Sci. Total Environ. 2017, 605, 219–229. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, R.S.; Ürge-Vorsatz, D.; Barau, A.S. Sustainable Development Goals and climate change adaptation in cities. Nat. Clim. Chang. 2018, 8, 181–183. [Google Scholar] [CrossRef]
- Qiu, H.; Chen, L.; Zhou, J.; He, Z.; Zhang, H. Risk analysis of water supply-hydropower generation-environment nexus in the cascade reservoir operation. J. Clean. Prod. 2021, 283, 124239. [Google Scholar] [CrossRef]
- Qiu, H.; Zhou, J.; Chen, L.; Zhu, Y. Multiple Strategies Based Salp Swarm Algorithm for Optimal Operation of Multiple Hydropower Reservoirs. Water 2021, 13, 2753. [Google Scholar] [CrossRef]
- Baloch, M.A.; Mahmood, N.; Zhang, J.W. Effect of natural resources, renewable energy and economic development on CO2 emissions in BRICS countries. Sci. Total Environ. 2019, 678, 632–638. [Google Scholar]
- Su, C.W.; Umar, M.; Khan, Z. Does fiscal decentralization and eco-innovation promote renewable energy consumption? Analyzing the role of political risk. Sci. Total Environ. 2021, 751, 142220. [Google Scholar] [CrossRef]
- Kang, J.N.; Wei, Y.M.; Liu, L.C.; Han, R.; Yu, B.Y.; Wang, J.W. Energy systems for climate change mitigation: A systematic review. Appl. Energy 2020, 263, 114602. [Google Scholar] [CrossRef]
- Xu, J.; Ni, T.; Zheng, B. Hydropower development trends from a technological paradigm perspective. Energy Convers. Manag. 2015, 90, 195–206. [Google Scholar] [CrossRef]
- Li, H.; Liu, P.; Guo, S.; Cheng, L.; Huang, K.; Feng, M.; He, S.; Ming, B. Deriving adaptive long-term complementary operating rules for a large-scale hydro-photovoltaic hybrid power plant using ensemble Kalman filter. Appl. Energy 2021, 301, 117482. [Google Scholar] [CrossRef]
- Berga, L. The role of hydropower in climate change mitigation and adaptation: A review. Engineering 2016, 2, 313–318. [Google Scholar] [CrossRef] [Green Version]
- Killingtveit, A. Hydropower. In Managing Global Warming; Academic Press: Cambridge, MA, USA, 2019; pp. 265–315. [Google Scholar]
- Provansal, M.; Dufour, S.; Sabatier, F.; Anthony, E.J.; Raccasi, G.; Robresco, S. The geomorphic evolution and sediment balance of the lower Rhône River (southern France) over the last 130 years: Hydropower dams versus other control factors. Geomorphology 2014, 219, 27–41. [Google Scholar] [CrossRef]
- Zhang, H.; Chang, J.; Gao, C.; Wu, H.; Wang, Y.; Lei, K.; Long, R.; Zhang, L. Cascade hydropower plants operation considering comprehensive ecological water demands. Energy Convers. Manag. 2019, 180, 119–133. [Google Scholar] [CrossRef]
- Brandão, J.L.B. Performance of the equivalent reservoir modelling technique for multi-reservoir hydropower systems. Water Resour. Manag. 2010, 24, 3101–3114. [Google Scholar] [CrossRef]
- Fu, X.; Li, A.; Wang, L.; Ji, C. Short-term scheduling of cascade reservoirs using an immune algorithm-based particle swarm optimization. Comput. Math. Appl. 2011, 62, 2463–2471. [Google Scholar] [CrossRef] [Green Version]
- Allawi, M.F.; Jaafar, O.; Ehteram, M.; Hamzah, F.M.; El-Shafie, A. Synchronizing artificial intelligence models for operating the dam and reservoir system. Water Resour. Manag. 2018, 32, 3373–3389. [Google Scholar] [CrossRef]
- Dobson, B.; Wagener, T.; Pianosi, F. An argument-driven classification and comparison of reservoir operation optimization methods. Adv. Water Resour. 2019, 128, 74–86. [Google Scholar] [CrossRef]
- Howson, H.R.; Sancho, N.G.F. A new algorithm for the solution of multi-state dynamic programming problems. Math. Program. 1975, 8, 104–116. [Google Scholar] [CrossRef]
- Hossain, M.S.; El-Shafie, A. Intelligent systems in optimizing reservoir operation policy: A review. Water Resour. Manag. 2013, 27, 3387–3407. [Google Scholar] [CrossRef]
- Yeh, W.W.G. Reservoir management and operations models: A state-of-the-art review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Feng, M.; Liu, P.; Guo, S.; Shi, L.; Deng, C.; Ming, B. Deriving adaptive operating rules of hydropower reservoirs using time-varying parameters generated by the E n KF. Water Resour. Res. 2017, 53, 6885–6907. [Google Scholar] [CrossRef]
- Kumar, D.N.; Baliarsingh, F. Folded dynamic programming for optimal operation of multireservoir system. Water Resour. Manag. 2003, 17, 337–353. [Google Scholar] [CrossRef]
- Pant, M.; Rani, D. Large scale reservoir operation through integrated meta-heuristic approach. Memetic Comput. 2021, 13, 359–382. [Google Scholar]
- Srinivasan, K.; Kumar, K. Multi-objective simulation-optimization model for long-term reservoir operation using piecewise linear hedging rule. Water Resour. Manag. 2018, 32, 1901–1911. [Google Scholar] [CrossRef]
- Mehta, R.; Jain, S.K. Optimal operation of a multi-purpose reservoir using neuro-fuzzy technique. Water Resour. Manag. 2009, 23, 509–529. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Wu, X.Y. Optimization of hydropower system operation by uniform dynamic programming for dimensionality reduction. Energy 2017, 134, 718–730. [Google Scholar] [CrossRef]
- Bhaskar, N.R.; Whitlatch, E.E., Jr. Derivation of monthly reservoir release policies. Water Resour. Res. 1980, 16, 987–993. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Zhang, R.; Wang, S.; Cheng, C.T. Operation rule derivation of hydropower reservoir by k-means clustering method and extreme learning machine based on particle swarm optimization. J. Hydrol. 2019, 576, 229–238. [Google Scholar] [CrossRef]
- He, S.; Guo, S.; Yang, G.; Chen, K.; Liu, D.; Zhou, Y. Optimizing operation rules of cascade reservoirs for adapting climate change. Water Resour. Manag. 2020, 34, 101–120. [Google Scholar] [CrossRef]
- Niu, W.J.; Feng, Z.K.; Feng, B.F.; Min, Y.W.; Cheng, C.T.; Zhou, J.Z. Comparison of multiple linear regression, artificial neural network, extreme learning machine, and support vector machine in deriving operation rule of hydropower reservoir. Water 2019, 11, 88. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Li, L.; Chen, G.; Rheinheimer, D.E. Parameter uncertainty analysis of reservoir operating rules based on implicit stochastic optimization. J. Hydrol. 2014, 514, 102–113. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef]
- Li, L.L.; Zhao, X.; Tseng, M.L.; Tan, R.R. Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm. J. Clean. Prod. 2020, 242, 118447. [Google Scholar] [CrossRef]
- Albardan, M.; Klein, J.; Colot, O. SPOCC: Scalable POssibilistic Classifier Combination-toward robust aggregation of classifiers. Expert Syst. Appl. 2020, 150, 113332. [Google Scholar] [CrossRef] [Green Version]
- Chilakala, L.R.; Kishore, G.N. Optimal deep belief network with opposition-based hybrid grasshopper and honeybee optimization algorithm for lung cancer classification: A DBNGHHB approach. Int. J. Imaging Syst. Technol. 2021, 31, 1404–1423. [Google Scholar] [CrossRef]
- Henry, W. Experiments on the quantity of gases absorbed by water, at different temperatures, and under different pressures. Philos. Trans. R. Soc. Lond. 1803, 93, 29–274. [Google Scholar]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Yang, Y.; Zong, X.; Yao, D.; Li, S. Improved Alopex-based evolutionary algorithm (AEA) by quadratic interpolation and its application to kinetic parameter estimations. Appl. Soft Comput. 2017, 51, 23–38. [Google Scholar] [CrossRef]
- Guo, W.Y.; Wang, Y.; Dai, F.; Xu, P. Improved sine cosine algorithm combined with optimal neighborhood and quadratic interpolation strategy. Eng. Appl. Artif. Intell. 2020, 94, 103779. [Google Scholar] [CrossRef]
- Zhang, H.; Cai, Z.; Ye, X.; Wang, M.; Kuang, F.; Chen, H.; Li, C.; Li, Y. A multi-strategy enhanced salp swarm algorithm for global optimization. Eng. Comput. 2020, 38, 1177–1203. [Google Scholar] [CrossRef]
- Scholkopf, B.; Smola, A.J. Learning with kernels: Support vector machines, regularization, optimization, and beyond. In Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Courant, R.; Hilbert, D. The calculus of variations. In Methods of Mathematical Physics; Interscience Publishers: New York, NY, USA, 1953; pp. 164–274. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-international conference on neural networks, Perth, WA, Australia, 27 November 1995–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Oliva, D.; Xiong, S. An improved opposition-based sine cosine algorithm for global optimization. Expert Syst. Appl. 2017, 90, 484–500. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
- Carrasco, J.; García, S.; Rueda, M.M.; Das, S.; Herrera, F. Recent trends in the use of statistical tests for comparing swarm and evolutionary computing algorithms: Practical guidelines and a critical review. Swarm Evol. Comput. 2020, 54, 100665. [Google Scholar] [CrossRef] [Green Version]
- Muthusamy, H.; Ravindran, S.; Yaacob, S.; Polat, K. An improved elephant herding optimization using sine–cosine mechanism and opposition based learning for global optimization problems. Expert Syst. Appl. 2021, 172, 114607. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar]
- Young, G.K., Jr. Finding reservoir operating rules. J. Hydraul. Div. 1967, 93, 297–322. [Google Scholar] [CrossRef]

| Function | Dim | Range | fmin |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−10, 10] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−30, 30] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−1.28, 1.28] | 0 |
| Function | Dim | Range | fmin |
|---|---|---|---|
| 30 | [−500, 500] | −418.9829 × 5 | |
| 30 | [−5.12, 5.12] | 0 | |
| 30 | [−32, 32] | 0 | |
| 30 | [−600, 600] | 0 | |
| 30 | [−50, 50] | 0 | |
| 30 | [−50, 50] | 0 |
| Function | Dim | Range | fmin |
|---|---|---|---|
| 2 | [−65, 65] | 1 | |
| 4 | [−5, 5] | 0.00030 | |
| 2 | [−5, 5] | −1.0316 | |
| 2 | [−5, 5] | 0.398 | |
| 2 | [−2, 2] | 3 | |
| 3 | [1, 3] | −3.86 | |
| 6 | [0, 1] | −3.32 | |
| 4 | [0, 10] | −10.1532 | |
| 4 | [0, 10] | −10.4028 | |
| 4 | [0, 10] | −10.5363 |
| Functions | Indicator | MVQIHGSO | HGSO | PSO | DE | MVO | SCA | OBSCA | GWO | IGWO | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Unimodal | F1 | Mean | 0.00 | 1.71 × 10−71 | 2.33 × 10−40 | 5.29 × 10−12 | 1.79 × 10−1 | 2.74 × 10−3 | 1.11 × 10−27 | 2.48 × 10−70 | 2.57 × 10−71 |
| Std | 9.34 × 10−71 | 0.00 | 1.04 × 10−39 | 2.22 × 10−12 | 5.80 × 10−2 | 7.88 × 10−3 | 4.22 × 10−27 | 7.10 × 10−70 | 6.07 × 10−71 | ||
| F2 | Mean | 4.10 × 10−185 | 1.25 × 10−43 | 8.79 × 10−3 | 4.65 × 10−8 | 3.55 | 3.17 × 10−6 | 4.21 × 10−25 | 6.67 × 10−41 | 1.95 × 10−42 | |
| Std | 6.83 × 10−43 | 0.00 | 3.15 × 10−2 | 1.23 × 10−8 | 1.81 × 101 | 4.67 × 10−6 | 2.18 × 10−24 | 7.20 × 10−41 | 3.62 × 10−42 | ||
| F3 | Mean | 0.00 | 1.04 × 10−69 | 1.09 × 10−1 | 2.41 × 104 | 1.83 × 101 | 2.10 × 103 | 1.32 × 10−3 | 7.80 × 10−19 | 8.61 × 10−13 | |
| Std | 5.66 × 10−69 | 0.00 | 1.28 × 10−1 | 2.77 × 103 | 6.90 | 1.73 × 103 | 5.17 × 10−3 | 3.92 × 10−18 | 4.38 × 10−12 | ||
| F4 | Mean | 2.06 × 10−72 | 1.51 × 10−183 | 1.09 × 10−1 | 2.00 | 6.33 × 10−1 | 1.36 × 101 | 1.55 × 10−5 | 1.15 × 10−17 | 7.93 × 10−15 | |
| Std | 1.13 × 10−71 | 0.00 | 7.10 × 10−2 | 2.44 × 10−1 | 2.77 × 10−1 | 9.40 | 2.88 × 10−5 | 1.69 × 10−17 | 6.16 × 10−15 | ||
| F5 | Mean | 2.85 × 101 | 2.80 × 101 | 4.06 × 101 | 4.65 × 101 | 3.08 × 102 | 5.54 × 102 | 2.79 × 101 | 2.65 × 101 | 2.25 × 101 | |
| Std | 2.70 × 10−1 | 6.13 × 10−1 | 2.77 × 101 | 2.31 × 101 | 5.98 × 102 | 2.18 × 103 | 3.06 × 10−1 | 7.80 × 10−1 | 2.79 × 10−1 | ||
| F6 | Mean | 1.74 × 10−1 | 3.44 | 3.63 × 10−23 | 4.92 × 10−12 | 1.66 × 10−1 | 4.29 | 4.10 | 4.13 × 10−1 | 1.01 × 10−5 | |
| Std | 6.39 × 10−2 | 5.26 × 10−1 | 1.84 × 10−22 | 1.84 × 10−12 | 4.89 × 10−2 | 3.92 × 10−1 | 2.73 × 10−1 | 2.57 × 10−1 | 2.39 × 10−6 | ||
| F7 | Mean | 6.76 × 10−5 | 7.92 × 10−4 | 9.32 × 10−3 | 2.59 × 10−2 | 1.22 × 10−2 | 2.35 × 10−2 | 1.47 × 10−3 | 4.72 × 10−4 | 8.64 × 10−4 | |
| Std | 4.35 × 10−4 | 4.84 × 10−5 | 4.00 × 10−3 | 4.70 × 10−3 | 5.04 × 10−3 | 2.54 × 10−2 | 1.03 × 10−3 | 3.15 × 10−4 | 3.80 × 10−4 | ||
| Multimodal | F8 | Mean | −1.02 × 104 | −2.64 × 105 | −6.68 × 103 | −1.25 × 104 | −8.18 × 103 | −3.97 × 103 | −4.08 × 103 | −6.09 × 103 | −9.62 × 103 |
| Std | 1.08 × 103 | 6.38 × 105 | 5.86 × 102 | 8.39 × 101 | 7.31 × 102 | 2.69 × 102 | 2.26 × 102 | 7.63 × 102 | 1.29 × 103 | ||
| F9 | Mean | 0.00 | 0.00 | 4.67 × 101 | 6.20 × 101 | 1.05 × 102 | 1.29 × 101 | 0.00 | 1.78 × 10−1 | 1.39 × 101 | |
| Std | 0.00 | 0.00 | 1.45 × 101 | 5.96 | 3.31 × 101 | 1.98 × 101 | 0.00 | 8.08 × 10−1 | 6.96 | ||
| F10 | Mean | 1.01 × 10−15 | 1.72 × 10−15 | 6.36 × 10−1 | 6.01 × 10−7 | 7.92 × 10−1 | 1.11 × 101 | 1.09 × 10−1 | 1.26 × 10−14 | 9.06 × 10−15 | |
| Std | 1.53 × 10−15 | 6.49 × 10−16 | 7.67 × 10−1 | 1.10 × 10−7 | 7.47 × 10−1 | 9.72 | 5.12 × 10−1 | 2.97 × 10−15 | 2.31 × 10−15 | ||
| F11 | Mean | 0.00 | 0.00 | 1.66 × 10−2 | 7.82 × 10−11 | 4.49 × 10−1 | 1.72 × 10−1 | 4.67 × 10−11 | 4.53 × 10−4 | 1.89 × 10−3 | |
| Std | 0.00 | 0.00 | 2.13 × 10−2 | 1.51 × 10−10 | 8.69 × 10−2 | 2.35 × 10−1 | 2.56 × 10−10 | 2.48 × 10−3 | 4.56 × 10−3 | ||
| F12 | Mean | 7.73 × 10−4 | 3.43 × 10−1 | 4.49 × 10−2 | 6.66 × 10−13 | 8.71 × 10−1 | 1.17 | 4.48 × 10−1 | 3.01 × 10−2 | 7.46 × 10−7 | |
| Std | 3.65 × 10−4 | 1.18 × 10−1 | 7.04 × 10−2 | 3.91 × 10−13 | 8.25 × 10−1 | 1.89 | 9.21 × 10−2 | 2.30 × 10−2 | 2.44 × 10−7 | ||
| F13 | Mean | 2.00 × 10−2 | 2.49 | 2.07 × 10−2 | 3.01 × 10−12 | 3.78 × 10−2 | 3.20 | 2.28 | 3.05 × 10−1 | 1.63 × 10−2 | |
| Std | 8.67 × 10−3 | 3.23 × 10−1 | 3.65 × 10−2 | 1.72 × 10−12 | 1.87 × 10−2 | 1.52 | 1.47 × 10−1 | 2.03 × 10−1 | 3.70 × 10−2 | ||
| Fixed-dimension multimodal | F14 | Mean | 9.98 × 10−1 | 1.14 | 2.58 | 9.98 × 10−1 | 9.98 × 10−1 | 1.33 | 1.20 | 3.22 | 9.98 × 10−1 |
| Std | 1.61 × 10−12 | 2.87 × 10−1 | 2.01 | 0.00 | 6.12 × 10−12 | 7.52 × 10−1 | 6.05 × 10−1 | 3.54 | 4.12 × 10−17 | ||
| F15 | Mean | 3.08 × 10−4 | 3.53 × 10−4 | 3.84 × 10−4 | 6.49 × 10−4 | 3.33 × 10−3 | 9.72 × 10−4 | 7.45 × 10−4 | 4.35 × 10−3 | 3.34 × 10−4 | |
| Std | 4.16 × 10−8 | 4.13 × 10−5 | 2.95 × 10−4 | 9.37 × 10−5 | 6.80 × 10−3 | 4.47 × 10−4 | 1.14 × 10−4 | 8.14 × 10−3 | 1.43 × 10−4 | ||
| F16 | Mean | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | -1.03 | −1.03 | −1.03 | |
| Std | 5.34 × 10−12 | 2.10 × 10−5 | 6.78 × 10−16 | 6.78 × 10−16 | 4.39 × 10−8 | 1.50 × 10−5 | 7.18 × 10−7 | 2.78 × 10−9 | 6.78 × 10−16 | ||
| F17 | Mean | 0.398 | 0.399 | 0.398 | 0.398 | 0.398 | 0.399 | 0.398 | 0.398 | 0.398 | |
| Std | 1.49 × 10−10 | 9.22 × 10−4 | 0.00 | 0.00 | 7.35 × 10−8 | 6.37 × 10−4 | 2.89 × 10−4 | 3.25 × 10−7 | 0.00 | ||
| F18 | Mean | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | |
| Std | 2.86 × 10−10 | 1.13 × 10−5 | 1.50 × 10−15 | 1.90 × 10−15 | 6.23 × 10−7 | 1.51 × 10−5 | 4.30 × 10−6 | 3.90 × 10−6 | 7.14 × 10−16 | ||
| F19 | Mean | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | |
| Std | 1.53 × 10−9 | 2.17 × 10−3 | 2.71 × 10−15 | 2.71 × 10−15 | 2.67 × 10−7 | 2.89 × 10−3 | 1.76 × 10−3 | 1.30 × 10−3 | 2.71 × 10−15 | ||
| F20 | Mean | −3.32 | −3.12 | −3.29 | −3.31 | −3.29 | −2.96 | −3.16 | −3.29 | −3.31 | |
| Std | 3.02 × 10−2 | 7.03 × 10−2 | 5.54 × 10−2 | 1.38 × 10−15 | 5.56 × 10−2 | 3.10 × 10−1 | 4.12 × 10−2 | 5.20 × 10−2 | 3.02 × 10−2 | ||
| F21 | Mean | −10.2 | −4.89 | −6.15 | −9.96 | −7.28 | −4.28 | −9.30 | −9.31 | −9.82 | |
| Std | 1.93 | 8.91 × 10−2 | 3.44 | 1.68 × 10−3 | 2.79 | 2.16 | 1.07 × 10−1 | 1.92 | 1.28 | ||
| F22 | Mean | −10.4 | −4.91 | −9.06 | −10.0 | −8.58 | −4.05 | −10.2 | −10.2 | −10.4 | |
| Std | 1.35 | 1.15 × 10−1 | 2.77 | 5.07 × 10−8 | 2.90 | 2.26 | 1.44 × 10−1 | 9.63 × 10−1 | 7.32 × 10−9 | ||
| F23 | Mean | −10.5 | −4.96 | −8.11 | −10.5 | −9.56 | −4.97 | −10.4 | −10.4 | −10.5 | |
| Std | 2.59 × 10−5 | 1.02 × 10−1 | 3.55 | 1.49 × 10−13 | 2.25 | 1.70 | 1.04 × 10−1 | 9.79 × 10−1 | 1.09 × 10−14 | ||
| Algorithms | Friedman Ranks | Final Ranks |
|---|---|---|
| MVQIHGSO | 2.543 | 1 |
| HGSO | 4.608 | 3 |
| PSO | 5.652 | 7 |
| DE | 4.608 | 4 |
| MVO | 6.456 | 8 |
| SCA | 7.804 | 9 |
| OBSCA | 5.260 | 6 |
| GWO | 4.695 | 5 |
| IGWO | 3.369 | 2 |
| Compared Algorithms | Unimodal Functions | Multimodal Functions | Fixed-Dimension Functions |
|---|---|---|---|
| MVQIHGSO vs. HGSO | 2.5940 × 10−8 | 0.1012 | 7.4567 × 10−4 |
| MVQIHGSO vs. PSO | 1.4838 × 10−12 | 4.1333 × 10−10 | 0.8573 |
| MVQIHGSO vs. DE | 6.6342 × 10−19 | 2.5731 × 10−4 | 0.0916 |
| MVQIHGSO vs. MVO | 1.7618 × 10−32 | 5.2700 × 10−31 | 0.0273 |
| MVQIHGSO vs. SCA | 9.6394 × 10−27 | 6.4376 × 10−25 | 3.2725 × 10−5 |
| MVQIHGSO vs. OBSCA | 1.0240 × 10−9 | 4.1657 × 10−4 | 0.0227 |
| MVQIHGSO vs. GWO | 5.5859 × 10−7 | 0.0072 | 0.0654 |
| MVQIHGSO vs. IGWO | 7.5243 × 10−5 | 0.0011 | 0.0402 |
| Characteristics | Hydropower Stations | Units | |
|---|---|---|---|
| Xiluodu | Xiangjiaba | ||
| Completion date | 2013 | 2012 | - |
| Watershed area | 0.45 | 0.45 | million km2 |
| Dead water level | 540 | 370 | m |
| Flood control limited water level | 560 | 370 | m |
| Normal water level | 600 | 380 | m |
| Regulated storage | 6.46 | 0.903 | billion m3 |
| The minimum release | 1200 | 1200 | m3/s |
| The minimum output | 1000 | 1000 | MW |
| Installed capacity | 12,600 | 6000 | MW |
| Efficiency coefficient | 8.8 | 8.8 | - |
| Reservoirs | Models | R2 | RMSE | MAE | MAPE |
|---|---|---|---|---|---|
| XLD | MVQIHGSO-SVM | 0.998 | 0.340 | 0.126 | 0.021% |
| HGSO-SVM | 0.997 | 0.411 | 0.151 | 0.025% | |
| SCA-SVM | 0.997 | 0.405 | 0.149 | 0.025% | |
| PSO-SVM | 0.998 | 0.405 | 0.150 | 0.025% | |
| Grid-SVM | 0.998 | 0.357 | 0.151 | 0.025% | |
| XJB | MVQIHGSO-SVM | 0.998 | 0.164 | 0.075 | 0.019% |
| HGSO-SVM | 0.997 | 0.192 | 0.098 | 0.026% | |
| SCA-SVM | 0.997 | 0.189 | 0.092 | 0.025% | |
| PSO-SVM | 0.996 | 0.192 | 0.096 | 0.025% | |
| Grid-SVM | 0.997 | 0.187 | 0.086 | 0.023% |
| Reservoirs | Hydropower Generation (TWh) | ||||||
|---|---|---|---|---|---|---|---|
| Observed | MVQIHGSO-SVM | HGSO-SVM | SCA-SVM | PSO-SVM | Grid-SVM | Optimization | |
| XLD | 129.82 | 131.30 | 131.03 | 131.03 | 131.03 | 131.12 | 131.41 |
| XJB | 64.03 | 64.78 | 64.56 | 64.56 | 64.56 | 64.61 | 65.00 |
| Total | 193.85 | 196.08 | 195.59 | 195.58 | 195.58 | 195.73 | 196.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, H.; Hu, T.; Zhang, S.; Xiao, Y. Deriving Operating Rules of Hydropower Reservoirs Using Multi-Strategy Ensemble Henry Gas Solubility Optimization-Driven Support Vector Machine. Water 2023, 15, 437. https://doi.org/10.3390/w15030437
Qiu H, Hu T, Zhang S, Xiao Y. Deriving Operating Rules of Hydropower Reservoirs Using Multi-Strategy Ensemble Henry Gas Solubility Optimization-Driven Support Vector Machine. Water. 2023; 15(3):437. https://doi.org/10.3390/w15030437
Chicago/Turabian StyleQiu, Hongya, Ting Hu, Song Zhang, and Yangfan Xiao. 2023. "Deriving Operating Rules of Hydropower Reservoirs Using Multi-Strategy Ensemble Henry Gas Solubility Optimization-Driven Support Vector Machine" Water 15, no. 3: 437. https://doi.org/10.3390/w15030437





