Designing Water Inter-Plant Networks of Single and Multiple Contaminants through Mathematical Programming
Abstract
:1. Introduction
2. Methods
- Given a set of sources, reaching up to one hundred sources, where each source (n) has a flowrate (FRn) in a multi-contaminant reach up to six contaminants (A, B, C, D, E and F), where the concentrations of contaminants in sources are XRnA, XRnB, XRnC, XRnD, XRnE and XRnF, the flowrate of each source has the probability to send to sinks by flowrate gn-i or send to waste by flowrate Gn_waste.
- Given a set of sinks, reaching up to one hundred sinks, where each sink (i) has a flowrate (Gi) with a limiting concentration of contaminants XgiA, XgiB, XgiC, XgiD, XgiE and XgiF, then:
- The freshwater flowrate (FW) has the probability to feed each sink (i) with a concentration of contaminants XA, XB, XC, XD, XE and XF.
- The total wastewater flowrate is Gwaste with a concentration of XwA, XwB, XwC, XwD, XwE and XwF.
3. Case Studies
3.1. Case Study 1
3.2. Case Study 2
3.3. Case Study 3
4. Results and Discussions
4.1. Results and Discussions of Case Study 1
4.2. Results and Discussions of Case Study 2
4.3. Results and Discussions of Case Study 3
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Redhwan, S.A.; Crittenden, B.D.; Lababidi, H.M.S. Wastewater minimization under uncertain operational conditions. Comput. Chem. Eng. 2005, 29, 1009–1021. [Google Scholar] [CrossRef]
- Ami, P.; Avi, O.; Asce, M. Multiobjective contaminant sensor network design for water distribution system. J. Water Resour. Plann. Manag. 2008, 134, 366–377. [Google Scholar] [CrossRef]
- Chew, I.M.L.; Foo, D.C.Y. Automated targeting for inter-plant water integration. Chem. Eng. J. 2009, 153, 23–36. [Google Scholar] [CrossRef]
- Satyawali, Y.; Balakrishnan, M. Wastewater treatment in molasses-based alcohol distilleries for COD and color removal: A review. J. Environ. Manag. 2008, 86, 481–497. [Google Scholar] [CrossRef] [PubMed]
- Iancu, P.; Plesu, V.; Lavric, V. Regeneration of internal streams as an effective tool for wastewater network optimization. Comput. Chem. Eng. 2009, 33, 731–742. [Google Scholar] [CrossRef]
- Tian, J.R.; Zhou, P.J.; Lv, B. A process integration approach to industrial water conservation: A case study for a Chinese steel plant. J. Environ. Manag. 2008, 86, 682–687. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kim, J.; Kim, J.; Yoo, C.; Moon, I. A simultaneous optimization approach for the design of wastewater and heat exchange networks based on cost estimation. J. Clean. Prod. 2009, 17, 162–171. [Google Scholar] [CrossRef]
- Chew, I.M.L.; Foo, D.C.Y.; Tan, R.R. Flowrate targeting algorithm for interplant resource conservation network. Part 2: Assisted integration scheme. Ind. Eng. Chem. Res. 2010, 49, 6456–6468. [Google Scholar] [CrossRef]
- Chen, C.L.; Hung, S.W.; Lee, J.Y. Design of inter-plant water network with central and decentralized water mains. Comput. Chem. Eng. 2010, 34, 1522–1532. [Google Scholar] [CrossRef]
- Julien, P.; Nouho, K.; Jean, M.; Vincent, R.; Pierre, S. Impact of an intense combined sewer overflow event on the microbiological water quality of the Seine River. Water Res. 2011, 45, 893–903. [Google Scholar] [CrossRef]
- Poplewski, G.; Jezowski, J.M.; Jezowska, A. Water network design with stochastic optimization approach. Chem. Eng. Res. Des. 2011, 89, 2085–2101. [Google Scholar] [CrossRef]
- Sahu, G.; Garg, A.; Majozi, T.; Bandyopadhyay, S. Optimum Design of Waste Water Treatment Network. Am. Chem. Soc. 2013, 52, 5161–5171. [Google Scholar] [CrossRef]
- Yang, L.; Diaz, R.S.; Grossmann, I.E. Water network optimization with wastewater regeneration models. Ind. Eng. Chem. Res. 2014, 53, 17680–17695. [Google Scholar] [CrossRef]
- Ahmetovic, E.; Ibric, N.; Kravanja, Z. Optimal design for heat-integrated water-using and wastewater treatment networks. Appl. Energy 2014, 4, 63–81. [Google Scholar] [CrossRef]
- Buabeng, E.; Majozi, T. Effective Synthesis and Optimization Framework for Integrated Water and Membrane Networks: A Focus on Reverse Osmosis Membranes. Ind. Eng. Chem. Res. 2015, 54, 9394–9406. [Google Scholar] [CrossRef]
- Bozkurt, H.; Van Loosdrecht, M.C.M.; Gernaey, K.V.; Sin, G. Optimal WWTP process selection for treatment of domestic wastewater—A realistic full-scale retrofitting study. Chem. Eng. J. 2015, 286, 447–458. [Google Scholar] [CrossRef]
- Sueviriyapan, N.; Suriyaprapadilok, U.; Siemanond, K.; Quaglia, A.; Gani, R. Industrial wastewater treatment network based on recycling and rerouting strategies for retrofit design schemes. J. Clean. Prod. 2015, 111, 231–252. [Google Scholar] [CrossRef]
- Naderi, M.J.; Pishvaee, M.S.A. A stochastic programming approach to integrated water supply and wastewater collection network design problem. Comput. Chem. Eng. 2017, 104, 107–127. [Google Scholar] [CrossRef]
- Mostafa, B.; Mohammad, H.S.; Hashem, A.; Hossein, N.F. Water management methods in food industry: Corn refinery as a case study. J. Food Eng. 2018, 74, 262–283. [Google Scholar]
- Han, H.G.; Zhang, L.; Liu, H.X.; Qiao, J.F. Multiobjective design of fuzzy neural network controller for wastewater treatment process. Appl. Soft Comput. 2018, 67, 467–478. [Google Scholar] [CrossRef]
- Fadzil, A.F.A.; Alwi, S.R.W.; Manan, Z.A.; Klemes, J.J. Maximizing total site water reuse via a two-way centralized water header. ACS Sustain. Chem. Eng. 2018, 6, 2563–2573. [Google Scholar] [CrossRef]
- Lv, Z.; Song, Y.; Chen, C.; Jiang, B.; Sun, H.; Lyu, Z. A novel step-by-step optimization method for interplant water. J. Environ. Manag. 2018, 213, 255–270. [Google Scholar] [CrossRef] [PubMed]
- Reinaldo, C.M.; Fernando, L.P.; Silvio, A.B. Industrial wastewater reuse in inter-plant water netwoks. Braz. J. Dev. 2019, 5, 8366–8374. [Google Scholar]
- Robles, C.E.; Ben-Ayed, A.; Bernier, J.; Rocher, V.; Dochain, D. Management of an integrated network of wastewater treatment plants for improving water quality in a river basin. IFAC-Pap. Online 2019, 52, 358–363. [Google Scholar] [CrossRef]
- Wang, X.; Fan, X.; Liu, Z.Y. Design of interplant water network of multiple contaminants with an interplant water main. Chem. Eng. Trans. 2019, 72, 295–300. [Google Scholar] [CrossRef]
- Fard, A.M.F.; Keshteli, M.H.; Tian, G.; Li, Z. An Adaptive Lagrangian Relaxation-based algorithm for a coordinated water supply and wastewater collection network design problem. Inf. Sci. 2019, 512, 1335–1359. [Google Scholar] [CrossRef]
- Mohammad, J.D.; Chang, K.Y. Modeling and extensive analysis of the energy and economics of cooling, heat, and power trigeneration (CCHP) from textile wastewater for industrial low-grade heat recovery. Energy Convers. Manag. 2020, 205, 112451. [Google Scholar] [CrossRef]
- Kumawat, P.K.; Chaturvedi, N.D. Robust targeting of resource requirement in a continuous water network. Chem. Eng. Trans. 2020, 81, 1003–1008. [Google Scholar] [CrossRef]
- Poplewski, G.; Foo, D.C.Y. An extended corner point method for the synthesis of flexible water network. Process Saf. Environ. Prot. 2020, 148, 210–224. [Google Scholar] [CrossRef]
- Bhoomi, S.; Deepak, C.; Ajit, P.S. Wastewater allocation and pricing model for the efficient functioning of CETP serving a textile industrial cluster. Adv. Energy Environ. 2021, 142, 247–263. [Google Scholar]
- Erkata, Y.; Rinaldi, I.; Roy, H.S.; Carolus, B.R.; Satriyo, K.W.; Rangga, K.M.; Juris, B.; Herry, S. Reducing energy and water consumption in textile dyeing industry with cleaner production by inlet-outlet modification to reuse wastewater. Phys. Comput. Sci. 2021, 58, 49–58. [Google Scholar]
- Mariacrocetta, S.; Gabriele, F. Strategies for improving optimal positioning of quality sensors in urban drainage systems for non-conservative contaminants. Water 2021, 13, 934. [Google Scholar] [CrossRef]
- Nessren, M.F.; Dina, A.K.; Ayat, O.G.; Mamdouh, A.G.; Mai, K.F. Graphical design and analysis of mass exchange networks using composition driving forces. S. Afr. J. Chem. Eng. 2021, 36, 94–104. [Google Scholar] [CrossRef]



| Plant | Sources and Sinks | Stream Number | Flow Rate (m3/h) | TSS (ppm) | Plant | Sources and Sinks | Stream Number | Flow Rate (m3/h) | TSS (ppm) |
|---|---|---|---|---|---|---|---|---|---|
| Plant A | Sources | S1 | 50 | 50 | Plant B | Sources | S1 | 20 | 100 |
| S2 | 100 | 100 | S2 | 100 | 100 | ||||
| S3 | 70 | 150 | S3 | 40 | 800 | ||||
| S4 | 60 | 250 | S4 | 10 | 800 | ||||
| Sinks | K1 | 50 | 20 | Sinks | K1 | 20 | 0 | ||
| K2 | 100 | 50 | K2 | 100 | 50 | ||||
| K3 | 80 | 100 | K3 | 40 | 50 | ||||
| K4 | 70 | 200 | K4 | 10 | 400 | ||||
| Plant C | Sources | S1 | 105 | 17 | Plant E | Sources | S1 | 40 | 200 |
| S2 | 182.35 | 44 | S2 | 50 | 200 | ||||
| S3 | 138.7 | 49 | S3 | 30 | 400 | ||||
| S4 | 92.55 | 83 | S4 | 60 | 400 | ||||
| S5 | 45.55 | 115 | S5 | 40 | 600 | ||||
| Sinks | K1 | 182.35 | 0 | Sinks | K1 | 40 | 0 | ||
| K2 | 45.55 | 10 | K2 | 50 | 100 | ||||
| K3 | 138.7 | 10 | K3 | 30 | 100 | ||||
| K4 | 92.55 | 10 | K4 | 60 | 300 | ||||
| K5 | 105 | 87 | K5 | 40 | 400 | ||||
| Plant D | Sources | S1 | 150 | 10 | Plant D | Sinks | K1 | 200 | 20 |
| S2 | 60 | 50 | |||||||
| S3 | 100 | 85 | K2 | 80 | 75 |
| Plant | Process | Stream Number | Flow Rate (m3/h) | Limiting Concentration of Contaminant COD (ppm) |
|---|---|---|---|---|
| Molasses treatment system (X) | Sources | S1 | 20 | 100 |
| S2 | 66.67 | 80 | ||
| S3 | 100 | 100 | ||
| S4 | 41.67 | 800 | ||
| S5 | 10 | 800 | ||
| Sinks | K1 | 20 | 0 | |
| K2 | 66.67 | 50 | ||
| K3 | 100 | 50 | ||
| K4 | 41.67 | 80 | ||
| K5 | 10 | 400 | ||
| Yeast production system (Y) | Sources | S1 | 20 | 100 |
| S2 | 66.67 | 80 | ||
| S3 | 15.63 | 400 | ||
| S4 | 42.86 | 800 | ||
| S5 | 6.67 | 1000 | ||
| Sinks | K1 | 20 | 0 | |
| K2 | 66.67 | 50 | ||
| K3 | 15.63 | 80 | ||
| K4 | 42.86 | 100 | ||
| K5 | 6.67 | 400 | ||
| Circulating cooling system (Z) | Sources | S1 | 20 | 100 |
| S2 | 80 | 50 | ||
| S3 | 50 | 125 | ||
| S4 | 40 | 800 | ||
| S5 | 300 | 150 | ||
| Sinks | K1 | 20 | 0 | |
| K2 | 80 | 25 | ||
| K3 | 50 | 25 | ||
| K4 | 40 | 50 | ||
| K5 | 300 | 100 |
| Plant | Sources and Sinks | Flowrate (m3/h) | Contaminant A (Hydrocarbon) (ppm) | Contaminant B (H2S) (ppm) | Contaminant C (TDS) (ppm) |
|---|---|---|---|---|---|
| Plant 1 | Source 1 | 30 | 100 | 90 | 50 |
| Source 2 | 16 | 50 | 70 | 70 | |
| Source 3 | 75 | 150 | 80 | 70 | |
| Source 4 | 21 | 160 | 100 | 90 | |
| Source 5 | 29 | 210 | 200 | 120 | |
| Source 6 | 65 | 80 | 70 | 80 | |
| Source 7 | 61 | 300 | 290 | 170 | |
| Source 8 | 57 | 210 | 170 | 100 | |
| Sink 1 | 30 | 0 | 0 | 0 | |
| Sink 2 | 16 | 0 | 0 | 0 | |
| Sink 3 | 75 | 40 | 60 | 20 | |
| Sink 4 | 21 | 30 | 40 | 70 | |
| Sink 5 | 29 | 110 | 135 | 60 | |
| Sink 6 | 65 | 0 | 0 | 0 | |
| Sink 7 | 61 | 100 | 75 | 20 | |
| Sink 8 | 57 | 90 | 50 | 34 | |
| Plant 2 | Source 1 | 35 | 110 | 120 | 100 |
| Source 2 | 40 | 350 | 400 | 210 | |
| Source 3 | 40 | 150 | 180 | 210 | |
| Source 4 | 30 | 210 | 150 | 220 | |
| Source 5 | 30 | 350 | 320 | 310 | |
| Source 6 | 64 | 800 | 1100 | 1000 | |
| Source 7 | 50 | 1500 | 2100 | 1800 | |
| Sink 1 | 35 | 0 | 0 | 0 | |
| Sink 2 | 40 | 200 | 170 | 150 | |
| Sink 3 | 40 | 90 | 130 | 100 | |
| Sink 4 | 30 | 110 | 80 | 150 | |
| Sink 5 | 30 | 260 | 200 | 180 | |
| Sink 6 | 64 | 340 | 350 | 400 | |
| Sink 7 | 50 | 950 | 850 | 900 | |
| Plant 3 | Source 1 | 30 | 900 | 4500 | 3000 |
| Source 2 | 34 | 120 | 12,500 | 180 | |
| Source 3 | 56 | 220 | 45 | 9500 | |
| Sink 1 | 30 | 150 | 700 | 800 | |
| Sink 2 | 34 | 20 | 300 | 45 | |
| Sink 3 | 56 | 120 | 20 | 200 |
| Stream | Flowrate (t/h) | Stream | Flowrate (t/h) | Stream | Flowrate (t/h) | Stream | Flowrate (t/h) |
|---|---|---|---|---|---|---|---|
| Fw | 412.3 | G4-waste | 53 | G10-13 | 8.5 | G14-1 | 35.3 |
| Fw5 | 20 | G5-3 | 1.9 | G10-14 | 55.8 | G14-11 | 39.1 |
| Fw9 | 182.4 | G5-4 | 0.4 | G10-15 | 12.4 | G14-14 | 75.6 |
| Fw10 | 35.2 | G5-6 | 0.8 | G10-17 | 3.5 | G15-2 | 4 |
| Fw11 | 41 | G5-13 | 3 | G10-18 | 1.8 | G15-6 | 56 |
| Fw12 | 71.5 | G5-15 | 6.7 | G10-19 | 0.7 | G16-4 | 4.2 |
| Fw14 | 22.2 | G5-17 | 1.8 | G10-waste | 7 | G16-6 | 1.2 |
| Fw16 | 40 | G5-18 | 0.6 | G11-2 | 47.8 | G16-7 | 3.3 |
| G1-2 | 45 | G5-19 | 0.3 | G11-3 | 29.9 | G16-13 | 8.5 |
| G1-3 | 0.9 | G5-waste | 4.5 | G11-4 | 1.5 | G16-15 | 50 |
| G1-6 | 1.5 | G6-4 | 5.8 | G11-6 | 22.7 | G16-17 | 6.5 |
| G1-7 | 2 | G6-7 | 1 | G11-7 | 7.1 | G16-18 | 5.9 |
| G1-17 | 0.4 | G6-18 | 3.3 | G11-13 | 12.3 | G16-19 | 17.8 |
| G1-waste | 0.2 | G6-19 | 4.1 | G11-15 | 10.9 | G16-20 | 2.5 |
| G2-2 | 1.2 | G6-20 | 3 | G11-17 | 3.8 | G17-8 | 0.8 |
| G2-4 | 7.3 | G6-waste | 82.8 | G11-18 | 1.9 | G17-19 | 1.1 |
| G2-13 | 63.6 | G7-8 | 1.9 | G11-19 | 0.9 | G17-waste | 38.1 |
| G2-17 | 18 | G7-20 | 7 | G12-4 | 42.3 | G18-4 | 2.3 |
| G2-18 | 3.6 | G7-waste | 31.1 | G12-6 | 1.3 | G18-8 | 1.6 |
| G2-waste | 6.4 | G8-waste | 10 | G12-8 | 2 | G18-18 | 2.5 |
| G3-3 | 5.3 | G9-11 | 58.6 | G12-13 | 8.4 | G18-20 | 14.1 |
| G3-4 | 4.8 | G9-14 | 46.4 | G12-17 | 6 | G18-waste | 29.5 |
| G3-17 | 6.3 | G10-1 | 14.7 | G12-18 | 6.7 | G19-waste | 30 |
| G3-18 | 2.7 | G10-2 | 2 | G12-20 | 2.3 | G20-8 | 2.2 |
| G3-19 | 5.3 | G10-4 | 1.4 | G12-waste | 23.4 | G20-19 | 27 |
| G3-waste | 45.6 | G10-6 | 16.6 | G13-3 | 42 | G20-20 | 8.7 |
| G4-17 | 1.7 | G10-7 | 26.5 | G13-13 | 0.7 | G20-waste | 22.1 |
| G4-19 | 2.7 | G10-10 | 10.4 | G13-17 | 2 | G21-8 | 1.4 |
| G4-20 | 2.5 | G10-12 | 21 | G13-18 | 0.9 | G21-waste | 38.6 |
| Sinks | Fw (t/h) | Sources Flowrates (t/h) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | S13 | S14 | S15 | ||
| K1 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| K2 | 44.4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 22.2 |
| K3 | 47 | 20 | 0 | 0 | 0 | 0 | 0 | 25 | 0 | 0 | 0 | 0 | 0 | 8 | 0 | 0 |
| K4 | 11.7 | 0 | 0 | 16.6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13.4 | 0 | 0 |
| K5 | 0 | 0 | 0 | 0 | 0 | 2.8 | 0 | 0 | 2.7 | 0 | 0 | 0 | 0 | 0 | 0 | 4.5 |
| K6 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 00 | 0 | 0 | 0 | 0 |
| K7 | 25 | 0 | 0 | 0 | 0 | 0 | 0 | 41.7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| K8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10.9 | 0 | 0 | 4.7 |
| K9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14.3 | 28.6 | 0 | 0 |
| K10 | 0 | 0 | 0 | 0 | 0 | 1.1 | 0 | 0 | 1.8 | 0 | 0 | 0 | 0 | 0 | 0.7 | 3 |
| K11 | 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| K12 | 66.7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13.3 |
| K13 | 31.8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14.8 | 0 | 0 | 3.4 |
| K14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 40 | 0 | 0 | 0 |
| K15 | 27.7 | 0 | 66.7 | 83.4 | 0 | 0 | 20 | 0 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 82.1 |
| waste | 0 | 0 | 0 | 0 | 41.7 | 6.1 | 0 | 0 | 11.1 | 42.9 | 6.7 | 0 | 0 | 0 | 39.3 | 166.8 |
| Integration Scheme | The Introduced Method | Optimization Method (Chew et al. [3]) | Step-by-Step Optimization Method (Lv et al. [22]) |
|---|---|---|---|
| Used Technique | Nonlinear Programming (NLP) | Mixed integer nonlinear programming (MINLP) | Linear Programming (LP) |
| Freshwater consumption (t/h) | 314.36 | 314.96 | 330 |
| Wastewater discharge (t/h) | 314.36 | 538 | 329.54 |
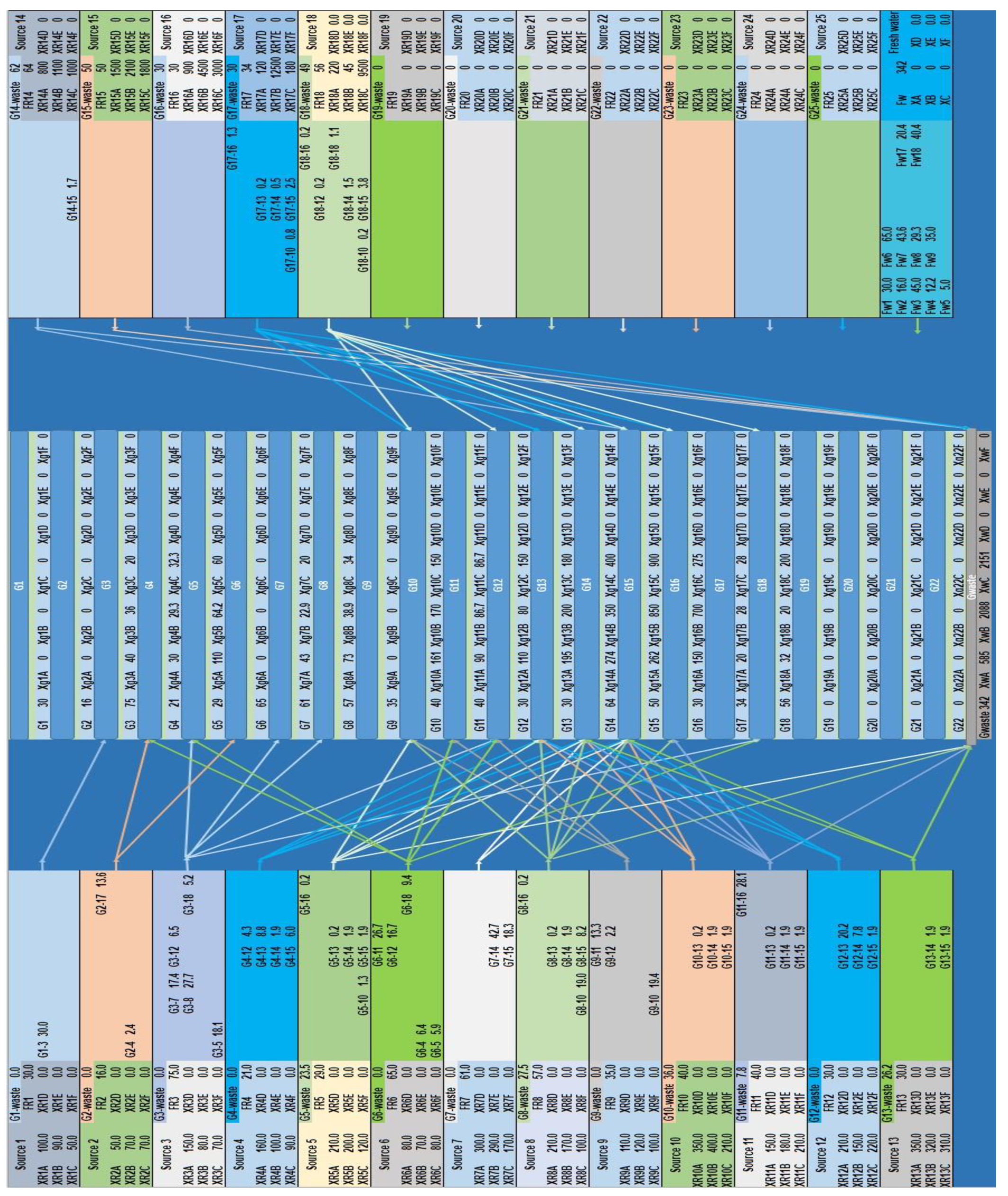
| Sources and Fresh Water | Sinks | Waste | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K1 | K2 | K3 | K4 | K5 | K6 | K7 | K8 | K9 | K10 | K11 | K12 | K13 | K14 | K15 | K16 | K17 | K18 | ||
| Fw | 30 | 16 | 45 | 12.2 | 5 | 65 | 43.6 | 29.3 | 35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20.4 | 40.4 | 0 |
| S1 | 0 | 0 | 30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| S2 | 0 | 0 | 0 | 2.4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13.6 | 0 | 0 |
| S3 | 0 | 0 | 0 | 0 | 18.1 | 0 | 17.4 | 27.7 | 0 | 0 | 0 | 6.5 | 0 | 0 | 0 | 0 | 0 | 5.2 | 0 |
| S4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4.3 | 8.8 | 1.9 | 6 | 0 | 0 | 0 | 0 |
| S5 | 0 | 0 | 0 | 0 | 00 | 0 | 0 | 0 | 0 | 1.3 | 0 | 0 | 0.2 | 1.9 | 1.9 | 0.2 | 0 | 0 | 0 |
| S6 | 0 | 0 | 0 | 6.4 | 5.9 | 0 | 0 | 0 | 0 | 0 | 26.7 | 16.7 | 0 | 0 | 0 | 0 | 0 | 9.4 | 0 |
| S7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 42.7 | 18.3 | 0 | 0 | 0 | 0 |
| S8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 0 | 0 | 0.2 | 1.9 | 8.2 | 0.2 | 0 | 0 | 27.5 |
| S9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19.4 | 13.3 | 2.2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| S10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 1.9 | 1.9 | 0 | 0 | 0 | 36 |
| S11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 1.9 | 1.9 | 28.1 | 0 | 0 | 7.8 |
| S12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20.2 | 7.8 | 1.9 | 0 | 0 | 0 | 0 |
| S13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.9 | 1.9 | 0 | 0 | 0 | 26.2 |
| S14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.7 | 0 | 0 | 0 | 62 |
| S15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 50 |
| S16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30 |
| S17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.8 | 0 | 0 | 0.2 | 0.5 | 2.5 | 1.3 | 0 | 0 | 30 |
| S18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0 | 0.2 | 0 | 1.5 | 3.8 | 0.2 | 0 | 1.1 | 49 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shoaib, A.M.; Atawia, A.A.; Hassanean, M.H.; Gadallah, A.G.; Bhran, A.A. Designing Water Inter-Plant Networks of Single and Multiple Contaminants through Mathematical Programming. Water 2023, 15, 4315. https://doi.org/10.3390/w15244315
Shoaib AM, Atawia AA, Hassanean MH, Gadallah AG, Bhran AA. Designing Water Inter-Plant Networks of Single and Multiple Contaminants through Mathematical Programming. Water. 2023; 15(24):4315. https://doi.org/10.3390/w15244315
Chicago/Turabian StyleShoaib, Abeer M., Amr A. Atawia, Mohamed H. Hassanean, Abdelrahman G. Gadallah, and Ahmed A. Bhran. 2023. "Designing Water Inter-Plant Networks of Single and Multiple Contaminants through Mathematical Programming" Water 15, no. 24: 4315. https://doi.org/10.3390/w15244315
APA StyleShoaib, A. M., Atawia, A. A., Hassanean, M. H., Gadallah, A. G., & Bhran, A. A. (2023). Designing Water Inter-Plant Networks of Single and Multiple Contaminants through Mathematical Programming. Water, 15(24), 4315. https://doi.org/10.3390/w15244315






