An Optimal Model and Application of Hydraulic Structure Regulation to Improve Water Quality in Plain River Networks
Abstract
:1. Introduction
2. Methods
2.1. Traditional Gravitational Search Algorithm
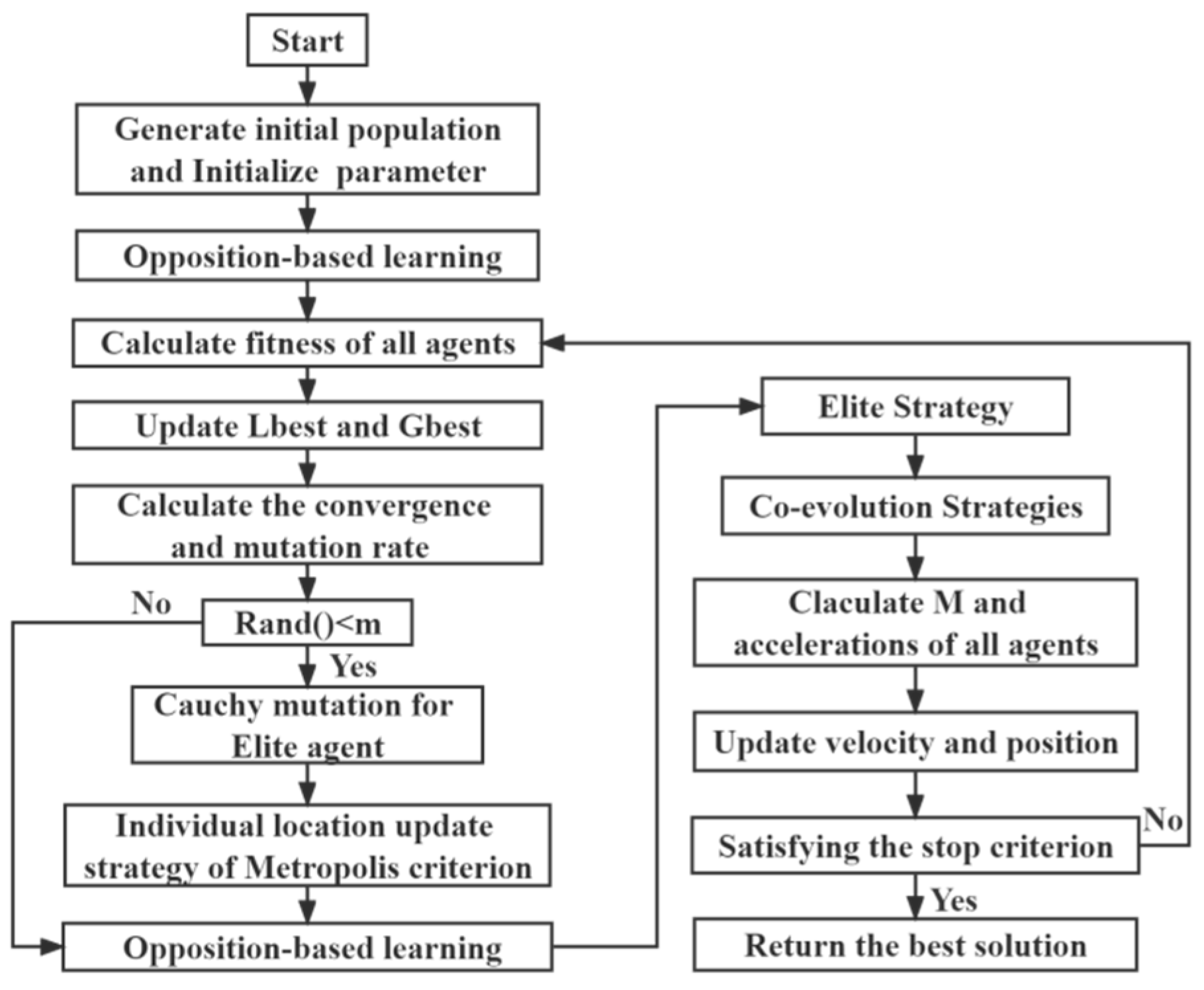
2.2. Proposed Algorithm: IPSOGSA
2.2.1. Opposition-Based Learning
2.2.2. Elite Mutation Strategy
2.2.3. Local Search Strategy
2.2.4. Co-Evolution Strategies
2.2.5. Location Update Strategy
2.2.6. The Procedure of IPSOGSA
2.3. Experiment Results and Discussion
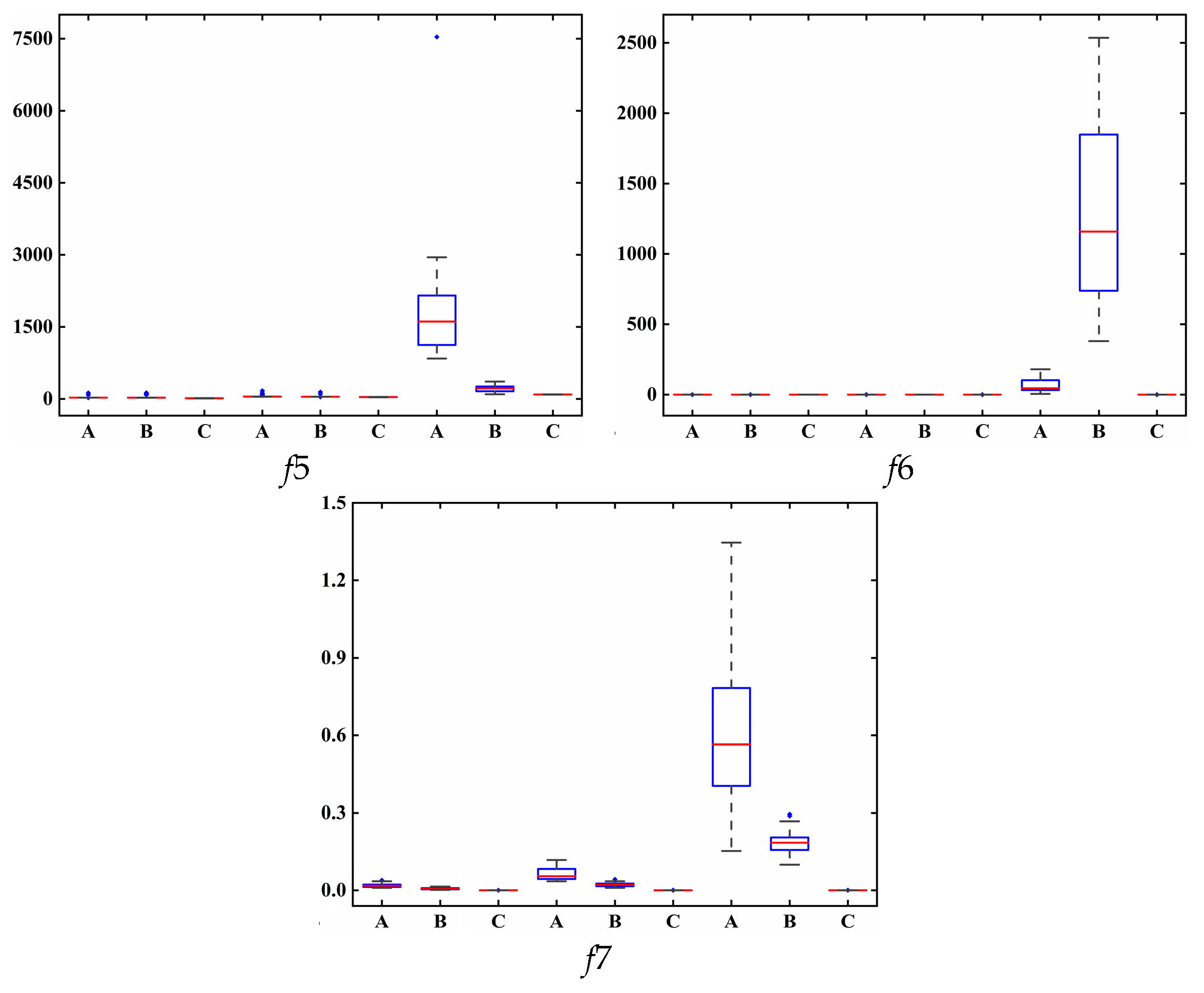
2.3.1. Classical Benchmark Functions Set
2.3.2. Modern Benchmark Functions Set
3. Optimal Scheduling Model of Hydraulic Structures
3.1. Mathematical Problem Formulation
3.1.1. Economic Objective
3.1.2. Water Quality Constraints
3.1.3. Hydraulic Constraints
3.2. Water Quality Prediction Model
4. Practical Application
4.1. Case Study
4.2. Backpropagation Neural Network
4.3. Optimal Operation Scheduling of Water Diversion Project
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hosper, H.; Meyer, M.-L. Control of phosphorus loading and flushing as restoration methods for Lake Veluwe, The Netherlands. Hydrobiol. Bull. 1986, 20, 183–194. [Google Scholar] [CrossRef]
- Welch, E.B.; Barbiero, R.P.; Bouchard, D.; Jones, C.A. Lake trophic state change and constant algal composition following dilution and diversion. Ecol. Eng. 1992, 1, 173–197. [Google Scholar] [CrossRef]
- Bode, H.; Evers, P.; Albrecht, D.R. Integrated water resources management in the Ruhr River Basin, Germany. Water Sci. Technol. 2003, 47, 81–86. [Google Scholar] [CrossRef] [PubMed]
- Lane, R.R.; Day, J.W.; Kemp, G.P.; Demcheck, D.K. The 1994 experimental opening of the Bonnet Carre Spillway to divert Mississippi River water into Lake Pontchartrain, Louisiana. Ecol. Eng. 2001, 17, 411–422. [Google Scholar] [CrossRef]
- Yin, W.; Xin, X.K.; Jia, H.Y. Preliminary research on hydrodynamic dispatch method of algal blooms in Three Gorges Reservoir Bays. Appl. Mech. Mater. 2014, 675–677, 811–817. [Google Scholar] [CrossRef]
- Gao, X.P.; Xu, L.P.; Zhang, C. Modelling the effect of water diversion projects on renewal capacity in an urban artificial lake in China. J. Hydroinformatics 2015, 17, 990–1002. [Google Scholar] [CrossRef]
- Kumar, D.N.; Baliarsingh, F.; Raju, K.S. Optimal reservoir operation for flood control using folded dynamic programming. Water Resour. Manag. 2010, 24, 1045–1064. [Google Scholar] [CrossRef]
- Chang, L.C. Guiding rational reservoir flood operation using penalty-type genetic algorithm. J. Hydrol. 2008, 354, 65–74. [Google Scholar] [CrossRef]
- Chen, H.-t.; Wang, W.-c.; Chau, K.-w.; Xu, L.; He, J. Flood Control Operation of Reservoir Group Using Yin-Yang Firefly Algorithm. Water Resour. Manag. 2021, 35, 5325–5345. [Google Scholar] [CrossRef]
- Li, Q.; Ouyang, S. Research on multi-objective joint optimal flood control model for cascade reservoirs in river basin system. Nat. Hazards 2015, 77, 2097–2115. [Google Scholar] [CrossRef]
- Niu, W.-j.; Feng, Z.-k.; Liu, S. Multi-strategy gravitational search algorithm for constrained global optimization in coordinative operation of multiple hydropower reservoirs and solar photovoltaic power plants. Appl. Soft Comput. 2021, 107, 107315. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Guo, S.L.; Chang, F.J.; Liu, P.; Chen, A.B. Methodology that improves water utilization and hydropower generation without increasing flood risk in mega cascade reservoirs. Energy 2018, 143, 785–796. [Google Scholar] [CrossRef]
- Xu, Z.; Mo, L.; Zhou, J.; Zhang, X. Optimal dispatching rules of hydropower reservoir in flood season considering flood resources utilization: A case study of Three Gorges Reservoir in China. J. Clean. Prod. 2023, 388, 135975. [Google Scholar] [CrossRef]
- Moazeni, F.; Khazaei, J. Optimal design and operation of an islanded water-energy network including a combined electrodialysis-reverse osmosis desalination unit. Renew. Energy 2021, 167, 395–408. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, Z.; Lei, X.; Hou, Q.; Wang, H. A multi-objective optimal control model of cascade pumping stations considering both cost and safety. J. Clean. Prod. 2022, 345, 131171. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, H.; Wan, W.; Zhao, J. Optimal operation toward energy efficiency of the long-distance water transfer project. J. Hydrol. 2023, 618, 129152. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Zhang, H.P.; Chen, L.; Zhao, J.F. Influence of the South–North Water Diversion Project and the Mitigation Projects on the water quality of Han River. Sci. Total Environ. 2008, 406, 57–68. [Google Scholar] [CrossRef]
- Yang, H.; Wang, J.; Li, J.; Zhou, H.; Liu, Z. Modelling impacts of water diversion on water quality in an urban artificial lake. Environ. Pollut. 2021, 276, 116694. [Google Scholar] [CrossRef]
- Zhou, H.P.; Shao, W.Y.; Jiang, L.J. Optimal model of hydrodynamic controlling on pumps and slice gates for water quality improvement. Appl. Mech. Mater. 2013, 316–317, 732–740. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Grosan, C. Experienced Gray Wolf Optimization Through Reinforcement Learning and Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 681–694. [Google Scholar] [CrossRef]
- Heidari, A.A.; Faris, H.; Aljarah, I.; Mirjalili, S. An efficient hybrid multilayer perceptron neural network with grasshopper optimization. Soft Comput. 2019, 23, 7941–7958. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Improved whale trainer for sonar datasets classification using neural network. Appl. Acoust. 2019, 154, 176–192. [Google Scholar] [CrossRef]
- Khishe, M.; Safari, A. Classification of Sonar Targets Using an MLP Neural Network Trained by Dragonfly Algorithm. Wirel. Pers. Commun. 2019, 108, 2241–2260. [Google Scholar] [CrossRef]
- Zheng, X.; Nguyen, H. A novel artificial intelligent model for predicting water treatment efficiency of various biochar systems based on artificial neural network and queuing search algorithm. Chemosphere 2022, 287, 132251. [Google Scholar] [CrossRef]
- Aarts, E.H.L.; van Laarhoven, P.J.M. Simulated annealing: An introduction. Stat. Neerl. 1989, 43, 31–52. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J. Parameters identification of hydraulic turbine governing system using improved gravitational search algorithm. Energy Convers. Manag. 2011, 52, 374–381. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. Filter modeling using gravitational search algorithm. Eng. Appl. Artif. Intell. 2011, 24, 117–122. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, D.; Shen, X. A Simplified and Efficient Gravitational Search Algorithm for Unconstrained Optimization Problems. In Proceedings of the 2017 International Conference on Vision, Image and Signal Processing (ICVISP), Osaka, Japan, 22–24 September 2017; pp. 11–17. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L.; Zhang, Y.; Wang, J. Immune Gravitation Inspired Optimization Algorithm. In Advanced Intelligent Computing; Huang, D.S., Gan, Y., Bevilacqua, V., Figueroa, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 178–185. [Google Scholar] [CrossRef]
- Shaw, B.; Mukherjee, V.; Ghoshal, S.P. A novel opposition-based gravitational search algorithm for combined economic and emission dispatch problems of power systems. Int. J. Electr. Power Energy Syst. 2012, 35, 21–33. [Google Scholar] [CrossRef]
- Hatamlou, A.; Abdullah, S.; Othman, Z. Gravitational search algorithm with heuristic search for clustering problems. In Proceedings of the 2011 3rd Conference on Data Mining and Optimization (DMO), Putrajaya, Malaysia, 28–29 June 2011; pp. 190–193. [Google Scholar] [CrossRef]
- Darzi, S.; Sieh Kiong, T.; Tariqul Islam, M.; Rezai Soleymanpour, H.; Kibria, S. A memory-based gravitational search algorithm for enhancing minimum variance distortionless response beamforming. Appl. Soft Comput. 2016, 47, 103–118. [Google Scholar] [CrossRef]
- Yin, B.; Guo, Z.; Liang, Z.; Yue, X. Improved gravitational search algorithm with crossover. Comput. Electr. Eng. 2017, 66, 505–516. [Google Scholar] [CrossRef]
- Mirjalili, S.; Hashim, S.Z.M. A new hybrid PSOGSA algorithm for function optimization. In Proceedings of the 2010 International Conference on Computer and Information Application, Tianjin, China, 3–5 December 2010; pp. 374–377. [Google Scholar] [CrossRef]
- Duman, S.; Yorukeren, N.; Altas, I.H. A novel modified hybrid PSOGSA based on fuzzy logic for non-convex economic dispatch problem with valve-point effect. Int. J. Electr. Power Energy Syst. 2015, 64, 121–135. [Google Scholar] [CrossRef]
- Xiao, J.; Niu, Y.; Chen, P.; Leung, S.C.H.; Xing, F. An improved gravitational search algorithm for green partner selection in virtual enterprises. Neurocomputing 2016, 217, 103–109. [Google Scholar] [CrossRef]
- Salajegheh, F.; Salajegheh, E.; Shojaee, S. An enhanced approach for optimizing mathematical and structural problems by combining PSO, GSA and gradient directions. Soft Comput. 2022, 26, 11891–11913. [Google Scholar] [CrossRef]
- Tian, H.; Yuan, X.; Ji, B.; Chen, Z. Multi-objective optimization of short-term hydrothermal scheduling using non-dominated sorting gravitational search algorithm with chaotic mutation. Energy Convers. Manag. 2014, 81, 504–519. [Google Scholar] [CrossRef]
- Duman, S.; Li, J.; Wu, L.; Guvenc, U. Optimal power flow with stochastic wind power and FACTS devices: A modified hybrid PSOGSA with chaotic maps approach. Neural Comput. Appl. 2020, 32, 8463–8492. [Google Scholar] [CrossRef]
- Li, N.; Su, Z.; Jerbi, H.; Abbassi, R.; Latifi, M.; Furukawa, N. Energy management and optimized operation of renewable sources and electric vehicles based on microgrid using hybrid gravitational search and pattern search algorithm. Sustain. Cities Soc. 2021, 75, 103279. [Google Scholar] [CrossRef]
- Hui, W.; Zhijian, W.; Shahryar, R.; Yong, L.; Mario, V. Enhancing particle swarm optimization using generalized opposition-based learning. Inf. Sci. 2011, 181, 4699–4714. [Google Scholar] [CrossRef]
- Lou, Y.; Li, J.L.; Shi, Y.H.; Jin, L.P. Gravitational Co-evolution and Opposition-based Optimization Algorithm. Int. J. Comput. Intell. Syst. 2013, 6, 849–861. [Google Scholar] [CrossRef]
- Xin, Y.; Yong, L.; Guangming, L. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef]
- Joshi, S.K. Chaos embedded opposition based learning for gravitational search algorithm. Appl. Intell. 2023, 53, 5567–5586. [Google Scholar] [CrossRef]
- Khishe, M.; Mosavi, M.R. Chimp optimization algorithm. Expert Syst. Appl. 2020, 149, 113338. [Google Scholar] [CrossRef]
- Dhiman, G. SSC: A hybrid nature-inspired meta-heuristic optimization algorithm for engineering applications. Knowl. -Based Syst. 2021, 222, 106926. [Google Scholar] [CrossRef]
- Dhiman, G. ESA: A hybrid bio-inspired metaheuristic optimization approach for engineering problems. Eng. Comput. 2021, 37, 323–353. [Google Scholar] [CrossRef]
- Aydilek, İ.B. A hybrid firefly and particle swarm optimization algorithm for computationally expensive numerical problems. Appl. Soft Comput. 2018, 66, 232–249. [Google Scholar] [CrossRef]
- Askarzadeh, A. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm. Comput. Struct. 2016, 169, 1–12. [Google Scholar] [CrossRef]
- Civicioglu, P. Backtracking Search Optimization Algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Salajegheh, F.; Salajegheh, E. PSOG: Enhanced particle swarm optimization by a unit vector of first and second order gradient directions. Swarm Evol. Comput. 2019, 46, 28–51. [Google Scholar] [CrossRef]



| Algorithm | α | rate | |||||
|---|---|---|---|---|---|---|---|
| GSA | 100 | 20 | - | - | - | - | - |
| PSOGSA | 100 | 20 | - | - | - | - | - |
| IPSOGSA | 100 | 20 | 0.1 | 0.2 | 1000 | 0.96 | 0.01 |
| Dimension | IPSOGSA vs. | w (+) | t (=) | l) |
|---|---|---|---|---|
| 30 | GSA | 12 | 0 | 1 |
| PSOGSA | 11 | 1 | 1 | |
| 50 | GSA | 12 | 0 | 1 |
| PSOGSA | 11 | 0 | 2 | |
| 100 | GSA | 13 | 0 | 0 |
| PSOGSA | 13 | 0 | 0 |
| Phase | Indicators | GA | GSA | IGSA | |||
|---|---|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | RMSE | R2 | ||
| Training phase | CODMn | 0.591 | 0.961 | 0.582 | 0.962 | 0.472 | 0.975 |
| NH3-N | 0.075 | 0.969 | 0.073 | 0.971 | 0.058 | 0.981 | |
| TP | 0.023 | 0.933 | 0.020 | 0.946 | 0.020 | 0.950 | |
| Test phase | CODMn | 0.496 | 0.971 | 0.572 | 0.962 | 0.463 | 0.975 |
| NH3-N | 0.080 | 0.966 | 0.087 | 0.960 | 0.066 | 0.976 | |
| TP | 0.019 | 0.950 | 0.019 | 0.954 | 0.016 | 0.967 | |
| Scenario Number | Description: Water Quality (mg/L) |
|---|---|
| S1 | Upstream: CODMn:5; NH3-N:0.75; TP:0.15 Initial: CODMn:15; NH3-N:2.0; TP:0.4 |
| S2 | Upstream: CODMn:4; NH3-N:0.5; TP:0.1 Initial: CODMn:15; NH3-N:2.0; TP:0.4 |
| S3 | Upstream: CODMn:4; NH3-N:0.5; TP:0.1 Initial: CODMn:10; NH3-N:1.5; TP:0.3 |
| S4 | Upstream: CODMn:4; NH3-N:0.5; TP:0.1 Initial: CODMn:6; NH3-N:1.0; TP:0.2 |
| S5 | Upstream: CODMn:6; NH3-N:1.3; TP:0.25 Initial: CODMn:6; NH3-N:1.2; TP:0.25 |
| Scenario Number | Algorithm | Height of Gate (m) | Flow (m3/s) | Run Time (h) | Economic Cost | ||||
|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P1 | P2 | P3 | ||||
| S1 | GSA | 1.4 | 0 | 36 | 24 | 0 | 170 | 34 | 2.50 × 107 |
| IPSOGSA | 1.4 | 12 | 12 | 24 | 5 | 173 | 1 | 7.78 × 106 | |
| S2 | GSA | 0.7 | 72 | 12 | 12 | 45 | 177 | 53 | 2.16 × 107 |
| IPSOGSA | 1.4 | 12 | 12 | 0 | 3 | 167 | 0 | 7.34 × 106 | |
| S3 | GSA | 1.2 | 12 | 0 | 12 | 104 | 0 | 145 | 1.08 × 107 |
| IPSOGSA | 1.2 | 0 | 12 | 12 | 0 | 132 | 4 | 5.88 × 106 | |
| S4 | No scheduling required | ||||||||
| S5 | No scheduling required | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, F.; Zhang, H.; Wu, Q.; Chi, S.; Yang, M. An Optimal Model and Application of Hydraulic Structure Regulation to Improve Water Quality in Plain River Networks. Water 2023, 15, 4297. https://doi.org/10.3390/w15244297
Huang F, Zhang H, Wu Q, Chi S, Yang M. An Optimal Model and Application of Hydraulic Structure Regulation to Improve Water Quality in Plain River Networks. Water. 2023; 15(24):4297. https://doi.org/10.3390/w15244297
Chicago/Turabian StyleHuang, Fan, Haiping Zhang, Qiaofeng Wu, Shanqing Chi, and Mingqing Yang. 2023. "An Optimal Model and Application of Hydraulic Structure Regulation to Improve Water Quality in Plain River Networks" Water 15, no. 24: 4297. https://doi.org/10.3390/w15244297
APA StyleHuang, F., Zhang, H., Wu, Q., Chi, S., & Yang, M. (2023). An Optimal Model and Application of Hydraulic Structure Regulation to Improve Water Quality in Plain River Networks. Water, 15(24), 4297. https://doi.org/10.3390/w15244297





