Leakage Risk Assessment of Urban Water Distribution Network Based on Unascertained Measure Theory and Game Theory Weighting Method
Abstract
:1. Introduction
- (1)
- How to incorporate the correlation between leakage probability and leakage loss to provide a more comprehensive understanding of leakage risk?
- (2)
- How to select a comprehensive range of evaluation indices that cover different forms of leakage threats to guarantee a more all-inclusive risk assessment?
- (3)
- How to efficiently manage uncertain data? Techniques including using probabilistic approaches or sensitivity analysis may be employed to conduct a more precise assessment.
- (4)
- How to develop a systematic approach to weigh the subjective and objective indices, taking into consideration their relative importance in overall risk assessment?
2. Literature Review
2.1. Past Studies on Micro Models
2.2. Past Studies on Macro Models
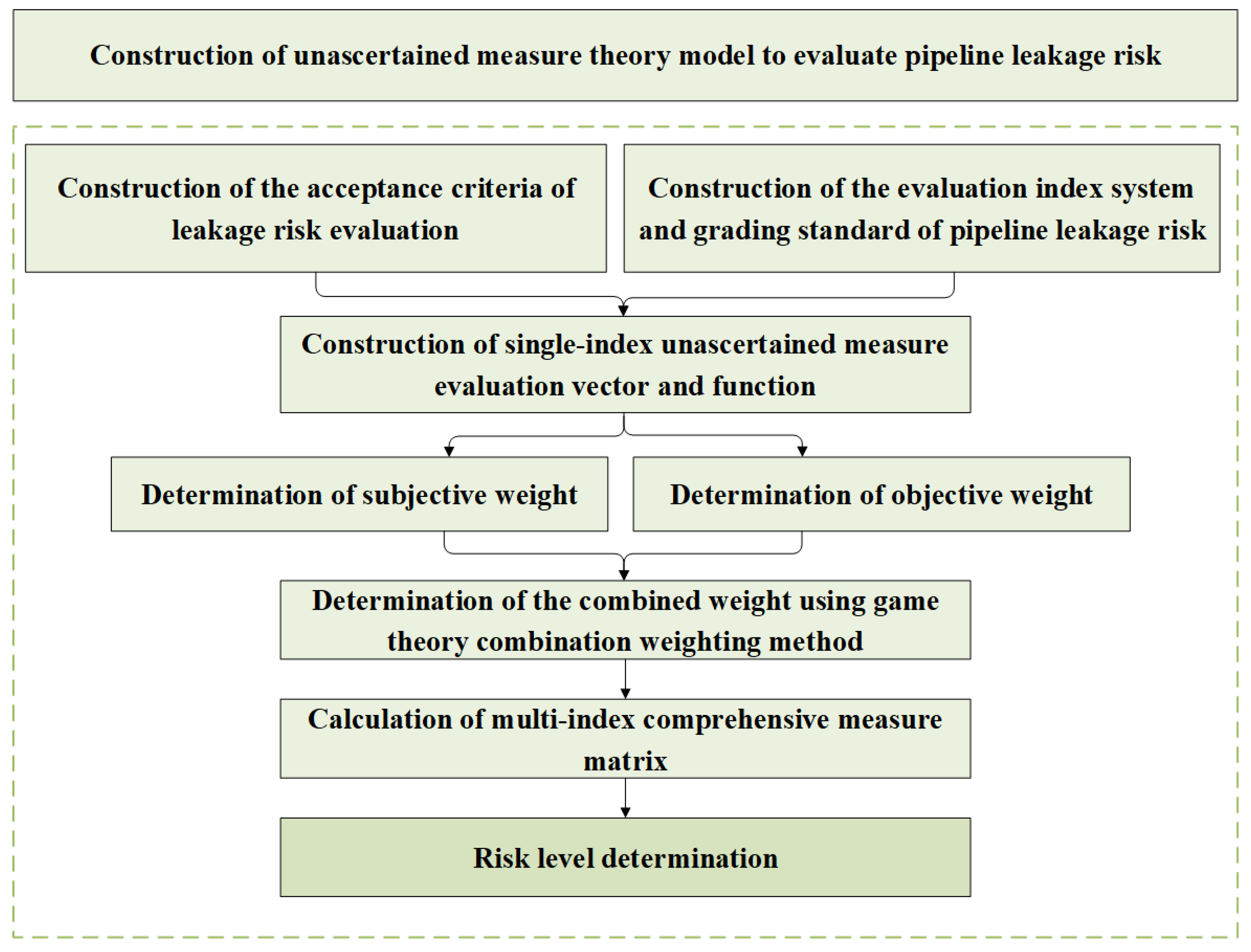
3. Research Methodology
3.1. Evaluation Index System of Pipeline Leakage Risk
3.2. Pipeline Leakage Risk Assessment Model
4. Case Analysis
4.1. Project Overview
4.2. Selection of Evaluation Indexes
4.3. Application of Pipeline Leakage Risk Assessment Model
- (1)
- Construction of single-index measurement function
- (2)
- Weight calculation using the combination weighting method
- (3)
- Multi-index comprehensive measure vector and risk level determination
4.4. Arrangement of Evaluation Objects
4.5. Discussion
5. Conclusions
- (1)
- This study introduced the concept that risk comprises both the probability of occurrence and loss resulting from such an occurrence, providing a resolution to the problem of recent research’s singular focus on the probability of pipeline leakage. Based on insights from the relevant literature and statistical data collected from various regions of China, this study identified four primary categories as the criterion layer: pipeline intrinsic factors, external environmental factors, operational management factors, and leakage loss factors. A detailed analysis of 14 evaluation indices was carried out within these categories, resulting in the establishment of a comprehensive evaluation system for the risk of pipeline leakage. This system categorized the evaluation space into five sequential levels based on the level of risk.
- (2)
- The implementation of the theory of unascertained measures to assess pipeline risks empowered researchers and water companies to manage uncertainties linked with historical data efficiently. In order to create an evaluation model for the risk of leaks in UWDN, it was necessary to follow specific steps. These steps included constructing single-index unascertained measure evaluation matrixes, determining combination weights, establishing multi-index comprehensive measurement vectors, and applying the confidence recognition criterion. The resulting model was able to precisely evaluate the likelihood of leaks occurring in particular water supply pipelines during the evaluation timeframe.
- (3)
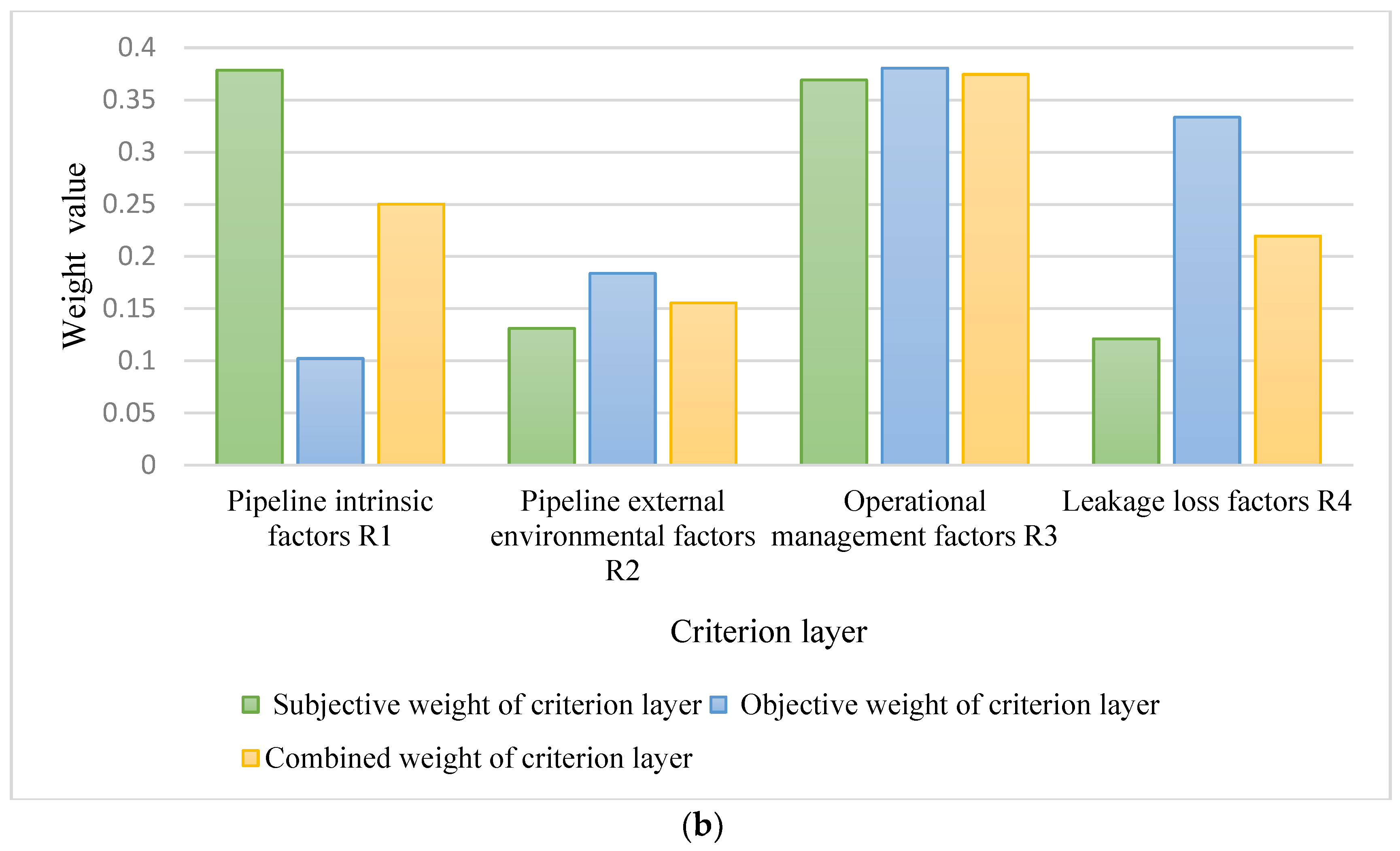
- The game theory combination weighting method was utilized in this study to determine the weight of each evaluation index, resulting in a balanced blend of subjective and objective information. Assigning weights was not only a crucial component of risk assessment but also established a basis for controlling and managing water leakage. For example, this study identified that the indexes with the greatest weights were construction conditions and repair or reconstruction costs. Interestingly, previous studies on leakage risk assessment largely disregarded these factors. This discovery enables the water company to concentrate on mitigating the impact of these specific indices, ultimately reducing overall leakage risk. This strategic insight outlines the practical implications of using a weighting methodology to guide targeted interventions for improving the control and management of water leakages.
- (4)
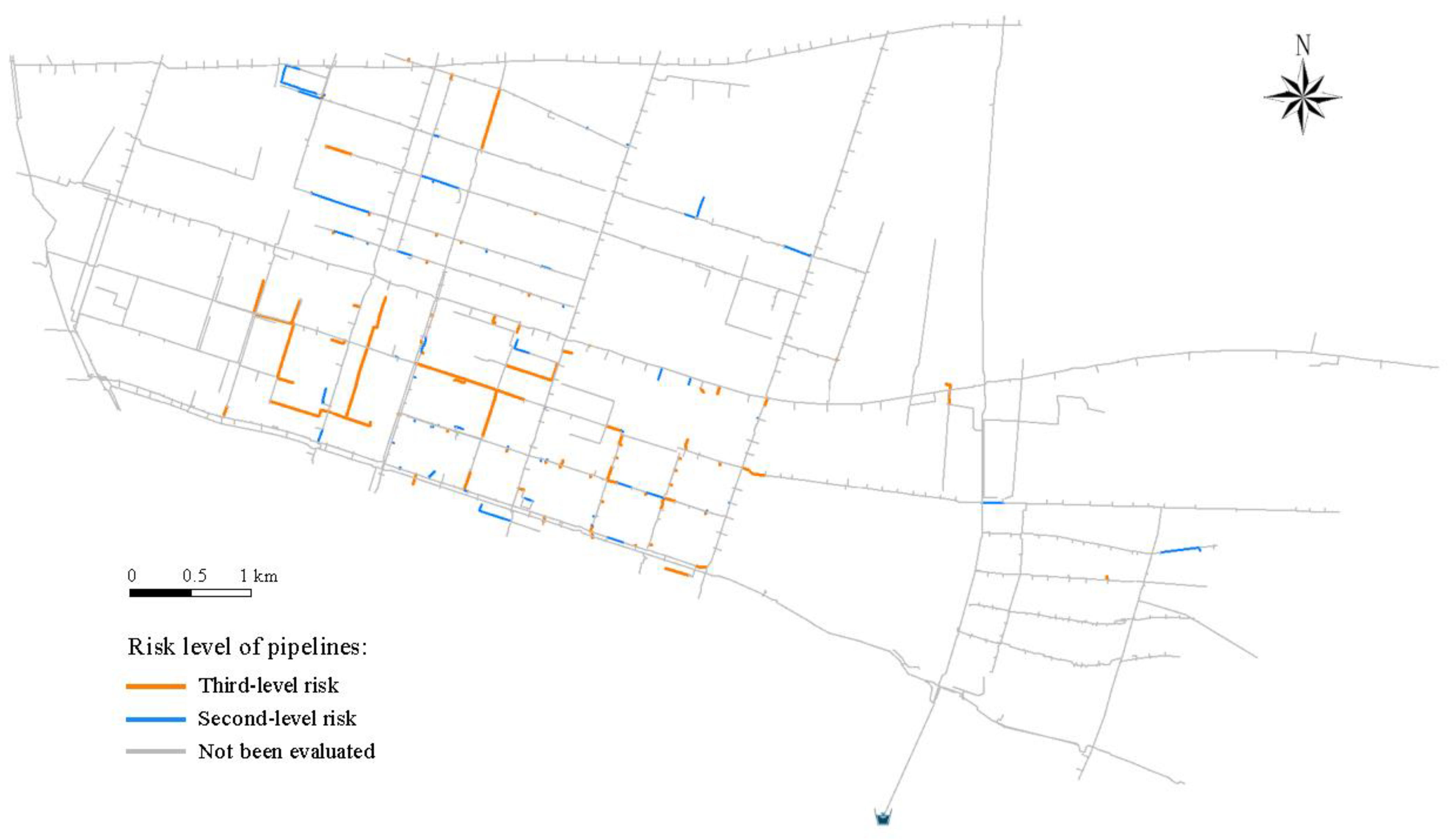
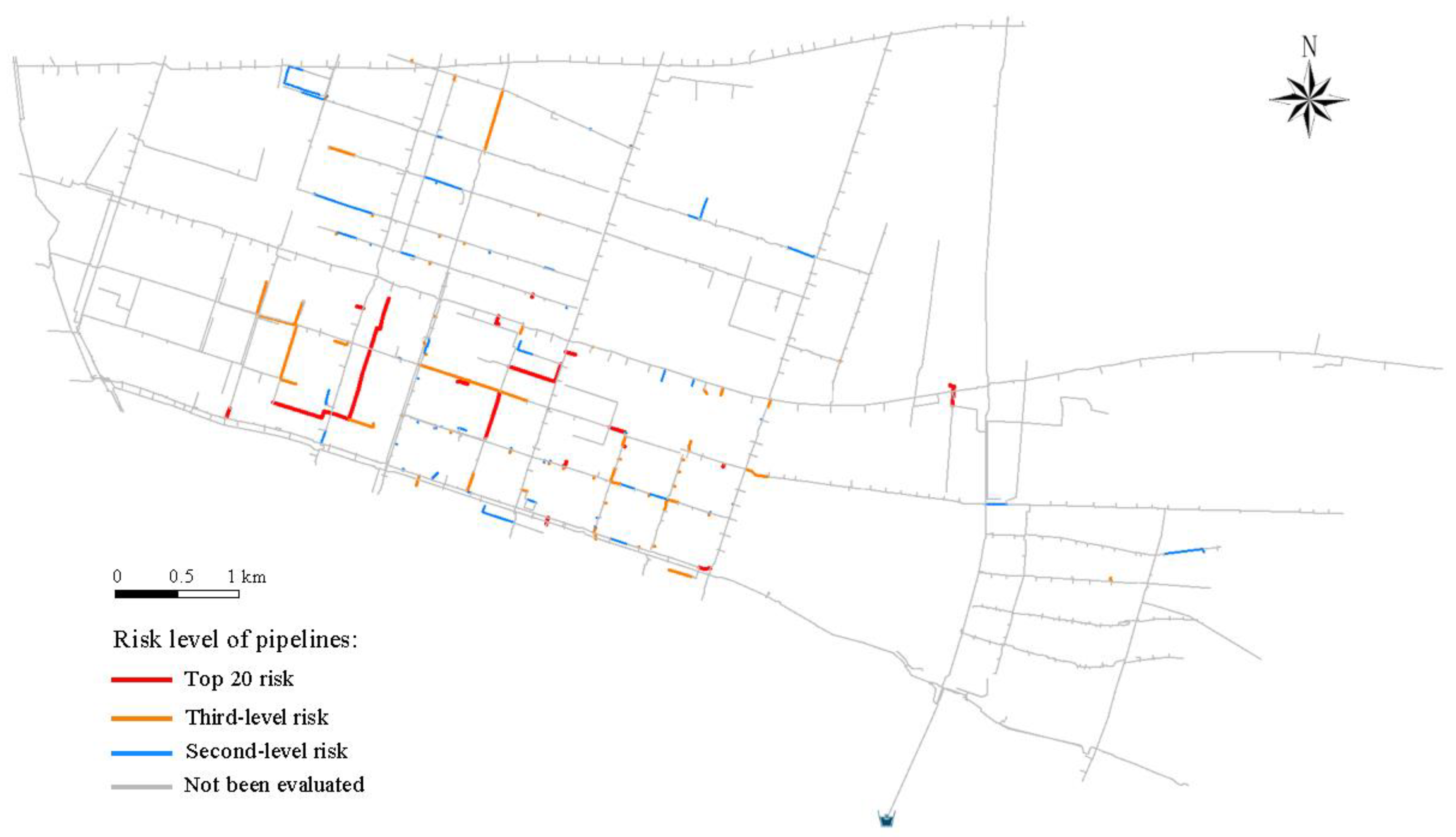
- To evaluate the practicability and dependability of this study, the research methodology was employed to conduct a risk assessment on pipelines that have recorded leaks in the M district of W city, China. As a result of this evaluation, the risk level of the tested pipe section lines was found to be at a second to third level of risk. It is vital to continue monitoring the pipeline for leaks, which should be performed daily, as supported by field studies. Uncertain significance values can facilitate the sorting of pipeline risks within a specific level, creating a valuable reference for the water company to develop comprehensive and detailed leak control strategies.
- (5)
- By integrating theoretical models, statistical analyses, and innovative methodologies, this study presents a durable and methodical method for evaluating and managing leakage risks. This comprehensive approach facilitates decision-making, the allocation of resources, and proactive risk mitigation. In pipeline leakage risk assessment, identifying the precise location of the leak is not the only crucial factor, and ensuring that water companies can repair leaks more efficiently is another factor. This approach holds considerable practical value for decision-makers. Broadening the model’s application and improving its interaction design can enable water companies to make informed decisions and develop effective strategies for managing pipeline leak risks in diverse geographical locations. The model’s versatility guarantees its adjustability to varying contexts, thus supplying water management authorities with a valuable instrument to customize and design their interventions to suit the specific challenges and characteristics of each location.
- (1)
- It is important to note that the approach presented in this study has certain limitations. Conducting a risk assessment for every single pipeline in a specific area would not be practical. Therefore, it is recommended that a select number of crucial pipelines be chosen for assessment, as demonstrated in this paper, and that leak detection procedures be performed on those key pipelines first. A global risk assessment should be conducted on all pipelines in the study area using machine learning classification and regression methods. The suggested approach includes using key pipelines as a sample and a test set and is a follow-up task of this research.
- (2)
- This study has room for improvement in selecting influencing factors and evaluation indices. For example, when considering the “Special location” index (R43), it primarily evaluates the placement of the pipeline below buildings or in densely populated urban areas. Nonetheless, it is worth mentioning that tourism can notably impact water consumption and treatment costs [49]. In the case area, there are ancient towns and various tourist attractions. This indicates that the index system could be enhanced in future iterations by incorporating tourist destinations.
- (3)
- The agenda ahead involves implementing a model to conduct further risk evaluations of pipeline leakage in the region. To accomplish this, it is necessary to complete the interaction design of the leakage risk evaluation model by utilizing procedural design functions and integrating it with the database, which is a critical aspect. This will allow for the model to be applied in numerous regions that demand risk assessment. This collaborative endeavor aims to offer dependable technical assistance to the water companies in creating comprehensive leak prevention strategies for diverse locations and circumstances.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Geng, W.M. Control the leakage of water supply network. Urban Public Util. 2005, 2, 17–18. (In Chinese) [Google Scholar] [CrossRef]
- National Development and Reform Commission. National Development and Reform Commission and Other Departments on the Issuance of “14th Five-Year” Water-Saving Society Construction Plan Notice. Available online: https://www.ndrc.gov.cn/xxgk/zcfb/ghwb/202111/t20211108_1303414.html (accessed on 13 November 2023).
- National Bureau of Statistics. China City Statistical Yearbook 2021; China Statistical Publishing House: Beijing, China, 2022; ISBN 978-7-5037-9786-6. [Google Scholar]
- De Silva, D.; Moglia, M.; Davis, P.; Burn, S. Condition Assessment to Estimate Failure Rates in Buried Metallic Pipelines. J. Water Supply Res. Technol.-Aqua 2006, 55, 179–191. [Google Scholar] [CrossRef]
- Al-Barqawi, H.; Zayed, T. Infrastructure Management: Integrated AHP/ANN Model to Evaluate Municipal Water Mains’ Performance. J. Infrastruct. Syst. 2008, 14, 305–318. [Google Scholar] [CrossRef]
- Zheng, C.Z. Analysis and Evaluation of Urban Water Supply Pipeline Integrity. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2010. [Google Scholar] [CrossRef]
- Kutyłowska, M. K-Nearest Neighbours Method as a Tool for Failure Rate Prediction. Period. Polytech. Civ. Eng. 2018, 62, 318–322. [Google Scholar] [CrossRef]
- Zhang, H.X. Research and Application of Pipeline Risk Assessment for Urban Water Supply Network. Master’s Thesis, Chang’an University, Xi’an, China, 2020. [Google Scholar] [CrossRef]
- Rogers, P.D.; Grigg, N.S. Failure Assessment Modeling to Prioritize Water Pipe Renewal: Two Case Studies. J. Infrastruct. Syst. 2009, 15, 162–171. [Google Scholar] [CrossRef]
- Fayaz, M.; Ahmad, S.; Hang, L.; Kim, D. Water Supply Pipeline Risk Index Assessment Based on Cohesive Hierarchical Fuzzy Inference System. Processes 2019, 7, 182. [Google Scholar] [CrossRef]
- Zhang, W.; Lai, T.; Li, Y. Risk Assessment of Water Supply Network Operation Based on ANP-Fuzzy Comprehensive Evaluation Method. J. Pipeline Syst. Eng. Pract. 2022, 13, 04021068. [Google Scholar] [CrossRef]
- Lambert, A.; Merks, C.; Trow, S. Good Practices in Leakage Management: Lessons from Europe. 2015. Available online: https://search.ebscohost.com/login.aspx?direct=true&db=eih&AN=102656122&lang=zh-cn&site=ehost-live (accessed on 13 November 2023).
- Adedeji, K.B.; Hamam, Y.; Abe, B.T.; Abu-Mahfouz, A.M. Towards Achieving a Reliable Leakage Detection and Localization Algorithm for Application in Water Piping Networks: An Overview. IEEE Access 2017, 5, 20272–20285. [Google Scholar] [CrossRef]
- Henry, R.; Luxmoore, A.R. A Pipe-Profiling Adapter for CCTV Inspection Cameras: Development of a Pipe-Profiling Instrument. Meas. Sci. Technol. 1996, 7, 495–504. [Google Scholar] [CrossRef]
- Muntakim, A.H.; Dhar, A.S.; Dey, R. Interpretation of Acoustic Field Data for Leak Detection in Ductile Iron and Copper Water-Distribution Pipes. J. Pipeline Syst. Eng. Pract. 2017, 8, 05017001. [Google Scholar] [CrossRef]
- Sikder, M.N.K.; Nguyen, M.B.T.; Elliott, E.D.; Batarseh, F.A. Deep H2O: Cyber Attacks Detection in Water Distribution Systems Using Deep Learning. J. Water Process Eng. 2023, 52, 103568. [Google Scholar] [CrossRef]
- Ramos, H.M.; Morani, M.C.; Carravetta, A.; Fecarrotta, O.; Adeyeye, K.; López-Jiménez, P.A.; Pérez-Sánchez, M. New Challenges towards Smart Systems’ Efficiency by Digital Twin in Water Distribution Networks. Water 2022, 14, 1304. [Google Scholar] [CrossRef]
- Rajani, B.; Zhan, C. On the Estimation of Frost Loads. Can. Geotech. J. 1996, 33, 629–641. [Google Scholar] [CrossRef]
- Rajani, B.; Zhan, C.; Kuraoka, S. Pipesoil Interaction Analysis of Jointed Water Mains. Can. Geotech. J. 1996, 33, 393–404. [Google Scholar] [CrossRef]
- Zhao, S.; Jiang, X.B.; Gao, H.L. Reliability Method for the Assessment of the Failure Probability and Remaining Life of the Corroded Pipeline. Oil Gas Storage Transp. 2006, 12, 28–31. (In Chinese) [Google Scholar] [CrossRef]
- Shen, W.M. Study on Soil-Culvert Interaction and Structural Characteristics of Culvert in Transverse and Longitudinal Direction. Ph.D. Dissertation, Zhejiang University, Hangzhou, China, 2011. Available online: https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C447WN1SO36whHG-SvTYjkCc7dJWN_daf9c2-IbmsiYfKjYNsgKsVO4GjtplRcsdDhIppMOEPvr7zSIb9F6xl0A2&uniplatform=NZKPT (accessed on 13 November 2023).
- Jur, T.A.; Middleton, J.I.; Yurko III, A.A.; Windham, R.L.; Grey, J.R. Case Studies in Graphitic Corrosion of Cast Iron Pipe. J. Fail. Anal. Prev. 2021, 21, 376–386. [Google Scholar] [CrossRef]
- Lin, P.; Zhang, B.; Wang, Y.; Li, Z.; Li, B.; Wang, Y.; Chen, F. Data Driven Water Pipe Failure Prediction: A Bayesian Nonparametric Approach. In Proceedings of the 24th ACM International on Conference on Information and Knowledge Management (CIKM ‘15). Association for Computing Machinery, New York, NY, USA, 19–23 October 2015; pp. 193–202. [Google Scholar] [CrossRef]
- Diaz-Ortiz, J.; Alvarado-Medellin, P.; Ramirez-Aguilera, A.M.; Badillo-Almaraz, H.; Gomez, R.O.; Capetillo, C.B. Water Distribution System Calibration Using the Finite Element Method Coupled to a Genetic Algorithm. J. Water Process Eng. 2023, 54, 104017. [Google Scholar] [CrossRef]
- Yamijala, S.; Guikema, S.D.; Brumbelow, K. Statistical Models for the Analysis of Water Distribution System Pipe Break Data. Reliab. Eng. Syst. Saf. 2009, 94, 282–293. [Google Scholar] [CrossRef]
- Wang, C.W.; Zhang, H.W.; Niu, Z.G.; Peng, S. Assessment of Operation Conditions of Gray Cast lron Pipes. China Water Wastewater 2010, 26, 50–52+56. (In Chinese) [Google Scholar] [CrossRef]
- Kizilöz, B. Prediction Model for the Leakage Rate in a Water Distribution System. Water Supply 2021, 21, 4481–4492. [Google Scholar] [CrossRef]
- Wang, J.L.; Hu, Y.M.; Xu, Q.; Zhang, X.Z.; Li, S. Evaluation of influencing factors of pipe leakage for water distribution network based on fuzzy analytic hierarchy process and grey relation analysis methods. Water Wastewater Eng. 2022, 58, 116–122. (In Chinese) [Google Scholar] [CrossRef]
- Li, H.C. Research on Risk Assessment of Urban Water Supply Pipeline Network Leakage Based on Unascertained Measure Theory. Ph.D. Dissertation, Taiyuan University of Technology, Taiyuan, China, 2019. Available online: https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C475KOm_zrgu4lQARvep2SAkOsSuGHvNoCRcTRpJSuXuqfnlfiV7zWsMx7W9OKuUqHWPfwxWPMuwGJE90k1PYltS&uniplatform=NZKPT (accessed on 13 November 2023).
- Zhong, H.; Tang, Y.; Yan, H.; Zhang, Y.; Dong, L.; Wang, B. Corrosion of Pipelines in Urban Water Systems: Current Research Status and Future Trends Based on Bibliometric Analysis. J. Water Process Eng. 2023, 56, 104288. [Google Scholar] [CrossRef]
- Tian, C. Methodology and Application of Pipe Condition Assessment in Urban Water Distribution System. Ph.D. Dissertation, Tsinghua University, Beijing, China, 2016. Available online: https://kns.cnki.net/kcms2/article/abstract?v=hqt_j-uEELGGf6RiMZxxl2MYvYAjrKIgiiQ2dtoGJHEkOeMnRsykeOV6jmSpIjN3W5VHu9NYimdwvk7dT1TjtbI4_wAxwsOrE2BCFVq9OO1JNEF-HY5nXTQJeLL6ZhGWb302FmXFL-o=&uniplatform=NZKPT (accessed on 13 November 2023).
- Jiang, M. The Study of Water Supply Network Leakage Evaluation Based on Improved Analytic Hierarchy Process. Ph.D. Dissertation, Harbin Institute of Technology, Harbin, China, 2017. [Google Scholar] [CrossRef]
- Zhang, G.L.; Wang, Q.B.; Zhang, F.R.; Wu, K.N.; Cai, C.F.; Zhang, M.K.; Li, D.C.; Zhao, Y.G.; Yang, Y.L. Criteria for Establishment of Soil Family and Soil Series in Chinese Soil Taxonomy. Acta Pedol. Sin. 2013, 50, 826–834. (In Chinese) [Google Scholar] [CrossRef]
- Wu, K.N.; Zhao, R. Soil Texture Classification and lts Application in China. Acta Pedol. Sin. 2019, 56, 227–241. (In Chinese) [Google Scholar]
- Wu, S.; Liu, Y.H.; Zhang, S.H.; Wang, W.Y.; Ma, Z.Z. Experimental study on influences of pressure regulation and con-trol in water supply pipes on volume of water leakage. Adv. Sci. Technol. Water Resour. 2007, 3, 27–29. (In Chinese) [Google Scholar] [CrossRef]
- Li, C.C.; Li, J. Numerical simulation of leakage flow in pipeline leak point. City Town Water Supply 2020, 2, 33–36+11. (In Chinese) [Google Scholar] [CrossRef]
- Tan, X. Leakage of Water Supply Pipe Network Prediction and Evaluation of Healthy. Ph.D. Dissertation, Hunan University, Changsha, China, 2009. [Google Scholar] [CrossRef]
- Wang, G.Y. Unascertained information and its mathematical treatment. J. Harbin Inst. Archit. Eng. 1990, 4, 1–9. Available online: https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C44YLTlOAiTRKjkpgKvIT9NkyGkCpOZCCacPWZoIEaDzzFLQvQYWq1hBw8IhE0OJMAszlUkyfAYMSMciESwvSz0q&uniplatform=NZKPT (accessed on 13 November 2023). (In Chinese).
- Li, L.; Sheng, Z.H.; Xu, N.R. An improved analytic hierarchy process. Syst. Eng. 1989, 3, 5–7+2. Available online: https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C44YLTlOAiTRKqd0WnNPv0wTDjtDUwHroNyoRyUmZKOvx4-642obkUlr5iipJ_mUIDOyiIt2zZtPIdQaXLmjpQha&uniplatform=NZKPT (accessed on 13 November 2023). (In Chinese).
- Niu, L.; Chen, K.; Cheng, Y. Application of Improved Analytic Hierarchy Process in Employment Comprehensive Evaluation. Comput. Simul. 2011, 28, 376–379. (In Chinese) [Google Scholar] [CrossRef]
- Chen, J.L. Research on combination weighting evaluation method based on game theory. Fujian Comput. 2003, 9, 15–16. (In Chinese) [Google Scholar] [CrossRef]
- Zhong, L.M.; Xie, Q.M.; Luo, Y. Stability evaluation of tunnel surrounding rock based on game-extension theory. China Saf. Prod. Sci. Technol. 2019, 15, 56–61. (In Chinese) [Google Scholar] [CrossRef]
- Sun, Y.Y.; Hao, W. Application of information entropy-unascertained measure theory in quality optimization of concrete recycled coarse aggregate. Civ. Eng. Environ. Eng. 2017, 39, 87–92. (In Chinese) [Google Scholar] [CrossRef]
- Fu, Y.F. Distribution Systems Control on Leakage of Urban Water. Ph.D. Dissertation, Tianjin University, Tianjin, China, 2004. [Google Scholar] [CrossRef]
- Zhang, C.; Nong, X.; Zhong, H.; Shao, D.; Chen, L.; Liang, J. A Framework for Exploring Environmental Risk of the Longest Inter-Basin Water Diversion Project under the Influence of Multiple Factors: A Case Study in China. J. Environ. Manag. 2022, 322, 116036. [Google Scholar] [CrossRef] [PubMed]
- Zehtabian, E.; Masoudi, R.; Yazdandoost, F.; Sedghi-Asl, M.; Loáiciga, H.A. Investigation of Water Allocation Using Integrated Water Resource Management Approaches in the Zayandehroud River Basin, Iran. J. Clean. Prod. 2023, 395, 136339. [Google Scholar] [CrossRef]
- Hu, X.; Huang, L.; Chen, J.; Li, X.; Zhang, H. Rockburst Prediction Based on Optimization of Unascertained Measure Theory with Normal Cloud. Complex Intell. Syst. 2023, 9, 7321–7336. [Google Scholar] [CrossRef]
- Wu, Q.; Zhao, D.; Wang, Y.; Shen, J.; Mu, W.; Liu, H. Method for Assessing Coal-Floor Water-Inrush Risk Based on the Variable-Weight Model and Unascertained Measure Theory. Hydrogeol. J. 2017, 25, 2089–2103. [Google Scholar] [CrossRef]
- Pérez, D.M.G.; Martín, J.M.M.; Martínez, J.M.G.; Sáez-Fernández, F.J. An Analysis of the Cost of Water Supply Linked to the Tourism Industry. An Application to the Case of the Island of Ibiza in Spain. Water 2020, 12, 2006. [Google Scholar] [CrossRef]


| Goal Layer | Criterion Layer | Index Layer | Evaluation Method | First-Level Risk: Very Low Risk | Second-Level Risk: Low Risk | Third-Level Risk: General Risk | Fourth-Level Risk: High Risk | Fifth-Level Risk: Very High Risk | Quantitative Classification Method Description |
|---|---|---|---|---|---|---|---|---|---|
| Leakage risk of urban water distribution network | Pipeline intrinsic factors R1 | Pipe material R11 | Characterization | Ductile iron pipe | Plastic pipe | Galvanized steel pipe | Steel pipe | Cast iron pipe | |
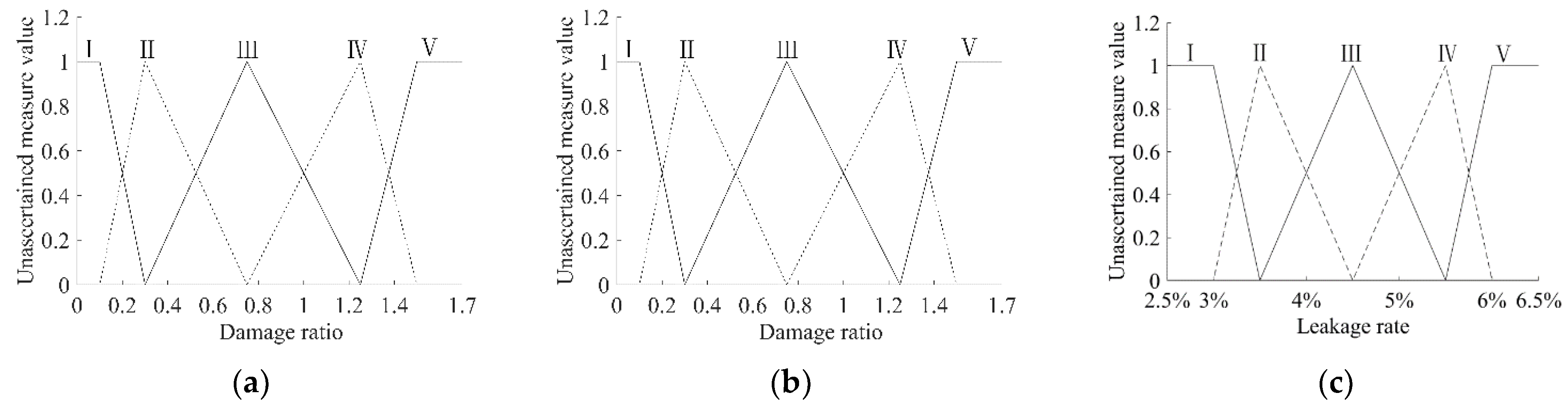
| Diameter R12 | Quantification | ≤0.1 | 0.1–0.5 | 0.5–1.0 | 1.0–1.5 | ≥1.5 | Damage ratio | ||
| Age of the pipeline R13 | Quantification | ≤0.1 | 0.1–0.5 | 0.5–1.0 | 1.0–1.5 | ≥1.5 | Damage ratio | ||
| Corrosion condition R14 [29,30] | Characterization | The pipeline exhibits high resistance to corrosion. | The pipeline exhibits high resistance to corrosion. | Pipeline corrosion is a prevalent issue. | The pipeline is susceptible to corrosion. | The pipeline is extremely vulnerable to corrosion. | |||
| Joint condition R15 [31,32] | Characterization | Flexible interface, high toughness, good interface strength and tightness. | Flexible interface, strong shock resistance, can resist a certain tensile deformation. | Strong sealing, relatively strong, water leakage easy to occur on such a pipeline because of poor welding. | The rigidity is strong, and the uneven settlement or temperature change of the foundation will break the joint. | The rigidity is strong, and the pipeline joint is easily broken due to thermal expansion and cold contraction. | |||
| Pipeline external environmental factors R2 | Depth of embedment R21 | Quantification | ≤3% | 3–4% | 4–5% | 5–6% | ≥6% | Leakage rate per unit pipe length | |
| Nature of soil R22 [33,34] | Characterization | Coarse bone soil | Coarse bone sandy soil | Sandy soil | Loam | Clay soil | |||
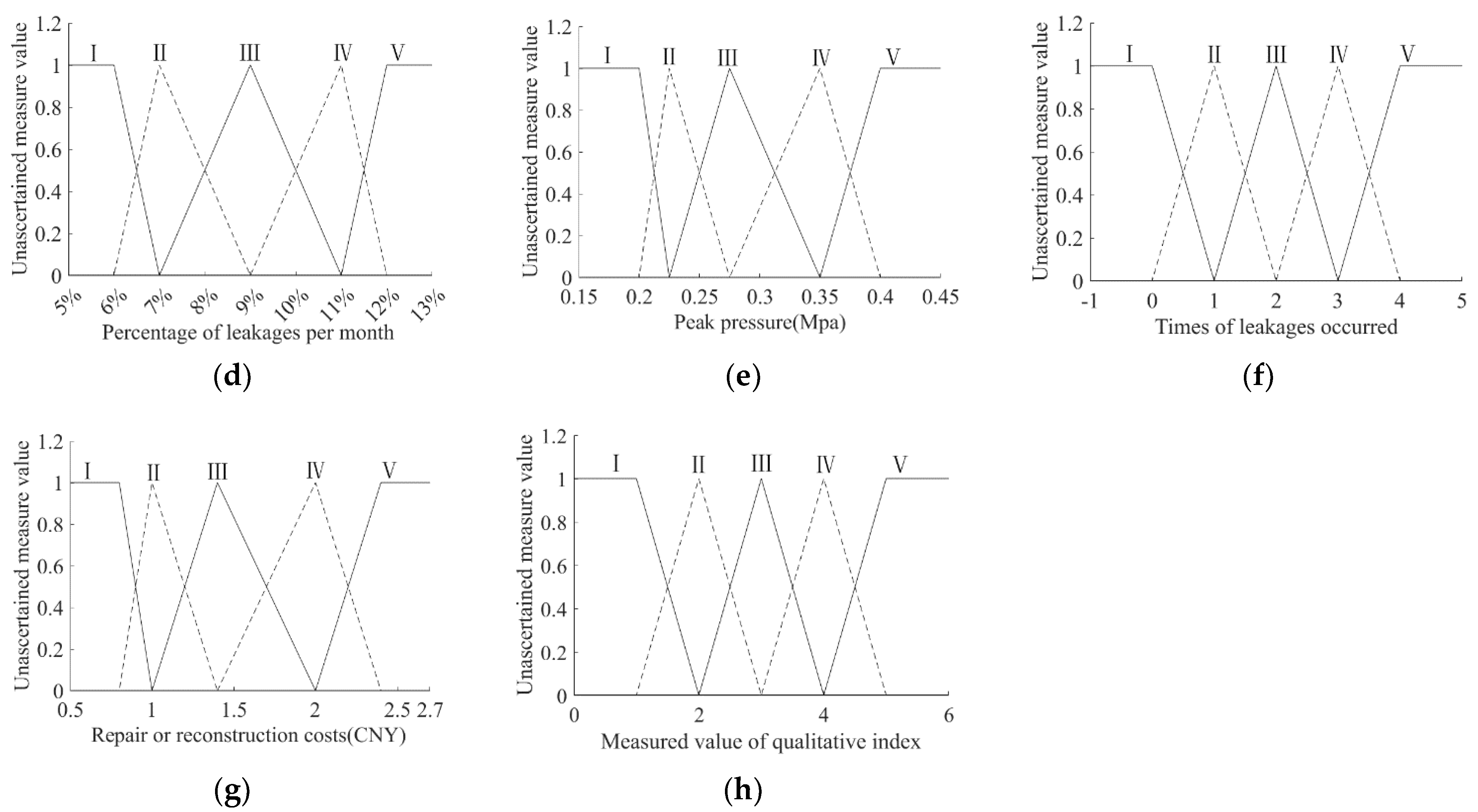
| Temperature and frozen R23 | Quantification | ≤6% | 6–8% | 8–10% | 10–12% | ≥12% | Percentage of leakages per month | ||
| Operational management factors R3 | Peak pressure R31 [35,36] | Quantification | ≤0.20 | 0.20–0.25 | 0.25–0.30 | 0.30–0.40 | ≥0.40 | Unit: Mpa | |
| Times of leakages occurred R32 | Quantification | 0 | 1 | 2 | 3 | ≥4 | Unit: times | ||
| Construction condition R33 [37] | Characterization | The construction process is in full compliance with the specification. | The construction process is in line with the specifications. | The construction process is generally in line with the specifications. | There are obvious omissions in the construction process. | There are many non-compliant processes in the construction. | |||
| Leakage loss factors R4 | Repair or reconstruction costs R41 | Quantification | <8000 | 8000–12,000 | 12,000–16,000 | 16,000–24,000 | >24,000 | Uni: CNY | |
| Road grade R42 | Characterization | Roads within the district. | Branch roads to the interior of the district. | Third-level road. | Second-level road. | First-level road. | |||
| Special location R43 | Characterization | The special location of the pipeline has no effect on the leakage maintenance. | The special location of the pipeline has little effect on the leakage maintenance. | The special location of the pipeline has some effect on the leakage maintenance. | The special location of the pipeline has a large effect on the leakage maintenance. | The special location of the pipeline has a great effect on the leakage maintenance. | |||
| Qualitative index value | 1 | 2 | 3 | 4 | 5 | ||||
| Pipeline Number | Upstream Node Number | Downstream Node Number | Diameter (DN) | Length (m) | Pipe Material | Year of Construction | Depth of Embedment (m) | Nature of Soil |
|---|---|---|---|---|---|---|---|---|
| P01739 | V00018-B | J1363 | 200 | 18.38 | Ductile iron pipe | 2010 | 1.575 | Sandy soil |
| Pipeline Number | Peak Pressure (Mpa) | The number of Leakages Occurred | Condition of Construction | Pipeline repair or Reconstruction Costs (CNY) [44] | Road Grade of Pipeline | Special Circumstances | ||
| P01739 | 0.276 | 1 | The construction process is in line with the specifications | 13,842.39 | Third-level road | Located in dense urban areas, passing through sewers or drains | ||
| Evaluation Index | Pipe Material R11 | Diameter R12 | Age of the Pipeline R13 | Corrosion Condition R14 | Joint Condition R15 | Depth of Embedment R21 | Nature of Soil R22 |
|---|---|---|---|---|---|---|---|
| Value of index of P01739 | 1 | 0.72 | 3.3 | 3 | 2 | 2.74% | 3 |
| Evaluation Index | Temperature and Frozen R23 | Peak Pressure R31 | Times of Leakages Occurred R32 | Construction Condition R33 | Repair or Reconstruction Costs R41 | Road Grade R42 | Special Location R43 |
| Value of index of P01739 | 12.93% | 0.276 | 1 | 2 | 13,842.39 | 3 | 2 |
| Goal Layer | Criterion Layer | Subjective Weight of Criterion Layer | Objective Weight of Criterion Layer | Combined Weight of Criterion Layer | Index Layer | Subjective Weight for Each Index | Objective Weight for Each Index | Combined Weight for Each Index |
|---|---|---|---|---|---|---|---|---|
| Leakage risk of urban water distribution network | Pipeline intrinsic factors R1 | 0.3785 | 0.1023 | 0.2503 | Pipe material R11 | 0.2278 | 0.2063 | 0.2258 |
| Diameter R12 | 0.0462 | 0.1749 | 0.0579 | |||||
| Age of the pipeline R13 | 0.278 | 0.2063 | 0.2715 | |||||
| Corrosion condition R14 | 0.3348 | 0.2063 | 0.3232 | |||||
| Joint condition R15 | 0.1131 | 0.2063 | 0.1216 | |||||
| Pipeline external environmental factors R2 | 0.1312 | 0.1838 | 0.1556 | Depth of embedment R21 | 0.3186 | 0.3333 | 0.3186 | |
| Nature of soil R22 | 0.4044 | 0.3333 | 0.4044 | |||||
| Temperature and Frozen R23 | 0.277 | 0.3333 | 0.277 | |||||
| Operational management factors R3 | 0.3691 | 0.3806 | 0.3744 | Peak pressure R31 | 0.2067 | 0.3259 | 0.2105 | |
| Times of leakages occurred R32 | 0.2868 | 0.337 | 0.2884 | |||||
| Construction condition R33 | 0.5065 | 0.337 | 0.5012 | |||||
| Leakage loss factors R4 | 0.1212 | 0.3334 | 0.2197 | Repair or reconstruction costs R41 | 0.4167 | 0.3096 | 0.4003 | |
| Road grade R42 | 0.2251 | 0.3452 | 0.2435 | |||||
| Special location R43 | 0.3582 | 0.3452 | 0.3562 |
| Pipeline Number | Risk Level Result | First-Level Risk Membership | Second-Level Risk Membership | Third-Level Risk Membership | Fourth-Level Risk Membership | Fifth-Level Risk Membership | Uncertain Significance | Risk Ranking |
|---|---|---|---|---|---|---|---|---|
| P0896 | 3 | 0.0983 | 0.1892 | 0.3231 | 0.2535 | 0.1360 | 3.1395 | 1 |
| P1394 | 3 | 0.0623 | 0.2096 | 0.4791 | 0.0603 | 0.1886 | 3.1033 | 2 |
| P1192 | 3 | 0.1027 | 0.3067 | 0.2405 | 0.1875 | 0.1626 | 3.0005 | 3 |
| P1440 | 3 | 0.0864 | 0.2434 | 0.4276 | 0.0813 | 0.1613 | 2.9878 | 4 |
| P1588 | 3 | 0.1172 | 0.2260 | 0.4261 | 0.0303 | 0.2004 | 2.9706 | 5 |
| P0461 | 3 | 0.0000 | 0.4735 | 0.2938 | 0.0318 | 0.2009 | 2.9599 | 6 |
| P1406 | 3 | 0.1385 | 0.2099 | 0.4149 | 0.0448 | 0.1920 | 2.9419 | 7 |
| P1605 | 3 | 0.1085 | 0.2858 | 0.3205 | 0.1361 | 0.1492 | 2.9319 | 8 |
| P0981 | 3 | 0.1289 | 0.3065 | 0.1820 | 0.2815 | 0.1011 | 2.9194 | 9 |
| P0175 | 3 | 0.0560 | 0.3438 | 0.3341 | 0.1577 | 0.1084 | 2.9188 | 10 |
| P1451 | 3 | 0.0538 | 0.4089 | 0.3041 | 0.0591 | 0.1741 | 2.8909 | 11 |
| P1508 | 3 | 0.0855 | 0.3465 | 0.3308 | 0.0661 | 0.1711 | 2.8907 | 12 |
| P1183 | 3 | 0.1301 | 0.2376 | 0.4147 | 0.0627 | 0.1548 | 2.8744 | 13 |
| P1358 | 3 | 0.1377 | 0.2102 | 0.4114 | 0.1407 | 0.1000 | 2.8551 | 14 |
| P01756 | 3 | 0.2114 | 0.1908 | 0.2381 | 0.2672 | 0.0925 | 2.8386 | 15 |
| P1441 | 3 | 0.1285 | 0.3854 | 0.2004 | 0.1302 | 0.1556 | 2.7990 | 16 |
| P1388 | 3 | 0.0739 | 0.2981 | 0.4992 | 0.0162 | 0.1125 | 2.7953 | 17 |
| P1450 | 3 | 0.1032 | 0.3343 | 0.3749 | 0.0423 | 0.1453 | 2.7924 | 18 |
| P01738 | 3 | 0.2026 | 0.2117 | 0.3774 | 0.0154 | 0.1929 | 2.7842 | 19 |
| P1721 | 3 | 0.0858 | 0.4824 | 0.2010 | 0.0374 | 0.1934 | 2.7701 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, C.; Wang, J.; Gao, W.; Huang, X.; Tao, T. Leakage Risk Assessment of Urban Water Distribution Network Based on Unascertained Measure Theory and Game Theory Weighting Method. Water 2023, 15, 4294. https://doi.org/10.3390/w15244294
Xiong C, Wang J, Gao W, Huang X, Tao T. Leakage Risk Assessment of Urban Water Distribution Network Based on Unascertained Measure Theory and Game Theory Weighting Method. Water. 2023; 15(24):4294. https://doi.org/10.3390/w15244294
Chicago/Turabian StyleXiong, Chuyu, Jiaying Wang, Wei Gao, Xianda Huang, and Tao Tao. 2023. "Leakage Risk Assessment of Urban Water Distribution Network Based on Unascertained Measure Theory and Game Theory Weighting Method" Water 15, no. 24: 4294. https://doi.org/10.3390/w15244294
APA StyleXiong, C., Wang, J., Gao, W., Huang, X., & Tao, T. (2023). Leakage Risk Assessment of Urban Water Distribution Network Based on Unascertained Measure Theory and Game Theory Weighting Method. Water, 15(24), 4294. https://doi.org/10.3390/w15244294






