1. Introduction
In recent years, fractured oil and gas reservoirs have accounted for the majority of newly discovered oil and gas reserves, attracting widespread attention from the petroleum industry and academia [
1,
2,
3,
4,
5]. The efficient development of low-permeability oil fields can accelerate the replacement of energy resources, can extend the service life of oil and gas resources, and is of great significance for improving China’s energy security level.
By utilizing reservoir numerical simulation technology, reservoir engineers can gain a more quantitative understanding of the production and development mechanisms of fractured reservoirs, thus making correct decisions on key issues during their development process. Common fracture models include dual/multiple medium models (DPDK/MPMK), discrete fracture mesh models (DFM), and embedded discrete fracture models (EDFM) [
6,
7,
8]. The dual/multi medium model assumes that the geometric shape of fractures is regular and their distribution within the unit follows a certain assumed shape. Among them, the porous model assumes that fractures evenly cut the matrix into multiple blocks, and each matrix block can be subdivided into multiple nested matrices. The dual pore/porous model simulates the reservoir space of fractures by allocating porosity. In simulation, it is often assumed that the first layer of mesh is a fracture mesh. Fluids can flow through the same layer, as in the dual-porosity and single-permeability model, or through multiple layers, as in the dual-porosity and double-permeability model. The conductivity of fractures within the matrix can be analytically calculated based on the pre-assumed morphology of fractures within the unit. Due to the assumption of regularity in the geometry of fractures, the dual medium method is suitable for reservoirs with smaller and uniformly distributed fractures but has huge limitations for large-scale fractured reservoirs. Unlike the dual medium method, both EDFM and DFM can consider the geometric shape of fractures in a simulation. EDFM simulates fractures as flat plates embedded in the background grid, uses “non adjacent connections” to obtain grid connectivity, and calculates conductivity. DFM uses solid grids to simulate fractures, and its conductivity calculation is no different than that between traditional grids [
9,
10].
Although EDFM and DFM have no limitations on the geometric shape of fractures, they are limited by the topological structure of the grid, and DFM cannot simulate some complex fractures, such as “X” type intersecting fractures. Compared to DFM, due to the use of virtual flat plates to simulate fractures, the EDFM method is more flexible in the geometric representation of fractures; however, the accuracy of EDFM is lower than that of DFM, specifically manifested through the following factors: (1) EDFM has grid dependency, and background grids with too large scales can affect accuracy; (2) When calculating the normal flow of fractures, due to the fact that the EDFM method does not truly segment the grids on both sides of the fracture, the calculation results of EDFM for the normal flow of fractures are not accurate. The coupling method of EDFM+DFM integrates the advantages of EDFM and DFM by using the unstructured grid of DFM as the background grid of EDFM and can compensate for the respective disadvantages of EDFM and DFM methods, thereby improving the simulation accuracy to a certain extent. However, whether it is EDFM, DFM, or coupled EDFM+DFM, these methods will still face the problem of simulation accuracy, which is due to the non-orthogonality of the grid.
Figure 1 shows the effect of grid orthogonality on EDFM and DFM. It can be seen that for EDFM, non-orthogonal grids are mainly generated by the background grid cutting the fracture slices and exist in the two-dimensional grid on the fracture slices; as for DFM, its non-orthogonal mesh is generated due to the deformation of the fracture and surrounding mesh to meet the geometric shape of the fracture inclination and exists around the inclined fracture mesh.
There are two strategies to overcome the influence of grid non-orthogonality: (1) improve the grid quality and (2) improve the accuracy of flow formats. In considering this problem, on the one hand, the non-orthogonal mesh of EDFM is caused by the intersection of fracture slices and background mesh, and due to the large number and random distribution of fractures, the background mesh of EDFM cannot be optimized for each fracture. On the other hand, the non-orthogonal mesh of DFM is generated because the fracture mesh simulates the inclination angle of fractures, resulting in a certain degree of compression and stretching of the surrounding mesh. Li’s research indicates that this non orthogonal effect cannot be eliminated. Therefore, adopting strategies to improve grid quality cannot solve this problem [
11,
12,
13,
14,
15].
The flow format plays a decisive role in the accuracy and efficiency of numerical simulation. A high-quality flow format should have the characteristics of simplicity, monotony, and accuracy. Simplicity refers to the sparsity of the solution matrix generated by the flow scheme. Monotonicity means that the flow always points from the grid with high pressure to the grid with low pressure. Accuracy refers to the solution of the solving matrix satisfying first-order or second-order accuracy.
Most flow format calculation methods of reservoir simulators are based on the control volume finite difference of a two-point format, which is also called two-point flow approximation (TPFA). The conductivity of TPFA is only related to the geometric shape of the grid. If the permeability is constant, the conductivity only needs to be calculated once before the simulation starts. But TPFA is only accurate in k-orthogonal grids, and in practical problems, due to the presence of fractures, faults, and wells, k-orthogonal grids are almost impossible to establish.
The multi-point flow approximation (MPFA) method can ensure the accuracy of flow calculations in non-k-orthogonal grids. It is called multipoint flow approximation because calculating the flow between two grids requires the pressure and conductivity of multiple surrounding grids. MPFA assumes that pressure is first-order continuous in space. From the pressure equation, MPFA is equivalent to a first-order finite volume scheme. However, MPFA does not assume a continuous distribution of saturation and mole fraction, so MPFA is not a strict finite volume scheme. It is not assumed that the continuous distribution of saturation and mole fraction is in line with physical reality, and MPFA can use the same “pressure + saturation” variable system as TPFA. The conductivity calculation of MPFA involves multiple grids. Taking a three-dimensional hexahedral grid as an example, using the O method to calculate all flow terms in a grid requires 27 grids and 26 conductivity calculations. As a comparison, TPFA only involves five grids in two-dimensional quadrilateral grids and seven grids in three-dimensional hexahedral grids. More grids will result in a high density of Jacobi matrices generated during the solving process, resulting in low solving efficiency. In addition, MPFA-L has better monotonicity in the problems of irregular grids and strong permeability anisotropy. Nonlinear flow discretization is also known as the nonlinear two-point flow scheme (NTPFA) [
16,
17,
18,
19,
20].
Similar to MPFA, NTPFA is also based on a multi-point flow format. The construction idea of NTPFA is based on multi-directional decomposition of traffic, which decomposes the traffic of the main grid on both sides of a certain intersection into the weighted traffic of the auxiliary grid around the main grid. Nonlinear refers to the dynamic variation of its conductivity, and within a time step, the conductivity of NTPFA is a function of the auxiliary grid pressure at the current time. In practical applications, although conductivity is a function of pressure, it is not necessary to derive it in the solving matrix, which makes NTPFA have the same Jacobi matrix structure as TPFA. The research shows that NTPFA has second-order precision and strict monotonicity. Compared to MPFA, the Jacobi matrix of NTPFA is sparser, and the solution accuracy of NTPFA is higher than that of TPFA. At present, NTPFA is only used in the conventional two-dimensional structured and triangular grids. Based on the development idea of NTPFA, this paper designs the flow format of DFM and EDFM and proposes the conductivity calculation method of DFM and EDFM by combining the grid non-orthogonality problems faced by EDFM and DFM, respectively [
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31].
2. Methodology
Due to the use of solid grids to simulate fractures in the DFM method, calculating the flow between fractures, fracture-matrix flow, and matrix-matrix flow through the DFM method actually involves calculating the flow between grid elements. Taking
Figure 2 as an example, the process of applying nonlinear discretization to calculate DFM conductivity is illustrated by calculating the flow from matrix unit C
− to fracture unit C
+.
The traditional two-point flow calculation format (TPFA) has advantages, such as simplicity and stability. Under the framework of TPFA, the flow from grid C
+ to grid C
− through unit surface f can be expressed as:
Among them, the conductivity of T
+ and T
− is the conductivity of C
+ to C
− and C
− to C
+, respectively. In the two-point flow format, the values of the two are equal:
From the above formula, it can be seen that the calculation of two-point flow conductivity only depends on the geometry of the grid, and its accuracy depends on the orthogonality of the grid. When the grid skew is large, the difference between nf and tf is large, resulting in a large error in the results. Only when nf and tf are relatively close can this format obtain accurate solutions.
Further decompose the flow process between the two unit center points described in Equation (1) into two flow engineering:
According to the continuity of flow and the principle of mass conservation, within a unit time, the flow rate of process 1 passing through surface f is equal to the flow rate of process 2 passing through surface f. Therefore, the flow calculation of the entire process can be represented as the weighted sum of Process 1 and Process 2.
Firstly, the idea of nonlinear discretization is applied to construct the conductivity of process 1. The core idea of nonlinear discretization is to counteract the influence of the non-orthogonality of the grid through traffic decomposition. Flow decomposition refers to the decomposition of a unit to surface flow (taking C+ to f as an example) into the sum of three adjacent unit to surface subflows of C+, where adjacent units refer to units that have at least one common edge with C+.
Here, the Nikitin method is introduced to complete the traffic decomposition process. For a tetrahedron, a vector starts along one of its vertices. If the vector happens to pass through the opposite side of the vertex, the vector can be decomposed into the sum of the weights of the three prism edges along the vertex, and the weight is greater than 0 but less than 1. Taking
Figure 2 as an example, starting from the centroid of unit C
+, if the vector Kn
f passes through the surface T
1-T
2-T
3, then Kn
f can be represented as:
According to Nikitin’s weight calculation method, the weight coefficient is:
On this basis, according to the derivative decomposition rule, the pressure gradient from C
+ to f can be expressed as:
Substituting Equation (7) into Darcy’s formula, the flow rate from C
+ to f can be expressed as:
We define the flow rate from C
+ to C
− as the sum of the weights of the flow rate from C
+ to f and the flow rate from f to C
−, as follows:
Referring to the format of the two-point flow in Equation (1), further transform the above equation to include the terms of the main grid C
+ and C
− pressure:
Combining the format of the two-point flow, it is not difficult to see that the above formula contains multiple terms from other units. To simplify it to the two-point flow format, it is necessary to adjust the weight values to eliminate each other, so that
The calculation method for weight is:
At this point, we have obtained the nonlinear flow discretization format of DFM as follows:
where:
In the above equation, the values of conductivity T+ and T− depend on the pressure of the auxiliary units in the grid. Therefore, during the simulation process, conductivity is not a fixed value and changes with the change of pressure. Under the fully implicit solution strategy, each Newton step requires the derivative of the conductivity. In this case, the format is actually a multi-point flow format, and the Jacobi matrix is also more dense. In fact, in seepage mechanics problems, the variation of conductivity in each Newtonian step is not significant. Based on this, Nikitin proposed an explicit solution framework, where the conductivity is fixed within each time step and updated outside the time step. Nikitin and other scholars have shown through numerical experiments that there is no difference in accuracy between the two methods, and both exhibit excellent stability. But it shows that the Jacobi matrix under the solving framework is more sparse and the solving efficiency is higher.
Based on the nonlinear discrete conductivity calculation process described earlier, the specific implementation steps for flow calculation are proposed as follows:
(1) Determine the adjacent relationship of grid cells and obtain a group of neighboring cells. In 2018, Li proposed a data storage structure for layered unstructured grids suitable for DFM in which unstructured grids are stored in a prism format. Based on this structure, determine the same layer connectivity relationship of the grid. Firstly, traverse the prism. If two grids C1 and C2 have the same prism number, then the two grids are adjacent but do not have a common face. If C1 and C2 have two identical prism numbers, the grid is adjacent and has a common face. If two grid numbers are evenly divided by each layer’s grid number, and the remaining numbers are the same and adjacent to each other, then the two grids have a common face. The above situations are all adjacent grids. When there is a longitudinal connectivity relationship between two grids C1+ and C1−, the same layer grids of C1+ are all adjacent grids of C1−, and vice versa.
(2) Build a flow matrix. This article uses an explicit method to calculate and update the conductivity, so the structure of the Jacobi matrix is the same as that of the matrix for two-point flow. Find the adjacent grid table in list T1 for a certain side of grid C1, C1-F1. If there is only C1 in the table, then this face is an edge interface. If there is another adjacent grid C2, then C1 and C2 are two-point flow adjacent grids, marked separately in the C1 row, C2 column and in the C2 row, C1 column of the flow matrix. Traverse all grids and mark the T1 list during the traversal process to reduce unnecessary repetitive operations.
(3) Obtain auxiliary unit weight coefficients. Taking unit intersection unit C1-f-C2 as an example, based on the permeability tensor of unit C1 and the surface normal vector of f, the flow decomposition criterion used in this article is used to obtain its auxiliary units C1-1, C1-2, and C1-3, and calculate their weight coefficients α1, β1, and γ1. Similarly, obtain the auxiliary units C2-1, C2-2, and C2-3 and their weight coefficients α 2, β 2, and γ 2 for C2.
(4) Calculate conductivity and assemble flow matrix. Calculate the conductivity T1 of C1 to C2 and the conductivity T2 of C2 to C1 according to Equations (11)–(13). Among them, the flow pressure and gravity of the auxiliary unit are calculated step by step using the results from the previous time. This article decomposes the nonlinear discretization of flow into pressure-driven and gravity-driven components and calculates the conductivity of the two driving forces separately. The final flow is a linear superposition of the two. According to the flow matrix marker in step 1, update the corresponding conductivity coefficient and update the flow residual term in the corresponding row. The fluid properties of the flow surface are calculated using nonlinear upstream weights. In a two-point flow, it is only necessary to determine the size of the two grid potentials, which is different from the two-point flow format. For nonlinear discretization, it is necessary to compare the sum of the products of the conductivity of two grids and their respective driving forces. The relevant expression is shown in Equation (14).
Among them, Tp1, Tg1, Tp2, and Tg2 are the conductivity calculated based on pressure for grid C1, gravity for grid C1, pressure for grid C2, and gravity for grid C2. z1 and z2 represent the unit centroid heights of C1 and C2.
(5) After each Newton step iteration is completed, repeat step 3 until convergence is achieved.
3. Transmissibility for EDFM
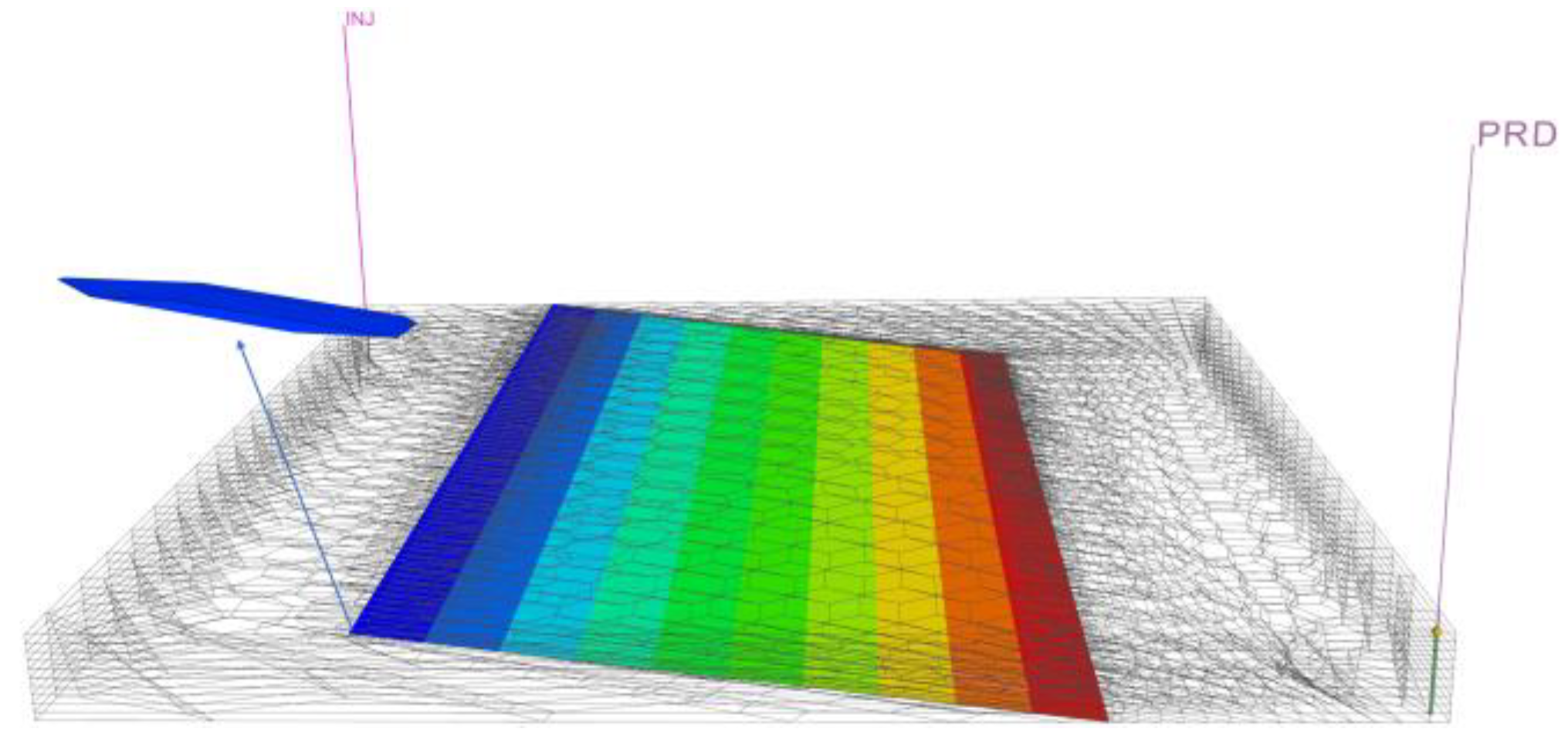
Unlike DFM, EDFM does not use solid grids, but instead uses virtual “flat plates” to simulate fractures. These “flat plates” overlap with the reservoir grid in space. Therefore, in EDFM, the flow between fracture mesh units and matrix mesh units cannot be directly calculated through mesh geometry. In addition, due to the different computational domains between fractures and matrix rocks, there is no material exchange between fractures and matrix in the fluid mass balance equation, which requires the establishment of additional connections to simulate material exchange between fractures and the matrix. This additional connection is called a nonadjacent connection (NNC). Three types of NNCs are required in EDFM (
Figure 3): (1) the NNC between the fracture element and adjacent background grid blocks; (2) the NNC between two units of a single fracture; and (3) the NNC between two intersecting fractures.
We use a component flow model to illustrate the calculation process of the EDFM method. After adding nonadjacent connections, the new mass balance equation can be expressed as follows:
Among them,
xi and
yi are the molar fractions of component
i in the oil and gas phases, respectively;
μo and
μg are the viscosity of the oil and gas phases, respectively; k
ro and k
rg are the relative permeability of the oil and gas phases, respectively; K is the absolute permeability tensor;
qi is the mass flow rate of component
i;
qNNCi is the mass flow rate of component
i passing through NNC. The calculation method for the mass flow rate term is similar to that for the flow term, which can be expressed as:
is defined as the conductivity term, where An and dn represent the characteristic area and characteristic distance, respectively. These two parameters can be understood as the flow characteristic parameters of two control volumes connected through NNC. The calculation method for T varies for different types of NNC.
For the first type of NNC, A
n is the intersection area between the fracture and the background grid, and K is the harmonic average of the permeability between the fracture and the matrix. Assuming that the pressure changes linearly along the normal direction of the fracture,
dn can be calculated as follows:
Among them, V is the control volume of the mesh.
For the second type of NNC, the conductivity can be calculated using the harmonic averaging method:
Among them,
T1 and
T2 are the conductivity of the two fractures, which can be calculated by the following equation:
Among them, Lint is the length of the intersection line of two fractures; wf is the fracture opening; Kf is the permeability of the fracture. df is the distance between the fracture center and the intersection line, and df is the weighted average distance between two fracture segments. For the third type of NNC, the conductivity can be directly calculated using Equation (19), simply replacing dn with the distance between the centroids of two fracture segments.
The grid orthogonality problem mainly exists in the second and third types of NNC. Due to the fact that fractures are cut into several pieces and the diversity of fracture morphology and distribution patterns, the shape of these pieces is likely to be non-orthogonal polygons. Therefore, calculating the flow inside EDFM fractures is essentially a flow problem under two-dimensional unstructured grids.
Similar to three-dimensional problems, nonlinear discretization in two-dimensional situations is also based on the flow decomposition method to calculate conductivity. Taking
Figure 4 as an example, the fracture piece in the figure is divided into several unstructured grids by the background grid: F1 and F2 are two of them, respectively, and the flow through the intersection side E
F1−F2 of F1 and F2 is calculated.
Firstly, calculate the flow rate from F1 to F2. If the vector Kn
f starting from the centroid of F1 falls within the angle range of vectors t1 and t2 composed of the centroid of F1 and its two adjacent unit centroids, then Kn
f can be expressed as:
According to Lipnikov’s weight calculation method, the weight coefficient is:
On this basis, according to the derivative decomposition rule, the pressure gradient from C+ to f can be expressed as:
According to Darcy’s law, the flow rate from + to f can be expressed as:
We define the flow rate from C
+ to C
− as the sum of the weights of the flow rate from C
+ to f and the flow rate from f to C
−, as follows:
To transform the above equation into a two-point flow format that includes independent terms of the pressure F1 and F2 of the main unit, Equation (25) can be written as:
Combining the format of the two-point flow, the above formula includes multiple redundant terms from other units. To simplify it to the two-point flow format, the weight calculation method is as follows:
Therefore, the flow discretization format applied by NTPFA to the second type of NNC is: