Pressure Pulsation Characteristics of Agricultural Irrigation Pumps under Cavitation Conditions

Abstract

Agricultural irrigation pumps are the main agricultural irrigation machinery, and their performance is closely related to the flow characteristics inside them. This paper combines experimental research and numerical simulation analysis. Based on the good agreement between the experimental results and numerical simulation data, this paper focuses on studying the characteristics of pressure fluctuations of agricultural irrigation pumps under cavitation conditions. The study found that under non-cavitation conditions, the pressure fluctuations at different monitoring points in pumps with different numbers of blades showed periodic variations, which are related to the number of blades. Under cavitation conditions, the pressure fluctuation coefficients of agricultural irrigation pumps with different impeller blade numbers increased, with a significant impact on the distribution of radial forces on the impeller. The research results supplement the relevant theoretical analysis and have certain practical significance for the application of agricultural irrigation pumps to practical production.

1. Introduction

In recent years, centrifugal pumps have been widely used in the agricultural field due to their advantages, such as saving water resources and improving irrigation efficiency, as they have the characteristics of high flow rate and relatively low head [1,2,3]. Following decades of development, research on the internal flow of these pumps has become increasingly profound. With the continuous development of computer technology, Computational Fluid Dynamics (CFD) techniques have been adopted for the in-depth study of flow [4,5,6].

Yang et al. [7] conducted a study on the influence of discharge guide vanes on the tailwater tube of a centrifugal pump turbine, comparing and analyzing the flow state inside the tailwater tube and impeller under different operating conditions with and without discharge guide vanes. They revealed the influence of discharge guide vanes on the flow state of various flow components in the hydraulic turbine and provided insights into the effects. Yuan et al. [8] conducted numerical simulations of two-phase flow in a centrifugal pump using the MUSIG model. The results showed that the external characteristics under this model were more consistent with experimental results than those obtained using the regular Euler–Euler model. Shen et al. [9] studied the influence of groove structure on the performance and flow structure of the centrifugal pump, suggesting that the arrangement of grooves can improve the pump’s performance under high flow conditions and expand its stable operating range. Lu et al. [10] conducted numerical simulations of the internal flow of a two-stage centrifugal pump at seven different time positions for the first-stage and second-stage impellers. They analyzed the flow field and pressure fluctuation characteristics inside the impellers and volutes and found that the hydraulic performance and pressure fluctuation characteristics of the centrifugal pump were better when the second-stage impeller rotated to the middle of the first-stage impeller. Si et al. [11] conducted a study on the flow-induced characteristics of gas–liquid two-phase flow centrifugal pumps, pointing out that the performance of the centrifugal pump under gas–liquid inflow conditions is more sensitive to gas at low flow rates. Wang et al. [12] conducted numerical studies on vortex structures, vortex evolution, and vortex interactions in centrifugal pumps using the RNG turbulence model and vortex dynamics diagnostic methods, such as regularized vorticity, Q-criterion, and BVF. Lin et al. [13] conducted steady-state numerical simulations to analyze the influence of inlet ribs on the internal flow of centrifugal pumps, finding optimal inlet rib designs for improving internal flow characteristics at low flow rates. Wu et al. [14] analyzed the erosion failure of a centrifugal fan pump using the Zwart cavitation model and found that erosion failure on the surface is caused by the collapse of cavities in the vortex core, When deviating from the optimal operating conditions, various forms of secondary flow exist in the impeller imports and exports, leading to fatigue failure and the prevalence of static and dynamic interference in centrifugal pumps. These phenomena may cause large pressure pulsations, exacerbating the vibration and noise. Gu et al. [15] found that multi-stage centrifugal pumps are frequently used in high-lift applications and consume considerable energy but suffer from poor performance and large axial force. The rear shroud of the impeller is trimmed for reducing axial thrust, but this degrades performance. This study analyzes performance degradation and optimizes performance and axial force. Hu et al., [16] studied the flow characteristics within the pre-swirl system of a marine gas turbine at low rotational speed by varying the pressure at the pre-swirl nozzle. Xi et al.’s [17] study show that water hammer occurs and the pressure of the oil casing annulus increases at the inside and outside walls with the increase in eccentricity. The water hammer pressure forms a double imbalance in the internal and external walls of eccentric annulus tubing. With the increase in eccentricity, flow velocity decreases in the small flow passage, and flow velocity attenuation is fast at the oil casing annulus. Zhang et al. [18] conducted a detailed analysis of the cavitation mechanism in coolant pumps under high flow conditions, combining experimental research and numerical simulation. Their research provides a theoretical basis for understanding incipient cavitation in uncalibrated blade passages. Hu et al. [19] optimized the design of centrifugal fire pumps for cavitation performance at various flow rates, which has practical significance. the energy transition mechanism of nonlinear fluid-induced vibration was revealed. Kim et al. [20] analyzed the influence of blade leading-edge shape on cavitation in pumps and found that square groups have lower net head, providing a useful reference for blade selection. Chen et al. [21] conducted a study on the cavitation characteristics of a high-speed submersible axial-flow pump with a specific speed of n_s = 700. They utilized ANSYS CFX 19.2 software for numerical calculations to obtain the external characteristic curve. The analysis focused on investigating the impact of variations in inlet pressure and operating flow rate on the cavitation volume fraction of the submersible axial-flow pump. The findings highlighted that increasing the inlet pressure and adjusting the operating flow rate to the design value effectively mitigates cavitation. Bai et al. [22] investigated the hydraulic performance and anti-cavitation properties of the thrust plate-assisted impeller using experimental methods under different speeds, temperatures, and outlet conditions. The experimental results revealed that the speed variation pattern differs from that of traditional centrifugal pumps and is not applicable to the head produced by the thrust plate-assisted impeller. Gong et al. [23] employed a combination of experimental validation and numerical simulation to enhance the hydraulic performance of multi-stage submersible electric pumps. They quantified the relationship between the angle of the space guide vane leading to each flow surface using a linear equation and explored the influence of the equation’s slope variation on the separation flow within the guide vane and its impact on the guide vane performance. Their research outcomes provide a foundation and scientific support for investigating the impact of the guide vane’s outlet edge shape on the hydraulic performance of multi-stage submersible electric pumps. Kan et al. [24] utilized the immersed boundary method with large eddy simulation (IBM–LES) to examine the three-dimensional unsteady turbulent flow field of a specific mixed-flow pump operating under design conditions in cylindrical coordinates. The results contribute theoretical references and engineering applications for enhancing the stability of mixed-flow pump operation. Lang et al. [25] employed LIGHTHILL acoustic analogy theory and the FW–H equation in conjunction with computational fluid dynamics and computational acoustics to solve the internal hydrodynamic noise of a single-blade centrifugal pump. The investigation concluded that the distribution characteristics of pressure fluctuation directly impact the internal hydrodynamic noise of the single-blade centrifugal pump. Xu et al. [26] established a simulation model using the characteristic line method to study the hydraulic transition process. The model’s validity was confirmed by comparing it with actual load rejection test data. The simulation focused on the closing law of the guide vane during the hydraulic transition process.

With the development of society and the need to meet the living standards and quality of the people, the requirements for centrifugal pump performance have become increasingly demanding. Not only is high efficiency expected, but also smooth operation in various environments. However, in practical production, agricultural irrigation pumps are prone to cavitation, which severely affects the stable operation and hydraulic performance of the pumps. Scholars have conducted extensive research on this issue. In the studies conducted by Chen et al. [27], which consider both the dynamic characteristics and load cases, a novel uncertain load-dependent sensor placement method was developed using the non-probabilistic theory for response reconstruction, which has a two-step strategy. Using multi-source vibration sensing methods, Li et al. [28] reported nonlinear vibration patterns in the critical transition states of MVCT. Bu et al. [29] showed that the flow pattern inside the runner is stable under partial load conditions, and turbulent flow areas appear at the runner outlet and in the lower annular flow passage. There is a cylindrical cavity vortex belt in the draft tube, which is derived from the runner discharge cone and develops in the straight cone section of the draft tube. Ni et al. [30] investigated the changes in internal flow field, pressure pulsation in the lobe-free zone, the efficiency of turbine working conditions and the hydraulic performance of a water pump under working conditions were analyzed after optimizing the active guide vane profile of a variable-speed pump turbine through numerical simulation. Additionally, the effect of active guide vane optimization on the hydraulic performance was examined. The results show that, after optimization of the movable guide vane, the internal flow pattern of the hydraulic turbine working condition is improved, the amplitude of pressure pulsation in the lobe-free zone is reduced, the efficiency is improved, and the effect is more obvious in the case of partial load. Wang et al. [31] showed that the pressure pulsation peak-to-peak value of the impeller monitoring point gradually decreases along the flow direction, and the main frequency is eight times the rotation frequency and its multiplication frequency. With the intensification of cavitation, the peak-to-peak value of impeller pressure pulsation gradually decreases. The main frequencies of the pressure pulsation of the forward and reverse guide vanes are both the vane frequency and its multiplier, and the amplitude increases with the development of cavitation. The cavitation in the axial direction shows that the cavitation volume fraction gradually increases from the front cover plate to the rear cover plate of the impeller. Zheng et al., [32] in wavelet analysis, found that the jet velocity increases, the wavelet energy value at each scale in the region near the nozzle inlet decreases by 25% when the jet inclines upward. However, there is still limited research on the influence of cavitation conditions on the pressure fluctuation characteristics of high-speed centrifugal pumps with different numbers of blades. The phenomenon of cavitation is described as the formation and collapse of bubbles when the local pressure of a liquid is lower than its saturation vapor pressure at the corresponding temperature. When these bubbles flow to a high-pressure zone, they collapse under the action of pressure, causing a shock wave that can lead to erosion of the components. This theory of bubble collapse, which explains the causes of cavitation, was initially established by the British physicist Rayleigh [33] in 1917 and has since been further improved and developed by numerous scholars from different perspectives [34,35,36,37]. Different researchers have established several cavitation models using different methods, with the most commonly used being the cavitation model based on the Rayleigh–Plasset equation. Common models include the Singhai model [38], Zwart–Gerber–Belamri model [39], Schnerr–Sauer model [40], and Kunz model [41]. Therefore, this study focuses on high-speed centrifugal pumps and analyzes the pressure fluctuation characteristics under cavitation conditions, contributing to the relevant theoretical research of agricultural irrigation pumps.Currently, in-depth research on the pressure pulsation characteristics in the impeller domain mainly relies on numerical simulation methods. Weidong Shi et al. found, through numerical simulation of a centrifugal pump, that the dominant frequency of pulsation at different blade positions was mainly the blade frequency [42]. However, Cao et al. found in their numerical simulation that the dominant frequency of pulsation at different blade positions was mainly the rotational frequency [43].

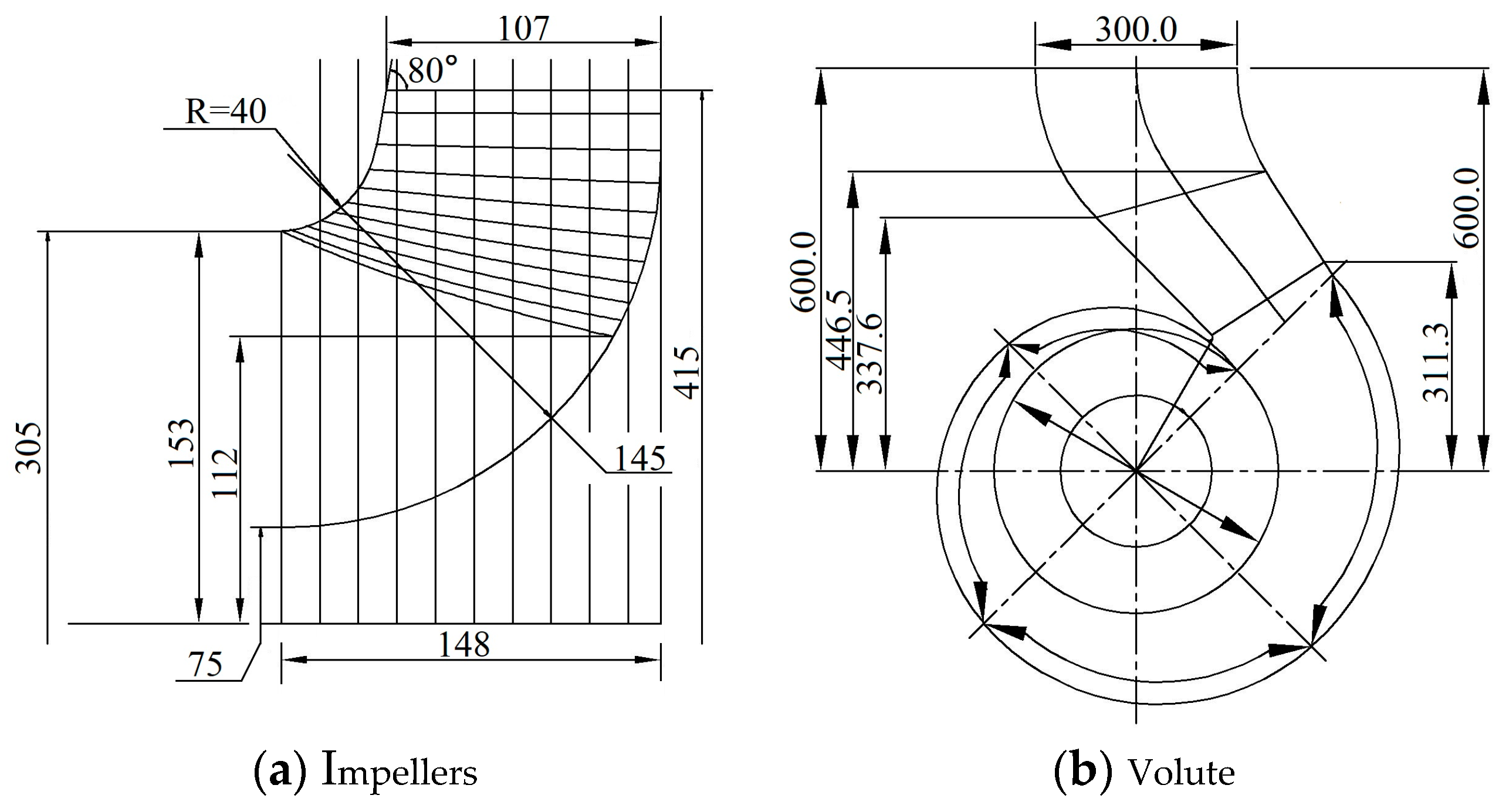
2. Model Parameters

2.1. Three-Dimensional Modeling

In this paper, a single-stage high specific speed centrifugal pump is used as the object of study, whose main components are impeller, volute, rotor, and bearings. The pump’s rated flow Q = 1000 m³/h, head H = 20 m, rated speed n = 980 r/min, and specific speed size n_s = 200. The impeller inlet diameter D₁ = 107 mm, impeller outer diameter D₂ = 415 mm, number of vanes Z = 6, vane outlet angle β₂ = 30°, volute base diameter D₃ = 425 mm, and volute inlet width b₃ = 220 mm. The hydraulic model of impeller and volute is shown in Figure 1. In this paper, Creo is used to model the main flow components of the centrifugal pump in point–line–plane 3D, respectively, as shown in Figure 2.

2.2. Cavitation Model

In this paper, the Zwart model, which is included in CFX, is chosen for cavitation simulation. The Zwart model is one of the widely used cavitation simulation models, and the expressions of its evaporation source term and condensation source term are based on the transport equations that are solved by the Rayleigh–Plesset vacuole growth equations, which take into account the changes in the volume of the vacuole during the generation and development of individual vacuoles. The expressions for the evaporation source term and condensation source term are provided below:

$$R_e=F_{vap}\frac{3{\alpha }_{ruc}(1-\alpha ){\rho }_v}{R_B}\sqrt{\frac{2}{3}\frac{P_v-P}{{\rho }_l}}; P<P_v$$

(1)

$$R_c=F_{cond}\frac{3{\alpha }_v{\rho }_v}{R_B}\sqrt{\frac{2}{3}\frac{P-P_v}{{\rho }_l}}; P>P_v$$

(2)

where: α_ruc is the volume fraction of nucleation position, taken as 5 × 10⁻⁴; R_B is the radius of the vacuole, m, taken as 1 × 10⁻⁶; P is the flow field pressure, Pa; P_v is the vaporization pressure, Pa; F_vap is the empirical correction coefficient for the evaporation process, taken as 50; and F_cond is the empirical correction coefficient for the condensation process, taken as 0.01.

3. Numerical Calculation

3.1. Models and Meshes

The ANSYS ICEM19.2 software is selected for grid calculation generation and optimization. Because a high specific speed centrifugal pump has a twist blade and wide flow channel, an unstructured mesh is selected for the impeller of the pump, while a structural mesh is performed for the other overflow parts of the pump. The quality values of all the meshes are above 0.31, thus meeting the requirements of the mesh quality calculations. The mesh is shown in Figure 3.

In order to ensure that the grid division meets the calculation requirements and the calculation time can be reduced, the independence of the grid is verified, and a suitable number of grids is obtained. As shown in Figure 4, when the total number of grids is greater than 1.2 million, the head of the pump no longer changes significantly, and finally the total number of grids can be determined to be 1.2 million. The number of grids for the impeller, volute, inlet straight section, and outlet straight section are 469,873, 554,281, 1,250,810, and 67,000, respectively. The grid number of each overflow component is shown in

Table 1. Grid number of each flow part.

Flow Parts	Impeller	Guide Vane	Inlet Section	Export Section
Grid number	469,873	554,281	1,250,810	67,000

. The grid numbers of impeller, worm shell, inlet straight section, and outlet straight section are 469,873, 554,281, 1,250,810, and 67,000, respectively.

3.2. Boundary Condition

In the CFX pre-processing boundary condition settings, the turbulence model is the SST k-ω turbulence model. The SST k-ε model retains its initial k-ω model in the region close to the wall and uses the k-ε model in the region away from the wall. It has good adaptability to the problem set by a wide range of flow velocity variations. The dynamic–static interface coordinate system transformation is set to Transient Rotor Stator. The analysis type is set to Transient. The nonstationary total time is 0.367 s and the computation time for each step is 0.00068 s.

In this paper, the main monitoring points of pressure pulsation are set up in the regions of the blade working surface, back surface, and volute outlet, and the position of monitoring points for pumps with different numbers of vanes is consistent. The monitoring points are set as shown in Figure 5; the blade working surface monitoring points are P1–P4, the blade back monitoring points are P5–P8, and the volute outlet monitoring points are P13–P16.

In order to visually monitor the difference in pressure fluctuation variations, the pressure pulsation dimensionless pressure coefficients are introduced, viz:

$$C_{\mathrm{p}}=(p-p^{\prime })/0.5\rho u^2$$

(3)

where p is the static pressure at the monitoring point (Pa), p′ is the average static pressure at the monitoring point during the sampling cycle (Pa), ρ is the fluid density (kg/m³), and u is the impeller outlet circumferential velocity (m/s).

4. Experimental Verification

In this paper, the external characteristic test of a centrifugal pump with a three-vane impeller and a six-vane impeller was carried out in an integrated experimental platform with secondary precision. The test bench, shown in Figure 6, includes inlet and outlet bypass valves, inlet and outlet pressure gauges, and pressure sensors, which transmit the collected pump head and flow rate data to the computer, recording and calculating to obtain the pump efficiency values.

Table 2. Head data of three blades.

Flow (m3/h)	Head (m)
	CFD	Experimental	Relative Deviation (%)
800	17.30	16.90	2.36
1000	15.95	15.70	1.59
1100	15.10	14.50	4.13
1200	13.60	13.00	4.61
1300	11.63	11.30	2.92
1400	10.15	9.80	3.57

,

Table 3. Efficiency data of three blades.

Flow (m3/h)	Efficiency (m)
	CFD	Experimental	Relative Deviation (%)
800	73.50	72.50	1.37
1000	77.10	76.00	1.44
1100	75.00	73.80	1.62
1200	73.80	72.30	2.07
1300	70.60	68.20	3.51
1400	67.80	64.90	4.46

,

Table 4. External characteristic data of six blades.

Flow (m3/h)	Head (m)
	CFD	Experimental	Relative Deviation (%)
800	21.11	20.50	2.97
1000	19.60	19.40	1.03
1100	17.45	17.10	2.04
1200	16.50	16.45	0.30
1300	15.83	15.20	4.14
1400	12.50	12.00	4.16

and

Table 5. Efficiency data of six blades.

Flow (m3/h)	Efficiency (m)
	CFD	Experimental	Relative Deviation (%)
800	74.50	72.98	2.08
1000	75.80	75.01	1.05
1100	74.04	72.93	1.52
1200	73.80	71.50	3.21
1300	72.60	71.15	2.03
1400	64.00	61.50	4.06

show the numerical simulation results and test results of two types of blade numbers under different flow conditions. As shown in the table, under the design conditions, when the number of impeller blades is 6, the test head is 19.40 m and the predicted head is 19.60 m, with a relative deviation of 1.03%; when the number of impeller blades is 3, the test head is 15.70 m, and the predicted head is 15.95 m, with a relative deviation of 1.59%, which is a small error. However, the relative deviation value of the head under high flow conditions is larger, and with the increase of flow, as the blade numbers differ, it is evident that the difference between the test data and the numerical prediction has increased. this is because the pump has undergone unavoidable cavitation under high flow conditions.

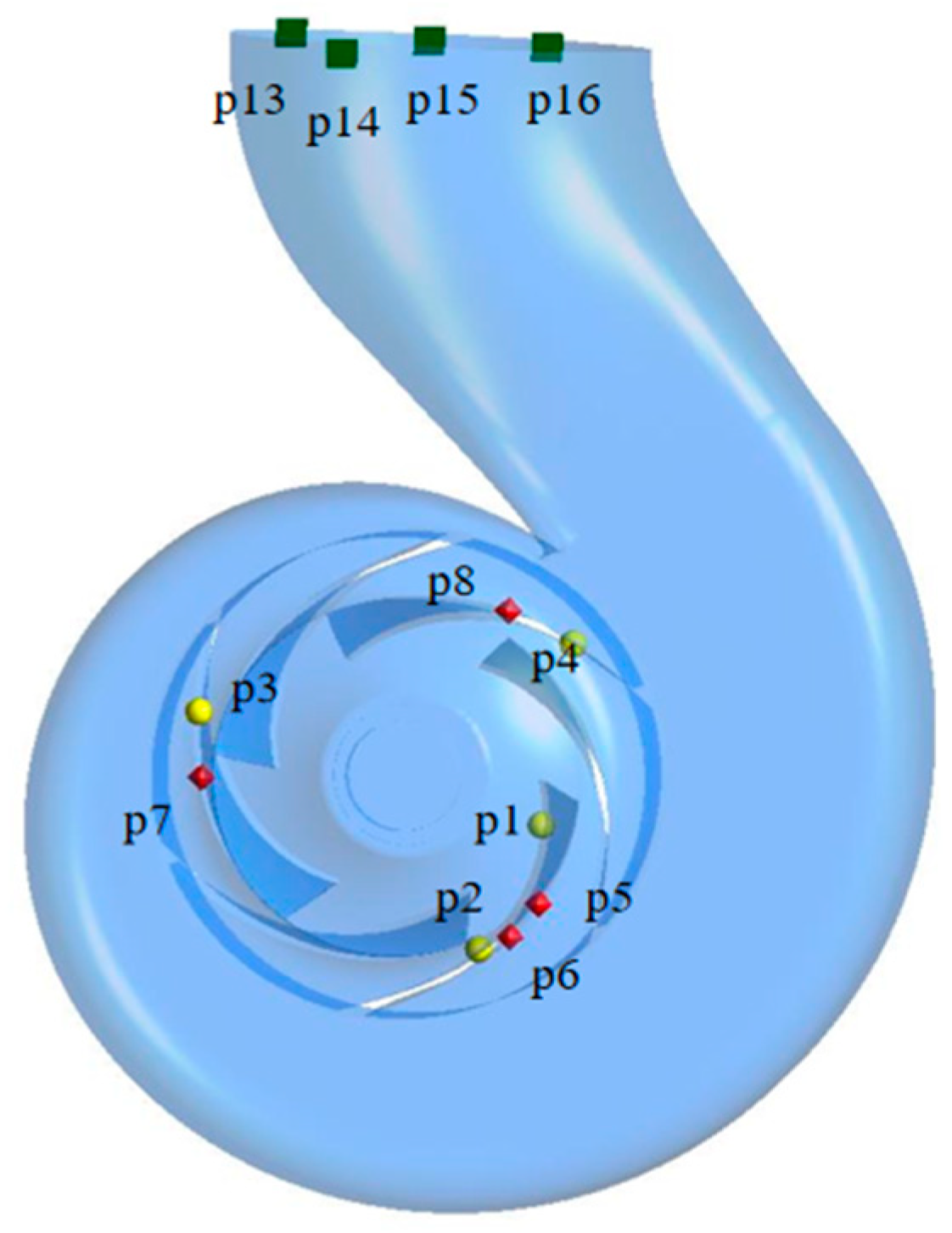
5. Pressure Pulsation Analysis of Pumps with Different Numbers of Vanes

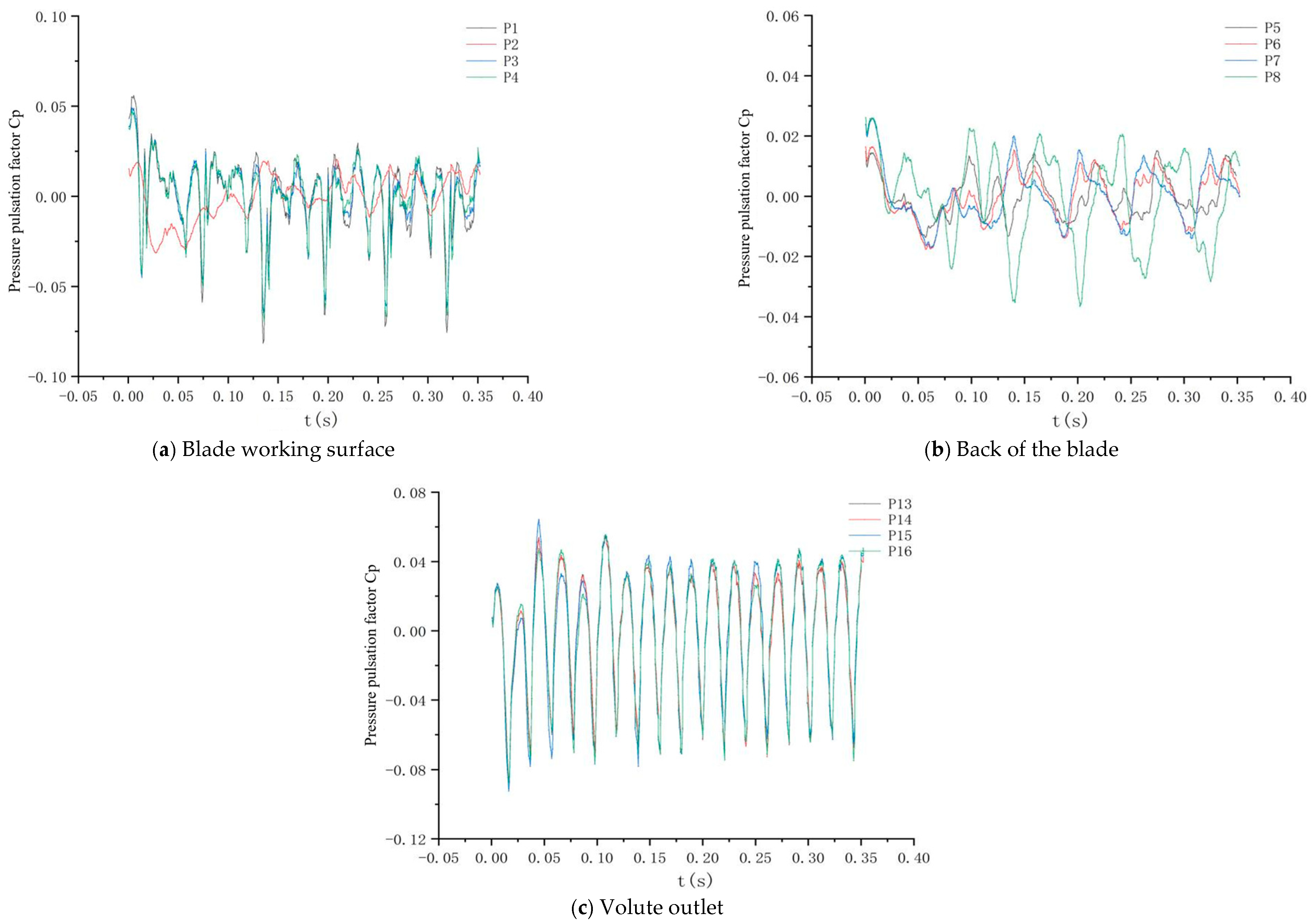
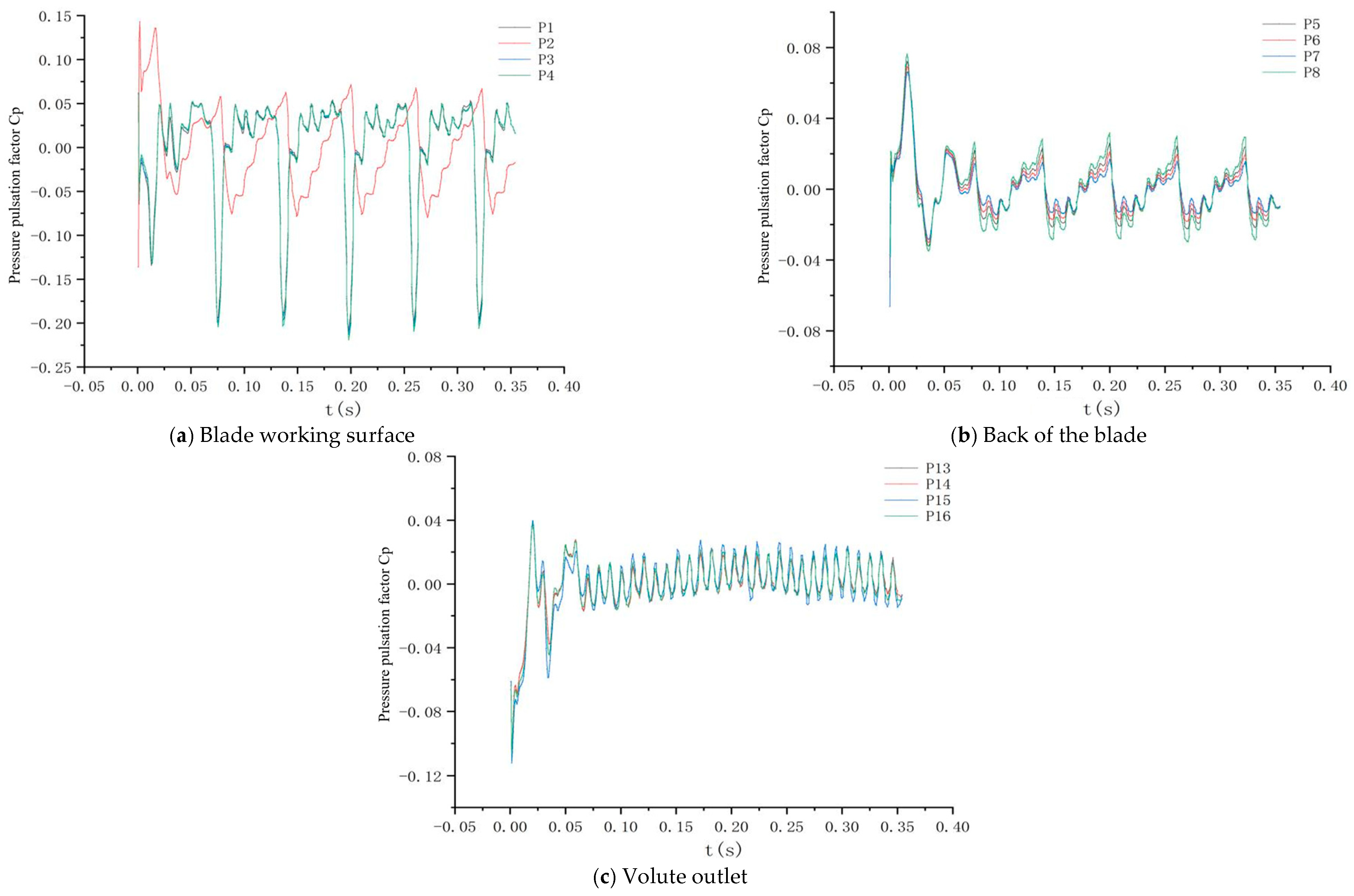
5.1. Time-Domain Characterization of Pressure Pulsations

The time-domain diagrams of pressure pulsation at each monitoring point of the three-bladed impeller are shown in Figure 7. Here, (a) is the working surface of the blade, (b) is the back of the blade, and (c) is the outlet of the volute. We can see that, under 1000 m³/h working conditions, the trend of pressure change at the monitoring point in the blade working surface and backside monitoring area is more complicated; the regularity change is not obvious, but we can still see that the amplitude is cyclic, that six obvious troughs appear in the working surface and backside, and that the amplitude fluctuation of the working surface is bigger than the amplitude fluctuation of the backside. The difference between the test data and the numerical prediction becomes larger as the blade numbers vary. The pressure fluctuation at the outlet of the volute is relatively large, and for the three-bladed impeller, a total of 18 peaks and valleys appear at the outlet of the volute in six cycles, which is a periodic change.

The pressure pulsation time-domain diagram at each monitoring point of the six-bladed impeller in Figure 8 shows that, under the working condition of 1000 m³/h, the pressure fluctuation at the monitoring point is larger than that of the three-bladed impeller in the monitoring area of the working surface and the back of the blades. The peaks and valleys of the waveforms show the same cyclic changes with the number of blades, and the values of the pressure coefficient of pulsation are basically the same, which indicates that the working surface of the six-bladed impeller and its back are more uniformly pressurized than those of the three-bladed impeller. It shows that the working surface and the back of the six-bladed impeller are more uniform than those of the three-bladed impeller. The amplitude fluctuation of the volute outlet is reduced compared with that of the three-bladed impeller, which indicates that the pressure fluctuation at the volute outlet of the six-bladed impeller is smaller, and the force is more uniform.

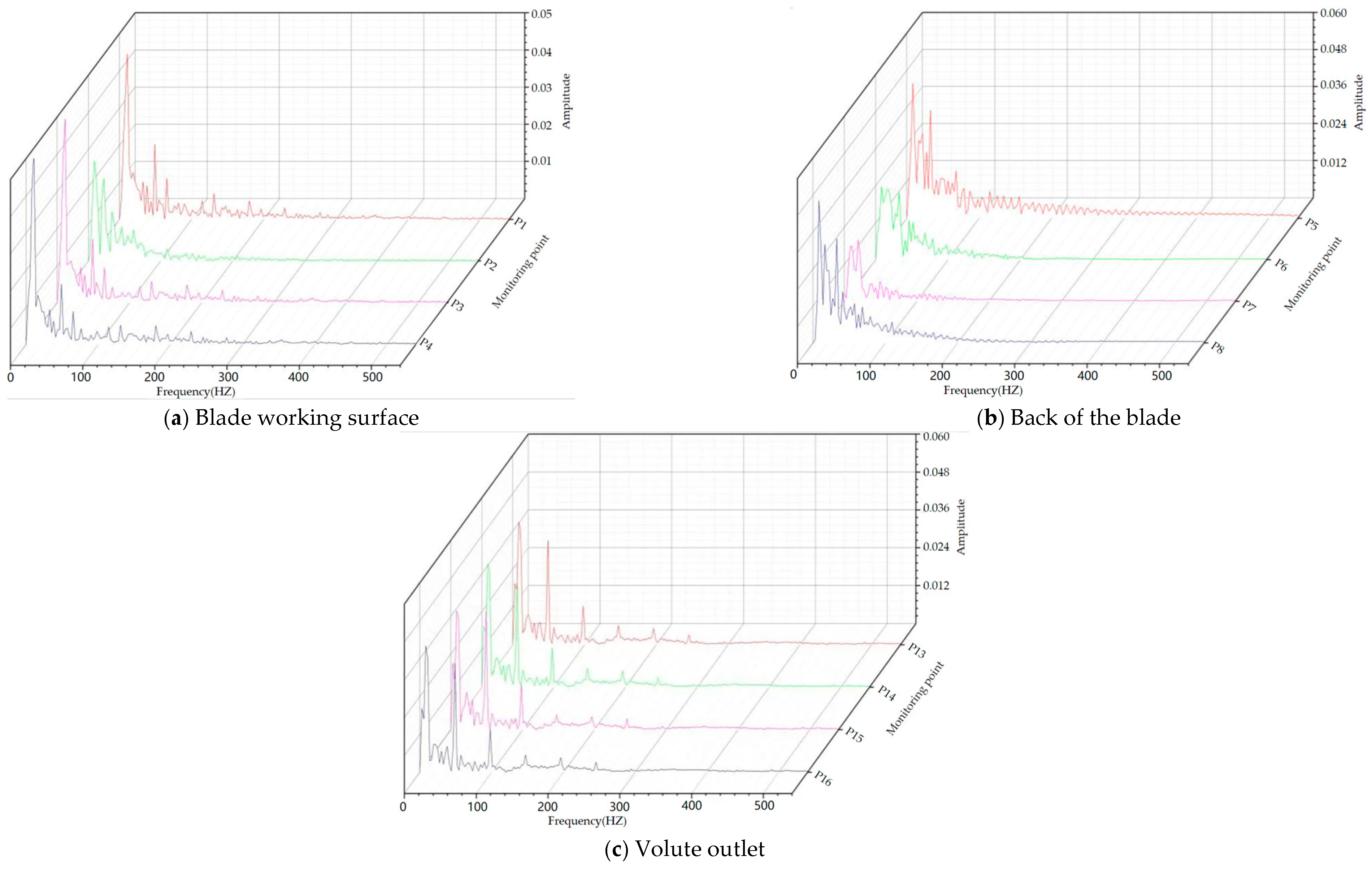
5.2. Pressure Pulsation Frequency Domain Characterization

The time-domain relationship of the pressure monitoring points of the high specific speed centrifugal pump is subjected to a fast Fourier transform, which results in the frequency-domain plots for different blade number states. The monitoring points are analyzed in the frequency domain as follows: The rotational speed is 980 r/min, the shaft frequency is 16.33 Hz, the three-blade blade frequency is 49 Hz, and the six-blade blade frequency is 98Hz. As Figure 9 shows, the three-bladed impeller work surface monitoring point pressure pulsation frequency is mainly concentrated in the 0~400 Hz band, with the main frequency in the leaf frequency, while each monitoring point also exists in other sub-frequencies, in which the amplitude is greater in the axial frequency integer multiples of the place, the back of the blade monitoring point pressure pulsation frequency is mainly concentrated in the 0~100 Hz, the pressure fluctuations are less than on the face of the workpiece, the main frequency is in the axial frequency, and other sub-frequency amplitudes are more in the axial frequency. The main frequency is the shaft frequency, while other secondary frequency amplitudes are mostly integer multiples of the shaft frequency. The pressure pulsation frequency of the monitoring point at the outlet of the volute is mainly concentrated at 0~300 Hz, the main frequency is the leaf frequency, and others are at the integer multiple of the axial frequency, which also shows that the flow inside the three blades is relatively stable under the working condition of 1000 m³/h.

6. Analysis of Pump Pressure Pulsation under Cavitation Conditions

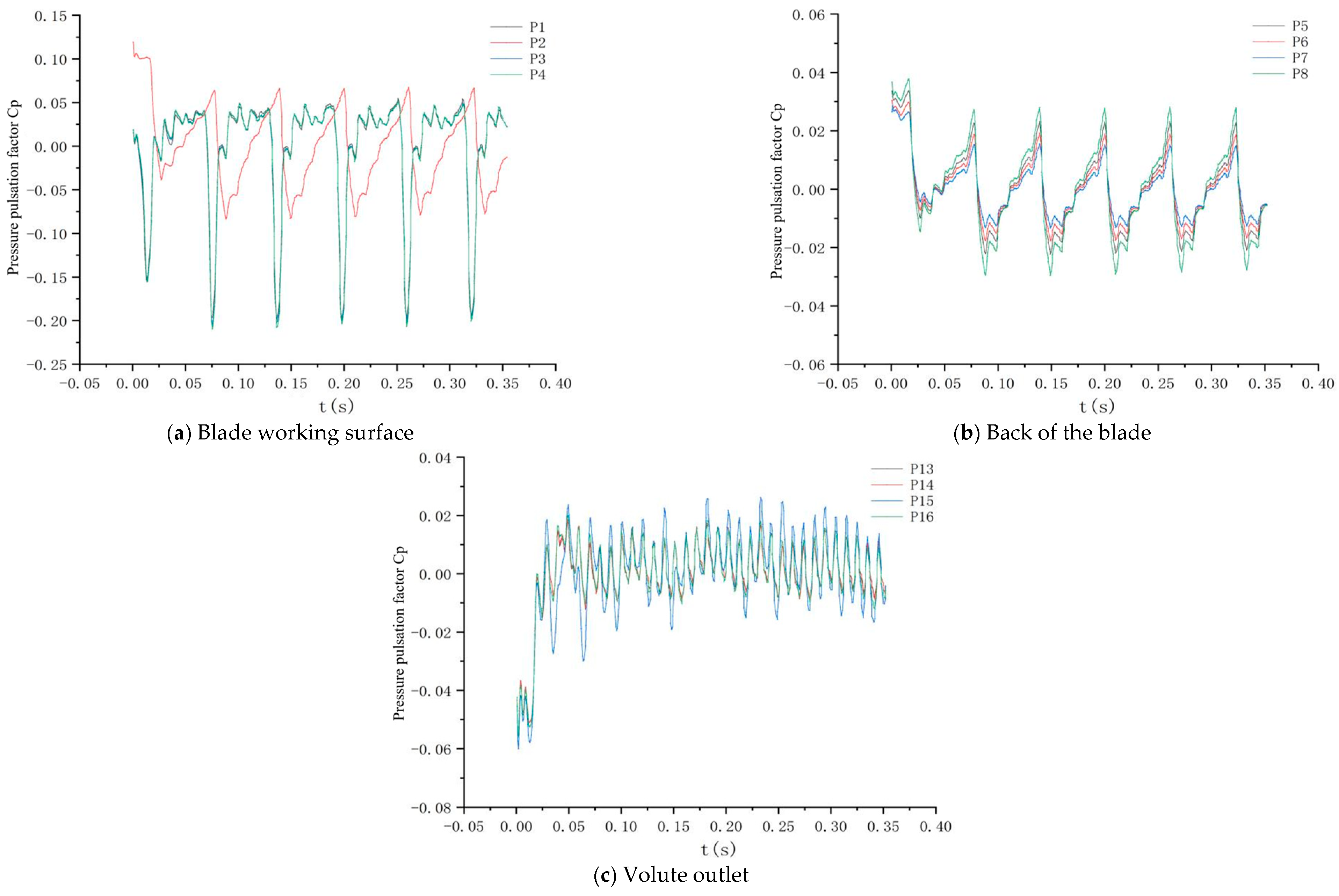
6.1. Time-Domain Characterization of a Pump under Cavitation Conditions

In Figure 10, the pressure pulsation time-domain diagram at each monitoring point of the three-bladed impeller under cavitation conditions, with the cavitation number of 0.55 (at this time for the development stage of cavitation), it can be seen that the pressure changes in the monitoring area of the monitoring point do not exhibit an obviously regular distribution. Compared with the three-blade pressure pulsation time-domain graph without cavitation, the pressure pulsation coefficients of the blade working surface and back surface, as well as the outlet of the volute, are greatly increased, indicating that the unevenness of the pressure in the monitoring area is aggravated under cavitation conditions. Under the cavitation number condition, the volute outlet does not show the same regular changes observed in the cavitation condition that are seen in the no-cavitation condition, indicating that cavitation also has a significant effect on the pressure at the volute outlet.

In Figure 11, showing the cavitation conditions for the six-bladed impeller at each monitoring point of the pressure pulsation time-domain plot, the cavitation number of 0.55 (at this time for the initial stage of cavitation), it can be seen that, in the 1000 m³/h working condition, the monitoring point pressure fluctuations in the blade working surface and the backside of the monitoring area appear to be undergoing cyclical change, and, compared to the six-bladed impeller, which showed no cavitation at the monitoring point, the overall trend of change is a slight increase in the pressure pulsation. It shows that when the cavitation number is 0.55, the cavitation has little effect on the pressure of the monitoring point of the six-bladed impeller, and the pressure pulsation of the monitoring point of the three-bladed impeller with the same cavitation number is more gentle and regular, which shows that under the working condition of 1000 m³/h, the pressure fluctuation of the working surface, the back surface, and the outlet of the volute of the six-bladed impeller is smaller than that of the three-bladed impeller.

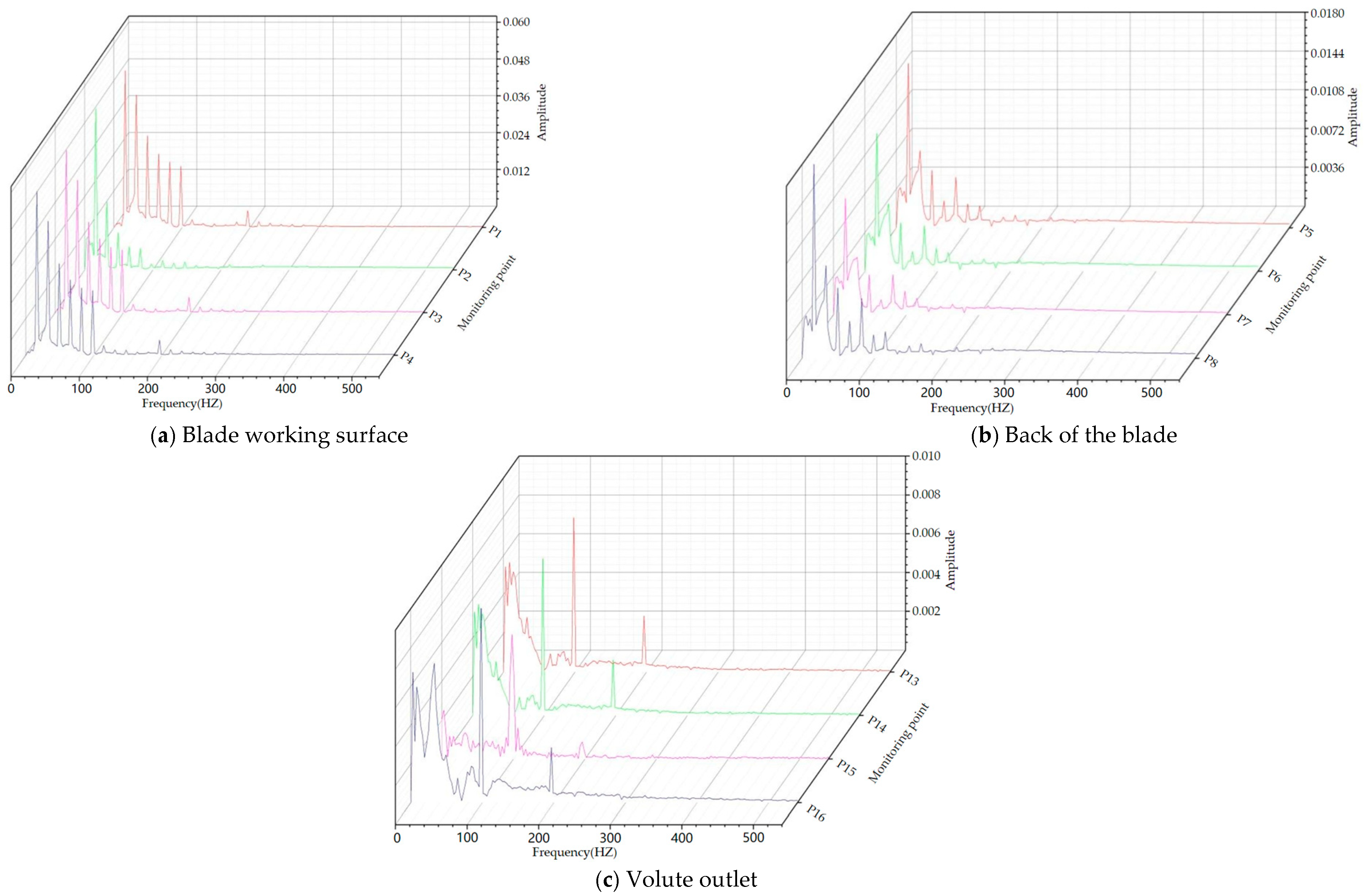
6.2. Frequency Domain Characterization of Pumps under Cavitation Conditions

Figure 12 shows that, under cavitation conditions, the impeller working surface monitoring point pressure pulsation frequency of the three-bladed impeller is mainly concentrated in the 0~300 Hz band. The main frequency is the shaft frequency and each monitoring point exists in other sub-frequencies, in which amplitude is more in the integer multiples of the shaft frequency, the back of the blade monitoring point pressure pulsation frequency is mainly concentrated in the 0~200 Hz band, pressure fluctuations are reduced compared to the work surface, the main frequency is at the shaft frequency, the other sub-frequency is at the shaft frequency, and the rest of the secondary frequency amplitudes are integer multiples of the shaft frequency. The pressure pulsation frequency of the monitoring point at the outlet of the volute is mainly concentrated at 0~300 Hz, the main frequency is the axial frequency, and the other sub-frequency amplitudes are integer multiples of the axial frequency. Compared with the monitoring point of the uncavitated three -bladed impeller, the pressure pulsation coefficient of the working surface and the back surface increases and the pressure fluctuation at the outlet of the volute becomes larger, which indicates that, under cavitation conditions, the cavitation has a greater impact on the internal flow.

Figure 13 shows the monitoring points of the three-bladed impeller under cavitation conditions. The unchanged pressure pulsation frequencies are mainly concentrated in the 0~200 Hz band, each regional monitoring point primary frequency and secondary frequency changes rules, and under no-cavitation conditions the six-bladed impeller monitoring point trend change is consistent; the difference being that pressure fluctuations at the back of the blade become complex under cavitation conditions. There is no obvious change at the outlet of the volute, indicating that the internal flow in the region is not significantly changed by the cavitation of the blade.

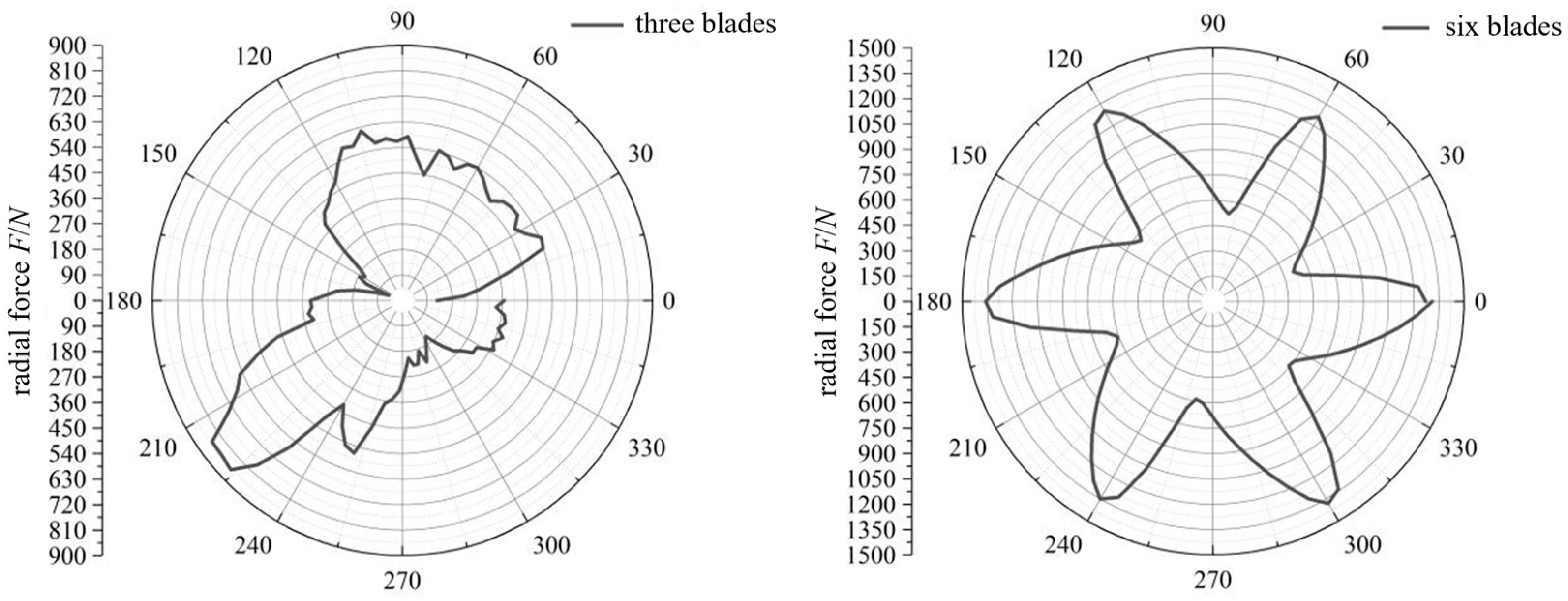
7. Radial Force Analysis

In the operation process of a high-speed centrifugal pump, the pump impeller is subjected to uneven pressure due to the fluid excitation force. These pressures are the main reason for the formation of radial force, which has a great impact on the smooth and safe operation of the pump. Therefore, the analysis of radial force on the impeller of a high-speed centrifugal pump is necessary.

To calculate the radial force of the impeller, it is necessary to edit the formula for the radial force on the impeller when performing. During non-stationary calculations, the axis of rotation of the impeller is taken in the coordinate system as the Z-axis, and the radial force is the vector sum of the component forces on the impeller blades and front and rear cover plates in the X- and Y-directions. The formula is edited as follows:

forcex = force_x()@shroud + force_x()@hub + force_x()@blade

(4)

forcey = force_y()@shroud + force_y()@hub + force_y()@blade

(5)

forcer = sqr (forcex × forcex + forcey × forcry)

(6)

In order to analyze more intuitively and conveniently, the radial force non-constant characteristics of three and six blades and the radial force non-constant characteristics of three and six blades under cavitation conditions are analyzed comparatively in this paper.

From Figure 14, it can clearly be seen that the radial force distributions of three and six blades have three and six distinct peaks and valleys, respectively, which are consistent with the corresponding number of blades and are distributed in a circular pattern. It shows that the radial force on the impeller is affected by the number of blades. The radial force on the six-bladed impeller is significantly higher than that on the three-bladed impeller. This indicates that the six-bladed impeller is subjected to a higher pressure peak when operating at 1000 m³/h. Many irregular fluctuations can be seen in the graph of the three-bladed impeller. From the perspective of the formula, it is speculated that they may be caused by the differences in the radial force on the impeller under the same instantaneous node.

As can be seen from Figure 15, other conditions remain unchanged. Under the same cavitation number and occurrence of cavitation, the radial force distribution of the three blades has changed significantly compared to that of the uncavitated condition. Respectively, the number and distribution of peaks and valleys have changed, unlike the previous obvious periodic changes. The amplitude of the radial force is also significantly larger, indicating that the cavitation number and impact of cavitation on the radial force of the three-bladed impeller are more substantial. In the case of the six-bladed impeller, compared with the uncavitated condition, the wave peaks and valleys did not change significantly. The amplitude of the radial force increased slightly, but the occurrence of cavitation had no effect on the radial force of the six-bladed impeller. Comparison of the radial force distributions of different impeller blades with the same cavitation number and occurrence of cavitation leads to the conclusions that the number of impeller blades will have an impact on the pump cavitation and that cavitation will also have a significant impact on the distribution of the impeller’s radial force.

8. Conclusions

This article combines numerical simulation and experimental research to study the pressure pulsation characteristics of agricultural irrigation pumps with different impeller blade numbers under cavitation conditions. The following conclusions are drawn:

(1)

Under the head and efficiency test, data were obtained through pump performance tests and the values were compared with the numerical simulation results. The results show that the data have small errors under the design conditions, indicating that the numerical simulation in this article has a certain level of reliability.

(2)

Under non-cavitating conditions, the pressure fluctuations at monitoring points on the working surface, back surface, and volute exit of impellers with different blade numbers show periodic variations and are related to the number of blades. The pressure fluctuation on the working surface is greater than that on the back surface. The pressure fluctuation of the six-bladed impeller is more uniform than that of the three-bladed impeller, and the internal flow is more stable. Under cavitation conditions, the pressure pulsation coefficients increase compared to the non-cavitating conditions, but the pressure fluctuations are affected by cavitation, which it’s uncertain. The pressure fluctuations at monitoring points on the three-bladed impeller are more complex and do not show obvious periodicity, while the overall trend of the six-bladed impeller changes less.

(3)

The frequency of pressure pulsation in the impeller is a multiple of its rotational frequency. Under non-cavitating conditions, the amplitude of the pressure pulsation on the working surface of the six-bladed impeller is larger than that of the three-bladed impeller at the same frequency. The pressure fluctuation at the volute exit is more complex, while the variations in other monitoring areas are not significant. Under cavitation conditions, the overall trend of the three-bladed and six-bladed impellers remains consistent with the non-cavitating conditions. The amplitude of the pressure pulsation at the same frequency on the three-bladed impeller is larger than that under non-cavitating conditions, while the increase in amplitude at monitoring points on the six-bladed impeller is slight.

(4)

By analyzing the unsteady characteristics of the radial force of centrifugal pumps with different impeller blade numbers during high-speed operation, it is found that, under constant flow rate conditions, the radial force on the impeller is significantly influenced by the number of blades, with the six-bladed impeller experiencing higher radial forces than the three-bladed impeller. Under cavitation conditions, the number of impeller blades and the distribution of radial forces are mutually influenced by the cavitation effect.