Phosphorus Threshold for the Growth of Microcystis wesenbergii, Microcystis aeruginosa, and Chlorella vulgaris Based on the Monod Formula
Abstract
:1. Modified Monod Model and Its Significance
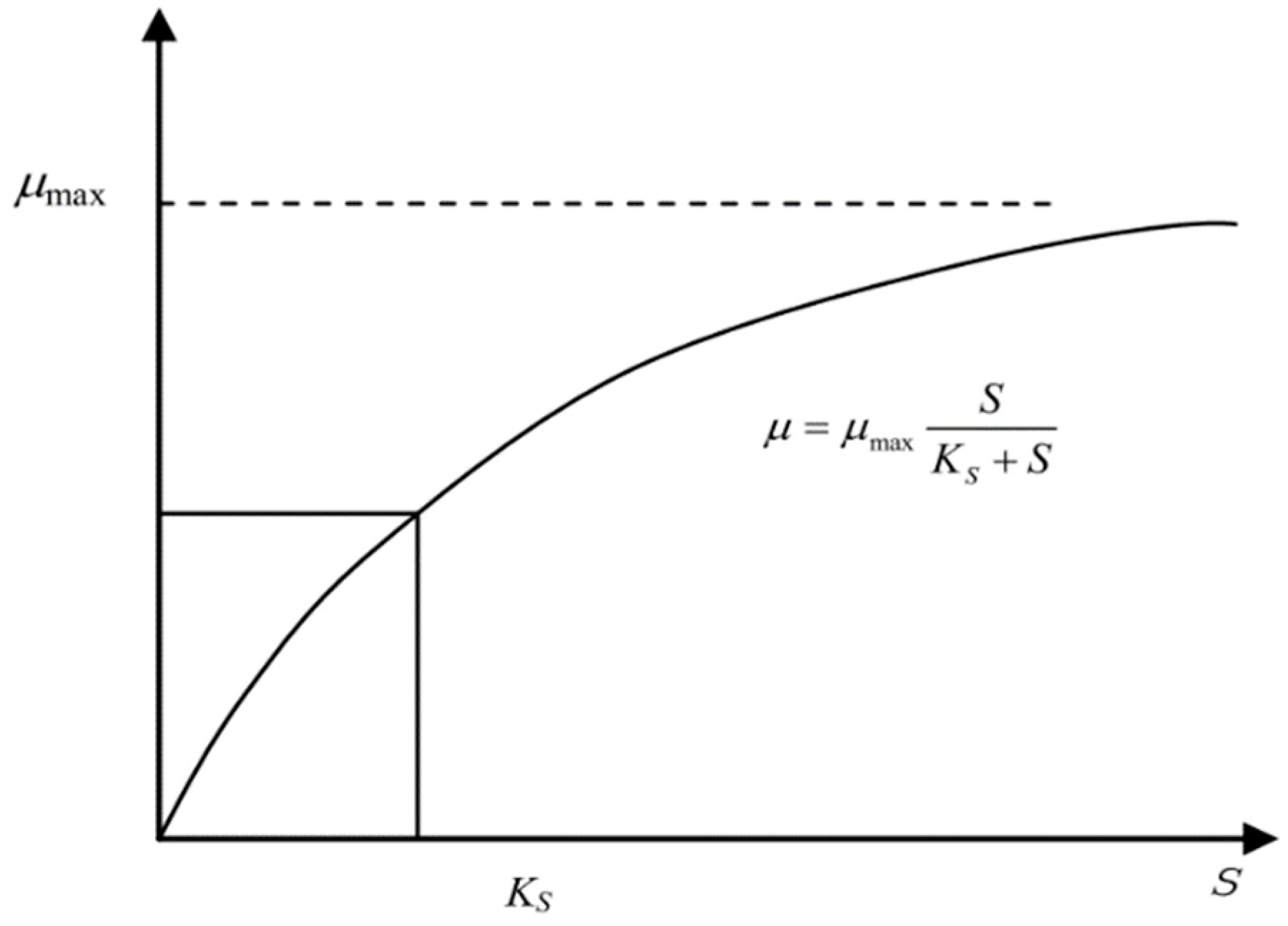
1.1. Monod Equation
1.2. Modified Monod Model
2. Materials and Methods
2.1. Experimental Materials
2.2. Medium Design
2.3. Experimental Design
2.4. Data Analysis Methods
3. Results and Analysis
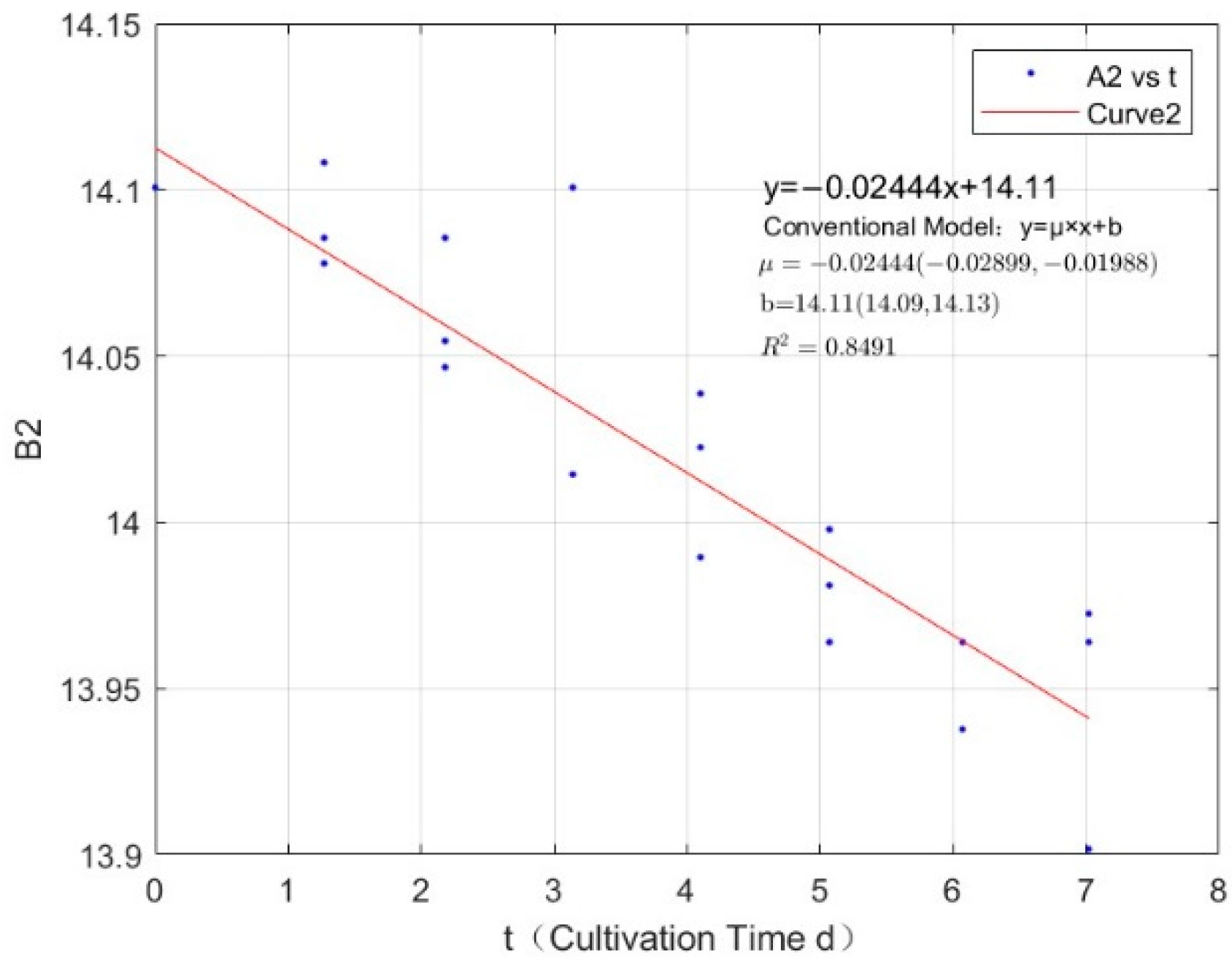
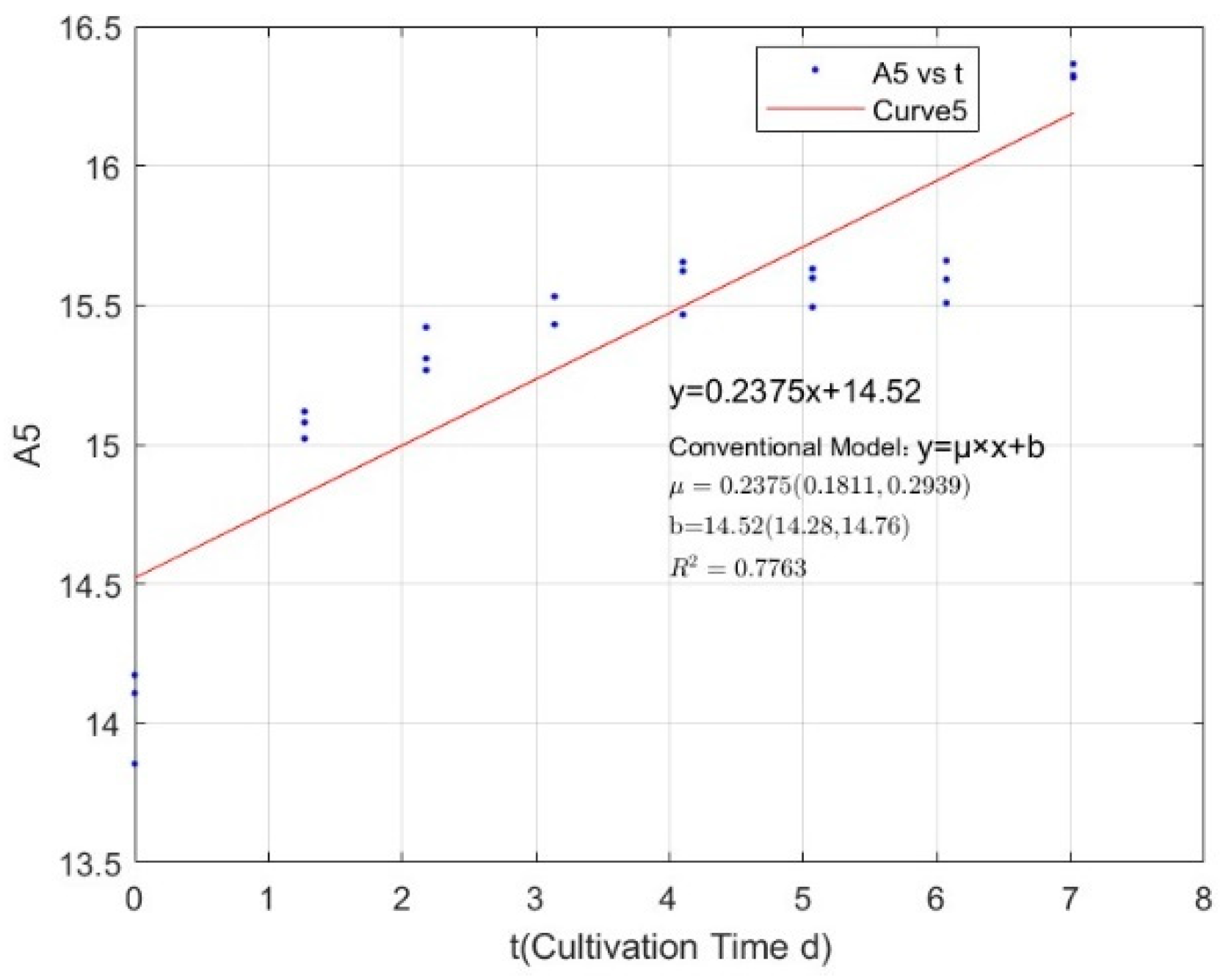
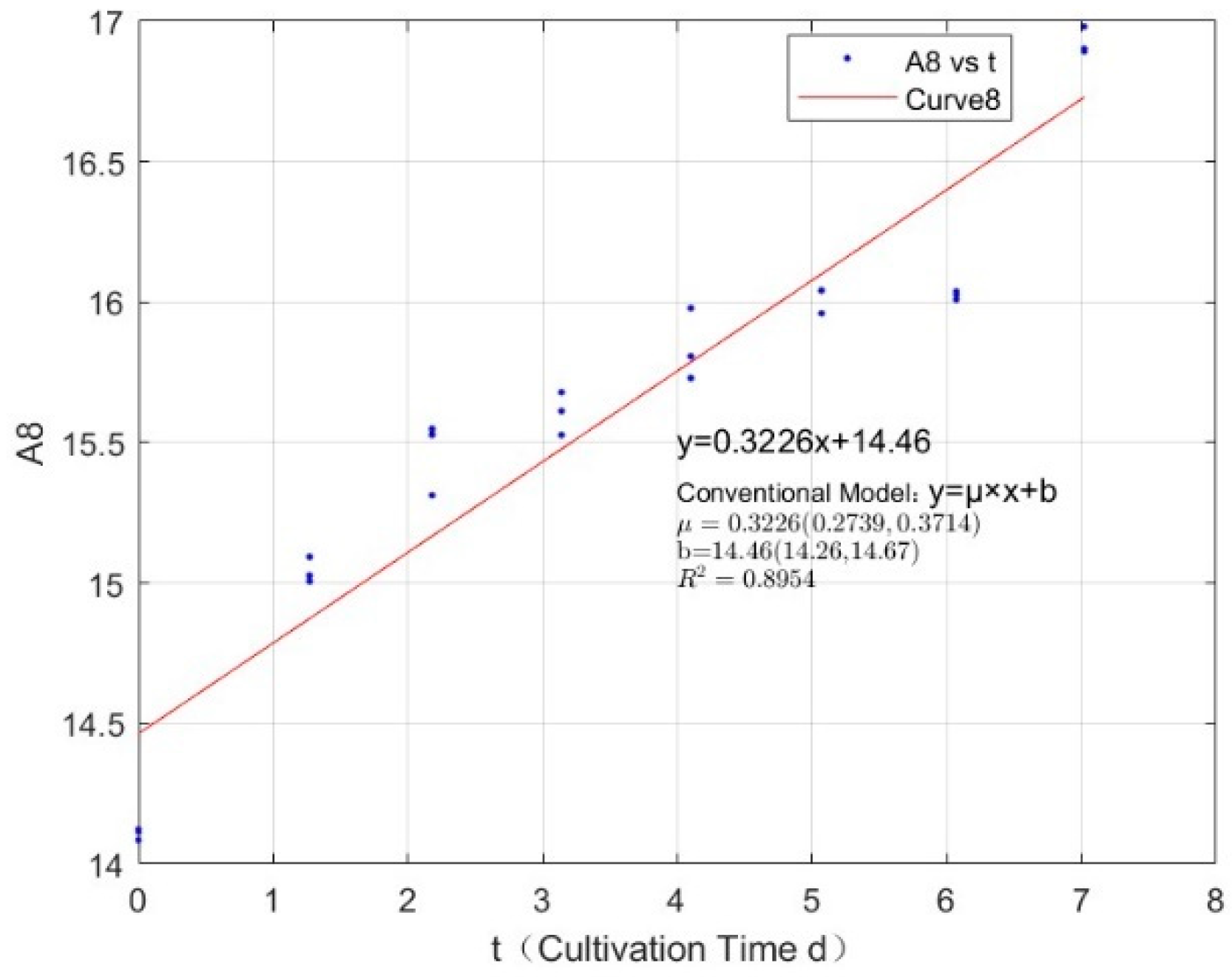
3.1. Specific Growth Rate of C. vulgaris
3.2. Growth Rate of M. aeruginosa
3.3. Growth Rate of M. wesenbergii
4. Comparison and Discussion Based on the Experiment of Specific Growth Rate of Three Kinds of Algae
4.1. Comparison of the Specific Growth Rates of Three Algal Species
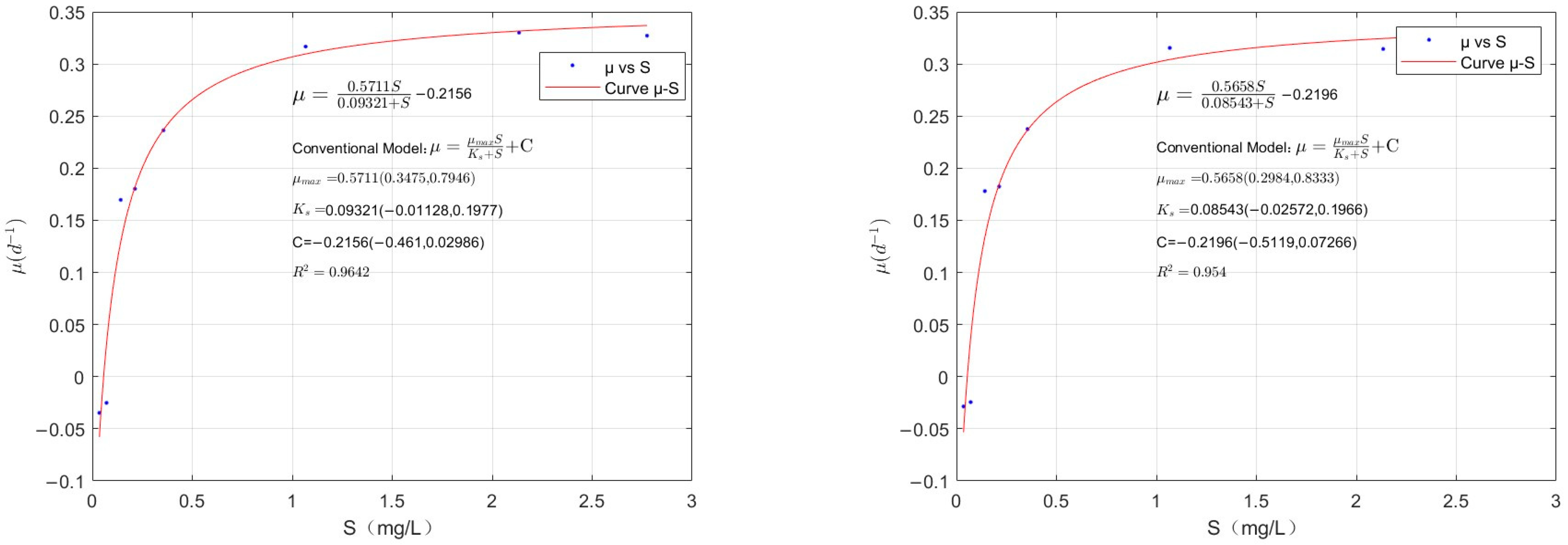
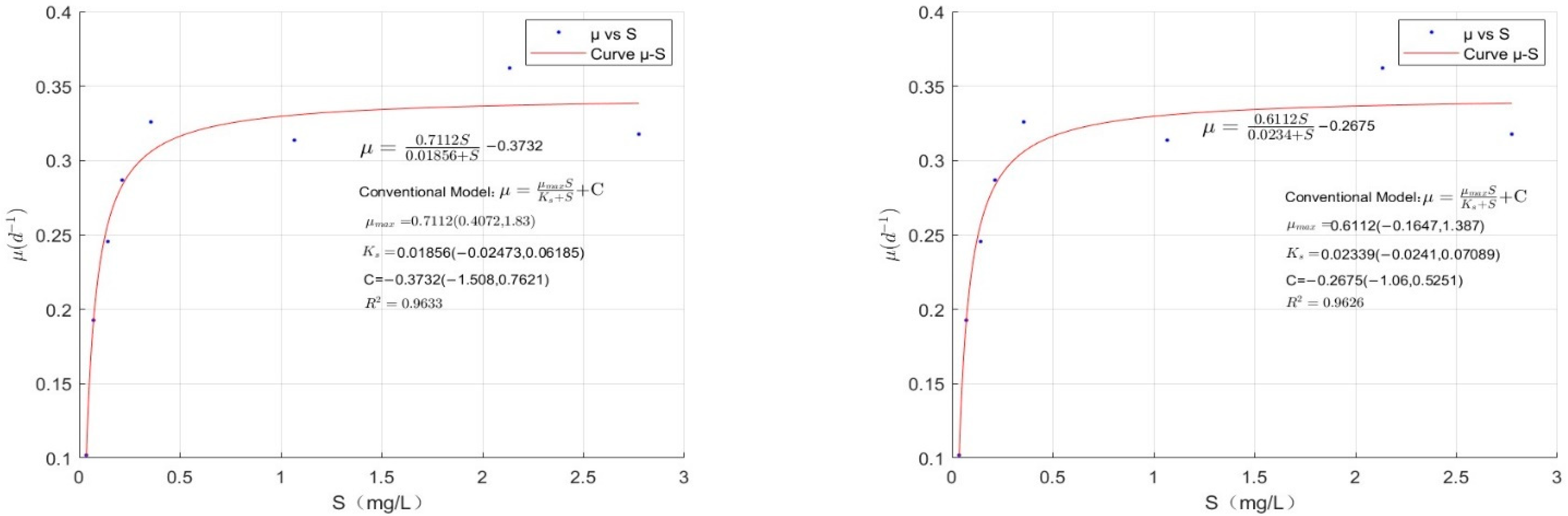
4.2. Fitting of the Modified Monod Model for C. vulgaris
4.3. Fitting of the Modified Monod Model for M. aeruginosa
4.4. Fitting of the Modified Monod Model for M. wesenbergii
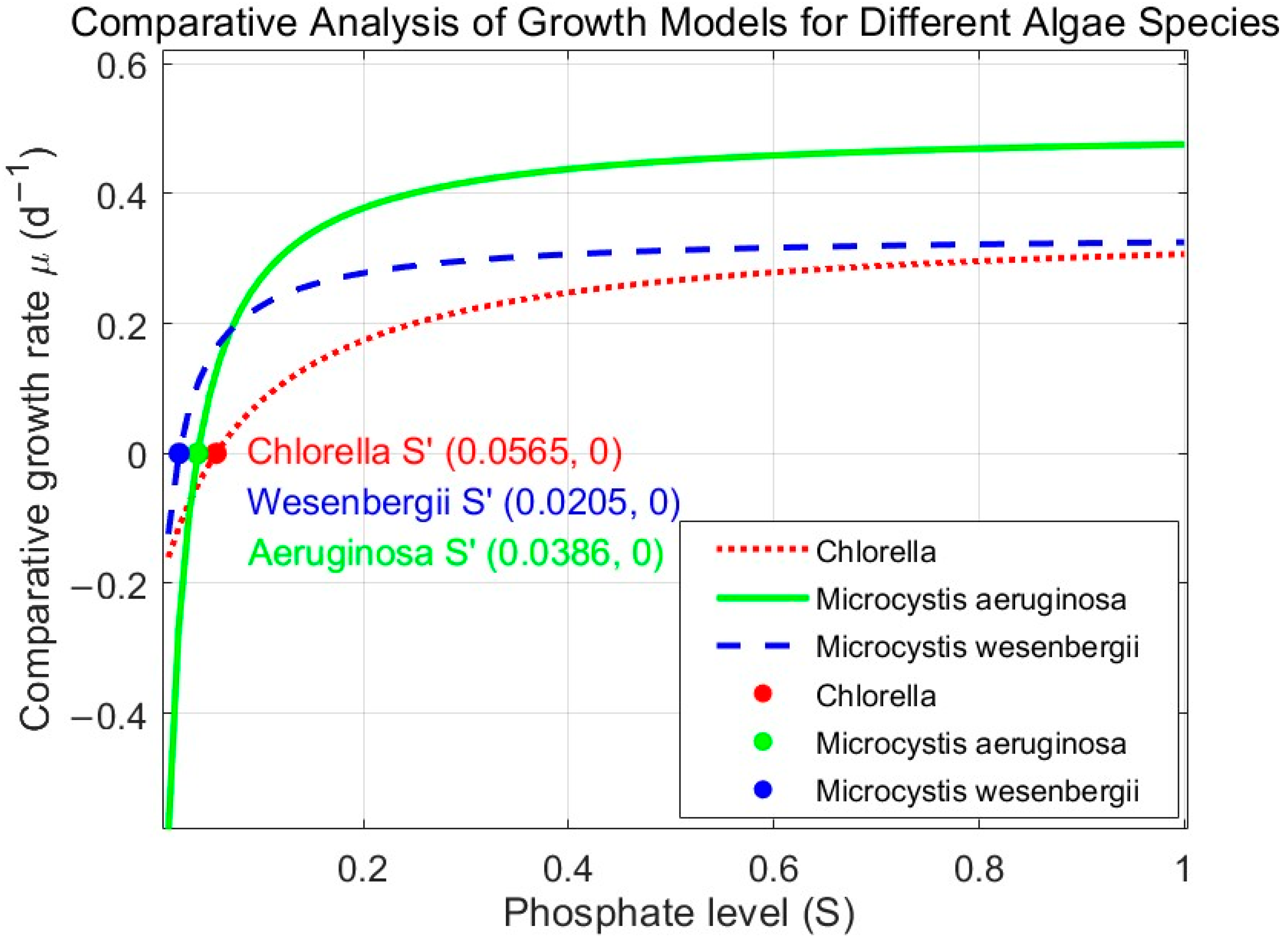
4.5. Comparison of Modified Monod Models for C. vulgaris, M. aeruginosa, and M. wesenbergii
5. Conclusions
- (a)
- The conventional Monod equation has certain limitations. In this study, we proposed the modified Monod equation and designed experiments to validate it. The resulting fit had R2 values of 0.954, 0.964, 0.977, 0.978, 0.9633, and 0.9626, indicating that the modified Monod equation effectively describes algal growth when phosphorus is limited.
- (b)
- By using the modified Monod model, we calculated the lower threshold of phosphorus nutrients, which is the phosphorus nutrient concentration at which algal growth reaches a dynamic equilibrium. The calculated values were 0.0565 mg/L for C. vulgaris, 0.0386 mg/L for M. aeruginosa, and 0.0205 mg/L for M. wesenbergii. Controlling phosphorus concentrations at or near these S′ values can theoretically prevent excessive algal proliferation, providing guidance for algal growth control using nutrient limitation.
- (c)
- The S′ of the three algal species followed the order of M. wesenbergii S′ < M. aeruginosa S′ < C. vulgaris S′. M. wesenbergii requires the lowest theoretical phosphorus nutrient concentration for growth, followed by M. aeruginosa, and C. vulgaris requires the highest. The results suggest that cyanobacteria (Microcystis and similar species) have lower phosphorus nutrient thresholds, explaining why algal blooms in China are mainly composed of cyanobacteria and why other algal species do not bloom during cyanobacterial bloom events.
- (d)
- Among the three algal species, M. aeruginosa exhibited the highest maximum specific growth rate, whereas C. vulgaris had the lowest. This result suggests that in natural water bodies with fluctuating phosphorus concentrations, M. aeruginosa would dominate in terms of biomass, followed by M. wesenbergii and C. vulgaris. This observation implies that cyanobacterial biomass tends to be higher than that of green algae, making cyanobacteria the dominant species in freshwater ecosystems.
- (e)
- At high phosphorus concentrations (>2 mg/L), the growth of M. aeruginosa and M. wesenbergii is inhibited to some extent and that of C. vulgaris is unaffected. This result indicates that phosphorus inhibition does not occur in all algal species. The results of this experiment suggest that phosphorus inhibition is evident in cyanobacteria, and future research may explore this phenomenon further by investigating internal phosphorus forms and phosphorus absorption gene sequences in different algal species.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Materials and Methods
Appendix A.1. Experimental Materials
| Lab Equipment | Lab Equipment |
|---|---|
| BG11 medium (Changde Det Bio-Tech Co., Ltd.) | Photobioreactor |
| Centrifuge | Centrifuge tubes |
| Autoclave | Count Star cell counter |
| Count Star counting chamber | Analytical balance |
| 1000 mL volumetric flasks | 1000 mL volumetric flasks |
| 500 mL Erlenmeyer flasks | Breathable membrane caps |
| Aseptic workbench | Alcohol lamp |
| Glass rods | Graduated cylinders |
| Wash bottles | Beakers |
| Pipettes | Wide-mouth bottles |
| Wide-mouth bottles (brown) |
Appendix A.2. Medium Design
Appendix A.2.1. Initial Culture Medium
| Drug Name | Dosage per Liter of Medium |
|---|---|
| NaNO3 | 1.5 g |
| K2HPO4 | 0.04 g |
| MgSO4·7H2O | 0.075 g |
| CaCl2·2H2O | 0.036 g |
| Citric acid | 0.006 g |
| Ferric ammonium citrate | 0.006 g |
| EDTANa2 | 0.001 g |
| Na2CO3 | 0.02 g |
| A5 | 1 ml |
| Drug Name | Usage per Liter of A5/mg |
|---|---|
| H3BO3 | 2.86 |
| MnCl2·4H2O | 1.86 |
| ZnSO4·7H2O | 0.22 |
| NaMoO4·2H2O | 0.021 |
| CuSO4·5H2O | 0.08 |
| Co(NO3)2·6H2O | 0.05 |
Appendix A.2.2. Phosphate-Deficient Medium
Appendix A.2.3. Phosphate Concentration Gradient Medium
| Stock Solution | Preparation Method |
|---|---|
| Stock1 | 0.30 g C6H8O7, 0.30 g C6H8FeNO7, 0.050 g EDTANa2, Dissolve and make up to 100 mL in a volumetric flask. |
| Stock2 | 30.0 g NaNO3, 0.78 g K2HPO4, 1.50 g MgSO4·7H2O, Dissolve and make up to 1000 mL in a volumetric flask. |
| Stock3 | 1.90 g CaC12·2H2O, Dissolve and make up to 100 mL in a volumetric flask. |
| Stock4 | 2.00 g Na2CO3, Dissolve and make up to 100 mL in a volumetric flask. |
| Stock5 | 2.860 g H3BO3, 1.8100 g MnCl2·4H2O, 0.2220 g ZnSO4·7H2O, 0.3910 g Na2MoO4, 0.0790 g CuSO4·5H2O, 0.0490 g Co(NO3)2·6H2O, Dissolve and make up to 1000 mL in a volumetric flask. |
| P gradient Stock Solution | Amount of K2HPO4 to Be Added (in Grams) |
|---|---|
| a1 | 0.01 |
| a2 | 0.02 |
| a3 | 0.04 |
| a4 | 0.06 |
| a5 | 0.1 |
| a6 | 0.3 |
| a7 | 0.6 |
| a8 | 0.78 |
| Phosphorus Concentration Gradient Culture Medium | P Concentration (mg/L) |
|---|---|
| A1 | 0.03557 |
| A2 | 0.07114 |
| A3 | 0.14228 |
| A4 | 0.2134 |
| A5 | 0.3557 |
| A6 | 1.0671 |
| A7 | 2.1342 |
| A8 | 2.7745 |
Appendix A.3. Experimental Design
Appendix B
Appendix B.1. Specific Growth Rate of M. aeruginosa
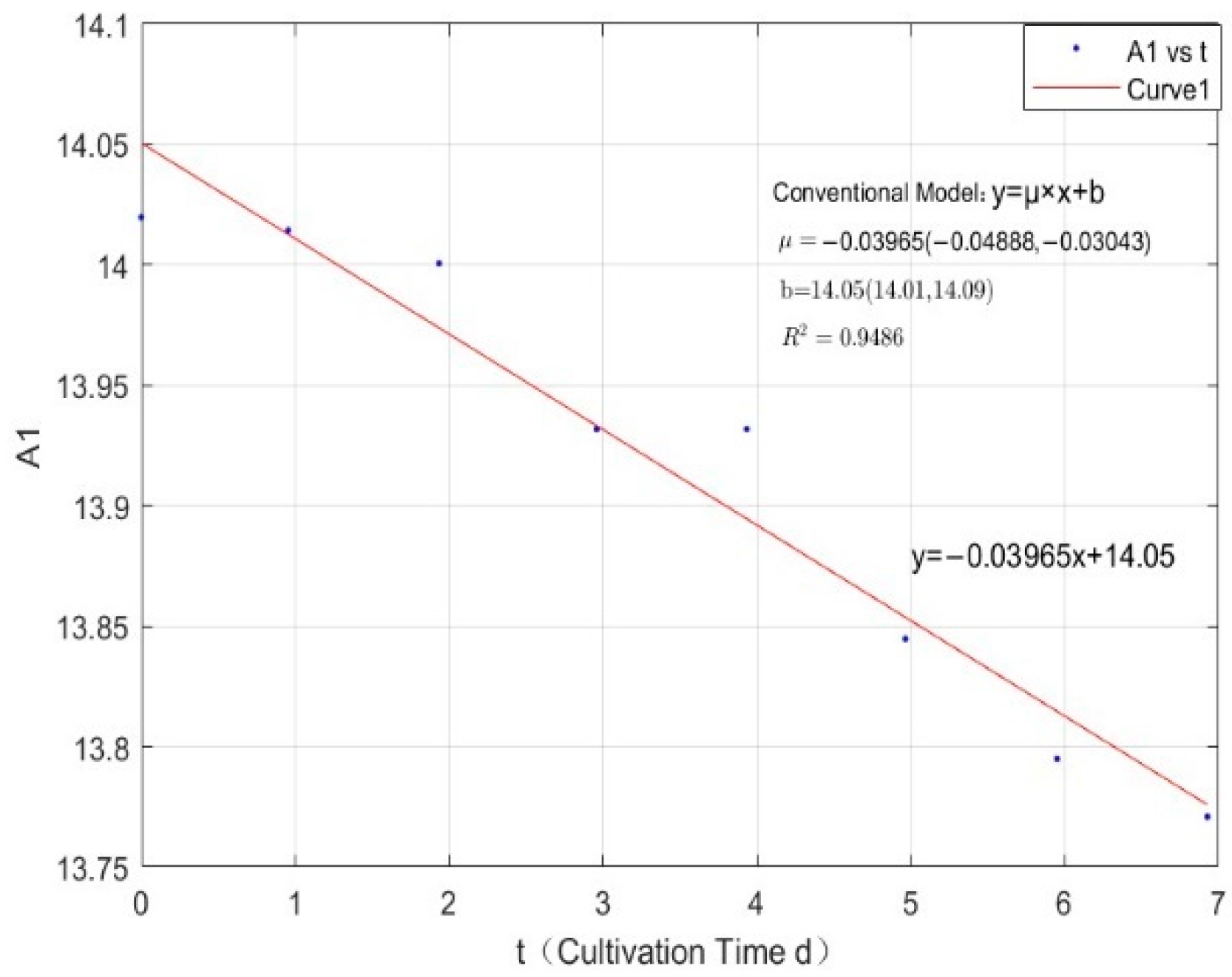

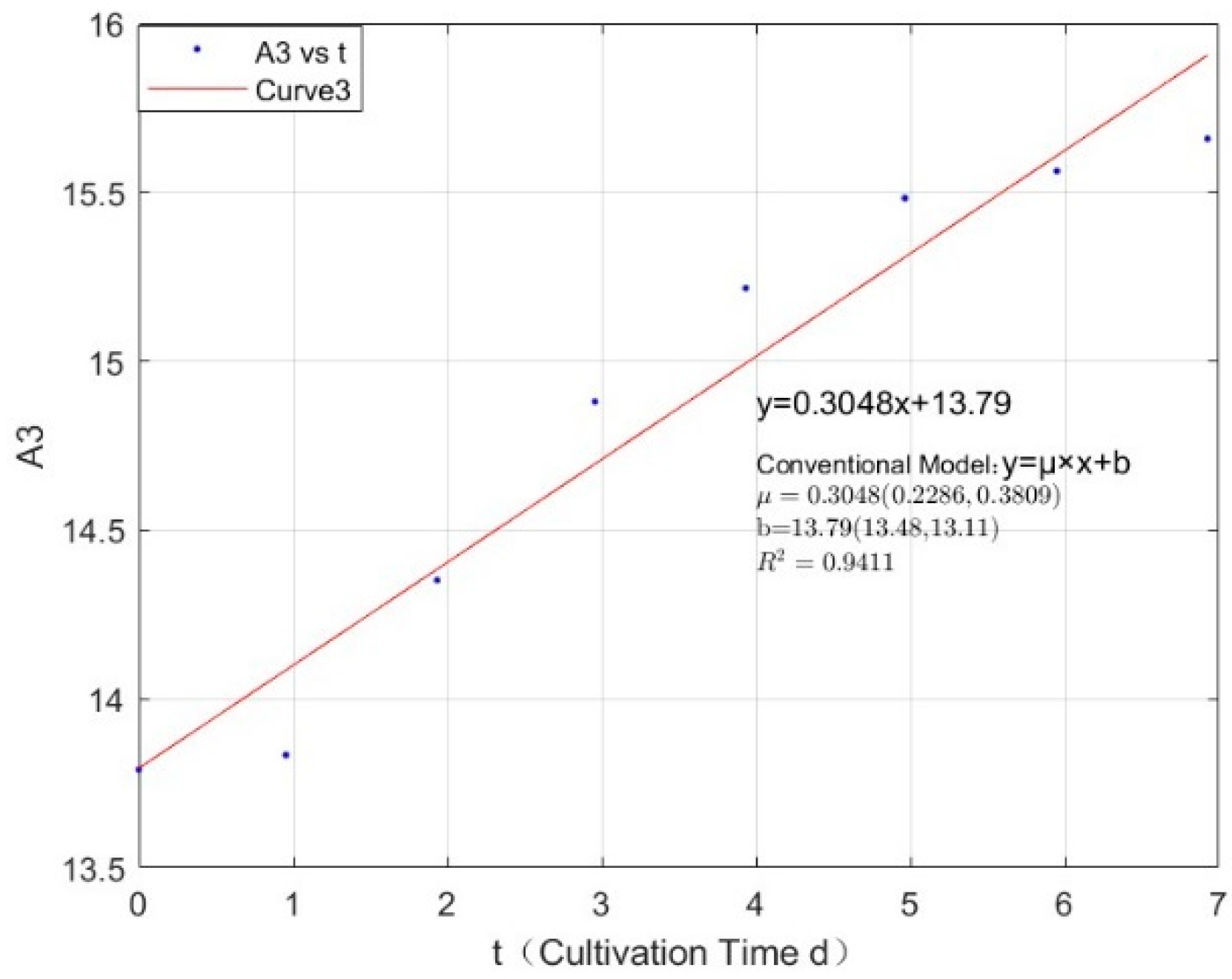
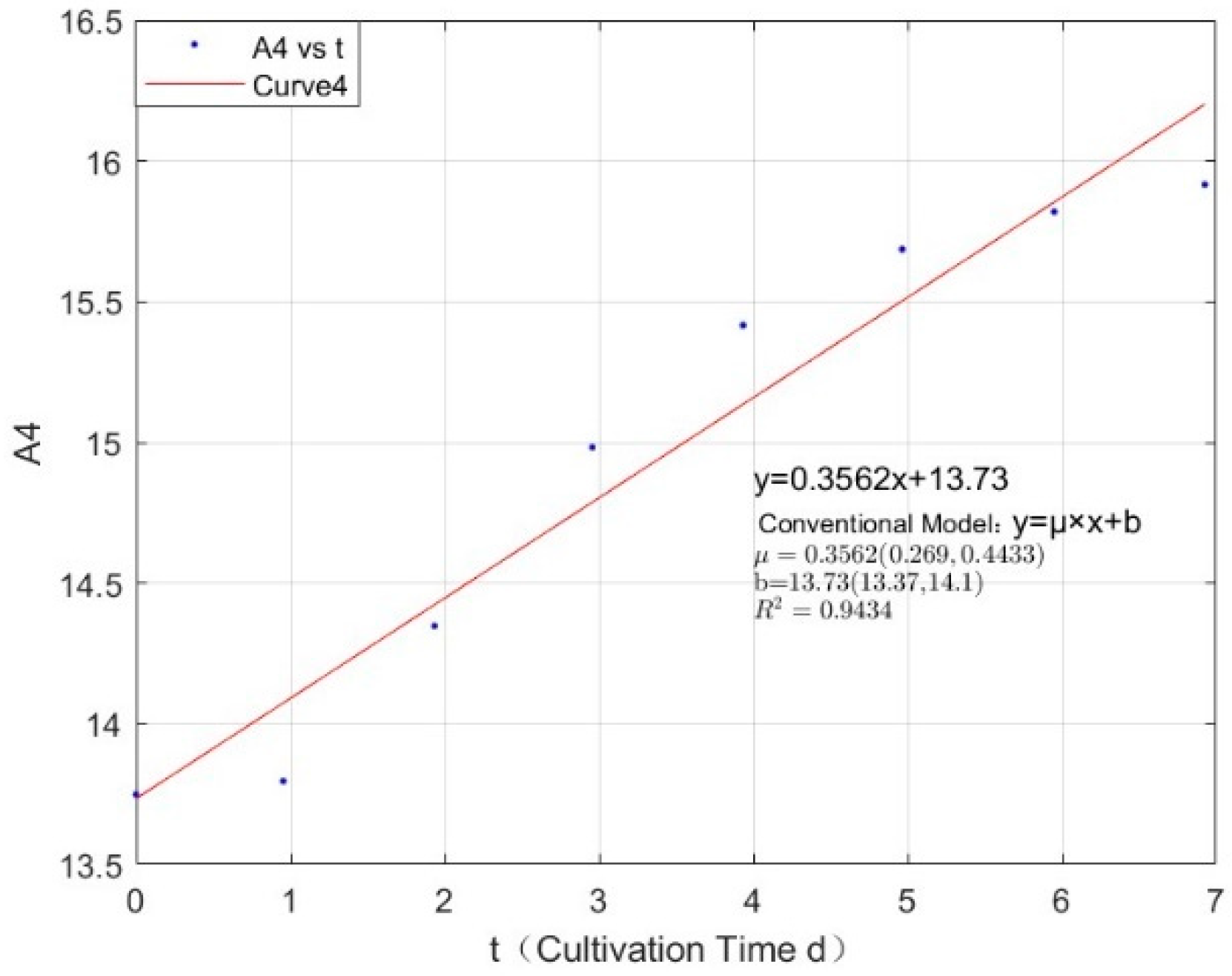
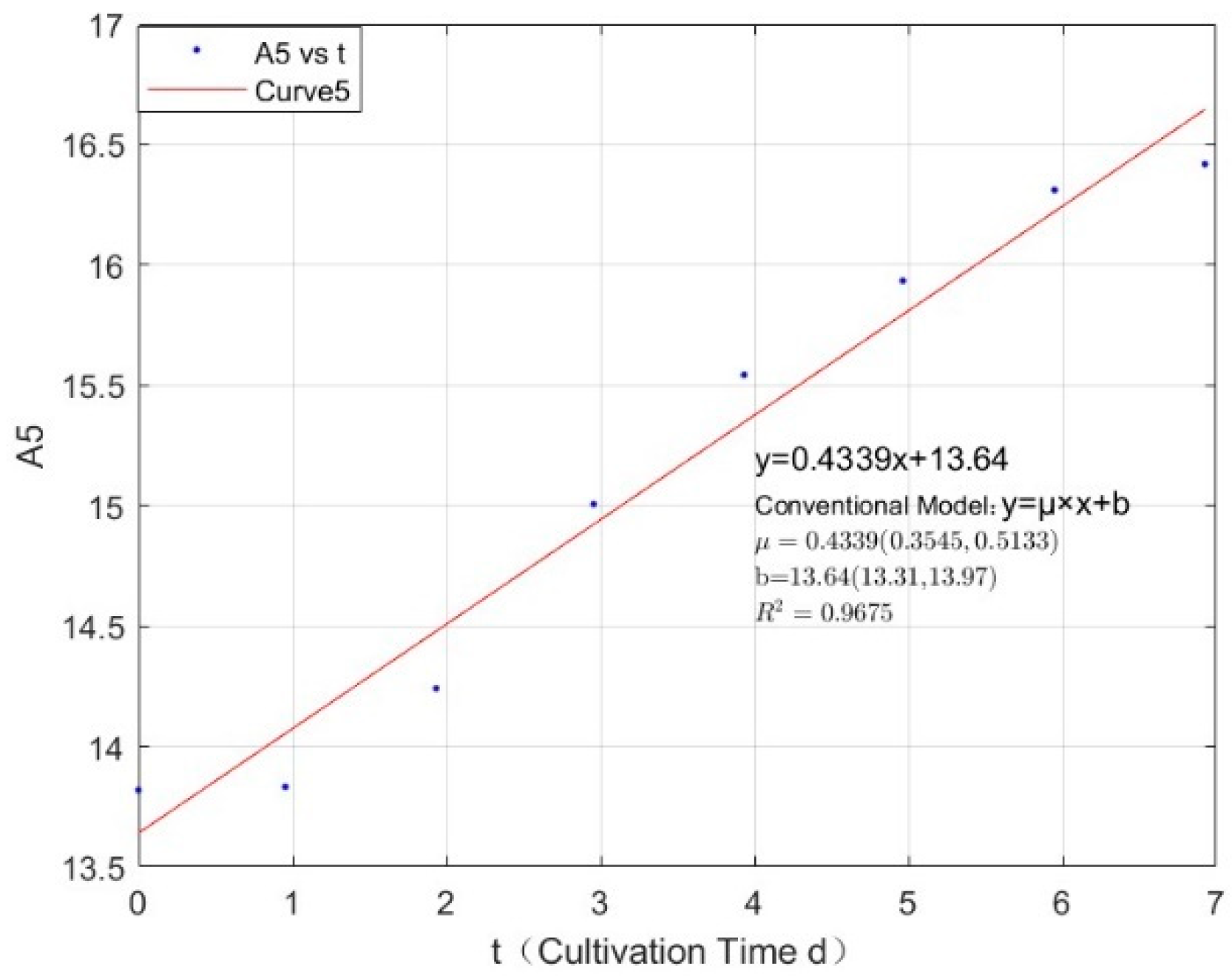
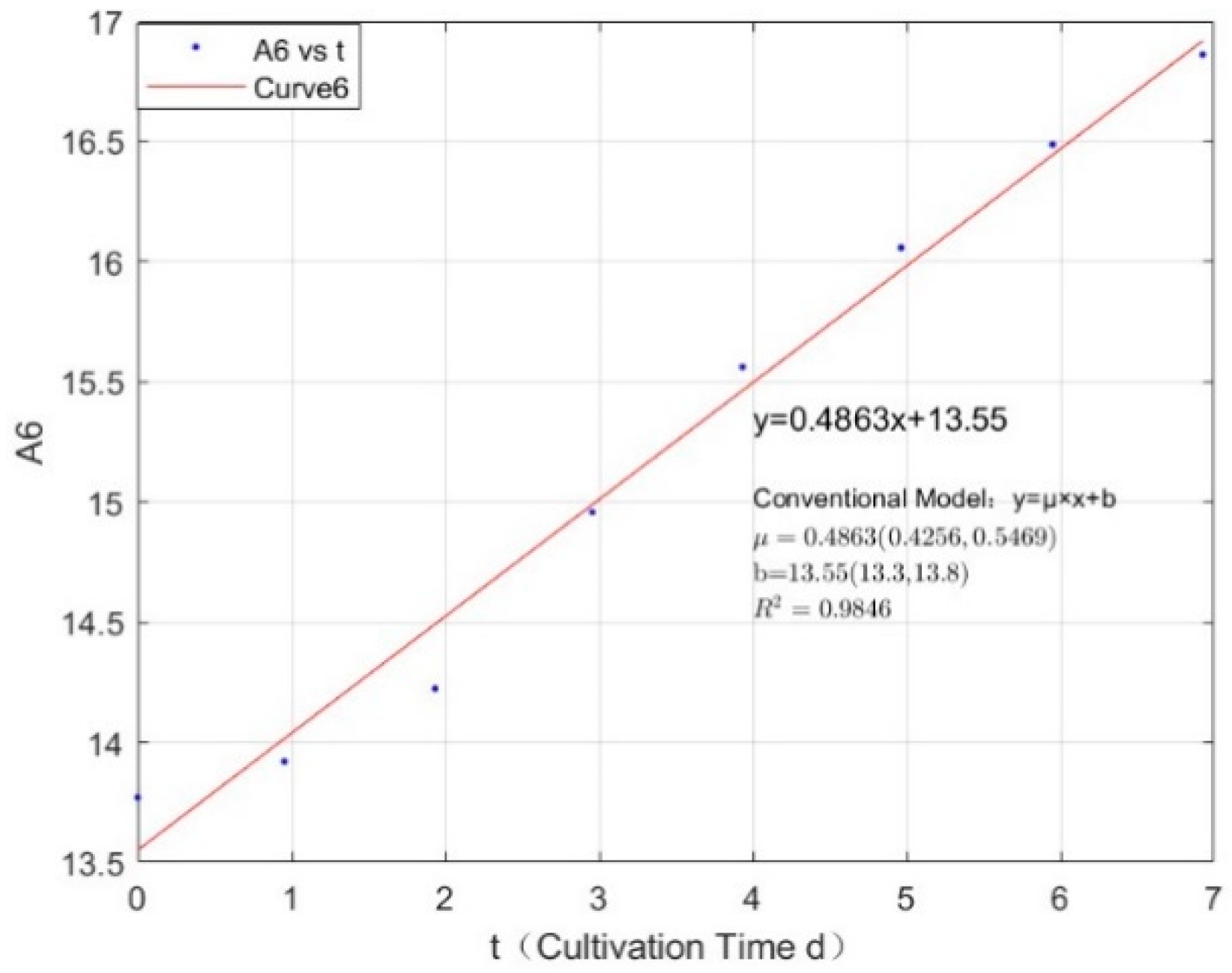
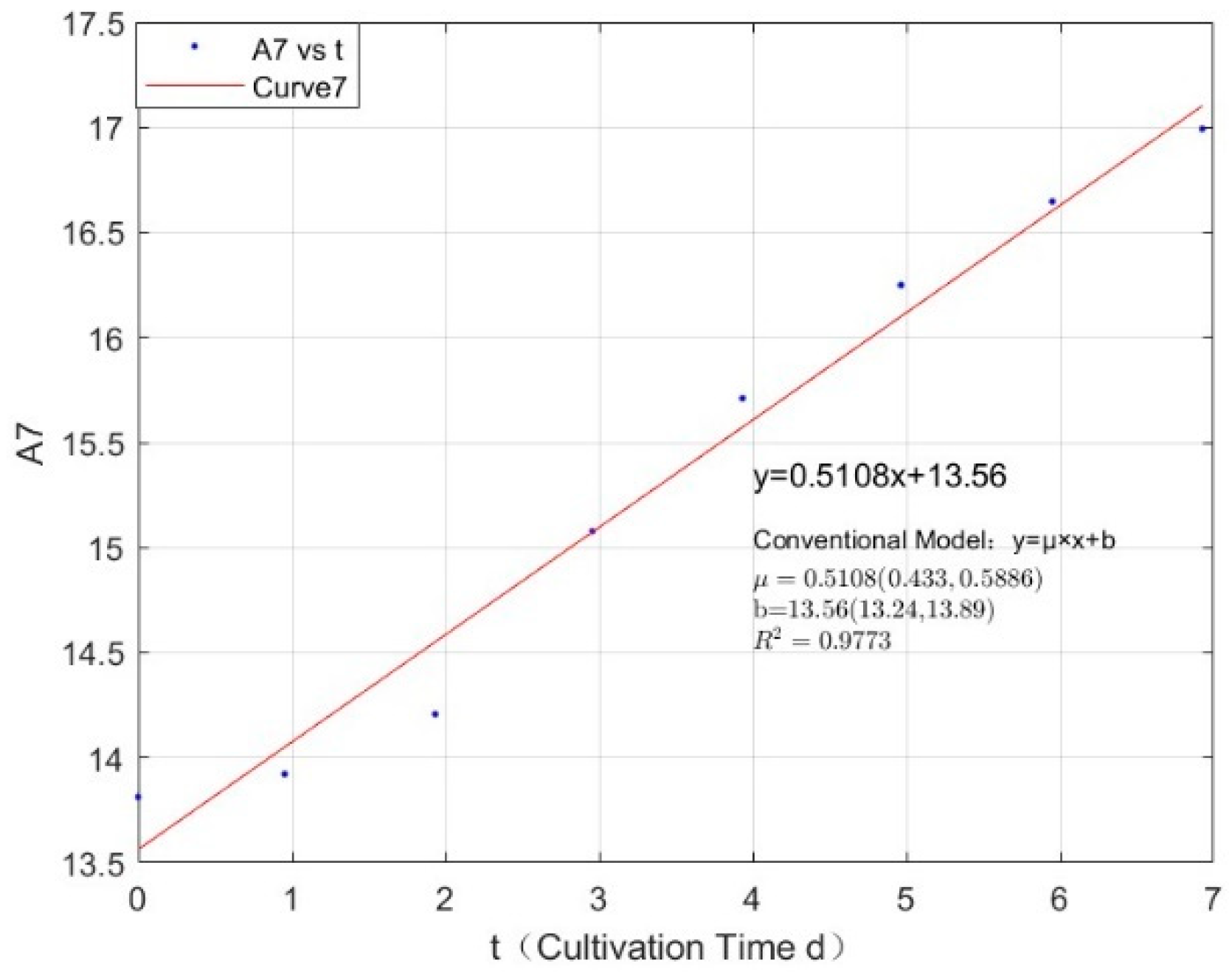
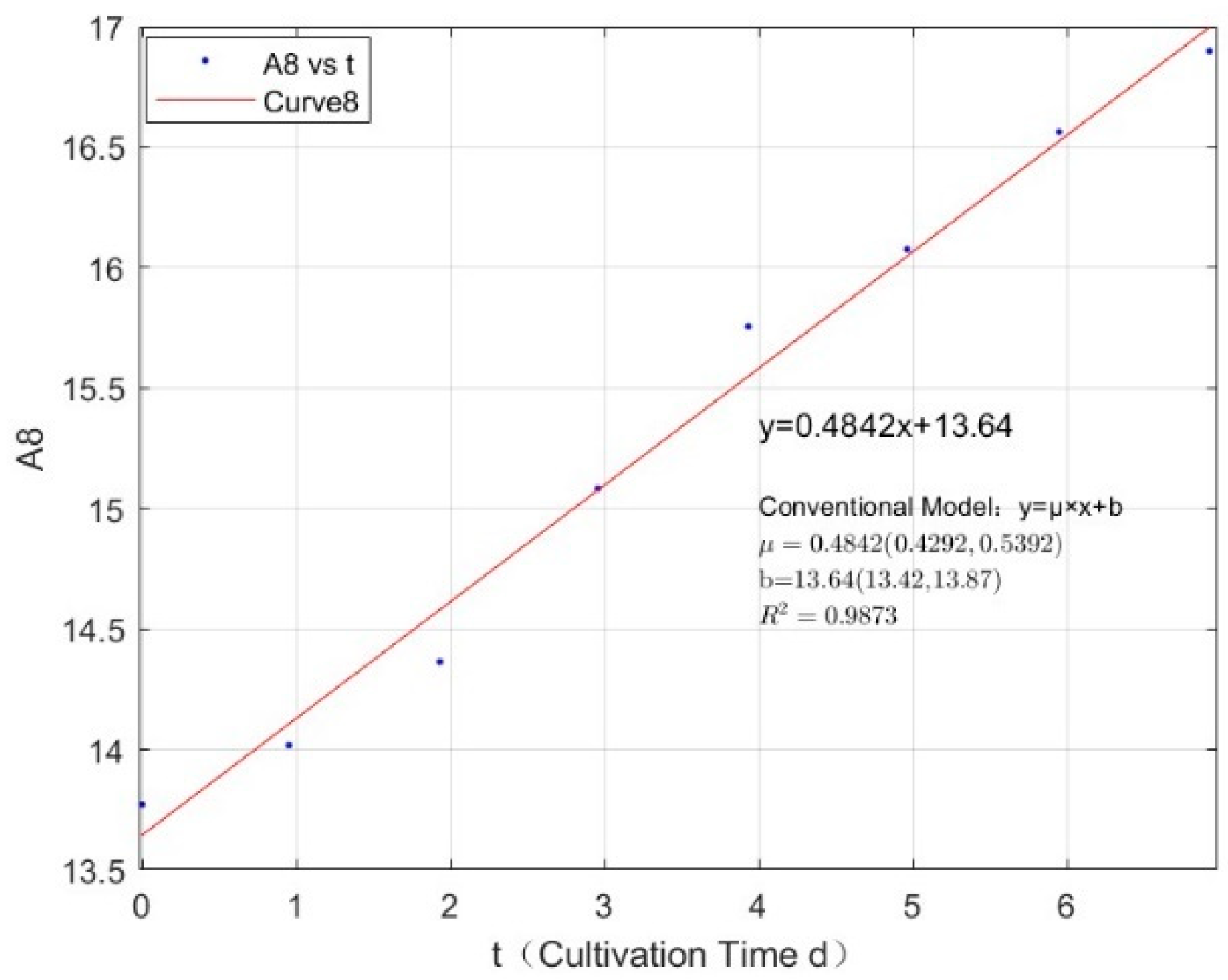
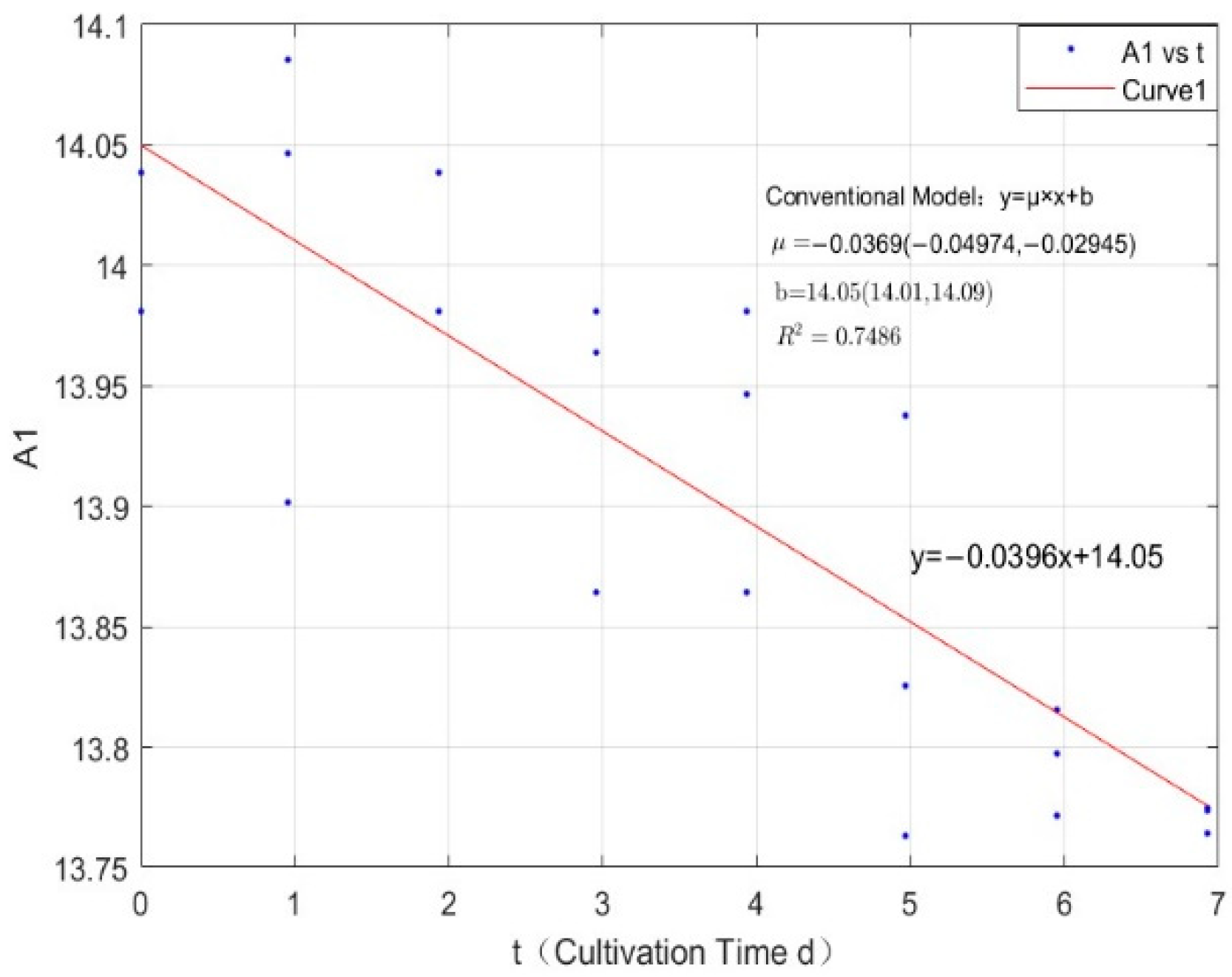
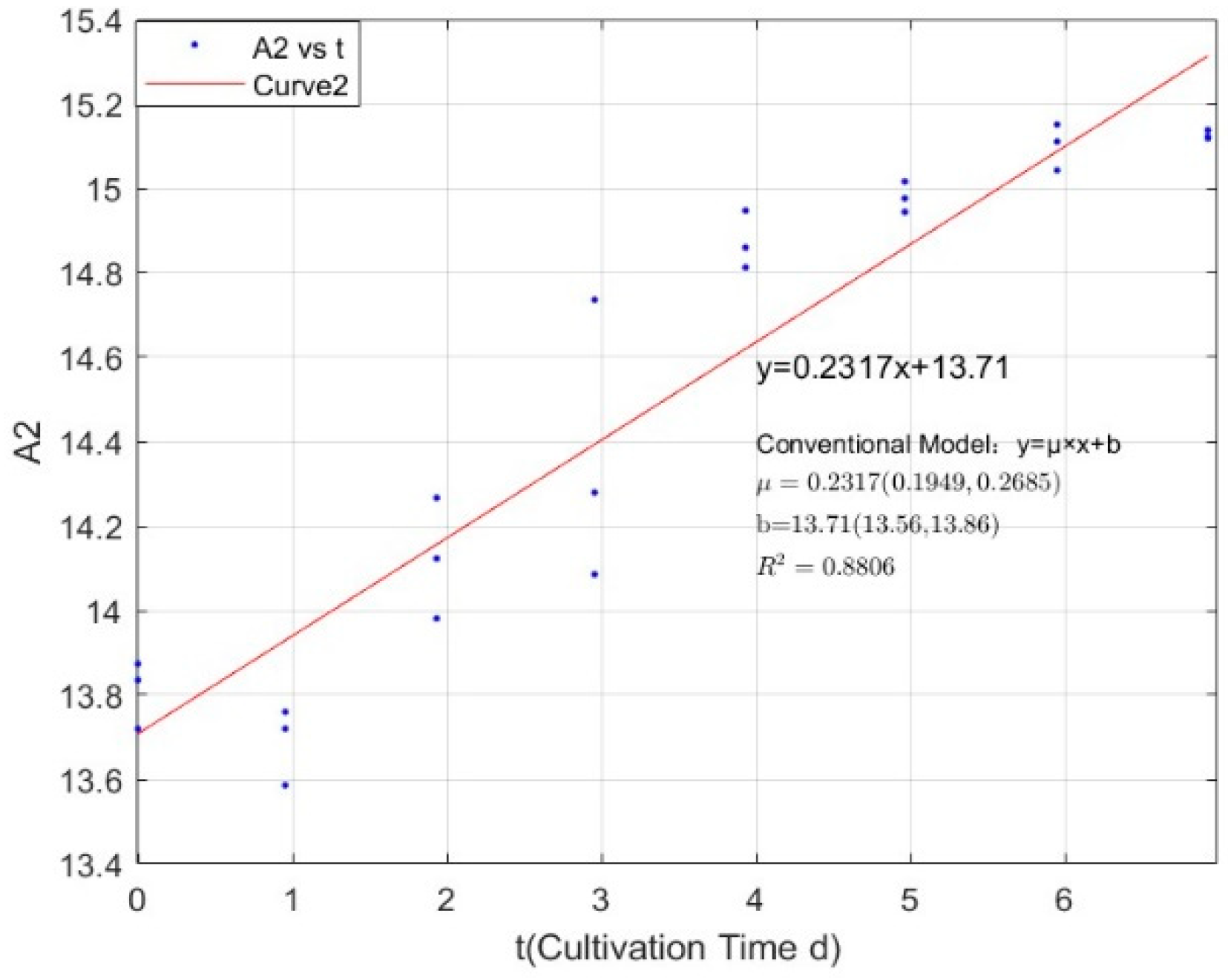
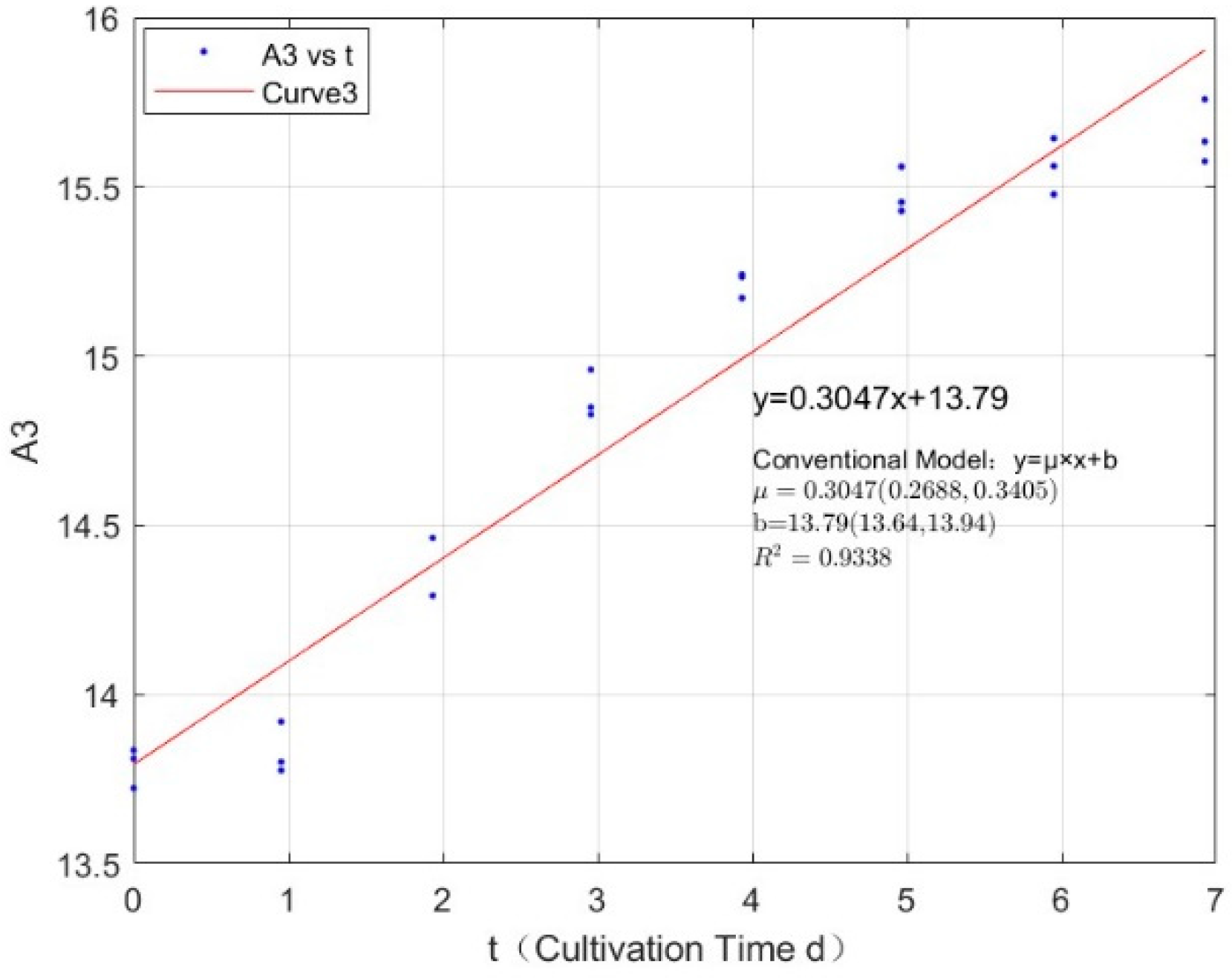
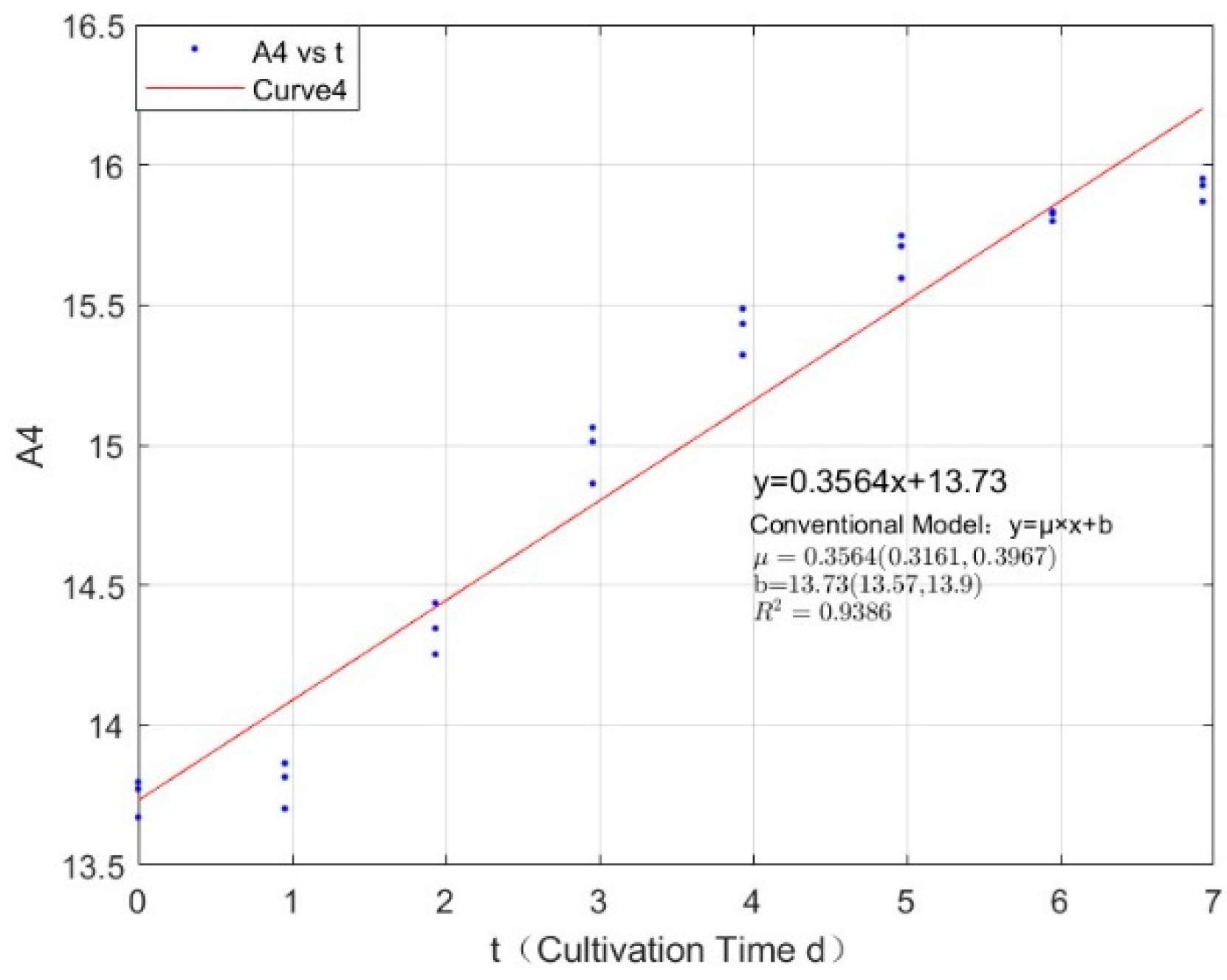
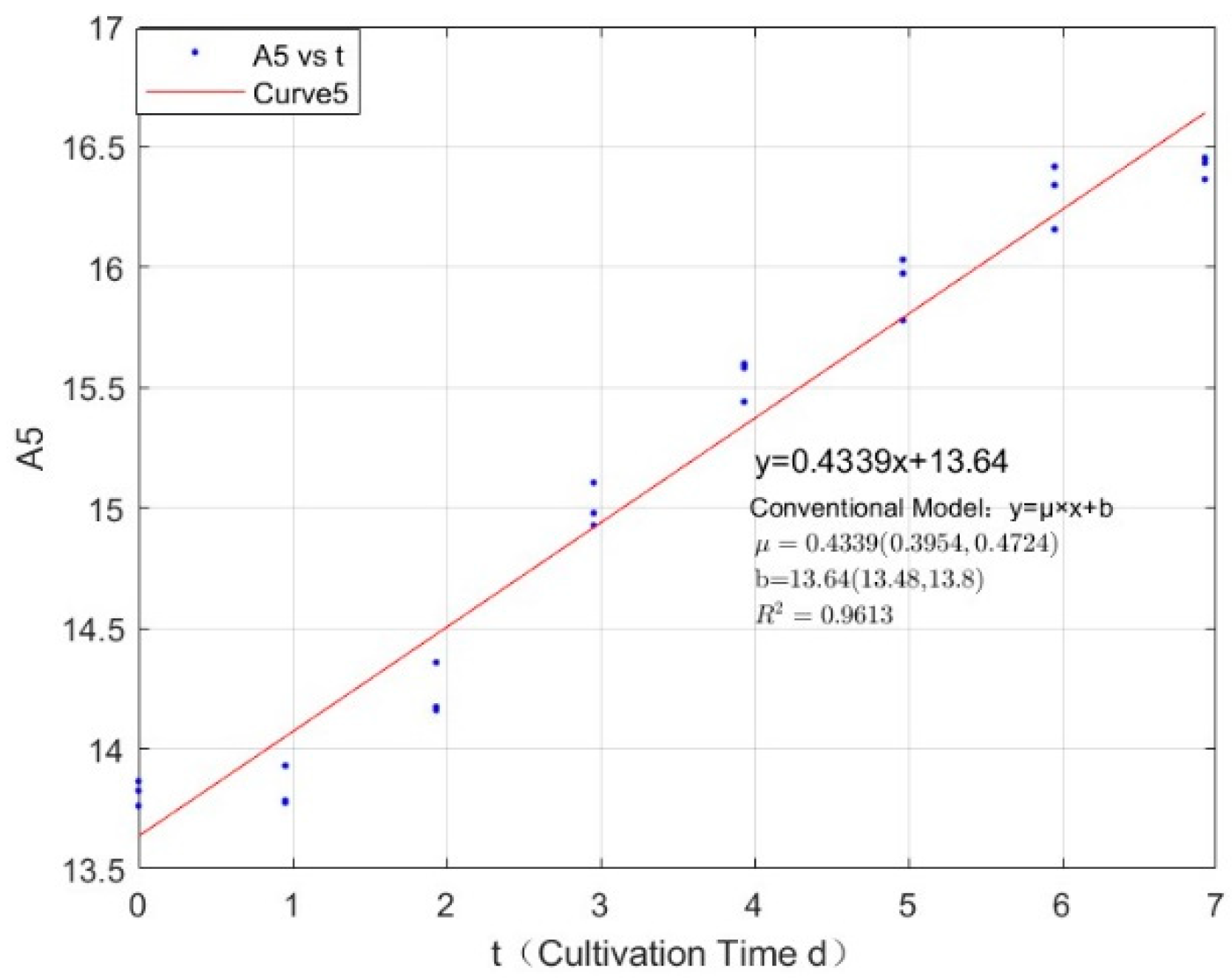
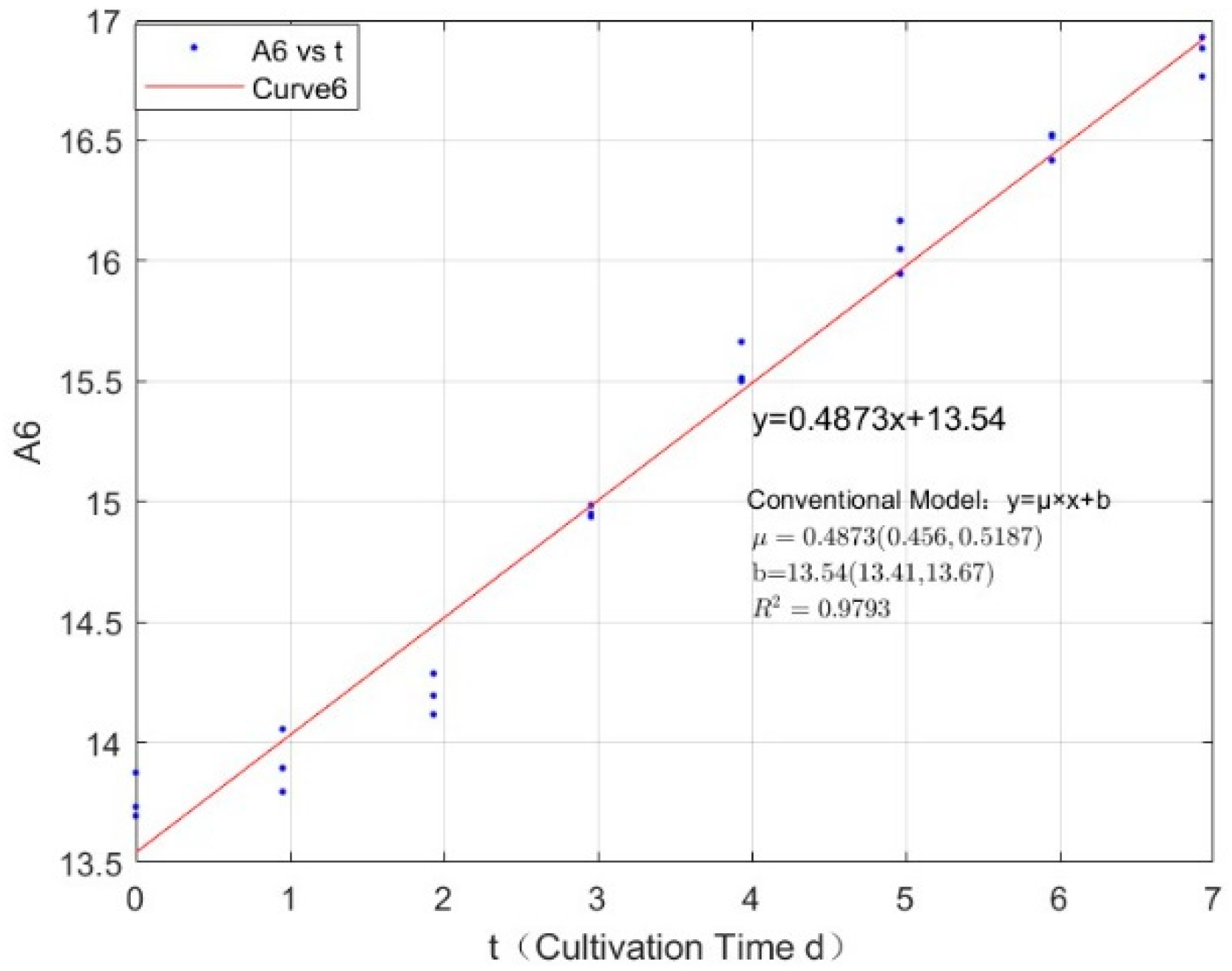
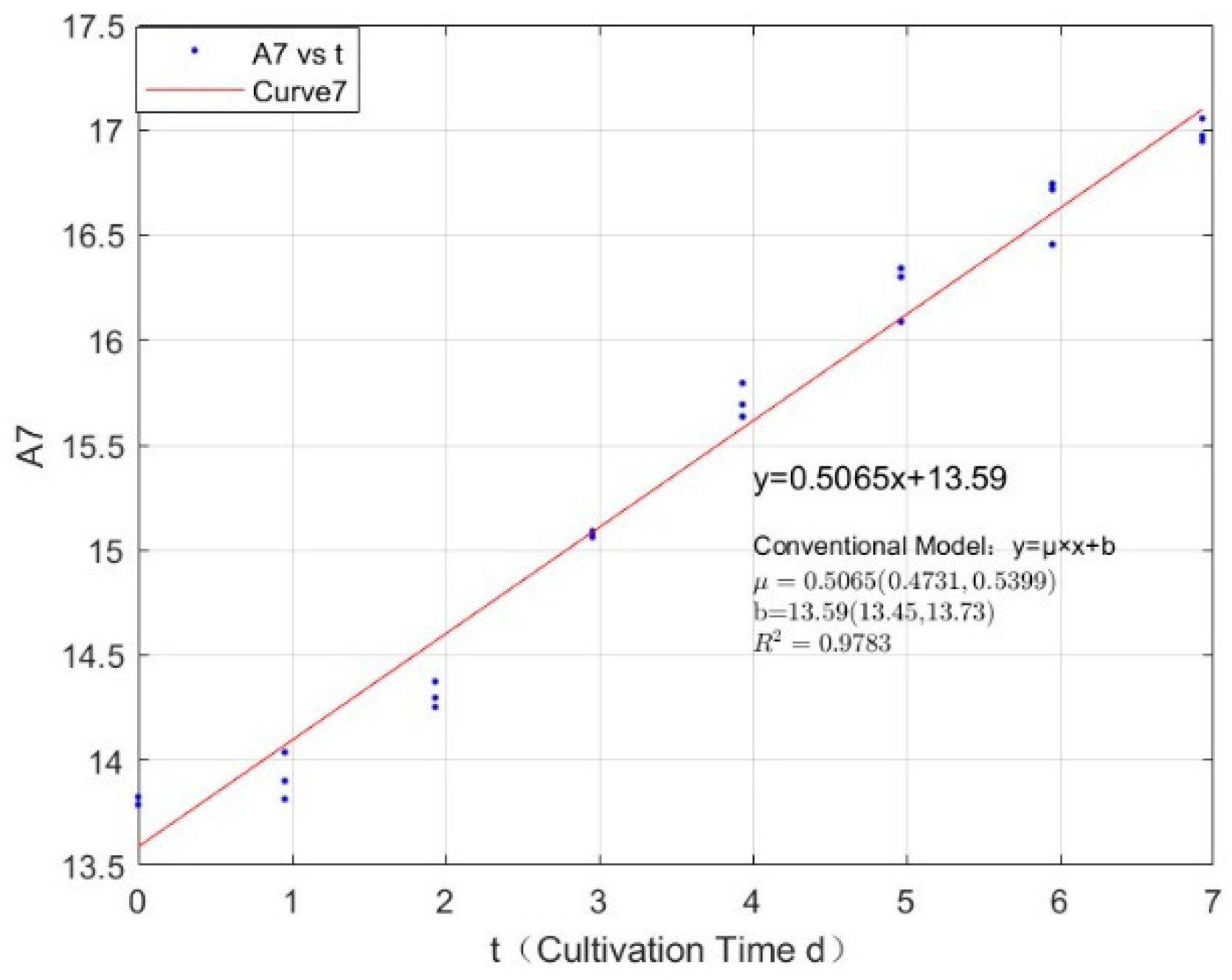
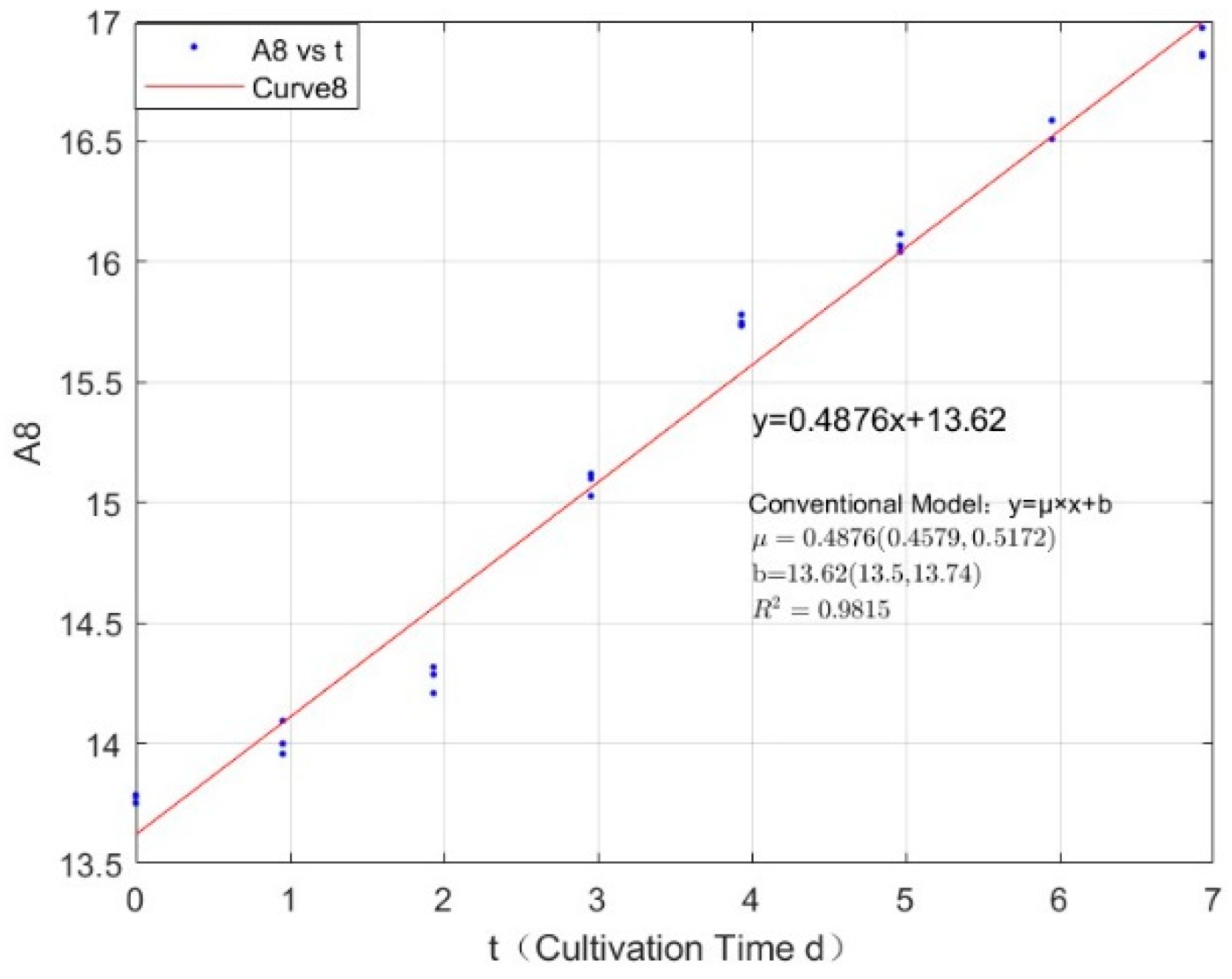
Appendix B.2. Specific Growth Rate of M. wesenbergii
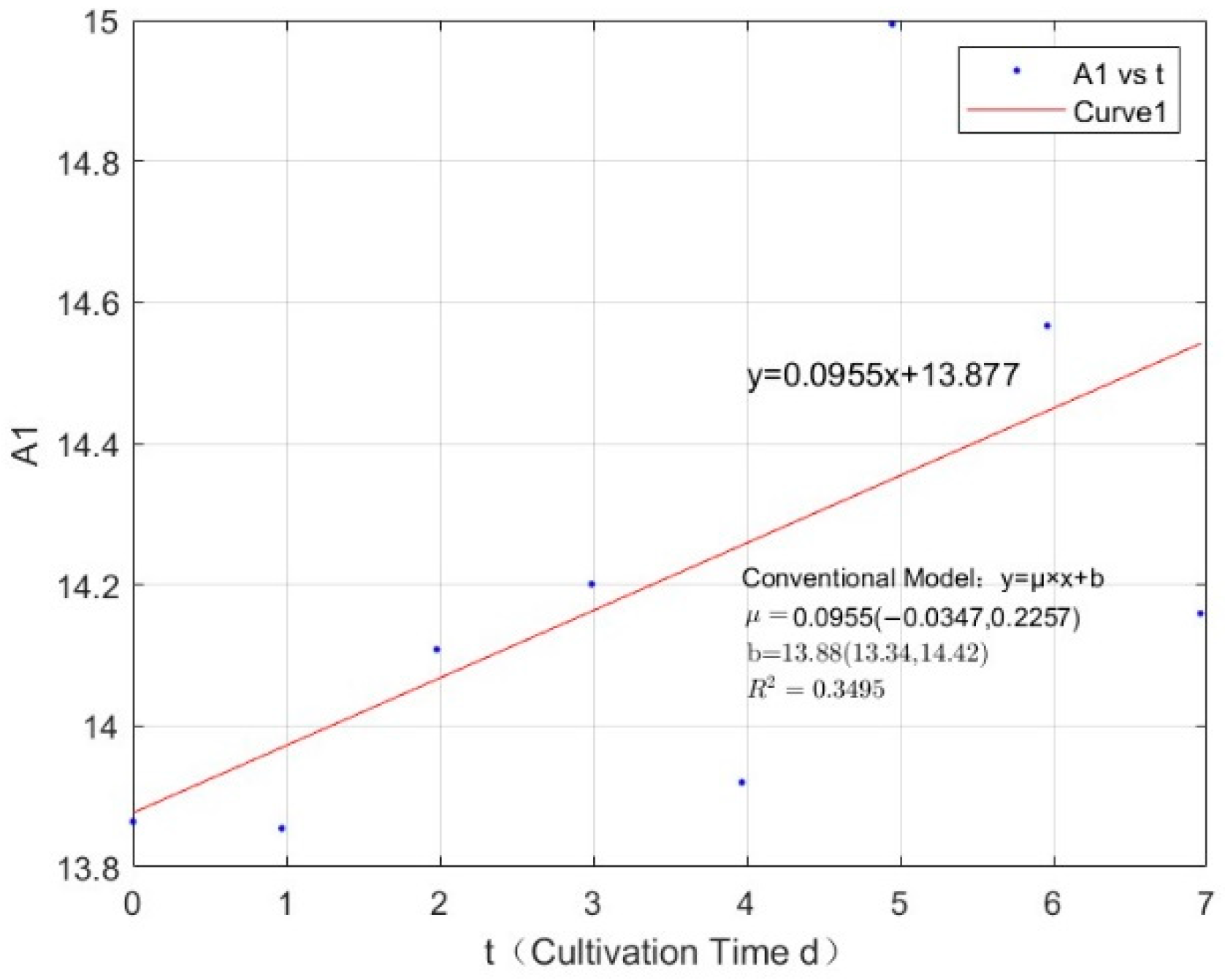
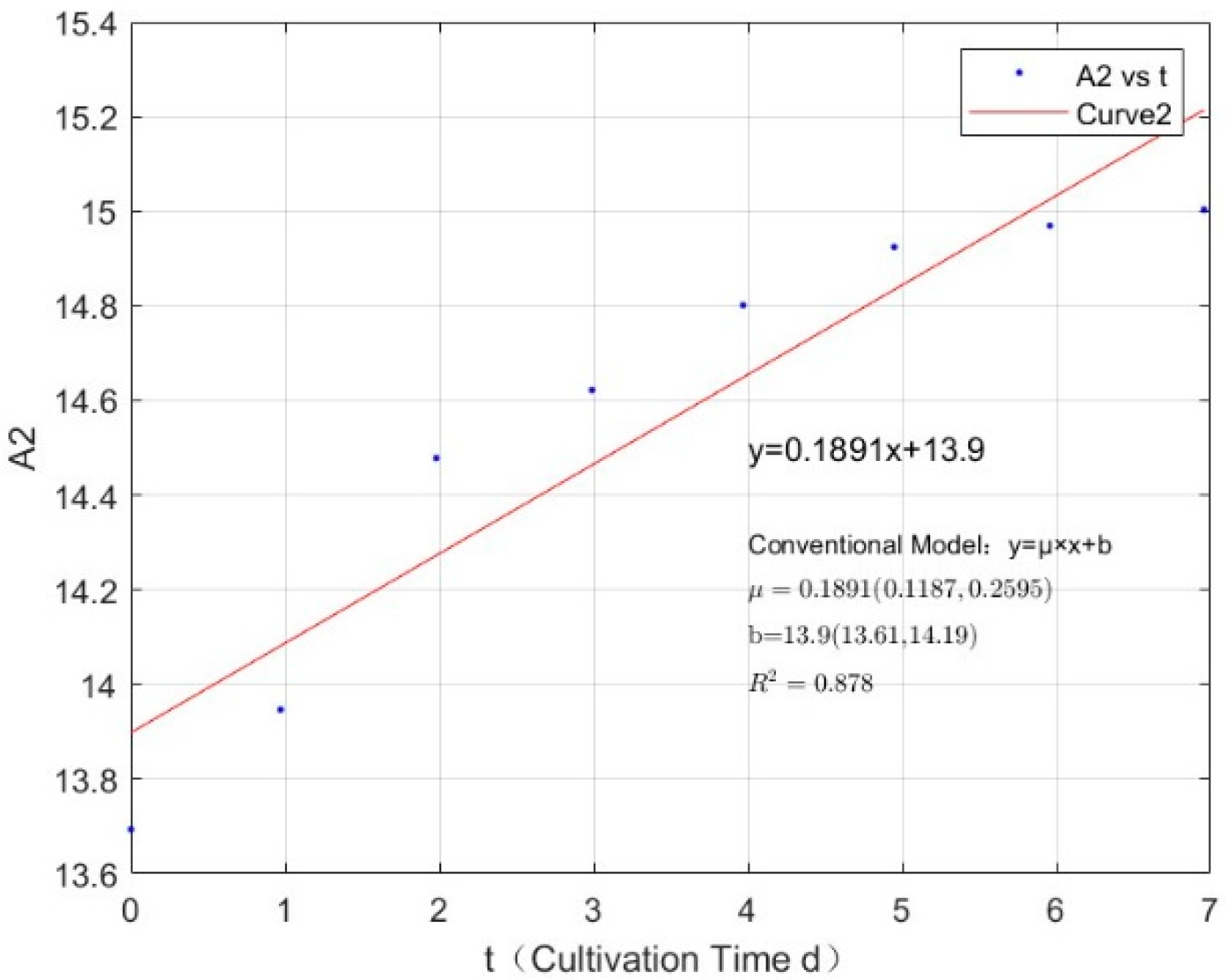
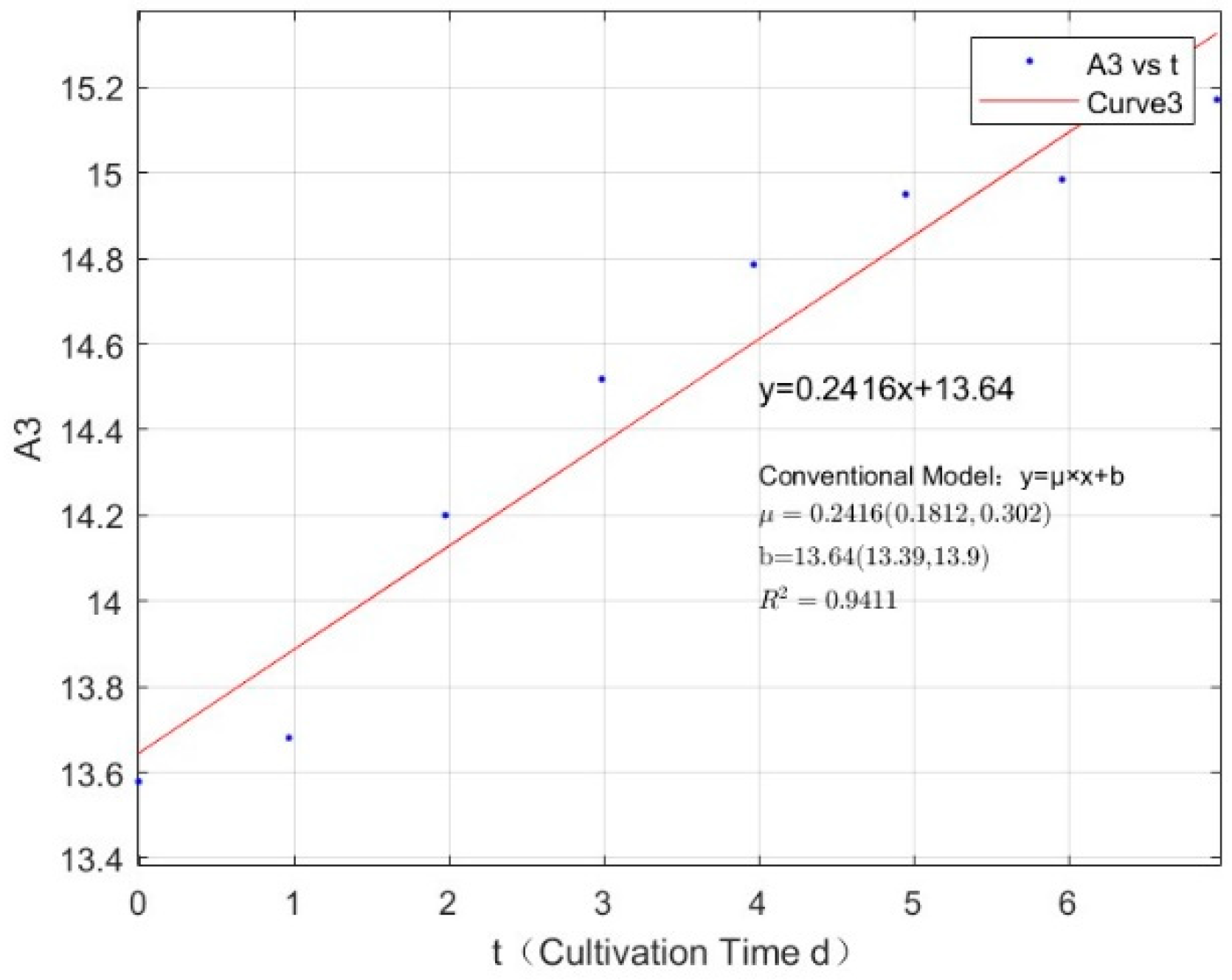
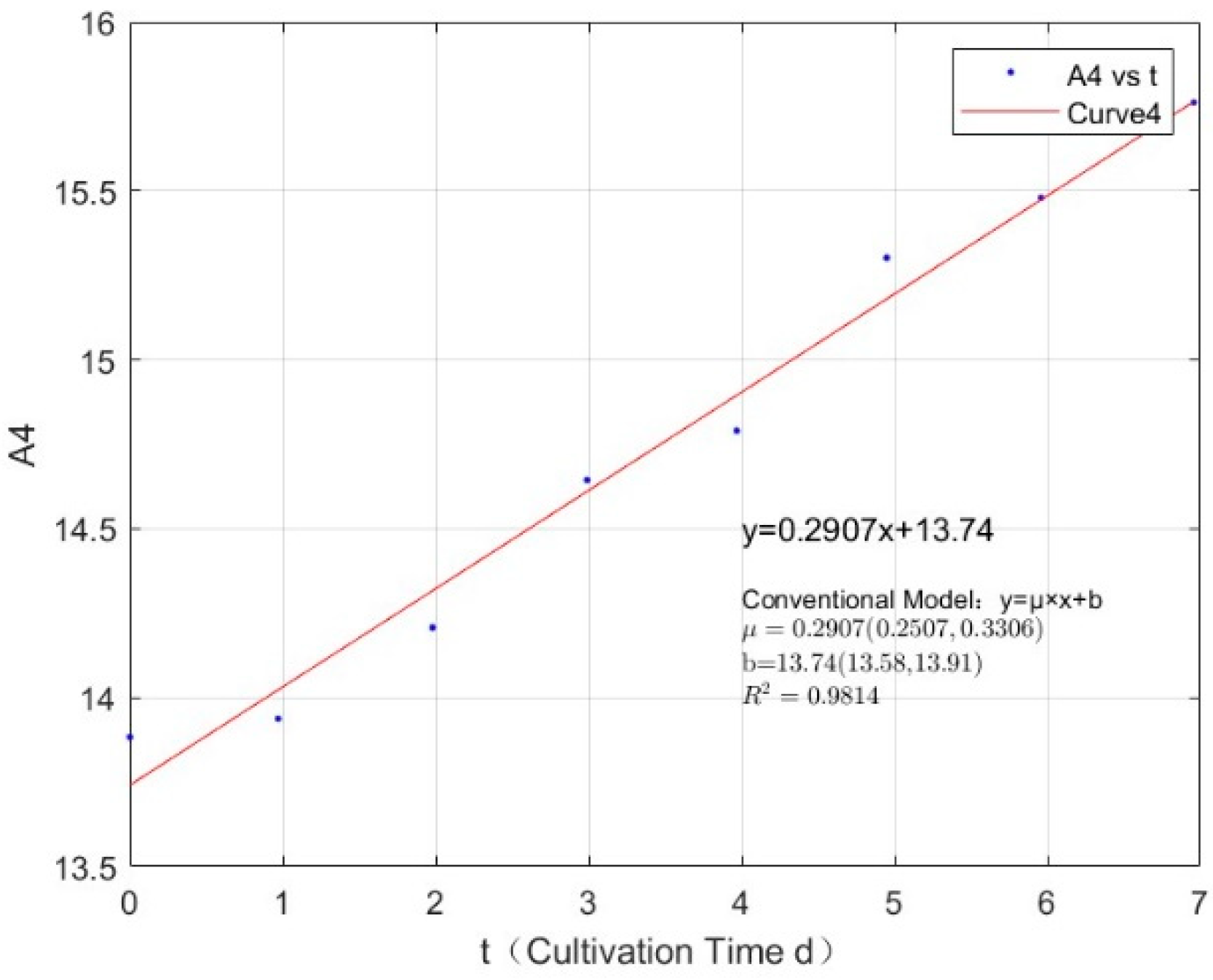
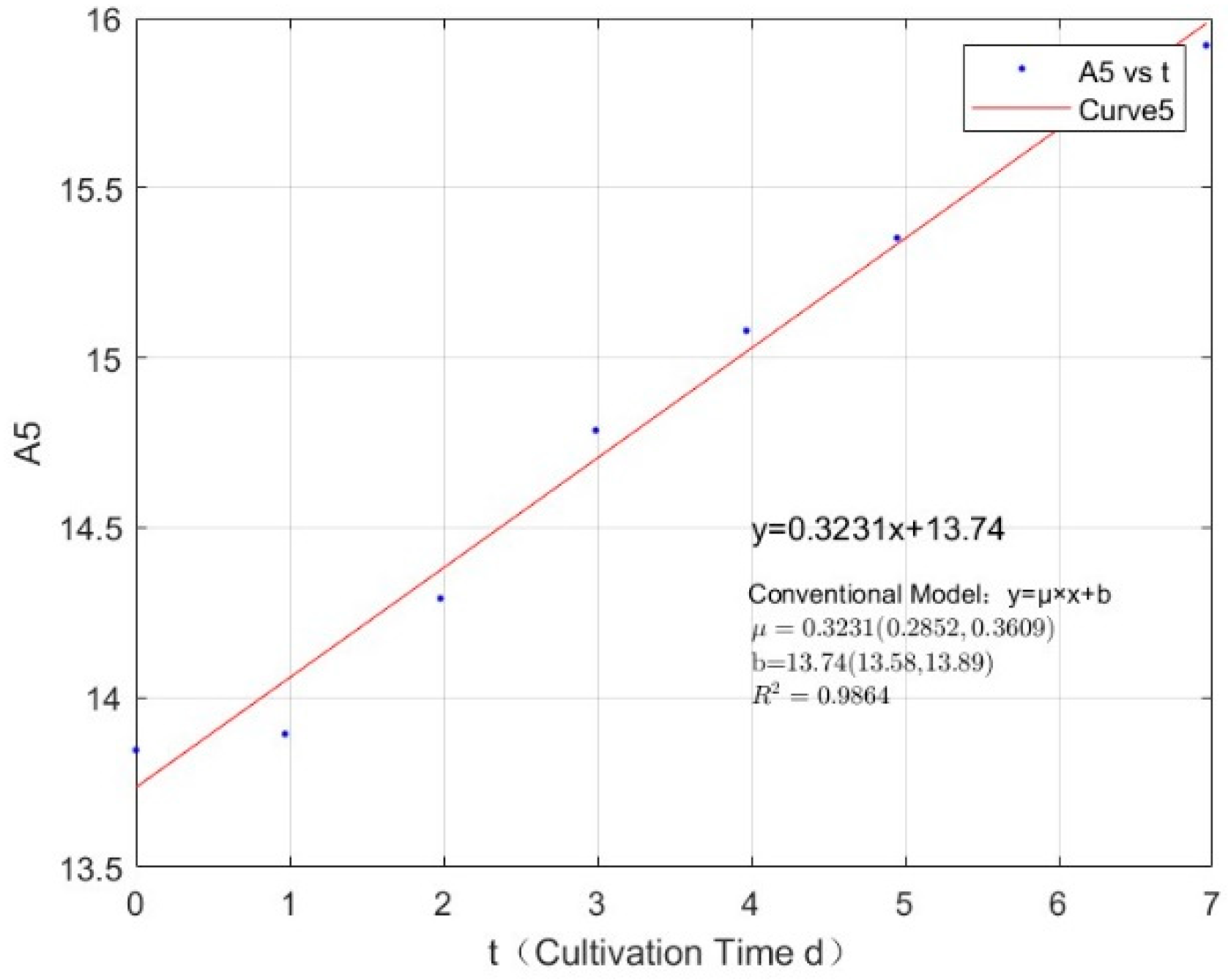
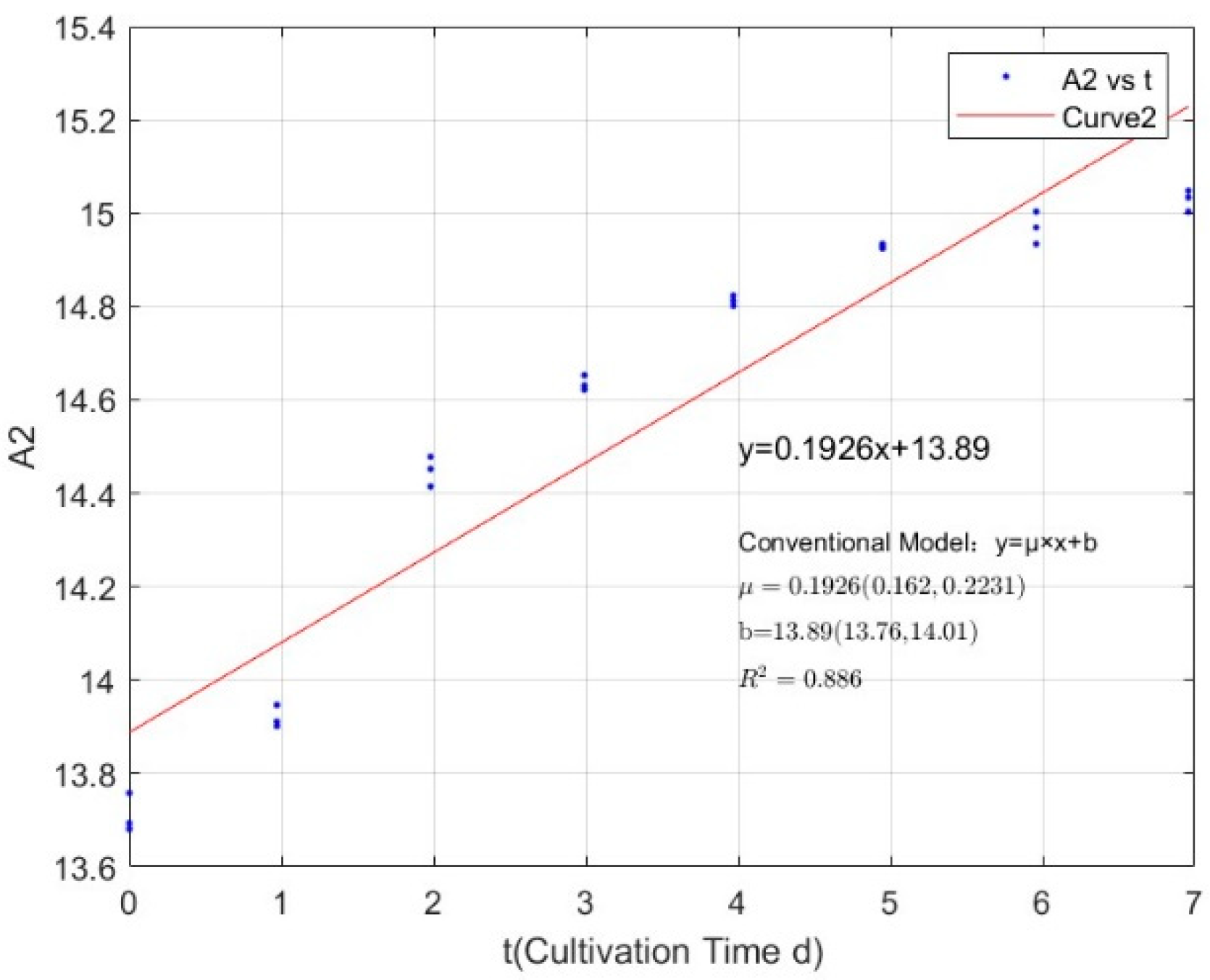
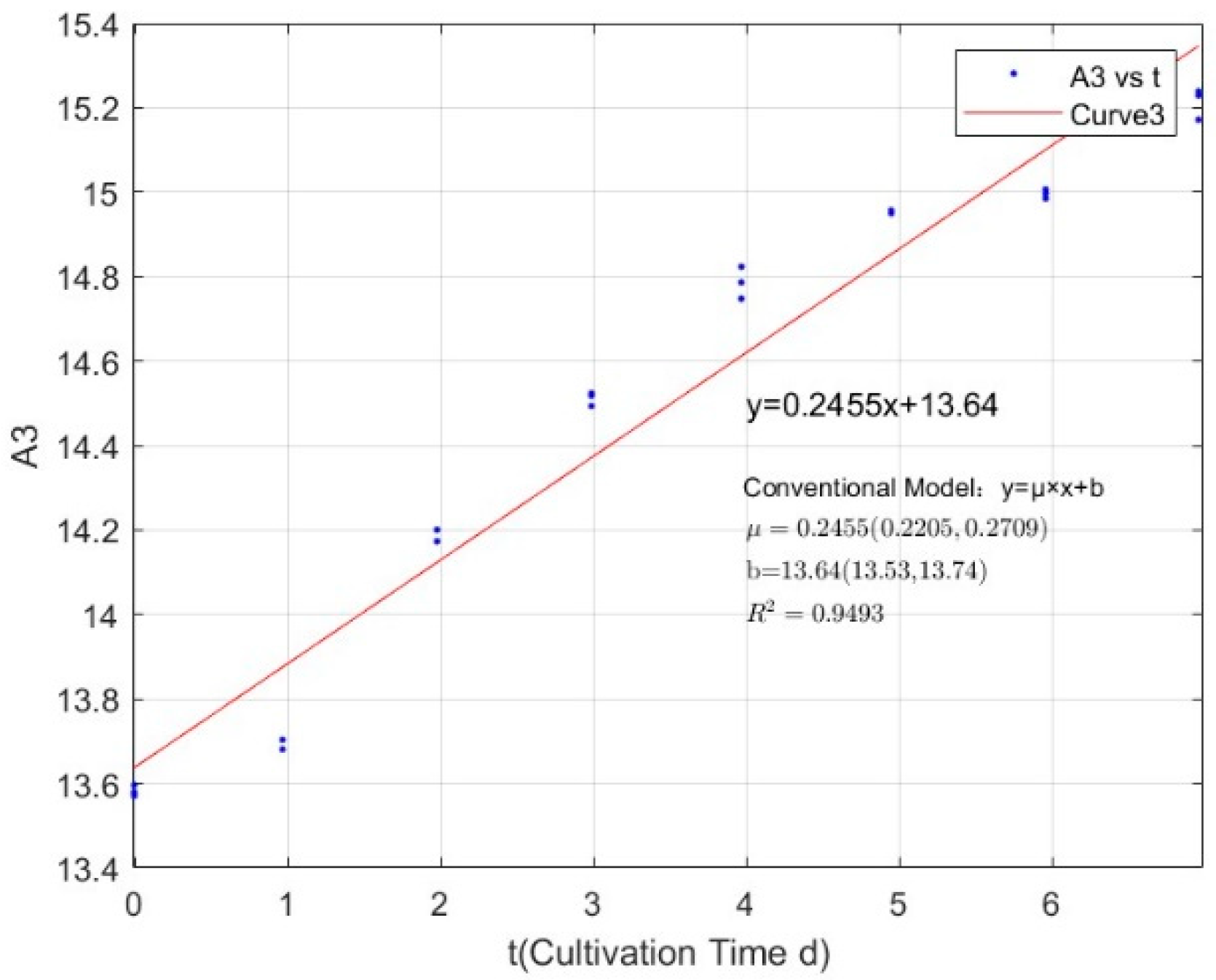
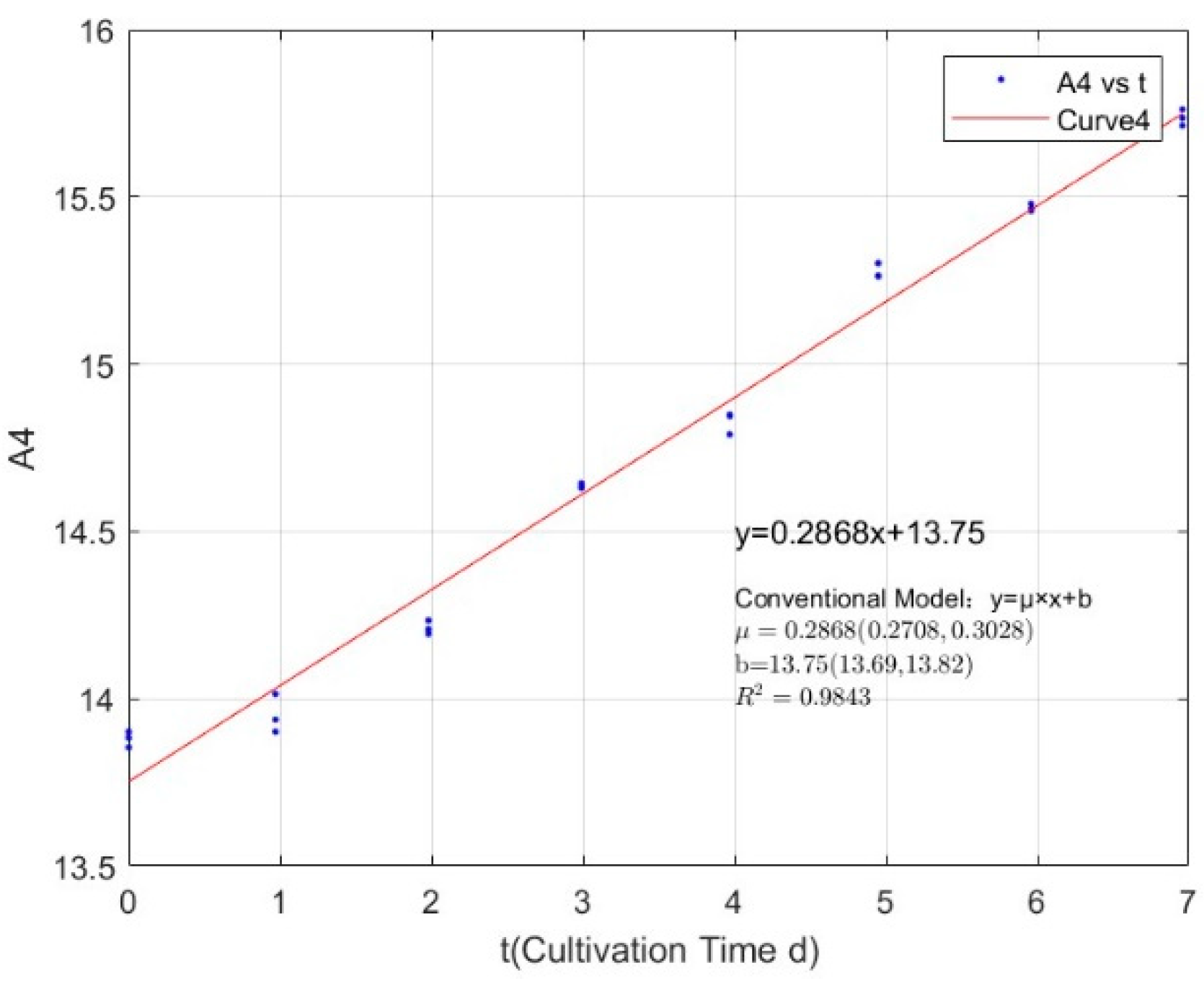
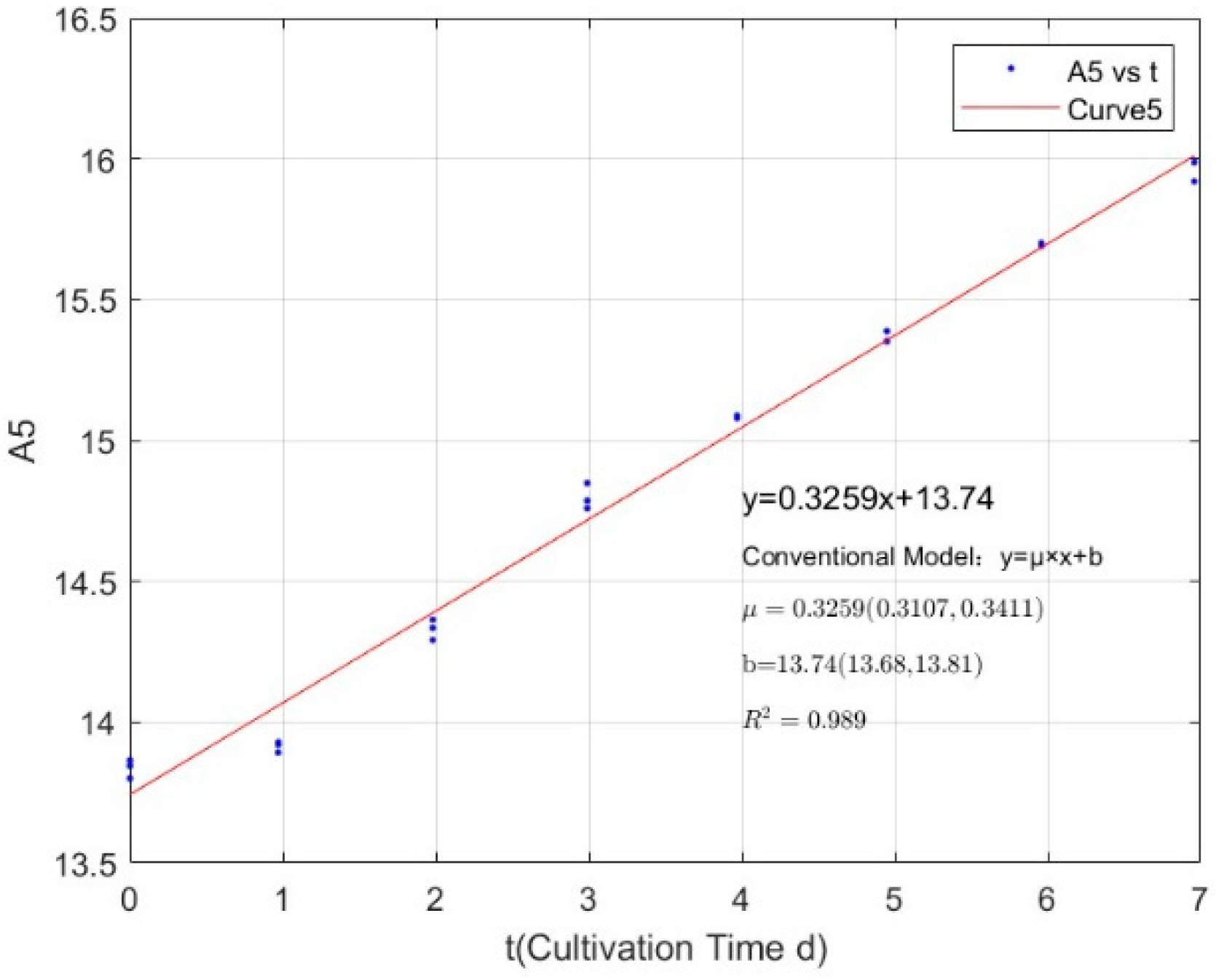
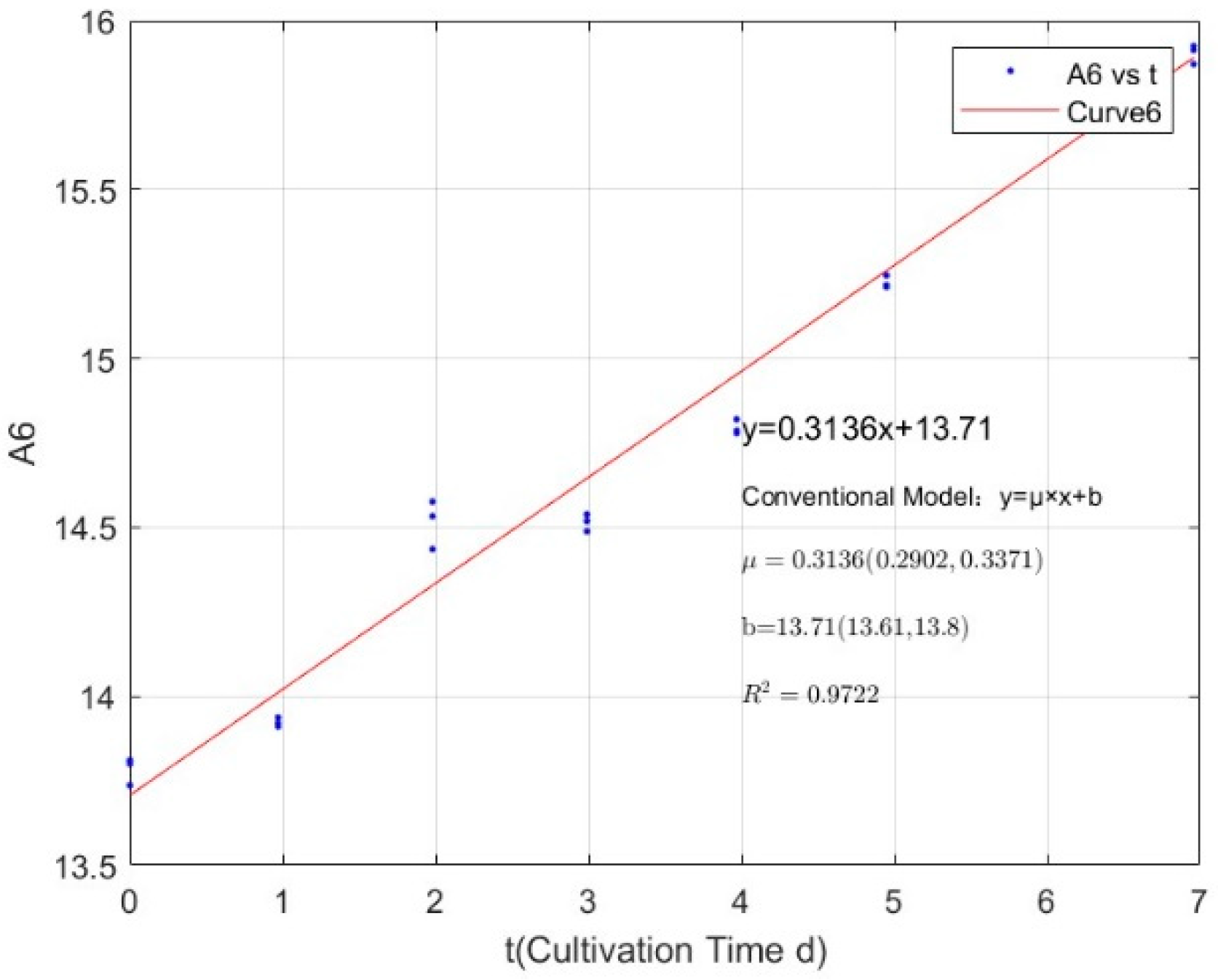
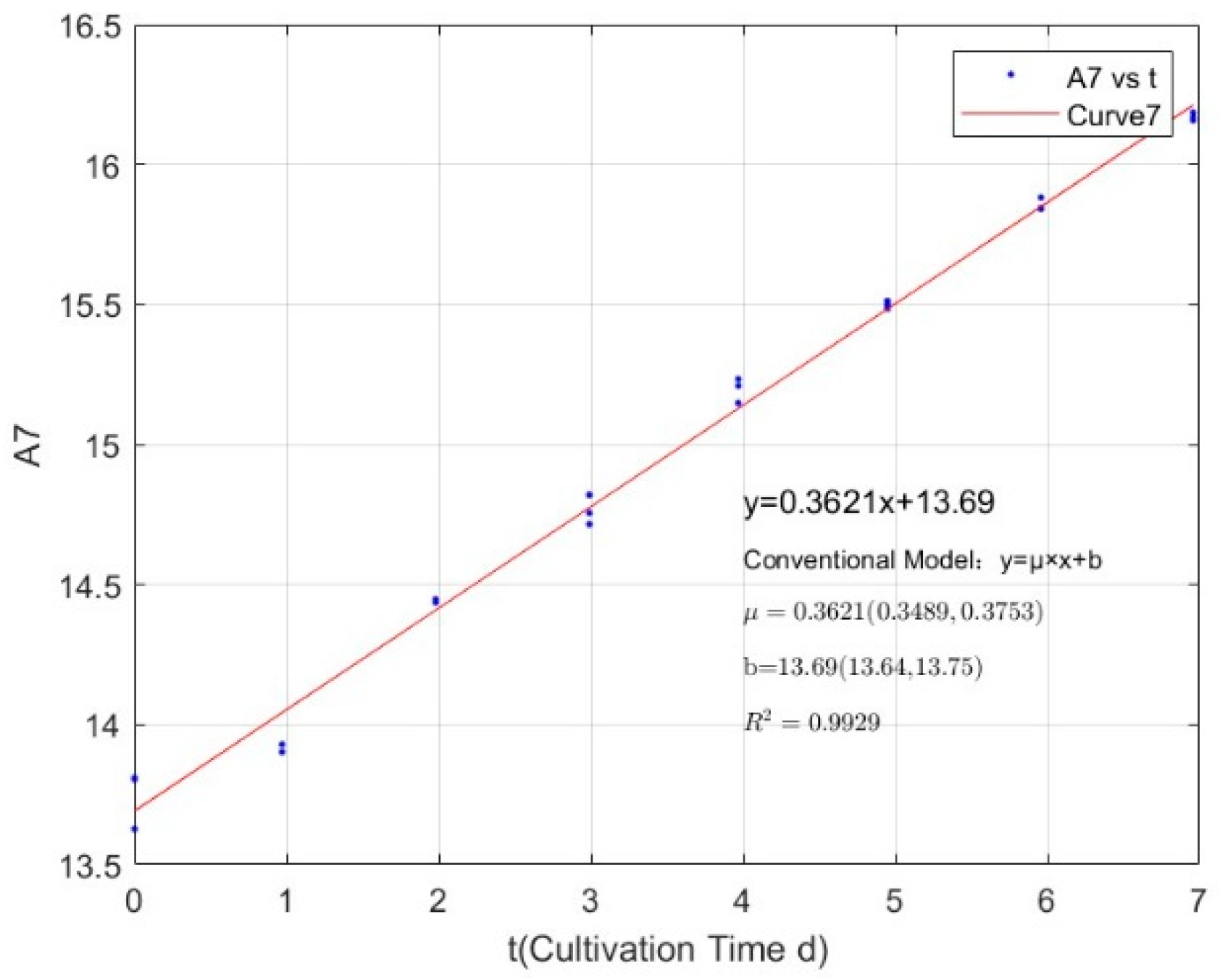
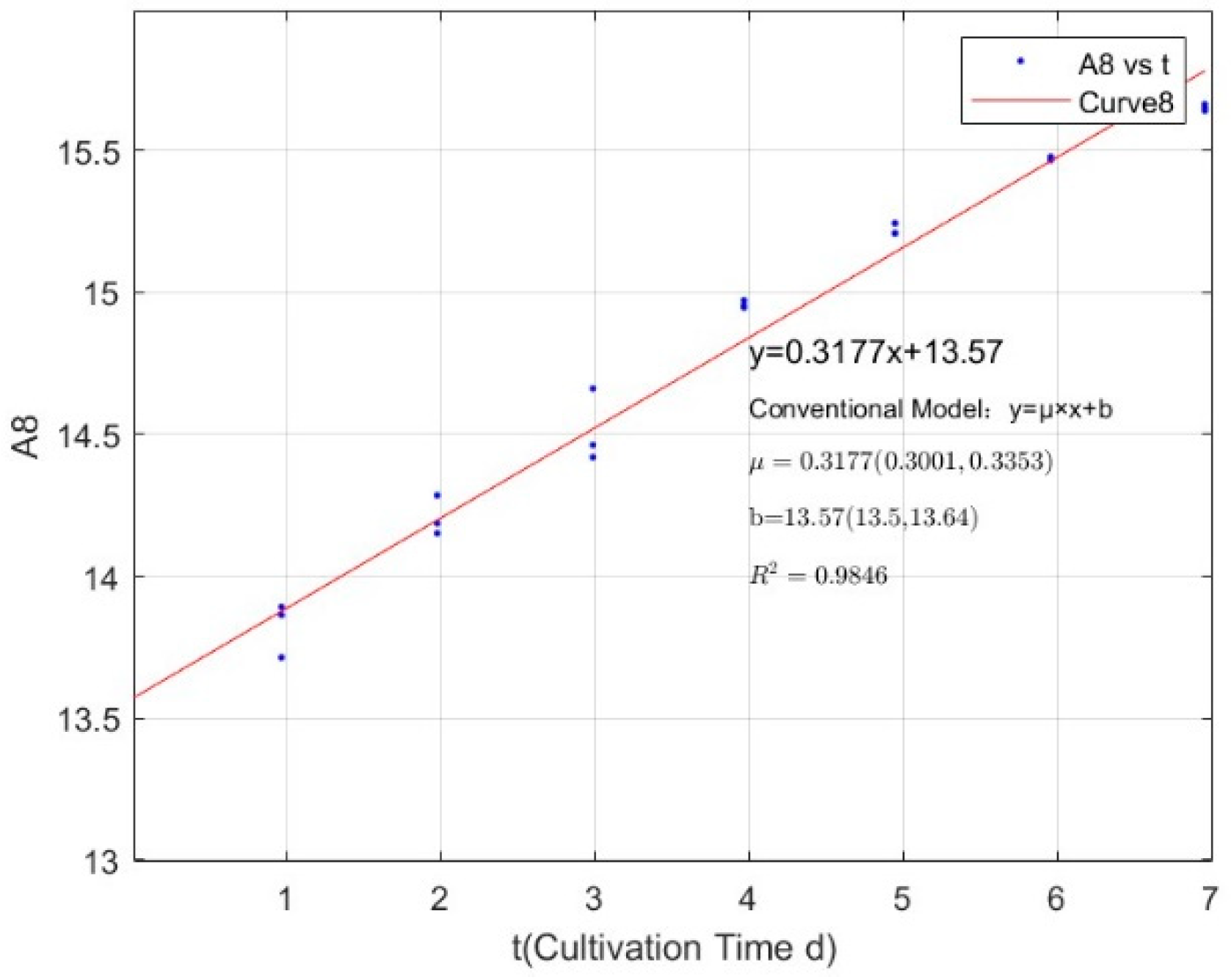
References
- Xia, R.; Zhang, Y.; Wang, G.; Zhang, Y.; Dou, M.; Hou, X.; Qiao, Y.; Wang, Q.; Yang, Z. Multi-factor identification and modelling analyses for managing large river algal blooms. Environ. Pollut. 2019, 254, 113056. [Google Scholar] [CrossRef] [PubMed]
- Paerl, H.W.; Fulton, R.S., 3rd; Moisander, P.H.; Dyble, J. Harmful freshwater algal blooms, with an emphasis on cyanobacteria. Sci. World J. 2001, 1, 76–113. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.R.; Lv, H.; Isabwe, A.; Liu, L.; Yu, X.; Chen, H. Disturbance-induced phytoplankton regime shifts and recovery of cyanobacteria dominance in two subtropical reservoirs. Water Res. 2017, 120, 52–63. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Zhang, M.; Shi, X.; Kong, F.; Ma, R.; Yu, Y. Nutrient reduction magnifies the impact of extreme weather on cyanobacterial bloom formation in large shallow Lake Taihu (China). Water Res. 2016, 103, 302–310. [Google Scholar] [CrossRef] [PubMed]
- Koeller, P.; Fuentes-Yaco, C.; Platt, T.; Sathyendranath, S.; Richards, A.; Ouellet, P.; Orr, D.; Skúladóttir, U.; Wieland, K.; Savard, L.; et al. Basin-scale coherence in phenology of shrimps and phytoplankton in the North Atlantic Ocean. Science 2009, 324, 791–793. [Google Scholar] [CrossRef] [PubMed]
- Metsoviti, M.N.; Katsoulas, N.; Karapanagiotidis, I.T.; Papapolymerou, G. Effect of nitrogen concentration, two-stage and prolonged cultivation on growth rate, lipid and protein content of Chlorella vulgaris. J. Chem. Technol. Biotechnol. 2019, 94, 1466–1473. [Google Scholar] [CrossRef]
- Lehtola, M.J.; Miettinen, I.T.; Keinänen, M.M.; Kekki, T.K.; Laine, O.; Hirvonen, A.; Vartiainen, T.; Martikainen, P.J. Microbiology, chemistry and biofilm development in a pilot drinking water distribution system with copper and plastic pipes. Water Res. 2004, 38, 3769–3779. [Google Scholar] [CrossRef]
- Chokshi, K.; Pancha, I.; Ghosh, A.; Mishra, S. Nitrogen starvation-induced cellular crosstalk of ROS-scavenging antioxidants and phytohormone enhanced the biofuel potential of green microalga Acutodesmus dimorphus. Biotechnol. Biofuels 2017, 10, 60. [Google Scholar] [CrossRef]
- Lee, T.A.; Rollwagen-Bollens, G.; Bollens, S.M. The influence of water quality variables on cyanobacterial blooms and phytoplankton community composition in a shallow temperate lake. Environ. Monit. Assess. 2015, 187, 315. [Google Scholar] [CrossRef]
- O’Neil, J.M.; Davis, T.W.; Burford, M.A.; Gobler, C.J. The rise of harmful cyanobacteria blooms: The potential roles of eutrophication and climate change. Harmful Algae 2012, 14, 313–334. [Google Scholar] [CrossRef]
- Smith, V.H. Eutrophication of freshwater and coastal marine ecosystems a global problem. Environ. Sci. Pollut. Res. 2003, 10, 126–139. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Qin, B.; Teubner, K.; Dokulil, M.T. Long-term dynamics of phytoplankton assemblages: Microcystis-domination in Lake Taihu, a large shallow lake in China. J. Plankton Res. 2003, 25, 445–453. [Google Scholar] [CrossRef]
- Yan, K.; Xu, J.-C.; Gao, W.; Li, M.-J.; Yuan, Z.-W.; Zhang, F.-S.; Elser, J. Human perturbation on phosphorus cycles in one of China’s most eutrophicated lakes. Resour. Environ. Sustain. 2021, 4, 100026. [Google Scholar] [CrossRef]
- Redfield, A.C. The biological control of chemical factors in the environment. Am. Sci. 1958, 46, 230A-221. [Google Scholar]
- Liebig, J.V. Die Organische Chemie in Ihrer Anwendung Auf Agricultur Und Physiologie; Springer: Berlin/Heidelberg, Germany, 1841. [Google Scholar]
- Caperon, J. Population growth in micro-organisms limited by food supply. Ecology 1967, 48, 715–722. [Google Scholar] [CrossRef] [PubMed]
- Morrison, K.; Thérien, N.; Marcos, B. Comparison of six models for nutrient limitations on phytoplankton growth. Can. J. Fish. Aquat. Sci. 1987, 44, 1278–1288. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, X.; Zhang, C.; Sang, G. The effects of turbulence on phytoplankton and implications for energy transfer with an integrated water quality-ecosystem model in a shallow lake. J. Environ. Manag. 2020, 256, 109954. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, Y.; Li, R.; Xin, Q.; Lin, X. Mechanisms and Countermeasures for the Outbreak of Cyanobacterial Blooms in Lake Taihu. Lake Sci. 2019, 31, 18–27. [Google Scholar]
- Zhang, M.; Shi, X. The variation of water quality from 2012 to 2018 in Lake Chaohu and the mitigating strategy on cyanobacterial blooms. J. Lake Sci. 2020, 32, 11–20. [Google Scholar]
- Zhao, H.; Li, J.; Yan, X.; Fang, S.; Du, Y.; Xue, B.; Yu, K.; Wang, C. Monitoring Cyanobacteria Bloom in Dianchi Lake Based on Ground-Based Multispectral Remote-Sensing Imaging: Preliminary Results. Remote Sens. 2021, 13, 3970. [Google Scholar] [CrossRef]
- Zhu, G.; Qin, B.-Q.; Zhang, Y.; Xu, H. Variation and driving factors of nutrients and chlorophyll-a concentrations in northern region of Lake Taihu, China, 2005–2017. J. Lake Sci. 2018, 30, 279–295. [Google Scholar]
- Xu, H.; Paerl, H.W.; Qin, B.; Zhu, G.; Gaoa, G. Nitrogen and phosphorus inputs control phytoplankton growth in eutrophic Lake Taihu, China. Limnol. Oceanogr. 2010, 55, 420–432. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, H.; Yang, G.; Zhu, G.; Qin, B. Developing the critical phosphorus threshold for spring algal growth in Lake Taihu, China. China Environ. Sci. 2013, 33, 1622–1629. [Google Scholar]
- Xu, H.; Paerl, H.W.; Qin, B.; Zhu, G.; Hall, N.S.; Wu, Y. Determining critical nutrient thresholds needed to control harmful cyanobacterial blooms in eutrophic Lake Taihu, China. Environ. Sci. Technol. 2015, 49, 1051–1059. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Paerl, H.W.; Zhu, G.; Qin, B.; Hall, N.S.; Zhu, M. Long-term nutrient trends and harmful cyanobacterial bloom potential in hypertrophic Lake Taihu, China. Hydrobiologia 2017, 787, 229–242. [Google Scholar] [CrossRef]
- Vollenwelder, R.A.; Janus, L.L. OECD Cooperative Programme on Eutrophication; Citeseer; Environment Canada: Burlington, ON, Canada, 1981. [Google Scholar]
- Gibson, G.; Carlson, R.; Simpson, J.; Smeltzer, E.; Kennedy, R. Nutrient Criteria Technical Guidance Manual Lake and Reservoirs; United States Environmental Protection Agency: Washington, DC, USA, 2000.
- Monod, J. The growth of bacterial cultures. Annu. Rev. Microbiol. 1949, 3, 371–394. [Google Scholar] [CrossRef]
- Chen, L.-M.; Chai, L.-H. Mathematical model and mechanisms for biofilm wastewater treatment systems. World J. Microbiol. Biotechnol. 2005, 21, 1455–1460. [Google Scholar] [CrossRef]
- Rittmann, B.E.; McCarty, P.L. Environmental Biotechnology: Principles and Applications; McGraw-Hill Education: New York, NY, USA, 2001. [Google Scholar]
- Ketchum, B.H. The absorption of phosphate and nitrate by illuminated cultures of Nitzschia closterium. Am. J. Bot. 1939, 26, 399–407. [Google Scholar] [CrossRef]
- Ketchum, B.H. The development and restoration of deficiencies in the phosphorus and nitrogen composition of unicellular plants. J. Cell. Comp. Physiol. 1939, 13, 373–381. [Google Scholar] [CrossRef]
- Aitchison, P.; Butt, V. The relation between the synthesis of inorganic polyphosphate and phosphate uptake by Chlorella vulgaris. J. Exp. Bot. 1973, 24, 497–510. [Google Scholar] [CrossRef]
- Albi, T.; Serrano, A. Inorganic polyphosphate in the microbial world. Emerging roles for a multifaceted biopolymer. World J. Microbiol. Biotechnol. 2016, 32, 27. [Google Scholar] [CrossRef] [PubMed]
- Caperon, J. Population growth response of Isochrysis galbana to nitrate variation at limiting concentrations. Ecology 1968, 49, 866–872. [Google Scholar] [CrossRef]
- Fuhs, G.W. Phosphorus content and rate of growth in the diatoms Cyclotella nana and Thalassiosira fluviatilis. J. Phycol. 1969, 5, 312–321. [Google Scholar] [CrossRef] [PubMed]
- Rhee, G.Y. A continuous culture study of phosphate uptake, growth rate and polyphosphate in Scenedesmus sp. 1. J. Phycol. 1973, 9, 495–506. [Google Scholar] [CrossRef]
- Chu, F.-F.; Chu, P.-N.; Cai, P.-J.; Li, W.-W.; Lam, P.K.; Zeng, R.J. Phosphorus plays an important role in enhancing biodiesel productivity of Chlorella vulgaris under nitrogen deficiency. Bioresour. Technol. 2013, 134, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Xiao, P.; Qing, S.; Jin, G.; Yong, W.P. Research Progress on the Effects of Inorganic Phosphorus on Plant Leaf Photosynthesis and Its Mechanisms. J. Plant Nutr. Fertil. 1997, 3, 201–208. [Google Scholar]
- Yin, C.; Liang, Y.; Zhang, Q. Effects of Nitrogen Concentration on Chlorophyll Fluorescence Characteristics and Growth of Chlorella vulgaris 3011 and 8701. Fish. Sci. 2008, 27, 27–31. [Google Scholar]
- Sun, Y. The Effects of Fe3+ on the Growth and Lipid Content of Chlorella. Biotechnol. Bull. 2014, 4, 181. [Google Scholar]

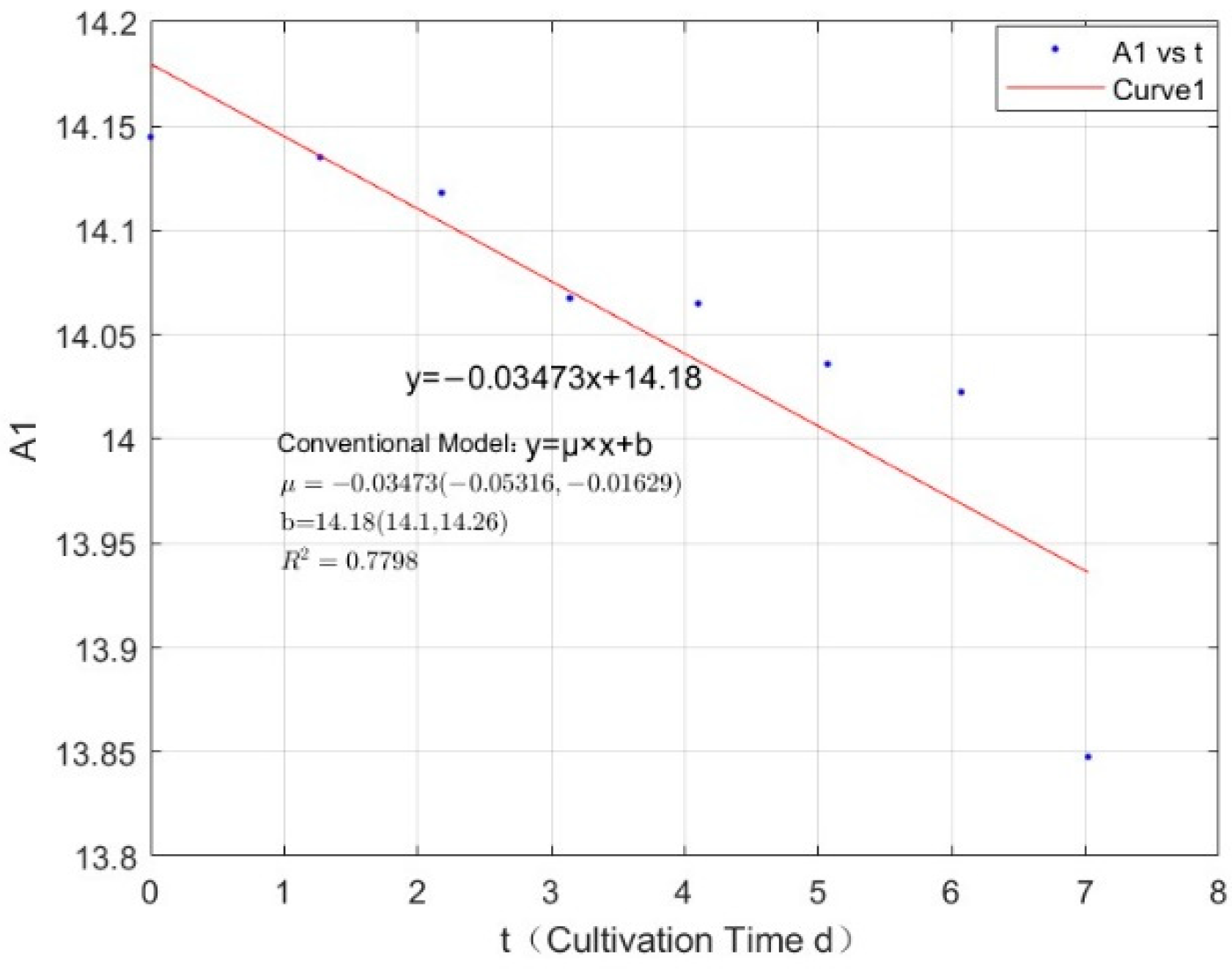
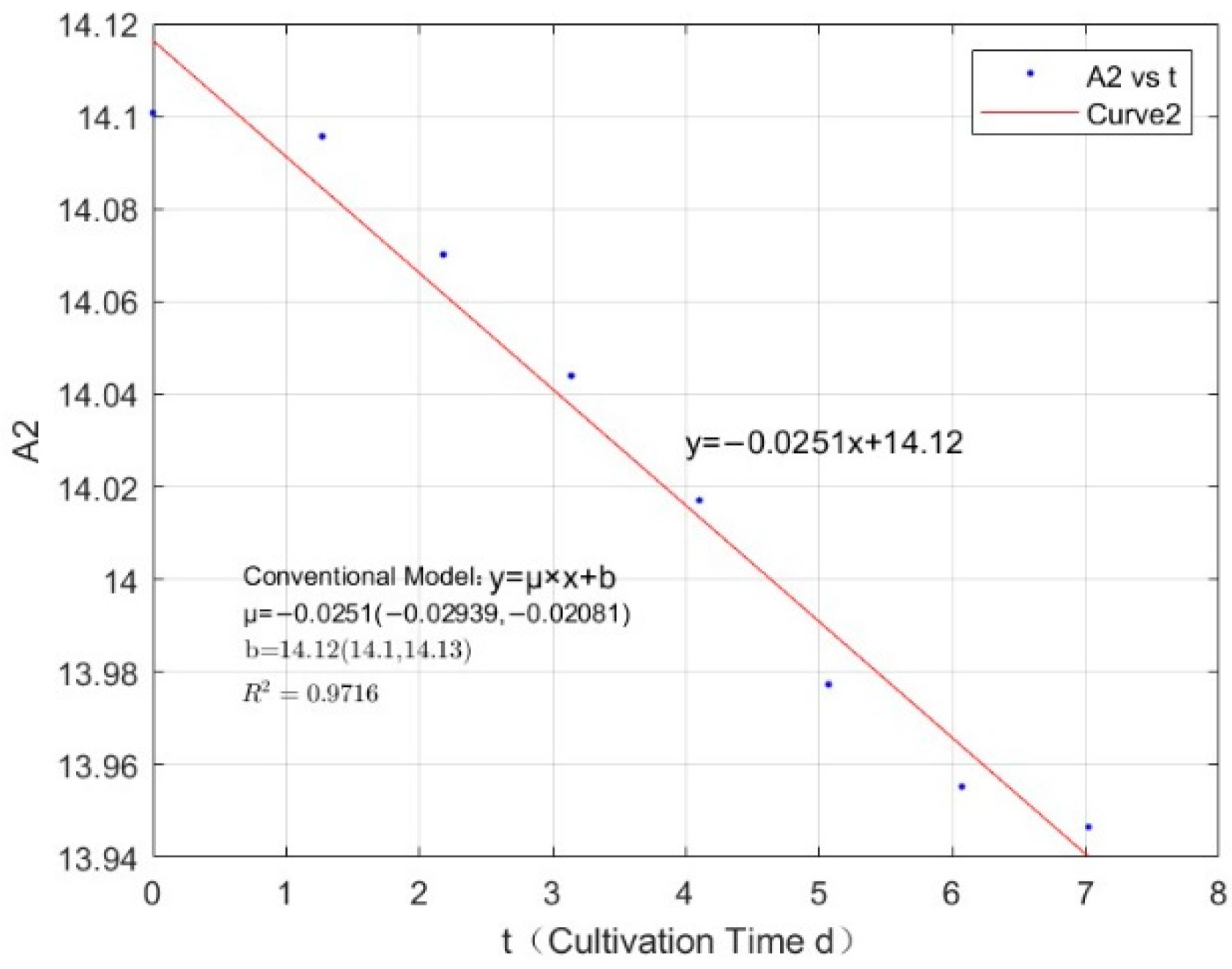



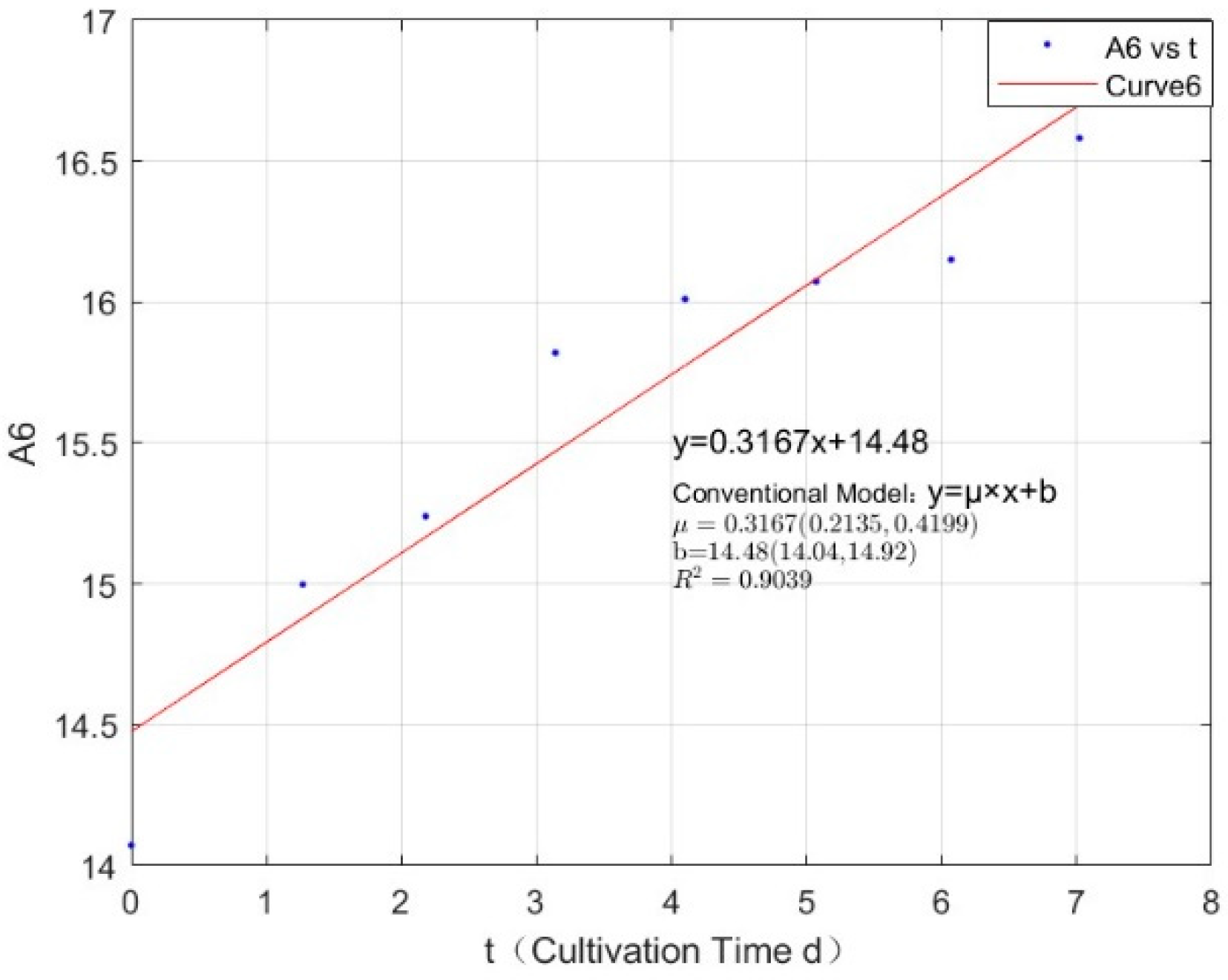


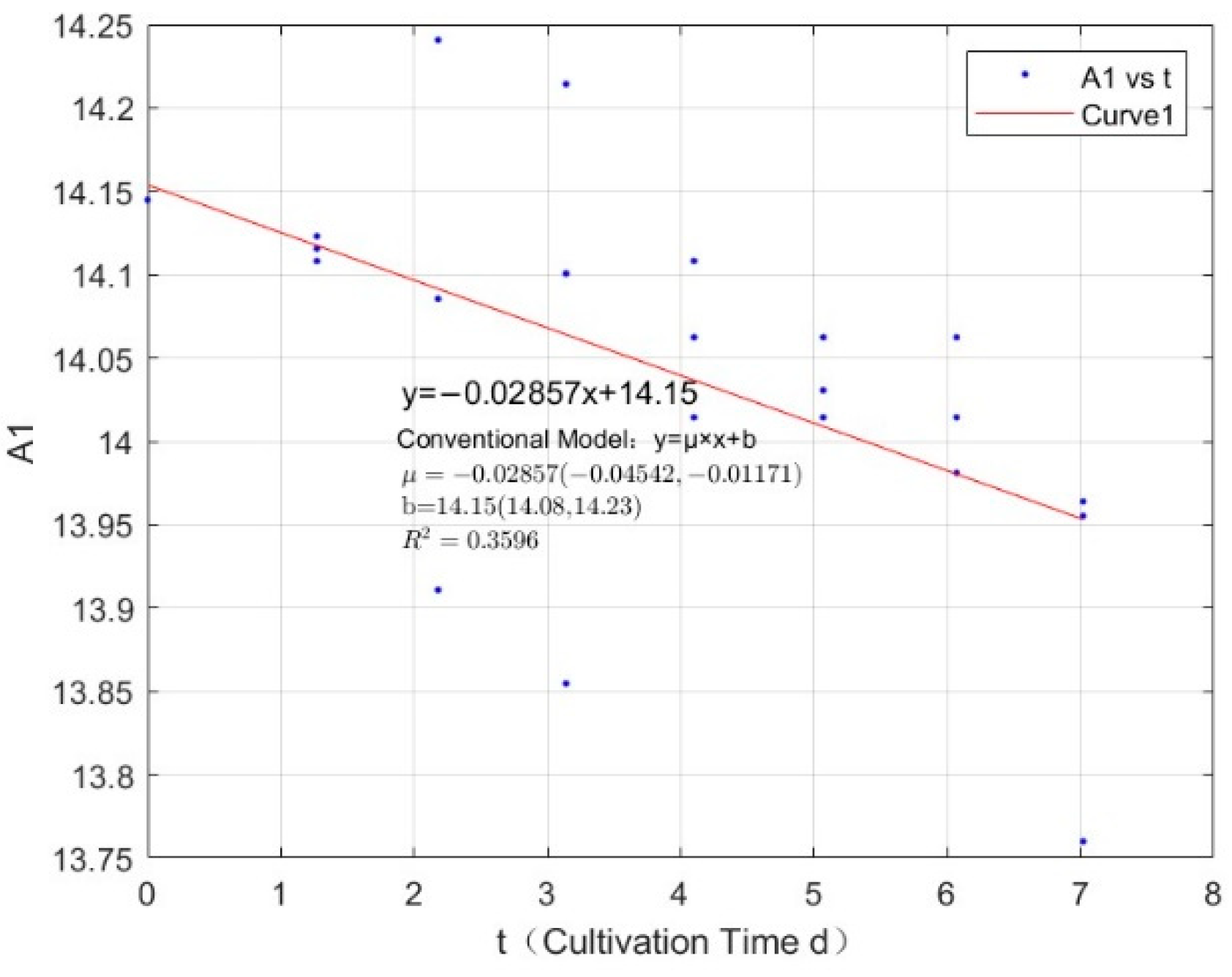






| Phosphorus Concentration (mg/L) | Specific Growth Rate (day−1) | Fitted R-Squared Value (R²) |
|---|---|---|
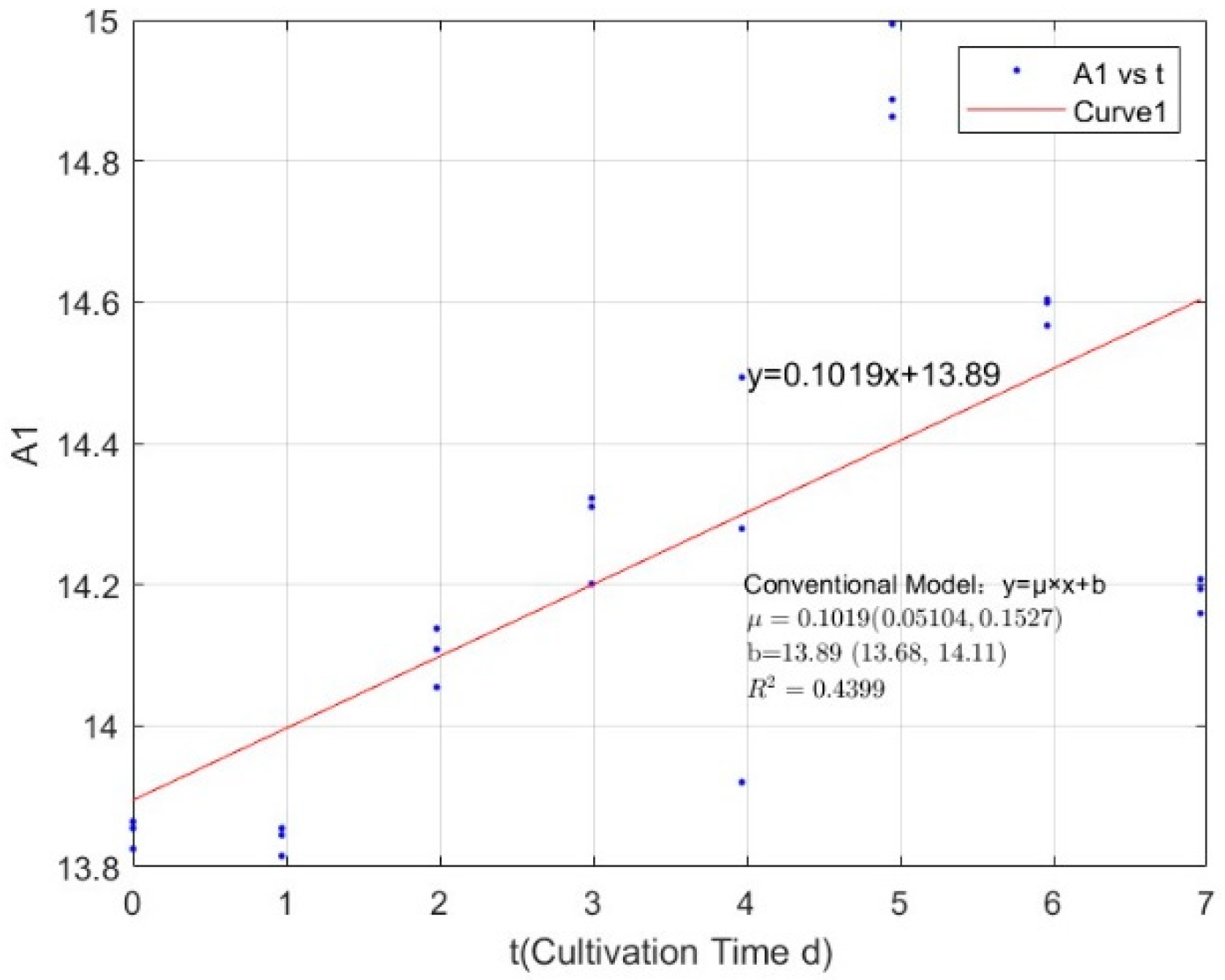
| 0.0356 | −0.0347 | 0.7798 |
| 0.0711 | −0.0251 | 0.9716 |
| 0.1423 | 0.1696 | 0.7126 |
| 0.2134 | 0.1802 | 0.6222 |
| 0.3557 | 0.2363 | 0.7709 |
| 1.0671 | 0.3167 | 0.9039 |
| 2.1342 | 0.3301 | 0.9112 |
| 2.7745 | 0.3271 | 0.8985 |
| Phosphorus Concentration (mg/L) | Specific Growth Rate (day−1) | Fitted R-Squared Value (R²) |
|---|---|---|
| 0.0356 | −0.0286 | 0.3596 |
| 0.0711 | −0.0244 | 0.8491 |
| 0.1423 | 0.178 | 0.6019 |
| 0.2134 | 0.1824 | 0.6214 |
| 0.3557 | 0.2375 | 0.7763 |
| 1.0671 | 0.3154 | 0.8986 |
| 2.1342 | 0.3144 | 0.8899 |
| 2.7745 | 0.3226 | 0.8954 |
| Phosphorus Concentration (mg/L) | Specific Growth Rate (day−1) | Fitted R-Squared Value (R2) |
|---|---|---|
| 0.0356 | −0.0397 | 0.9486 |
| 0.0711 | 0.2308 | 0.9238 |
| 0.1423 | 0.3048 | 0.9411 |
| 0.2134 | 0.3562 | 0.9434 |
| 0.3557 | 0.4339 | 0.9675 |
| 1.0671 | 0.4863 | 0.9846 |
| 2.1342 | 0.5108 | 0.9773 |
| 2.7745 | 0.4842 | 0.9873 |
| Phosphorus Concentration (mg/L) | Specific Growth Rate (day−1) | Fitted R-Squared Value (R2) |
|---|---|---|
| 0.0356 | −0.0369 | 0.7486 |
| 0.0711 | 0.2317 | 0.8806 |
| 0.1423 | 0.3047 | 0.9338 |
| 0.2134 | 0.3564 | 0.9386 |
| 0.3557 | 0.4339 | 0.9613 |
| 1.0671 | 0.4873 | 0.9793 |
| 2.1342 | 0.5065 | 0.9783 |
| 2.7745 | 0.4876 | 0.9815 |
| Phosphorus Concentration (mg/L) | Specific Growth Rate (day−1) | Fitted R-Squared Value (R2) |
|---|---|---|
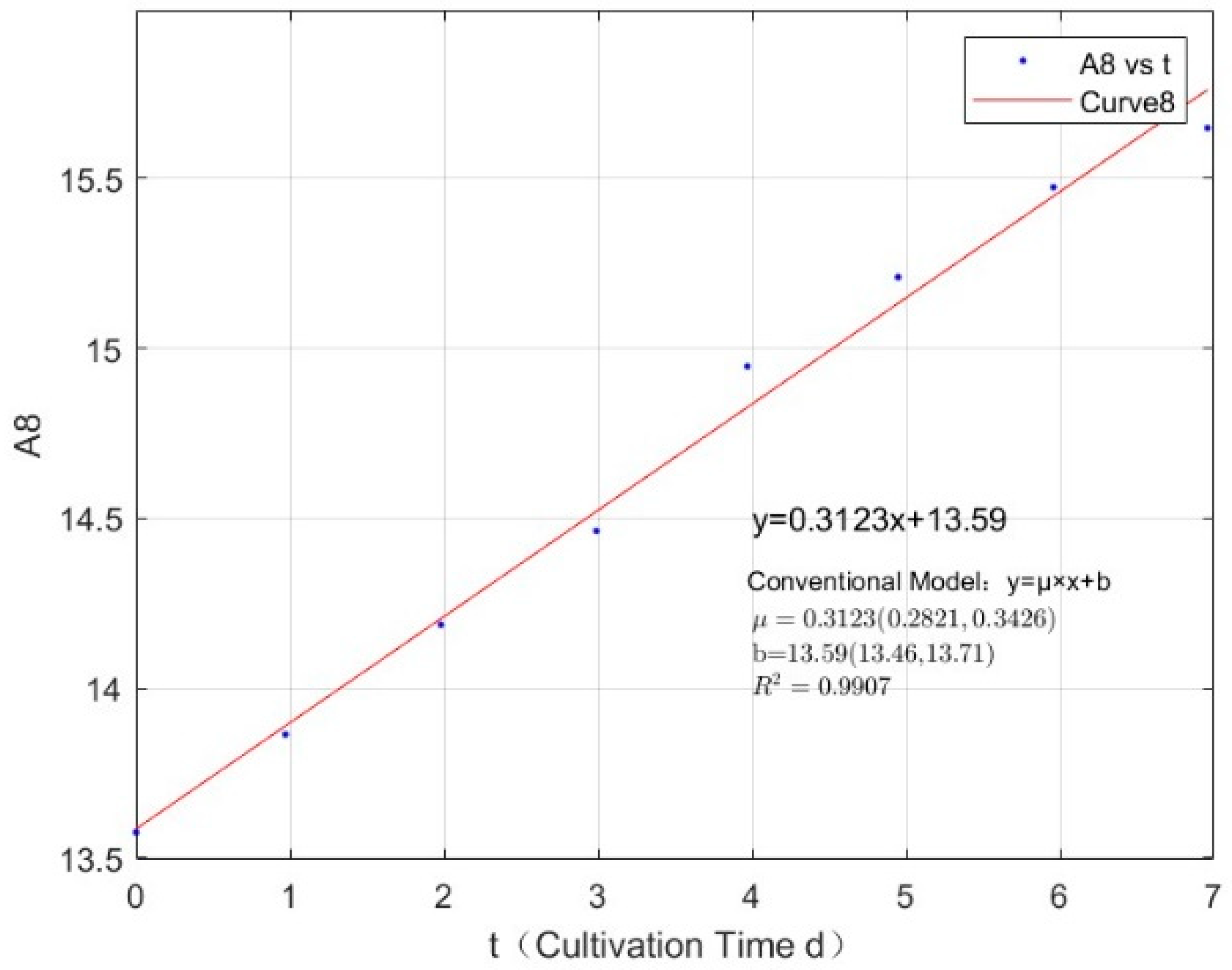
| 0.0356 | 0.0955 | 0.3495 |
| 0.0711 | 0.1891 | 0.8780 |
| 0.1423 | 0.2416 | 0.9411 |
| 0.2134 | 0.2907 | 0.9814 |
| 0.3557 | 0.3231 | 0.9864 |
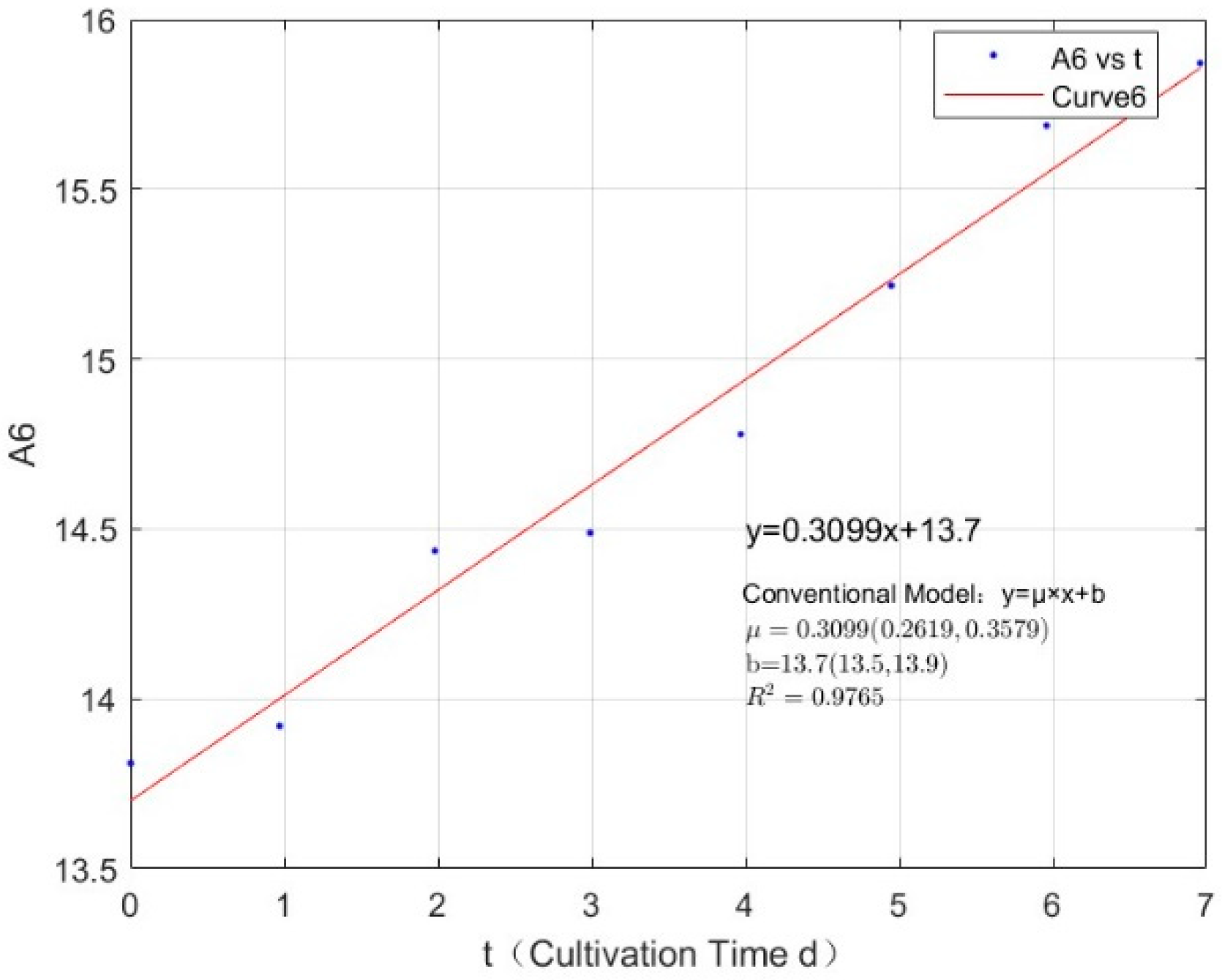
| 1.0671 | 0.3099 | 0.9765 |
| 2.1342 | 0.3535 | 0.9946 |
| 2.7745 | 0.3123 | 0.9907 |
| Phosphorus Concentration (mg/L) | Specific Growth Rate (day−1) | Fit R-Squared Value (R2) |
|---|---|---|
| 0.0356 | 0.1019 | 0.4399 |
| 0.0711 | 0.1926 | 0.8860 |
| 0.1423 | 0.2455 | 0.9493 |
| 0.2134 | 0.2868 | 0.9843 |
| 0.3557 | 0.3259 | 0.9890 |
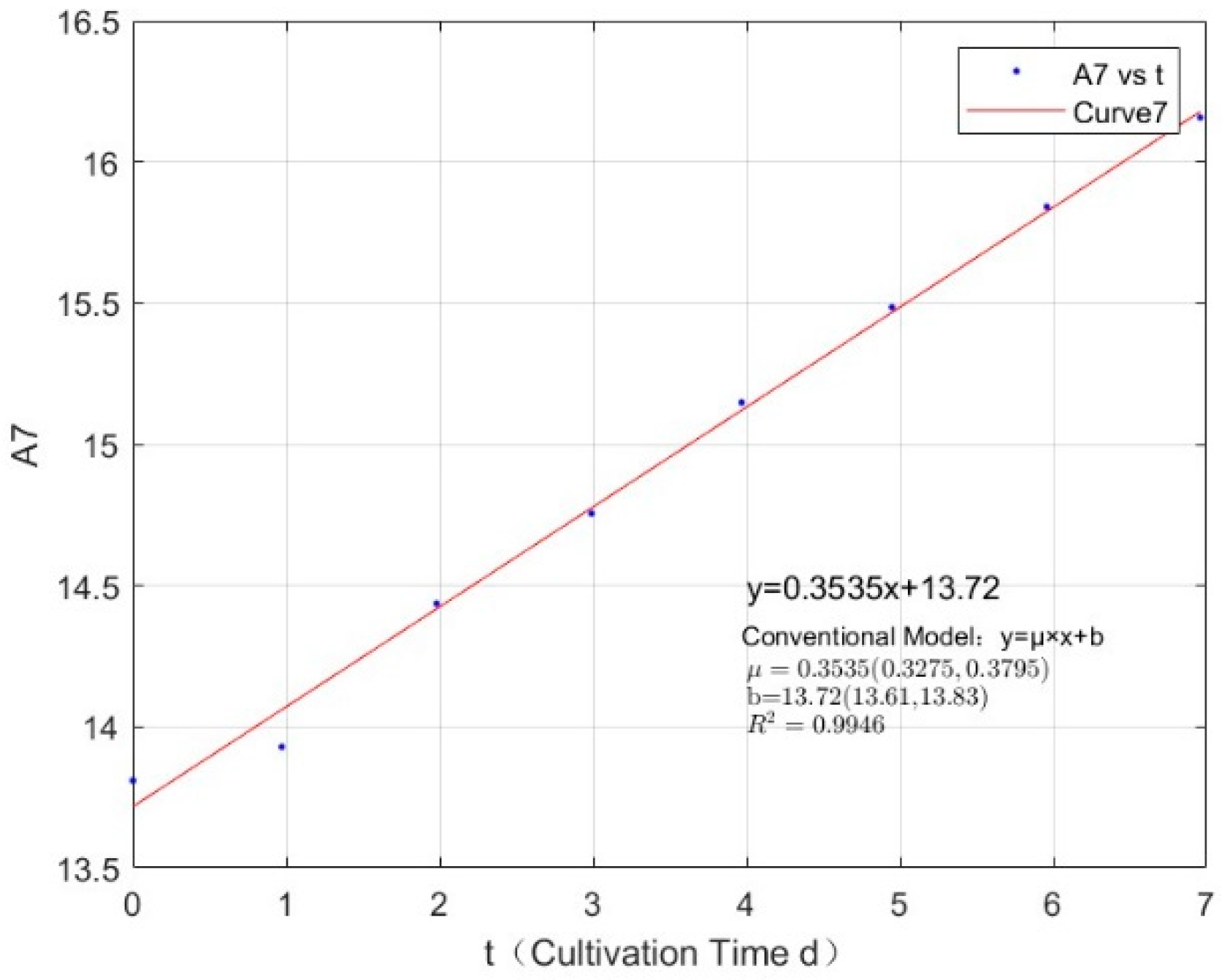
| 1.0671 | 0.3136 | 0.9722 |
| 2.1342 | 0.3621 | 0.9929 |
| 2.7745 | 0.3177 | 0.9846 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Fu, W.; Xiong, N.; He, J.; Zheng, Z. Phosphorus Threshold for the Growth of Microcystis wesenbergii, Microcystis aeruginosa, and Chlorella vulgaris Based on the Monod Formula. Water 2023, 15, 4249. https://doi.org/10.3390/w15244249
Guo Y, Fu W, Xiong N, He J, Zheng Z. Phosphorus Threshold for the Growth of Microcystis wesenbergii, Microcystis aeruginosa, and Chlorella vulgaris Based on the Monod Formula. Water. 2023; 15(24):4249. https://doi.org/10.3390/w15244249
Chicago/Turabian StyleGuo, Yansen, Wenrui Fu, Nan Xiong, Jian He, and Zheng Zheng. 2023. "Phosphorus Threshold for the Growth of Microcystis wesenbergii, Microcystis aeruginosa, and Chlorella vulgaris Based on the Monod Formula" Water 15, no. 24: 4249. https://doi.org/10.3390/w15244249
APA StyleGuo, Y., Fu, W., Xiong, N., He, J., & Zheng, Z. (2023). Phosphorus Threshold for the Growth of Microcystis wesenbergii, Microcystis aeruginosa, and Chlorella vulgaris Based on the Monod Formula. Water, 15(24), 4249. https://doi.org/10.3390/w15244249








