Analytical Determination of Irrotational Flow Profiles in Open-Channel Transitions
Abstract
:1. Introduction
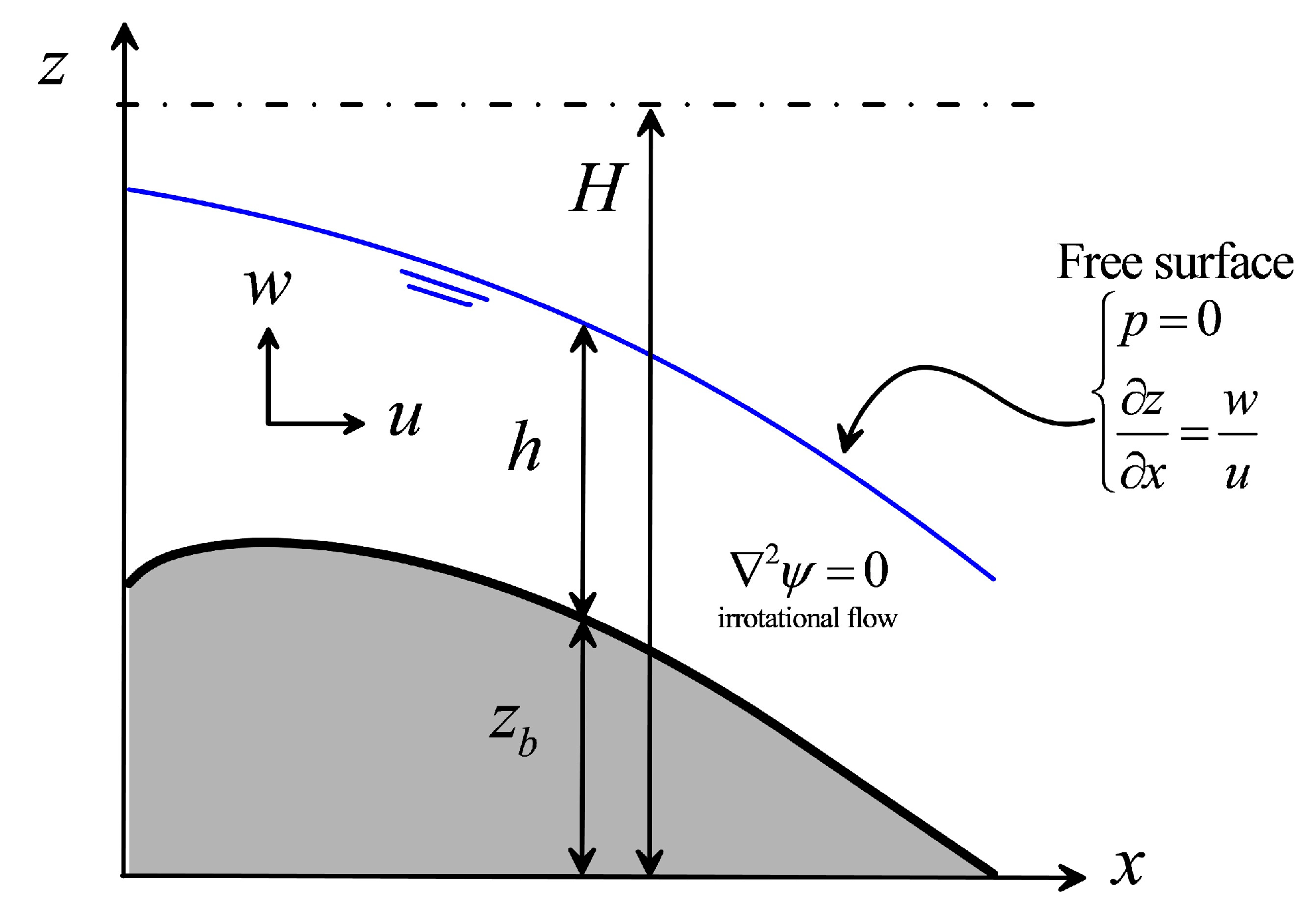
2. Irrotational Flow Modeling
2.1. The x-ψ Method
2.2. Free Surface Boundary Condition
2.3. Critical Point
3. Solution Method
- Select a discharge q;
- Determine the critical point and total energy head H. Start assuming α(i) = 0 (initial hydrostatic flow profile);
- Compute the sub- and supercritical portions of the flow profile using Equations (28) and (29);
- For the new free surface position, solve the Laplace equation by SOR and compute a new set of coefficients α(i) at each node on the free surface;
- Compute the free surface pressure residuals. If their average is not below a tolerance, go back to 2 and start a new free surface iteration.
4. Test Cases
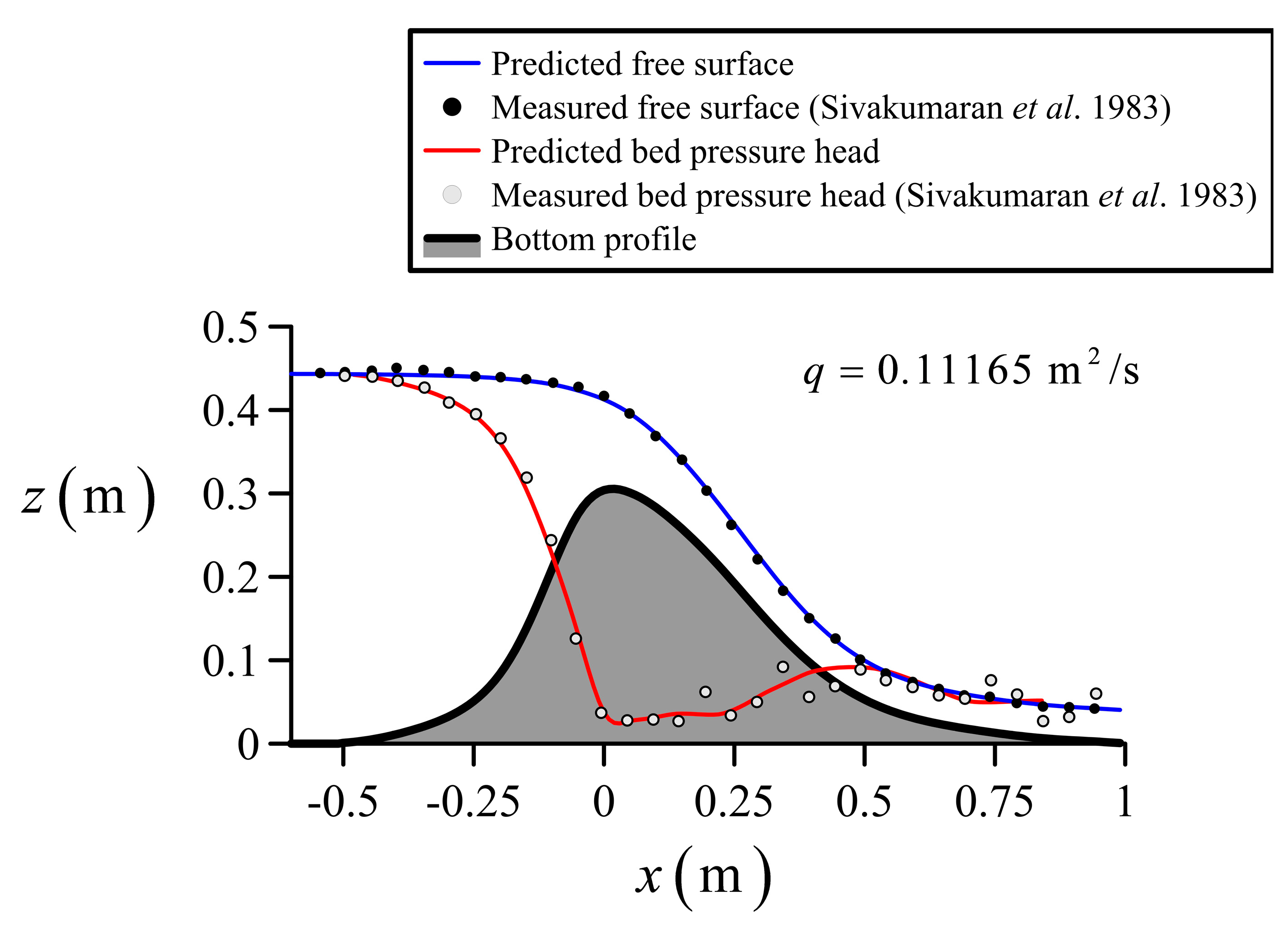
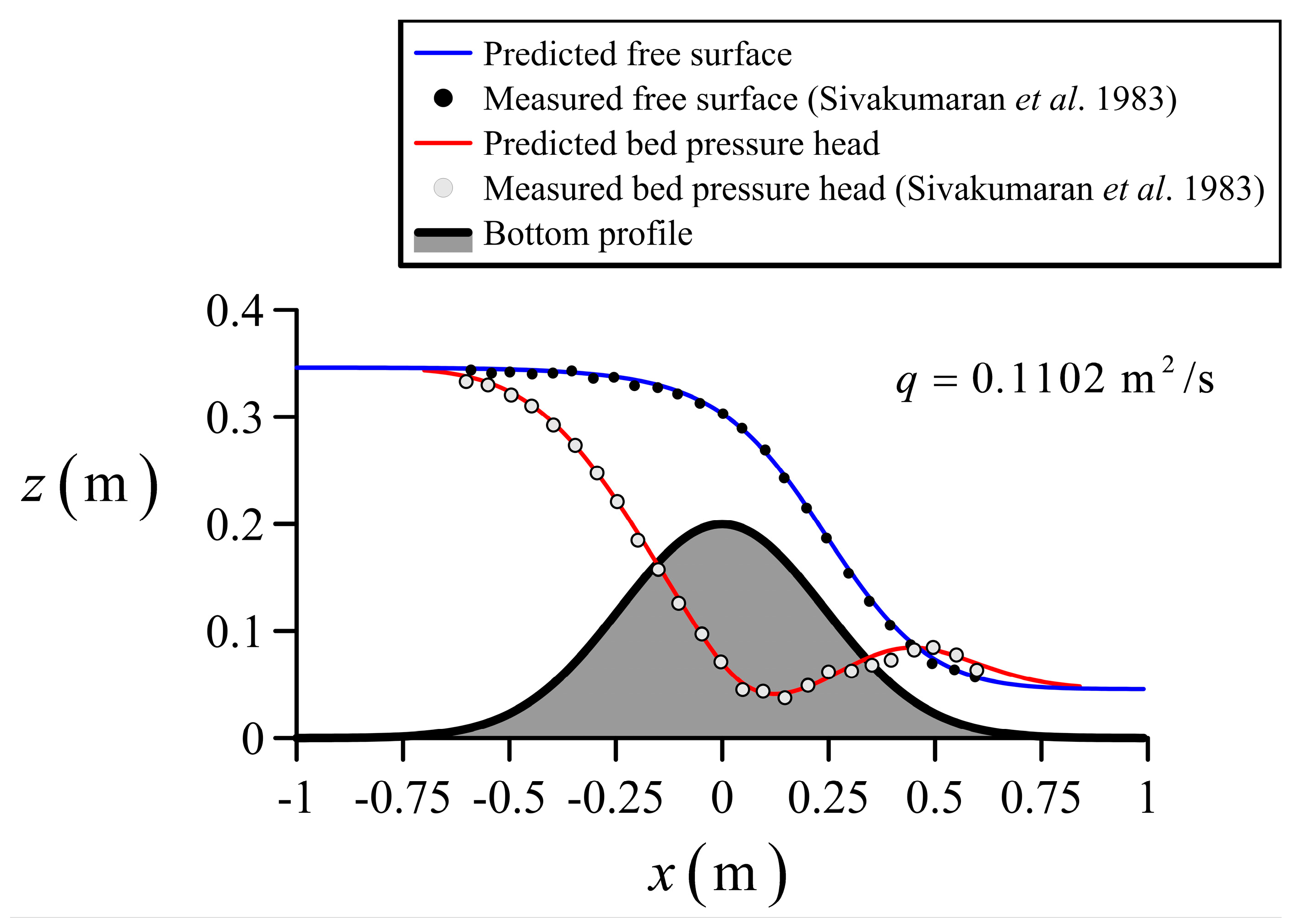
4.1. Flow over Low Humps
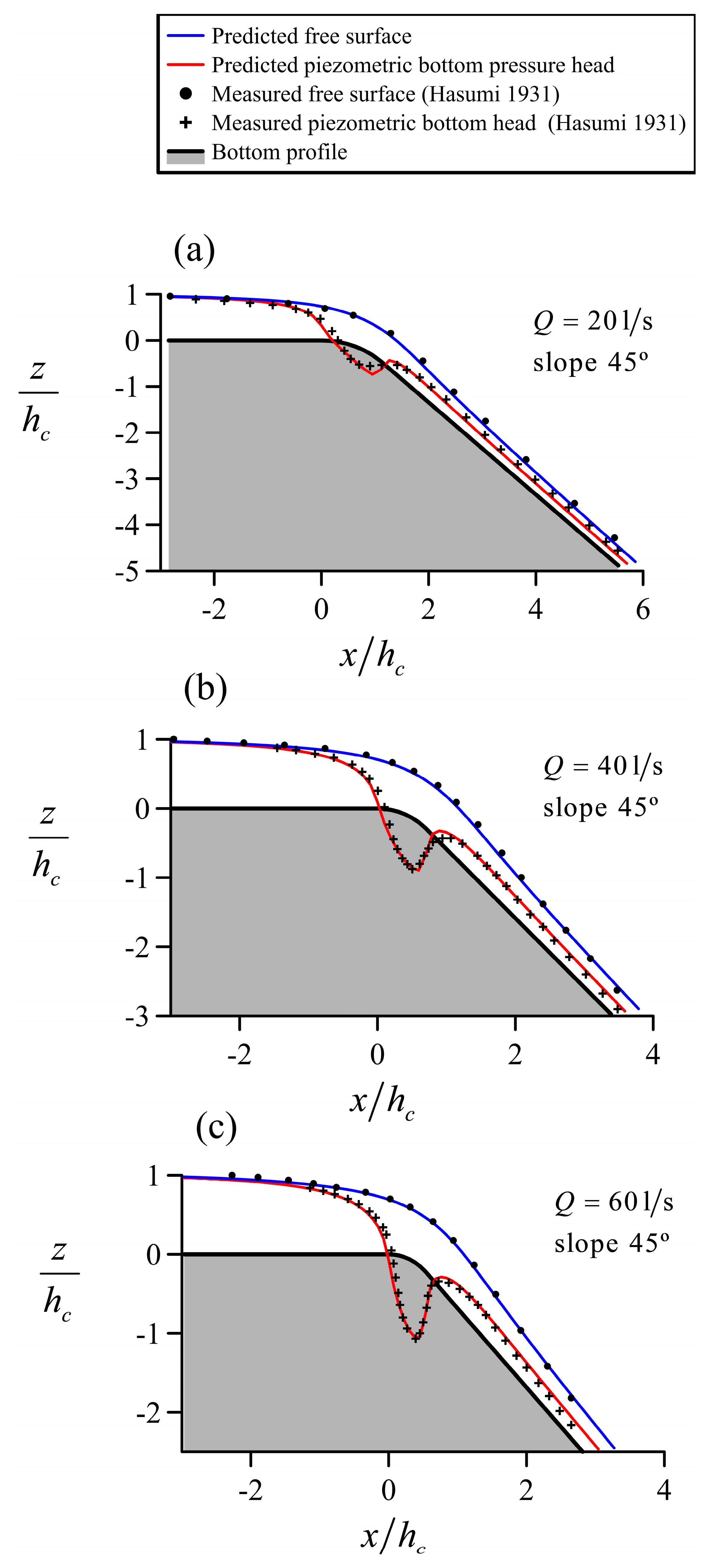
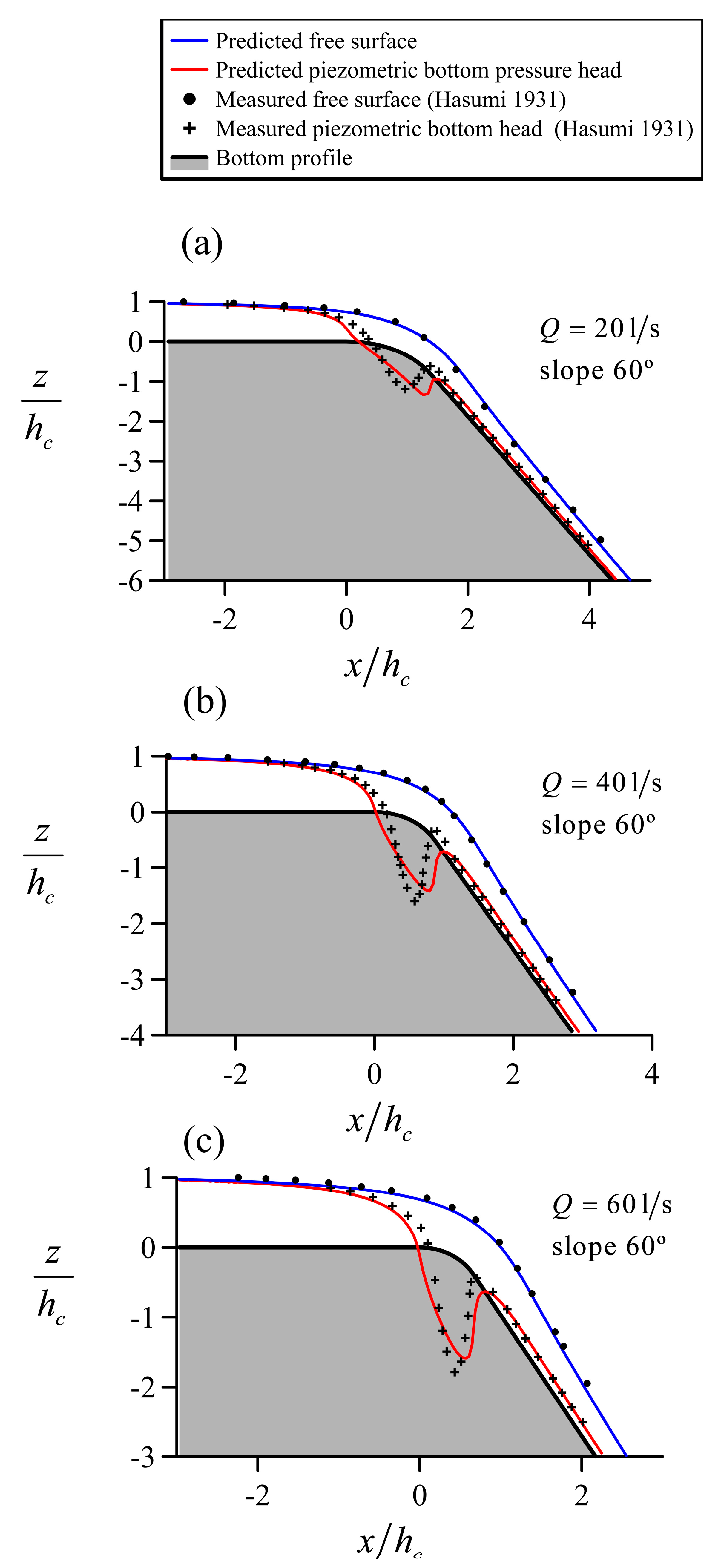
4.2. Flow Transition from Mild to Steep Slopes
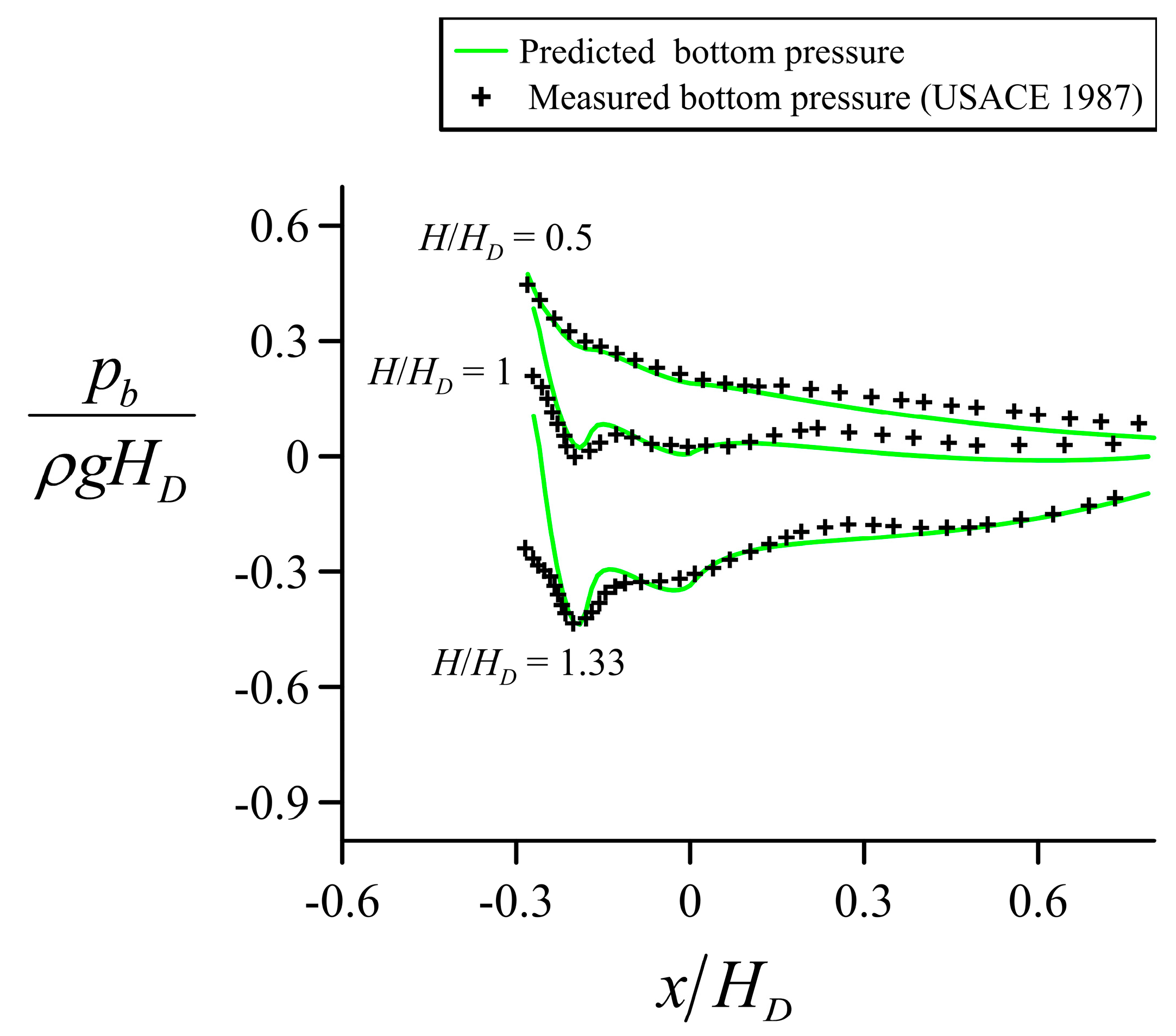
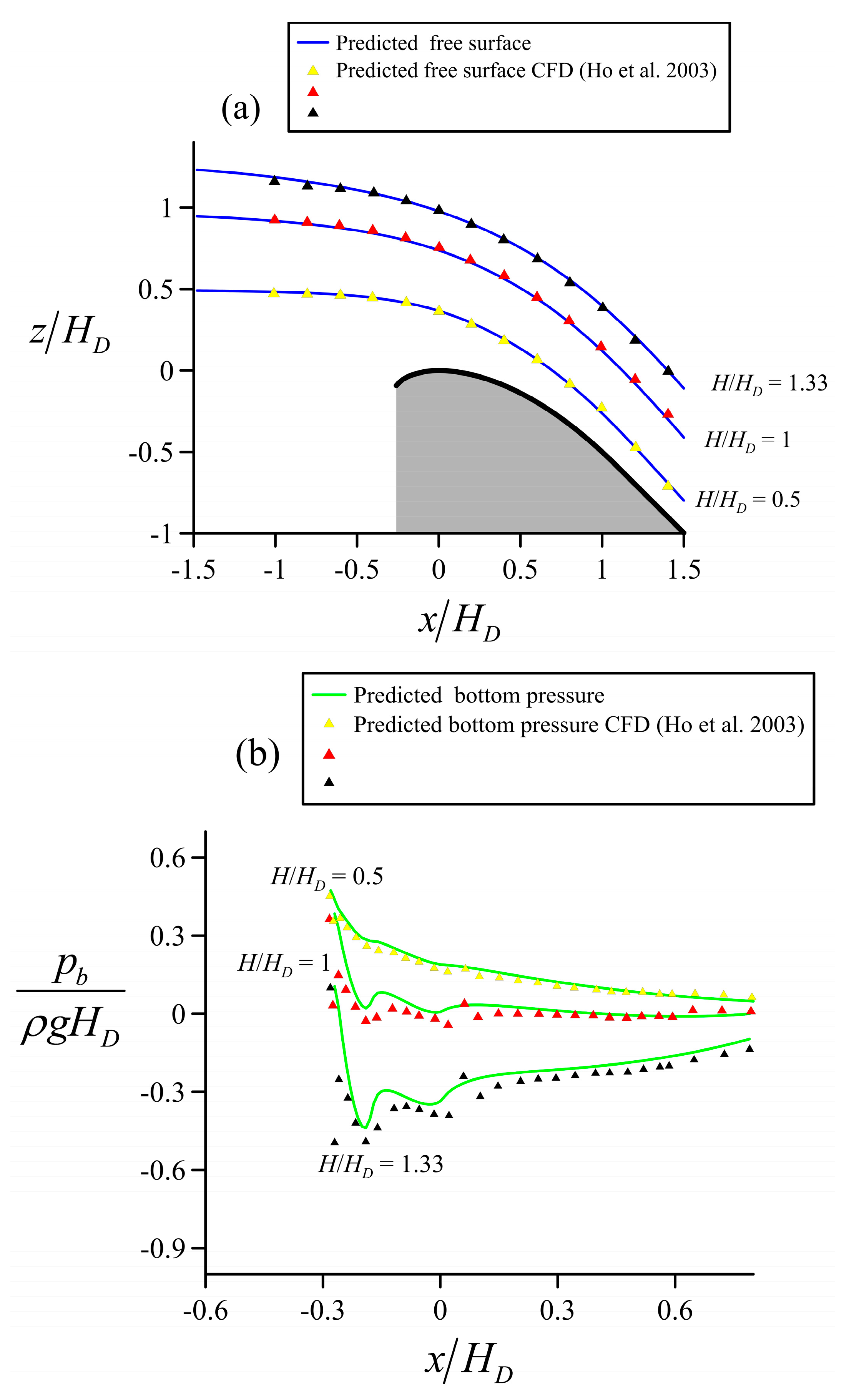
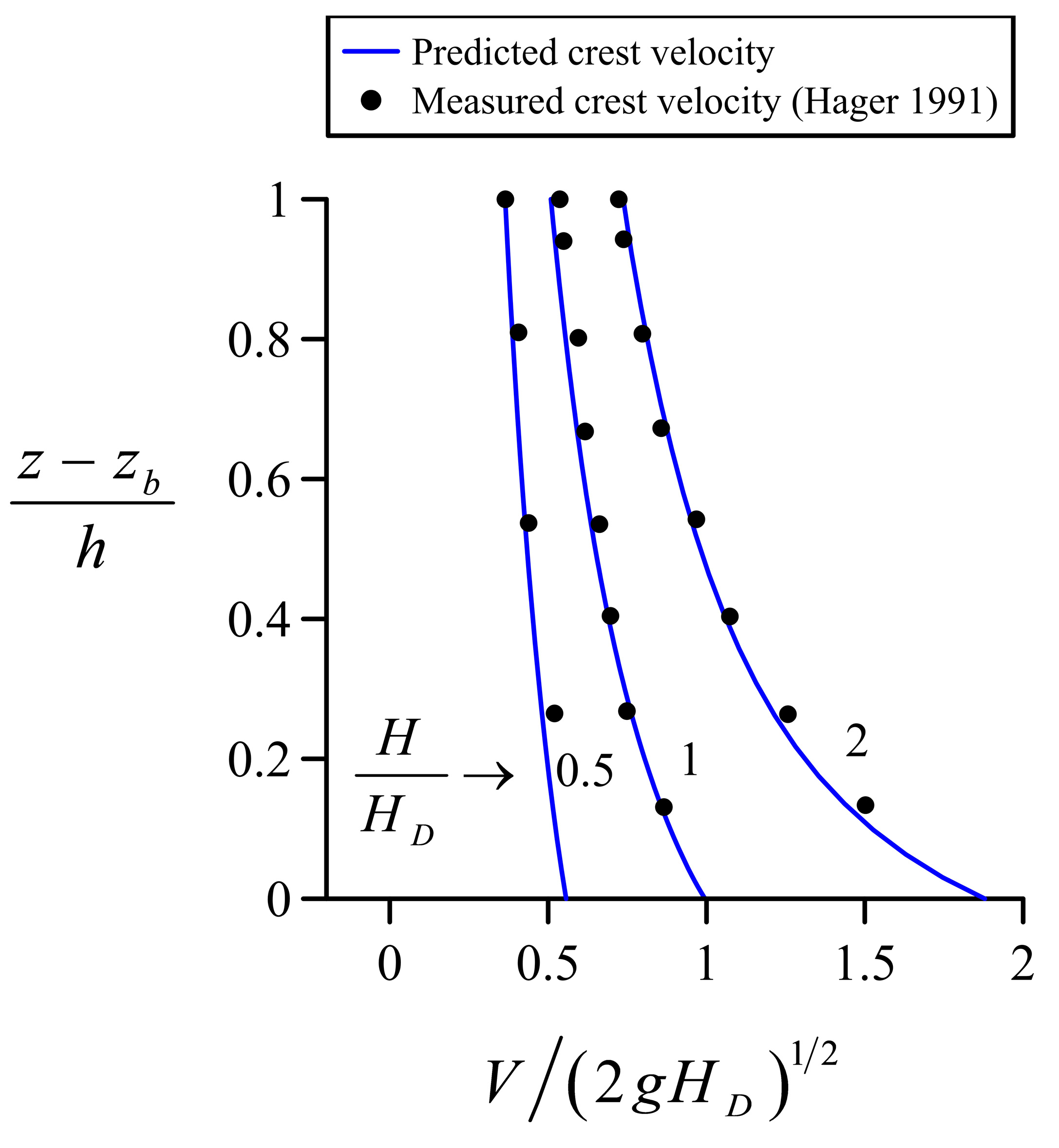
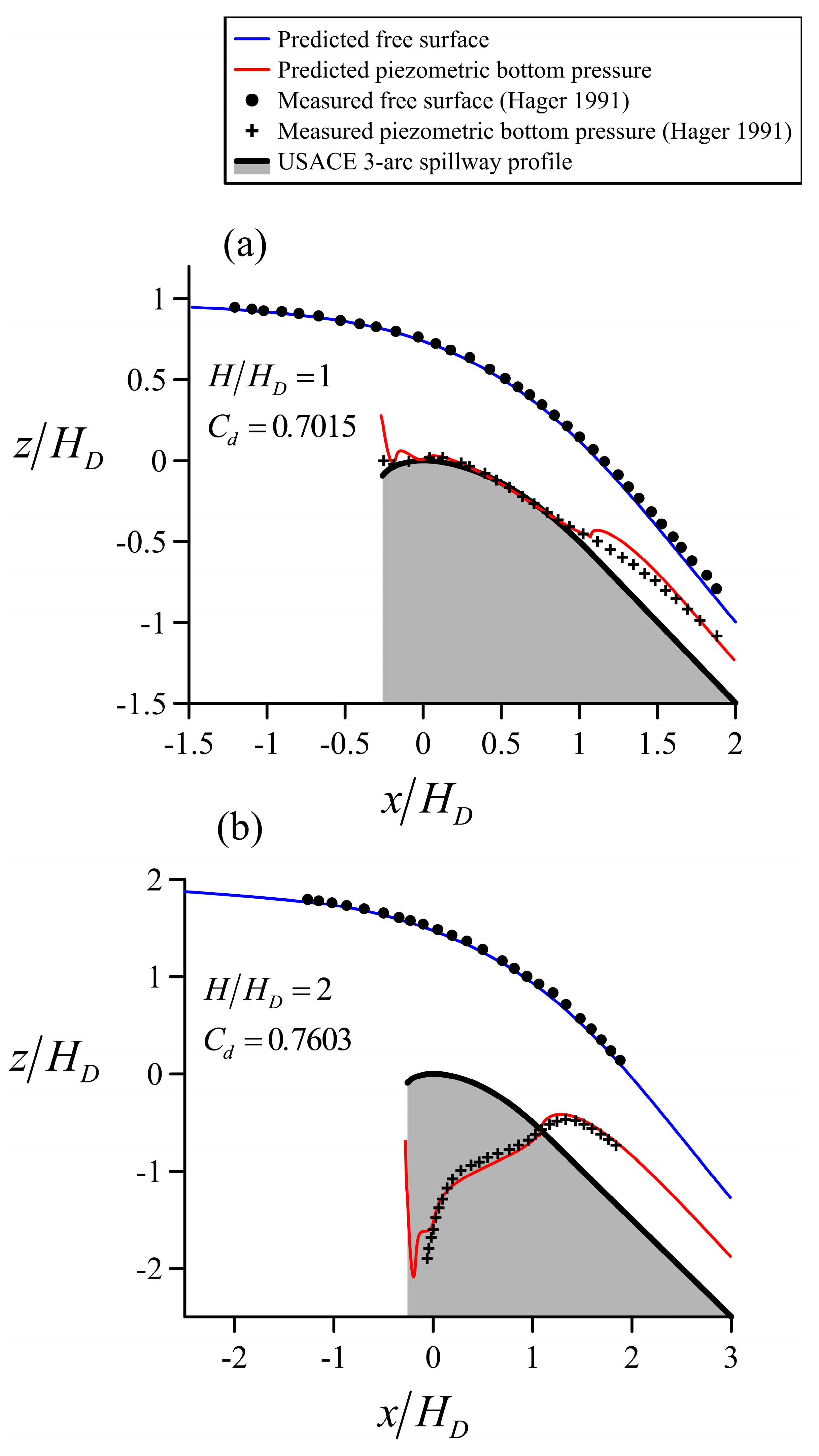
4.3. Flow over the Spillway of a High Dam
5. Discussion of Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| u | horizontal velocity |
| w | vertical velocity |
| ψ | stream function |
| z | elevation |
| x | horizontal coordinate |
| V | modulus of velocity vector |
| θ | streamline inclination |
| p | pressure head |
| ρ | water density |
| g | gravity acceleration |
| H | total energy head |
| zs | free surface elevation |
| zb | channel bed elevation |
| E | specific energy |
| Vs | free surface velocity |
| q | discharge per unit channel width |
| α | ratio of surface velocity to depth-averaged velocity |
| hc | critical depth of 2D irrotational flow |
| X, a, b | auxiliar variables |
| Γ | auxiliar function in specific energy |
| i | mesh index |
References
- Castro-Orgaz, O. Steady open channel flows with curved streamlines: The Fawer approach revised. Environ. Fluid Mech. 2010, 10, 297–310. [Google Scholar] [CrossRef]
- Ramamurthy, A.S.; Vo, N.-D.; Balachandar, R. A Note on Irrotational Curvilinear Flow Past a Weir. J. Fluids Eng. 1994, 116, 378–381. [Google Scholar] [CrossRef]
- Rouse, H. The Distribution of Hydraulic Energy in Weir Flow in Relation to Spillway Design. Master’s Thesis, MIT, Boston, MA, USA, 1932. [Google Scholar]
- Rouse, H. Verteilung der Hydraulischen Energie Bei Einem Lotrechten Absturz (Distribution of Hydraulic Energy at a Vertical Drop). Ph.D. Thesis, TU Karlsruhe, Karlsruhe, Germany, 1938. (In Germany). [Google Scholar]
- Rouse, H. Fluid Mechanics for Hydraulic Engineers; McGraw-Hill: New York, NY, USA, 1938. [Google Scholar]
- Hager, W.H. Critical flow condition in open channel hydraulics. Acta Mech. 1985, 54, 157–179. [Google Scholar] [CrossRef]
- Bos, M.G. Discharge Measurement Structures; Intl. Inst. for Land Reclamation (ILRI): Wageningen, The Netherlands, 1976. [Google Scholar]
- Castro-Orgaz, O. Curvilinear flow over round-crested weirs. J. Hydraul. Res. 2008, 46, 543–547. [Google Scholar] [CrossRef]
- Hager, W.H.; Schleiss, A. Constructions Hydrauliques: Ecoulements Stationnaires (Hydraulic Structures: Steady Flows). Traité de Génie Civil 15; Presses Polytechniques Universitaires Romandes: Lausanne, Switzerland, 2009. (In French) [Google Scholar]
- Rouse, H.; Reid, L. Model research on spillway crests. Civ. Engng. 1935, 5, 10–14. [Google Scholar]
- Bettess, P.; Bettess, J.A. Analysis of free surface flows using isoparametric finite elements. Int. J. Numer. Methods Eng. 1983, 19, 1675–1689. [Google Scholar] [CrossRef]
- Thom, A.; Apelt, C. Field Computations in Engineering and Physics; Van Nostrand: London, UK, 1961. [Google Scholar]
- Katopodes, N.D. Free Surface Flow: Computational Methods; Butterworth-Heinemann: Oxford, UK, 2019. [Google Scholar]
- Ganguli, M.K.; Roy, S.K. On the standardisation of the relaxation treatment of systematic pressure computations for overflow spillway discharge. Irrig. Power 1952, 9, 187–204. [Google Scholar]
- Hay, N.; Markland, E. The determination of the discharge over weirs by the electrolytic tank. Proc. Inst. Civ. Eng. 1958, 10, 59–86. [Google Scholar] [CrossRef]
- Montes, J.S. Potential Flow Analysis of Flow Over a Curved Broad Crested Weir. In Proceedings of the 11th Australasian Fluid Mechanics Conference, University of Tasmania, Hobart, Australia, 14–18 December 1992; pp. 1293–1296. [Google Scholar]
- Montes, J.S. Potential-Flow Solution to 2D Transition from Mild to Steep Slope. J. Hydraul. Eng. 1994, 120, 601–621. [Google Scholar] [CrossRef]
- Southwell, R.V.; Vaisey, G. Relaxation methods applied to engineering problems XII. Fluid motions characterized by ‘free’ stream-lines. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1946, 240, 117–161. [Google Scholar] [CrossRef]
- Barbier, C. Computer Algebra and Transputers Applied to the Finite Element Method. Ph.D. Thesis, Durham University, Durham, UK, 1992. [Google Scholar]
- Betts, P. A variational principle in terms of stream function for free-surface flows and its application to the finite element method. Comput. Fluids 1979, 7, 145–153. [Google Scholar] [CrossRef]
- Dao-Yang, D.; Man-Ling, L. Mathematical Model of Flow Over a Spillway Dam. In Proceedings of the 13th Intl. Congress of Large Dams New Delhi Q50(R55), New Delhi, India, 29 October 1979; pp. 959–976. [Google Scholar]
- Diersch, H.-J.; Schirmer, A.; Busch, K.-F. Analysis of flows with initially unknown discharge. J. Hydraul. Div. 1977, 103, 213–232. [Google Scholar] [CrossRef]
- Ikegawa, M.; Washizu, K. Finite element method applied to analysis of flow over a spillway crest. Int. J. Numer. Methods Eng. 1973, 6, 179–189. [Google Scholar] [CrossRef]
- Nakayama, T.; Ikegawa, M. Finite element analysis of flow over a weir. Comput. Struct. 1984, 19, 129–135. [Google Scholar] [CrossRef]
- Tu, R. Free Boundary Potential Flow Using Finite Elements. Ph.D. Thesis, University of Arizona, Dept. of Civil Engineering and Engineering Mechanics, Tucson, AZ, USA, 1971. [Google Scholar]
- Varoḡlu, E.; Finn, W.L. Variable domain finite element analysis of free surface gravity flow. Comput. Fluids 1978, 6, 103–114. [Google Scholar] [CrossRef]
- Cheng, A.H.-D.; Liu, P.L.-F.; Liggett, J.A. Boundary calculations of sluice and spillway flows. J. Hydraul. Div. 1981, 107, 1163–1178. [Google Scholar] [CrossRef]
- Henderson, H.C.; Kok, M.; De Koning, W.L. Computer-aided spillway design using the boundary element method and non-linear programming. Int. J. Numer. Methods Fluids 1991, 13, 625–641. [Google Scholar] [CrossRef]
- Liggett, J.A. The Boundary Element Method. In Chapter 8, Vol. I of Engineering Applications of Computational Hydraulics; Pitman Publ.: Boston, MA, USA, 1982. [Google Scholar]
- Castro-Orgaz, O.; Hager, W.H. Non-Hydrostatic Free Surface Flows. In Advances in Geophysical and Environmental Mechanics and Mathematics; Springer: Berlin/Heidelberg, Germany, 2017; 696p. [Google Scholar] [CrossRef]
- Castro-Orgaz, O.; Hager, W.H. Shallow Water Hydraulics; Springer: Berlin/Heidelberg, Germany, 2019; 563p. [Google Scholar] [CrossRef]
- Montes, J.S. Hydraulics of Open Channel Flow; ASCE Press: Reston, VA, USA, 1998. [Google Scholar]
- Vallentine, H.R. Applied Hydrodynamics; Butterworths: London, UK, 1969. [Google Scholar]
- Milne-Thomson, L.M. Theoretical Hydrodynamics; MacMillan: London, UK, 1962. [Google Scholar]
- Cassidy, J.J. Irrotational flow over spillways of finite height. J. Eng. Mech. Div. 1965, 91, 155–173. [Google Scholar] [CrossRef]
- Boadway, J.D. Transformation of elliptic partial differential equations for solving two-dimensional boundary value problems in fluid flow. Int. J. Numer. Methods Eng. 1976, 10, 527–533. [Google Scholar] [CrossRef]
- Wilkinson, D.L. Free surface slopes at controls in channel flow. J. Hydraul. Div. 1974, 100, 1107–1117. [Google Scholar] [CrossRef]
- Selby, S.M. Standard Mathematical Tables; CRC: Boca Raton, FL, USA, 1973. [Google Scholar]
- Chanson, H. The Hydraulics of Open Channel Flows: An Introduction; Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Henderson, F.M. Open Channel Flow; MacMillan: New York, NY, USA, 1966. [Google Scholar]
- Fawer, C. Etude de Quelques Écoulements Permanents à Filets Courbes (Study of Some Steady Flows with Curved Streamlines). Ph.D. Thesis, Université de Lausanne, La Concorde, Lausanne, Switzerland, 1937. (In French). [Google Scholar]
- Jaeger, C. Remarques sur quelques écoulements le long des lits à pente variant graduellement (Remarks on some flows along bottoms of gradually varied slope). Schweiz. Bauztg. 1939, 114, 231–234. (In French) [Google Scholar]
- Dao-Yang, D. A numerical method of flow over spillway dam with unknown energy head. Acta Mech. Sin. 1985, 17, 300–308. (In Chinese) [Google Scholar]
- Iwasa, Y. Hydraulic significance of transitional behaviours of flows in channel transitions and controls. Mem. Fac. Eng. Kyoto Univ. 1958, 20, 237–276. [Google Scholar]
- Castro-Orgaz, O. Potential Flow Solution for Open-Channel Flows and Weir-Crest Overflow. J. Irrig. Drain. Eng. 2013, 139, 551–559. [Google Scholar] [CrossRef]
- Jaeger, C. Engineering Fluid Mechanics; Blackie and Son: Edinburgh, UK, 1956. [Google Scholar]
- Sivakumaran, N.S.; Hosking, R.J.; Tingsanchali, T. Steady shallow flow over a spillway. J. Fluid Mech. 1981, 111, 411–420. [Google Scholar] [CrossRef]
- Sivakumaran, N.S.; Tingsanchali, T.; Hosking, R.J. Steady shallow flow over curved beds. J. Fluid Mech. 1983, 128, 469–487. [Google Scholar] [CrossRef]
- Sivakumaran, N.S. Shallow Flow over Curved Beds. Ph.D. Thesis, Asian Institute of Technology, Bangkok, Thailand, 1981. [Google Scholar]
- Castro-Orgaz, O.; Hager, W.H. Curved-streamline transitional flow from mild to steep slopes. J. Hydraul. Res. 2009, 47, 574–584. [Google Scholar] [CrossRef]
- Westernacher, A. Abflussbestimmung an Ausgerundeten Abstürzen mit Fliesswechsel (Discharge Determination at Rounded Drops under Transitional Flow); TU Karlsruhe: Karlsruhe, Germany,, 1965. (In Germany) [Google Scholar]
- Weyermuller, R.G.; Mostafa, M.G. Flow at grade-break from mild to steep slopes. J. Hydraul. Div. 1976, 102, 1439–1448. [Google Scholar] [CrossRef]
- Cassidy, J.J. Designing spillway crests for high-head operation. J. Hydraul. Div. 1970, 96, 745–753. [Google Scholar] [CrossRef]
- Creager, W.P. Engineering for Masonry Dams; Wiley and Sons: New York, NY, USA, 1917. [Google Scholar]
- Escande, L. Détermination pratique du profile optimum d’un barrage déversoir: Tracé des piles par les méthodes aérodynamiques. Application à un ouvrage déterminé (Practical determination of the optimum weir profile: Pier shape using aerodynamic methods, application to prototype structure). Sci. Ind. 1933, 17, 467–474. (In French) [Google Scholar]
- Guo, Y.; Wen, X.; Wu, C.; Fang, D. Numerical modelling of spillway flow with free drop and initially unknown discharge. J. Hydraulic Res. 1998, 36, 785–801. [Google Scholar]
- USACE. Hydraulic Design of Spillways; U.S. Army Corps of Engineers: Washington, DC, USA, 1990. [Google Scholar]
- Ishihara, T.; Iwasa, Y.; Ihda, K. Basic studies on hydraulic performances of overflow spillways and diversion weirs. Bull. Disaster Prev. Res. Inst. 1960, 33, 1–30. [Google Scholar]
- Castro-Orgaz, O.; Cantero-Chinchilla, F.N.; Hager, W.H. High-order shallow water expansions in free surface flows: Application to steady overflow processes. Ocean Eng. 2022, 250, 110717. [Google Scholar] [CrossRef]
- Hasumi, M. Untersuchungen über die Verteilung der hydrostatischen Drücke an Wehrkronen und-Rücken von Überfallwehren infolge des abstürzenden Wassers (Studies on the distribution of hydrostatic pressure distributions at overflows due to water flow). J. Dept. Agric. Kyushu Imp. Univ. 1931, 3, 1–97. (In Germany) [Google Scholar]
- Melsheimer, E.S.; Murphy, T.E. Investigations of Various Shapes of the Upstream Quadrant of the Crest of a High Spillway: Hydraulic Laboratory Investigation; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1970. [Google Scholar]
- USACE. Hydraulic Design Criteria; U.S. Army Waterways Experiment Station: Vicksburg, MS, USA, 1987. [Google Scholar]
- Maynord, S.T. General Spillway Investigation: Hydraulic Model Investigation; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1985. [Google Scholar]
- Murphy, T.E. Spillway Crest Design; U.S. Army Engineer Waterways Experiment Station: Vicksburg, MS, USA, 1973. [Google Scholar]
- Reese, A.J.; Maynord, S.T. Design of Spillway Crests. J. Hydraul. Eng. 1987, 113, 476–490. [Google Scholar] [CrossRef]
- Knapp, F.H. Ausfluss, Überfall und Durchfluss im Wasserbau; Braun: Karlsruhe, Germany, 1960. (In Germany) [Google Scholar]
- Hager, W.H. Continuous crest profile for standard spillway. J. Hydraul. Eng. 1987, 113, 1453–1457. [Google Scholar] [CrossRef]
- Hager, W.H. Experiments on standard spillway flow. Proc. ICE 1991, 91, 399–416. [Google Scholar]
- Lai, C.; Hromadka, T.D. Modeling Complex Two-Dimensional Flows by the Complex-Variable Boundary-Element Method. In Proceedings of the Intl. Symp. of Refined Flow Modeling and Turbulence Measurements, Volume II, G-26-1/10, The University of Iowa, Iowa City, IA, USA, 16–18 September 1985. [Google Scholar]
- Ho, D.; Boyes, K.; Donohoo, S.; Cooper, B. Numerical flow analysis for spillways. In Proceedings of the 43rd ANCOLD Conference, Hobart, Tasmania, Australia, 24–29 October 2003. [Google Scholar]
- Savage, B.M.; Johnson, M.C. Flow over ogee spillway: Physical and numerical model case study. J. Hydraul. Eng. 2001, 127, 640–649. [Google Scholar] [CrossRef]




| Cd | Error | ||
|---|---|---|---|
| H/HD | Experimental | Irrotational | % |
| 0.5 | 0.6320 | 0.6406 | +1.36 |
| 1 | 0.7044 | 0.7015 | −0.41 |
| 1.38 | 0.7378 | 0.7328 | −0.68 |
| 1.88 | 0.7680 | 0.7574 | −1.38 |
| 2.46 | 0.7818 | 0.7784 | −0.43 |
| 3.06 | 0.7910 | 0.7917 | +0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro-Orgaz, O.; Hager, W.H. Analytical Determination of Irrotational Flow Profiles in Open-Channel Transitions. Water 2023, 15, 4217. https://doi.org/10.3390/w15244217
Castro-Orgaz O, Hager WH. Analytical Determination of Irrotational Flow Profiles in Open-Channel Transitions. Water. 2023; 15(24):4217. https://doi.org/10.3390/w15244217
Chicago/Turabian StyleCastro-Orgaz, Oscar, and Willi H. Hager. 2023. "Analytical Determination of Irrotational Flow Profiles in Open-Channel Transitions" Water 15, no. 24: 4217. https://doi.org/10.3390/w15244217
APA StyleCastro-Orgaz, O., & Hager, W. H. (2023). Analytical Determination of Irrotational Flow Profiles in Open-Channel Transitions. Water, 15(24), 4217. https://doi.org/10.3390/w15244217





