Fragility Analysis for Water-Retaining Structures Resting on Spatially Random Soil
Abstract
:1. Introduction
2. Methodology
2.1. Probabilistic Seepage Analysis
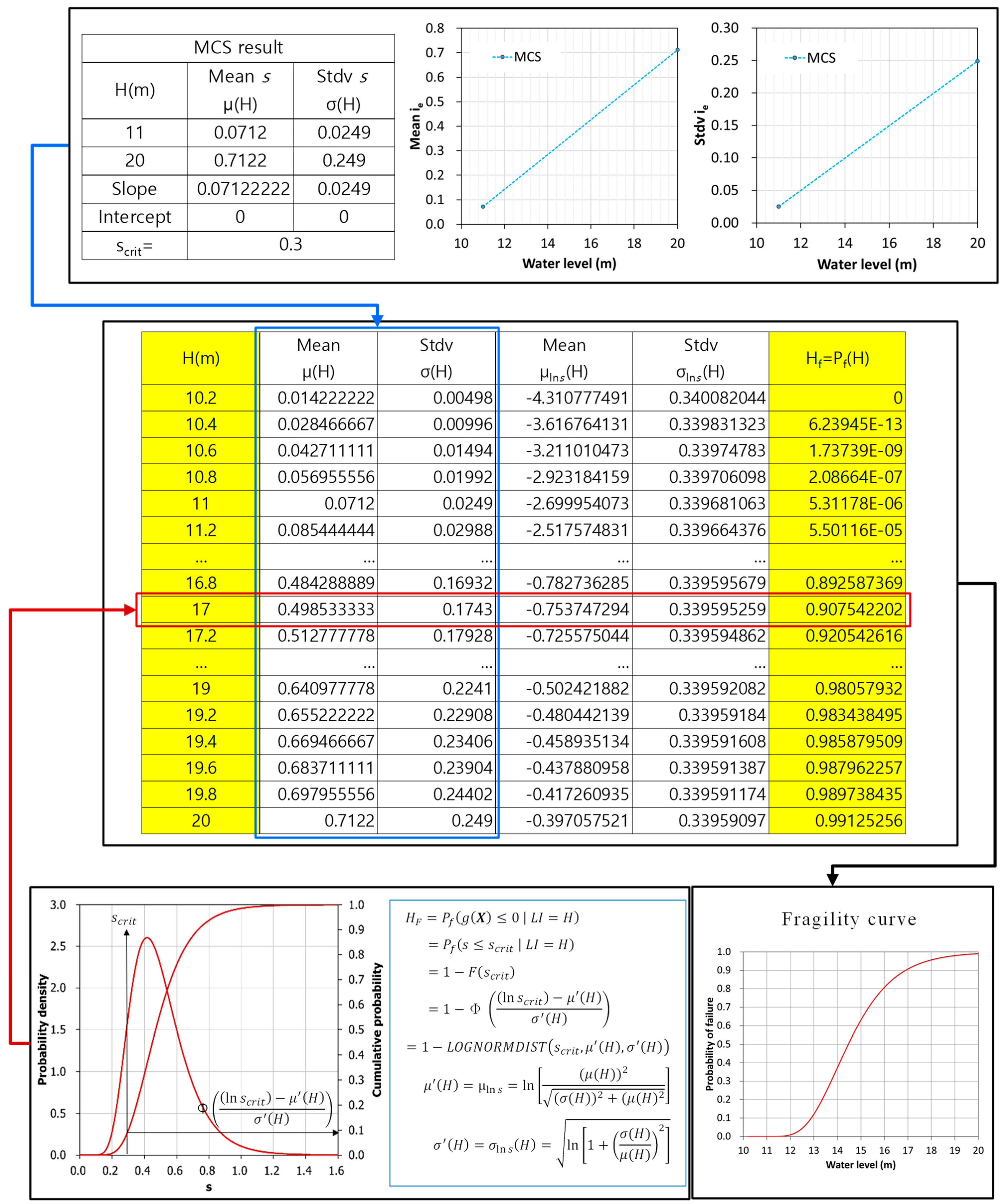
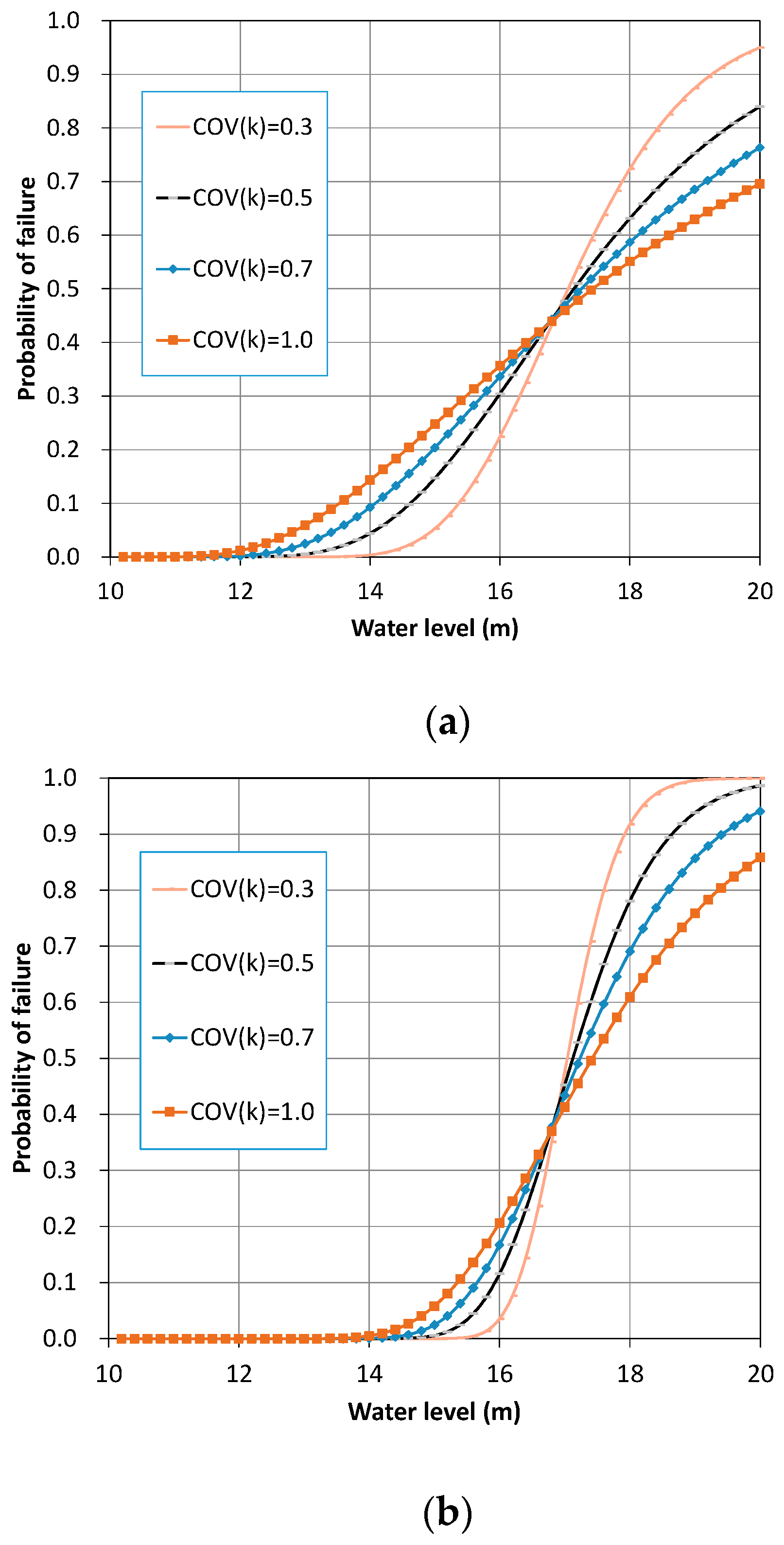
2.2. Fragility Curve
2.2.1. Method A
2.2.2. Method B
3. Fragility Curve for Seepage through the Soil Foundation of the Water-Retaining Structure
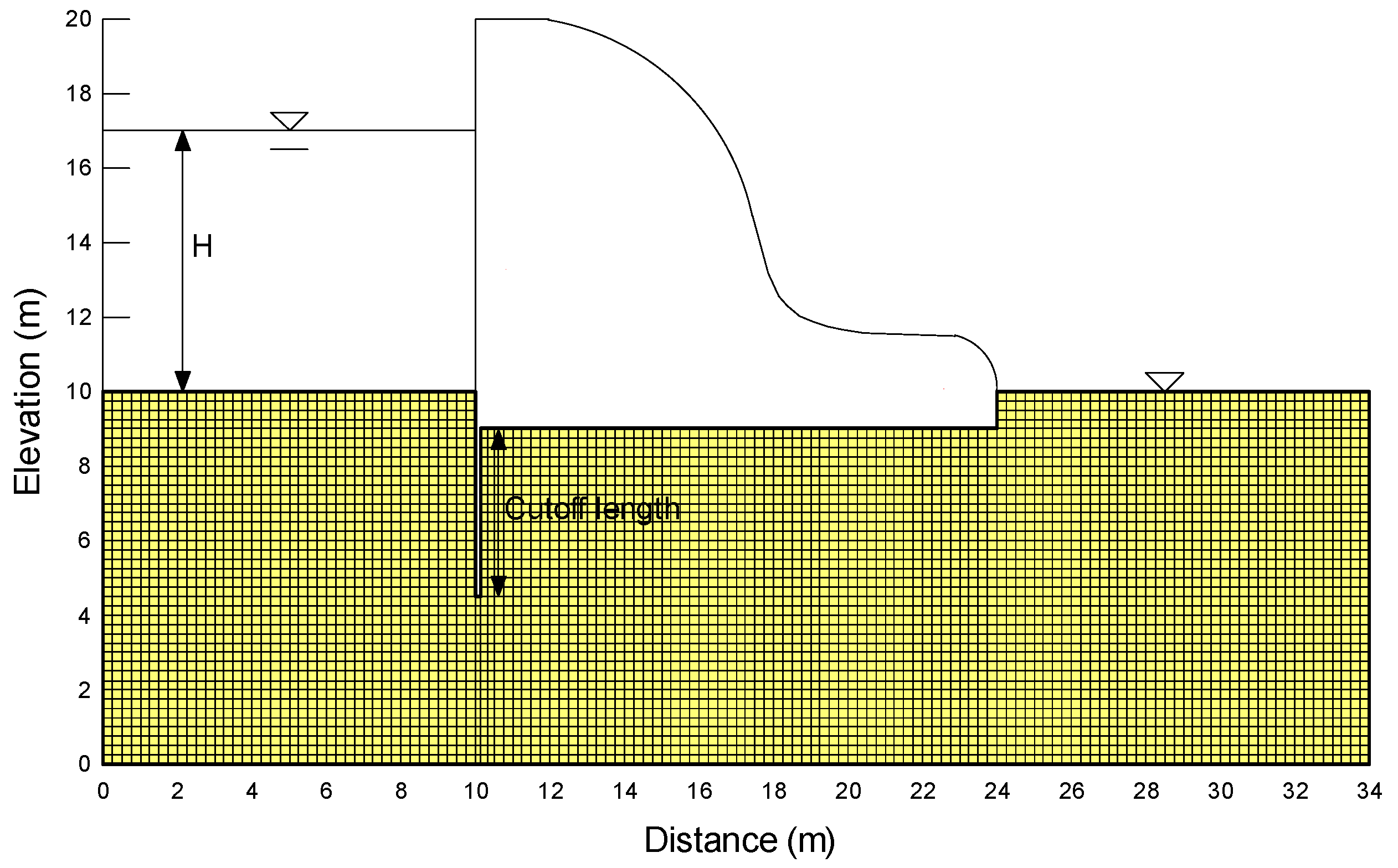
3.1. Soil Properties and Analysis Conditions
3.2. Stochastic Simulations
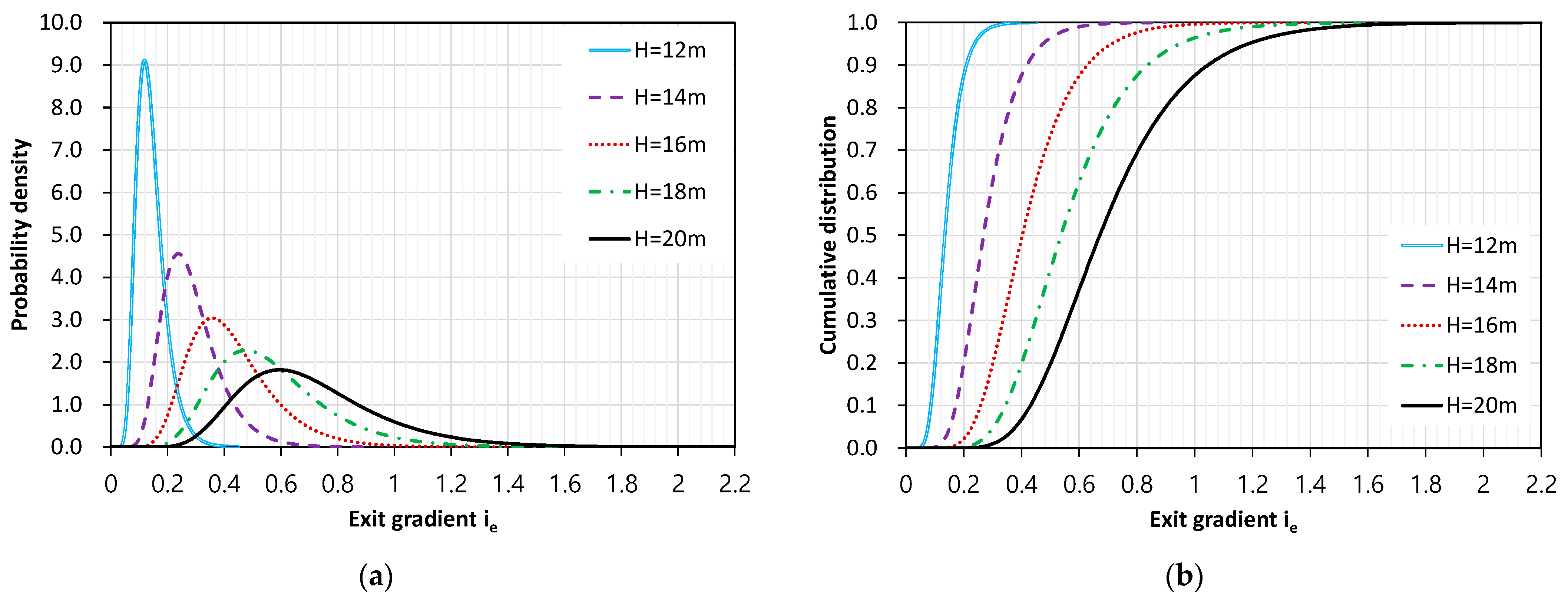
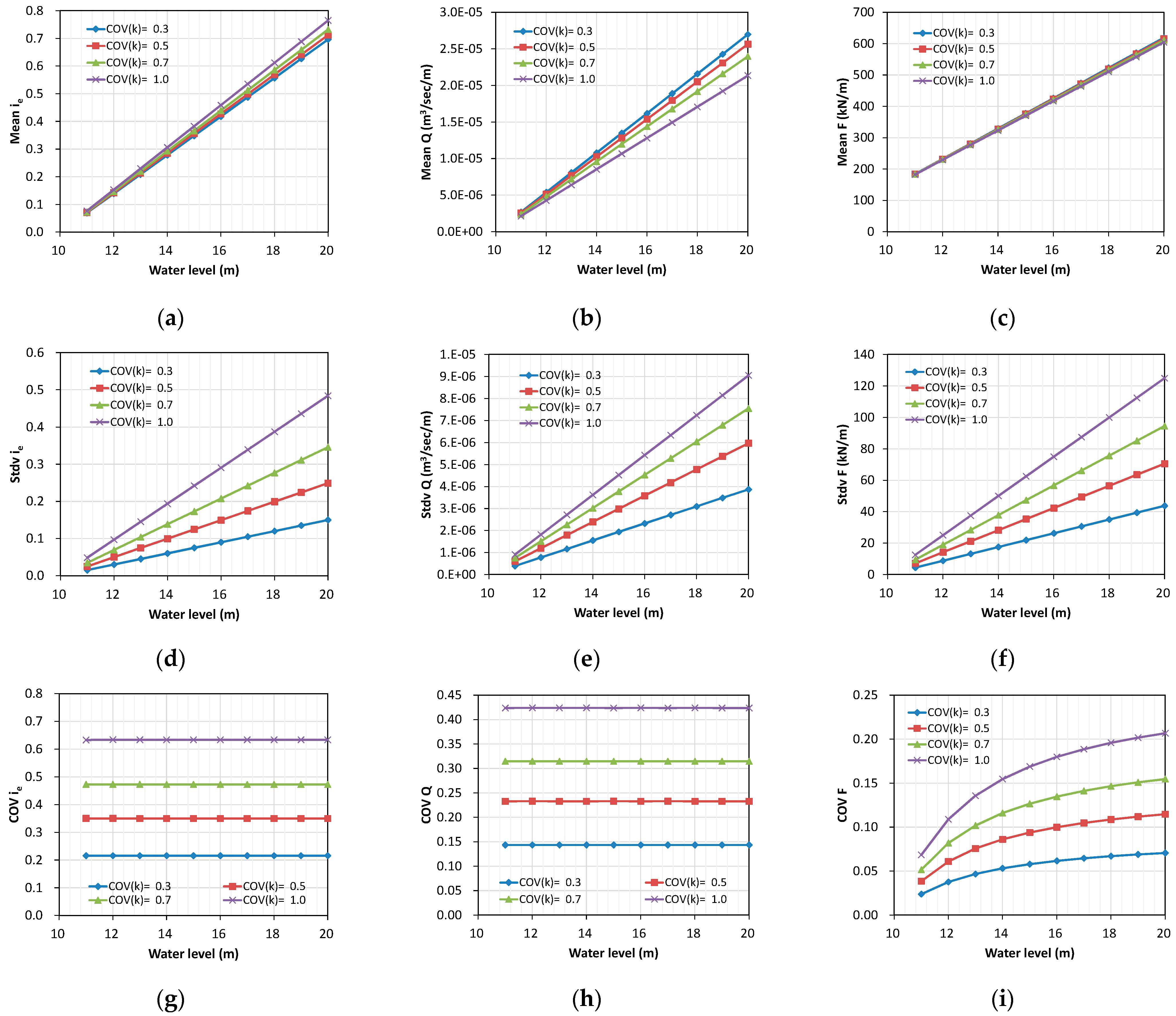
3.2.1. Fragility for Piping
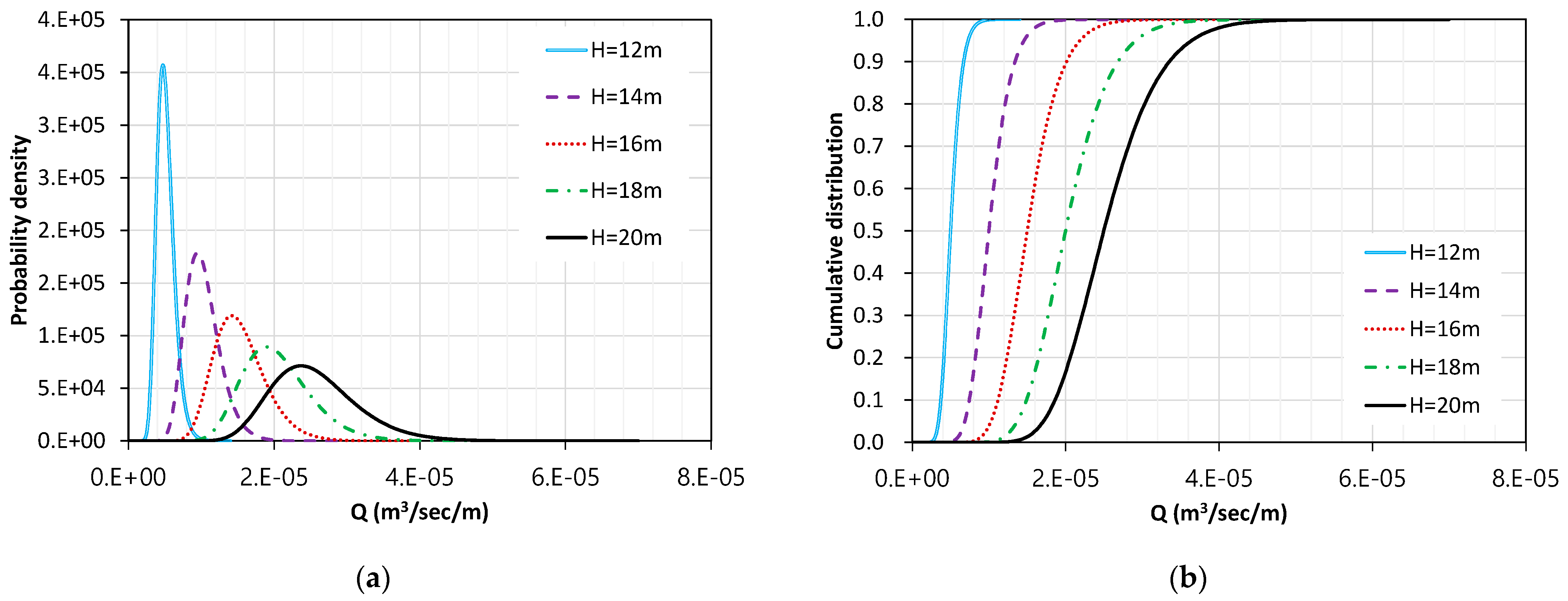
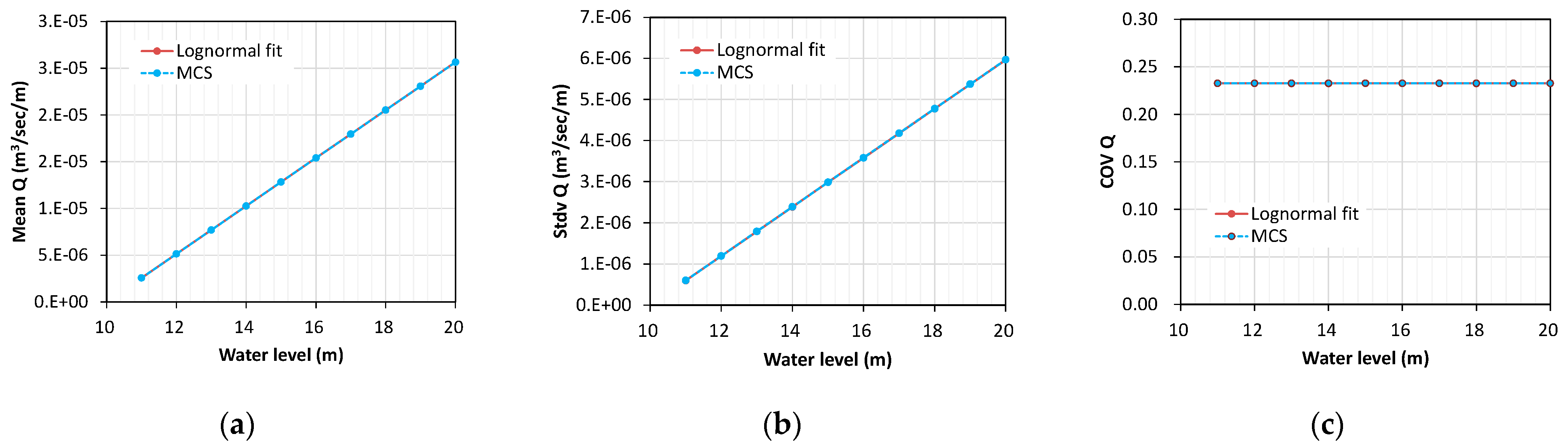
3.2.2. Fragility for Seepage Rate
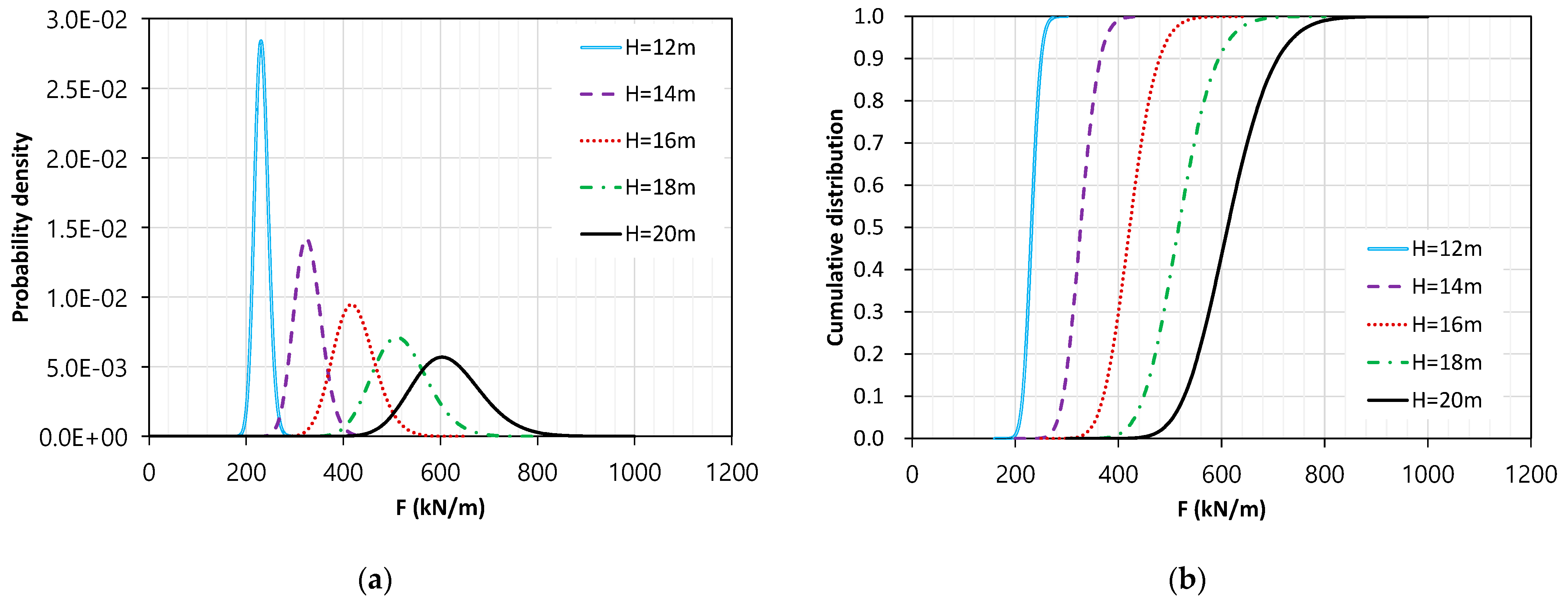
3.2.3. Fragility for Uplift Force
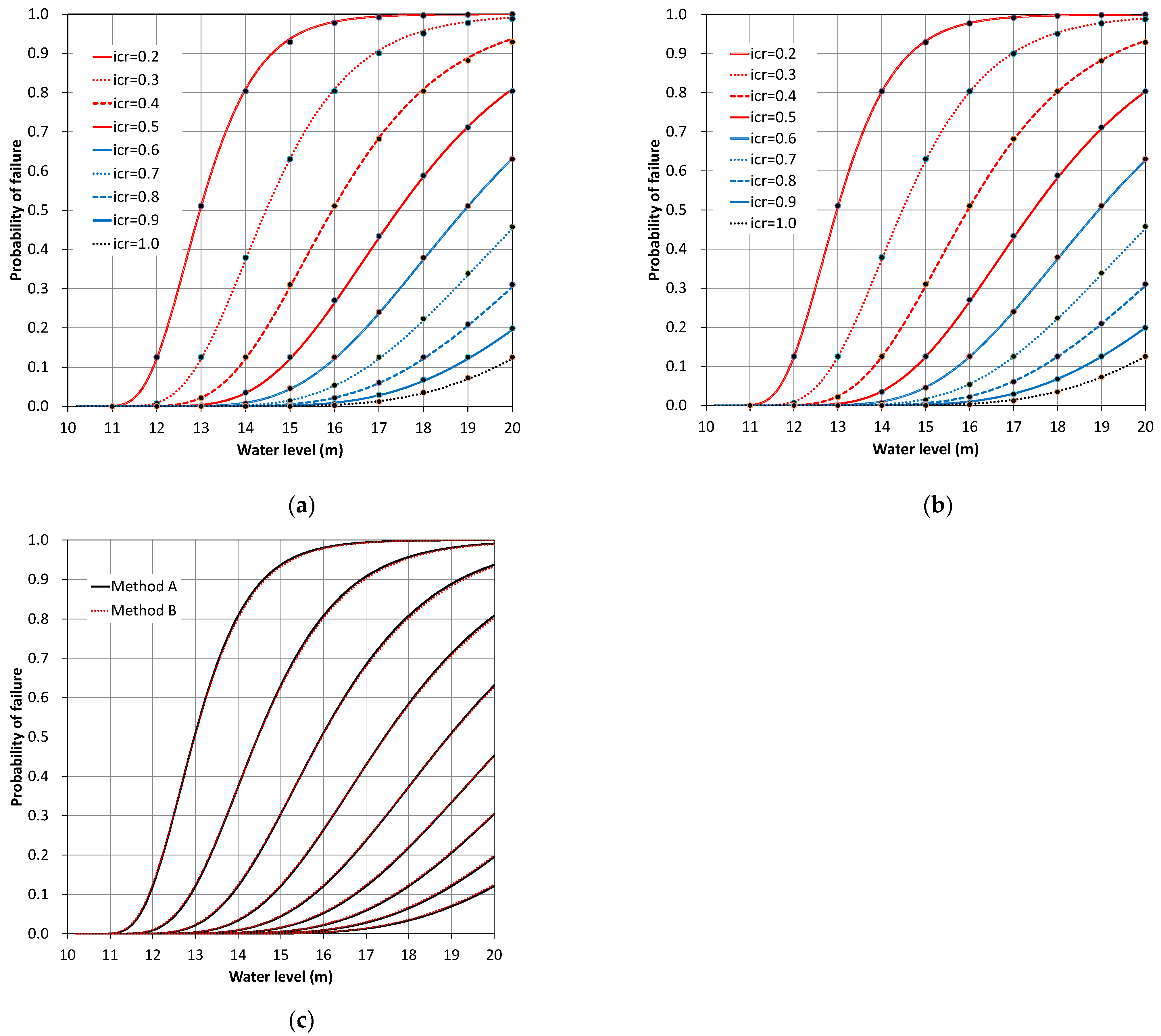
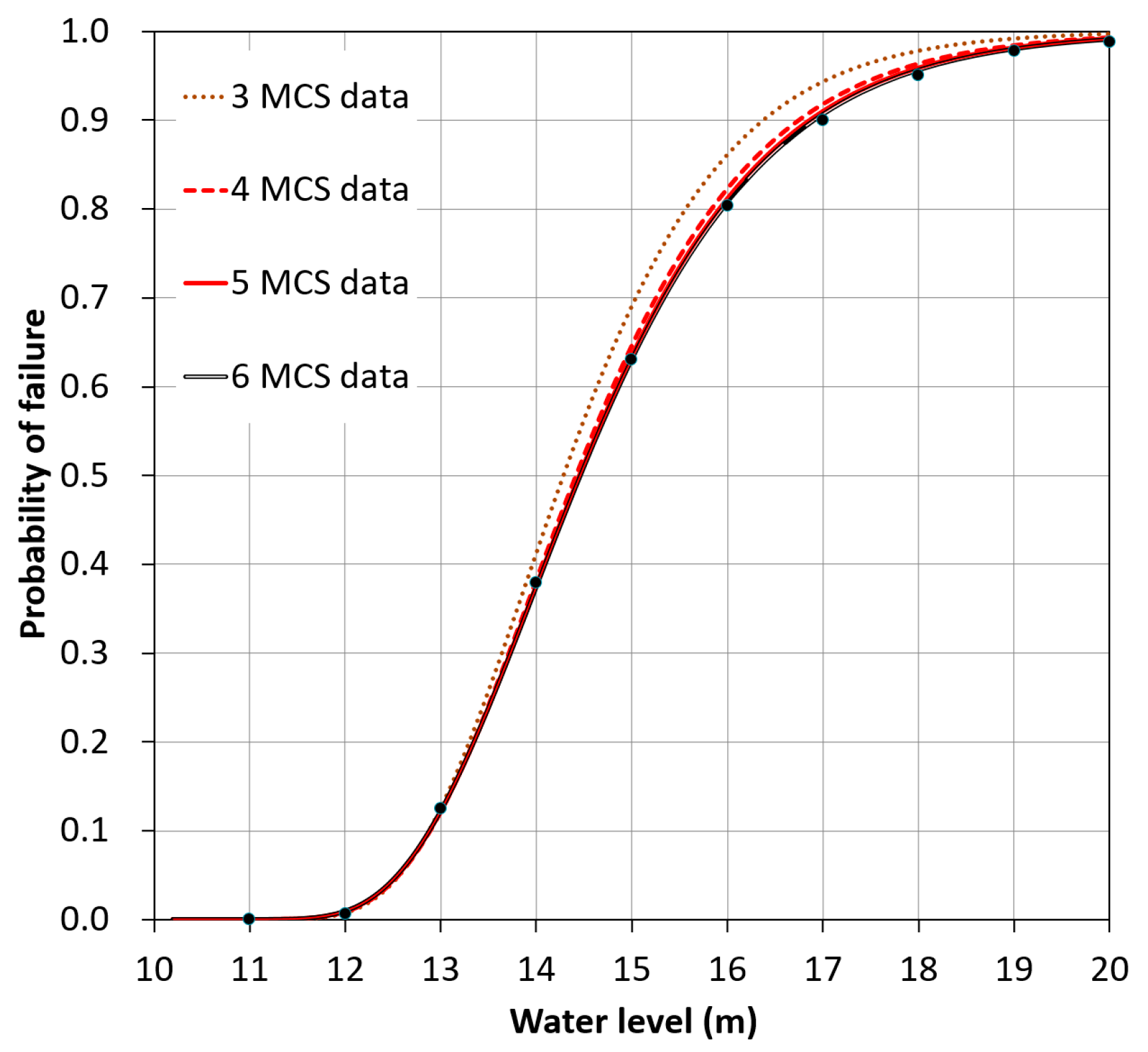
3.3. Effect of on the Fragility Curve
3.4. Effect of Variation in the Cutoff Length
4. Discussion
5. Summary and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- USACE. Risk-Based Analysis for Flood Damage Reduction Studies; Engineer Manual 1110-2-1619; US Army Corps of Engineers: Washington, DC, USA, 1996; Available online: https://apps.dtic.mil/sti/pdfs/ADA401763.pdf (accessed on 27 November 2023).
- Simm, J.; Tarrant, O. Development of fragility curves to describe the performance of UK levee systems. In Proceedings of the Twenty-Sixth International Congress on Large Dams, Vienna, Austria, 1–7 July 2018. [Google Scholar]
- Rossi, N.; Bačić, M.; Kovačević, M.S.; Librić, L. Development of fragility curves for piping and slope stability of river levees. Water 2021, 13, 738. [Google Scholar] [CrossRef]
- Kennedy, R.P.; Cornell, C.A.; Campbell, R.D.; Kaplan, S.; Perla, H.F. Probabilistic seismic safety study of an existing nuclear power plant. Nucl. Eng. Des. 1980, 59, 315–338. [Google Scholar] [CrossRef]
- Tsompanakis, Y.; Lagaros, N.D.; Psarropoulos, P.N.; Georgopoulos, E.C. Probabilistic seismic slope stability assessment of geostructures. Struct. Infrastruct. Eng. 2010, 6, 179–191. [Google Scholar] [CrossRef]
- Porter, K. A Beginner’s Guide to Fragility, Vulnerability, and Risk; University of Colorado Boulder: Boulder, CO, USA, 2018; Available online: https://www.sparisk.com/pubs/Porter-beginners-guide.pdf (accessed on 27 November 2023).
- Cho, S.E. Failure distribution analysis of shallow landslides under rainfall infiltration based on fragility curves. Landslides 2020, 17, 79–91. [Google Scholar] [CrossRef]
- Vorogushyn, S.; Merz, B.; Apel, H. Development of dike fragility curves for piping and micro-instability breach mechanisms. Nat. Hazards Earth Syst. Sci. 2009, 19, 1383–1401. [Google Scholar] [CrossRef]
- Wu, X.Z. Development of fragility functions for slope instability analysis. Landslides 2015, 12, 165–175. [Google Scholar] [CrossRef]
- Martinović, K.; Reale, C.; Gavin, K. Fragility curves for rainfall-induced shallow landslides on transport networks. Can. Geotech. J. 2018, 55, 852–861. [Google Scholar] [CrossRef]
- McKenna, G.; Argyroudis, S.A.; Winter, M.G.; Mitoulis, S.A. Multiple hazard fragility analysis for granular highway embankments: Moisture ingress and scour. Transp. Geotech. 2021, 26, 100431. [Google Scholar] [CrossRef]
- Hall, J.W.; Dawson, R.J.; Sayers, P.B.; Rosu, C.; Chatterton, J.B.; Deakin, R. A methodology for national-scale flood risk assessment. Proc. Inst. Civ. Eng.-Water Marit. Eng. 2003, 156, 235–247. [Google Scholar] [CrossRef]
- Dawson, R.J.; Hall, J.; Sayers, P.; Bates, P.; Rosu, C. Sampling-based flood risk analysis for fluvial dike systems. Stoch. Environ. Res. Risk Assess. 2005, 19, 388–402. [Google Scholar] [CrossRef]
- Wojciechowska, K.; Pleijter, G.; Zethof, M.; Havinga, F.; Haaren, D.V.; Ter Horst, W. Application of fragility curves in operational flood risk assessment. In Proceedings of the 5th International Symposium on Geotechnical Safety and Risk, Rotterdam, The Netherlands, 13–16 October 2015; IOS Press: Amsterdam, The Netherlands, 2015; pp. 528–534. [Google Scholar] [CrossRef]
- Mainguenaud, F.; Peyras, L.; Khan, U.T.; Carvajal, C.; Sharma, J.; Beullac, B. A probabilistic approach to levee reliability based on sliding, backward erosion and overflowing mechanisms: Application to an inspired Canadian case study. J. Flood Risk Manag. 2023, 16, e12921. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D.V. Extreme hydraulic gradient statistics in stochastic earth dam. J. Geotech. Geoenviron. Eng. 1997, 123, 995–1000. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Probabilistic analysis of exit gradients due to steady seepage. J. Geotech. Geoenviron. Eng. 1998, 124, 789–797. [Google Scholar] [CrossRef]
- Srivastava, A.; Sivakumar Babu, G.L.; Haldar, S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis. Eng. Geol. 2010, 110, 93–101. [Google Scholar] [CrossRef]
- Ahmed, A.A. Stochastic analysis of seepage under hydraulic structures resting on anisotropic heterogeneous soils. J. Geotech. Geoenviron. Eng. 2012, 139, 1001–1004. [Google Scholar] [CrossRef]
- Cho, S.E. Probabilistic analysis of seepage that considers the spatial variability of permeability for an embankment on soil foundation. Eng. Geol. 2012, 133–134, 30–39. [Google Scholar] [CrossRef]
- Liu, L.L.; Cheng, Y.M.; Jiang, S.H.; Zhang, S.H.; Wang, X.M.; Wu, Z.H. Effects of spatial autocorrelation structure of permeability on seepage through an embankment on a soil foundation. Comput. Geotech. 2017, 87, 62–75. [Google Scholar] [CrossRef]
- Tan, X.; Wang, X.; Khoshnevisan, S.; Hou, X.; Zha, F. Seepage analysis of earth dams considering spatial variability of hydraulic parameters. Eng. Geol. 2017, 228, 260–269. [Google Scholar] [CrossRef]
- Hekmatzadeh, A.A.; Zarei, F.; Johari, A.; Haghighi, A.T. Reliability analysis of stability against piping and sliding in diversion dams, considering four cutoff wall configurations. Comput. Geotech. 2018, 98, 217–231. [Google Scholar] [CrossRef]
- Johari, A.; Heydari, A. Reliability analysis of seepage using an applicable procedure based on stochastic scaled boundary finite element method. Eng. Anal. Bound. Elem. 2018, 94, 44–59. [Google Scholar] [CrossRef]
- Liu, K.; Vardon, P.J.; Hicks, M.A. Probabilistic analysis of seepage for internal stability of earth embankments. Environ. Geotech. 2019, 6, 294–306. [Google Scholar] [CrossRef]
- Chi, F.; Breul, P.; Carvajal, C.; Peyras, L. Stochastic seepage analysis in embankment dams using different types of random fields. Comput. Geotech. 2023, 162, 105689. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Seepage beneath water retaining structures founded on spatially random soil. Géotechnique 1993, 43, 577–587. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Three-dimensional seepage through spatially random soil. J. Geotech. Geoenviron. Eng. 1997, 123, 153–160. [Google Scholar] [CrossRef]
- Robbins, B.A.; Griffiths, D.V.; Fenton, G.A. Random finite element analysis of backward erosion piping. Comput. Geotech. 2021, 138, 104322. [Google Scholar] [CrossRef]
- Cho, S.E. Probabilistic assessment of seepage stability of soil foundation under water retaining structures by fragility curves. J. Korean Geotech. Soc. 2021, 37, 41–54. [Google Scholar] [CrossRef]
- Cho, S.E. Probabilistic seepage analysis by the finite element method considering spatial variability of soil permeability. J. Korean Geotech. Soc. 2011, 27, 93–104. [Google Scholar] [CrossRef]
- Lacasse, S.; Nadim, F. Uncertainties in characterizing soil properties. In Proceedings of the Uncertainty 96, Madison, WI, USA, 31 July–3 August 1996; ASCE: Reston, VA, USA, 1996; pp. 49–75. [Google Scholar]
- Vanmarcke, E.H. Random Fields: Analysis and Synthesis; World Scientific: Singapore, 1983. [Google Scholar]
- Fenton, G.A.; Griffiths, D.V. Risk Assessment in Geotechnical Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kennedy, R.P.; Ravindra, M.K. Seismic fragilities for nuclear power plant risk studies. Nucl. Eng. Des. 1980, 79, 47–68. [Google Scholar] [CrossRef]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Jeon, O.H.; Jung, W.Y. Fragility analysis of weir structure subjected to flooding water damage. Int. J. Civ. Environ. Eng. 2018, 12, 75–80. Available online: https://publications.waset.org/10008936/pdf (accessed on 27 November 2023).
- Bodda, S.S.; Gupta, A.; Ju, B.S.; Jung, W.Y. Fragility of a weir structure due to scouring. Comput. Eng. Phys. Model. 2020, 3, 1–15. [Google Scholar] [CrossRef]
- Freeze, R.A. A stochastic-conceptual analysis of one-dimensional groundwater flow in nonuniform homogeneous media. Water Resour. Res. 1975, 11, 725–741. [Google Scholar] [CrossRef]
- Hoeksema, R.J.; Kitanidis, P.K. Analysis of the spatial structure of properties of selected aquifers. Water Resour. Res. 1985, 21, 563–572. [Google Scholar] [CrossRef]
- Sudicky, E.A. A natural gradient experiment on solute transport in a sand aquifer: Spatial variability of hydraulic conductivity and its role in the dispersion process. Water Resour. Res. 1986, 22, 2069–2083. [Google Scholar] [CrossRef]
- Duncan, J.M. Factors of safety and reliability in geotechnical engineering. J. Geotech. Geoenviron. Eng. 2000, 126, 307–316. [Google Scholar] [CrossRef]
- El-Ramly, H.; Morgenstern, N.R.; Cruden, D.M. Probabilistic stability analysis of a tailings dyke on presheared clay-shale. Can. Geotech. J. 2003, 40, 192–208. [Google Scholar] [CrossRef]









| Parameter | (m/s) | Autocorrelation Distance (m) | |
|---|---|---|---|
| K | 0.3, 0.5, 0.7, 1.0 |
| 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
| 2.981 | 4.470 | 5.960 | 7.450 | 8.940 | 10.427 | 11.913 | 13.392 | 14.862 | |
| 0.346 | 0.346 | 0.346 | 0.346 | 0.346 | 0.346 | 0.346 | 0.345 | 0.345 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, S.-E. Fragility Analysis for Water-Retaining Structures Resting on Spatially Random Soil. Water 2023, 15, 4165. https://doi.org/10.3390/w15234165
Cho S-E. Fragility Analysis for Water-Retaining Structures Resting on Spatially Random Soil. Water. 2023; 15(23):4165. https://doi.org/10.3390/w15234165
Chicago/Turabian StyleCho, Sung-Eun. 2023. "Fragility Analysis for Water-Retaining Structures Resting on Spatially Random Soil" Water 15, no. 23: 4165. https://doi.org/10.3390/w15234165
APA StyleCho, S.-E. (2023). Fragility Analysis for Water-Retaining Structures Resting on Spatially Random Soil. Water, 15(23), 4165. https://doi.org/10.3390/w15234165








