Location and Extents of Scour Hole around an Erodible Spill-through Abutment under Clear Water Condition and the Abutment Classification
Abstract
:1. Introduction
2. Methodology
2.1. Model Specifications
2.2. Experimental Setting
3. Experimental Results and Discussion
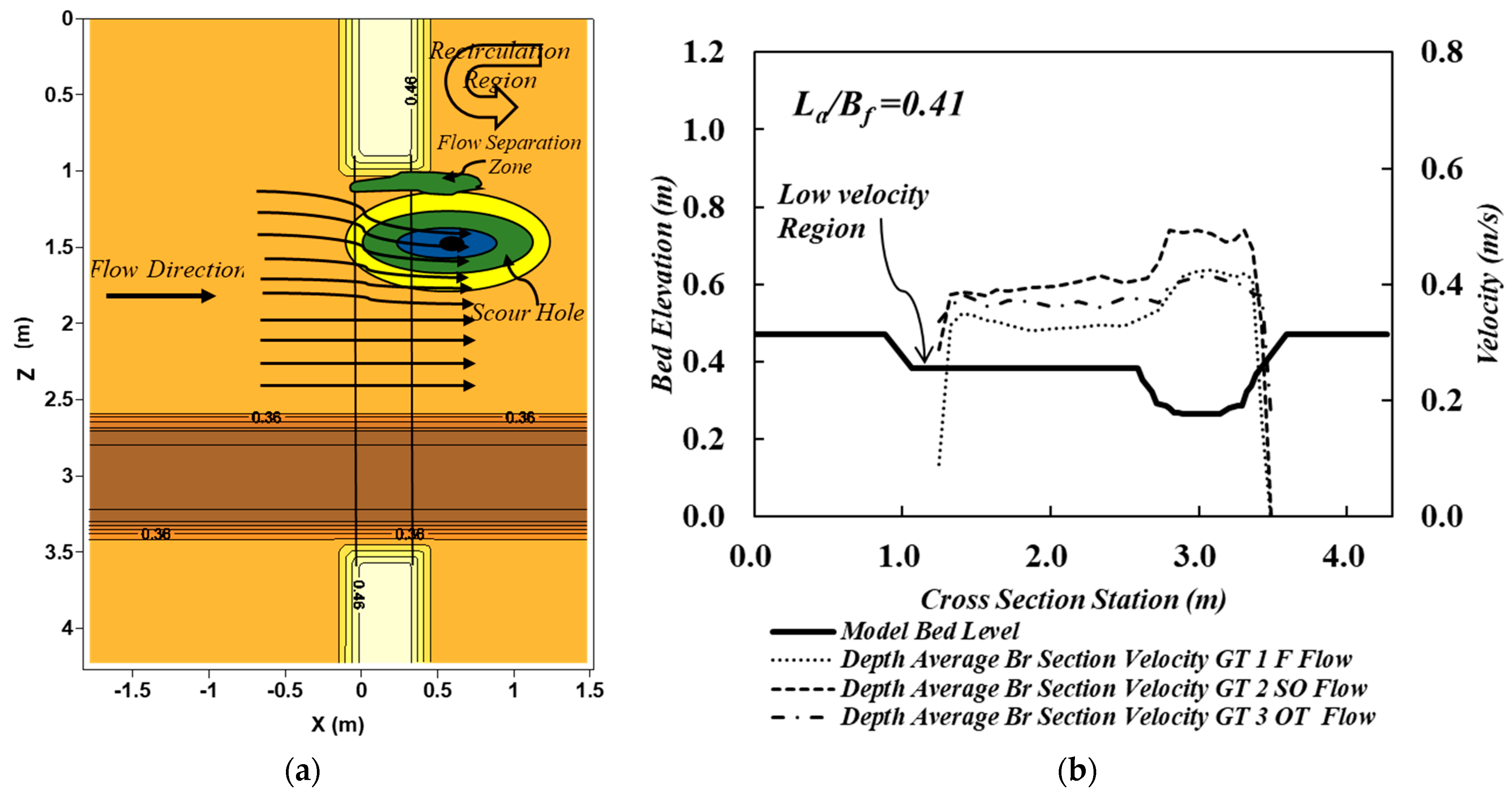
3.1. Experimental Results
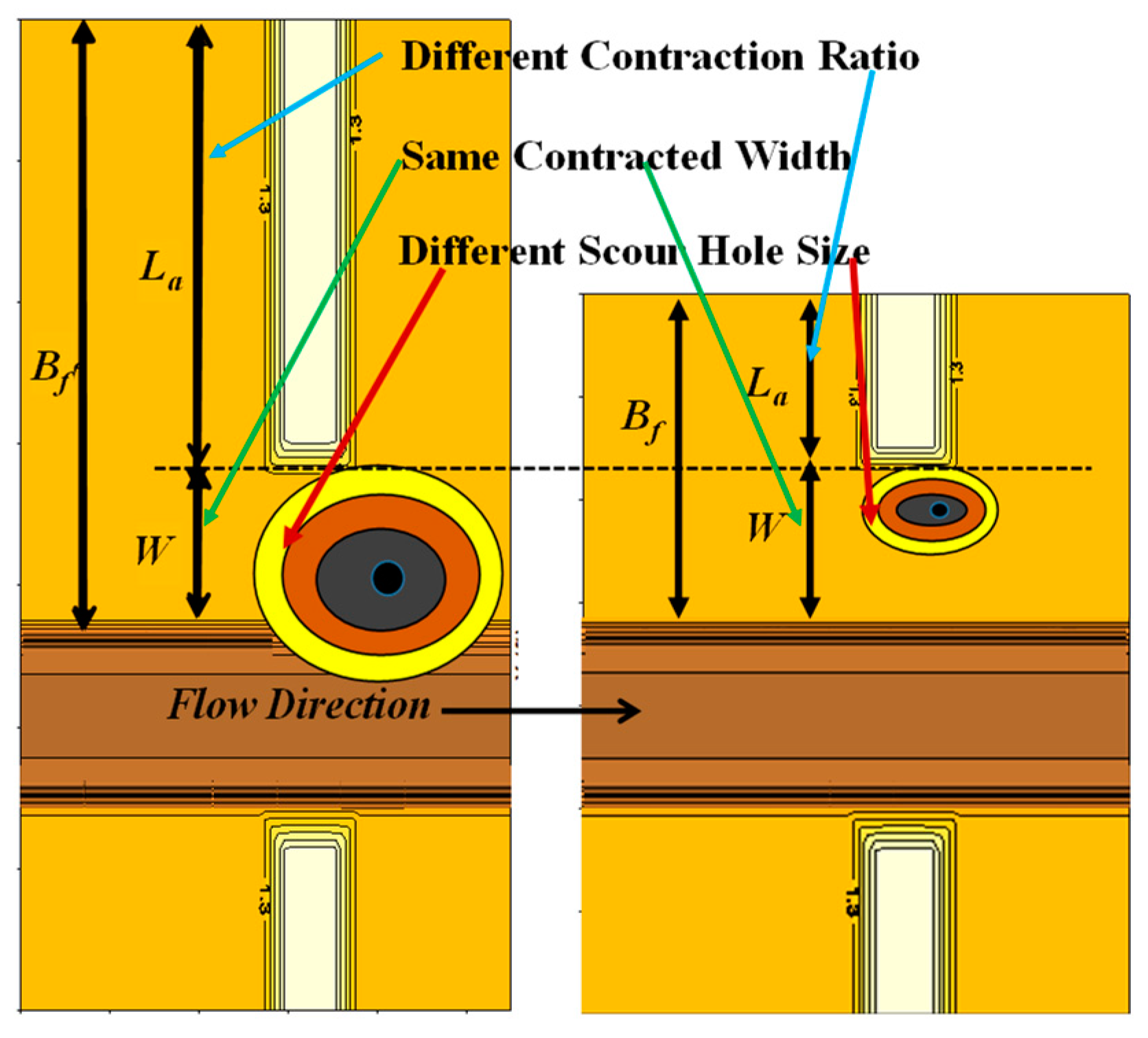
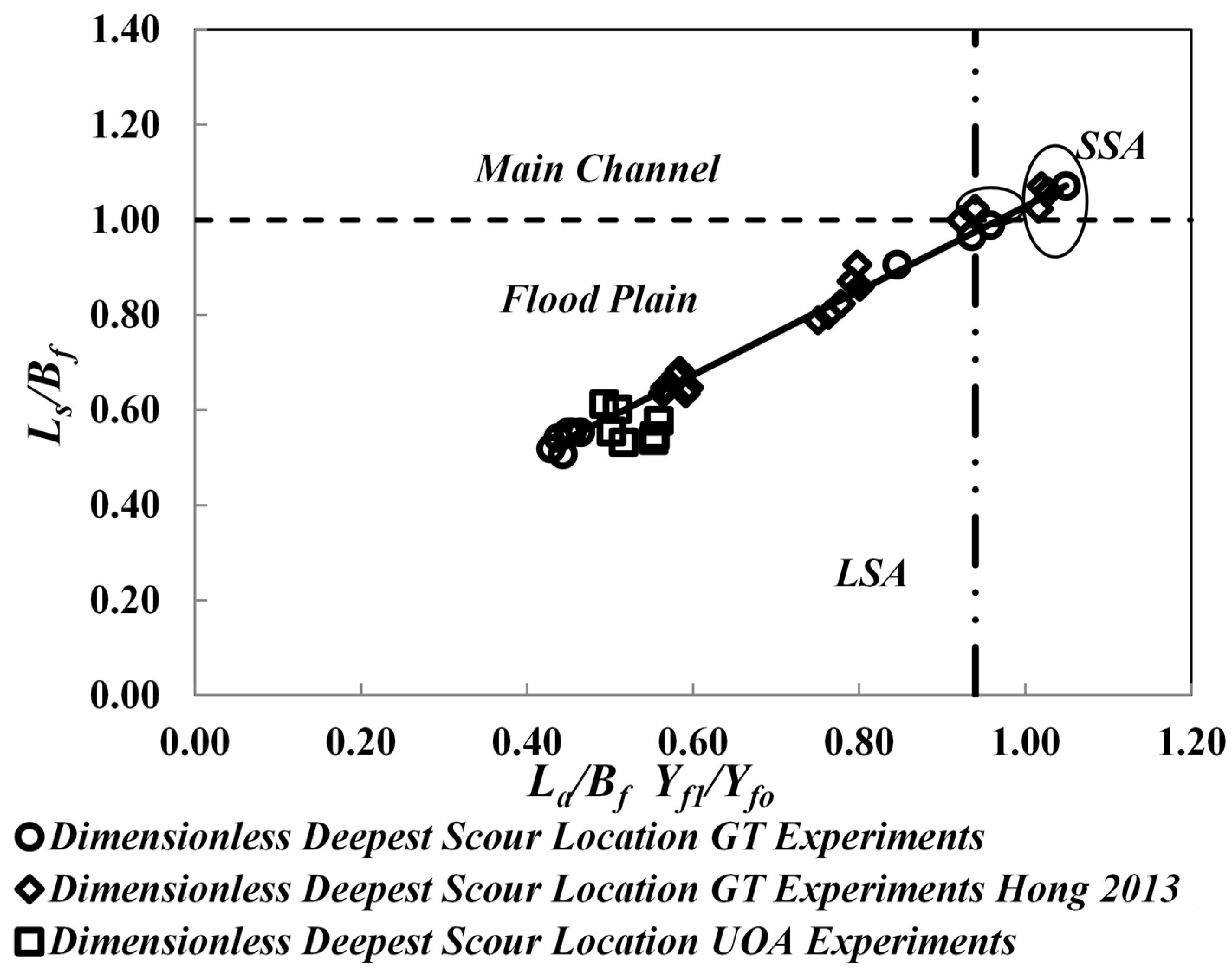
3.2. Classification of Abutment and Prediction of Maximum Scour Location in Transverse Direction
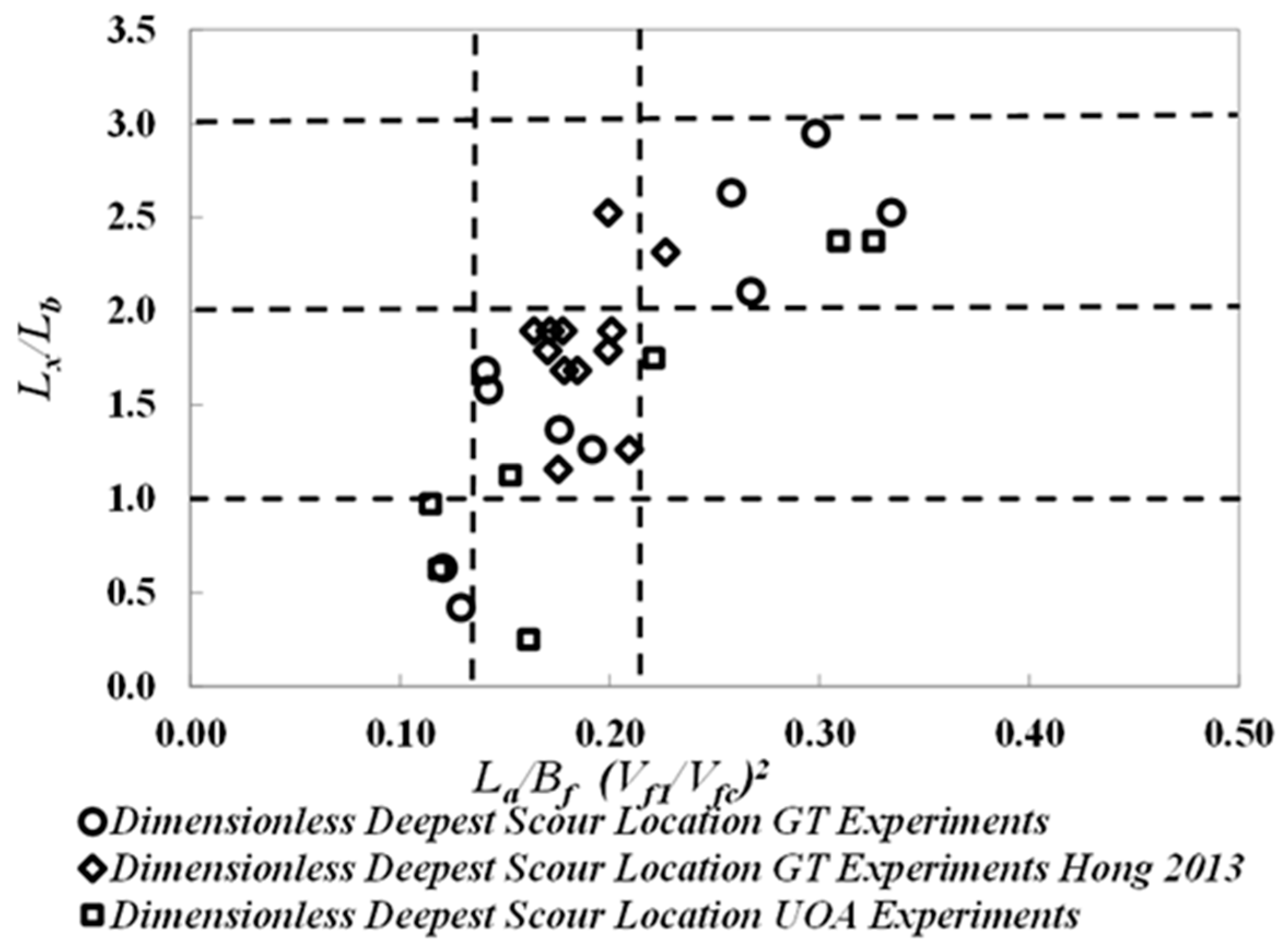
3.3. Prediction of Maximum Scour Location in Flow Direction
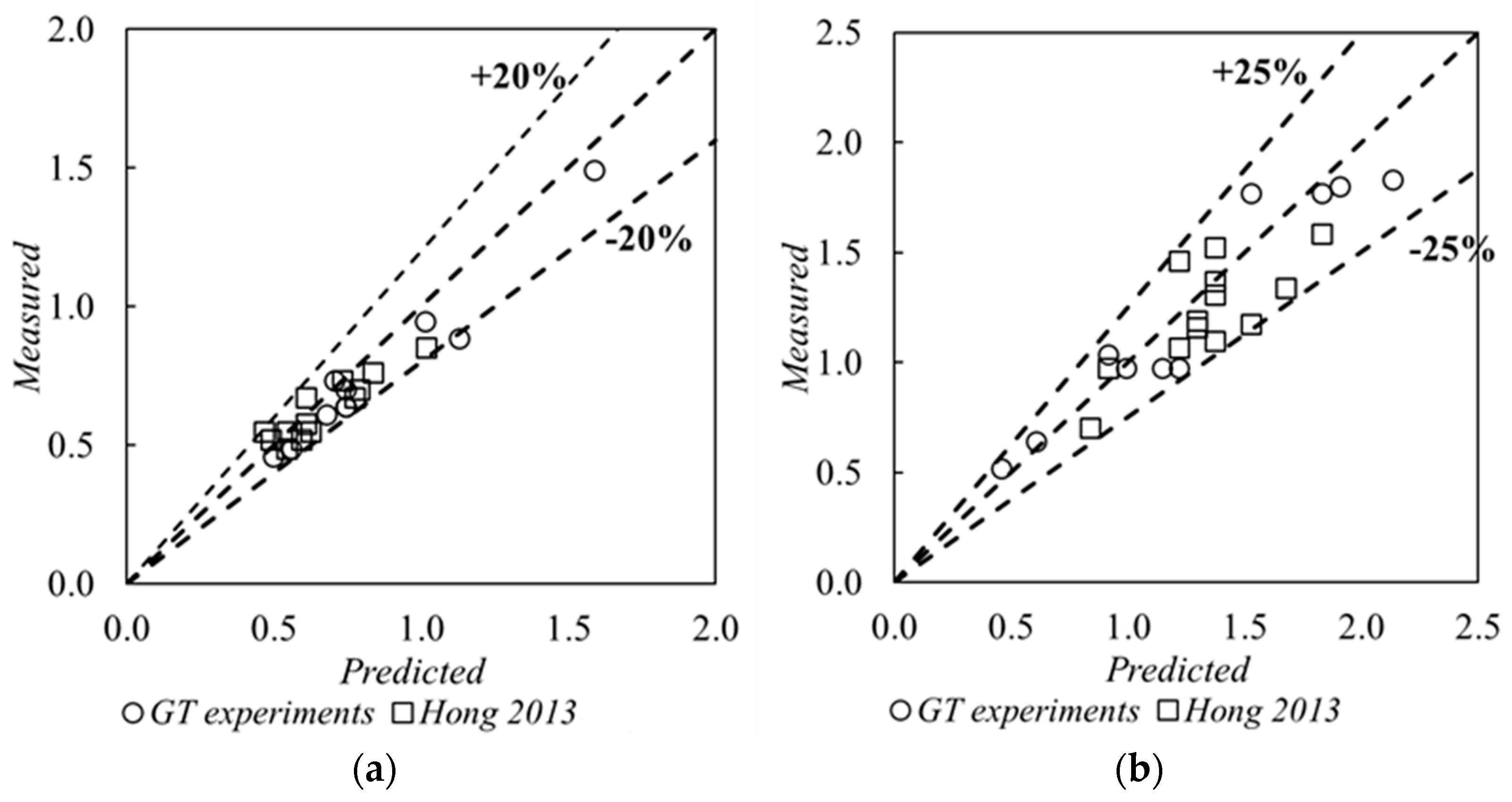
3.4. Prediction of Extent of Scour Hole
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Landers, M.N. Bridge scour data management. In Proceedings of the ASCE Water Forum ’92, Baltimore, MD, USA, 2–6 August 1992; pp. 1094–1099. [Google Scholar]
- Rehman, K.; Wang, Y.-C.; Waseem, M.; Hong, S.H. Tree-based machine learning models for prediction of bed elevation around bridge piers. Phys. Fluids 2022, 34, 085105. [Google Scholar] [CrossRef]
- Shirole, A.M.; Holt, R.C. Planning for a comprehensive bridge safety assurance program. Transp. Res. Record. 1991, 1290, 39–50. [Google Scholar]
- Lee, S.O.; Abid, I.; Hong, S.H. Effect of complex shape of pier foundation exposure on time development of scour. Environ. Fluid Mech. 2020, 21, 103–127. [Google Scholar] [CrossRef]
- Rehman, K.; Hong, S.H. Influence of lateral flow contraction on bed shear stress estimation by using measured turbulent kinetic energy. Exp. Therm. Fluid Sci. 2022, 139, 110742. [Google Scholar] [CrossRef]
- Arneson, L.A.; Zevenbergen, L.W.; Lagasse, P.F.; Clopper, P.E. Evaluating scour at bridges. In Hydraulic Engineering Circular 18 (HEC-18); U.S. Federal Highway Administration: Washington, DC, USA, 2012. [Google Scholar]
- Wu, P.; Hirshfield, F.; Sui, J.-Y. Local scour around bridge abutments under ice covered condition—An experimental study. Int. J. Sediment Res. 2015, 30, 39–47. [Google Scholar] [CrossRef]
- Yang, Y.; Melville, B.W.; Xiong, X.; Wang, L. Temporal evolution of scour at bridge abutments in compound channels. Int. J. Sediment Res. 2022, 37, 662–674. [Google Scholar] [CrossRef]
- Pandey, M.; Sharma, P.K.; Ahmad, Z.; Singh, U.K. Experimental investigation of clear-water temporal scour variation around bridge pier in gravel. Environ. Fluid Mech. 2017, 18, 871–890. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Pandey, M.; Debnath, K.; Oliveto, G. A comparative study on equilibrium scour volume around circular cylinders in clay-sand mixed cohesive beds, at near threshold velocity of sand- an experimental approach. Water 2022, 22, 6777–6791. [Google Scholar] [CrossRef]
- Straub, L.G. Effect of channel contraction works upon regimen of moveable bed streams. Trans. Am. Geophys. Union 1934, 15, 454–463. [Google Scholar]
- Laursen, E.M. Scour at bridge crossings. J. Hydraul. Div. 1960, 86, 39–54. [Google Scholar] [CrossRef]
- Laursen, E.M. An analysis of relief bridge scour. J. Hydraul. Div. 1963, 89, 93–118. [Google Scholar] [CrossRef]
- Gill, M.A. Bed erosion in rectangular long contraction. J. Hydraul. Div. 1981, 107, 273–284. [Google Scholar] [CrossRef]
- Froehlich, D.C. Local scour at bridge abutments. In Proceedings of the National Conference of Hydraulic Engineering, ASCE, New Orleans, LA, USA, 14–18 August 1989; pp. 13–18. [Google Scholar]
- Sturm, T.W.; Janjua, N.S. Clear-water scour around abutments in floodplains. J. Hydraul. Eng. 1994, 120, 956–972. [Google Scholar] [CrossRef]
- Sturm, T.W. Scour around bankline and setback abutments in compound channels. J. Hydraul. Eng. 2006, 132, 21–32. [Google Scholar] [CrossRef]
- Oben-Nyarko, K.; Ettema, R. Pier and abutment scour interaction. J. Hydraul. Eng. 2011, 137, 1598–1605. [Google Scholar] [CrossRef]
- Sturm, T.W.; Ettema, R.; Melville, B. Evaluation of Bridge-Scour Research: Abutment and Contraction Scour Progresses and Prediction; Final Report, NCHRP Project 24-27(02); Transportation Research Board, The National Academies: Washington, DC, USA, 2011. [Google Scholar]
- Hong, S. Prediction of Clear-Water Abutment Scour Depth in Compound Channel for Extreme Hydrologic Events. Ph.D. Thesis, Smartech Home @ Georgia Tech, Atlanta, GA, USA, 2013. Available online: https://smartech.gatech.edu/handle/1853/47535?show=full (accessed on 14 January 2013).
- Khosronejad, A.; Diplas, P.; Angelidis, D.; Zhang, Z.; Heydari, N.; Sotiropoulos, F. Scour depth prediction at the base of longitudinal walls: A combined experimental, numerical, and field study. Environ. Fluid Mech. 2020, 20, 459–478. [Google Scholar] [CrossRef]
- Zolghadr, M.; Zomorodian, S.M.A.; Fathi, A.; Tripathi, R.P.; Jafari, N.; Mehta, D.; Sihag, P.; Azamathulla, H.M. Experimental study on the optimum installation depth and dimensions of roughening elements on abutment as scour countermeasures. Fluids 2023, 8, 175. [Google Scholar] [CrossRef]
- Nabaei, S.F.; Afzalimehr, H.; Sui, J.; Kumar, B.; Nabaei, S.H. Investigation of effect of vegetation on flow structures and turbulence anisotropy around semi-elliptical abutment. Water 2021, 13, 3108. [Google Scholar] [CrossRef]
- Fathi, A.; Zomorodian, S.M.A.; Zolghadr, M.; Chadee, A.; Chiew, Y.-M.; Kumar, B.; Martin, H. Combination of riprap and submerged vane as an abutment scour countermeasure. Fluids 2023, 8, 41. [Google Scholar] [CrossRef]
- Raikar, R.V.; Hong, J.-H.; Deshmukh, A.R.; Guo, W.-D. Parametric study on abutment scour under unsteady flow. Water 2022, 14, 1820. [Google Scholar] [CrossRef]
- Bonakdari, H.; Moradi, F.; Ebtehaj, I.; Gharabaghi, B.; Sattar, A.A.; Azimi, A.H.; Radecki-Pawlik, A. A non-tuned machine learning technique for abutment scour depth in clear water condition. Water 2020, 12, 301. [Google Scholar] [CrossRef]
- Choo, H.; Zhao, Q.; Burns, S.; Sturm, T.; Hong, S. Laboratory and theoretical evaluation of impact of packing density, particle shape, and uniformity coefficient on erodibility of coarse-grained soil particles. Earth Surf. Process. Landf. 2020, 45, 1499–1509. [Google Scholar] [CrossRef]
- Gotvald, A.J.; McCallum, B.E. Epic Flooding in Georgia, 2009 (No. 2010-3107); US Geological Survey: Atlanta GA USA, 2010. [Google Scholar]
- Umbrell, E.R.; Young, G.K.; Stein, S.M.; Jones, J.S. Clear-water contraction scour under bridges in pressure flow. J. Hydraul. Eng. 1998, 124, 236–240. [Google Scholar] [CrossRef]
- Lyn, D. Pressure-flow scour: A Reexamination of the HEC-18 equation. J. Hydraul. Eng. 2008, 134, 1015–1020. [Google Scholar] [CrossRef]
- Lyn, D. Turbulence models in sediment transport engineering. In Chapter 16 in Sedimentation Engineering: Measurements, Modeling, and Practice; Garcia, M., Ed.; ASCE Manual of Practice No. 110; ASCE: Reston, VA, USA, 2008. [Google Scholar]
- Guo, J.; Kerenyi, K.; Pagan-Ortiz, J.E.; Flora, K. Bridge pressure flow scour at clear water threshold condition. Trans. Tianjin Univ. 2009, 15, 79–94. [Google Scholar] [CrossRef]
- Shan, H.; Xie, A.; Bojanowski, C.; Suaznabar, O.; Lottes, S.; Shen, J.; Kerenyi, K. Submerged Flow Bridge Scour under Clear Water Conditions; Report FHWA-HRT-12-034; Federal Highway Administration: McClean, VA, USA, 2012.
- Hong Seung Ho Sturm, T.W.; Stoesser, T. Clear-water abutment scour depth in compound channel for extreme hydrologic events. J. Hydraul. Eng. 2015, 141. [Google Scholar] [CrossRef]
- Koushki, M.; Chamani, M.R.; Moghim, M.N. Assessment of equilibrium pressure-scour depth using jet flow theory. Int. J. Sediment Res. 2023, 38, 141–151. [Google Scholar] [CrossRef]
- Abdelhaleem, F.S.; Mohamed, I.M.; Shaaban, I.G.; Ardakanian, A.; Fahmy, W.; Ibrahim, A. Pressure-flow scour under bridge deck in clear water conditions. Water 2023, 15, 404. [Google Scholar] [CrossRef]
- Sui, J.; Afzalimehr, H.; Samani, A.K.; Maherani, M. Clear-water scour around semi-elliptical abutments with armored beds. Int. J. Sediment Res. 2010, 25, 233–245. [Google Scholar] [CrossRef]
- Pandey, M.; Valyrakis, M.; Qi, M.; Sharma, A.; Lodhi, A.S. Experimental assessment and prediction of temporal scour depth around a spur dike. Int. J. Sediment Res. 2020, 36, 17–28. [Google Scholar] [CrossRef]
- Sodjavi, K.; Montagné, B.; Bragança, P.; Meslem, A.; Byrne, P.; Degouet, C.; Sobolik, V. PIV and electrodiffusion diagnostics of flow field, wall shear stress and mass transfer beneath three round submerged impinging jets. Exp. Therm. Fluid Sci. 2016, 70, 417–436. [Google Scholar] [CrossRef]
- Zhang, W.; Zapata, M.U.; Bai, X.; Pham-Van-Bang, D.; Nguyen, K.D. Three-dimensional simulation of horseshoe vortex and local scour around a vertical cylinder using an unstructured finite-volume technique. Int. J. Sediment Res. 2020, 35, 295–306. [Google Scholar] [CrossRef]
- Melville, B.W. Local scour at bridge abutments. J. Hydraul. Eng. 1992, 118, 615–631. [Google Scholar] [CrossRef]
- Chang, F.; Davis, S. Maryland SHA Procedure for Estimating Scour at Bridge Abutments Part 2-Clear Water Scour. Stream Stability and Scour at Highway Bridges: Compendium of Stream Stability and Scour Papers Presented at Conferences Sponsored by the Water Resources Engineering (Hydraulics) Division of the American Society of Civil Engineers; ASCE: Memphis, TN, USA, 1998. [Google Scholar]
- Xu, P.; Cheng, N.; Wei, M. Length parameter for scaling abutment scour depth. Water 2020, 12, 3058. [Google Scholar] [CrossRef]
- Hong, S.H.; Abid, I. Scour around an erodible abutment with riprap apron over time. J. Hydraul. Eng. 2019, 145, 06019007. [Google Scholar] [CrossRef]
- Melville, B.W.; Chiew, Y.-M. Time Scale for Local Scour at Bridge Piers. J. Hydraul. Eng. 1999, 125, 59–65. [Google Scholar] [CrossRef]
- Sturm, T.W. Open Channel Hydraulics, 2nd ed.; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Pagliara, S.; Hassanabadi, S.; Kurdistani, M. Log-Vane scour in Clear water conditions. River Res. Appl. 2014, 31, 1176–1182. [Google Scholar] [CrossRef]
- Carnacina, I.; Pagliara, S.; Leonardi, N. Bridge pier scour under pressure flow conditions. River Res. Appl. 2019, 35, 844–854. [Google Scholar] [CrossRef]
- Roy, D.; Pagliara, S. Equilibrium morphology and scour evolution at blunt nosed chevrons. River Res. Appl. 2021, 38, 499–512. [Google Scholar] [CrossRef]
- Sturm, T.W. Enhanced Abutment Scour Studies for Compound Channels; FHWA-RD-99-156; Federal Highway Administration: Mclean, VA, USA, 2004. [Google Scholar]
- Kara, S.; Stoesser, T.; Sturm, T.W. Turbulence statistics in compound channels with deep and shallow overbank flows. J. Hydraul. Res. 2012, 50, 482–493. [Google Scholar] [CrossRef]
- Abdelaziz, A.A.; Lim, S.Y. Effect of abutment aspect ratio on clear-water scour in floodplains. River Res. Appl. 2019, 36, 148–160. [Google Scholar] [CrossRef]
- Xiong, X. Combined Abutment and Contraction Scour in Compound Channels for Extreme Flood Events. Ph.D. Thesis, Libraries and Learning Services @ The University of Auckland, Auckland, New Zealand, 2017. [Google Scholar]
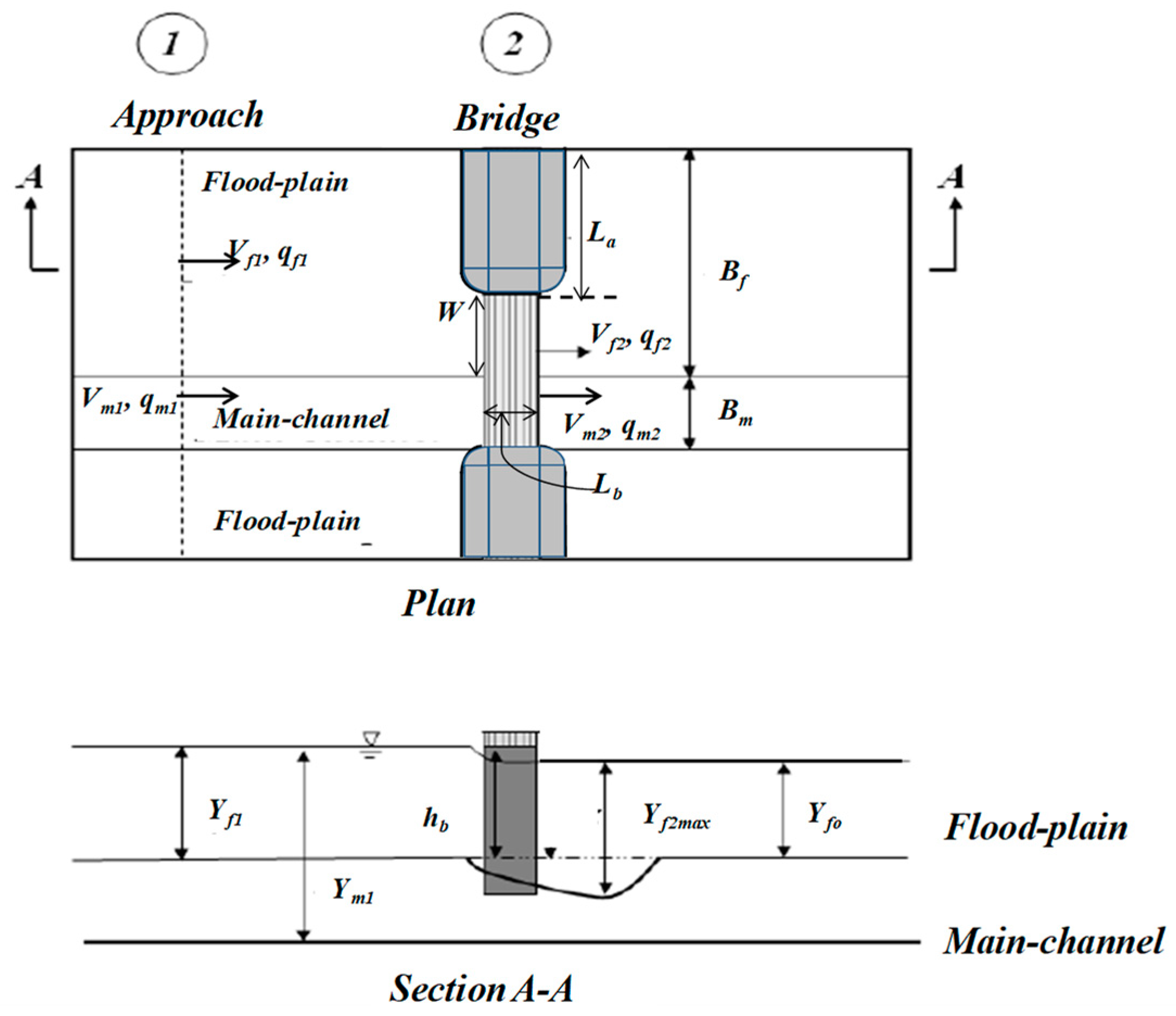
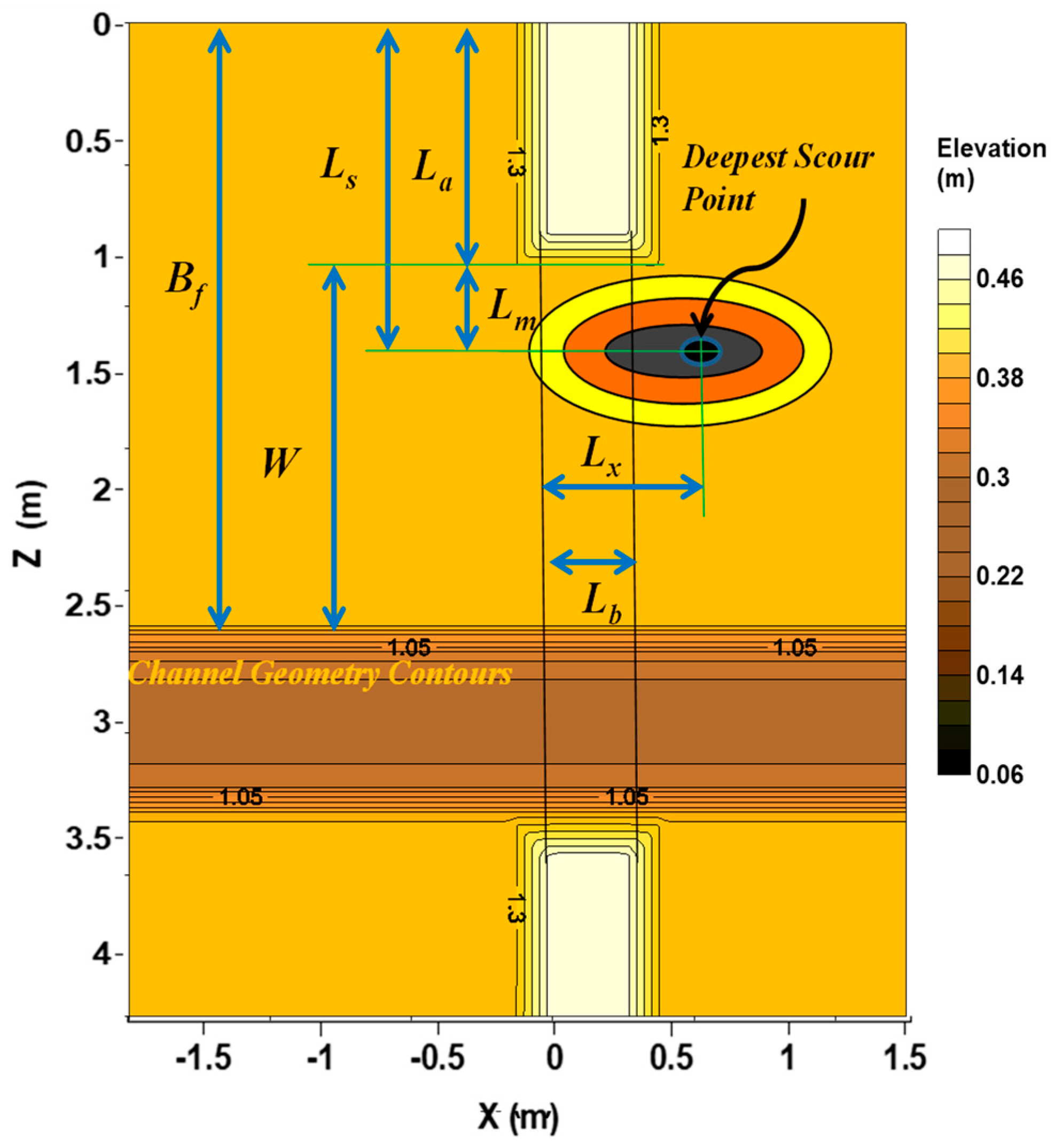
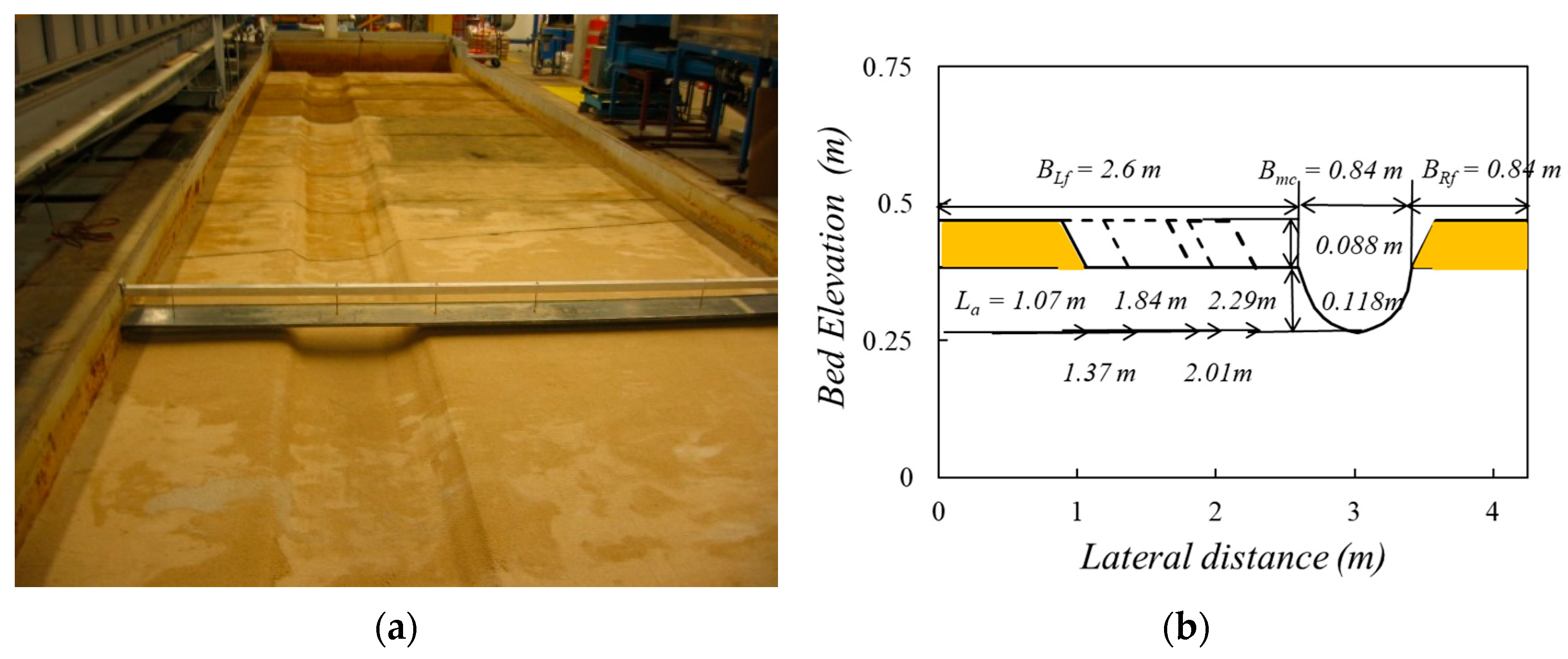

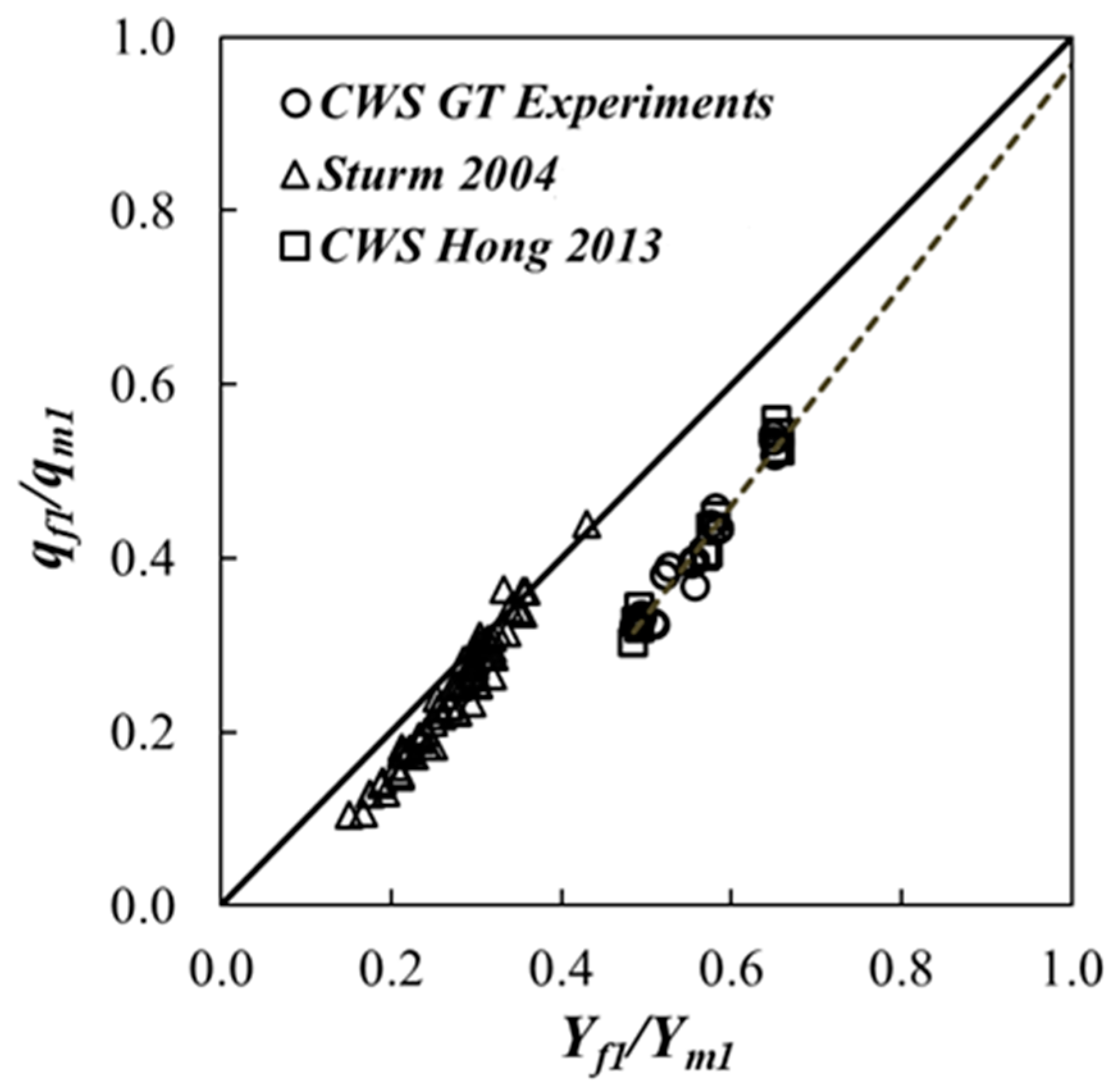

| Run | La/Bf | Flow Type | Ls/Bf | Lx/Lb | Yf1/Yf0 | Vf1/Vfc | qf2/qf1 | W/Yf1 |
|---|---|---|---|---|---|---|---|---|
| GT 1 | 0.41 | F | 0.51 | 0.63 | 1.080 | 0.542 | 1.548 | 20.746 |
| GT 2 | 0.41 | SO | 0.55 | 1.58 | 1.106 | 0.589 | 1.519 | 15.576 |
| GT 3 | 0.41 | OT | 0.52 | 0.84 | 1.046 | 0.561 | 1.043 | 10.460 |
| GT 4 | 0.41 | F | 0.55 | 1.37 | 1.132 | 0.655 | 1.500 | 20.080 |
| GT 5 | 0.41 | OT | 0.54 | 1.26 | 1.067 | 0.684 | 1.014 | 10.183 |
| GT 10 | 0.77 | F | 0.99 | 2.53 | 1.244 | 0.659 | 1.821 | 7.547 |
| GT 11 | 0.77 | SO | 0.31 | 2.63 | 1.362 | 0.579 | 1.865 | 5.540 |
| GT 12 | 0.77 | OT | 0.91 | 2.95 | 1.098 | 0.622 | 1.154 | 3.984 |
| GT 18 | 0.41 | F | 0.55 | 1.68 | 1.096 | 0.586 | 1.670 | 15.723 |
| GT 19 | 0.77 | F | 0.97 | 2.11 | 1.215 | 0.589 | 2.103 | 6.211 |
| Hong 1 * | 0.88 | OT | 1.00 | 2.11 | 1.048 | 0.420 | 1.339 | 2.087 |
| Hong 2 * | 0.53 | F | 0.64 | 1.79 | 1.115 | 0.613 | 1.818 | 16.460 |
| Hong 3 * | 0.53 | F | 0.65 | 1.68 | 1.122 | 0.580 | 1.755 | 16.194 |
| Hong 4 * | 0.71 | F | 0.86 | 1.26 | 1.127 | 0.543 | 2.236 | 10.080 |
| Hong 5 * | 0.71 | F | 0.82 | 1.16 | 1.095 | 0.497 | 2.208 | 10.373 |
| Hong 6 * | 0.53 | SO | 0.68 | 1.68 | 1.102 | 0.590 | 1.875 | 11.527 |
| Hong 7 * | 0.53 | SO | 0.67 | 1.90 | 1.092 | 0.569 | 1.781 | 11.268 |
| Hong 8 * | 0.71 | SO | 0.91 | 1.90 | 1.123 | 0.532 | 2.257 | 7.418 |
| Hong 9 * | 0.71 | SO | 0.87 | 1.79 | 1.114 | 0.490 | 2.223 | 7.289 |
| Hong 10 * | 0.53 | OT | 0.65 | 2.53 | 1.068 | 0.613 | 1.148 | 8.197 |
| Hong 11 * | 0.53 | OT | 0.64 | 1.90 | 1.064 | 0.556 | 1.250 | 8.264 |
| Hong 12 * | 0.71 | OT | 0.80 | 2.32 | 1.074 | 0.565 | 1.176 | 5.091 |
| Hong 13 * | 0.71 | OT | 0.79 | 1.90 | 1.057 | 0.500 | 1.278 | 5.176 |
| Run | La/Bf | Flow Type | Lm (m) | 2 Lm (m) | Measured Scour Width, (m) | Lx (m) | 2.5 Lx (m) | Measured Scour Length, (m) |
|---|---|---|---|---|---|---|---|---|
| GT 1 | 0.41 | F | 0.249 | 0.497 | 0.457 | 0.183 | 0.458 | 0.518 |
| GT 2 | 0.41 | SO | 0.371 | 0.741 | 0.701 | 0.457 | 1.143 | 0.975 |
| GT 3 | 0.41 | OT | 0.280 | 0.560 | 0.488 | 0.243 | 0.608 | 0.640 |
| GT 4 | 0.41 | F | 0.371 | 0.741 | 0.640 | 0.396 | 0.990 | 0.975 |
| GT 5 | 0.41 | OT | 0.340 | 0.679 | 0.610 | 0.366 | 0.914 | 1.036 |
| GT 10 | 0.77 | F | 0.565 | 1.130 | 0.884 | 0.732 | 1.829 | 1.768 |
| GT 11 | 0.77 | SO | 0.792 | 1.585 | 1.494 | 0.762 | 1.904 | 1.798 |
| GT 12 | 0.77 | OT | 0.352 | 0.705 | 0.732 | 0.853 | 2.134 | 1.829 |
| GT 18 | 0.41 | F | 0.371 | 0.741 | 0.640 | 0.488 | 1.219 | 0.975 |
| GT 19 | 0.77 | F | 0.505 | 1.010 | 0.945 | 0.610 | 1.524 | 1.768 |
| Hong 1 * | 0.88 | OT | 0.311 | 0.622 | 0.549 | 0.610 | 1.524 | 1.173 |
| Hong 2 * | 0.53 | F | 0.272 | 0.544 | 0.549 | 0.518 | 1.295 | 1.158 |
| Hong 3 * | 0.53 | F | 0.303 | 0.606 | 0.579 | 0.488 | 1.219 | 1.067 |
| Hong 4 * | 0.71 | F | 0.386 | 0.772 | 0.671 | 0.366 | 0.914 | 0.975 |
| Hong 5 * | 0.71 | F | 0.295 | 0.591 | 0.518 | 0.335 | 0.838 | 0.701 |
| Hong 6 * | 0.53 | SO | 0.394 | 0.788 | 0.701 | 0.488 | 1.219 | 1.463 |
| Hong 7 * | 0.53 | SO | 0.365 | 0.731 | 0.732 | 0.549 | 1.372 | 1.524 |
| Hong 8 * | 0.71 | SO | 0.508 | 1.016 | 0.853 | 0.549 | 1.372 | 1.372 |
| Hong 9 * | 0.71 | SO | 0.417 | 0.834 | 0.762 | 0.518 | 1.295 | 1.189 |
| Hong 10 * | 0.53 | OT | 0.303 | 0.606 | 0.671 | 0.732 | 1.829 | 1.585 |
| Hong 11 * | 0.53 | OT | 0.272 | 0.544 | 0.488 | 0.549 | 1.372 | 1.311 |
| Hong 12 * | 0.71 | OT | 0.233 | 0.466 | 0.549 | 0.671 | 1.676 | 1.341 |
| Hong 13 * | 0.71 | OT | 0.244 | 0.488 | 0.518 | 0.549 | 1.372 | 1.097 |
| No. | Finding | Criteria | Remarks |
|---|---|---|---|
| 1. | Abutment Classification | ||
| 2. | Location in Transverse Direction | Point of Deepest Scour | |
| 3. | Location in Flow Direction | Point of Deepest Scour | |
| 4. | Size of the Scour Hole | 2 Lm for the transverse direction 2.5 Lx for the flow direction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abid, I.; Sturm, T.W.; Hong, S.H. Location and Extents of Scour Hole around an Erodible Spill-through Abutment under Clear Water Condition and the Abutment Classification. Water 2023, 15, 4155. https://doi.org/10.3390/w15234155
Abid I, Sturm TW, Hong SH. Location and Extents of Scour Hole around an Erodible Spill-through Abutment under Clear Water Condition and the Abutment Classification. Water. 2023; 15(23):4155. https://doi.org/10.3390/w15234155
Chicago/Turabian StyleAbid, Irfan, Terry W. Sturm, and Seung Ho Hong. 2023. "Location and Extents of Scour Hole around an Erodible Spill-through Abutment under Clear Water Condition and the Abutment Classification" Water 15, no. 23: 4155. https://doi.org/10.3390/w15234155
APA StyleAbid, I., Sturm, T. W., & Hong, S. H. (2023). Location and Extents of Scour Hole around an Erodible Spill-through Abutment under Clear Water Condition and the Abutment Classification. Water, 15(23), 4155. https://doi.org/10.3390/w15234155






