An Improved Flow Direction Algorithm That Considers Mass Conservation for Sediment Transport Simulations
Abstract
:1. Introduction
2. Materials and Methods
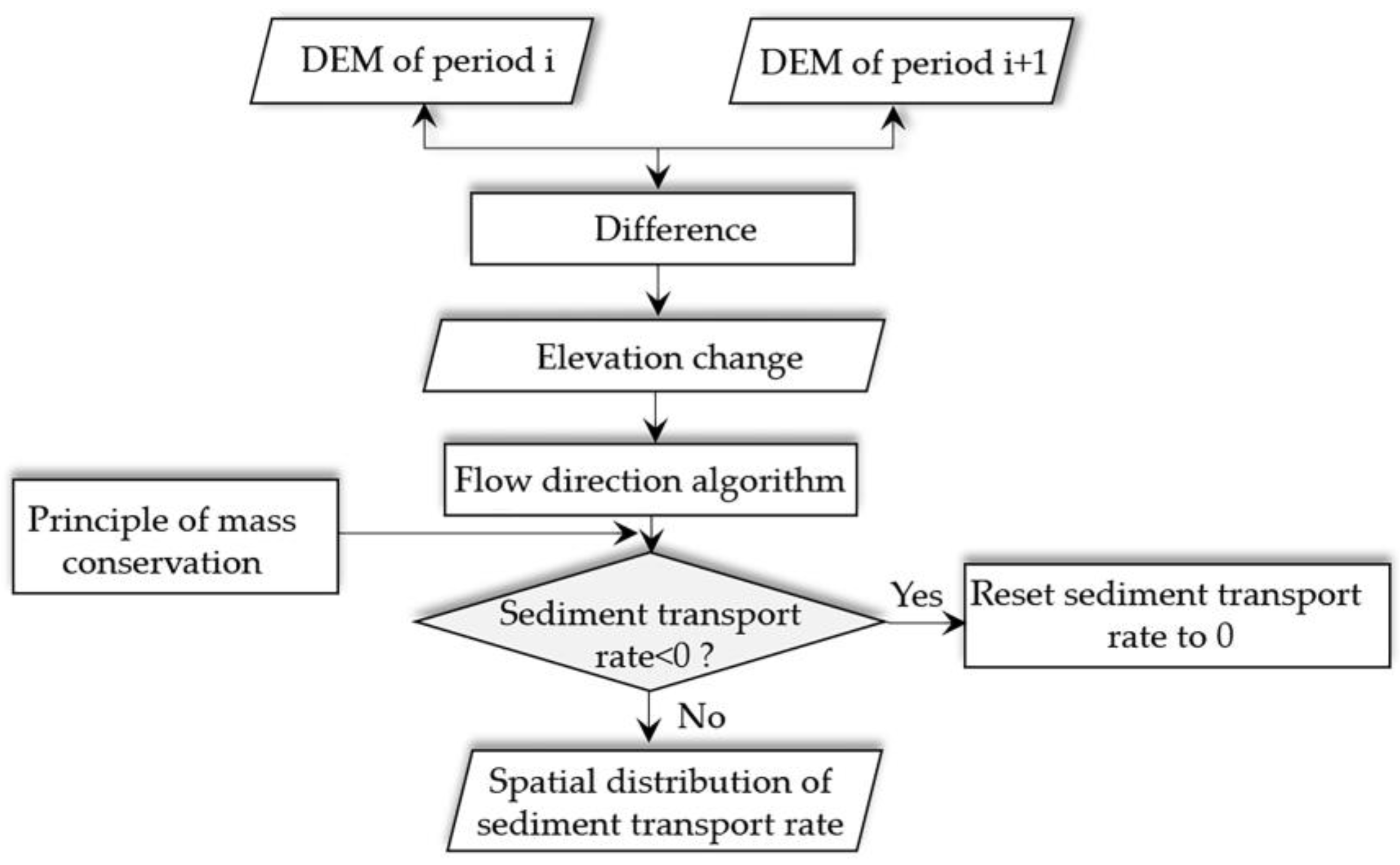
2.1. Algorithm Design
- (1)
- Simulation of the sediment transport process based on the SFD algorithm
- (2)
- Simulation of the sediment transport process based on the MFD algorithm
2.2. Evaluation of Model Performance
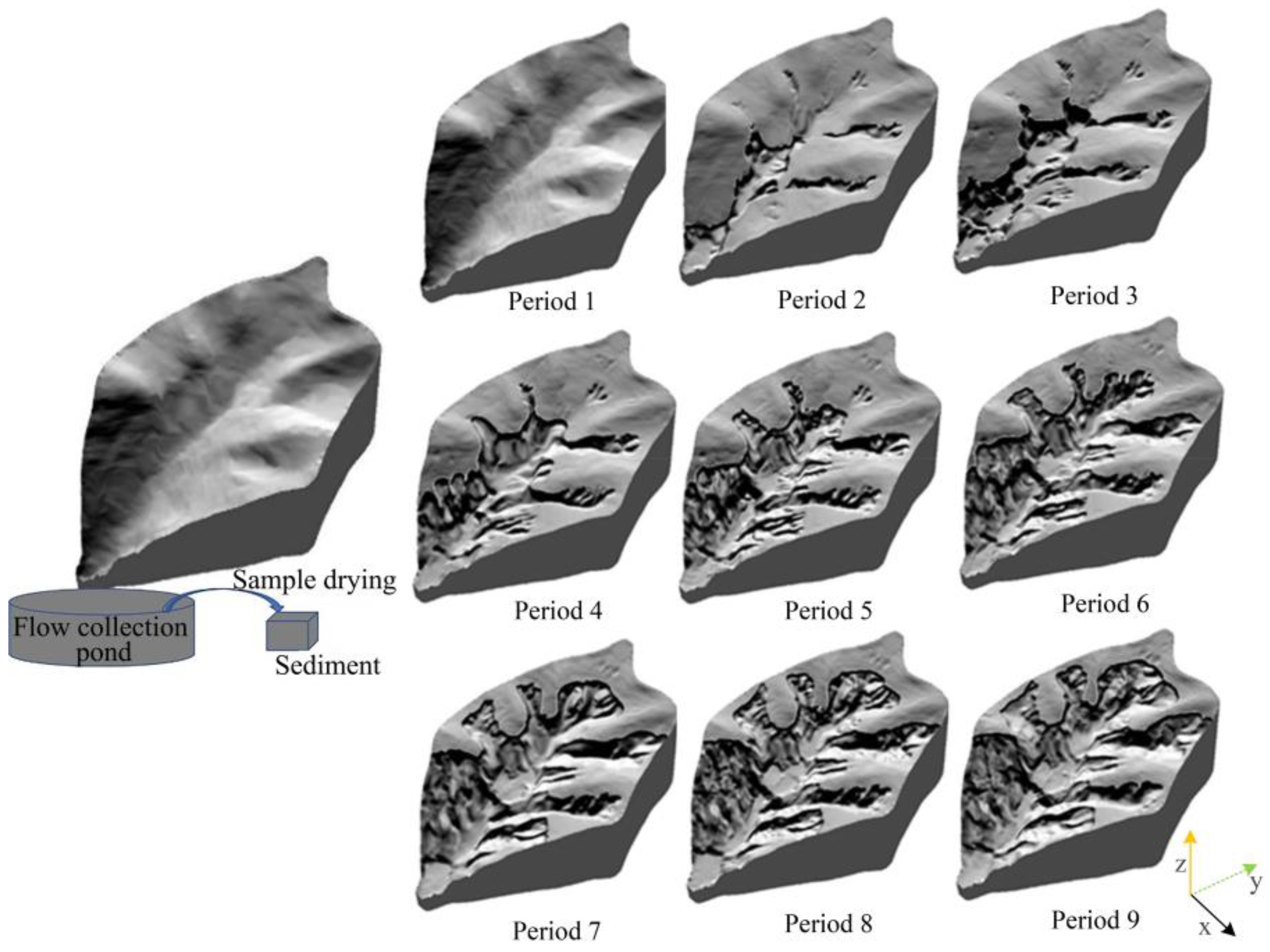
2.3. Experimental Sample Area and Data
3. Results
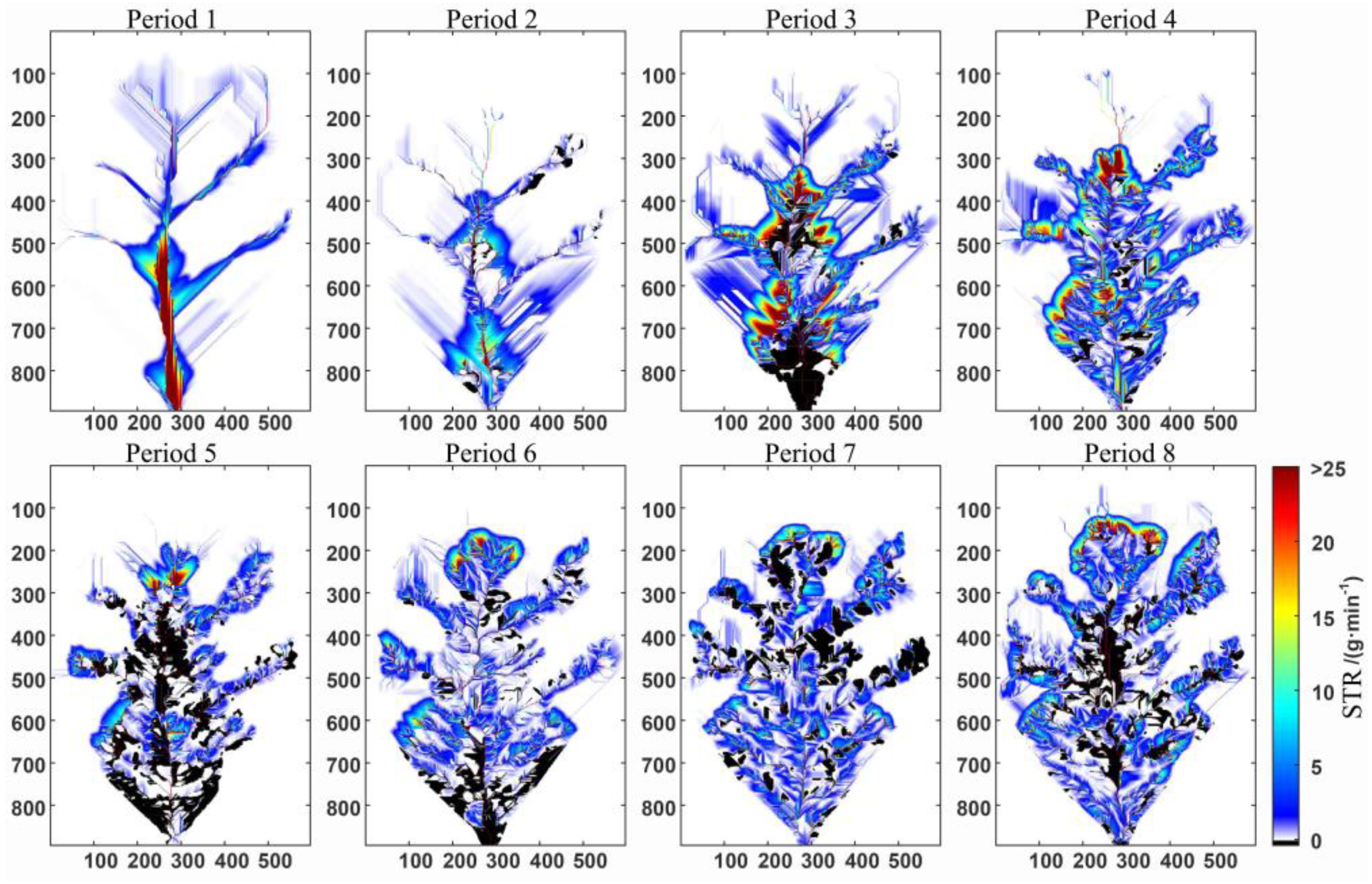
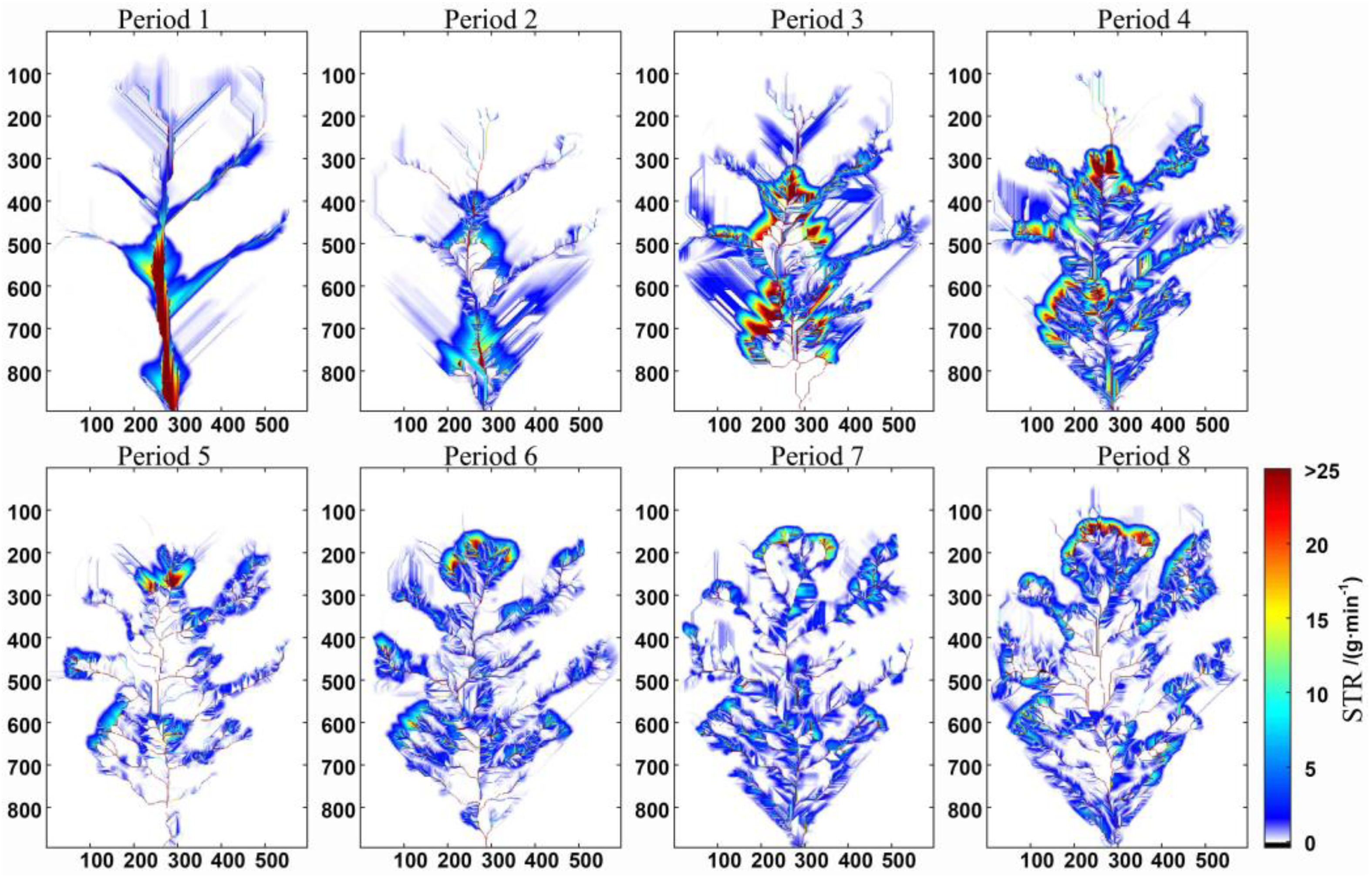
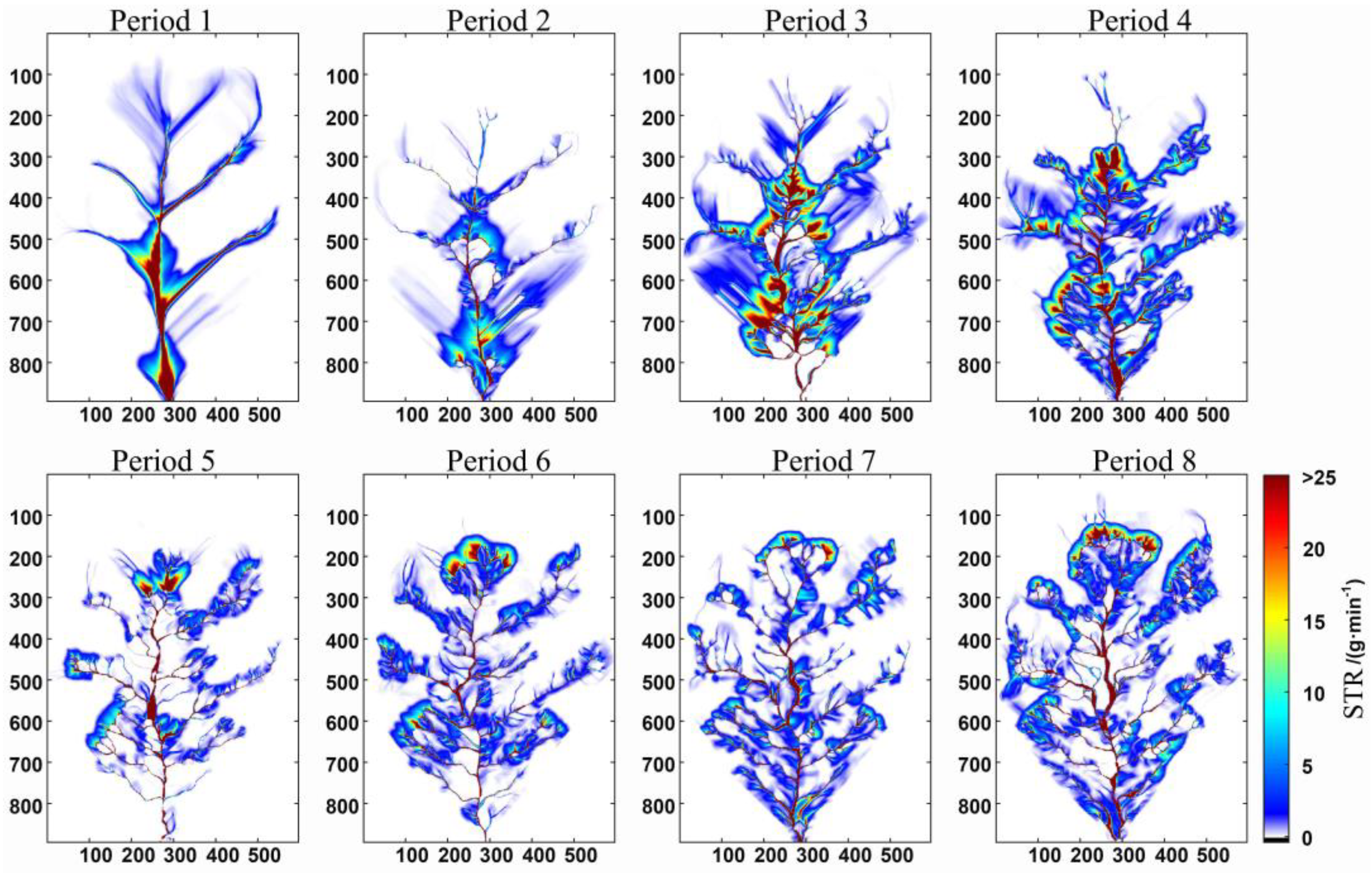
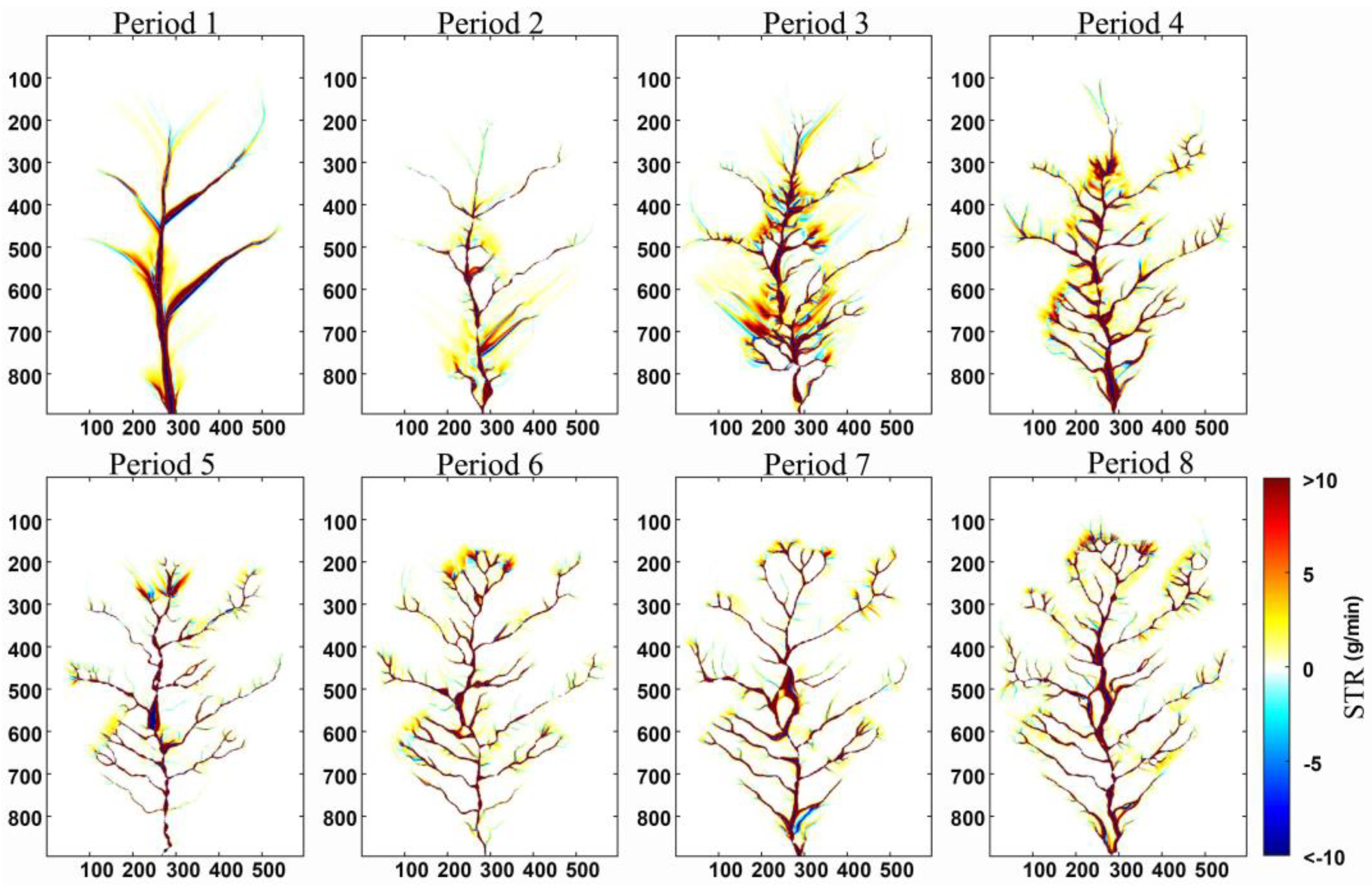
3.1. Analysis of the Improvement Effect of the SFD Algorithm
3.2. Analysis of the Improvement Effect of the MFD Algorithm
3.2.1. Simulation of the Sediment Transport Process Based on the MFD–se Algorithm
3.2.2. Simulation of the Sediment Transport Process Based on the MFD–md Algorithm
3.2.3. Comparison of MFD–se and MFD–md Algorithms
4. Discussion
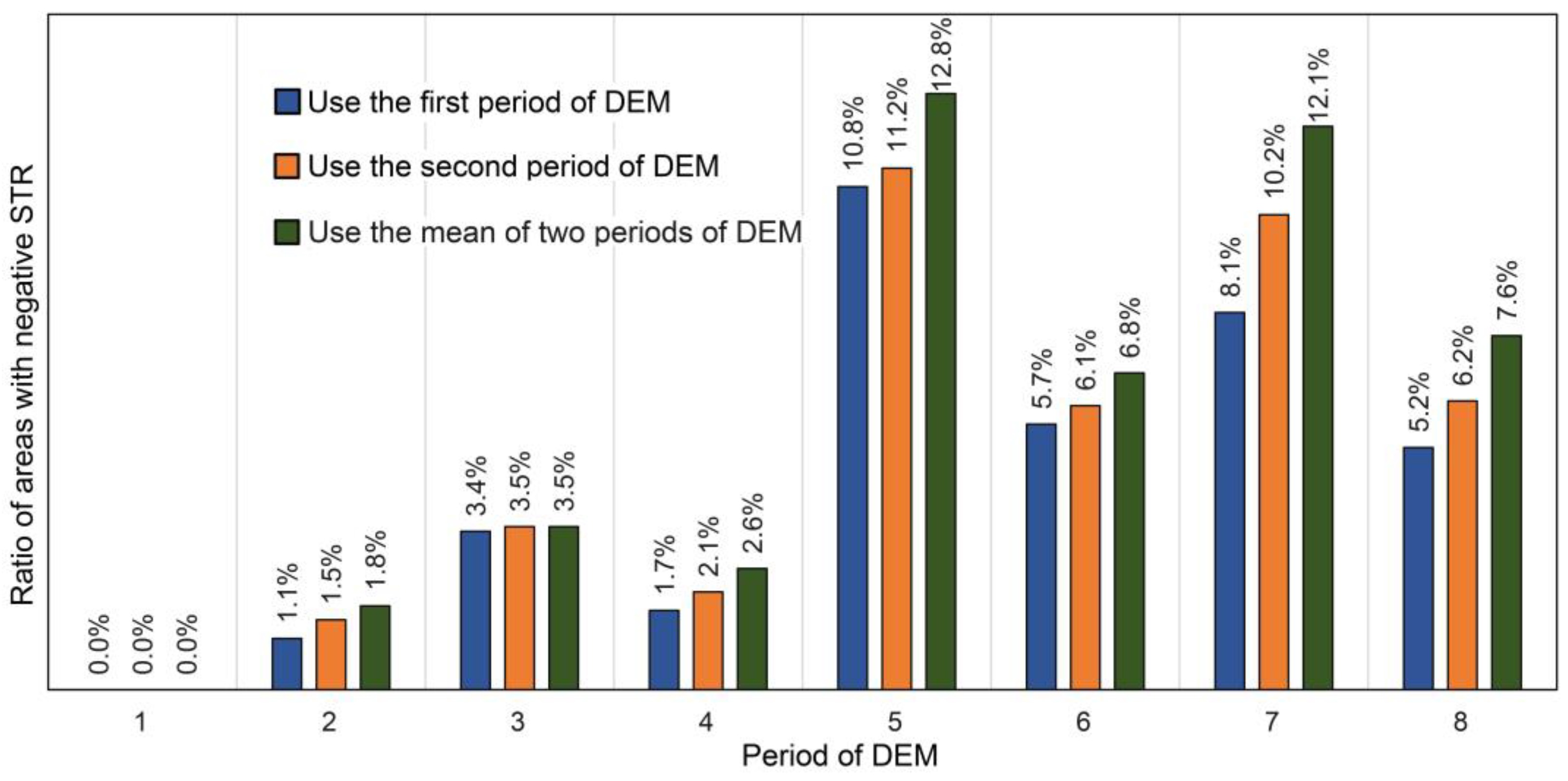
4.1. Influence of DEM Data Selection
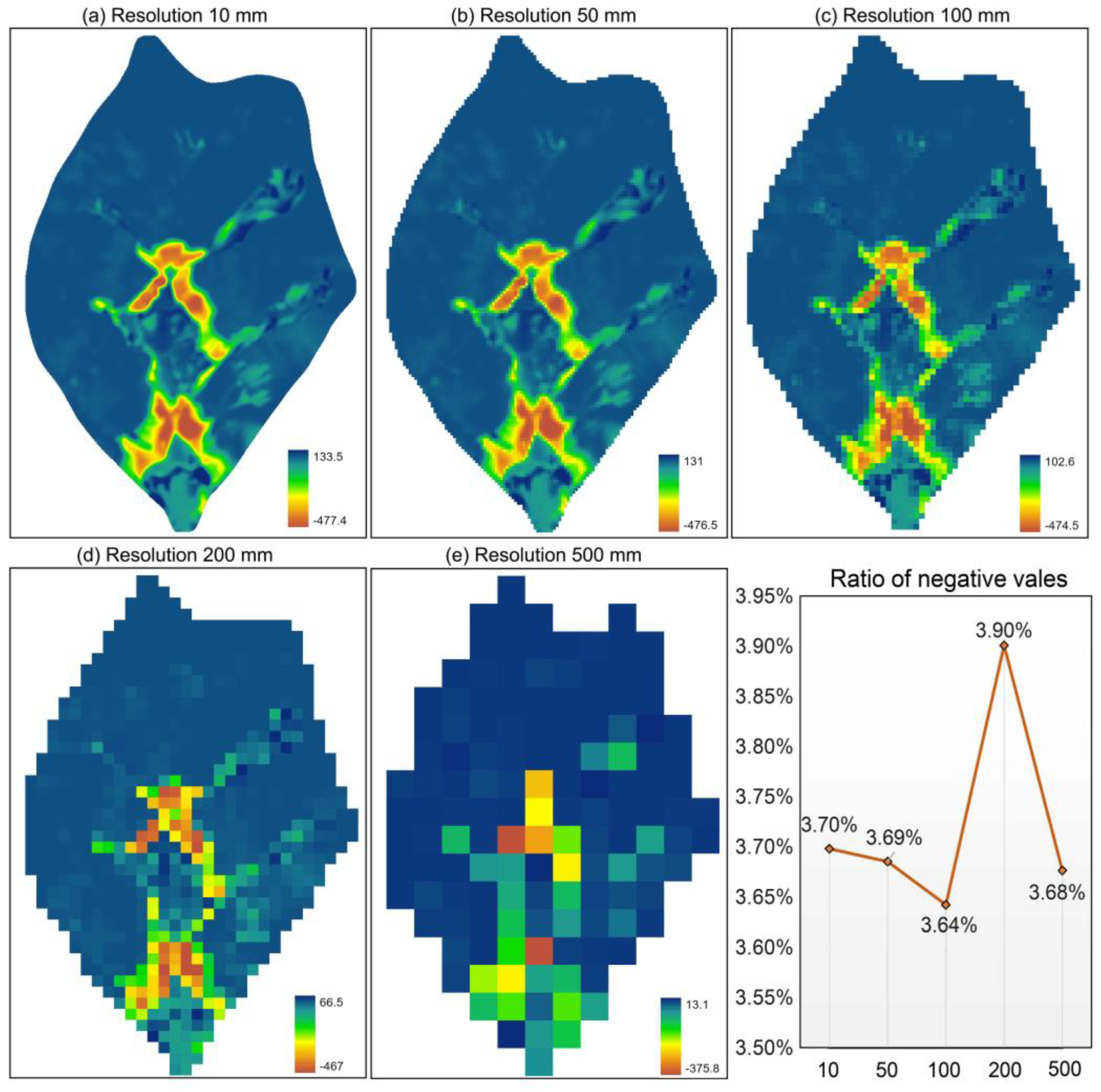
4.2. Influence of Spatial Resolution of the DEM Data
4.3. Analysis of the Reasons for a Negative STR
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Orlandini, S.; Moretti, G. Determination of Surface Flow Paths from Gridded Elevation Data. Water Resour. Res. 2009, 45, W03417. [Google Scholar] [CrossRef]
- Chorowicz, J.; Ichoku, C.; Riazanoff, S.; Kim, Y.-J.; Cervelle, B. A Combined Algorithm for Automated Drainage Network Extraction. Water Resour. Res. 1992, 28, 1293–1302. [Google Scholar] [CrossRef]
- Shin, S.; Paik, K. An Improved Method for Single Flow Direction Calculation in Grid Digital Elevation Models. Hydrol. Process. 2017, 31, 1650–1661. [Google Scholar] [CrossRef]
- Scarpa, G.M.; Braga, F.; Manfè, G.; Lorenzetti, G.; Zaggia, L. Towards an Integrated Observational System to Investigate Sediment Transport in the Tidal Inlets of the Lagoon of Venice. Remote Sens. 2022, 14, 3371. [Google Scholar] [CrossRef]
- Han, X.; Liu, J.; Mitra, S.; Li, X.; Srivastava, P.; Guzman, S.M.; Chen, X. Selection of Optimal Scales for Soil Depth Prediction on Headwater Hillslopes: A Modeling Approach. CATENA 2018, 163, 257–275. [Google Scholar] [CrossRef]
- Tarboton, D.G. A New Method for the Determination of Flow Directions and Upslope Areas in Grid Digital Elevation Models. Water Resour. Res. 1997, 33, 309–319. [Google Scholar] [CrossRef]
- Zhao, F.; Xiong, L.; Zhang, C.; Wei, H.; Liu, K.; Tang, G. Hydrological Object-Based Flow Direction Model for Constructing a Lake-Stream Topological System. Water Resour. Res. 2023, 59, e2022WR033681. [Google Scholar] [CrossRef]
- Xiong, L.; Jiang, R.; Lu, Q.; Yang, B.; Li, F.; Tang, G. Improved Priority-Flood Method for Depression Filling by Redundant Calculation Optimization in Local Micro-Relief Areas. Trans. GIS 2019, 23, 259–274. [Google Scholar] [CrossRef]
- Liu, X.; Wang, N.; Shao, J.; Chu, X. An Automated Processing Algorithm for Flat Areas Resulting from DEM Filling and Interpolation. ISPRS Int. J. Geo-Inf. 2017, 6, 376. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Sosa, J.; Bates, P.D.; Allen, G.H.; Pavelsky, T.M. MERIT Hydro: A high-resolution global hydrography map based on latest topography dataset. Water Resour. Res. 2019, 55, 5053–5073. [Google Scholar] [CrossRef]
- Lehner, B.; Grill, G. Global River Hydrography and Network Routing: Baseline Data and New Approaches to Study the World’s Large River Systems. Hydrol. Process. 2013, 27, 2171–2186. [Google Scholar] [CrossRef]
- Jain, M.K.; Kothyari, U.C. Estimation of Soil Erosion and Sediment Yield Using GIS. Hydrol. Sci. J. 2000, 45, 771–786. [Google Scholar] [CrossRef]
- Moore, I.D.; Wilson, J.P. Length-Slope Factors for the Revised Universal Soil Loss Equation: Simplified Method of Estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Xia, Y.; Li, X.; Wang, T. A Hybrid Flow Direction Algorithm for Water Routing on DEMs. Acta Geod. Cartogr. Sin. 2018, 47, 683. [Google Scholar]
- Xiong, L.; Tang, G.; Yan, S.; Zhu, S.; Sun, Y. Landform-oriented flow-routing algorithm for the dual-structure loess terrain based on digital elevation models. Hydrol. Process. 2014, 28, 1756–1766. [Google Scholar] [CrossRef]
- Pei, T.; Qin, C.-Z.; Zhu, A.-X.; Yang, L.; Luo, M.; Li, B.; Zhou, C. Mapping Soil Organic Matter Using the Topographic Wetness Index: A Comparative Study Based on Different Flow-Direction Algorithms and Kriging Methods. Ecol. Indic. 2010, 10, 610–619. [Google Scholar] [CrossRef]
- Zhang, H.; Shao, Z.; Sun, J.; Huang, X.; Yang, J. An Extended Watershed-Based AHP Model for Flood Hazard Estimation: Constraining Runoff Converging Indicators via MFD-Derived Sub-Watershed by Maximum Zonal Statistical Method. Remote Sens. 2022, 14, 2465. [Google Scholar] [CrossRef]
- O’Callaghan, J.F.; Mark, D.M. The Extraction of Drainage Networks from Digital Elevation Data. Comput. Vis. Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Freeman, T.G. Calculating Catchment Area with Divergent Flow Based on a Regular Grid. Comput. Geosci. 1991, 17, 413–422. [Google Scholar] [CrossRef]
- Gallant, J.C.; Wilson, J.P. TAPES-G: A Grid-Based Terrain Analysis Program for the Environmental Sciences. Comput. Geosci. 1996, 22, 713–722. [Google Scholar] [CrossRef]
- Quinn, P.; Beven, K.; Chevallier, P.; Planchon, O. The Prediction of Hillslope Flow Paths for Distributed Hydrological Modelling Using Digital Terrain Models. Hydrol. Process. 1991, 5, 59–79. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.; Li, J.; Wang, Y.; Bai, J.; Zhou, Z. Quantifying the Spatial Flow of Soil Conservation Service to Optimize Land-Use Pattern under Ecological Protection Scenarios. Front. Earth Sci. 2022, 10, 957520. [Google Scholar] [CrossRef]
- Dai, W.; Xiong, L.; Antoniazza, G.; Tang, G.; Lane, S.N. Quantifying the Spatial Distribution of Sediment Transport in an Experimental Gully System Using the Morphological Method. Earth Surf. Process. Landf. 2021, 46, 1188–1208. [Google Scholar] [CrossRef]
- Dietrich, W.E.; Smith, J.D.; Dunne, T. Flow and Sediment Transport in a Sand Bedded Meander. J. Geol. 1979, 87, 305–315. [Google Scholar] [CrossRef]
- Dai, W.; Qian, W.; Liu, A.; Wang, C.; Yang, X.; Hu, G.; Tang, G. Monitoring and Modeling Sediment Transport in Space in Small Loess Catchments Using UAV–SfM Photogrammetry. CATENA 2022, 214, 106244. [Google Scholar] [CrossRef]
- Jenson, S.K.; Domingue, J.O. Extracting Topographic Structure from Digital Elevation Data for Geographic Information-System Analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- Lai, Z.; Li, S.; Lv, G.; Pan, Z.; Fei, G. Watershed Delineation Using Hydrographic Features and a DEM in Plain River Network Region. Hydrol. Process. 2016, 30, 276–288. [Google Scholar] [CrossRef]
- Turcotte, R.; Fortin, J.-P.; Rousseau, A.N.; Massicotte, S.; Villeneuve, J.-P. Determination of the Drainage Structure of a Watershed Using a Digital Elevation Model and a Digital River and Lake Network. J. Hydrol. 2001, 240, 225–242. [Google Scholar] [CrossRef]
- Qin, C.; Zhu, A.-X.; Pei, T.; Li, B.; Zhou, C.; Yang, L. An Adaptive Approach to Selecting a Flow-partition Exponent for a Multiple-flow-direction Algorithm. Int. J. Geogr. Inf. Sci. 2007, 21, 443–458. [Google Scholar] [CrossRef]
- Hairsine, P.B.; Rose, C.W. Rainfall Detachment and Deposition: Sediment Transport in the Absence of Flow-Driven Processes. Soil Sci. Soc. Am. J. 1991, 55, 320–324. [Google Scholar] [CrossRef]
- Antoniazza, G.; Bakker, M.; Lane, S.N. Revisiting the Morphological Method in Two-Dimensions to Quantify Bed-Material Transport in Braided Rivers. Earth Surf. Process. Landf. 2019, 44, 2251–2267. [Google Scholar] [CrossRef]
- Bakker, M.; Antoniazza, G.; Odermatt, E.; Lane, S.N. Morphological Response of an Alpine Braided Reach to Sediment-Laden Flow Events. J. Geophys. Res. Earth Surf. 2019, 124, 1310–1328. [Google Scholar] [CrossRef]
- Cui, L. The Coupling Relationship between the Sediment Yield from Rainfall Erosion and the Topographic Feature of the Watershed; Northwest A&F University: Xianyang, China, 2002. [Google Scholar]
- Hengl, T. Finding the Right Pixel Size. Comput. Geosci. 2006, 32, 1283–1298. [Google Scholar] [CrossRef]
- Wechsler, S.P. Uncertainties Associated with Digital Elevation Models for Hydrologic Applications: A Review. Hydrol. Earth Syst. Sci. 2007, 11, 1481–1500. [Google Scholar] [CrossRef]
- Picco, L.; Mao, L.; Cavalli, M.; Buzzi, E.; Rainato, R.; Lenzi, M.A. Evaluating Short-Term Morphological Changes in a Gravel-Bed Braided River Using Terrestrial Laser Scanner. Geomorphology 2013, 201, 323–334. [Google Scholar] [CrossRef]

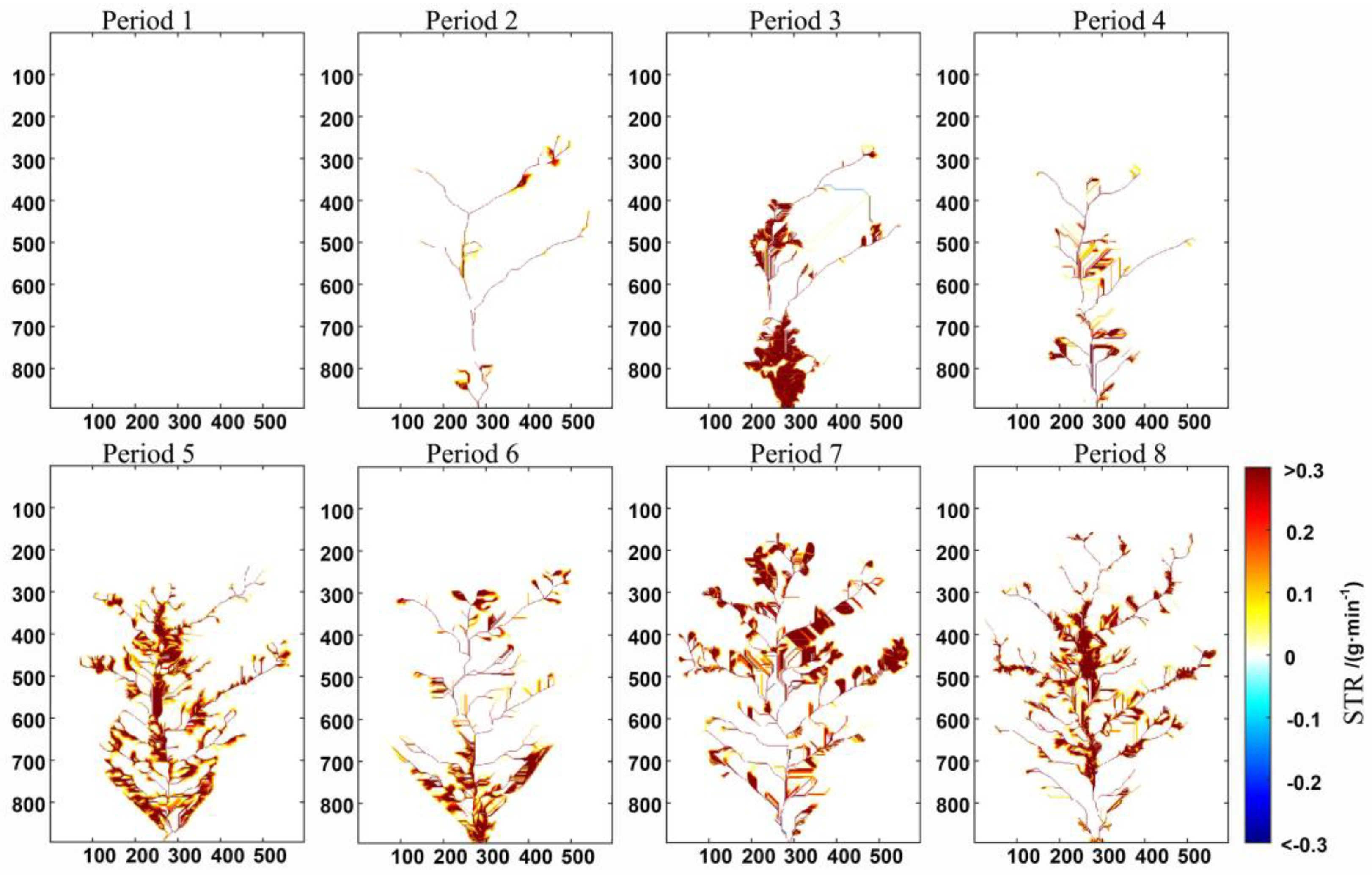
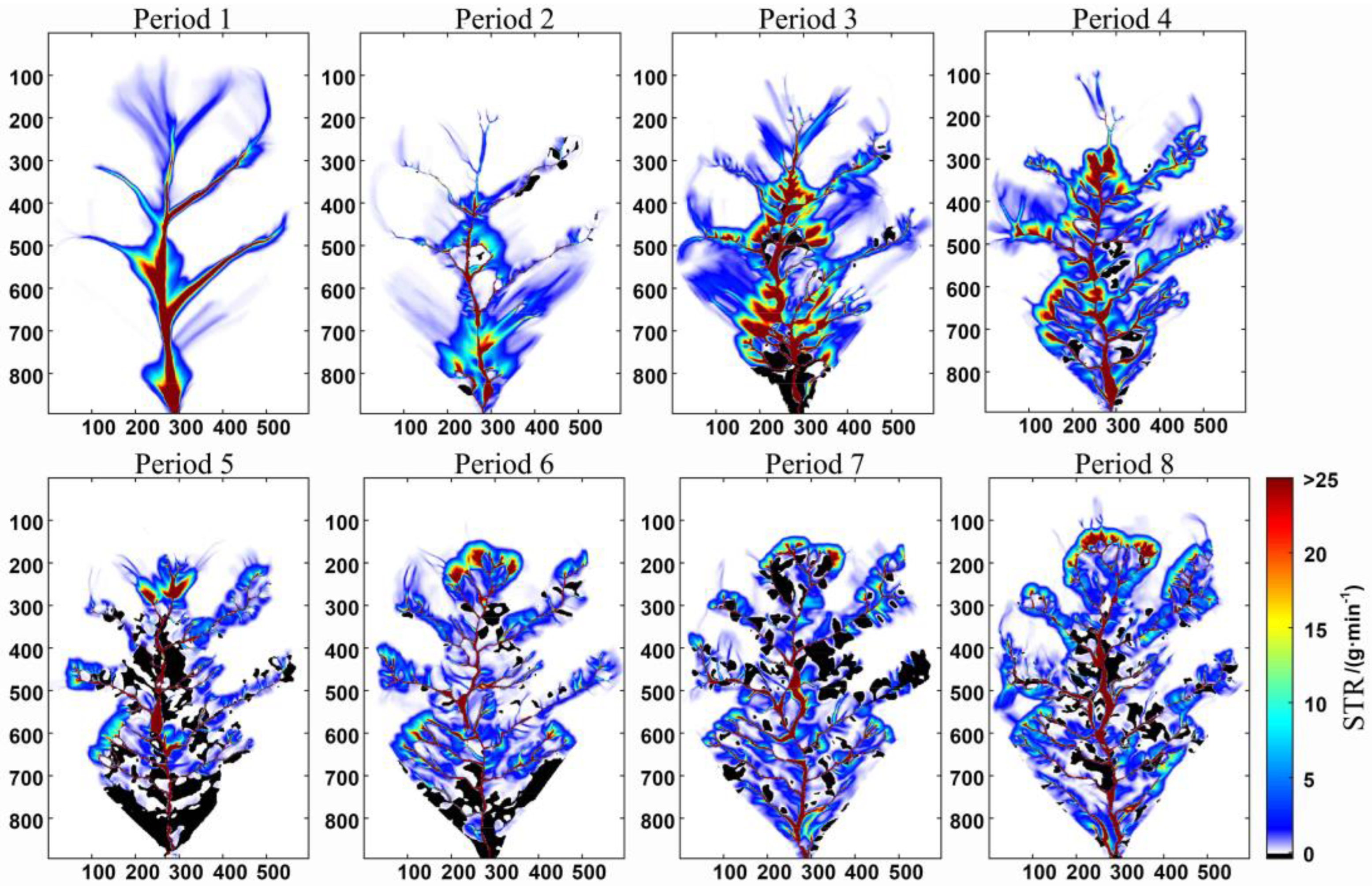
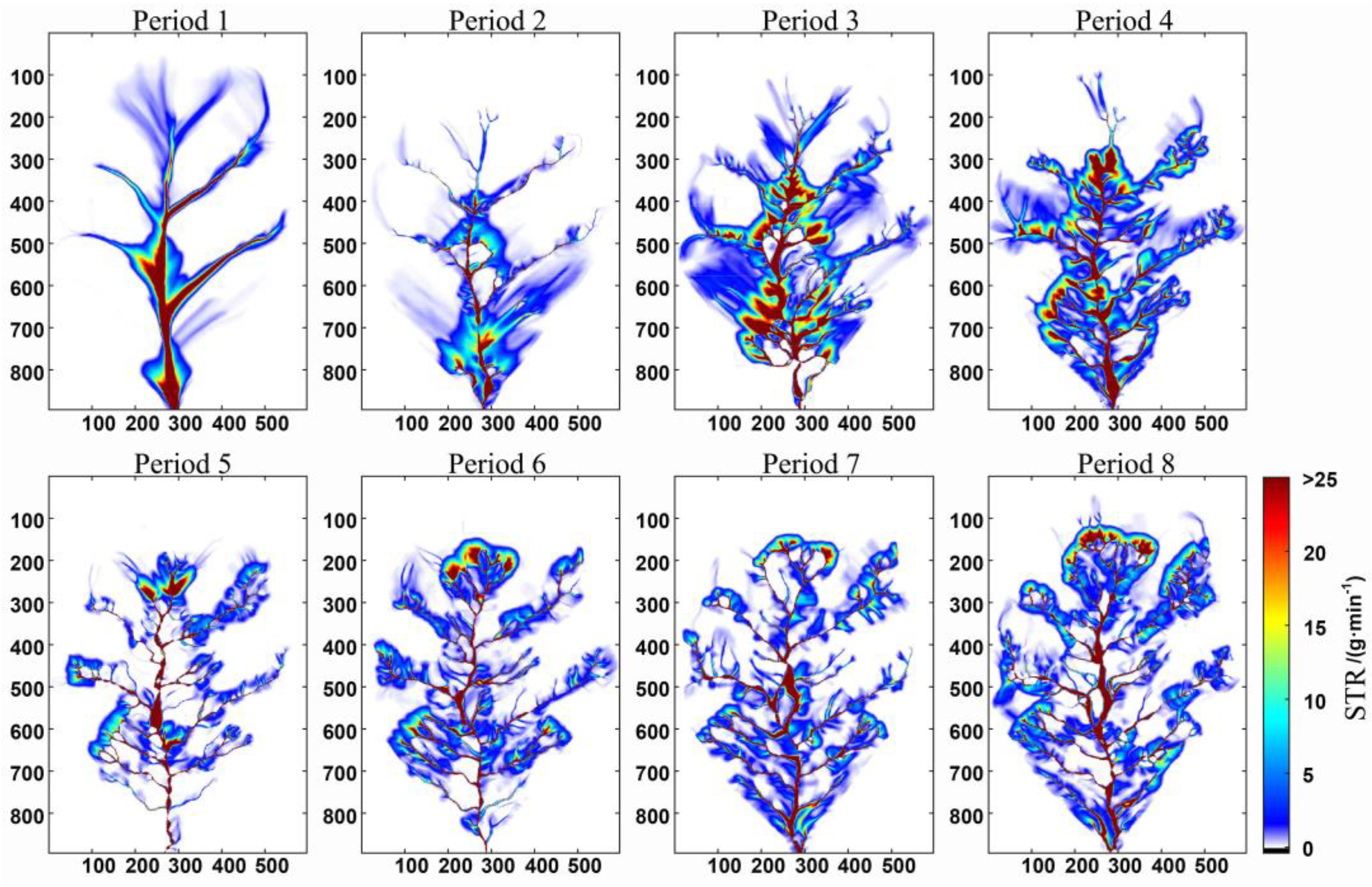

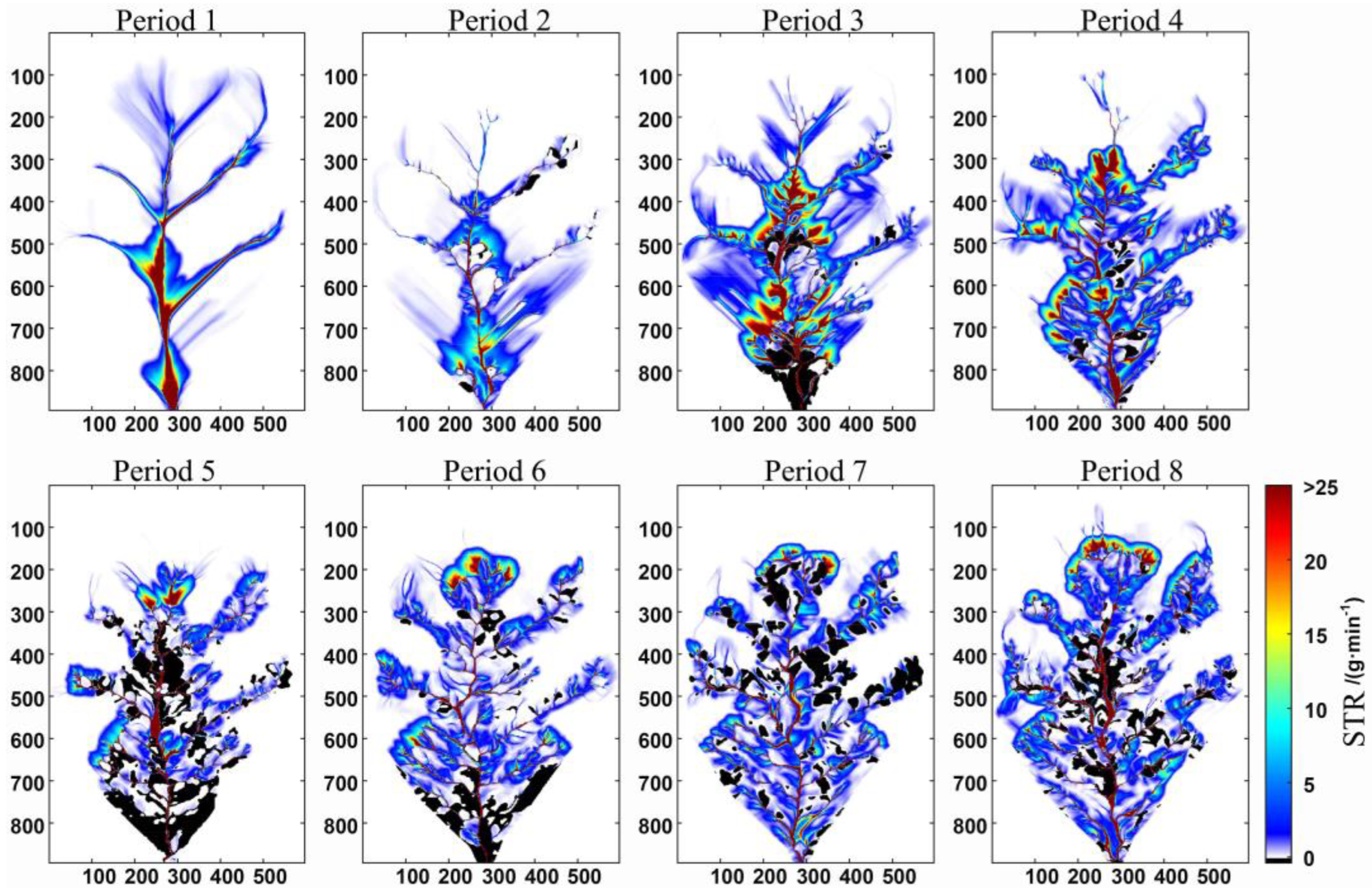

| Aera | Length | Max Width | Perimeter | Height Difference | Longitudinal Gradient | Mean Slope | Soil Bulk Density |
|---|---|---|---|---|---|---|---|
| 31.49 m2 | 9.1 m | 5.8 m | 23.3 m | 2.57 m | 28.24% | 15° | 1.39 g/cm3 |
| Period | Rainfall Number | Rainfall Intensity (mm/min) | Rainfall Duration (min) | Rainfall Level (mm) | Mean STR at the Outlet (kg/min) |
|---|---|---|---|---|---|
| DEM1 | 1 | 0.54 | 90.5 | 48.87 | 1.86 |
| 2 | 0.52 | 89.5 | 46.54 | 1.11 | |
| 3 | 0.49 | 89.5 | 43.86 | 1.73 | |
| 4 | 1.18 | 47.52 | 56.07 | 5.11 | |
| 5 | 1.21 | 45.86 | 55.49 | 14.07 | |
| DEM2 | 6 | 2.41 | 30.53 | 73.58 | 26.12 |
| 7 | 1.19 | 46.17 | 54.94 | 13.88 | |
| DEM3 | 8 | 0.57 | 90.18 | 51.40 | 7.52 |
| 9 | 0.59 | 61.95 | 36.55 | 7.81 | |
| DEM4 | 10 | 1.20 | 47.92 | 57.50 | 17.82 |
| 11 | 2.15 | 31.17 | 67.02 | 35.97 | |
| DEM5 | 12 | 0.52 | 62.94 | 32.73 | 5.23 |
| 13 | 0.58 | 61.53 | 35.69 | 6.02 | |
| 14 | 0.56 | 60.83 | 34.06 | 4.26 | |
| DEM6 | 15 | 1.12 | 46.82 | 52.44 | 10.98 |
| 16 | 1.08 | 45.83 | 49.50 | 9.63 | |
| 17 | 0.98 | 47.02 | 46.08 | 7.97 | |
| 18 | 1.04 | 45.37 | 47.18 | 6.45 | |
| DEM7 | 19 | 2.12 | 30.37 | 64.38 | 16.73 |
| 20 | 1.98 | 34.35 | 68.01 | 13.70 | |
| DEM8 | 21 | 0.53 | 91.27 | 48.37 | 3.01 |
| 22 | 0.55 | 90.60 | 49.83 | 2.58 | |
| 23 | 0.60 | 89.72 | 53.83 | 2.83 | |
| DEM9 | 24 | 1.05 | 61.35 | – | – |
| 25 | 2.03 | 31.65 | – | – |
| Period 1 | Period 2 | Period 3 | Period 4 | Period 5 | Period 6 | Period 7 | Period 8 | ||
|---|---|---|---|---|---|---|---|---|---|
| D8 | Max | 7470.44 | 8397.05 | 35,344.23 | 44,611.56 | 10,894.10 | 22,376.86 | 18,787.41 | 26,478.01 |
| Min | 15.00 | 14.32 | 74.02 | 96.99 | 31.03 | 52.28 | 41.26 | 60.29 | |
| Mean | 0.25 | 0.22 | 0.87 | 1.22 | 0.15 | 0.40 | 0.48 | 0.54 | |
| PPA | 33.60% | 33.51% | 35.66% | 37.10% | 25.44% | 38.49% | 35.72% | 40.77% | |
| PNA | 0.00% | 1.00% | 4.48% | 1.49% | 10.93% | 5.71% | 8.29% | 7.86% | |
| Improved D8 | Max | 7470.44 | 8471.36 | 37,217.53 | 44,816.52 | 12,479.17 | 22,969.26 | 20,806.58 | 28,824.86 |
| Min | 15.00 | 14.79 | 84.43 | 99.86 | 45.57 | 58.42 | 52.90 | 72.67 | |
| Mean | 0.25 | 0.23 | 1.13 | 1.31 | 0.42 | 0.53 | 0.71 | 0.76 | |
| PPA | 33.60% | 33.83% | 36.37% | 37.57% | 27.43% | 40.19% | 38.31% | 43.05% | |
| PNA | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | |
| Period 1 | Period 2 | Period 3 | Period 4 | Period 5 | Period 6 | Period 7 | Period 8 | ||
|---|---|---|---|---|---|---|---|---|---|
| MFD–se | Max | 3815.63 | 7207.58 | 35,378.31 | 39,770.87 | 10,894.10 | 20,285.19 | 17,331.12 | 26,474.16 |
| Min | 8.71 | 9.90 | 52.61 | 69.77 | 21.31 | 44.09 | 34.36 | 50.44 | |
| Mean | 0.04 | 0.10 | 0.50 | 0.63 | 0.02 | 0.33 | 0.36 | 0.55 | |
| PPA | 60.36% | 52.17% | 55.48% | 54.75% | 45.20% | 49.54% | 47.41% | 55.62% | |
| PNA | 0.00% | 0.72% | 3.08% | 1.22% | 10.30% | 5.51% | 8.27% | 5.44% | |
| Improved MFD–se | Max | 3815.63 | 7256.98 | 36,211.57 | 39,822.40 | 12,006.44 | 20,582.70 | 19,034.43 | 27,676.04 |
| Min | 8.71 | 10.01 | 53.96 | 69.89 | 23.03 | 44.82 | 38.18 | 52.14 | |
| Mean | 0.04 | 0.11 | 0.53 | 0.64 | 0.05 | 0.36 | 0.43 | 0.58 | |
| PPA | 60.36% | 52.89% | 58.09% | 55.97% | 55.24% | 54.89% | 55.44% | 61.00% | |
| PNA | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | |
| Period 1 | Period 2 | Period 3 | Period 4 | Period 5 | Period 6 | Period 7 | Period 8 | ||
|---|---|---|---|---|---|---|---|---|---|
| MFD–md | Max | 4740.49 | 8289.73 | 35,364.24 | 39,675.66 | 10,894.87 | 22,139.55 | 16,562.19 | 26,480.26 |
| Min | 8.38 | 9.44 | 50.72 | 68.95 | 20.62 | 42.21 | 32.63 | 48.03 | |
| Mean | 0.03 | 0.08 | 0.41 | 0.58 | 0.01 | 0.27 | 0.29 | 0.40 | |
| PPA | 60.34% | 51.71% | 54.37% | 52.95% | 44.21% | 49.07% | 47.00% | 54.44% | |
| PNA | 0.00% | 0.79% | 3.59% | 1.33% | 10.95% | 5.73% | 8.62% | 6.59% | |
| Improved MFD–md | Max | 4740.49 | 8349.73 | 36,390.77 | 39,733.96 | 12,186.44 | 22,627.60 | 18,263.32 | 28,061.01 |
| Min | 8.38 | 9.54 | 52.21 | 69.09 | 22.57 | 42.94 | 36.40 | 50.19 | |
| Mean | 0.03 | 0.08 | 0.43 | 0.59 | 0.03 | 0.29 | 0.34 | 0.42 | |
| PPA | 60.34% | 52.51% | 57.49% | 54.28% | 54.78% | 54.63% | 55.37% | 60.98% | |
| PNA | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Dai, W.; Wang, B.; Zhu, H.; Zhao, F.; Jiao, H.; Li, P. An Improved Flow Direction Algorithm That Considers Mass Conservation for Sediment Transport Simulations. Water 2023, 15, 4111. https://doi.org/10.3390/w15234111
Wei H, Dai W, Wang B, Zhu H, Zhao F, Jiao H, Li P. An Improved Flow Direction Algorithm That Considers Mass Conservation for Sediment Transport Simulations. Water. 2023; 15(23):4111. https://doi.org/10.3390/w15234111
Chicago/Turabian StyleWei, Hong, Wen Dai, Bo Wang, Hui Zhu, Fei Zhao, Haoyang Jiao, and Penghui Li. 2023. "An Improved Flow Direction Algorithm That Considers Mass Conservation for Sediment Transport Simulations" Water 15, no. 23: 4111. https://doi.org/10.3390/w15234111
APA StyleWei, H., Dai, W., Wang, B., Zhu, H., Zhao, F., Jiao, H., & Li, P. (2023). An Improved Flow Direction Algorithm That Considers Mass Conservation for Sediment Transport Simulations. Water, 15(23), 4111. https://doi.org/10.3390/w15234111






