Bed Topography Inference from Velocity Field Using Deep Learning
Abstract
:1. Introduction
2. Methodology
2.1. Data Generation
2.2. Entropy-Based Velocity Profile
2.2.1. Shannon Entropy-Based Method
- Assume a maximum velocity (e.g., m/s) in the initial iteration;
- Calculate the section flow area A using the measured local flow depth data with the assistance of the function in MatLab;
- Determine the mean cross-sectional flow velocity by dividing the flow rate L/s by the section area A;
- Compute the entropy parameter M based on Equation (2);
- Iterate over each set of 60 data points along the channel width, and calculate the velocity profiles for the cross-section using Equation (1);
- Estimate the flow discharge based on the calculated velocity profiles;
- Adjust the maximum velocity in the initial step and repeat the process until the error is less than .
2.3. Neural Network
2.3.1. Basic Parameters
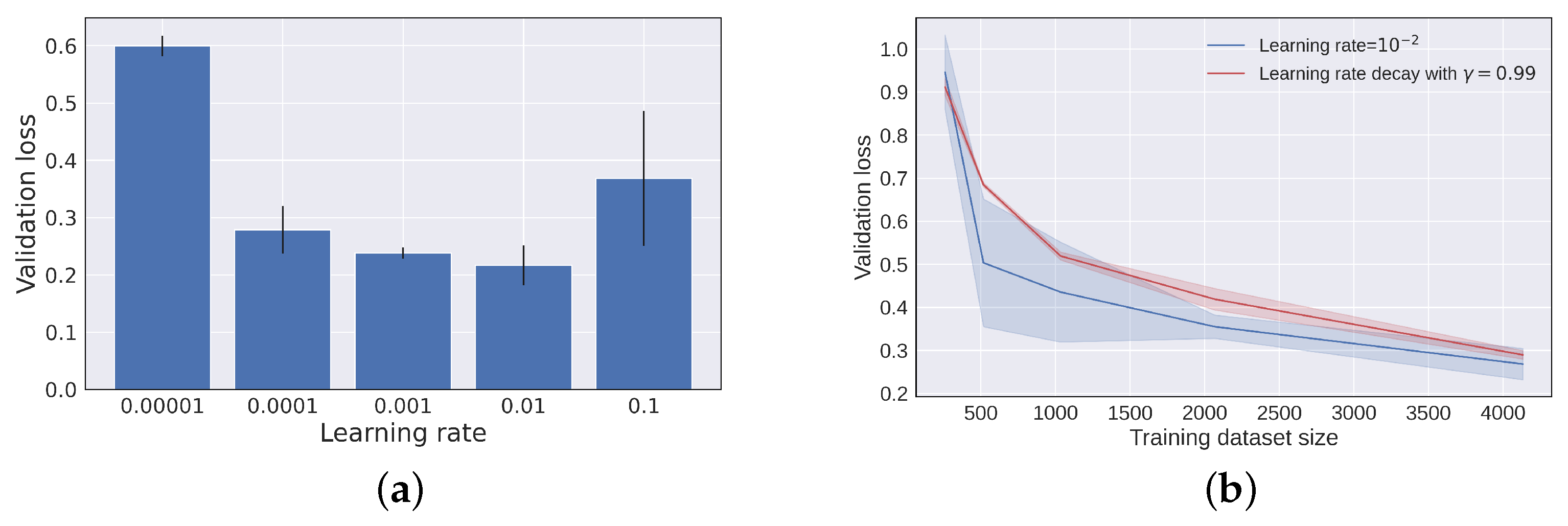
2.3.2. Regularization and Hyperparameters
3. Results and Performance
3.1. Model Performance
3.2. Model’s Predictions
3.2.1. Model’s Predictions Based on Experiments
3.2.2. Model’s Predictions Based on Numerical Simulation
3.2.3. Model’s Predictions Based on Field Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Model Architecture
| Layer (Type) | Output Shape | Function Parameters |
|---|---|---|
| InputLayer | [1, 256, 64] | |
| Conv2-D-1 | [16, 128, 32] | = 2, kernel size 4 × 4, stride = 2, pad = 1 |
| BatchNorm2-D-2 | [16, 128, 32] | |
| Dropout2-D-3 | [16, 128, 32] | p = 0, inplace = True |
| LeakyReLU-4 | [16, 128, 32] | negative slope = 0.2, inplace = True |
| Conv2-D-5 | [16, 64, 16] | = 2, kernel size 4 × 4, stride = 2, pad = 1 |
| BatchNorm2-D-6 | [16, 64, 16] | |
| Dropout2-D-7 | [16, 64, 16] | p = 0, inplace = True |
| LeakyReLU-8 | [16, 64, 16] | negative slope = 0.2, inplace = True |
| Conv2-D-9 | [32, 32, 8] | = 4, kernel size 4 × 4, stride = 2, pad = 1 |
| BatchNorm2-D-10 | [32, 32, 8] | |
| Dropout2-D-11 | [32, 32, 8] | p = 0, inplace = True |
| LeakyReLU-12 | [32, 32, 8] | negative slope = 0.2, inplace = True |
| Conv2-D-13 | [64, 16, 4] | = 8, kernel size 4 × 4, stride = 2, pad = 1 |
| BatchNorm2-D-14 | [64, 16, 4] | |
| Dropout2-D-15 | [64, 16, 4] | p = 0, inplace = True |
| LeakyReLU-16 | [64, 16, 4] | negative slope = 0.2, inplace = True |
| Conv2-D-17 | [64, 8, 2] | = 8, kernel size 2 × 2, stride = 2, pad = 0 |
| BatchNorm2-D-18 | [64, 8, 2] | |
| Dropout2-D-19 | [64, 8, 2] | p = 0, inplace = True |
| LeakyReLU-20 | [64, 8, 2] | negative slope = 0.2, inplace = True |
| Conv2-D-21 | [64, 4, 1] | = 8, kernel size 2 × 2, stride = 2, pad = 0 |
| BatchNorm2-D-22 | [64, 4, 1] | |
| Dropout2-D-23 | [64, 4, 1] | p = 0, inplace = True |
| LeakyReLU-24 | [64, 4, 1] | negative slope = 0.2, inplace = True |
| Upsample-25 | [64, 8, 2] | scale factor = 2, mode = ’bilinear’ |
| Conv2-D-26 | [64, 8, 2] | = 8, kernel size 1 × 1, stride = 1, pad = 0 |
| BatchNorm2-D-27 | [64, 8, 2] | |
| Dropout2-D-28 | [64, 8, 2] | p = 0, inplace = True |
| ReLU-29 | [64, 8, 2] | inplace = True |
| Upsample-30 | [128, 16, 4] | scale factor = 2, mode = ’bilinear’ |
| Conv2-D-31 | [64, 16, 4] | = 8, kernel size 1 × 1, stride = 1, pad = 0 |
| BatchNorm2-D-32 | [64, 16, 4] | |
| Dropout2-D-33 | [64, 16, 4] | p = 0, inplace = True |
| ReLU-34 | [64, 16, 4] | inplace = True |
| Upsample-35 | [128, 32, 8] | scale factor = 2, mode = ’bilinear’ |
| Conv2-D-36 | [32, 32, 8] | = 4, kernel size 3 × 3, stride = 1, pad = 1 |
| BatchNorm2-D-37 | [32, 32, 8] | |
| Dropout2-D-38 | [32, 32, 8] | p = 0, inplace = True |
| ReLU-39 | [32, 32, 8] | inplace = True |
| Upsample-40 | [64, 64, 16] | scale factor = 2, mode = ’bilinear’ |
| Conv2-D-41 | [16, 64, 16] | = 2, kernel size 3 × 3, stride = 1, pad = 1 |
| BatchNorm2-D-42 | [16, 64, 16] | |
| Dropout2-D-43 | [16, 64, 16] | p = 0, inplace = True |
| ReLU-44 | [16, 64, 16] | inplace = True |
| Upsample-45 | [32, 128, 32] | scale factor = 2, mode = ’bilinear’ |
| Conv2-D-46 | [16, 128, 32] | = 2, kernel size 3 × 3, stride = 1, pad = 1 |
| BatchNorm2-D-47 | [16, 128, 32] | |
| Dropout2-D-48 | [16, 128, 32] | p = 0, inplace = True |
| ReLU-49 | [16, 128, 32] | inplace = True |
| Upsample-50 | [32, 256, 64] | scale factor = 2, mode = ’bilinear’ |
| Conv2-D-51 | [1, 256, 64] | = 1, kernel size 3 × 3, stride = 1, pad = 1 |
| Dropout2-D-52 | [1, 256, 64] | p = 0, inplace = True |
Appendix B. Tsallis Entropy-Based Method
References
- Marcus, W.A. Mapping of stream microhabitats with high spatial resolution hyperspectral imagery. J. Geogr. Syst. 2002, 4, 113–126. [Google Scholar] [CrossRef]
- Wozencraft, J.; Millar, D. Airborne lidar and integrated technologies for coastal mapping and nautical charting. Mar. Technol. Soc. J. 2005, 39, 27–35. [Google Scholar] [CrossRef]
- Hilldale, R.C.; Raff, D. Assessing the ability of airborne LiDAR to map river bathymetry. Earth Surf. Process. Landforms 2008, 33, 773–783. [Google Scholar] [CrossRef]
- Zaron, E.D. Recent developments in bottom topography mapping using inverse methods. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. III); Springer: Berlin/Heidelberg, Germany, 2017; pp. 241–258. [Google Scholar]
- Durand, M.; Andreadis, K.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Moller, D.; Wilson, M. Estimation of bathymetric depth and slope from data assimilation of swath altimetry into a hydrodynamic model. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Simeonov, J.A.; Holland, K.T.; Anderson, S.P. River discharge and bathymetry estimation from inversion of surface currents and water surface elevation observations. J. Atmos. Ocean. Technol. 2019, 36, 69–86. [Google Scholar] [CrossRef]
- Emery, L.; Smith, R.; McNeal, D.; Hughes, B.; Swick, L.W.; MacMahan, J. Autonomous collection of river parameters using drifting buoys. In Proceedings of the OCEANS 2010 MTS/IEEE SEATTLE, Seattle, WA, USA, 20–23 September 2010; pp. 1–7. [Google Scholar]
- Almeida, T.G.; Walker, D.T.; Warnock, A.M. Estimating river bathymetry from surface velocity observations using variational inverse modeling. J. Atmos. Ocean. Technol. 2018, 35, 21–34. [Google Scholar] [CrossRef]
- Smith, J.D.; McLean, S. A model for flow in meandering streams. Water Resour. Res. 1984, 20, 1301–1315. [Google Scholar] [CrossRef]
- Wilson, G.; Özkan-Haller, H.T. Ensemble-based data assimilation for estimation of river depths. J. Atmos. Ocean. Technol. 2012, 29, 1558–1568. [Google Scholar] [CrossRef]
- Landon, K.C.; Wilson, G.W.; Özkan-Haller, H.T.; MacMahan, J.H. Bathymetry estimation using drifter-based velocity measurements on the Kootenai River, Idaho. J. Atmos. Ocean. Technol. 2014, 31, 503–514. [Google Scholar] [CrossRef]
- Lee, J.; Ghorbanidehno, H.; Farthing, M.W.; Hesser, T.J.; Darve, E.F.; Kitanidis, P.K. Riverine bathymetry imaging with indirect observations. Water Resour. Res. 2018, 54, 3704–3727. [Google Scholar] [CrossRef]
- Ghorbanidehno, H.; Lee, J.; Farthing, M.; Hesser, T.; Darve, E.F.; Kitanidis, P.K. Deep learning technique for fast inference of large-scale riverine bathymetry. Adv. Water Resour. 2021, 147, 103715. [Google Scholar] [CrossRef]
- Honnorat, M.; Monnier, J.; Rivière, N.; Huot, É.; Le Dimet, F.X. Identification of equivalent topography in an open channel flow using Lagrangian data assimilation. Comput. Vis. Sci. 2010, 13, 111–119. [Google Scholar] [CrossRef]
- MacMahan, J.; Brown, J.; Thornton, E. Low-cost handheld global positioning system for measuring surf-zone currents. J. Coast. Res. 2009, 25, 744–754. [Google Scholar] [CrossRef]
- Najar, M.A.; Benshila, R.; Bennioui, Y.E.; Thoumyre, G.; Almar, R.; Bergsma, E.W.; Delvit, J.M.; Wilson, D.G. Coastal bathymetry estimation from Sentinel-2 satellite imagery: Comparing deep learning and physics-based approaches. Remote Sens. 2022, 14, 1196. [Google Scholar] [CrossRef]
- Liu, X.; Song, Y.; Shen, C. Bathymetry Inversion using a Deep-Learning-Based Surrogate for Shallow Water Equations Solvers. arXiv 2022, arXiv:2203.02821. [Google Scholar]
- Forghani, M.; Qian, Y.; Lee, J.; Farthing, M.W.; Hesser, T.; Kitanidis, P.K.; Darve, E.F. Application of deep learning to large scale riverine flow velocity estimation. Stoch. Environ. Res. Risk Assess. 2021, 35, 1069–1088. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J. Deep learning for geophysics: Current and future trends. Rev. Geophys. 2021, 59, e2021RG000742. [Google Scholar] [CrossRef]
- Jackson, J.E. A User’s Guide to Principal Components; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Maximenko, N.; Hafner, J.; Niiler, P. Pathways of marine debris derived from trajectories of Lagrangian drifters. Mar. Pollut. Bull. 2012, 65, 51–62. [Google Scholar] [CrossRef]
- Bradley, A.A.; Kruger, A.; Meselhe, E.A.; Muste, M.V. Flow measurement in streams using video imagery. Water Resour. Res. 2002, 38, 51-1–51-8. [Google Scholar] [CrossRef]
- Lewis, Q.W.; Rhoads, B.L. Resolving two-dimensional flow structure in rivers using large-scale particle image velocimetry: An example from a stream confluence. Water Resour. Res. 2015, 51, 7977–7994. [Google Scholar] [CrossRef]
- Biondi, F.; Addabbo, P.; Clemente, C.; Orlando, D. Measurements of surface river doppler velocities with along-track InSAR using a single antenna. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 987–997. [Google Scholar] [CrossRef]
- Yoon, Y.; Durand, M.; Merry, C.J.; Clark, E.A.; Andreadis, K.M.; Alsdorf, D.E. Estimating river bathymetry from data assimilation of synthetic SWOT measurements. J. Hydrol. 2012, 464, 363–375. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Drozdzal, M.; Vorontsov, E.; Chartrand, G.; Kadoury, S.; Pal, C. The importance of skip connections in biomedical image segmentation. In Proceedings of the International Workshop on Deep Learning in Medical Image Analysis, International Workshop on Large-Scale Annotation of Biomedical Data and Expert Label Synthesis, Athens, Greece, 21 October 2016; pp. 179–187. [Google Scholar]
- Orhan, A.E.; Pitkow, X. Skip connections eliminate singularities. arXiv 2017, arXiv:1701.09175. [Google Scholar]
- Dhont, B.E.M. Sediment Pulses in a Gravel-Bed Flume with Alternate Bars; Technical report; EPFL: Lausanne, Switzerland, 2017. [Google Scholar]
- Griffiths, G.A. Sediment translation waves in braided gravel-bed rivers. J. Hydraul. Eng. 1993, 119, 924–937. [Google Scholar] [CrossRef]
- Venditti, J.; Nelson, P.; Minear, J.; Wooster, J.; Dietrich, W. Alternate bar response to sediment supply termination. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Singh, V.P. Introduction to Tsallis Entropy Theory in Water Engineering; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Vyas, J.K.; Perumal, M.; Moramarco, T. Discharge estimation using Tsallis and Shannon entropy theory in natural channels. Water 2020, 12, 1786. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- Singh, V.P.; Yang, C.T.; Deng, Z. Downstream hydraulic geometry relations: 1. Theoretical development. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Bechle, A.J.; Wu, C.H. An entropy-based surface velocity method for estuarine discharge measurement. Water Resour. Res. 2014, 50, 6106–6128. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 1987, 113, 583–599. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and 2-D velocity distribution in open channels. J. Hydraul. Eng. 1988, 114, 738–756. [Google Scholar] [CrossRef]
- Chiu, C.L. Velocity distribution in open channel flow. J. Hydraul. Eng. 1989, 115, 576–594. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Ghoshal, K.; Singh, V.P. Two-dimensional distribution of streamwise velocity in open channel flow using maximum entropy principle: Incorporation of additional constraints based on conservation laws. Comput. Methods Appl. Mech. Eng. 2020, 361, 112738. [Google Scholar] [CrossRef]
- Moramarco, T.; Saltalippi, C.; Singh, V.P. Estimation of mean velocity in natural channels based on Chiu’s velocity distribution equation. J. Hydrol. Eng. 2004, 9, 42–50. [Google Scholar] [CrossRef]
- Song, T.; Graf, W.H. Velocity and Turbulence Distribution in Unsteady Open-Channel Flows. J. Hydraul. Eng. 1996, 122, 141–154. [Google Scholar] [CrossRef]
- Kohl, S.; Romera-Paredes, B.; Meyer, C.; De Fauw, J.; Ledsam, J.R.; Maier-Hein, K.; Eslami, S.; Jimenez Rezende, D.; Ronneberger, O. A probabilistic u-net for segmentation of ambiguous images. Adv. Neural Inf. Process. Syst. 2018, 31. [Google Scholar]
- Siddique, N.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V. U-net and its variants for medical image segmentation: A review of theory and applications. IEEE Access 2021, 9, 82031–82057. [Google Scholar] [CrossRef]
- Rafique, M.U.; Zhu, J.; Jacobs, N. Automatic segmentation of sinkholes using a convolutional neural network. Earth Space Sci. 2022, 9, e2021EA002195. [Google Scholar] [CrossRef]
- Sudhan, M.; Sinthuja, M.; Pravinth Raja, S.; Amutharaj, J.; Charlyn Pushpa Latha, G.; Sheeba Rachel, S.; Anitha, T.; Rajendran, T.; Waji, Y.A. Segmentation and classification of glaucoma using U-net with deep learning model. J. Healthc. Eng. 2022, 2022. [Google Scholar] [CrossRef]
- Yan, C.; Fan, X.; Fan, J.; Wang, N. Improved U-Net remote sensing classification algorithm based on Multi-Feature Fusion Perception. Remote Sens. 2022, 14, 1118. [Google Scholar] [CrossRef]
- Windheuser, L.; Karanjit, R.; Pally, R.; Samadi, S.; Hubig, N. An end-to-end flood stage prediction system using deep neural networks. Earth Space Sci. 2023, 10, e2022EA002385. [Google Scholar] [CrossRef]
- Thuerey, N.; Weißenow, K.; Prantl, L.; Hu, X. Deep learning methods for Reynolds-averaged Navier–Stokes simulations of airfoil flows. AIAA J. 2020, 58, 25–36. [Google Scholar] [CrossRef]
- Yao, W.; Zeng, Z.; Lian, C.; Tang, H. Pixel-wise regression using U-Net and its application on pansharpening. Neurocomputing 2018, 312, 364–371. [Google Scholar] [CrossRef]
- Jiang, Z.; Tahmasebi, P.; Mao, Z. Deep residual U-net convolution neural networks with autoregressive strategy for fluid flow predictions in large-scale geosystems. Adv. Water Resour. 2021, 150, 103878. [Google Scholar] [CrossRef]
- Beheshti, N.; Johnsson, L. Squeeze u-net: A memory and energy efficient image segmentation network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 364–365. [Google Scholar]
- Huet-Dastarac, M.; Nguyen, D.; Jiang, S.; Lee, J.; Montero, A.B. Can input reconstruction be used to directly estimate uncertainty of a regression U-Net model?–Application to proton therapy dose prediction for head and neck cancer patients. arXiv 2023, arXiv:2310.19686. [Google Scholar]
- Alom, M.Z.; Hasan, M.; Yakopcic, C.; Taha, T.M.; Asari, V.K. Recurrent residual convolutional neural network based on u-net (r2u-net) for medical image segmentation. arXiv 2018, arXiv:1802.06955. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Guo, C.; Szemenyei, M.; Hu, Y.; Wang, W.; Zhou, W.; Yi, Y. Channel attention residual u-net for retinal vessel segmentation. In Proceedings of the ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 1185–1189. [Google Scholar]
- Shekhar, S.; Bansode, A.; Salim, A. A comparative study of hyper-parameter optimization tools. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Brisbane, Australia, 8–10 December 2021; pp. 1–6. [Google Scholar]
- Ghosh, S.; Singh, A.; Kumar, S. BBBC-U-Net: Optimizing U-Net for automated plant phenotyping using big bang big crunch global optimization algorithm. Int. J. Inf. Technol. 2023, 15, 4375–4387. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 19 November 2023).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Santurkar, S.; Tsipras, D.; Ilyas, A.; Madry, A. How does batch normalization help optimization? In Proceedings of the Advances in Neural Information Processing Systems 31 (NeurIPS 2018), Montréal, QC, Canada, 3–8 December 2018; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 7–9 July 2015; pp. 448–456. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Chia Laguna Resort, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Loshchilov, I.; Hutter, F. Fixing Weight Decay Regularization in Adam. 2018. Available online: https://openreview.net/forum?id=rk6qdGgCZ (accessed on 19 November 2023).
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning (still) requires rethinking generalization. Commun. ACM 2021, 64, 107–115. [Google Scholar] [CrossRef]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de simulación numérica del flujo en ríos. Rev. Int. Métodos Numéricos Cálculo Diseño Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef]
- Lewis, Q.W.; Rhoads, B.L. LSPIV measurements of two-dimensional flow structure in streams using small unmanned aerial systems: 1. Accuracy assessment based on comparison with stationary camera platforms and in-stream velocity measurements. Water Resour. Res. 2018, 54, 8000–8018. [Google Scholar] [CrossRef]
- Lewis, Q.W.; Rhoads, B.L. LSPIV measurements of two-dimensional flow structure in streams using small unmanned aerial systems: 2. Hydrodynamic mapping at river confluences. Water Resour. Res. 2018, 54, 7981–7999. [Google Scholar] [CrossRef]
- Farahani, A.; Voghoei, S.; Rasheed, K.; Arabnia, H.R. A brief review of domain adaptation. In Advances in Data Science and Information Engineering: Proceedings from ICDATA 2020 and IKE 2020, Las Vegas, NV, USA, 27–30 July 2020; Springer: Berlin/Heidelberg, Germany, 2021; pp. 877–894. [Google Scholar]
- Tsai, W.P.; Feng, D.; Pan, M.; Beck, H.; Lawson, K.; Yang, Y.; Liu, J.; Shen, C. From calibration to parameter learning: Harnessing the scaling effects of big data in geoscientific modeling. Nat. Commun. 2021, 12, 5988. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Pan, M.; Beck, H.E.; Fisher, C.K.; Beighley, R.E.; Kao, S.C.; Hong, Y.; Wood, E.F. In quest of calibration density and consistency in hydrologic modeling: Distributed parameter calibration against streamflow characteristics. Water Resour. Res. 2019, 55, 7784–7803. [Google Scholar] [CrossRef]
- Gao, H.; Birkel, C.; Hrachowitz, M.; Tetzlaff, D.; Soulsby, C.; Savenije, H.H. A simple topography-driven and calibration-free runoff generation module. Hydrol. Earth Syst. Sci. 2019, 23, 787–809. [Google Scholar] [CrossRef]
- Acuña, G.J.; Ávila, H.; Canales, F.A. River model calibration based on design of experiments theory. A case study: Meta River, Colombia. Water 2019, 11, 1382. [Google Scholar] [CrossRef]
- Song, T.; Graf, W.; Lemmin, U. Uniform flow in open channels with movable gravel bed. J. Hydraul. Res. 1994, 32, 861–876. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]












| Exp. 1 | Exp. 2 | Exp. 3 | |
|---|---|---|---|
| Flow rate (L/s) | 15 | 15 | 15 |
| Flume slope (%) | 1.6 | 1.7 | 1.6 |
| Sediment feed rate (g/s) | 2.5 | 7.5 | 5.0 |
| Duration (hours) | 250 | 556 | 118 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiani-Oshtorjani, M.; Ancey, C. Bed Topography Inference from Velocity Field Using Deep Learning. Water 2023, 15, 4055. https://doi.org/10.3390/w15234055
Kiani-Oshtorjani M, Ancey C. Bed Topography Inference from Velocity Field Using Deep Learning. Water. 2023; 15(23):4055. https://doi.org/10.3390/w15234055
Chicago/Turabian StyleKiani-Oshtorjani, Mehrdad, and Christophe Ancey. 2023. "Bed Topography Inference from Velocity Field Using Deep Learning" Water 15, no. 23: 4055. https://doi.org/10.3390/w15234055
APA StyleKiani-Oshtorjani, M., & Ancey, C. (2023). Bed Topography Inference from Velocity Field Using Deep Learning. Water, 15(23), 4055. https://doi.org/10.3390/w15234055






